Influence of organic films on the evaporation and condensation of water in aerosol

Abstract

Uncertainties in quantifying the kinetics of evaporation and condensation of water from atmospheric aerosol are a significant contributor to the uncertainty in predicting cloud droplet number and the indirect effect of aerosols on climate. The influence of aerosol particle surface composition, particularly the impact of surface active organic films, on the condensation and evaporation coefficients remains ambiguous. Here, we report measurements of the influence of organic films on the evaporation and condensation of water from aerosol particles. Significant reductions in the evaporation coefficient are shown to result when condensed films are formed by monolayers of long-chain alcohols [C_nH_(2n+1)OH], with the value decreasing from 2.4 × 10⁻³ to 1.7 × 10⁻⁵ as n increases from 12 to 17. Temperature-dependent measurements confirm that a condensed film of long-range order must be formed to suppress the evaporation coefficient below 0.05. The condensation of water on a droplet coated in a condensed film is shown to be fast, with strong coherence of the long-chain alcohol molecules leading to islanding as the water droplet grows, opening up broad areas of uncoated surface on which water can condense rapidly. We conclude that multicomponent composition of organic films on the surface of atmospheric aerosol particles is likely to preclude the formation of condensed films and that the kinetics of water condensation during the activation of aerosol to form cloud droplets is likely to remain rapid.

The transport of volatile and semivolatile components between the condensed and gas phases in aerosol during evaporation or condensation is important for understanding cloud microphysics, atmospheric chemistry, the delivery of drugs to the lungs, and the applications of aerosols in materials and combustion science. For example, the uptake of chemical species to atmospheric aerosol particles facilitates chemical reactions (1), the condensation of water on cloud condensation nuclei allows cloud droplets to form (2), the uptake of water on pharmaceutical aerosol can affect their deposition pattern within the lungs (3), and the evaporation rates of solvents in spray drying processes influence the structure and morphology of the final microparticle (4). The rate of mass transport to or from an aerosol particle can be considered to involve the interplay of three mechanistic steps: gas phase diffusion, interfacial transfer, and bulk condensed phase diffusion. Different limiting regimes can be identified under which the rate of evaporation or condensation is determined by any one of these steps (5).

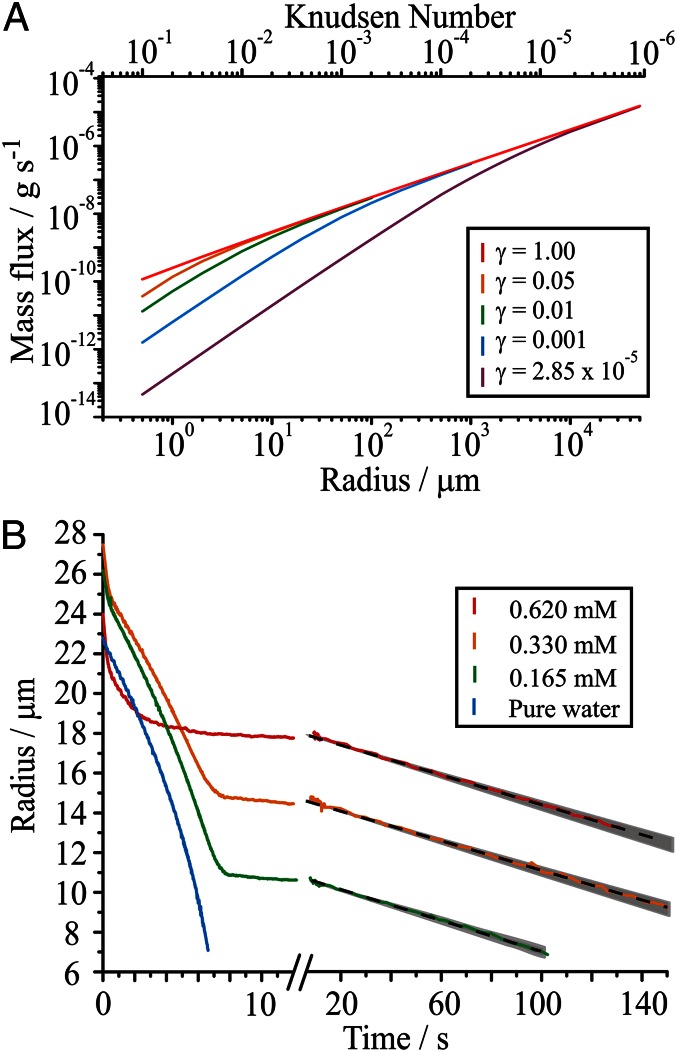
The Knudsen number is the ratio of the mean free path of gas phase molecules to the particle radius. At low Knudsen number, in the limits of large particle size and high gas pressure, gas phase diffusion usually determines evaporation and condensation rates. Bulk phase diffusion is limiting when the viscosity of the particle impedes transport to or from the surface and kinetically arrested states are formed, for example, glassy (6) and semisolid aerosol particles (7). The magnitude of any limitation imposed on the rate of mass transfer across the interface is characterized by the mass accommodation coefficient (α_m), which is defined as the fraction of molecules colliding with the surface that accommodate into the bulk liquid phase. By microscopic reversibility, the mass accommodation coefficient can be assumed to be equivalent to the evaporation coefficient (γ) with the two parameters describing the depression in the net flux of molecular traffic below that expected from gas kinetic theory and the Hertz–Knudsen equation (8). Numerous attempts to measure mass accommodation and evaporation coefficients for water at an aqueous–gas surface have reported values ranging over orders of magnitude (9, 10). More recent work, including a sensitivity analysis of previous studies, has narrowed the possible value of α_m for pure water to greater than 0.5 (11). The interplay of the limiting regimes governed by slow gas phase diffusion and slow interfacial transport is shown in Fig. 1A. Evaporation and condensation fluxes from small particles (Knudsen numbers of >0.1) are suppressed by even small deviations of the evaporation coefficient from unity; larger particles only show a measurable suppression in flux due to slow interfacial transport when the evaporation coefficient is <<1 and gas phase diffusion is otherwise limiting.

Fig. 1.

(A) Calculated values of the mass flux from evaporating water droplets with variation in evaporation coefficient over a size range covering four orders of magnitude. The gas phase pressure is 100 kPa and the temperature is 293 K. (B) Evaporation of 1:1 by volume water–ethanol droplets doped with hexadecanol at initial alcohol concentrations of 0.62, 0.33, and 0.165 mM (red, orange, and green, respectively) into a surrounding RH of ∼80%. The evaporation profile for pure water (blue) is shown for reference. Droplet evaporation shown over an extended timescale highlights the continued steady decrease in radius with time. The model simulation for γ = 2.85 × 10⁻⁵ is shown for comparison (black dash), along with the uncertainty in RH (gray envelope). This equates to a ±7% uncertainty in the value of the evaporation coefficient.

The extent of the suppression of evaporation/condensation by slow interfacial transport is expected to depend on the surface composition (12). Dissolved species in an aqueous solution can preferentially partition to the surface to lower the Gibbs energy by minimizing hydrophobic interactions with water, reducing the surface tension and possibly leading to profound changes in mass accommodation and evaporation coefficients. However, the limitations imposed on the interfacial transport of water between the gas and aqueous phases due to the presence of species at the surface of aerosol particles remains ambiguous (13, 14). For example, Saykally and coworkers (15) have investigated ion adsorption at water surfaces and the resulting impact on mass transfer. Although ammonium sulfate was not found to influence the evaporation kinetics of water (16), subtle effects due to the presence of more surface active perchlorate ions were observed (17).

Organic molecules are more surface active than ionic salts and would be expected to have a greater impact on interfacial transport. Organic films are of particular interest in cloud microphysics owing to their potential abundance in the atmosphere (18, 19). The effect of monomolecular films on the uptake coefficient of N₂O₅ has been investigated by Cosman et al. (20) and is one of few examples in which the effect of a surface film on mass transport at the surface of an aerosol has been unambiguously identified. The influence of organic surface films on water transport has been mostly inferred from studies on flat surfaces and large droplets (21–26), measurements that are largely insensitive to the kinetics of interfacial transfer due to the low Knudsen numbers involved, and the magnitude of the suppression for aerosol particles remains unclear.

The packing density and ordering of organic surfactant molecules in a monomolecular film can show 2D phase behavior analogous to that observed in bulk gas, liquid, and solid phases (27). For a densely packed film of a long-chain alcohol, with a surface area per molecule of <20 Ų, a 2D solid film is formed with long-range ordering and a coherent arrangement of hydrophobic chains. From molecular-dynamic simulations, the chains are predicted to align perpendicular to the surface with little tilt relative to the surface normal (28). As the packing density decreases and the film is allowed to expand, the surface area per molecule increases and the film behaves more like a liquid phase, retaining only short-range interactions but losing long-range order. The chains tilt relative to the surface normal and the layer is expected to become more permeable to water (28). Finally, a gaseous film is characterized by the loss of even short-range interactions, and individual surfactant molecules can be assumed to act independently. The accessible area theory, proposed by Barnes et al. (29), suggests that resistance to evaporation imposed by a molecular film is governed by the availability of holes large enough for water molecules to pass through. As such, tighter packing and longer chains are expected to increase resistance to evaporation.

In this study, we investigate the influence of monomolecular films of long-chain fatty alcohols [functional form C_nH_(2n+1)OH] on the evaporation of water from single aqueous aerosol droplets, 5–20 µm in radius. The size (and Knudsen) regime attainable through our technique confers significantly increased sensitivity to the evaporation coefficient compared with other single-particle and flat-surface measurements. Indeed, an evaporation coefficient of ≤0.05 can be unambiguously identified following an assessment of the associated uncertainties (5, 11). More specifically, we report the dependence of the evaporation coefficient on the length of the aliphatic chain and on temperature, and compare evaporation with the condensation of water on coated aqueous NaCl droplets.

Results and Discussion

Mass Transport of Water Across a Hexadecanol Monolayer.

The influence of initially submillimolar concentrations of hexadecanol (n = 16; Fluka; ≥99%) on the evaporation of water from a droplet held in a gas phase at a relative humidity (RH) of 80% is shown in Fig. 1B. Within the first 200 ms, the ethanol used to solubilize the fatty alcohol in the aqueous droplet rapidly evaporates, leaving only water and hexadecanol. Water then continues to evaporate at a rate consistent with that observed from pure water droplets before an abrupt and marked decrease in the evaporation rate is observed. We have demonstrated previously that we can accurately track the concentration profile of an evaporating droplet through knowledge of the initial conditions, the droplet size and solute concentration (5). The concentration of the fatty alcohol in the droplet at the radius at which the evaporation rate decreases can be used to estimate the surface packing of the film, under the assumption that all of the fatty alcohol resides at the surface. The surface area per molecule was found to be between 20 and 22 Ų at the point where evaporation retardation was observed (Table 1) for all three of the starting solute concentrations studied. The calculated values are consistent with literature data for the surface area of a molecule in a condensed alkylic monolayer (30–32) and suggest that the slowing of the evaporation rate is due to the formation of a condensed monolayer film.

Table 1.

Initial size (R₀) and concentration (C₀) of the droplets reported in this work

n	C0, mM	R0, µm	Rdef, µm	Amol, Å2	γ
12*	0.200	22.5	8.9	16.1	2.35 ± 0.15 × 10−3
13	0.200	22.2	9.7	20.0	1.2 ± 0.1 × 10−3
14	0.090	25	7.9	20.7	4.0 ± 0.4 × 10−4
15	0.130	24.5	9.4	22.0	8.0 ± 0.6 × 10−5
16	0.620	22.5	17.8	22.4	2.85 ± 0.20 × 10−5
16	0.330	25.5	14.8	20.0	2.85 ± 0.20 × 10−5
16	0.165	25	10.4	20.9	2.85 ± 0.20 × 10−5
17	0.025	24	7.7	21.9	1.65 ± 0.05 × 10−5

The concentration of the fatty alcohol [functional form C_nH_(2n+1)OH] at the point of deflection in the evaporation rate was calculated from the particle size (R_def). Assuming all molecules resided at the surface, a surface area per molecule was calculated (A_mol).

^*Data for dodecanol data were recorded at 283 K, not 293 K, as explained in the text.

Following film formation, water loss continues at a reduced rate with an approximately linear decrease in radius with time. This can be contrasted with the linear dependence of the radius-squared on time observed when gas diffusion limits the rate of evaporation from pure water droplets in the continuum (gas diffusion limited) regime. The reduced evaporation rate can be used to estimate the value of the evaporation coefficient from the semianalytic treatment described in the Materials and Methods. Independent of the initial concentration of hexadecanol, the evaporation of water is consistent with a γ of (2.85 ± 0.20) × 10⁻⁵, with the model accurately reproducing both the rate and linearity of the time dependence in radius for the remainder of the droplet evaporation. The invariable value of the evaporation coefficient as the droplet radius (and total surface area) diminishes suggests that the packing density of molecules in the surface film remains constant. If the monolayer does not compress further, transfer of the fatty alcohol molecules from the surface film into the aqueous bulk must occur.

The uncertainty associated with interpreting the kinetics of mass transfer arises primarily from the uncertainty in RH (±2%), estimated from the rate of water evaporation following complete loss of ethanol and before the influence of the film. The influence of this uncertainty on the model predictions is shown in Fig. 1B as a gray envelope and equates to an uncertainty in the evaporation coefficient of ±7%. From our previous work, we have noted uncertainties associated with the thermophysical parameters, specifically the gas phase diffusion and thermal conductivity constants (11). However, when the evaporation coefficient is <<1, as in the case here, these uncertainties have negligible effect on the value estimated for the evaporation coefficient.

Previous studies have qualitatively investigated the effect of hexadecanol on the evaporation rate of water. Garrett (23) noted a decrease in the evaporation rate for water droplets 50–250 µm in radius coated with hexadecanol sitting on a Teflon mesh, although the exact droplet size was not reported. A decrease in the evaporation rate of around an order of magnitude was reported compared with the evaporation of pure water droplets, much less pronounced than the decrease in evaporation rate observed in our measurements of around two orders of magnitude. When the difference in Knudsen number is accounted for, however, these observations are broadly consistent. A decrease in the mass flux of an order of magnitude below that expected from a water surface is expected for a droplet size of ∼160 µm in radius (Fig. 1A), well within the size range measured by Garrett.

Dependence of the Evaporation Coefficient on the Carbon Chain Length.

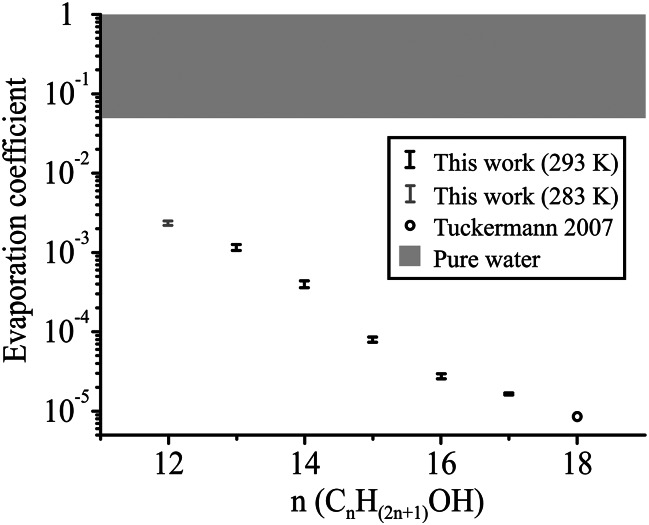
Measurements of evaporation from droplets containing fatty alcohols of varying chain length have been used to investigate the influence of the thickness of the monolayer film on the evaporation rate (Fig. 2), retaining the same OH head group for all measurements. In addition to hexadecanol, we have studied dodecanol (n = 12; Fluka; ≥98%), tridecanol (n = 13; Sigma-Aldrich; 97%), tetradecanol (n = 14; Fluka; ≥99%), pentadecanol (n = 15; Sigma-Aldrich; 99%), and heptadecanol (n = 17; Sigma-Aldrich; 98%). As the carbon chain length is increased, the degree of slowing in the evaporation rate following monolayer formation becomes more significant.

Fig. 2.

The evaporation coefficient (on a log₁₀ scale) as a function of carbon chain length. The low-temperature data (283 K) associated with n = 12 is shown in gray, and the calculated value for data presented by Tuckermann et al. (33) for octadecanol (n = 18) is shown as a black circle. The range of evaporation coefficients possible for pure water, as discernible by our technique, is shown by the gray shaded region.

The evaporation of water from droplets doped with dodecanol (n = 12) is consistent with that observed from pure water droplets at room temperature with no slowing that could be attributed to the formation of a monolayer. Despite the droplets reaching a concentration of dodecanol required for monolayer formation at around 10 µm, they continued to decrease in size at the same rate until they were lost from the trap when <6 µm in radius. However, at a lower gas phase temperature (283 K as opposed to 293 K), a marked decrease in the evaporation rate was once again observed at a dodecanol concentration corresponding to monolayer formation. The melting point of dodecanol is 297 K, and at room temperature it exists as a waxy liquid. On reducing the temperature, the dodecanol forms a condensed solid film with long-range coherence of the alkyl chains and an evaporation coefficient consistent with the trend observed at 293 K for the longer-chain alcohols.

An evaporation coefficient inferred from the data presented by Tuckermann et al. (33) of the evaporation rate of water from aqueous droplets doped with octadecanol (n = 18), held in an acoustic trap at 293 K, is also included in Fig. 2. The authors observed a reduction in the evaporation rate following formation of a monolayer consistent with an evaporation coefficient of 8.5 × 10⁻⁶, a value in consistent with the trend found in our experiments.

For each of the alcohols studied at 293 K, the surface area per molecule at the onset of monolayer formation was estimated and fell within the range of 20–22 Ų (Table 1), with a slightly lower area for film formation in dodecanol-doped droplets at 283 K. Henry et al. (28) reported that the hydrocarbon chains are fully extended with very little tilt when the area falls below 24 Ų, providing the maximum barrier to water transport. Although the surface packing density responsible for inhibiting water transport does not change significantly along the homologous series, the magnitude of the suppression does. An increasing resistance to water transport through the film is indeed expected (28), consistent with an increase in the escape path (barrier length) that water molecules must pass through from the aqueous phase into the gas phase.

Dependence of the Evaporation Coefficient on Temperature.

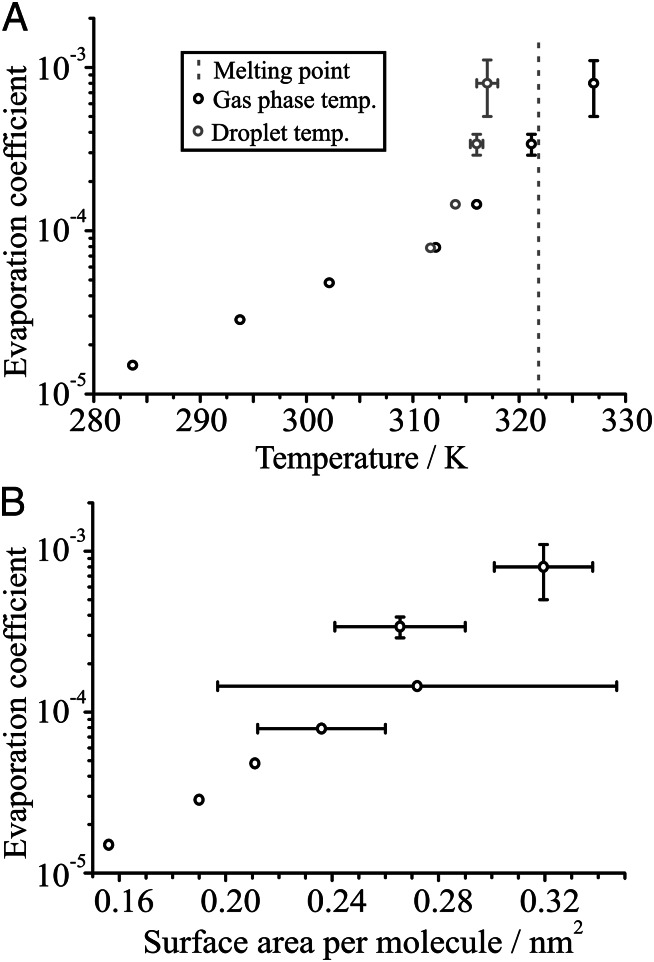
Evaporation rates from hexadecanol-doped droplets were measured over a range of temperatures (Fig. 3A). The evaporation coefficient shows a marked increase with temperature over the range of 283 to 312 K, above which the increase becomes even more pronounced. It is worth noting that, in this regime, the droplet and gas phase will be at significantly different temperatures, due to the removal of latent heat during the evaporation of water. The ambient and low-temperature measurements reported in the previous sections were performed under humid conditions, in which the droplet temperature depression due to loss of latent heat via evaporation of water from the droplet is minimal. When the gas phase temperature is increased, there is an associated increase in the saturation vapor pressure of water, leading to a reduction in the RH at which the evaporation rate is measured. Thus, measurements at higher temperatures are performed under much drier conditions, with an associated increase in the uncertainty in the RH (<20% ± 10% RH) at T > 315 K. The semianalytic treatment of mass flux can be used to estimate the steady droplet temperature during evaporation, and the results of these calculations are also shown by correcting the apparent droplet temperature in Fig. 3A. The dramatic rise in evaporation coefficient appears to be consistent with the approach to the melting temperature of the condensed surface film, mirroring the effect of decreasing the temperature on the effect of a dodecanol film.

Fig. 3.

(A) The effect of varying the gas phase temperature (black points) on the evaporation coefficient for water droplets doped with 0.2 mM hexadecanol. The melting point of hexadecanol is indicated. Note that the droplet will be at a lower temperature than the gas phase due to evaporative cooling, an effect that becomes more important at high temperatures where the RH is lower and evaporation is more rapid. The droplet temperature, estimated from the mass flux equations, is plotted in gray, and the uncertainty in both axes is estimated based on the uncertainty in the RH. In cases in which no error bar is present, the point itself is equal to or much larger than the uncertainty in the measurement. (B) The dependence of the evaporation coefficient on the surface area per molecule of the monolayer, calculated for each of the temperatures presented in A. The uncertainty in surface area comes primarily from the initial size uncertainty, which increases with more the rapid evaporation at higher temperatures. The largest error bar is due to an anomaly in the observed formation of the monolayer, and the radius at the point of monolayer formation was less clear.

The surface area per molecule at the point of monolayer formation is reported for each temperature in Fig. 3B. As the temperature increases, the packing density decreases, and a correlation between packing density and the associated evaporation coefficient is observed. This behavior is qualitatively consistent with previous work measuring reactive uptake of N₂O₅ onto aqueous surfaces coated with organic species of varying packing density (20) and is again consistent with the phase of the monolayer, as described by Donaldson et al. (27). Indeed, Henry et al. (28) suggested that an increase in temperature would lead to expansion of an octadecanol monolayer film and increased permeability.

Water Condensation on Monolayer-Coated Aqueous Aerosol.

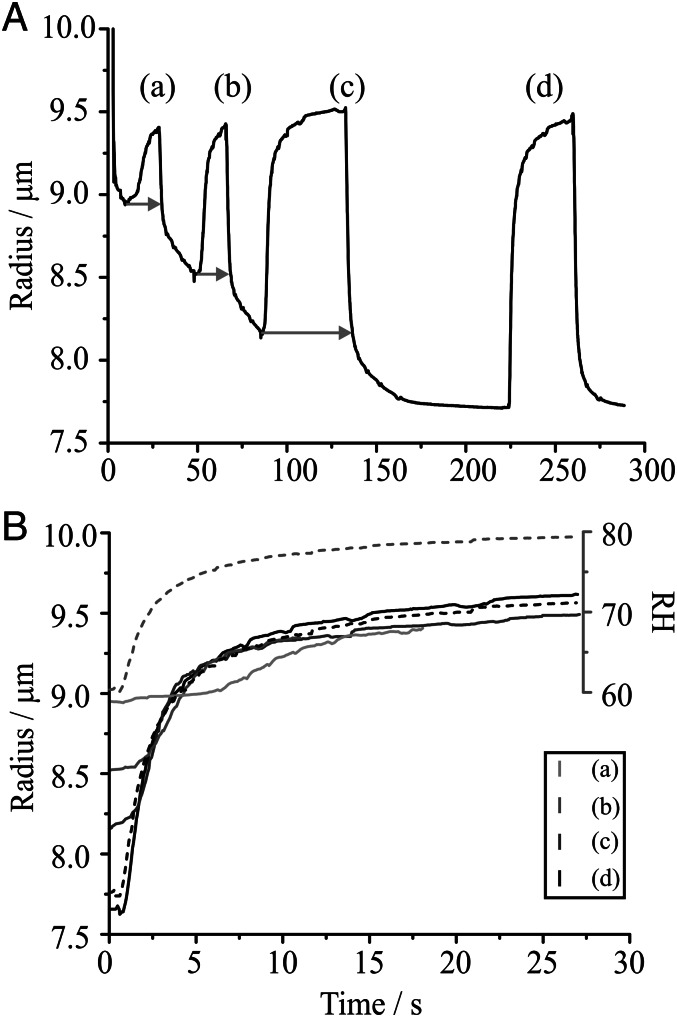
Water condensation has been studied by first forming, by evaporation, a droplet with a complete monolayer coverage of hexadecanol. Specifically, an aqueous sodium chloride droplet, doped with hexadecanol, was allowed to evaporate into a gas phase held at an RH of 60% (Fig. 4A). The monolayer reduced considerably the evaporation rate at the point at which a condensed film was formed. To then study water condensation on the coated droplet, the RH was rapidly increased from 60% to 80%. Measurements were performed on both coated and uncoated (pure sodium chloride solution) droplets for comparison. Following equilibration at 60% RH, the uncoated droplet responded rapidly to the increase in RH and displayed a repeatable size change on cycling the RH between 60% and 80%. Indeed, the time dependence of the droplet size was used to retrieve the typical time variance in water activity experienced by a growing droplet in these measurements (shown in Fig. 4B). Perhaps surprisingly, the coated droplet also responded rapidly to the increase in RH, even after the monolayer had formed. On subsequent decrease in RH, the droplet size response was again rapid until it reached its size before the RH increase. Evaporation then continued in a slow manner and another cycle of the RH displayed similar behavior. Following equilibrium, both condensation and subsequent evaporation of water behaved in the same way as the uncoated droplet.

Fig. 4.

(A) Kinetics of evaporation and condensation during RH cycling between 60% and 80% for a sodium chloride droplet coated with a hexadecanol monolayer. (B) Size changes for events a–d (labeled in A). t = 0 s on this plot indicates when the RH change was initiated. The size response of an uncoated droplet is shown by the dashed black line, whereas the corresponding change in RH inferred from the response of this pure sodium chloride droplet, is indicated by the dashed gray line.

Fig. 4B compares more closely the sequential condensation profiles (a–d), confirming that the timescales for condensational growth are similar to the variation in water activity retrieved from the uncoated droplet. Notably, the direction of mass flux does not reverse and water does not start to condense on the coated droplet until the RH has surpassed the water activity that the droplet has reached during evaporation. For example, there is a significant time lag between the RH change and the response in droplet size for the first increase in RH, with the RH in the gas phase first needing to climb up to a value that surpasses the water activity in the droplet. We suggest that the strong cohesion of alcohol chains as the droplet surface area begins to expand, with the alcohol persisting as islands, leads to regions of the droplet surface that are free from surfactant and condensation kinetics that show no inhibition. The coherence of surfactant molecules in islands on film expansion is not uncommon and has, for example, been seen for palmitic acid and stearic acid films on a water surface (34). On such a short timescale, the long-chain alcohol molecules that have partitioned into the particle bulk (largely as micelles) are unable to sustain a complete condensed film on growth.

Implications for Water Transport in Atmospheric Aerosol.

The dependence of the evaporation coefficient on the composition and phase of an organic surface film is now clear. The packing density at the point at which the evaporation rate arrests, the lowering of temperature required for dodecanol-coated droplets to show a similar behavior to longer chain alcohols, and the temperature dependence of the evaporation coefficient for hexadecanol films, all indicate that a solid condensed film must form for the evaporation coefficient of water to be reduced below a value of 0.05. Increasing the length of the carbon chain from n = 12 to 18 reduces the evaporation coefficient by a factor of 300, decreasing the value from 2.4 × 10⁻³ to 8.5 × 10⁻⁶. The trend of decreasing evaporation coefficient with increased packing density (Fig. 3B) is qualitatively consistent with molecular-dynamic simulations of the mass accommodation coefficient of water on aqueous surfaces coated by long-chain fatty acids. For example, Takahama and Russell (35) reported a value of 0 (upper possible limit, 0.04) for water accommodating on a surface coated with myristic acid at approaching full coverage. These observations strongly suggest that, for all but the most coherent of films, the evaporation coefficient, and by microscopic reversibility the mass accommodation coefficient, will be larger than 0.05. It should be noted that the thermal accommodation coefficient is assumed to remain unaffected, and future work may elucidate whether this is valid through the use of gas phases with different thermal conductivities, such as helium.

For ambient aerosol, it can be largely assumed that the full complexity of organic composition prevents the formation of a solid coherent film of long-range order with the high packing density characteristic of a condensed film required for suppression of water transport. This conclusion is broadly consistent with a recent analysis of a wide range of growth kinetic measurements made on ambient aerosols at various geographic locations, which concluded that the mass accommodation coefficient must be larger than 0.1 for cloud condensation nuclei (36). It is also consistent with laboratory-based measurements that have shown that the presence of surface-active ions or low–molecular-weight organic compounds (e.g., acetic acid) have little to no effect on the evaporation coefficient (16, 17). However, it must be remembered that tropospheric temperatures are largely lower than studied here. This fact may yet lead to a role for organic films in leading to marked suppressions of interfacial transport under certain circumstances.

The increasing impermeability to water transport of organic films with increasing carbon chain length will provide invaluable data for molecular-dynamic simulations and should allow us to more fully understand the mechanism of water transport across an organic layer. Furthermore, the apparent sustained coherence of an organic film when water condensation occurs, and the rapid response in droplet size through condensation, suggests that the growth of a droplet preserves islands of organic surfactants and opens up areas of uncoated water surface on which water condensation can occur rapidly. Molecular-dynamic simulations for droplets coated in a long-chain fatty acid could provide further insights into the dynamics that are occurring (11, 28, 37). Finally, although it is not possible to determine the lowest possible limit on the evaporation coefficient, with the value declining up to n = 18 chain length, the influence of longer-chain surfactants will provide greater insight into the mechanism of interfacial transport.

Materials and Methods

The experimental technique has been discussed by us previously and will be only briefly reviewed here (5, 38). The sample solution is placed in the reservoir of a microdispenser (Microfab MJ-ABP-01; 30-µm orifice). Single droplets are produced by the application of a voltage pulse, and an induction electrode imparts a charge on the droplet as it forms, allowing it to be manipulated by the fields of an electrodynamic balance (EDB), formed from two pairs of concentric cylindrical electrodes. The strong electric field confines the droplet within 100 ms of generation. The trapped droplet is illuminated with a cw-laser beam (532 nm) and the evolving droplet size is estimated from the angularly resolved elastic scattering pattern using a geometrical optics approximation to determine the radius (39). The time resolution of size measurements made during the initial rapid evaporation is chosen to be 10 ms, with measurements following slower size changes averaged every second. During confinement, a flow of nitrogen of fixed RH is passed over the droplet surface, allowing precise control of the gas phase environment. The chamber design allowed the temperature to be controlled between 283 and 330 K, with a stability of <<1 K, and a nitrogen airflow although the outer cylindrical electrode to be introduced, permitting the use of greater flow rates. Coupled with a four-way valve, the chamber could be rapidly cycled between two fixed gas phase conditions, with a half-time of <5 s for the change in RH.

The fatty alcohols used in this study are largely insoluble in water, but partially soluble in ethanol. Solutions of these fatty alcohols at submillimolar concentrations (Table 1) were made up in a 50% (vol/vol) aqueous mixture of ethanol and water. Droplets generated from these solutions were introduced into the cylindrical EDB and the effect of the fatty alcohol on water evaporation alone was investigated at an RH of ∼80%, following the initial rapid evaporation of ethanol in the first few 100 ms. Measurements were made on multiple droplets with the same initial size and composition, and an average evaporation trend determined. No dependence of the long-time evaporation from the water droplet due to the initial presence of ethanol was observed. For measurements of water uptake, droplets generated from a sodium chloride solution in water/ethanol containing hexadecanol were confined in the EDB at an RH of ∼60%. The RH was cycled between 60% and 80% RH, and the droplet response was recorded as water condensation and evaporation occurred.

To quantitatively interpret our measurements, the evaporation measurements are compared with simulations from a semianalytic mass flux model based on the well-established framework of Kulmala et al. (40). We have discussed previously the applicability of this model in the interpretation of our measurements (5, 11, 13, 38). The transition regime correction factors of Fuchs–Sutugin are used to account for the marked reduction in the continuum mass and heat fluxes observed due to the slow interfacial transfer kinetics and the considerable diminution of the evaporation coefficient when an organic film is formed. The thermal accommodation coefficient is assumed to be unity throughout, consistent with previous experimental work (41) on water surfaces. However, it should be noted that the effect of surface films on the thermal accommodation coefficient is unknown. Values of the thermophysical parameters required by the model were taken from the recommendations of Miles et al. (11).