Abstract
Model-based analyses of natural selection often categorize sites into a relatively small number of site classes. Forcing each site to belong to one of these classes places unrealistic constraints on the distribution of selection parameters, which can result in misleading inference due to model misspecification. We present an approximate hierarchical Bayesian method using a Markov chain Monte Carlo (MCMC) routine that ensures robustness against model misspecification by averaging over a large number of predefined site classes. This leaves the distribution of selection parameters essentially unconstrained, and also allows sites experiencing positive and purifying selection to be identified orders of magnitude faster than by existing methods. We demonstrate that popular random effects likelihood methods can produce misleading results when sites assigned to the same site class experience different levels of positive or purifying selection—an unavoidable scenario when using a small number of site classes. Our Fast Unconstrained Bayesian AppRoximation (FUBAR) is unaffected by this problem, while achieving higher power than existing unconstrained (fixed effects likelihood) methods. The speed advantage of FUBAR allows us to analyze larger data sets than other methods: We illustrate this on a large influenza hemagglutinin data set (3,142 sequences). FUBAR is available as a batch file within the latest HyPhy distribution (http://www.hyphy.org), as well as on the Datamonkey web server (http://www.datamonkey.org/).
Keywords: evolutionary model, coding sequence evolution, approximate Bayesian inference, parallel algorithms
Introduction
Codon-based models of evolution have proved extremely useful for identifying sites evolving under selection in protein-coding genes (Anisimova and Kosiol 2009; Delport et al. 2009). These models use a probabilistic approach to infer whether the nonsynonymous substitution rate (β) at a specific site is faster or slower than the neutral rate, which is typically set to the synonymous rate (α) at the same site (or to the mean synonymous rate for the entire alignment). However, existing software tools are simply too slow to allow analysis of many large data sets that are currently available.
The codon-modeling literature has largely focused on two ways of inferring the selection parameters 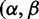 ), either jointly or as the ratio
), either jointly or as the ratio 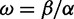 . First, in fixed effects likelihood (FEL) models (Kosakovsky Pond and Frost 2005; Massingham and Goldman 2005) the parameters are inferred independently for each site. This approach avoids assumptions about the distribution of selection parameters over sites, yielding greater flexibility to describe such distributions. However, the absence of parametric assumptions means that evidence from one site cannot inform our expectations regarding another: The inference at an individual site is based only on the limited amount of data from that site. The effect of this is that point estimates of site-specific parameter values can be unreliable, although robust inference is still possible by taking the uncertainty about these point estimates into account (Kosakovsky Pond and Frost 2005). Furthermore, methods where the number of parameters increases with the number of observations can be asymptotically inconsistent (Felsenstein 2001).
. First, in fixed effects likelihood (FEL) models (Kosakovsky Pond and Frost 2005; Massingham and Goldman 2005) the parameters are inferred independently for each site. This approach avoids assumptions about the distribution of selection parameters over sites, yielding greater flexibility to describe such distributions. However, the absence of parametric assumptions means that evidence from one site cannot inform our expectations regarding another: The inference at an individual site is based only on the limited amount of data from that site. The effect of this is that point estimates of site-specific parameter values can be unreliable, although robust inference is still possible by taking the uncertainty about these point estimates into account (Kosakovsky Pond and Frost 2005). Furthermore, methods where the number of parameters increases with the number of observations can be asymptotically inconsistent (Felsenstein 2001).
By contrast, random effects likelihood (REL) models (Nielsen and Yang 1998; Kosakovsky Pond and Muse 2005) are designed to share information across sites by inferring a gene-specific distribution for the selection parameters, with the assumption that the rates at each site are an independent draw from this distribution. Site-specific distributions for the selection parameters can then be obtained by application of Bayes’ rule. Many parametric forms have been investigated for the gene-specific distribution of selection parameters (Yang 2000) but to make parameter estimation tractable and to obtain reliable point estimates of parameter values, all of them are restricted to a small number of parameters. In addition, the distribution is either discrete or is discretized to allow numerical computation of the likelihood. The number of discrete components must be small, because the computational complexity of the likelihood calculation increases linearly with the number of discrete components. It is worth emphasizing that the synonymous and nonsynonymous substitution rates are inherently continuous-valued quantities and that their discretization is an approximation for computational convenience; as we show in later sections, overly coarse discretizations can mislead inference.
Huelsenbeck et al. (2006) proposed a nonparametric Bayesian approach, which addresses both the choice of distribution over selection parameters and the discretization, but at a prohibitive computational cost. Data augmentation techniques have improved the speed of inference under complex models (Lartillot 2006; Rodrigue et al. 2008; de Koning et al. 2012), but they remain intractable for large alignments.
In this article, we introduce FUBAR (a Fast Unconstrained Bayesian AppRoximation), which exploits several computational shortcuts to speed up the detection of positive or purifying selection, and to relax the above REL restrictions, leading to improved robustness against model misspecification and permitting the analysis of large data sets for which selection analysis was previously intractable. The key idea is to precompute a number of conditional likelihoods, arranged on an a priori-selected grid of values for α and β (in contrast to existing REL methods that shift the locations of the 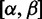 categories during optimization, depending on the data). Inference of selection parameters then proceeds without requiring further phylogenetic likelihood computation, instead repeatedly reusing the precomputed values. Our default recommendation for the number of grid points is 400: This is large and therefore finely discretized compared with the number of
categories during optimization, depending on the data). Inference of selection parameters then proceeds without requiring further phylogenetic likelihood computation, instead repeatedly reusing the precomputed values. Our default recommendation for the number of grid points is 400: This is large and therefore finely discretized compared with the number of 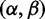 categories in typical random effects approaches, for example, that of Kosakovsky Pond and Muse (2005), which uses nine categories. However, as evidenced by the speedups we obtain, it is vastly smaller than the number of likelihood calculations performed during either optimization-based or sampling-based inference in existing methods, regardless of whether they use fixed or random effects models.
categories in typical random effects approaches, for example, that of Kosakovsky Pond and Muse (2005), which uses nine categories. However, as evidenced by the speedups we obtain, it is vastly smaller than the number of likelihood calculations performed during either optimization-based or sampling-based inference in existing methods, regardless of whether they use fixed or random effects models.
Although we have also used this approach to obtain large speedups in fixed effects models and in random effects models employing rate distributions with a small number of parameters, one of its key features is that it allows the implementation of far more parametrically complex models without extra computational cost. For this reason, we see the greatest utility in Bayesian approaches that allow large numbers of parameters to be used without being subject to overparameterization. Here, we present such an approach: following conventional random effects models, the selection parameters at each site are drawn from a gene-specific distribution for 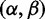 , but instead of using a low-dimensional parametric form for this distribution we adopt the general bivariate discrete distribution, parameterized by a weight at each point of the grid (fig. 1), and imposing no further constraints on the individual weights. Using a hierarchical Bayesian framework, we assume a Dirichlet prior for the gene-specific distribution of rate class weights, and use a Markov Chain Monte Carlo (MCMC) approach to integrate over the uncertainty in the posterior gene-specific and site-specific distributions. We show that this approach is less vulnerable to model misspecification than existing approaches, while also running orders of magnitude faster.
, but instead of using a low-dimensional parametric form for this distribution we adopt the general bivariate discrete distribution, parameterized by a weight at each point of the grid (fig. 1), and imposing no further constraints on the individual weights. Using a hierarchical Bayesian framework, we assume a Dirichlet prior for the gene-specific distribution of rate class weights, and use a Markov Chain Monte Carlo (MCMC) approach to integrate over the uncertainty in the posterior gene-specific and site-specific distributions. We show that this approach is less vulnerable to model misspecification than existing approaches, while also running orders of magnitude faster.
Fig. 1.
The synonymous and nonsynonymous rates ( ) are continuous model parameters that vary from one site to another, illustrated by a hypothetical distribution in (A). Typical random effects models, as exemplified by Dual REL (Kosakovsky Pond and Muse 2005) in (B) use a small number of discrete categories to approximate this continuous distribution, allowing the location (represented by the green bars) and the probability mass of the discrete points to vary; a change in the location of a point necessitates a re-evaluation of the phylogenetic likelihood function. FUBAR, in (C), uses a much denser grid of values chosen a priori, relying on the grid density to circumvent the need to move the parameter locations, and on MCMC to sample the weights assigned to each point. Without the need for movable grid lines, FUBAR needs to compute the conditional likelihood associated with each point only once, eliminating the bottleneck hindering traditional random effects models. Note that the uniform grid spacing depicted here is stylized. As the uncertainty in the selection parameters grows with their magnitude, FUBAR uses larger spacing for larger values (see text for details).
) are continuous model parameters that vary from one site to another, illustrated by a hypothetical distribution in (A). Typical random effects models, as exemplified by Dual REL (Kosakovsky Pond and Muse 2005) in (B) use a small number of discrete categories to approximate this continuous distribution, allowing the location (represented by the green bars) and the probability mass of the discrete points to vary; a change in the location of a point necessitates a re-evaluation of the phylogenetic likelihood function. FUBAR, in (C), uses a much denser grid of values chosen a priori, relying on the grid density to circumvent the need to move the parameter locations, and on MCMC to sample the weights assigned to each point. Without the need for movable grid lines, FUBAR needs to compute the conditional likelihood associated with each point only once, eliminating the bottleneck hindering traditional random effects models. Note that the uniform grid spacing depicted here is stylized. As the uncertainty in the selection parameters grows with their magnitude, FUBAR uses larger spacing for larger values (see text for details).
New Approaches
Following Muse and Gaut (1994), we model the evolution of a particular site along a particular branch of the phylogenetic tree as a continuous-time Markov process, governed by the instantaneous rate matrix  , with elements that describe the rate of substitution of codon i with codon j:
, with elements that describe the rate of substitution of codon i with codon j:
 |
(1) |
 counts the number of nucleotide differences between codons i and j, and AA(i) is the amino acid encoded by i. α and β are the rates of synonymous and nonsynonymous substitutions respectively. nij (comprising
counts the number of nucleotide differences between codons i and j, and AA(i) is the amino acid encoded by i. α and β are the rates of synonymous and nonsynonymous substitutions respectively. nij (comprising 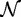 ) are the nucleotide mutational biases, which we model using the 5-parameter general time reversible (GTR) nucleotide model (Tavaré 1986).
) are the nucleotide mutational biases, which we model using the 5-parameter general time reversible (GTR) nucleotide model (Tavaré 1986).  (comprising Π) denote the equilibrium frequency parameters.
(comprising Π) denote the equilibrium frequency parameters.
We denote a phylogenetic tree  , specifying both the tree topology and a branch length parameter, tb, for every branch b. The probability of changing from codon i to j at a site along branch b in time tb is recorded in the corresponding element of the transition matrix
, specifying both the tree topology and a branch length parameter, tb, for every branch b. The probability of changing from codon i to j at a site along branch b in time tb is recorded in the corresponding element of the transition matrix  . The likelihood of observing the site given the model parameters is calculated using Felsenstein’s pruning algorithm (Felsenstein 1981). The goal of a selection analysis is to infer values for α and β for each site, and to provide a measure of evidence for the hypotheses that
. The likelihood of observing the site given the model parameters is calculated using Felsenstein’s pruning algorithm (Felsenstein 1981). The goal of a selection analysis is to infer values for α and β for each site, and to provide a measure of evidence for the hypotheses that  or
or 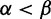 .
.
Modeling Variation in α and β
Calculating the Likelihood
The model used by FUBAR requires that the synonymous and nonsynonymous rates vary across sites. To achieve this, we follow Kosakovsky Pond and Muse (2005) and treat α and β as random effects, specifying a distribution from which they are drawn, and we integrate over that distribution to calculate the marginal likelihoods. To ensure identifiably, we require that 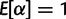 . For computational tractability, these distributions are discrete. Furthermore, the sites are assumed to evolve independently, with the overall likelihood being the product of the site likelihoods. Thus, if xk denotes the kth site of the alignment X, the overall likelihood can be calculated as:
. For computational tractability, these distributions are discrete. Furthermore, the sites are assumed to evolve independently, with the overall likelihood being the product of the site likelihoods. Thus, if xk denotes the kth site of the alignment X, the overall likelihood can be calculated as:
| (2) |
where 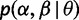 specifies the probability of each (
specifies the probability of each ( ) combination, θ is a set of parameters governing this distribution, and
) combination, θ is a set of parameters governing this distribution, and 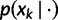 is computed by the standard phylogenetic pruning algorithm (Felsenstein 1981).
is computed by the standard phylogenetic pruning algorithm (Felsenstein 1981).
Recycling Conditional Likelihoods
To prevent having to recalculate the conditional likelihoods 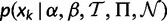 in equation (2), we estimate the parameters that would affect them in advance and use the estimated values throughout. The equilibrium frequency parameters,
in equation (2), we estimate the parameters that would affect them in advance and use the estimated values throughout. The equilibrium frequency parameters, 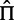 , are derived directly from nucleotide frequency counts using the CF3 × 4 estimator (Kosakovsky Pond et al. 2010). The nucleotide substitution rates,
, are derived directly from nucleotide frequency counts using the CF3 × 4 estimator (Kosakovsky Pond et al. 2010). The nucleotide substitution rates,  , and the tree topology and branch length parameters,
, and the tree topology and branch length parameters, 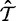 , are fixed at the maximum likelihood estimates (MLEs) under a nucleotide model.
, are fixed at the maximum likelihood estimates (MLEs) under a nucleotide model.
To construct a distribution over the selection parameters, a set of allowable values of α and β and their associated probabilities, 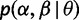 , must be specified. Random effects models typically specify parametric distributions for α and β as a function of θ. These distributions are either discrete or are subsequently discretized, in such a way that the allowable values of α and β depend on θ and therefore change at every step of the optimization or sampling procedure used to infer θ. As a result, existing random effects methods are forced to recompute the conditional likelihood many times during inference. We avoid this by fixing the locations of α and β to a prespecified grid (fig. 1).
, must be specified. Random effects models typically specify parametric distributions for α and β as a function of θ. These distributions are either discrete or are subsequently discretized, in such a way that the allowable values of α and β depend on θ and therefore change at every step of the optimization or sampling procedure used to infer θ. As a result, existing random effects methods are forced to recompute the conditional likelihood many times during inference. We avoid this by fixing the locations of α and β to a prespecified grid (fig. 1).
The analyses in this manuscript use a square 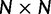 (N = 20) grid, with points used to represent negative selection (
(N = 20) grid, with points used to represent negative selection ( ), neutral evolution (
), neutral evolution (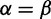 ), and positive selection (
), and positive selection ( ). Along a given axis, 70% of the points are used to describe rates
). Along a given axis, 70% of the points are used to describe rates 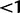 (for N = 20, there are 14 points at
(for N = 20, there are 14 points at  ), a point is placed at 1, and the remainder of the points are spaced out over
), a point is placed at 1, and the remainder of the points are spaced out over  using cubic steps (for N = 20, there are 5 such points at
using cubic steps (for N = 20, there are 5 such points at  for
for 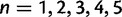 and
and  ). The nonlinear spacing of values above 1 can be justified by the empirical observation that the variance of rate estimates generally mirror the magnitude of the rate, that is, faster rates are more difficult to estimate precisely. The cap of rate values at 50 can be similarly justified by noting that, for most empirical data sets, any values above 50 are essentially infinite. Our preliminary experiments with different grids (results not shown) indicated that the inference of which sites are under selection was relatively robust to the choice of the grid. The software implementation permits the user to choose N, and it is straightforward to modify the grid definition if desired.
). The nonlinear spacing of values above 1 can be justified by the empirical observation that the variance of rate estimates generally mirror the magnitude of the rate, that is, faster rates are more difficult to estimate precisely. The cap of rate values at 50 can be similarly justified by noting that, for most empirical data sets, any values above 50 are essentially infinite. Our preliminary experiments with different grids (results not shown) indicated that the inference of which sites are under selection was relatively robust to the choice of the grid. The software implementation permits the user to choose N, and it is straightforward to modify the grid definition if desired.
Finally, we parameterize  as the general bivariate distribution, such that θ is a vector containing a probability weight for each point on the grid.
as the general bivariate distribution, such that θ is a vector containing a probability weight for each point on the grid.
Markov Chain Monte Carlo
We model the probability weight vector θ (and hence the gene-wide distribution of 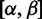 ) as a draw from a symmetric Dirichlet hyperprior:
) as a draw from a symmetric Dirichlet hyperprior:
 |
(3) |
where N is the number of points in the grid and 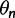 are the elements of the probability weight vector. The concentration parameter
are the elements of the probability weight vector. The concentration parameter  , which controls the “clumpiness” of the distribution, is set to 0.5 for all analyses, but can be tuned by the user.
, which controls the “clumpiness” of the distribution, is set to 0.5 for all analyses, but can be tuned by the user.
To perform the MCMC sampling, we implemented the Metropolis algorithm in the HyPhy software package (Kosakovsky Pond et al. 2005), seeking to obtain a set of samples from the posterior distribution of θ, given the alignment. We begin in an initial state based on relative cumulative weights assigned to each grid point derived from the precomputed conditional likelihoods at each site k: 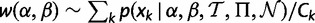 , where Ck =
, where Ck = 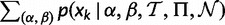 . We multiplicatively perturb each weight by a value sampled uniformly from [0.8, 1.2]. The resulting vector,
. We multiplicatively perturb each weight by a value sampled uniformly from [0.8, 1.2]. The resulting vector,  , is normalized so that the elements sum up to 1.
, is normalized so that the elements sum up to 1.
To propose a change to  , we first randomly pick two elements of the vector (grid points). A perturbation η is sampled from a uniform distribution between 0 and
, we first randomly pick two elements of the vector (grid points). A perturbation η is sampled from a uniform distribution between 0 and 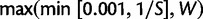 , where S is the number of sites in the alignment and W is the median weight in the initial state. We chose the upper bound as an empirically derived value to optimize the rate of chain mixing. We add η to the first element and subtract it from the second to obtain a proposed new state
, where S is the number of sites in the alignment and W is the median weight in the initial state. We chose the upper bound as an empirically derived value to optimize the rate of chain mixing. We add η to the first element and subtract it from the second to obtain a proposed new state 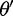 .
. 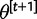 is then set to
is then set to 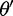 with probability
with probability
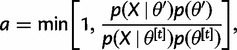 |
(4) |
and to  otherwise. Here,
otherwise. Here,  is obtained from equation (3) and
is obtained from equation (3) and  is the likelihood (eq. 2), calculated from our precomputed conditional likelihoods using matrix multiplication. The proposal distribution implied by this procedure is symmetric; hence, we have no need for a proposal ratio in equation (4). The resulting MCMC chain can be computed extremely efficiently, drawing
is the likelihood (eq. 2), calculated from our precomputed conditional likelihoods using matrix multiplication. The proposal distribution implied by this procedure is symmetric; hence, we have no need for a proposal ratio in equation (4). The resulting MCMC chain can be computed extremely efficiently, drawing  samples/second, which is sufficient to produce almost identical site posteriors on separate runs after a few minutes of run time.
samples/second, which is sufficient to produce almost identical site posteriors on separate runs after a few minutes of run time.
We assess MCMC convergence using potential scale reduction factors (PSRFs) and an effective sample size (Gelman et al. 2003) computed for the posterior probabilities of positive selection for each site. For all data sets tested, an MCMC chain length of  with the first half discarded as burn-in yielded good convergence (assessed by running 10 MCMC chains in parallel from random starting positions). Each chain is thinned to yield T samples from the posterior distribution (the default implementation sets T = 100). On the influenza analysis (discussed in later section), for example, all PSRFs were less than 1.03 and all effective sample sizes were more than 150. Our implementation in the HyPhy software package allows the user to specify the chain lengths, but does not use automated stopping because the MCMC step is not a computational bottleneck: instead, computation times are dominated by fitting the nucleotide model (parallelized using OpenMP) and precomputing the conditional likelihoods (parallelized using MPI).
with the first half discarded as burn-in yielded good convergence (assessed by running 10 MCMC chains in parallel from random starting positions). Each chain is thinned to yield T samples from the posterior distribution (the default implementation sets T = 100). On the influenza analysis (discussed in later section), for example, all PSRFs were less than 1.03 and all effective sample sizes were more than 150. Our implementation in the HyPhy software package allows the user to specify the chain lengths, but does not use automated stopping because the MCMC step is not a computational bottleneck: instead, computation times are dominated by fitting the nucleotide model (parallelized using OpenMP) and precomputing the conditional likelihoods (parallelized using MPI).
Site-Specific Inference
The MCMC procedure yields a set of T samples  . For each sample, we calculate the site-specific posterior distribution of
. For each sample, we calculate the site-specific posterior distribution of 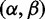 using Bayes’ theorem:
using Bayes’ theorem:
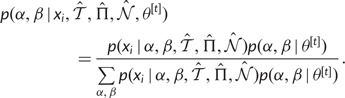 |
(5) |
The posterior probability that positive selection occurred at a site is the total probability that 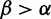 , averaging over the samples:
, averaging over the samples:
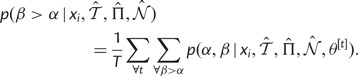 |
(6) |
Bayes factors can be calculated straightforwardly:
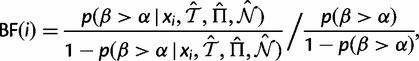 |
(7) |
where the prior probability  in the denominator is calculated by summing over the
in the denominator is calculated by summing over the 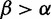 portion of all MCMC samples
portion of all MCMC samples  .
.
Results
Power and False-Positive Rates
To assess the statistical properties of FUBAR, we compared power and false-positive rates between FUBAR and FEL, using a collection of simulated alignments where the values for α and β varied from one site to another. These data were simulated over phylogenies estimated from three empirical data sets of varying size: 23 encephalitis virus env sequences, 38 vertebrate rhodopsin sequences, and 212 camelid VHH sequences (see Murrell, Wertheim, et al. 2012 for details).
Table 1 demonstrates the superiority of FUBAR over FEL. At a posterior threshold of 0.9, FUBAR achieves very low false-positive rates on data that were simulated under neutrality, and has better power in 21 of 27 configurations (and equal power in a further 2). To achieve a fair comparison between tests with different measures of evidence—P values vs. posterior probabilities—the thresholds were adjusted so that both FEL and FUBAR achieve false-positive rates of 0.05 on neutral data. This makes the superiority of FUBAR even clearer. FUBAR has greater power in every case, and the difference is sometimes substantial, especially for lower values of  .
.
Table 1.
Comparative Performance of FEL and FUBAR on Simulated Data.
| Simulation | FP : Power |
Power at FP  |
||
|---|---|---|---|---|
| FEL | FUBAR | FEL | FUBAR | |
| Encephalitis virus env | ||||
 |
0.01:0.03 | 0.00:0.01 | 0.04 | 0.10 |
 |
0.00:0.03 | 0.00:0.02 | 0.09 | 0.14 |
 |
0.00:0.03 | 0.00:0.04 | 0.08 | 0.17 |
 |
0.00:0.05 | 0.00:0.07 | 0.13 | 0.24 |
 |
0.00:0.09 | 0.00:0.20 | 0.19 | 0.38 |
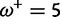 |
0.00:0.19 | 0.00:0.44 | 0.34 | 0.60 |
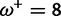 |
0.00:0.28 | 0.00:0.60 | 0.50 | 0.74 |
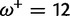 |
0.00:0.34 | 0.00:0.67 | 0.54 | 0.82 |
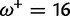 |
0.00:0.38 | 0.00:0.77 | 0.63 | 0.85 |
| Vertebrate Rhodopsin | ||||
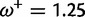 |
0.01:0.07 | 0.00:0.04 | 0.07 | 0.12 |
 |
0.01:0.08 | 0.00:0.08 | 0.08 | 0.18 |
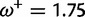 |
0.01:0.13 | 0.01:0.15 | 0.14 | 0.26 |
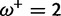 |
0.01:0.19 | 0.01:0.27 | 0.13 | 0.37 |
 |
0.01:0.32 | 0.01:0.57 | 0.34 | 0.59 |
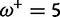 |
0.01:0.48 | 0.01:0.80 | 0.51 | 0.88 |
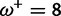 |
0.01:0.67 | 0.01:0.96 | 0.74 | 0.98 |
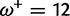 |
0.00:0.71 | 0.00:0.99 | 0.80 | 1.00 |
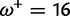 |
0.00:0.76 | 0.00:0.99 | 0.88 | 1.00 |
| Camelid VHH | ||||
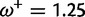 |
0.01:0.11 | 0.01:0.09 | 0.06 | 0.09 |
 |
0.02:0.19 | 0.01:0.20 | 0.14 | 0.21 |
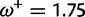 |
0.01:0.34 | 0.01:0.42 | 0.26 | 0.53 |
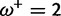 |
0.01:0.51 | 0.01:0.60 | 0.48 | 0.62 |
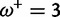 |
0.01:0.74 | 0.01:0.74 | 0.64 | 0.78 |
 |
0.01:0.93 | 0.01:0.95 | 0.93 | 0.97 |
 |
0.01:0.98 | 0.01:0.99 | 0.98 | 0.99 |
 |
0.01:0.97 | 0.01:1.00 | 0.97 | 1.00 |
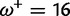 |
0.02:0.99 | 0.03:1.00 | 0.99 | 1.00 |
Note.—The rate of false positives (FP) and power are reported for a fixed nominal test P value of 0.05 for FEL, and a posterior threshold of 0.9 for FUBAR. To achieve a fair comparison between tests with different measures of evidence, power is also shown for the P value or posterior threshold that achieves FP of 0.05, estimated empirically from the distribution of P values or posteriors on the subset of sites evolving neutrally.
Speed Comparisons
We performed speed comparisons of FUBAR against the FEL and REL analyses implemented in HyPhy. REL methods are typically computationally intensive and nontrivial to parallelize, precluding their use on very large alignments with many sequences. Fixed effects methods are faster and typically parallelized, so FEL was used as our primary point of reference. A very large HIV-1 env alignment was obtained from LANL, stripped of gaps and subsampled to create alignments of varying size. To investigate how computation time increases with the number of sites, we sampled 100 taxa randomly from the env alignment and created 5 alignments with 50, 100, 200, 400, and 800 randomly sampled codon sites, respectively. To investigate how computation time increases with taxa, we fixed the number of sites to 200 and sampled alignments with 25, 50, 100, 200, 400, and 800 taxa. All phylogenies were estimated with FastTree 2 (Price et al. 2010) using the GTR nucleotide model. FEL and FUBAR were compared on a computing cluster, with the analyses running in parallel on 10 nodes each. FUBAR was consistently faster than FEL across all tested alignments. As can be seen in figure 2, FEL took from 3.3 times longer (214 s for FEL vs. 65 s for FUBAR) for the smallest alignment, to 19.5 times longer (1 h 2 min for FEL vs. 3 min for FUBAR) for the largest alignment, with the relative disparity increasing uniformly with alignment size. We also ran a discrete REL model, using three categories each for α and β and without parallelization, on the smallest and largest alignments. The running times were 22 min 25 s (20.7 times longer than FUBAR) and 35 h 29 min (709.7 times longer than FUBAR), respectively.
Fig. 2.
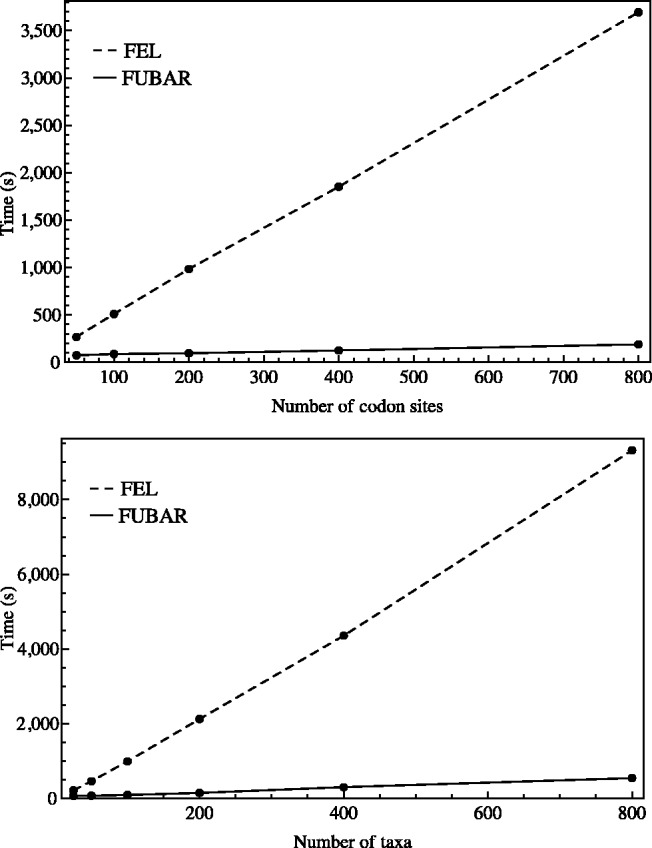
Execution times for FEL and FUBAR as a function of the number of codon sites (top) and number of taxa (bottom).
Additionally (table 2), we used 16 alignments from a previous paper by our group (Murrell, Wertheim, et al. 2012), ranging in size and divergence level to provide a sense of a real-world speedup that could be realized by FUBAR. We compared FUBAR, FEL, REL, and the M2 (3 rate classes) and M8 (9 rate classes) models implemented in PAML v4.16. FUBAR and FEL were run on 10 processors (a number readily available even to researchers on a desktop). REL was run using 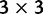 rate classes using built-in OpenMP parallelization in HyPhy (potentially using up to 9 processors). Finally, PAML was run on a single processor—to our knowledge no parallel version of the package exists—using the faster (by branch) optimization procedure (Yang 2000). All analyses were performed on systems equipped with 16-core 64-bit AMD Opteron 6272 processors running CentOS 6, and relied on gcc 4.4.6 to compile the source code.
rate classes using built-in OpenMP parallelization in HyPhy (potentially using up to 9 processors). Finally, PAML was run on a single processor—to our knowledge no parallel version of the package exists—using the faster (by branch) optimization procedure (Yang 2000). All analyses were performed on systems equipped with 16-core 64-bit AMD Opteron 6272 processors running CentOS 6, and relied on gcc 4.4.6 to compile the source code.
Table 2.
Run Time Comparisons between Different Selection Detection Methods on 16 Empirical Data Sets, Sorted on the Duration of the FUBAR Run.
| Data Set | Taxa | Codons | Mean Divergence Subs/Site | FUBAR Run Times (s) | Run Times (Times Slower than FUBAR) |
|||
|---|---|---|---|---|---|---|---|---|
| FEL | REL | PAML M2a | PAML M8 | |||||
| Echinoderm H3 | 37 | 111 | 0.33 | 40 | 5.1 | 12.0 | 7.1 | 46.1 |
| Flavivirus NS5 | 18 | 342 | 0.48 | 45 | 8.6 | 4.5 | 9.3 | 25.5 |
| Drosophila adh | 23 | 254 | 0.26 | 53 | 3.4 | 4.0 | 2.7 | 4.3 |
| West Nile virus NS3 | 19 | 619 | 0.13 | 58 | 6.1 | 5.9 | 37.2 | 105.5 |
| Hepatitis D virus Ag | 33 | 196 | 0.29 | 59 | 4.0 | 3.3 | 10.1 | 22.4 |
| Primate lysozyme | 19 | 130 | 0.08 | 62 | 0.5 | 3.0 | 0.7 | 1.8 |
| Vertebrate rhodopsin | 38 | 330 | 0.34 | 62 | 12.0 | 4.9 | 8.4 | 18.2 |
| Japanese encephalitis virus env | 23 | 500 | 0.13 | 68 | 4.8 | 8.8 | 1.6 | 4.0 |
| Mamallian β-globin | 17 | 144 | 0.38 | 74 | 1.5 | 8.4 | 2.3 | 5.6 |
| Abalone sperm lysin | 25 | 134 | 0.43 | 78 | 1.9 | 3.9 | 3.7 | 9.3 |
| HIV-1 vif | 29 | 192 | 0.08 | 84 | 2.6 | 3.8 | 2.3 | 4.5 |
| Salmonella recA | 42 | 353 | 0.04 | 102 | 2.1 | 2.9 | 2.6 | 12.3 |
| Camelid VHH | 212 | 96 | 0.27 | 120 | 6.3 | 17.2 | 141.0 | 311.1 |
| Diatom SIT | 97 | 300 | 0.54 | 136 | 10.2 | 5.1 | 21.5 | 19.3 |
| Influenza A virus H3N2 HA | 349 | 329 | 0.04 | 210 | 15.0 | 14.4 | 221.1 | 616.4 |
| HIV-1 rt | 476 | 335 | 0.08 | 278 | 15.2 | 14.4 |
 a a
|
 a a
|
Note.—Run times that are at least 10 times greater than those of FUBAR are italicized, and those at least 100 times greater are underlined.
aPAML reported an error regarding too many ambiguities in the data set.
Similar to the results in figure 2, FUBAR is the fastest of all methods except on the smallest alignments (e.g., the Primate Lysozyme alignment), and the benefit to using FUBAR becomes increasingly apparent with larger data sets, where, for example, PAML can run two orders of magnitude slower.
Robustness to Model Misspecification
Prior to FUBAR, random effects models typically used a small number of site categories to capture rate variation from one site to another. We wanted to investigate how empirical Bayesian inference behaves when the model is misspecified, and, in particular, when the model is too simple to accommodate the data, as this is almost universally true of most models for real data sets. An example of this is the M2a model implemented in PAML (Wong et al. 2004), which postulates three categories for ω
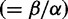 . We simulated 10 replicate alignments of 1,000 sites each, using a constant
. We simulated 10 replicate alignments of 1,000 sites each, using a constant  (i.e., no synonymous rate variation, as is assumed in PAML), but with β taking values of 0.2 (50% of sites), 1 (30%), 3 (10%), and 11 (10%). This represents a situation where most sites are under purifying selection or evolving neutrally, whereas a smaller proportion of sites are under either weak or strong positive selection. The use of four site categories is seemingly a small violation of the M2a model, whose alternative model allows the following three categories: one purifying (
(i.e., no synonymous rate variation, as is assumed in PAML), but with β taking values of 0.2 (50% of sites), 1 (30%), 3 (10%), and 11 (10%). This represents a situation where most sites are under purifying selection or evolving neutrally, whereas a smaller proportion of sites are under either weak or strong positive selection. The use of four site categories is seemingly a small violation of the M2a model, whose alternative model allows the following three categories: one purifying (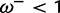 ), one neutral (
), one neutral ( ), and one positive selection (
), and one positive selection (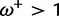 ). The point of this setup is that, in biological reality, the strength of positive selection is not constant across all sites experiencing positive selection—if this causes problems for M2a, it is reasonable to assume that coarse discretization is also problematic for many other models and not just for sites under positive selection.
). The point of this setup is that, in biological reality, the strength of positive selection is not constant across all sites experiencing positive selection—if this causes problems for M2a, it is reasonable to assume that coarse discretization is also problematic for many other models and not just for sites under positive selection.
The positive selection site category used by M2a must attempt to accommodate both the 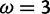 and the
and the 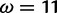 sites, and the resulting MLE (averaged over 10 replicates) is
sites, and the resulting MLE (averaged over 10 replicates) is  (SD 0.64). The evidence in favor of positive selection at a specific site is determined by the ratio
(SD 0.64). The evidence in favor of positive selection at a specific site is determined by the ratio  between the posterior probability of it belonging to the positive selection category and that of it belonging to a different category (LHS); in this example, the latter is dominated by the probability of the site belonging to the neutral category (RHS). For any given gene-specific distribution (acting as a prior for the site-specific distribution), this ratio is proportional to the likelihood ratio
between the posterior probability of it belonging to the positive selection category and that of it belonging to a different category (LHS); in this example, the latter is dominated by the probability of the site belonging to the neutral category (RHS). For any given gene-specific distribution (acting as a prior for the site-specific distribution), this ratio is proportional to the likelihood ratio 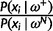 , i.e., the ratio between the likelihoods evaluated at
, i.e., the ratio between the likelihoods evaluated at 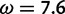 and at
and at  : this represents the contribution from the data at the site in question. The true peak of the likelihoods for most sites of interest is between these values, declining to either side. For some sites, the likelihood at
: this represents the contribution from the data at the site in question. The true peak of the likelihoods for most sites of interest is between these values, declining to either side. For some sites, the likelihood at  is higher than at
is higher than at 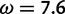 , and vice versa for other sites. See figure 3 (top) for a visual depiction.
, and vice versa for other sites. See figure 3 (top) for a visual depiction.
Fig. 3.

Site-specific inference under misspecified models. (Top) 100 log-likelihood curves as functions of  for a set of simulated sites (see text for description). Vertical lines indicate the value
for a set of simulated sites (see text for description). Vertical lines indicate the value 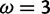 under which the sites were simulated, along with the values for the neutral and positive selection site categories (
under which the sites were simulated, along with the values for the neutral and positive selection site categories (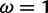 and
and 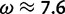 , respectively) used by the M2a model in PAML. The value of the positive selection site category does not match that under which the sites were simulated, due to the presence of other sites under stronger positive selection. The only evidence considered by M2a when classifying a site into the neutral or positive selection category is the value of the likelihood function at
, respectively) used by the M2a model in PAML. The value of the positive selection site category does not match that under which the sites were simulated, due to the presence of other sites under stronger positive selection. The only evidence considered by M2a when classifying a site into the neutral or positive selection category is the value of the likelihood function at 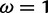 and the value at
and the value at 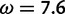 . With the peaks of the likelihood functions between these options, the model becomes overconfident, assigning strong evidence either for positive selection (exemplified by the blue curve) or against it (exemplified by the red curve), even when this conclusion is incorrect. (Bottom) Histograms of posterior site-specific probabilities of positive selection calculated for sites simulated under a true
. With the peaks of the likelihood functions between these options, the model becomes overconfident, assigning strong evidence either for positive selection (exemplified by the blue curve) or against it (exemplified by the red curve), even when this conclusion is incorrect. (Bottom) Histograms of posterior site-specific probabilities of positive selection calculated for sites simulated under a true 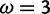 . M2a (left) confidently identifies positive selection in nearly half of these sites, but also incorrectly declares strong evidence against positive selection in half. FUBAR (right) detects most of the sites, and does not claim strong evidence for incorrect conclusions.
. M2a (left) confidently identifies positive selection in nearly half of these sites, but also incorrectly declares strong evidence against positive selection in half. FUBAR (right) detects most of the sites, and does not claim strong evidence for incorrect conclusions.
The effect of this (fig. 3, bottom) is that, among sites simulated with 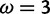 , M2a reports strong evidence in favor of positive selection (posterior probability
, M2a reports strong evidence in favor of positive selection (posterior probability 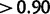 ) for 41% of sites, but strong evidence against selection (posterior probability
) for 41% of sites, but strong evidence against selection (posterior probability  ) for 43% of sites. Instead of resulting in increased uncertainty (which would yield moderate posteriors), the slight model misspecification causes M2a to report incorrect inferences with high confidence. Discussion of what we would hope for should go in Discussion. In contrast, the dense conditional likelihood grid of FUBAR allows it to infer the presence of both
) for 43% of sites. Instead of resulting in increased uncertainty (which would yield moderate posteriors), the slight model misspecification causes M2a to report incorrect inferences with high confidence. Discussion of what we would hope for should go in Discussion. In contrast, the dense conditional likelihood grid of FUBAR allows it to infer the presence of both  categories in the data and to base its site-specific inference on likelihoods evaluated much closer to the peak near
categories in the data and to base its site-specific inference on likelihoods evaluated much closer to the peak near 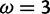 . Of sites simulated with
. Of sites simulated with  , 82% were detected with posteriors
, 82% were detected with posteriors 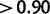 , 0.4%—with posteriors
, 0.4%—with posteriors 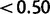 , and none with posteriors
, and none with posteriors  . The mean posterior probability of
. The mean posterior probability of 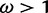 across sites simulated with
across sites simulated with 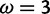 was 0.94 for FUBAR versus 0.49 for M2a.
was 0.94 for FUBAR versus 0.49 for M2a.
A Large Empirical Example—Influenza A Virus Hemagglutinin
To demonstrate the use of FUBAR, we analyzed a collection of global human influenza A virus (IAV) hemagglutinin subtype 3 (H3) sequences from the NCBI Influenza Virus Database (http://www.ncbi.nlm.nih.gov/genomes/FLU/, last accessed July 2012). The influenza hemagglutinin glycoprotein (HA) mediates the entry of the virus into cells and is the target of neutralizing antibodies.
We reconstructed the phylogeny (fig. 4) for 3,142 complete H3 nucleotide sequences isolated from Humans using FastTree 2 (Price et al. 2010). The FUBAR selection analysis (which we restricted to 10 CPUs, just as for the timing comparisons) took one and a half hours. Figure 4 shows the distribution of  across HA, with the mode at mild purifying selection
across HA, with the mode at mild purifying selection 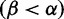 , and with a minority of sites under positive selection
, and with a minority of sites under positive selection 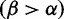 . We use
. We use 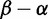 rather than the posterior
rather than the posterior 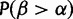 because, with so many sequences, the posteriors can confidently report positive selection even when it is very weak, and so we examine the estimated magnitude of positive selection instead. As a measure of the magnitude of selection,
because, with so many sequences, the posteriors can confidently report positive selection even when it is very weak, and so we examine the estimated magnitude of positive selection instead. As a measure of the magnitude of selection,  is very skewed (due to unreliability in estimates of this ratio when α is small), but
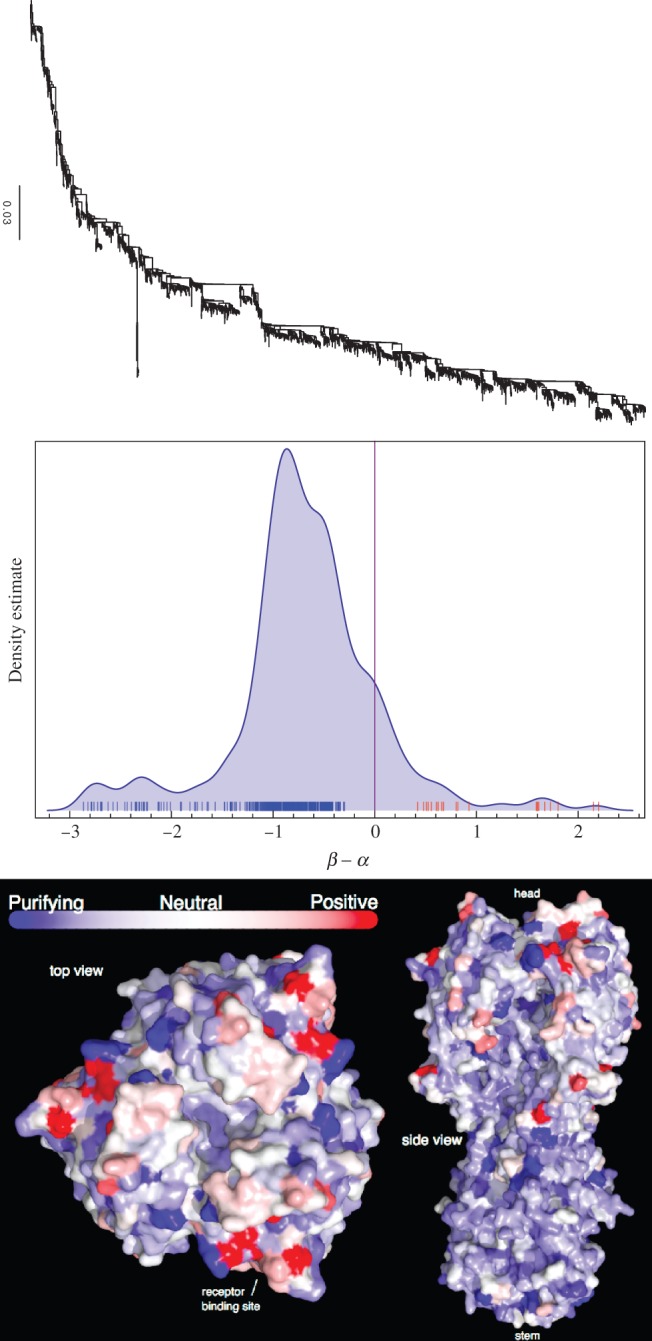
is very skewed (due to unreliability in estimates of this ratio when α is small), but 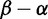 , with neutrality at 0, is more amenable to visualization. All sites described below are codon sites, given in H3 numbering (Winter et al. 1981), as opposed to the antigenic regions of the protein commonly referred to as “sites” in the influenza literature (but which we will refer to as “regions” here).
, with neutrality at 0, is more amenable to visualization. All sites described below are codon sites, given in H3 numbering (Winter et al. 1981), as opposed to the antigenic regions of the protein commonly referred to as “sites” in the influenza literature (but which we will refer to as “regions” here).
Fig. 4.
Influenza hemagglutinin analysis. (Top) The H3 phylogeny with 3,142 coding sequences. (Middle) The smoothed histogram of  across H3, with the greatest density at mild purifying selection
across H3, with the greatest density at mild purifying selection  , and fewer sites under positive selection
, and fewer sites under positive selection  . The notches depict sites with posteriors greater than 0.9 for positive (red) or purifying (blue) selection. (Bottom) The inferred
. The notches depict sites with posteriors greater than 0.9 for positive (red) or purifying (blue) selection. (Bottom) The inferred  values mapped to the HA protein (PDB 3ZTJ; Corti et al. 2011), displayed from two viewpoints. Red regions with stronger diversifying selection are likely involved in immune escape. These primarily occur on the “head” of the protein, with mostly purifying selection on the membrane proximal stem. See text for further detail.
values mapped to the HA protein (PDB 3ZTJ; Corti et al. 2011), displayed from two viewpoints. Red regions with stronger diversifying selection are likely involved in immune escape. These primarily occur on the “head” of the protein, with mostly purifying selection on the membrane proximal stem. See text for further detail.
Codon sites under positive selection are almost exclusively localized to the globular head. Using  as a working definition of strong positive selection, 11 codons were identified. Of these, seven sites (138, 145, 157, 194, 225, 226, and 229) are clustered in and around the receptor-binding site and fall broadly within three of the classical, major antigenic regions (regions A, B, and D; Wiley et al. 1981; Caton et al. 1982). Interestingly, site 226 projects into the receptor-binding pocket, and amino acid substitutions at this position can alter the receptor specificity (
as a working definition of strong positive selection, 11 codons were identified. Of these, seven sites (138, 145, 157, 194, 225, 226, and 229) are clustered in and around the receptor-binding site and fall broadly within three of the classical, major antigenic regions (regions A, B, and D; Wiley et al. 1981; Caton et al. 1982). Interestingly, site 226 projects into the receptor-binding pocket, and amino acid substitutions at this position can alter the receptor specificity ( vs.
vs. 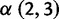 ) and consequently tissue tropism (Rogers et al. 1983). Sites 50 and 53 fall within region C (with site 45 located in close proximity). The remaining site under strong positive selection (site 3), does not lie within a previously defined antigenic region, and is likely located near the base of the membrane-proximal stem. The location of positively selected sites predominantly within the receptor binding site and antigenic regions is consistent with previous observations (Bush et al. 1999; Shih et al. 2007), and likely reflects selection for receptor binding avidity (Hensley et al. 2009) and immune escape.
) and consequently tissue tropism (Rogers et al. 1983). Sites 50 and 53 fall within region C (with site 45 located in close proximity). The remaining site under strong positive selection (site 3), does not lie within a previously defined antigenic region, and is likely located near the base of the membrane-proximal stem. The location of positively selected sites predominantly within the receptor binding site and antigenic regions is consistent with previous observations (Bush et al. 1999; Shih et al. 2007), and likely reflects selection for receptor binding avidity (Hensley et al. 2009) and immune escape.
The majority of sites under strong purifying selection are located within the stem. Antibodies to the HA stem are less common, but have nevertheless been shown to be able to mediate neutralization by inhibiting viral fusion with the host cell (Okuno et al. 1993; Varecková et al. 2003). This is consistent with the identification of broadly crossreactive antibodies that target this region (Ekiert et al. 2009; Sui et al. 2009; Wang et al. 2010; Corti et al. 2011), and reinforces the hemagglutinin stem as an attractive target for influenza vaccines.
Interestingly, HA2 site 172 is under extremely strong purifying selection (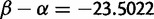 ), although its function is not clear.
), although its function is not clear.
Of the sites under strong purifying selection in the globular head, sites 165, 187, 218, and 222 are clustered together in the quaternary structure at the protomer interface of the globular head, potentially representing a more accessible target for cross-neutralizing antibodies. Although site 165 represents an N-linked glycosylation site, which could potentially shield this region from antibody binding, it is also conceivable that the glycan may contribute to epitope formation. Several potent and broadly crossneutralizing HIV antibodies (PG9/PG16-like and PGT128-like antibodies) are dependent on both a peptide and a glycan component for binding (McLellan et al. 2011; Pejchal et al. 2011), providing a precedent for this mode of recognition.
Discussion and Conclusion
It is strikingly evident from figure 2 how slowly the computation time required by FUBAR increases with data set size. This means that it is particularly useful for analyzing very large data sets, for which selection analysis is simply not feasible using traditional methods. This is illustrated by our IAV example, which is, to our knowledge, the largest alignment analyzed for evidence of positive selection using phylogenetic codon-substitution models. However, FUBAR even offers a speed advantage on small data sets, along with its superior statistical performance in cases of model misspecification. Successful applications of the FUBAR implementation on Datamonkey that have already been published include a study of positive selection in the sugarcane mosaic virus (Li et al. 2013), porcine parvoviruses (Cadar et al. 2013), and hepatitis E virus (Smith et al. 2012).
Phylogenetic models of evolution have long employed computational shortcuts to speed up likelihood optimization, some of which we have adopted here. One widespread example involves the equilibrium frequencies: an estimate of the equilibrium frequency parameters, 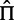 , is often counted directly off the sequence data, invoking a stationarity assumption to reduce the number of parameters that need to be optimized (Kosakovsky Pond et al. 2010). This works because inference under the model appears not to be very sensitive to the typical magnitude of the deviations of these estimators from those derived using maximum likelihood (Kosakovsky Pond et al. 2010). Another example is that estimates of the nucleotide substitution rates,
, is often counted directly off the sequence data, invoking a stationarity assumption to reduce the number of parameters that need to be optimized (Kosakovsky Pond et al. 2010). This works because inference under the model appears not to be very sensitive to the typical magnitude of the deviations of these estimators from those derived using maximum likelihood (Kosakovsky Pond et al. 2010). Another example is that estimates of the nucleotide substitution rates, 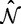 , may be calculated using a simpler model—such as a codon model that does not allow site-to-site variability in selection intensity—and then fixed for the optimization of the more complicated model (Kosakovsky Pond and Frost 2005). This works for the same reason as the shortcut estimate
, may be calculated using a simpler model—such as a codon model that does not allow site-to-site variability in selection intensity—and then fixed for the optimization of the more complicated model (Kosakovsky Pond and Frost 2005). This works for the same reason as the shortcut estimate  : inference is not usually affected. However, the justification for these shortcuts is merely empirical and their admissibility should be investigated further—comparing inference under the shortcuts to the full Bayesian solution—and situations where they mislead inference (if any) should be characterized.
: inference is not usually affected. However, the justification for these shortcuts is merely empirical and their admissibility should be investigated further—comparing inference under the shortcuts to the full Bayesian solution—and situations where they mislead inference (if any) should be characterized.
Other work has used a variety of computational and statistical shortcuts to improve the computational efficiency of inference under phylogenetic models of evolution. Quang et al. (2008) pre-estimate a number of amino acid profiles from a large database, and then an analysis on a new alignment of interest proceeds by inferring weights for each profile. However, the goal of this method is to estimate the phylogeny, which requires recomputing the conditional likelihoods whenever the branch lengths or tree are modified during maximization, so the approach cannot exploit the likelihood recycling to the same degree as FUBAR. Fast phylogeny inference methods (e.g., FastTree—Price et al. 2010) employ fixed discretizations to handle site to site rate variation. Rather than computing the conditional likelihoods only once, which is prevented because they optimize over the phylogeny, they hard-assign each site to 1 of 20 rate classes, and only compute the likelihoods for those sites at those rate classes. This hard-assignment reduces the likelihood calculation to an approximation, but one that does not appear to have a negative impact on phylogeny inference.
Another common shortcut used here is to estimate the relative branch lengths under a simple model and fix them, although the overall tree length is still allowed to vary. This is adopted in the fixed effects models of Kosakovsky Pond and Frost (2005) and in the Bayes empirical Bayes (BEB) approach of Yang et al. (2005). The BEB approach acknowledges that uncertainty about parameter values exists, but distinguishes between parameters for which these uncertainties matter (and where it is integrated out using a Bayesian approach) and parameters—such as relative branch lengths, nucleotide substitution rates, and equilibrium frequencies—for which it is sufficient to use the MLEs, ignoring the uncertainties in these point estimates. This approximation has been shown not to affect BEB inference on typical data sets (Scheffler and Seoighe 2005).
Inferring a gene-specific distribution of selection parameters allows information to be pooled across many sites, potentially resulting in improved power to detect selection at individual sites. Indeed, when we performed a FEL analysis (which does not do any information pooling) of the simulated data of the “Robustness to Model Misspecification” section, we detected only 31% of the sites simulated with  at the
at the 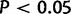 level, with a false-positive rate of 1.4% on the neutral and purifying sites, compared with 0.5% false-positives for FUBAR. The improved power of REL methods (including FUBAR) is not surprising in a simulation study where the data were generated using a gene-specific distribution of exactly the type assumed by these methods, but it seems reasonable to expect that information pooling should also be beneficial when analyzing biological data, provided the distributional assumptions used to do this do not cause problems due to model misspecification. Here, we have demonstrated a scenario in which traditional REL models suffer from exactly this problem: when the strength of selection is sufficiently heterogeneous across different sites in the same selective “category,” inference can be severely misleading. This happens because the gene-specific distributions used by traditional REL models have highly restrictive parametric forms, using only a small number of parameters and discrete components that may not always match biological reality. FUBAR avoids this problem by using a highly flexible and therefore far less restrictive distributional form that is more robust against model misspecification.
level, with a false-positive rate of 1.4% on the neutral and purifying sites, compared with 0.5% false-positives for FUBAR. The improved power of REL methods (including FUBAR) is not surprising in a simulation study where the data were generated using a gene-specific distribution of exactly the type assumed by these methods, but it seems reasonable to expect that information pooling should also be beneficial when analyzing biological data, provided the distributional assumptions used to do this do not cause problems due to model misspecification. Here, we have demonstrated a scenario in which traditional REL models suffer from exactly this problem: when the strength of selection is sufficiently heterogeneous across different sites in the same selective “category,” inference can be severely misleading. This happens because the gene-specific distributions used by traditional REL models have highly restrictive parametric forms, using only a small number of parameters and discrete components that may not always match biological reality. FUBAR avoids this problem by using a highly flexible and therefore far less restrictive distributional form that is more robust against model misspecification.
Historically, models of evolution have been hampered by a large number of biologically unrealistic constraints, often necessitated by computational and/or statistical considerations. Examples include neglecting synonymous rate variation, confining sites to a small number of rate classes, assuming that different nucleotide and/or amino acid pairs have equal exchangeabilities, and assuming independence between different sites. Some of these constraints have already been lifted, while others are still in place. Bayesian approaches such as the one presented here offer a solution to the statistical problem of overparameterization in maximum likelihood methods; in conjunction with more efficient computational approaches this opens the door to using more biologically realistic models with larger numbers of parameters and hence fewer restrictions. In particular, our grid-based methodology has broad application potential: for instance, random effects approaches are used by DEPS (Kosakovsky Pond et al. 2008), EDEPS and MEDS (Murrell, de Oliveira, et al. 2012) to model directional selection—where the substitution rate toward a specific amino acid is elevated at a specific site—and by Branch-site REL (Kosakovsky Pond et al. 2011) and MEME (Murrell, Wertheim, et al. 2012) to model selection that varies across lineages. Grid-based variants of these methods could be constructed, allowing a large number of nonneutral categories, which should improve the statistical performance of these methods.
Acknowledgments
This work was supported in part by the National Institutes of Health grants AI47745, AI57167, AI74621, and GM093939, the UC Laboratory Fees Research Program grant 12-LR-236617, the National Research Foundation of South Africa, the University of Cape Town's University Research Council, and Europeaid grant SANTE/2007/147-790 from the European Commission.
References
- Anisimova M, Kosiol C. Investigating protein-coding sequence evolution with probabilistic codon substitution models. Mol Biol Evol. 2009;26:255–271. doi: 10.1093/molbev/msn232. [DOI] [PubMed] [Google Scholar]
- Bush RM, Fitch WM, Bender CA, Cox NJ. Positive selection on the H3 hemagglutinin gene of human influenza virus A. Mol Biol Evol. 1999;16:1457–1465. doi: 10.1093/oxfordjournals.molbev.a026057. [DOI] [PubMed] [Google Scholar]
- Cadar D, Cságola A, Kiss T, Tuboly T. Capsid protein evolution and comparative phylogeny of novel porcine parvoviruses. Mol Phylogenet Evol. 2013;66:243–253. doi: 10.1016/j.ympev.2012.09.030. [DOI] [PubMed] [Google Scholar]
- Caton AJ, Brownlee GG, Yewdell JW, Gerhard W. The antigenic structure of the influenza virus A/PR/8/34 hemagglutinin (H1 subtype) Cell. 1982;31:417–427. doi: 10.1016/0092-8674(82)90135-0. [DOI] [PubMed] [Google Scholar]
- Corti D, Voss J, Gamblin SJ, et al. (23 co-authors) A neutralizing antibody selected from plasma cells that binds to group 1 and group 2 influenza A hemagglutinins. Science. 2011;333:850–856. doi: 10.1126/science.1205669. [DOI] [PubMed] [Google Scholar]
- de Koning APJ, Gu W, Castoe TA, Pollock DD. Phylogenetics, likelihood, evolution and complexity (PLEX) Bioinformatics. 2012;28:2989–2990. doi: 10.1093/bioinformatics/bts555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delport W, Scheffler K, Seoighe C. Models of coding sequence evolution. Brief Bioinform. 2009;10:97–109. doi: 10.1093/bib/bbn049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ekiert DC, Bhabha G, Elsliger MA, Friesen RHE, Jongeneelen M, Throsby M, Goudsmit J, Wilson IA. Antibody recognition of a highly conserved influenza virus epitope. Science. 2009;324:246–251. doi: 10.1126/science.1171491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. Evolutionary trees from DNA-sequences—a maximum-likelihood approach. J Mol Evol. 1981;17:368–376. doi: 10.1007/BF01734359. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. Taking variation of evolutionary rates between sites into account in inferring phylogenies. J Mol Evol. 2001;53:447–455. doi: 10.1007/s002390010234. [DOI] [PubMed] [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Rubin DB. 2nd ed. Boca Raton: Chapman & Hall/CRC; 2003. Bayesian data analysis (Texts in Statistical Science) [Google Scholar]
- Hensley SE, Das SR, Bailey AL, et al. (11 co-authors) Hemagglutinin receptor binding avidity drives influenza A virus antigenic drift. Science. 2009;326:734–736. doi: 10.1126/science.1178258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huelsenbeck JP, Jain S, Frost SW, Pond SKL. A Dirichlet process model for detecting positive selection in protein-coding DNA sequences. Proc Natl Acad Sci U S A. 2006;103:6263–6268. doi: 10.1073/pnas.0508279103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kosakovsky Pond S, Delport W, Muse SV, Scheffler K. Correcting the bias of empirical frequency parameter estimators in codon models. PLoS One. 2010;30:e11230. doi: 10.1371/journal.pone.0011230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kosakovsky Pond SL, Frost SDW. Not so different after all: a comparison of methods for detecting amino acid sites under selection. Mol Biol Evol. 2005;22:1208–1222. doi: 10.1093/molbev/msi105. [DOI] [PubMed] [Google Scholar]
- Kosakovsky Pond SL, Frost SDW, Muse SV. Hyphy: hypothesis testing using phylogenies. Bioinformatics. 2005;21:676–679. doi: 10.1093/bioinformatics/bti079. [DOI] [PubMed] [Google Scholar]
- Kosakovsky Pond SL, Murrell B, Fourment M, Frost SDW, Delport W, Scheffler K. A random effects branch-site model for detecting episodic diversifying selection. Mol Biol Evol. 2011;28:3033–3043. doi: 10.1093/molbev/msr125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kosakovsky Pond SL, Muse SV. Site-to-site variation of synonymous substitution rates. Mol Biol Evol. 2005;22:2375–2385. doi: 10.1093/molbev/msi232. [DOI] [PubMed] [Google Scholar]
- Kosakovsky Pond SL, Poon AFY, Leigh Brown AJ, Frost SDW. A maximum likelihood method for detecting directional evolution in protein sequences and its application to influenza a virus. Mol Biol Evol. 2008;25:1809–1824. doi: 10.1093/molbev/msn123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lartillot N. Conjugate Gibbs sampling for Bayesian phylogenetic models. J Comput Biol. 2006;13:1701–1722. doi: 10.1089/cmb.2006.13.1701. [DOI] [PubMed] [Google Scholar]
- Li Y, Liu R, Zhou T, Fan Z. Genetic diversity and population structure of sugarcane mosaic virus. Virus Res. 2013;17:242–246. doi: 10.1016/j.virusres.2012.10.024. [DOI] [PubMed] [Google Scholar]
- Massingham T, Goldman N. Detecting amino acid sites under positive selection and purifying selection. Genetics. 2005;169:1753–1762. doi: 10.1534/genetics.104.032144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLellan JS, Pancera M, Carrico C, et al. (47 co-authors) Structure of HIV-1 gp120 V1/V2 domain with broadly neutralizing antibody PG9. Nature. 2011;480:336–343. doi: 10.1038/nature10696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murrell B, de Oliveira T, Seebregts C, Kosakovsky Pond SL, Scheffler K, on behalf of the Southern African Treatment and R. N. S. Consortium Modeling HIV-1 drug resistance as episodic directional selection. PLoS Comput Biol. 2012;8:e1002507. doi: 10.1371/journal.pcbi.1002507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murrell B, Wertheim JO, Moola S, Weighill T, Scheffler K, Kosakovsky Pond SL. Detecting individual sites subject to episodic diversifying selection. PLoS Genet. 2012;8:e1002764. doi: 10.1371/journal.pgen.1002764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muse SV, Gaut BS. A likelihood approach for comparing synonymous and nonsynonymous nucleotide substitution rates, with application to the chloroplast genome. Mol Biol Evol. 1994;11:715–724. doi: 10.1093/oxfordjournals.molbev.a040152. [DOI] [PubMed] [Google Scholar]
- Nielsen R, Yang Z. Likelihood models for detecting positively selected amino acid sites and applications to the HIV-1 envelope gene. Genetics. 1998;148:929–936. doi: 10.1093/genetics/148.3.929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okuno Y, Isegawa Y, Sasao F, Ueda S. A common neutralizing epitope conserved between the hemagglutinins of influenza A virus H1 and H2 strains. J Virol. 1993;67:2552–2558. doi: 10.1128/jvi.67.5.2552-2558.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pejchal R, Doores KJ, Walker LM, et al. (31 co-authors) A potent and broad neutralizing antibody recognizes and penetrates the HIV glycan shield. Science. 2011;334:1097–1103. doi: 10.1126/science.1213256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price MN, Dehal PS, Arkin AP. FastTree 2—approximately maximum-likelihood trees for large alignments. PLoS One. 2010;5:e9490. doi: 10.1371/journal.pone.0009490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quang LS, Gascuel O, Lartillot N. Empirical profile mixture models for phylogenetic reconstruction. Bioinformatics. 2008;24:2317–2323. doi: 10.1093/bioinformatics/btn445. [DOI] [PubMed] [Google Scholar]
- Rodrigue N, Philippe H, Lartillot N. Uniformization for sampling realizations of Markov processes: applications to Bayesian implementations of codon substitution models. Bioinformatics. 2008;24:56–62. doi: 10.1093/bioinformatics/btm532. [DOI] [PubMed] [Google Scholar]
- Rogers GN, Paulson JC, Daniels RS, Skehel JJ, Wilson IA, Wiley DC. Single amino acid substitutions in influenza haemagglutinin change receptor binding specificity. Nature. 1983;304:76–78. doi: 10.1038/304076a0. [DOI] [PubMed] [Google Scholar]
- Scheffler K, Seoighe C. A Bayesian model comparison approach to inferring positive selection. Mol Biol Evol. 2005;22:2531–2540. doi: 10.1093/molbev/msi250. [DOI] [PubMed] [Google Scholar]
- Shih AC, Hsiao TC, Ho MS, Li WH. Simultaneous amino acid substitutions at antigenic sites drive influenza A hemagglutinin evolution. Proc Natl Acad Sci. 2007;104:6283–6288. doi: 10.1073/pnas.0701396104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith DB, Vanek J, Ramalingam S, Johannessen I, Templeton K, Simmonds P. Evolution of the hepatitis E virus hypervariable region. J Gen Virol. 2012;93:2408–2418. doi: 10.1099/vir.0.045351-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sui J, Hwang WC, Perez S, et al. (14 co-authors) Structural and functional bases for broad-spectrum neutralization of avian and human influenza A viruses. Nat Struct Mol Biol. 2009;16:265–273. doi: 10.1038/nsmb.1566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tavaré S. Some probabilistic and statistical problems in the analysis of DNA sequences. Lectures on mathematics in the life sciences. In: Miura RM, editor. Vol. 17. Providence (RI): American Mathematical Society; 1986. pp. 57–86. [Google Scholar]
- Varecková E, Mucha V, Wharton SA, Kostolanský F. Inhibition of fusion activity of influenza A haemagglutinin mediated by HA2-specific monoclonal antibodies. Arch Virol. 2003;148:469–486. doi: 10.1007/s00705-002-0932-1. [DOI] [PubMed] [Google Scholar]
- Wang TT, Tan GS, Hai R, Pica N, Petersen E, Moran TM, Palese P. Broadly protective monoclonal antibodies against H3 influenza viruses following sequential immunization with different hemagglutinins. PLoS Pathog. 2010;6:e1000796. doi: 10.1371/journal.ppat.1000796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiley DC, Wilson IA, Skehel JJ. Structural identification of the antibody-binding sites of Hong Kong influenza haemagglutinin and their involvement in antigenic variation. Nature. 1981;289:373–378. doi: 10.1038/289373a0. [DOI] [PubMed] [Google Scholar]
- Winter G, Fields S, Brownlee GG. Nucleotide sequence of the haemagglutinin gene of a human influenza virus H1 subtype. Nature. 1981;292:72–75. doi: 10.1038/292072a0. [DOI] [PubMed] [Google Scholar]
- Wong WSW, Yang Z, Goldman N, Nielsen R. Accuracy and power of statistical methods for detecting adaptive evolution in protein coding sequences and for identifying positively selected sites. Genetics. 2004;168:1041–1051. doi: 10.1534/genetics.104.031153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z. Maximum likelihood estimation on large phylogenies and analysis of adaptive evolution in human influenza virus A. J Mol Evol. 2000;51:423–432. doi: 10.1007/s002390010105. [DOI] [PubMed] [Google Scholar]
- Yang Z, Wong WSW, Nielsen R. Bayes empirical Bayes inference of amino acid sites under positive selection. Mol Biol Evol. 2005;22:1107–1118. doi: 10.1093/molbev/msi097. [DOI] [PubMed] [Google Scholar]



