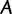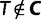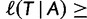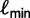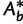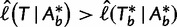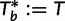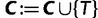Skip to main content
PMC home page
Molecular Biology and Evolution logoLink to Molecular Biology and Evolution
. 2013 Feb 15;30(5):1188–1195. doi: 10.1093/molbev/mst024

Ultrafast Approximation for Phylogenetic Bootstrap

Bui Quang Minh 1,*, Minh Anh Thi Nguyen 2, Arndt von Haeseler 1,*
PMCID: PMC3670741  PMID: 23418397

Abstract

Nonparametric bootstrap has been a widely used tool in phylogenetic analysis to assess the clade support of phylogenetic trees. However, with the rapidly growing amount of data, this task remains a computational bottleneck. Recently, approximation methods such as the RAxML rapid bootstrap (RBS) and the Shimodaira–Hasegawa-like approximate likelihood ratio test have been introduced to speed up the bootstrap. Here, we suggest an ultrafast bootstrap approximation approach (UFBoot) to compute the support of phylogenetic groups in maximum likelihood (ML) based trees. To achieve this, we combine the resampling estimated log-likelihood method with a simple but effective collection scheme of candidate trees. We also propose a stopping rule that assesses the convergence of branch support values to automatically determine when to stop collecting candidate trees. UFBoot achieves a median speed up of 3.1 (range: 0.66–33.3) to 10.2 (range: 1.32–41.4) compared with RAxML RBS for real DNA and amino acid alignments, respectively. Moreover, our extensive simulations show that UFBoot is robust against moderate model violations and the support values obtained appear to be relatively unbiased compared with the conservative standard bootstrap. This provides a more direct interpretation of the bootstrap support. We offer an efficient and easy-to-use software (available at http://www.cibiv.at/software/iqtree) to perform the UFBoot analysis with ML tree inference.

Keywords: phylogenetic inference, nonparametric bootstrap, tree reconstruction, maximum likelihood

Introduction

Since the groundbreaking work of Felsenstein (1985), nonparametric bootstrapping (Efron 1979) has become one of the widely used tools to estimate the phylogenetic support of certain clades or splits in an inferred phylogenetic tree. Here, the sequence alignment sites are sampled with replacement resulting in a number of pseudoreplicates. For every replicate, one applies a method of interest such as maximum likelihood (ML; Felsenstein 1981) to reconstruct a bootstrap tree. One then either constructs a consensus tree from the bootstrap trees or places the support values onto the reconstructed ML tree.

Because of the enormous computation time required for the standard bootstrap (SBS) with ML, several approaches have been published to approximate SBS. Resampling estimated log-likelihoods (RELL; Kishino et al. 1990; Hasegawa and Kishino 1994) was the first attempt to avoid a full ML inference per bootstrap replicate; it reuses the log-likelihood scores calculated for individual sites in the original alignment, given the tree. RELL was used to infer local bootstrap probabilities (LBP; Adachi and Hasegawa 1996) of every internal branch of the ML tree by comparing the three nearest neighbor interchange (NNI) tree topologies around the branch of interest. The approximate likelihood-ratio test (aLRT; Anisimova and Gascuel 2006) and its nonparametric variant (SH-aLRT; Guindon et al. 2010) differ slightly from the method used to calculate LBP by employing the SH test (Shimodaira and Hasegawa 1999) on these three NNI trees. Although RELL and SH-aLRT are very fast, it is currently unclear how they perform if the four subtrees incident to that branch are not fixed. The RAxML rapid bootstrap (RBS; Stamatakis 2006; Stamatakis et al. 2008) is a recent method to resemble SBS while performing 8–20 times faster on large data sets.

It has been shown that the SBS probabilities typically underestimate the true probabilities of a clade to be correct (Felsenstein and Kishino 1993; Hillis and Bull 1993). SBS is therefore biased but conservative. Efron et al. (1996) proposed a method to correct for this bias which, however, requires considerably more computation. Other methods include quartet puzzling (Strimmer and von Haeseler 1996; Schmidt et al. 2002) and Bayesian Markov chain Monte Carlo (MCMC) analysis (Yang and Rannala 1997; Huelsenbeck and Ronquist 2001). Bayesian MCMC methods, however, tend to overestimate the true probabilities in case of model misspecification or polytomies (Suzuki et al. 2002; Douady et al. 2003; Lewis et al. 2005; Anisimova et al. 2011). Both quartet puzzling and Bayesian MCMC methods are very time consuming for large data sets.

New Approaches

Here, we present an ultrafast bootstrap approach (UFBoot) as an alternative to the other nonparametric bootstrap approaches. To this end, we utilize the RELL concept with an efficient way of sampling plausible trees using the important quartet puzzling (IQP) with NNI (IQPNNI) algorithm (Vinh and von Haeseler 2004; Minh et al. 2005). In short, IQPNNI samples the local maxima and their neighborhoods in the tree space defined by the NNI operations. 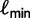Because the number of trees encountered during the IQPNNI search might be excessively large, we adaptively estimate a log-likelihood threshold Inline graphic such that we only investigate the trees with the RELL bootstrapping if their log-likelihoods are higher than Inline graphic. Taken together, UFBoot first generates a number of bootstrap alignments (typically 1,000) and initializes the corresponding bootstrap trees as null. UFBoot then performs the IQPNNI tree sampling on the original alignment. Whenever a new tree 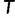Inline graphic whose log-likelihood exceeds 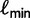Inline graphic is found, UFBoot quickly computes the RELL score of 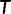Inline graphic for each bootstrap alignment. If 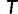Inline graphic has a higher RELL score than that of the current bootstrap tree, UFBoot updates the current bootstrap tree as 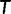Inline graphic for the corresponding bootstrap alignment. That way, UFBoot gradually rectifies the set of bootstrap trees. UFBoot stops collecting candidate trees when the correlation coefficient 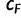Inline graphic of the split occurrence frequencies computed from the first half of the analysis and from the full analysis is larger than 0.99 (more details in Materials and Methods). Finally, UFBoot computes a consensus tree from the set of bootstrap trees and also maps the split support values onto the ML tree reconstructed during the IQPNNI sampling.

We provide an implementation of the whole framework in the IQ-TREE package (Nguyen L-T, Minh BQ, Schmidt HA, von Haeseler A, in preparation). In the following, we compare the performance of UFBoot against other bootstrap approaches in terms of accuracy (Hillis and Bull 1993) and computational time.

Results

Accuracy

We used simulated data (table 1; Materials and Methods) to compare four different methods (SBS with RAxML, RBS with RAxML, SH-aLRT with PhyML, and UFBoot) with respect to their accuracy defined in Hillis and Bull (1993). To this end, we plot the number of true splits (i.e., splits that occur in the true trees) having support of 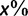Inline graphic divided by the number of all splits with support of 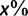Inline graphic (eq. 2; fig. 1). This ratio gives the estimated probability of a split to be true. Curves above the dashed diagonal line indicate that the inferred support values underestimate this probability, and thus the corresponding method exhibits a conservative behavior. In contrast, curves below the diagonal indicate that the method overestimates the true probabilities. Methods that generate curves around the diagonal are almost unbiased.

Table 1.

Simulation Settings.

True Tree Data Type No. Sequences No. Sites No. Alignments
Yule–Harding DNA 100 500 200
200 1,000 200
500 1,000 200
Protein 100 300 200
200 500 200
PANDIT DNA 4–403 24–6,891 6,222
Protein 4–545 12–2,297 6,182
Open in a new tab

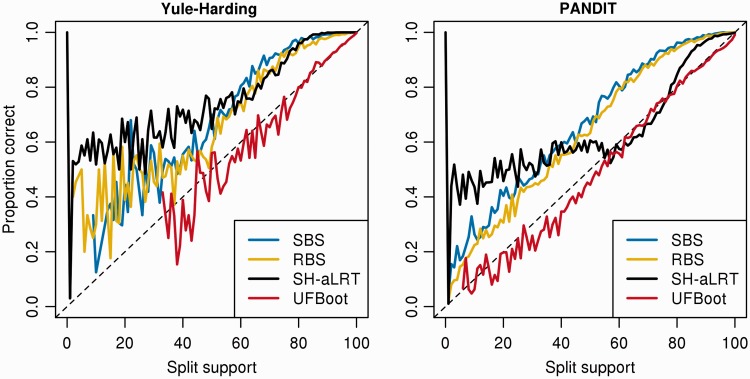
Fig. 1.

Fig. 1.

Open in a new tab

Accuracies of SBS, RBS with RAxML, SH-aLRT with PhyML, and UFBoot approximation from the Yule–Harding (left panel) and the PANDIT-based simulations (right panel).

Figure 1 summarizes the results for the Yule–Harding and PANDIT-based simulations (see Materials and Methods for more details). Note that the curves look similar for the seven simulation settings (table 1) and are thus not shown. SBS (blue curves) is the most conservative approach by substantially underestimating the probabilities of splits being correct for both Yule–Harding and PANDIT-based simulations. For example, a split with SBS support of 80% has indeed a probability of 0.95 to be correct. This biased but conservative behavior of SBS corroborates previous studies (Hillis and Bull 1993; Anisimova et al. 2011), which led to the widely accepted interpretation of “trusting” splits with SBS supports 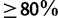Inline graphic. RBS (fig. 1, yellow curves) performs very similarly to SBS but with a tendency of being less conservative.

SH-aLRT (fig. 1, black curves) is generally as conservative as SBS and RBS in the Yule–Harding simulations but becomes apparently less conservative in the PANDIT-based simulations. Moreover, low SH-aLRT split supports (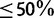Inline graphic) are not informative with respect to the true probabilities. For example, splits with SH-aLRT support of 20% are as correct as those with support of 50%.

UFBoot (fig. 1, red curves) appears to be almost unbiased compared with the other methods for both simulations (i.e., the split support values obtained closely reflect the probabilities of the split being correct). UFBoot is unbiased for support values higher than 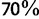Inline graphic. On the other side, UFBoot support values smaller than 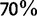Inline graphic slightly overestimate the true probability. Such unbiased behavior simplifies the interpretation of support values reported by UFBoot. For example, a split with support of 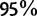Inline graphic will have a probability of 0.95 to be correct.

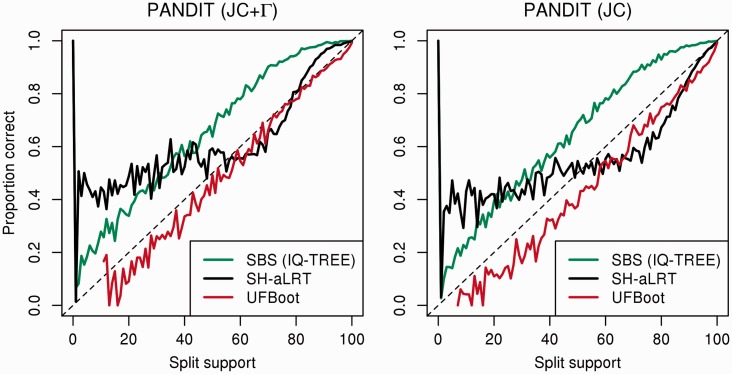
Moreover, we assessed the impact of model misspecification on the accuracies by repeating the analysis on the simulated DNA alignments using the simpler JC + 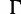Inline graphic model (Jukes and Cantor 1969; Yang 1994) and the simplest JC model (Jukes and Cantor 1969) for phylogenetic inference. Note that we could not repeat the same analysis with RBS and SBS, because RAxML supports only the GTR + 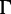Inline graphic model (Lanave et al. 1984; Yang 1994). Alternatively, we performed SBS with 100 replicates using IQ-TREE. Figure 2 shows that model violations have almost no influence on SBS estimates with IQ-TREE (green curves) in PANDIT-based simulations (Yule–Harding data not shown). Similarly, the accuracies of SH-aLRT and UFBoot do not change under moderate model violations (JC + 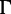Inline graphic). However, the split support values are inflated under severe model violations (JC). This agrees with previous studies showing that accounting for the rate heterogeneity among sites is more important than varying substitution rates (Sullivan and Swofford 2001; Nguyen et al. 2012).

Fig. 2.

Fig. 2.

Open in a new tab

Impact of moderate (JC + 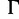Inline graphic) and severe model violations (JC) on the accuracies of SBS, SH-aLRT, and UFBoot in the PANDIT-based simulations.

Computational Time

For more than 96% of the Yule–Harding and PANDIT-based simulations the UFBoot stopping rule (see Materials and Methods) suggested to stop after 100 IQPNNI iterations. The remaining runs finished after at most 800 iterations. Thus, 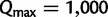Inline graphic is a conservative upper bound for the number of iterations to achieve high accuracy.

A more detailed picture emerges from the real PANDIT data. We compared the computational times of RBS and UFBoot on 308 large (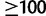Inline graphic sequences) DNA- and AA-PANDIT alignments. For a fair comparison of computing times, we apply the bootstopping criterion (-N autoMRE) (Pattengale et al. 2010) in the RBS search to automatically determine the number of bootstrap replicates required. For eight AA-PANDIT alignments (PF01261, PF00149, PF01546, PF01547, PF01636, PF00496, PF00501, and PF07690) RAxML did not finish after more than 1 week of computation, the runs were then stopped by our computing system. These alignments were excluded from our analysis, leaving us with 300 alignments. The bootstopping criterion of RBS yielded an average of 528 bootstrap replicates. The number of bootstrap replicates varied between 250 and 1,000 (the default upper limit in RAxML), where 5 alignments needed 250 replicates and 1 alignment hit the upper limit.

Our UFBoot stopping rule suggested on average 453 IQPNNI iterations for all alignments. We observed that for 80 (27%) alignments 100 iterations sufficed to obtain stable bootstrap estimates and for 69 (23%) alignments we hit the maximum of 1,000 iterations, indicating that the resulting split supports from these runs did not meet our convergence criterion. Among these 69 alignments 49, 15, and 5 alignments achieved a correlation coefficient 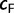Inline graphic of at least 0.95, between 0.9 and 0.95, and less than 0.9, respectively. However, the five alignments with 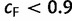Inline graphic comprise very divergent sequences and possibly nonalignable sequences. The percentages of alignment sites with low alignment confidence (Whelan et al. 2006) are ranging between 32% and 52%. Therefore, the nonconvergence in such cases is not surprising.

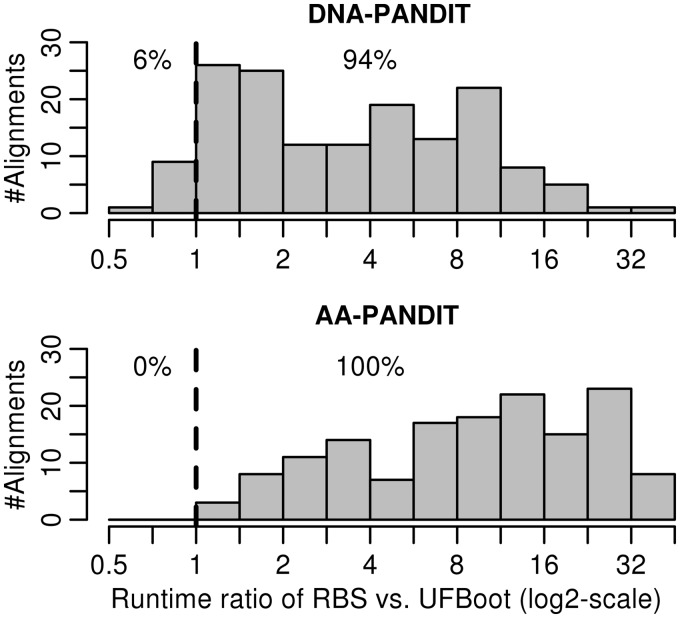
Finally, we computed the distribution of the ratio between the computational times of RBS and UFBoot for the 300 alignments (fig. 3). UFBoot was always faster than RBS except for 10 DNA alignments. The 69 alignments where UFBoot did not converge (discussed earlier) also caused the slowest UFBoot runs. UFBoot runs 3.1 times (median, range: 0.66–33.3) and 10.2 (median, range: 1.32–41.4) times faster than RBS for DNA and AA alignments, respectively. More impressive is the total computing time for the full PANDIT data analysis: UFBoot required 797 CPU core hours (1.1 month) on a computer cluster equipped with 2.2-GHz CPUs, whereas RBS needed 4,293 CPU hours (∼6 months).

Fig. 3.

Fig. 3.

Open in a new tab

Distributions of run-time ratios (log2-scale) between RBS and UFBoot for 300 DNA and AA PANDIT alignments. The percentages of alignments where UFBoot runs slower (left from the dashed line) or faster (right from the dashed line) than RBS are shown.

Discussion

We have suggested a very fast bootstrap approximation, namely UFBoot, and compared the performance with a collection of widely used methods. Although SBS and RBS estimates of clade support are conservative (see also Hillis and Bull 1993; Anisimova et al. 2011), the clade support estimated by UFBoot appears less biased according to our large-scale simulations. This leads to a different and easy-to-understand interpretation of the support values. For example, a support of at least 95% should be used if one wants to control the false-positive rate of 5%. The fact that UFBoot is a hybrid of parametric sampling of the tree space and the nonparametric bootstrap sampling of the alignment may be one explanation for reduction of the bias of the bootstrap probabilities. Parametric methods (aLRT, Bayesian MCMC) are unbiased if the true substitution model is known (Anisimova et al. 2011). UFBoot inherits this property as shown in our simulations. Moreover, UFBoot partly overcomes model misspecifications by applying the nonparametric RELL correction (Anisimova et al. 2011). However, we have to acknowledge that a thorough theoretical explanation for our observation is missing.

The interpretation of support values as unbiased has been used in Bayesian inference. However, Bayesian inference has been known to be sensitive even against mild model violations (Suzuki et al. 2002; Anisimova et al. 2011). In contrast, UFBoot appears robust against moderate model violations during phylogenetic inference (fig. 2). However, caution is advised under severe model violations (i.e., wrongly assumed rate homogeneity among sites) then UFBoot (also SH-aLRT) tends to infer unduly high support values. Here, methods to detect model violations (Goldman 1993; Weiss and von Haeseler 2003; Nguyen et al. 2011) should be applied before the UFBoot analysis (or any other analysis). At present it is not clear, if the number of IQPNNI iterations necessary to achieve bootstrap support convergence may be helpful to detect such artifacts.

Apart from oversimplified substitution models, other types of model violations such as polytomies and heterotachy (i.e., varying substitution rates among different tree branches and alignment sites) (Lopez et al. 2002) are known to cause systematic bias in the ML and Bayesian methods (Kolaczkowski and Thornton 2004; Lewis et al. 2005). For example, polytomies often lead to a tree space with a lot of local optima. This may hamper the underlying IQPNNI algorithm in exploring the tree space (Whelan and Money 2010; Money and Whelan 2012), which might in turn inflate UFBoot support values. It is necessary to investigate these and other factors (e.g., by looking at the support of conflicting splits) to understand further the mechanism of bias correction in UFBoot and under which conditions the correction might fail. Currently, these are still unclear to us. However, a more thorough analysis is beyond the scope of this study. Nevertheless, as our methodology works on any set of input candidate trees, it might be worthwhile to exploit UFBoot with other tree sampling strategies such as the genetic algorithm (Zwickl 2006) or the Bayesian MCMC (Drummond et al. 2012; Ronquist et al. 2012). We provide such an option in our implementation.

SH-aLRT behaves very differently between the Yule–Harding and PANDIT-based simulations (fig. 1), implying that there is no easy rule of thumb how to interpret SH-aLRT support values. This may be due to the fact that SH-aLRT computes the support value for every branch by only comparing the tree log-likelihood with the log-likelihoods of the two alternative NNI trees around the branch of interest (Adachi and Hasegawa 1996). That way, SH-aLRT ignores all other trees that may show higher log-likelihoods than the two NNI trees, which may result in an overconfidence of SH-aLRT support values. Nevertheless, SH-aLRT, being a very quick branch test method, is useful for extremely large data sets. In our implementation, we offer an option to report both SH-aLRT and UFBoot support values per branch so that users can directly compare them.

Our built-in UFBoot stopping rule provides an intuitive statistic 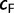Inline graphic, the correlation coefficient of the split support values inferred from the first half of the analysis and from the full analysis. 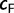Inline graphic values close to 1.0 imply that an extended tree search will not substantially change the resulting support values and we can therefore stop. Similar ideas have been employed in the bootstopping criterion (Pattengale et al. 2010). The fact that the UFBoot stopping rule suggested only 100 iterations for most simulated data are not surprising because the tree space for simulated data typically contains only a few local maxima and is therefore easy to sample. The situation is different for real data where our convergence criterion was not always met. But these cases were also characterized by low phylogenetic information (Money and Whelan 2012). This reinforces the observation that one should assess the phylogenetic signals in the data with, for example, the likelihood mapping (Strimmer and von Haeseler 1997) and saturation plots (Van de Peer et al. 2002; Xia et al. 2003) before carrying out an expensive bootstrap analysis. If the data appear to be appropriate for phylogenetic reconstruction, then UFBoot is a time-saving option compared with the other bootstrap inference tool.

Conclusion

We have presented the UFBoot approximation approach that 1) outperforms the RAxML RBS in terms of the computational time, 2) achieves almost unbiased support values like Bayesian methods, and 3) is relatively robust against moderate model violations. We provide an implementation of UFBoot within the IQ-TREE software package available from http://www.cibiv.at/software/iqtree. IQ-TREE is a substantially improved reimplementation of the IQPNNI algorithm with additional features (Nguyen L-T, Minh BQ, Schmidt HA, von Haeseler A, in preparation). IQ-TREE allows users to reconstruct the ML tree (with support values), the bootstrap trees, and the consensus tree by UFBoot within one single run. Users can also perform UFBoot from a user-defined set of trees sampled by other methods (e.g., genetic algorithm or MCMC sampling).

Materials and Methods

ML Principle

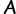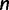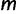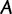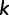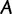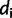Let Inline graphic denote a multiple sequence alignment with Inline graphic sequences and Inline graphic sites (columns), where sites in Inline graphic are grouped into Inline graphic site-patterns Inline graphic of identical sites. 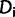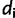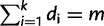Hence, we represent Inline graphic by a vector of site-pattern frequencies Inline graphic, where Inline graphic is the number of sites having site-pattern Inline graphic (Inline graphic > 0 and Inline graphic).

Under the assumption of independence of the sites, the log-likelihood 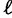Inline graphic of a tree 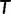Inline graphic (with branch lengths) given 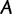Inline graphic is computed by:

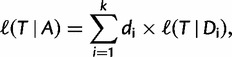graphic file with name mst024um1.jpg

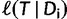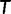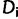where Inline graphic is the log-likelihood of Inline graphic at site-pattern Inline graphic.

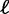Under the ML principle, the objective is to identify the most likely tree Inline graphic. Note that the computation of Inline graphic is implicitly based on a predefined substitution model, which we omit in this notation for the sake of simplicity.

RELL Method Revisited

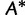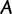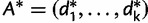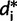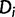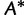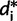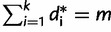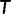A bootstrap sample Inline graphic of Inline graphic is simply a resampled frequency vector Inline graphic, where Inline graphic is the frequency of Inline graphic in Inline graphic (Inline graphic ≥ 0 and Inline graphic). To compute Inline graphic for a given tree Inline graphic under the SBS, one has to re-estimate the branch lengths and model parameters based on 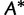Inline graphic. To save computation, RELL (Kishino et al. 1990) approximates Inline graphic by using 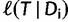Inline graphic (i.e., keeping branch lengths and model parameters fixed). Hence, the log-likelihood scores of individual sites remain the same, implying that calculating

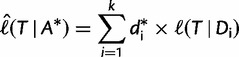graphic file with name mst024m1.jpg (1)

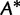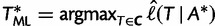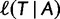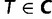for many bootstrap alignments on a fixed tree will be computationally inexpensive. In addition, one can quickly select an approximate ML tree for Inline graphic from a collection Inline graphic of candidate trees by computing Inline graphic if Inline graphic is known for all Inline graphic.

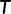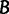RELL was used to infer the LBP (Adachi and Hasegawa 1996) for every internal branch of a fixed tree Inline graphic as follows: For each internal branch one computes Inline graphic and Inline graphic of the two NNI trees around this branch. Next, one generates Inline graphic bootstrap alignments 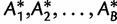Inline graphic and computes the three corresponding RELL scores 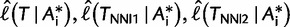Inline graphic for each 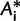Inline graphic according to equation (1). 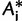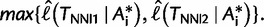The local support of the branch in question is the percentage of Inline graphic where Inline graphic Inline graphic In other words, the LBP method considers the set 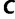Inline graphic of exactly three candidate trees and may overlook other “good” tree topologies (Adachi and Hasegawa 1996, p. 49). For that reason, we pursue another approach described in the following sections.

Tree Proposal

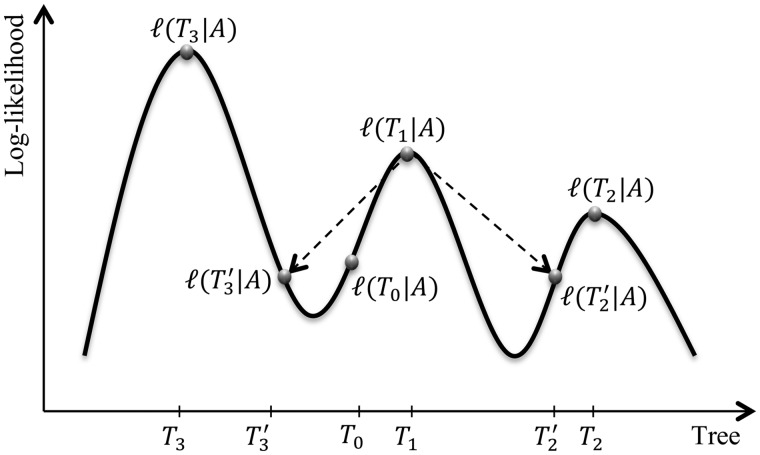
The applicability of RELL crucially depends on the collection of candidate trees. The naive way of evaluating all tree topologies of 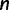Inline graphic taxa (Waddell et al. 2002) only works for small 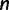Inline graphic. Here, we exploit a strategy of sampling trees using the IQPNNI algorithm (Vinh and von Haeseler 2004; Minh et al. 2005). In principle, IQPNNI does a sampling of local maxima in the tree space defined by the NNI operations (fig. 4). To this end, IQPNNI iteratively moves through the tree space in which the IQP operations help to escape local optimal regions and subsequently NNI moves toward the local optima within regions (T1, T2, and T3 in fig. 4). To escape local optima the IQP step randomly deletes a fraction 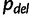Inline graphic of the leaves of the tree and re-inserts the leaves using the quartet puzzling method (Strimmer and von Haeseler 1996).

Fig. 4.

Fig. 4.

Open in a new tab

Schematic view of the tree space sampled by the IQPNNI algorithm. The solid curve reflects the log-likelihood surface on the tree space. The structure of tree space is defined by the NNI operations where each 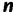Inline graphic-taxon tree has exactly 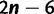Inline graphic neighboring trees.

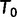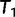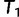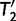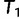The IQPNNI algorithm (fig. 4) works as follows. IQPNNI starts with the BIONJ (Gascuel 1997) tree Inline graphic and moves to Inline graphic via a series of NNIs. Here Inline graphic represents a local maximum of the tree space. This completes the first IQPNNI iteration. In the second IQPNNI iteration, IQPNNI applies the IQP operation to propose Inline graphic from Inline graphic and subsequently moves to 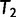Inline graphic (via NNI), which locates another local maximum. As 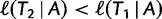Inline graphic, we keep 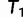Inline graphic as the current best tree. In the third iteration, 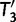Inline graphic is generated from 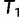Inline graphic and then 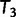Inline graphic reflects another local optimum. Now, as 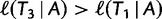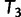Inline graphic, Inline graphic becomes the new ML tree as it has a higher likelihood. In other words, the IQPNNI algorithm allows us to escape the local optimum 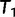Inline graphic. Because this search is carried out for many iterations, IQPNNI samples many local optima and thus provides a rough picture of the tree space.

As a by-product IQPNNI also samples the trees that are a few NNIs away from local optima. To get a collection 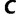Inline graphic of candidate trees, we collect all distinct trees encountered during the IQPNNI search.

Restricting the Number of Candidate Trees

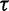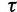As we might encounter millions of distinct trees during the IQPNNI search and as we are interested in plausible trees (i.e., those in the vicinity of local optima), we introduce the parameter Inline graphic to consider only trees in Inline graphic exceeding a certain log-likelihood threshold. In other words, based on Inline graphic we empirically determine a log-likelihood threshold 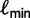Inline graphic during the search such that a tree 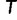Inline graphic will only be investigated with the RELL bootstrapping if 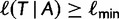Inline graphic. This works as follows: Let 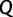Inline graphic be the total number of IQPNNI iterations and 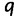Inline graphic the current iteration. On average, we aim to collect 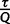Inline graphic trees per iteration. Hence, we expect 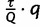Inline graphic trees after 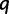Inline graphic iterations. If 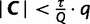Inline graphic after the qth iteration, we have collected fewer trees than we aimed for, so we set 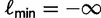Inline graphic to accept all subsequent trees. If however 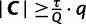Inline graphic, then the expected number of trees after 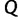Inline graphic iterations might exceed 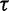Inline graphic. To avoid this, we set 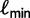Inline graphic equal to the log-likelihood of the 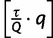Inline graphic-th best tree in Inline graphic. 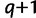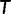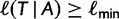In the subsequent iteration Inline graphic, a tree Inline graphic is assigned to Inline graphic only if it is not yet in Inline graphic and if Inline graphic. At the end of iteration 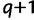Inline graphic, we update 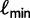Inline graphic as shown earlier. 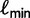Inline graphic will decrease or increase depending on the number of trees added to 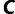Inline graphic during iteration 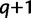Inline graphic. 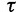We therefore adaptively adjust Inline graphic based on the number of trees encountered during the search. Note that because we do not remove any trees from Inline graphic, the size of Inline graphic might slightly exceed Inline graphic at the end.

UFBoot Approximation

The UFBoot works as follows:

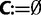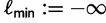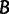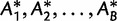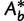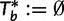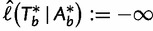  1. Initialization step: Initialize the collection of trees Inline graphic and the log-likelihood cutoff Inline graphic. Generate Inline graphic (typically 1,000 or 10,000) bootstrap alignments Inline graphic. For each Inline graphic initialize the bootstrap tree Inline graphic and Inline graphic.

  2. Exploration step: Perform the IQPNNI search with Inline graphic (fig. 4). Every time a new tree Inline graphic with Inline graphic Inline graphic is encountered during the search:
    1. Compute the approximate log-likelihood Inline graphic for each bootstrap replicate Inline graphic using RELL (eq. 1). If Inline graphic, update Inline graphic.
    2. Update Inline graphic.
    Re-estimate Inline graphic as explained upon finishing an IQPNNI iteration.

  3. Summarization step: Construct a consensus tree from the bootstrap trees 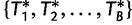Inline graphic or map the support values onto the ML tree reconstruced by the IQPNNI search.

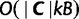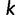The exploration step is the main step that simultaneously explores the tree space and updates the bootstrap trees. The computation of Inline graphic represents the only additional computation compared to the original IQPNNI algorithm and has a time-complexity of Inline graphic, where Inline graphic is the number of site-patterns in the input alignment. 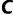We implement the collection of distinct trees Inline graphic as a hash table for computational efficiency, implying that we compute the approximate likelihoods for trees encountered during the search exactly once. Moreover, if the probability of revisiting a tree during the search is small (which often happens for large data), one can safely omit storing the trees in Inline graphic, and thus substantially reducing the memory consumption. We provide both options in our implementation.

UFBoot Stopping Rule

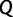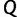In principle, the more IQPNNI iterations (Inline graphic) are carried out during the exploration step, the more candidate trees (Inline graphic) are considered and the better UFBoot performs. However, Inline graphic should not be too large since our goal is to provide an UFBoot approximation method. 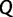Inline graphic should also not be unrealistically small because we want to achieve high accuracy. Thus, we introduce a so-called “UFBoot stopping rule” that automatically assesses the convergence of the split support values and stops collecting candidate trees once convergence is achieved.

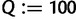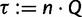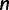To this end, we start with Inline graphic and Inline graphic, where Inline graphic is the number of sequences. That means, 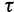Inline graphic is no more an independent parameter and we collect on average 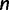Inline graphic trees per IQPNNI-iteration. This is motivated by the fact that each IQPNNI iteration generates 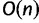Inline graphic trees, and we will therefore consider a constant factor (<1) of the number of trees encountered. During the exploration step, once 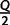Inline graphic iterations have been completed, we compute the vector of split occurrence frequencies 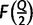Inline graphic for all splits in the current set of bootstrap trees 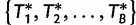Inline graphic. 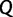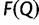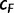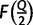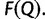At the end of the Inline graphic-th iteration we compute Inline graphic and the Pearson’s correlation coefficient Inline graphic between the two vectors Inline graphic and Inline graphic For splits occurring in one split set but not the other, a corresponding zero entry is added into the other vector. If 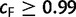Inline graphic, then more IQPNNI iterations do not substantially change the split support values. In such case, we stop and output the split support values in 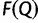Inline graphic. 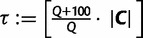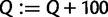Otherwise, we continue the exploration step with 100 more iterations (i.e., we increase Inline graphic and Inline graphic). Therefore, we compute the bootstrap split support every 50 iterations and evaluate the convergence every 100 iterations. Finally, we provide an option to specify a maximum number of iterations 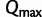Inline graphic such that we will also stop once 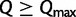Inline graphic. This ensures that the analysis will finish in case a 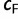Inline graphic of 0.99 is unlikely to be reached.

Performance Study with Yule–Harding Simulation

We simulated data with varying number of sequences and sites (table 1) to assess the performance of UFBoot. For each setting, we used IQ-TREE (Nguyen L-T, Minh BQ, Schmidt HA, von Haeseler A, in preparation) to generate 200 random trees (true trees) under the Yule–Harding model (Harding 1971) where the branch lengths follow an exponential distribution with the mean of 0.1. Seq-Gen (Rambaut and Grassly 1997) was used to evolve the DNA or protein sequences along the tree under the GTR + 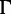Inline graphic (Lanave et al. 1984; Yang 1994) and WAG + 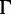Inline graphic (Yang 1994; Whelan and Goldman 2001) model, respectively. 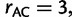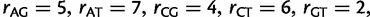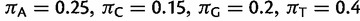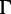The GTR model parameters are: Inline graphic Inline graphic Inline graphic. The Inline graphic distribution parameter is 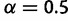Inline graphic. In total, we simulated 600 DNA alignments and 400 amino acid alignments for five settings (table 1).

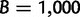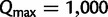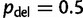For each simulated alignment, we then performed UFBoot with Inline graphic, Inline graphic, and Inline graphic. To compare the UFBoot results, we conducted SBS as implemented in RAxML-SSE3 7.3.0 with 100 replicates (Stamatakis 2006), RBS with 1,000 replicates (Stamatakis et al. 2008), and PhyML SH-aLRT (Guindon et al. 2010). For each bootstrap method, the inferred split support values were mapped onto the ML tree reconstructed by IQ-TREE.

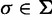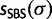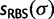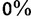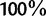Finally, we collected the set Inline graphic of unique splits occurring in the 1,000 ML trees reconstructed from the 1,000 alignments generated and classified them as true or false splits (i.e., splits that occur in the corresponding true tree or not). Each split Inline graphic was associated with four support values: Inline graphic, Inline graphic, Inline graphic, and Inline graphic rounded as integers between Inline graphic and Inline graphic. Then, we computed the fraction, 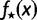Inline graphic, of true splits with support value 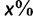Inline graphic against all splits with the same support value 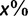Inline graphic, thus we computed:

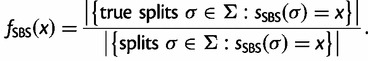graphic file with name mst024m2.jpg (2)

Similarly, we computed 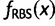Inline graphic, Inline graphic, and Inline graphic. This ratio is coined “accuracy” (Hillis and Bull 1993) and was used recently by Anisimova et al. (2011).

PANDIT-Based Simulation

Moreover, we performed a large-scale simulation based on the PANDIT database (Whelan et al. 2006) to examine the performance of different bootstrap strategies on trees inferred from biological data. To this end, we retrieved 6,491 DNA and 6,617 protein alignments with at least four sequences from the PANDIT website. Following the recommendation of Whelan et al. (2006), we removed all short alignments (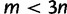Inline graphic for DNA and 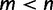Inline graphic for protein alignments). For the remaining 6,222 DNA and 6,182 protein alignments, we selected the best-fit models with the Bayesian information criterion using ModelTest (Posada and Crandall 1998) and ProtTest (Darriba et al. 2011), respectively. We then reconstructed an ML tree for each alignment using IQ-TREE under the selected model. The reconstructed ML trees were treated as true trees to generate alignments. We again used Seq-Gen to simulate alignments with the same alignment lengths as the original PANDIT alignments and under the estimated model parameters. We then superimposed the gap positions from the original PANDIT alignments onto corresponding simulated alignments. The use of PANDIT trees and the introduction of gaps into the simulated alignments are to reflect as much reality as possible in the simulation.

Finally, we compared the bootstrap strategies with respect to the accuracy as in the Yule–Harding simulations (eq. 2). Moreover, for 5,688 DNA alignments, where the selected best-fit models are more complex than JC + 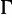Inline graphic (Jukes and Cantor 1969; Yang 1994), we assessed the impact of model misspecification on the accuracy (i.e., when the trees are reconstructed under JC + Inline graphic and JC models representing moderate and severe model violations, respectively).

Acknowledgments

The authors thank Dirk Metzler for discussions, Tina Koestler for helpful comments on the manuscript, and Manuel Gil for proofreading. They also thank Lars Jermiin and two anonymous reviewers for their constructive comments on the manuscript. This work was supported by the Austrian Science Fund—FWF (I760) to B.Q.M. and A.v.H. and the EU EURATRANS consortium (HEALTH-F4-2010-241504) to M.A.T.N. The computational results presented have been achieved in part using the Vienna Scientific Cluster (VSC).

References

  1. Adachi J, Hasegawa M. MOLPHY version 2.3—programs for molecular phylogenetics based on maximum likelihood. Minato-ku (Tokyo): Institute of Statistical Mathematics; 1996. [Google Scholar]
  2. Anisimova M, Gascuel O. Approximate likelihood-ratio test for branches: a fast, accurate, and powerful alternative. Syst Biol. 2006;55:539–552. doi: 10.1080/10635150600755453. [DOI] [PubMed] [Google Scholar]
  3. Anisimova M, Gil M, Dufayard JF, Dessimoz C, Gascuel O. Survey of branch support methods demonstrates accuracy, power, and robustness of fast likelihood-based approximation schemes. Syst Biol. 2011;60:685–699. doi: 10.1093/sysbio/syr041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Darriba D, Taboada GL, Doallo R, Posada D. ProtTest 3: fast selection of best-fit models of protein evolution. Bioinformatics. 2011;27:1164–1165. doi: 10.1093/bioinformatics/btr088. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Douady CJ, Delsuc F, Boucher Y, Doolittle WF, Douzery EJP. Comparison of Bayesian and maximum likelihood bootstrap measures of phylogenetic reliability. Mol Biol Evol. 2003;20:248–254. doi: 10.1093/molbev/msg042. [DOI] [PubMed] [Google Scholar]
  6. Drummond AJ, Suchard MA, Xie D, Rambaut A. Bayesian phylogenetics with BEAUti and the BEAST 1.7. Mol Biol Evol. 2012;29:1969–1973. doi: 10.1093/molbev/mss075. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Efron B. Bootstrap methods—another look at the kackknife. Ann Stat. 1979;7:1–26. [Google Scholar]
  8. Efron B, Halloran E, Holmes S. Bootstrap confidence levels for phylogenetic trees. Proc Natl Acad Sci U S A. 1996;93:13429–13434. doi: 10.1073/pnas.93.23.13429. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Felsenstein J. Evolutionary trees from DNA sequences—a maximum likelihood approach. J Mol Evol. 1981;17:368–376. doi: 10.1007/BF01734359. [DOI] [PubMed] [Google Scholar]
  10. Felsenstein J. Confidence limits on phylogenies—an approach using the bootstrap. Evolution. 1985;39:783–791. doi: 10.1111/j.1558-5646.1985.tb00420.x. [DOI] [PubMed] [Google Scholar]
  11. Felsenstein J, Kishino H. Is there something wrong with the bootstrap on phylogenies—a reply. Syst Biol. 1993;42:193–200. [Google Scholar]
  12. Gascuel O. BIONJ: an improved version of the NJ algorithm based on a simple model of sequence data. Mol Biol Evol. 1997;14:685–695. doi: 10.1093/oxfordjournals.molbev.a025808. [DOI] [PubMed] [Google Scholar]
  13. Goldman N. Statistical tests of models of DNA substitution. J Mol Evol. 1993;36:182–198. doi: 10.1007/BF00166252. [DOI] [PubMed] [Google Scholar]
  14. Guindon S, Dufayard JF, Lefort V, Anisimova M, Hordijk W, Gascuel O. New algorithms and methods to estimate maximum-likelihood phylogenies: assessing the performance of PhyML 3.0. Syst Biol. 2010;59:307–321. doi: 10.1093/sysbio/syq010. [DOI] [PubMed] [Google Scholar]
  15. Harding EF. The probabilities of rooted tree-shapes generated by random bifurcation. Adv Appl Prob. 1971;3:44–77. [Google Scholar]
  16. Hasegawa M, Kishino H. Accuracies of the simple methods for estimating the bootstrap probability of a maximum-likelihood tree. Mol Biol Evol. 1994;11:142–145. [Google Scholar]
  17. Hillis DM, Bull JJ. An empirical-test of bootstrapping as a method for assessing confidence in phylogenetic analysis. Syst Biol. 1993;42:182–192. [Google Scholar]
  18. Huelsenbeck JP, Ronquist F. MRBAYES: Bayesian inference of phylogenetic trees. Bioinformatics. 2001;17:754–755. doi: 10.1093/bioinformatics/17.8.754. [DOI] [PubMed] [Google Scholar]
  19. Jukes TH, Cantor CR. Evolution of protein molecules. In: Munro HN, editor. Mammalian protein metabolism. New York: Academic Press; 1969. pp. 21–132. [Google Scholar]
  20. Kishino H, Miyata T, Hasegawa M. Maximum-likelihood inference of protein phylogeny and the origin of chloroplasts. J Mol Evol. 1990;31:151–160. [Google Scholar]
  21. Kolaczkowski B, Thornton JW. Performance of maximum parsimony and likelihood phylogenetics when evolution is heterogeneous. Nature. 2004;431:980–984. doi: 10.1038/nature02917. [DOI] [PubMed] [Google Scholar]
  22. Lanave C, Preparata G, Saccone C, Serio G. A new method for calculating evolutionary substitution rates. J Mol Evol. 1984;20:86–93. doi: 10.1007/BF02101990. [DOI] [PubMed] [Google Scholar]
  23. Lewis PO, Holder MT, Holsinger KE. Polytomies and Bayesian phylogenetic inference. Syst Biol. 2005;54:241–253. doi: 10.1080/10635150590924208. [DOI] [PubMed] [Google Scholar]
  24. Lopez P, Casane D, Philippe H. Heterotachy, an important process of protein evolution. Mol Biol Evol. 2002;19:1–7. doi: 10.1093/oxfordjournals.molbev.a003973. [DOI] [PubMed] [Google Scholar]
  25. Minh BQ, Vinh LS, von Haeseler A, Schmidt HA. pIQPNNI: parallel reconstruction of large maximum likelihood phylogenies. Bioinformatics. 2005;21:3794–3796. doi: 10.1093/bioinformatics/bti594. [DOI] [PubMed] [Google Scholar]
  26. Money D, Whelan S. Characterizing the phylogenetic tree-search problem. Syst Biol. 2012;61:228–239. doi: 10.1093/sysbio/syr097. [DOI] [PubMed] [Google Scholar]
  27. Nguyen MAT, Gesell T, von Haeseler A. ImOSM: intermittent evolution and robustness of phylogenetic methods. Mol Biol Evol. 2012;29:663–673. doi: 10.1093/molbev/msr220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Nguyen MAT, Klaere S, von Haeseler A. MISFITS: evaluating the goodness of fit between a phylogenetic model and an alignment. Mol Biol Evol. 2011;28:143–152. doi: 10.1093/molbev/msq180. [DOI] [PubMed] [Google Scholar]
  29. Pattengale ND, Alipour M, Bininda-Emonds ORP, Moret BME, Stamatakis A. How many bootstrap replicates are necessary? J Comput Biol. 2010;17:337–354. doi: 10.1089/cmb.2009.0179. [DOI] [PubMed] [Google Scholar]
  30. Posada D, Crandall KA. MODELTEST: testing the model of DNA substitution. Bioinformatics. 1998;14:817–818. doi: 10.1093/bioinformatics/14.9.817. [DOI] [PubMed] [Google Scholar]
  31. Rambaut A, Grassly NC. Seq-Gen: an application for the Monte Carlo simulation of DNA sequence evolution along phylogenetic trees. Comput Appl Biosci. 1997;13:235–238. doi: 10.1093/bioinformatics/13.3.235. [DOI] [PubMed] [Google Scholar]
  32. Ronquist F, Teslenko M, van der Mark P, Ayres DL, Darling A, Hohna S, Larget B, Liu L, Suchard MA, Huelsenbeck JP. MrBayes 3.2: efficient Bayesian phylogenetic inference and model choice across a large model space. Syst Biol. 2012;61:539–542. doi: 10.1093/sysbio/sys029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Schmidt HA, Strimmer K, Vingron M, von Haeseler A. TREE-PUZZLE: maximum likelihood phylogenetic analysis using quartets and parallel computing. Bioinformatics. 2002;18:502–504. doi: 10.1093/bioinformatics/18.3.502. [DOI] [PubMed] [Google Scholar]
  34. Shimodaira H, Hasegawa M. Multiple comparisons of log-likelihoods with applications to phylogenetic inference. Mol Biol Evol. 1999;16:1114–1116. [Google Scholar]
  35. Stamatakis A. RAxML-VI-HPC: maximum likelihood-based phylogenetic analyses with thousands of taxa and mixed models. Bioinformatics. 2006;22:2688–2690. doi: 10.1093/bioinformatics/btl446. [DOI] [PubMed] [Google Scholar]
  36. Stamatakis A, Hoover P, Rougemont J. A rapid bootstrap algorithm for the RAxML web servers. Syst Biol. 2008;57:758–771. doi: 10.1080/10635150802429642. [DOI] [PubMed] [Google Scholar]
  37. Strimmer K, von Haeseler A. Quartet puzzling: a quartet maximum-likelihood method for reconstructing tree topologies. Mol Biol Evol. 1996;13:964–969. [Google Scholar]
  38. Strimmer K, von Haeseler A. Likelihood-mapping: a simple method to visualize phylogenetic content of a sequence alignment. Proc Natl Acad Sci U S A. 1997;94:6815–6819. doi: 10.1073/pnas.94.13.6815. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Sullivan J, Swofford DL. Should we use model-based methods for phylogenetic inference when we know that assumptions about among-site rate variation and nucleotide substitution pattern are violated? Syst Biol. 2001;50:723–729. doi: 10.1080/106351501753328848. [DOI] [PubMed] [Google Scholar]
  40. Suzuki Y, Glazko GV, Nei M. Overcredibility of molecular phylogenies obtained by Bayesian phylogenetics. Proc Natl Acad Sci U S A. 2002;99:16138–16143. doi: 10.1073/pnas.212646199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Van de Peer Y, Frickey T, Taylor JS, Meyer A. Dealing with saturation at the amino acid level: a case study based on anciently duplicated zebrafish genes. Gene. 2002;295:205–211. doi: 10.1016/s0378-1119(02)00689-3. [DOI] [PubMed] [Google Scholar]
  42. Vinh LS, von Haeseler A. IQPNNI: moving fast through tree space and stopping in time. Mol Biol Evol. 2004;21:1565–1571. doi: 10.1093/molbev/msh176. [DOI] [PubMed] [Google Scholar]
  43. Waddell PJ, Kishino H, Ota R. Very fast algorithms for evaluating the stability of ML and Bayesian phylogenetic trees from sequence data. Genome Inform. 2002;13:82–92. [PubMed] [Google Scholar]
  44. Weiss G, von Haeseler A. Testing substitution models within a phylogenetic tree. Mol Biol Evol. 2003;20:572–578. doi: 10.1093/molbev/msg073. [DOI] [PubMed] [Google Scholar]
  45. Whelan S, de Bakker PIW, Quevillon E, Rodriguez N, Goldman N. PANDIT: an evolution-centric database of protein and associated nucleotide domains with inferred trees. Nucleic Acids Res. 2006;34:D327–D331. doi: 10.1093/nar/gkj087. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Whelan S, Goldman N. A general empirical model of protein evolution derived from multiple protein families using a maximum-likelihood approach. Mol Biol Evol. 2001;18:691–699. doi: 10.1093/oxfordjournals.molbev.a003851. [DOI] [PubMed] [Google Scholar]
  47. Whelan S, Money D. The prevalence of multifurcations in tree-space and their implications for tree-search. Mol Biol Evol. 2010;27:2674–2677. doi: 10.1093/molbev/msq163. [DOI] [PubMed] [Google Scholar]
  48. Xia XH, Xie Z, Salemi M, Chen L, Wang Y. An index of substitution saturation and its application. Mol Phylogenet Evol. 2003;26:1–7. doi: 10.1016/s1055-7903(02)00326-3. [DOI] [PubMed] [Google Scholar]
  49. Yang Z. Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J Mol Evol. 1994;39:306–314. doi: 10.1007/BF00160154. [DOI] [PubMed] [Google Scholar]
  50. Yang ZH, Rannala B. Bayesian phylogenetic inference using DNA sequences: a Markov Chain Monte Carlo method. Mol Biol Evol. 1997;14:717–724. doi: 10.1093/oxfordjournals.molbev.a025811. [DOI] [PubMed] [Google Scholar]
  51. Zwickl DJ. Genetic algorithm approaches for the phylogenetic analysis of large biological sequence datasets under the maximum likelihood criterion. Austin (TX): The University of Texas; 2006. [Google Scholar]

Articles from Molecular Biology and Evolution are provided here courtesy of Oxford University Press

RESOURCES