Highly anisotropic stability and folding kinetics of a single coiled coil protein under mechanical tension

Abstract

Coiled coils are one of the most abundant protein structural motifs and widely mediate protein interactions and force transduction or sensation. They are thus model systems for protein engineering and folding studies, particularly the GCN4 coiled coil. Major single-molecule methods have also been applied to this protein and revealed its folding kinetics at various spatiotemporal scales. Nevertheless, the folding energy and kinetics of a single GCN4 coiled coil domain has not been well determined at a single-molecule level. Here we used high-resolution optical tweezers to characterize the folding and unfolding reactions of a single GCN4 coiled coil domain and their dependence on the pulling direction. In one axial and two transverse pulling directions, we observed reversible, two-state transitions of the coiled coil in real time. The transitions equilibrate at pulling forces ranging from 6 to 12 pN, showing different stabilities of the coiled coil in regard to pulling direction. Furthermore, the transition rates vary with both the magnitude and direction of the pulling force by greater than 1,000 folds, indicating a highly anisotropic and topology-dependent energy landscape for protein transitions under mechanical tension. We developed a new analytical theory to extract energy and kinetics of the protein transition at zero force. The derived folding energy does not depend on the pulling direction and is consistent with the measurement in bulk, which further confirms the applicability of the single-molecule manipulation approach for energy measurement. The highly anisotropic thermodynamics of proteins under tension should play important roles in their biological functions.

INTRODUCTION

Coiled coils are one of the most common structural motifs, estimated to exist in over 2,000 human proteins.^1,2 They generally mediate protein association³ and are widely involved in force transduction and sensation.^4,5 A prominent example is SNARE proteins, whose controlled assembly into a four-helix bundle provides the force to drive membrane fusion.⁶ Consistent with their broad biological functions, coiled coils exhibit versatile structures containing helices in various numbers, polarities, and lengths. Because isolated helices only have marginal stability in solution,^7,8 a long-standing and interesting question about coiled coils is how coil-to-helix transitions of individual polypeptides are coupled to their association.^9-12 This protein folding problem is best addressed by a model system-GCN4 coiled coil, a leucine zipper formed by two identical polypeptides of 33 amino acids in length.^13,14 Its folding kinetics has been extensively studied by ensemble-based experimental approaches, including circular dichroism spectroscopy,¹⁰ NMR,¹⁵ hydrogen exchange,^12,16 and laser-induced temperature jump.^8,11,17 These approaches have revealed the folding dynamic of the coiled coil in a large range of time scales and characterized the transition states in the folding process. It was shown that the coiled coil is formed mainly through a concurrent and coupled folding and association of the two polypeptides in a two-state manner.^10,12 However, the initial formation of short alpha-helical structures may be required to trigger the folding and association process,¹⁵ and transient intermediates are found in the folding pathway.^11,18 The existence of the intermediates is supported by inhomogeneous thermal unfolding profiles of the residues in the dimerization interface and non-exponential distributions of the relaxation time of the coiled coil in response to temperature jumps. Although these intermediates have not been well characterized, it has been suggested that they have structures close to the folded coiled coil.¹¹

Because of its small size and linear structure, GCN4 coiled coil has also become a model system for single-molecule studies. In the past decade, major single-molecule techniques, including single-molecule fluorescence resonance energy transfer (smFRET),^19,20 atomic force microscopy (AFM),^4,21,22 and optical tweezers,²³ were applied to this system. Although important insights were gained from these studies, reversible folding and unfolding transitions of a single GCN4 coiled coil domain have not been detected in real time with high spatiotemporal resolution. As a result, the folding energy and kinetics of this model coiled coil has not been accurately measured by single-molecule approaches. The reversible and clear transitions were only recently observed for a variant of GCN4 coiled coil using optical tweezers,²³ which reveals two folding intermediates in the presence of force and downhill folding in the absence of force. Nevertheless, like earlier AFM-based manipulation experiments,²⁴ the protein used in this study is an expanded coiled coil containing three repeats of a mutant GCN4 coiled coil domain with enhanced stability. The use of the triple zipper domain facilitates the detection of the protein transition due to its greater extension change and stability compared with a single domain. However, the measured energy and kinetics cannot be compared with that of a single, wild-type GCN4 coiled coil domain. Therefore, it is not clear whether the intermediate states and downhill folding reported in this study are unique to the triple domain or applicable to the single GCN4 coiled coil domain. In conclusion, a further high-resolution single-molecule study of the wild-type GCN4 coiled coil domain is necessary.

Optical tweezers have been emerging as a powerful tool for protein and nucleic acid folding studies, due to their capability of manipulating biomolecules with high force and spatiotemporal resolution in wide dynamic ranges.^25-32 Nevertheless, an important open question remains as to whether and how the energy and kinetics of the protein transition in the absence of force can be reliably extracted from the time-dependent extension traces detected in the presence of force.^29,32-38 A previous single-molecule manipulation experiment demonstrated that the rate of protein unfolding greatly varies with the direction of pulling force.³⁹ As a result, unique protein unfolding rates in the absence of force that correspond to ensemble measurements may⁴⁰ or may not³⁹ be extrapolated from the force-dependent rates measured by pulling protein molecules in single directions. Furthermore, because these early AFM-based experiments could not reveal protein refolding, it is unclear how protein folding rates depend on the pulling direction and correlate with the corresponding unfolding rates. Consequently, it remains to be tested whether the protein folding energy measured from the manipulation experiments, which can be determined by the ratio of the folding rate to the unfolding rate, is also anisotropic. The basic law of thermodynamics suggests that folding energy in the absence of force is a state function and should not depend on measurement methods, including the pulling direction in the single molecule manipulation approach. Although the energetic and kinetic parameters measured from single pulling directions are sometimes found to be consistent with those obtained in bulk,^25,26,28 to our knowledge a direct test of the independence of the folding energy on the pulling direction has not been performed so far. Such an explicit test has become important, given some recent questions about the accuracy or validity of the thermodynamic and kinetic measurements based on optical tweezers.³⁶

We have used high-resolution optical tweezers to characterize the folding/unfolding kinetics of a single GCN4 coiled coil domain pulled in one axial and two transverse directions. In all cases, we observed reversible zipping and unzipping transitions of the coiled coil in real time in a two-state manner. We found that the critical transition rates of the coiled coil at equilibrium forces (with an equilibrium constant of one) dramatically vary with the pulling directions and the linkage topology of the coiled coil, ranging from ~0.3 s⁻¹ to ~400 s⁻¹. Compared with the previous work on the coiled coil containing triple GCN4 domains, the single domain pulled from the same direction folded and unfolded cooperatively at an equilibrium force of 7.5 pN, about half of the corresponding force observed for the triple-domain protein.²³ Finally, based on an improved analytical theory for single molecules under tension, we verified that the folding energy of the GCN4 domain measured from the manipulation approach is independent of pulling direction and consistent with the corresponding ensemble result.

MATERIALS AND METHODS

Protein Synthesis and Crosslinking

All polypeptides were chemically synthesized and purified to > 95% purity. The coiled coil complexes were assembled, crosslinked, and tethered to beads as illustrated in Figure S3 in SI.^26,41

High-Resolution Optical Tweezers and Experiments

The dual-trap high-resolution optical tweezers were built, calibrated, and tuned to one base pair (0.34 nm) resolution, mainly as previously described.^42,43 Data were acquired at 20 kHz and mean filtered online to 5 or 10 kHz and saved on a hard disk. The protein folding/unfolding experiments were carried out at the room temperature in PBS buffer (137 mM NaCl, 2.7 mM KCl, 8.1 mM Na₂HPO₄, 1.8 mM KH₂ PO₄, pH 7.4), supplemented with the oxygen scavenging system.²⁹

Data Analysis

The time-dependent extension traces were typically analyzed using a two-state hidden Markov model⁴⁴ (HMM) and shown in the figures at 5 kHz if not otherwise specified, without any baseline correction or flattening. Model parameters, including state positions, state fluctuations, and transition rates, were optimized by maximizing the likelihood of the measured time series. The HMM analyses were performed by parallel computation using a Dell workstation containing eight CPU based on MATLAB codes. The codes implemented standard algorithms for HMM-based computations, including the forward-backward algorithm for the likelihood calculation, the Baum-Welch algorithm for parameter optimization, and the Viterbi algorithm for state idealization. The energetic and kinetic parameters at zero force were calculated using the formulae derived in the Supporting Information.

RESULTS AND DISCUSSION

Experimental Setup

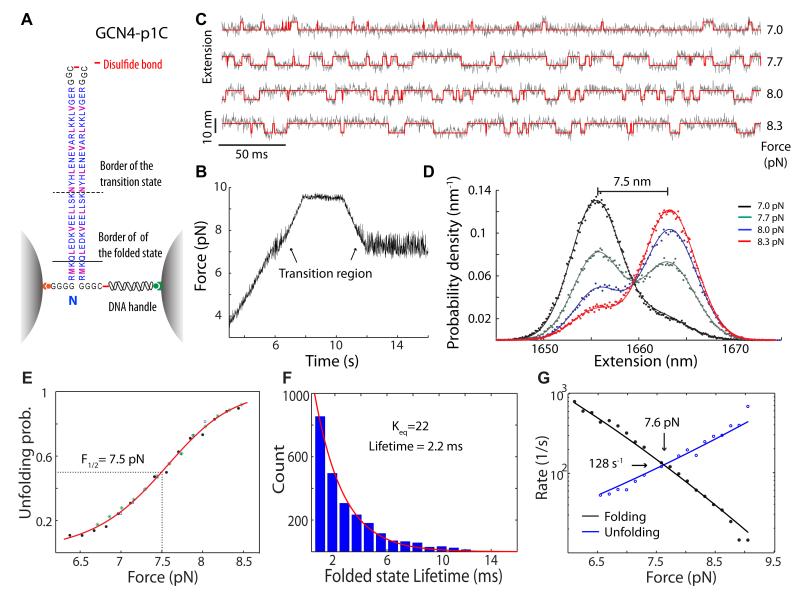
A single GCN4 coiled coil domain was tethered at its N-termini between two beads held in two optical traps (Figure 1A). One terminus was directly attached to a streptavidin-coated bead and the other terminus to another anti-digoxigenin-coated bead via a 2,260-bp DNA handle. The two polypeptides shown here were crosslinked at their C termini through a disulfide bond (GCN4-p1C), which allowed reversible zippering and unzippering of the protein without losing the peptide-DNA tether. Force was applied to the GCN4 protein by moving one of two traps. At each trap separation, time-dependent force and extension were recorded using the high-resolution optical tweezers with sub-nanometer spatial and sub-millisecond temporal resolution.^42,43

Figure 1.

The GCN4 coiled coil domain rapidly and cooperatively folds and unfolds when pulled from its N-termini. (A) Schematics of the experimental setup. A single coiled coil was crosslinked at its C-termini, tethered between two beads, and pulled using optical tweezers. Residues are highlighted in purple in the dimerization interface and blue elsewhere. Also indicated are boarders of the folded and transition states derived from this study. (B) The time-dependent instantaneous force shows reversible protein folding/unfolding transitions in a narrow force range. (C) The time-dependent extension (gray traces), or the distance between two bead centers, at different middle pulling forces (indicated on the right) and the corresponding idealized state transition traces determined by the hidden Markov modeling (red traces). (D) Probability density distributions (symbols) of the extension calculated from the traces shown in C and their double-Gaussian fitting (lines). The distributions are slightly shifted to align the peaks corresponding to the unfolded state. (E) The force-dependent probability of the coiled coil in the unfolded state. The probability data measured from three different molecules (symbols) were slightly shifted along the x-axis for a better comparison and for a correction of the systematic error in the absolute force measurement (~ 0.2 pN).⁴² The unfolding probability can be well fitted by a two-state model for the protein transitions (red line). The equilibrium force (7.5 pN) is indicated corresponding to an unfolding probability of 0.5. (F) The lifetime distribution of the coiled coil in the folded state follows a single exponential distribution. (G) The folding and unfolding rates versus the pulling force (the chevron plot).

The Coiled Coil Folds and Unfolds Rapidly in a Two-State Manner

To identify force-induced protein unfolding and refolding transitions, we first pulled the coiled coil by separating the two traps at a speed of 100 nm/s (Figure 1B, time t < ~8 s). Protein transitions appear as fast force hopping at around 7.5 pN when the force trace is mean filtered with a time window of 8 ms, indicating reversible folding and unfolding of the coiled coil. Further pulling to a higher force stabilizes the protein in the unfolded state and no additional unfolding event is found. To characterize the protein transitions in detail, we relaxed the molecule (10-12 s) just below the transition force range and then increased the trap separation (or the pulling force) in a step-wise manner to scan the whole transition range. At each trap separation, real-time, reversible protein transitions are clearly seen as fast hopping in extension (Figure 1C) or force (Figure S1A, SI) shown at 5 kHz. The probability density distributions of the extensions at all trap separations exhibit two peaks corresponding to the folded and unfolded states of the coiled coil (Figure 1D). Moreover, the distributions can be accurately fitted by double-Gaussian functions, which can be used to dissect the average position of each state and the unfolding probability. The two states differ in their average extension positions by 7.5 (±0.2, s.d.) nm at an equilibrium constant close to 1 (green curve in Figure 1D). The amplitude of the fluctuation around each state is determined by Brownian motion of the beads,⁴² which decreases when the extension trace is filtered to a lower bandwidth (Figure S1B). As a result, the two-state distribution becomes even more evident at the lower bandwidth. As the trap separation increases, the equilibrium is shifted to the unfolded state (Figures. 1C-E) with corresponding changes in state lifetimes (Figure 1F) and transition rates (Figure 1G), confirming that the observed transition is induced by force. The lifetime distribution of the coiled coil in each state can be accurately determined and well follows a single exponential distribution (Figure 1F), consistent with a two-state process. Taken together, we conclude that the single GCN4 coiled coil domain folds and unfolds cooperatively in an all-or-none manner under our experimental conditions and that the coil-to-helix transitions of individual polypeptides coincide with their association within our temporal resolution (or ~0.2 ms).

To accurately determine the transition kinetics, we took advantage of a two-state hidden-Markov model.^45-47 The HMM analysis reveals the idealized state transition traces (Figure 1C, red traces), the average unfolding probability (Figure 1E), the state lifetime distribution (Figure 1F), and the transition rates (Figure 1G). The unfolding probability exhibits a sigmoid dependence upon the pulling force, consistent with a two-state folding/unfolding process. Note that protein unfolding leads to an increase in extension (Figures 1C & D) and a corresponding decrease in force in our experiments (Figures S1A & S1C, SI). In the force range tested, the average forces or positions corresponding to both folded and unfolded states linearly increase with trap separation (Figure S1C). Therefore, we define the arithmetic mean of the two state forces as the middle pulling force and simply refer to it as force throughout the text if not otherwise specified. The thermodynamic average of the instantaneous force (Figure 1B and Figure S1A in SI) may not monotonically increase with the trap separation, thus is not used as an experimental control parameter. The folding or unfolding rate decreases or increases, respectively, with a force increase in an approximately exponential manner, suggesting a well-defined transition state. The folding and unfolding transition equilibrates at an average force of 7.5 (±0.2) pN and rate of 171 (±43) s⁻¹ (Table I).

Table I.

Energy and kinetic parameters of GCN4 coiled coils measured by pulling from different directions.

	Pulling ends	Contour length (nm)	Equilibrium force (pN)	Equilibrium rate (1/s)	Transition state* (nm)	Unfolding energy (kBT)	Rate (1/s)†
							Folding	Unfolding
GCN4-p1C	N	25.8 (0.8)	7.5 (0.2)	171 (43)	16.2 (0.8)	12.9 (0.7)	3.7(0.8)×105	0.9 (0.7)
GCN4-p1C’	N	17 (1)	6.6 (0.7)	359 (94)	10 (1)	6.6 (0.6)	2 (1)×104	25 (22)
GCN4-p1N	C	23.8 (0.7)	6.3 (0.3)	6 (2)	17.9 (0.9)	8.6 (0.6)	3 (1)×103	0.6 (0.4)
GCN4-p1Nc	N & C	7.8 (0.6)	12.1 (0.2)	~0.3	N.A.	8.5 (0.4)	N.A.	N.A.

^*The contour length distance to the unfolded state.

^†At zero force

A Thermodynamic and Kinetic Theory of Force-Induced Folding/Unfolding Transitions

Despite extensive studies, it remains challenging to quantitatively characterize the thermodynamics and kinetics of a single biomolecule under a constant or variable mechanical tension.^{29,33,34,36,37} Single-molecule manipulation studies are facilitated by performing experiments under a constant force, in which the kinetics of the biomolecule is minimally affected by many detailed experimental parameters, such as compliances of DNA handles and optical traps. Furthermore, the effect of force (f) on the folding rate (k) can be described by Bell’s formula k = k₀ exp(−fΔx^†/k_BT) where k₀ is the folding rate at zero force and Δx^† is the extension change to the transition state.⁴⁸ This formula is widely used to extract the reaction rate at zero force from the force-dependent rates measured by AFM or optical tweezers. However, it has been suggested that the extrapolated rate k₀ may depend upon the experimental conditions, such as bead size and DNA handle length, thus is not the true reaction rate of the biomolecule in the absence of force.^23,25,36 Besides the constant force mode, optical tweezers can also be operated in a linear force mode for higher spatiotemporal resolution and simpler instrumentation as in our case, in which mechanical force inversely changes with extension of the biomolecule (Figure S1A). Because the instantaneous energy associated with the conformational change of the biomolecule is coupled to the DNA handle and optical traps, the observed kinetics of the biomolecule is affected by the mechanical properties of the DNA handles and force constants of the traps. In this case Bell’s formula cannot be directly used and more complex methods, such as Monte Carlo or Langevin dynamic simulations,^24,36 are applied to dissect the coupling to extract the energetic and kinetic information of the biomolecule alone, especially at zero force. In conclusion, there has been no consistent and simple approach to quantify the energy and kinetics of the biomolecule studied by optical tweezers under constant or linear pulling force.

We developed a simplified analytical theory to describe the dynamics of protein folding and unfolding under mechanical tension exerted by optical traps, with detailed derivations shown in Supporting Info. Particularly, the unfolding probability (P_u) can be written as

$$P_u\left(f\right)=\frac{1}{1+\exp \left[-\frac{g_m\Delta l}{k_{B}T}(f-f_{1∕2})\right]},$$ (1)

where f and f_1/2 are the middle pulling force and the equilibrium force, respectively, Δ_l is the contour length increase accompanying protein unfolding, and g_m is the ratio of the corresponding extension to the contour length at the equilibrium force. The measured equilibrium force can be used to calculate the protein folding energy at zero force (ΔV), i.e.,

$$\Delta V=g_m\Delta l{f}_{1∕2}-\Delta l{E}_0,$$ (2)

where E₀ is the entropic energy of the polypeptide per unit contour length at the equilibrium force (SI). This equation represents the first law of thermodynamics at a single-molecule level: for a reversible process, the pulling work done to a single molecule (g_mΔlf_1/2) is used to unfold the protein (with energy ΔV) and to further stretch the unfolded polypeptide to the equilibrium force f_1/2 (with energy ΔlE₀) Finally, the folding rate (k_f) can be expressed as

$$k_f\left(f\right)=k_f\left(0\right)\exp \left(\frac{-g_m\Delta l_f^{†}f+\Delta l_f^{†}{E}_0+\frac{1}{2}{k}_t{g}_m^2\Delta l_f^{†}(\Delta l-\Delta l_f^{†})}{k_{B}T}\right),$$ (3)

with

$$k_f\left(0\right)=k_m\exp \left[-\frac{\Delta G_f^{†}}{k_{B}T}\right].$$ (4)

Here k_f(0) is the folding rate at zero force, $\Delta l_f^{†}$ the contour length difference between the unfolded state and the transition state, and k_t the overall force constant of the tether and traps (SI). The zero-force folding rate is determined by the folding energy barrier $\Delta G_f^{†}$ and the molecular transition rate k_m (Eq. (4)).^49,50 The rate k_m ≈ 1×10⁶ s⁻¹ sets an upper limit for the maximum protein folding rate observed for some small proteins.^12,49,50 Finally, the protein unfolding rate can be written similarly (SI).

Note that using the middle pulling force definition, Equations (1)-(2) are also applicable to the constant force case (SI). Compared with Bell’s formula, Equation (3) has two additional exponential terms, besides the first, force-dependent term ($-g_m\Delta l_f^{†}f$). The second term ($\Delta l_f^{†}{E}_0$) accounts for the energy decrease associated with the contour length decrease in forming the transition state. Because such contour length decrease also occurs in the constant force case, this term should be incorporated into Bell’s formula to correctly describe the effect of force in folding transitions of single biomolecules under tension. Thus we modify Bell’s formula for protein folding under constant tension as

$$k\left(f\right)=k_0\exp \left[\right(-f+E_0\left(f\right)∕g_m\left(f\right))\Delta x^{†}∕k_{B}T].$$ (5)

Due to the large contour length change ($\Delta l_f^{†}$ or Δx^†) generally involved in protein folding,^10,26,36 the second term in the exponential in both formulae (Equations (3) and (5)) is normally significant. Thus direct use of Bell’s formula may dramatically overestimate the protein folding rate (SI). Note that the rate in Equation (5) becomes generally non-exponential in regard to force, due to the contour length change in this case, instead of the force-induced shift in state position caused by force probes much stiffer than optical traps.³⁴ However, because the reversible protein folding and unfolding transitions are often detected in a narrow force range, the second term in the exponential in Equations (3) and (5) only weakly depends upon force. As a result, the force-dependent rate measured by optical tweezers only slightly deviates from an exponential function (Figure 1G). Only the third term in Equation (3) is unique to the linear force case and has a significant effect on the transition kinetics of the biomolecule studied under a linear force.⁵¹ Importantly, the effective activation energy for unfolding is lowered by an amount of $\frac{1}{2}{k}_t{g}_m^2\Delta l_f^{†}(\Delta l-\Delta l_f^{†})$ more by a linear force than by a constant force. Therefore, the linear force mode may be advantageous over the constant force mode to detect reversible folding and unfolding transitions of many biomolecules with high energy barriers.

Extracting Folding Energy and Transition Rates of the Coiled Coil at Zero Force

Based on our analytical theory, we simultaneously fit the measured unfolding probability, transition rates, and state forces using six fitting parameters: locations and free energy of the folded state and the transition state at zero force, the sum of the bead diameters, and the overall force constant of the detection system k_t (SI). Note that the diameter of the bead used in our experiment slightly varies from bead to bead and thus was chosen as a fitting parameter. The experimental data are well fitted by theoretical predictions (lines in Figures 1E, 1G and Figure S1C, SI), which yield the best-estimated sketch of the energy landscape for folding or unfolding transition of the coiled coil at zero force (Figure 2). The transition involves an average contour length change of 25.8 (±0.8) nm or 30 (±1) amino acids in each polypeptide (Table I). This length change is approximately equal to those derived from the corresponding extension changes at different trap separations (SI), indicating a relatively rigid structure of the folded coiled coil independent of the pulling force in the range of 7-10 pN (Figures 1E & G). Based on the average contour length change, the folded coiled coil observed in our experiments has 3 (±1) fraying amino acids in each polypeptide due to the presence of the pulling force (Figure 1A),^18,29 compared with the crystal structure of the coiled coil.^12,14 The average folding energy is measured as 12.9 (±0.7) k_BT, consistent with the value ~10 k_BT obtained in bulk experiment.¹²

Figure 2.

Sketches of the energy landscapes corresponding to folding of different GCN4 coiled coil constructs at zero force: wild-type ones crosslinked at C-termini (GCN4-p1C, Figure 1A) and N-termini (GCN4-p1N, Figure 4A), respectively, and the mutant version joined at C-termini (GCN4-p1C’, Figure 3A). Each sketch shows the positions of the unfolded state, the transition state, the folded state and their corresponding free energy. All three coiled coils have the same contour length of 32.4 nm for fully unfolded states and 4.2 nm for completely folded states.

We mapped the transition state of GCN4-p1C to be 16.2 (±0.8) nm away from the unfolded state (Table I). Interestingly, this transition state includes the middle asparagines in the dimerization interface at its N-termini (Figure 1A), which are shown to be crucial for the specific association of the coiled coil.^13,14 Thus, productive folding of the coiled coil requires zippering 55% of the C-terminal residues in the two polypeptides to register the two asparagines. Forming this transition state only creates a small energy barrier of 1 (±0.3) k_BT, which leads to a folding rate of 3.7 (±0.8) ×10⁵ s⁻¹ and an unfolding rate of 0.9 (±0.7) s⁻¹. The folding rate is close to the bulk value in the range of 1.7-5×10⁵ s⁻¹, whereas the unfolding rate is somewhat smaller than the bulk result 19 (±6) s⁻¹.^12,17 Interestingly, the folding rate of this coiled coil is close to the coil-to-helix transition rate measured for a polypeptide with similar length (~ 8×10⁵ s⁻¹)⁸, confirming a coupled folding and association mechanism for coiled coil formation.

The Coiled Coil with an N-terminal Mutation Is Partially Folded Under Pulling Force

Although we inferred a globally folded structure with small fraying ends for GCN4-p1C that is consistent with the previous observation,¹⁸ such inference depends upon the specific value for the persistence length of polypeptide (0.6 nm) chosen from a range of values reported in the literature (0.36-0.8 nm).^23,26,28 To further justify the folded structure identified by us, we repeated the experiment using a mutant coiled coil domain with the N-terminal methionine residue substituted by a serine residue to weaken the dimerization (Figure 3A). If the methionine is completely unfolded in the force range tested (6-9 pN), its substitution with serine will not alter the extension change and folding energy. Otherwise, the substitution will reduce both parameters. This latter scenario is exactly what we observed for the mutant. Its extension change decreases to 5.7 nm (Figure 3B) at a lower equilibrium force of 6.6 (±0.7) pN (Figure 3C). As a result, the point mutation significantly weakens the coiled coil, leading to a folding energy of only 6.6 (±0.6) k_BT (Table I). Consistent with these changes, the mutant coiled coil is only partially folded in our single-molecule manipulation experiment, with an average of 14 N-terminal residues unfolded in each polypeptide (Figure 3A). Correspondingly, the transition state is shifted towards the C-terminus by 6 residues compared with GCN4-p1C. Moreover, the mutant folds ~20-fold less efficiently compared with the wild-type at zero force (Table I), despite its two-fold increase in the folding rate at the critical force (Figure 3D). Thus the terminal methionine residue in the wild-type GCN4 coiled coil, despite being in a frayed state, is not completely unfolded and still greatly contributes to the stability of the folded coiled coil observed in our experiments. Taken together, we conclude that the folding energy and transition rates measured by us for the wild-type GCN4 coiled coil (GCN4-p1C) indeed correspond to an approximately complete coiled coil structure.

Figure 3.

The GCN4 coiled coil with an N-terminal point mutation is partially folded under mechanical tension. (A) Schematics of GCN4-p1C’. (B) Probability density distributions of the extension when mean filtered with time windows of 0.2 ms and 2 ms, respectively. The distributions can be well fitted by double-Gaussian functions (solid lines), revealing an average extension change of 5.7 nm as indicated. (C) The force-dependent unfolding probabilities (symbols) and their best-fit based on a two-state model (red line). Measurements from three different single molecules are overlaid and shown in different colors. (D) The force-dependent folding (hollow circles) and unfolding (stars) rates calculated from the same data sets as those in C. The rates can be fitted by a force-dependent two-state model for the transitions (lines). The two lines cross at an equilibrium force of 6.6 pN and a rate of 359 s⁻¹ as indicated. Note that the measured rate constants for this mutant are more scattered around the predicated lines than for the wild-type (Figure 1G). This is caused by the lower signal-to-noise to detect transitions at a lower force, a smaller extension change, and a faster rate by optical tweezers and possibly by higher amplitude of fluctuation in the N-terminal region of the mutant coiled coil.

GCN4 Coiled Coil Domain Folds Slowly When Pulled from Its C-termini

To investigate how the folding energy and kinetics of GCN4 coiled coil is affected by the pulling direction, we pulled the protein from its C-termini with its N-termini crosslinked (GCN4-p1N, Figure 4A). We again observed reversible and two-state folding and unfolding transitions (Figure 4B) and measured the folding energy and transition rates (Table I). We obtained a folding rate of 3(±1)×10³ s⁻¹, which is close to the previous measurement of 4.2 (±0.4)×10³ s⁻¹ in bulk.¹⁰ Furthermore, the transition state mapped by our method is consistent with that derived from the Φ analysis. The folding energy directly measured in our manipulation experiment is 8.6 (±0.6) k_BT. Considering the 5 fraying amino acids in each polypeptide in this construct (Figure 4A), we may correct the folding energy to 10.1 (±0.7) k_BT, assuming the same energy contribution per amino acid in the fraying region as in the associated region. This corrected unfolding energy is comparable to the bulk result of 14.8 (±0.6) k_BT for a coiled coil variant containing a single tyrosine to tryptophan substitution.¹⁰ Compared with the results obtained from two pulling directions, both GCN4-p1N and GCN4-p1C constructs start folding from their crosslinked end and require zippering of two central asparagines to overcome the energy barrier for productive folding (Figures 1A & 4A). Interestingly, both constructs share nearly entire triggering sequence in their folding transition states (Figure 4A), corroborating the critical role of this sequence in coiled coil folding.¹⁵ Nevertheless, GCN4-p1N differs from GCN4-p1C in three aspects: 1) GCN4-p1N folds and unfolds at about 10-fold lower critical rate than GCN4-p1C (Table I). Correspondingly, the energy barrier for the transition is much higher (5.8 vs 1 k_BT, Figure 2); 2) GCN4-p1N has smaller equilibrium force (Table I) and changes in extension (6.8 vs. 7.5 nm, Figure S2, SI) and contour length (Table I), confirming its smaller folding energy or lower stability; 3) GCN4-p1N has a transition state closer to the folded state than GCN4-p1C (compare Figure 4A with Figure 1A). These comparisons suggest that energy and kinetics of coiled coil folding critically depends on the pulling direction and/or the linkage topology because the two constructs also differ in their crosslinking sites.²⁸

Figure 4.

Energetics and kinetics of GCN4 coiled coil transition when pulled from its C-termini. (A) Schematics of the coiled coil construct (GCN4-p1Nc). The five critical amino acids in the triggering sequence are marked by dots. (B) A typical time-dependent extension trace (gray) at a force of 6.2 pN or a trap separation of 1718.43 nm and the corresponding idealized state transition trace (red). The probability density distribution of extension corresponding to this trace is shown in Figure S2, SI. (C) The force-dependent unfolding probability (symbols) and its best fit (line). (D) The folding and unfolding rates (symbols) and their theoretical fits (lines).

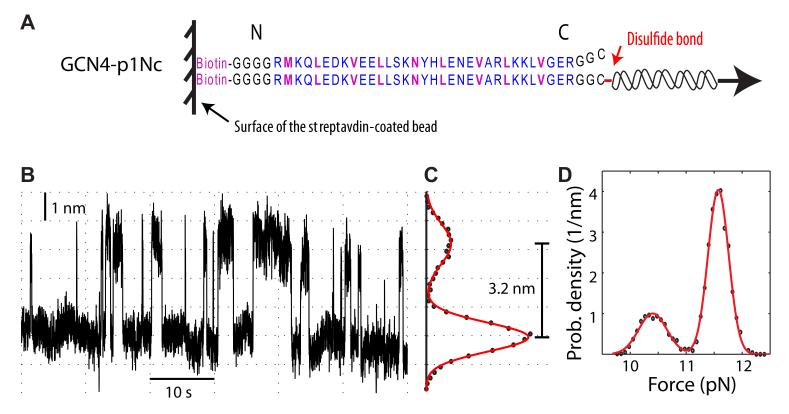
Pulling GCN4 Coiled Coil in an Axial Direction

To further dissect the effects of pulling direction and peptide linkage topology, we pulled the coiled coil in an axial direction. This construct (GCN4-p1Nc) has both N-termini attached to the same location on the surface of the streptavidin-coated bead (Figure 5A), thus has the same linkage topology as GCN4-p1N. The folding kinetics of this construct dramatically differs from the two constructs pulled in a transverse direction. First, the force-induced transition rate becomes the lowest among the three constructs (Figure 5B), with a critical transition rate down to 0.3 s⁻¹ (Table I). Second, the average length changes associated with the protein transition are reduced to 3.2 nm for the extension (Figure 5C) and 7.8 nm for the contour length, respectively, both of which are less than half of the corresponding length changes pulled in a transverse direction. Nevertheless, these length differences are expected because only one of the polypeptides in the coiled coil is directly stretched and its helix-to-coil transition contributes to a smaller contour length change of 0.25 nm per each amino acid (the contour length difference before (0.15 nm) and after (0.4 nm) the transition).¹⁴ Therefore, the measured total contour length change corresponds to 31 (±2) amino acids involved in the observed transitions. Third, the equilibrium force increases to 12.1 (±0.2) pN, indicating that the coiled coil can withstand a higher force in an axial direction than in a transverse direction. Fourth, the folding energy derived from axial pulling is equal within experimental error to the energy of the GCN4-p1N construct. This finding is important because energy is a state function and should not depend upon measurement methods, including the pulling direction in the manipulation approach. Thus, we directly verify that the energy change measured from a single-molecule manipulation experiment does not depend upon pulling directions, which further support the applicability of the manipulation approach for the energy measurement. Finally, we noticed that the transition kinetics in the presence of axial pulling force exhibits certain heterogeneity in transition rates. Specifically, the force-dependent transition rates cannot be fitted by a two-state model with a single transition state.^5,52 This observation is consistent with the previous result based on Φ-value analysis.¹⁰ Nevertheless, more extensive single-molecule measurements and theoretical modeling are required to further pinpoint the kinetic heterogeneity.

Figure 5.

The GCN4 coiled coil folds and unfolds slowly at a high force when pulled in an axial direction. (A) Schematic of the coiled coil construct and the pulling direction. (B) The extension versus time trace at 11.1 pN pulling force. Data are mean filtered to and shown at 50 Hz. (C-D) The probability density distribution (symbol) of extension (C) or force (D) corresponding to the trace in B, and its corresponding double-Gaussian fitting (red line).

Conclusion

Optical tweezers have been emerging as powerful tools for protein folding studies, due to their high spatiotemporal and force resolution and the corresponding large dynamic ranges in time, distance, and force measurement.^23,26,28 We typically stretched a single GCN4 protein for more than 20 minutes, observing folding events in real time up to a million times. Combined with the simplified analytical theory and efficient statistical modeling based on HMM, the extensive measurements make it possible to accurately and completely extract the energetic and kinetic parameters of protein transitions from a single molecule in a single experiment (e.g., Figures. 3C & D). Furthermore, measurements performed on different molecules are highly consistent (Figures 1E, 3C & 3D) and generally match the corresponding bulk results. Finally, the high dynamic ranges in time, distance, and force measurement offered by optical tweezers also help dissect more complex protein dynamics with multiple time scales and states.

We showed that the energy landscape of protein folding under mechanical tension is highly anisotropic in regard to pulling directions, which extends previous similar observations for protein unfolding dynamics.³⁹ The highly anisotropic energy landscape is important for numerous proteins whose functions involve coupling folding or unfolding to force generation or sensation.^6,23,53 Moreover, the folding and unfolding kinetics are also sensitive to protein topology, consistent with the conclusion from a recent single molecule experiment.²⁸ However, the ratio between the folding and unfolding rates (or the equilibrium constant), which determines the folding energy, does not depend on the pulling direction. This explicitly validates the energy measurement based on the manipulation approach. Nevertheless, it remains to be investigated whether consistent transition rates at zero force can be extrapolated from the force-dependent rates measured in different pulling directions.

Our results on a single GCN4 coiled coil domain differ from those of the recent study on the extended coiled coil containing three GCN4 coiled coil domains when pulled from the same N termini using optical tweezers.²³ First, we observed an equilibrium force about half of the value for the extended coil coil (7.5 vs. ~14 pN), indicating a reduced stability for the single GCN4 coiled coil domain. Second, we found that the single coiled coil domain folds and unfolds in a two-state process, like many small proteins investigated in a similar time scale (>0.2 ms), whereas the previous study showed two intermediate states. Thus these intermediates are probably unique to the folding process of the triple-domain coiled coil. Interestingly, whereas these intermediates are stabilized by the asparagines in the dimerization interface, the same residues are required to form the folding transition states of the single coiled coil domain in our study. Finally, the energy landscape derived by us at zero force has a small but well-defined energy barrier, whereas no energy barrier was found in the previous study, indicating a down-hill folding process. These different conclusions are partially caused by different methods and assumptions used to extract the energy landscape from the measured extension or force time series. Specifically, we adopted a higher molecular transition rate (k_m) of 1×10⁶ s⁻¹ than the one used in the latter study (1.2×10⁴ s⁻¹). Future work should assess these methods in detail.

It is interesting to compare the single-molecule manipulation approach with the traditional denaturant-based approach for protein folding studies. Force and denaturant have quantitatively similar effects on protein folding: both linearly tilt the energy of the folded and transition states towards the unfolded state.¹⁰ As a result, both lead to an exponential dependence of the transition rate on the force magnitude or denaturant concentration and the similar chevron plot for a two-state folding process. Moreover, the two methods rely on the same extrapolation approach to determine the transition rates at zero force or in a native environment from those measured at finite forces or denaturant concentrations. Because this extrapolation is model-dependent, the two methods also share the same weakness in determining the states and the transition rates in the absence of force or denaturant.³⁶ Nevertheless, the two experimental approaches have several important differences. First, the effect of force on the protein transition critically depends upon the distance change involved in the transition process, whereas no such simple relation exists for any denaturant. This leads to a significant advantage of the single-molecule manipulation approach for protein folding studies, which is their capability to reveal information about the transition state. Such information is generally difficult to obtain from ensemble or other single-molecule approaches.¹⁰ Second, in the single-molecule manipulation experiments, protein folding and unfolding take place in a natural environment, which allows an addition of other native proteins or nucleic acids to test their effects in protein folding. Finally, force is a vector quantity. Besides its magnitude mentioned above, its direction has equally significant impact in protein folding, which leads to highly anisotropic stability and folding kinetics of proteins. This is an important protein property that can be well studied by single-molecule manipulation approaches.