MR Guided PET Image Reconstruction

Abstract

The resolution of PET images is limited by the physics of positron-electron annihilation and instrumentation for photon coincidence detection. Model based methods that incorporate accurate physical and statistical models have produced significant improvements in reconstructed image quality when compared to filtered backprojection reconstruction methods. However, it has often been suggested that by incorporating anatomical information, the resolution and noise properties of PET images could be improved, leading to better quantitation or lesion detection. With the recent development of combined MR-PET scanners, it is possible to collect intrinsically co-registered MR images. It is therefore now possible to routinely make use of anatomical information in PET reconstruction, provided appropriate methods are available. In this paper we review research efforts over the past 20 years to develop these methods. We discuss approaches based on the use of both Markov random field priors and joint information or entropy measures. The general framework for these methods is described and their performance and longer term potential and limitations discussed.

1. Introduction

Positron Emission Tomography (PET) is a powerful functional imaging modality that can provide quantitative measurement of a broad range of biochemical and physiological processes in humans and animals in vivo (1). However, resolution and quantification accuracy in PET is limited by several factors including the intrinsic resolution of the detectors and the statistical noise in the data. In recent years, image quality in PET has been optimized using algorithms that explicitly account for both of these factors in the framework of maximum likelihood or penalized maximum likelihood reconstruction (2). An approach to further improving PET image quality is to use anatomical information from other imaging modalities, primarily Computed Tomography (CT) or Magnetic Resonance (MR), to guide the formation of the PET image. In this paper we review the computational approaches that have been developed for this purpose.

Combined PET/CT scanners are now routinely used for diagnostic PET studies (3). The CT scan provides the anatomical context for display and interpretation of the PET scans. However, soft tissue contrast in CT is typically poor, and CT images are therefore of limited value in terms of delineating organ and other tissue boundaries in a manner in which they can be used to guide PET image formation. Conversely, as a complementary imaging modality to the high sensitivity functional information gathered by PET, MR scanners are able to provide high-resolution anatomical information with excellent soft tissue contrast. Combined MR-PET images have been used extensively in brain research for many years. The PET images are typically co-registered to the MR images, which are then used to define anatomical regions of interest through manual or automated labeling (4). Until recently, these studies were performed with two separate scans of the subject, one in the MR and the other in the PET scanner. While retrospective coregistration of brain images is relatively straightforward, coregistration of other parts of the body is far more challenging because of differences in posture from scan to scan as well as the internal motion and non-rigid deformation of organs that can occur over time. For this reason, acquiring MR and PET images (almost) simultaneously in the same scanner is important for MR-PET studies, whether for clinical or research purposes.

The integration of PET and MR was first proposed about twenty years ago (5, 6). However, fully integrated simultaneous MR-PET systems have only recently become a reality (7). The major technical challenge of integrating PET and MR is the effect on PET detectors and electronics from the static and gradient magnetic fields and the radio-frequency (RF) signals used in MR. It is also important that the PET detectors don’t unduly compromise the uniformity of the MR system’s magnetic field. Finally, the PET detectors must fit within the bore of the MR magnet leaving sufficient room for the patient and RF coils. For these reasons, conventional photomultiplier tubes (PMTs) are impractical and solid-state devices are used. With the development of new detector materials and MR-compatible components, several combined MR-PET scanners have been designed and produced in the last decade (8).

Avalanche photodiodes (APDs) were first used for PET in a high magnetic field in 1998 (9), and then in the first preclinical MR-PET scanner in combination with LSO scintillators in 2006 (10). Silicon photomultipliers (SiPMs), a densely packed matrix of small Geiger-mode APD cells (11), are insensitive to magnetic fields and have higher gain than APDs as well as excellent intrinsic timing resolution of about 60 ps. The feasibility of applying SiPMs in a MR system was first demonstrated in 2007 (12) and a MR-PET prototype system for small animal imaging was recently reported in 2009 (13).

The first clinical MR-PET system, the Philips Ingenuity TF, is a clinical whole-body sequential MR-PET scanner combining time-of-flight (TOF) PET with 3T MR (14). Unlike the simultaneous MR-PET systems, the sequential systems do not need a new design of the PET system but allow for sequential acquisition of co-registered PET and MR images in a manner similar to that typically used in PET/CT systems. The Siemens Biograph mMR is the first commercially available clinical simultaneous whole body MR-PET scanner. The mMR uses LSO/APD PET detectors that are placed between the MR body coil and gradient coils. It has been shown that the performance of the PET system in the mMR scanner is equivalent to that of the Siemens Biograph PET/CT (15).

The availability of simultaneous MR-PET imaging offers several important advantages: first function and structural data are being acquired at the same point in time. Second, integrated MR-PET allows spatial co-registration of PET and MR images with minimal error. Third, the MR image can be used for attenuation correction of PET data, reducing the radiation exposure compared with PET/CT or a PET transmission scan using an external source. It is also possible to use the MR signal for motion correction of the PET data, and consequently generate motion corrected attenuation and scatters corrections. Finally, MR is a powerful modality that itself allows functional as well as anatomical imaging. Many of these advantages are described in other papers in this issue, here we focus only on using anatomical MR images specifically to improve the quality of the PET images.

In PET studies, the resolution of the images is limited by several physical factors (16), including positron range, photon pair non-collinearity, errors in localization of each detected photon caused by crystal penetration and scatter within the crystal, and the finite size of the detector elements. In addition, detection is photon limited due to limitations in the amount of activity injected, short scan times, and attenuation within the body. As a result Poisson noise is often the limiting factor in image quality. The current achievable spatial resolution of PET images is on the order of 4mm for whole body clinical scanners (17) and 1mm for preclinical scanners (18). Anatomical MR images can be routinely collected with both higher resolution and superior signal to noise ratio (SNR). It is therefore natural to ask where we can we use the anatomical information from MR to improve the quality of reconstructed PET images. Over the last two decades, several research groups have addressed this problem and many novel approaches have been proposed as we review below. We first summarize approaches to PET image reconstruction in Section 2 before proceeding to a review of how these methods can be modified to incorporate anatomical information in Section 3.

2. PET Image Reconstruction

The simplest model of PET data acquisition system assumes the measured data correspond to line integrals through the unknown image. In the 2D case the data, or sinogram, is the Radon transform of a 2D function. The Radon transform can be inverted in multiple ways, but most common among these is the filtered backprojection (FBP) algorithm, in which the sinogram is first filtered and then projected back into image space (19). For 3D systems the finite axial extent of the scanner results in missing data when the problem is viewed as a direct extension of the 2D case. Approaches to deal with these effects include the use of modified filters (20) and reprojection methods to estimate the missing data (21). An alternative analytic approach to the 3D problems first maps the data into a set of 2D Radon transforms using Fourier rebinning (22). The computation cost of this method is relatively low and for several years was the preferred method for 3D PET image reconstruction. Recently Fourier rebinning methods have also been extended to time-of-flight (TOF) data from the latest generation of PET/CT scanners (23, 24).

These analytical methods do not take into account the statistical variability inherent in photon-limited detection nor do they accurately model the true physical process of photon coincidence detection. In contrast, model based methods are able to combine accurate physical and statistical models, resulting in superior image quality. For this reason, model based methods are now routinely used in both research and clinical PET studies. The use of a model based method also facilitates the introduction of anatomical information as we describe below. First we will give a brief introduction to model based PET image reconstruction (see (2, 25) for more detailed reviews).

Model based reconstruction methods for PET are based on a statistical model in which the data are modeled as a collection of independent Poisson random variables with joint probability distribution function (PDF)

$$P(Y\mid \lambda )={\prod }_{j=1}^M\frac{{\overline{y}}_j^{y_j}{e}^{{\overline{y}}_j}}{y_j!}$$ (1)

where Y ∈ R^M×1 are the measured sinogram data, Ȳ ∈ R^M×1 are the mean (expected) values of the data, and M is the number of lines of response (LORs) in the sinogram. Ȳ can in turn be modeled as:

$$\overline{Y}=A\lambda +\overline{S}+\overline{R}$$ (2)

where λ is the unknown image, A is the system matrix, and S̄ and R̄ are the means of the scattered and random contributions, respectively, to the measured data. The system matrix A models the mapping from source to detector space and should take into account the geometry of the scanner, the properties of the detectors (including their intrinsic and geometric sensitivities), and the attenuation probabilities between each detector pair. These models can be either computed on the fly (26) or precomputed and stored in sparse matrix formats. As noted in (16), A can be usefully factored into geometric, detector response, attenuation, and detector normalization components for efficient storage and computation.

The most common approach to reconstruction of PET images based on the model in eqs (1,2) is to find the image that maximizes the log likelihood, Ln P(Y ∣ λ). This maximum likelihood (ML) solution can be found using the Expectation-Maximization (EM) algorithm (27). The EM algorithm has a simple iterative update equation with guaranteed convergence to the ML solution. Convergence of EM is slow so that in practice it is common to perform EM updates over subsets of the data which produces much faster initial convergence towards the ML solution (28). While this ordered subsets EM (OSEM) algorithm does not ultimately converge to the true ML solution, a judicious choice of the number of subsets and iterations, possibly with additional post-reconstruction smoothing, can produce excellent image quality in practice. For this reason OSEM remains the most widely used iterative reconstruction method in clinical scanners.

With either the EM or OSEM algorithms, iterating beyond a certain point will result in increased noise and decreasing image quality in the estimated image. This effect is caused by the inherent ill-posedness of the PET inverse problem. The system matrix A is ill-conditioned so that small differences in the data (which naturally occur due to photon counting noise) will produce large changes in the ML solution. This problem can be avoided in practice by using a limited number of iterations to reconstruct the image (29) or by post-filtering of an image obtained using a higher number of iterations (30).

An alternative approach to dealing with the instability of the ML problem is to work in a Bayesian framework by introducing a statistical prior distribution to describe the expected properties of the unknown image. The Bayesian formulation is of particular interest if one wants to include anatomical information since, as we show below, it provides a natural framework to do so. The effect of the prior distribution is to choose among those images that have similar likelihood values the one that is most probable with respect to the prior.

In Bayesian image reconstruction, the maximum a posterior (MAP) estimate of the image is found by maximizing the posterior function

$$\widehat{\lambda }=\arg {\max }_{\lambda \ge 0}\left\{P(\lambda \mid Y)=\frac{P(Y\mid \lambda )P(\lambda )}{P(Y)}\right\}$$ (3)

Equivalently, we can maximize the log of the posterior probability, noting that P(Y) is a constant once the data are acquired, so that

$$\widehat{\lambda }=\arg {\max }_{\lambda \ge 0}\{\mathit{Ln\; P}(Y\mid \lambda )+\mathit{Ln\; P}(\lambda )\}$$ (4)

When written in this way we see that MAP can also be viewed as maximizing a penalized likelihood function where the additive penalty is Ln P(λ). While Bayesian and frequentist statisticians (who favor ML approaches) differ widely in their views on statistical inference, for all practical purposes MAP and penalized maximum likelihood (PML) are essentially equivalent as used in most PET image reconstruction contexts. We will present the methods for incorporation of anatomical priors in a Bayesian framework here.

Different approaches have been proposed to design the prior distribution for the image P(λ). The simplest among these assume each voxel is statistically independent. These models are of limited value since the information we typically seek to capture in the prior is some degree of piecewise smoothness in the image. The Gibbs distribution, or Markov random field (MRF) (31), allows us to specify a prior in terms of local interactions since all MRFs have the property that the conditional probability for the value of any voxel in the images depends only on the values of the voxels in a local neighborhood of that voxel. This not only allows us to model the desired local properties but also leads to computationally tractable MAP reconstruction algorithms.

To define a MRF prior we need to specify the form of statistical interaction (or conditioning) between neighboring voxels. The simplest MRF models encourage uniform smoothness throughout the image using a multivariate Gaussian distribution. While these models have proven very useful in controlling the noise amplification issue encountered with EM and OSEM reconstruction, they are limited in their abilities to identify sharp changes in intensity that may occur, for example, at the boundaries between organs or substructures within an organ. The more complex compound MRFs are able to model these boundaries explicitly through introduction of “line process” as we described below in Section 3.2. An alternative approach to modeling piecewise smoothness is to use a hierarchical MRF in which we explicitly model the image as consisting of distinct segmented regions. While these MRF models can all be used for MAP reconstruction from PET data only, they also lend themselves to incorporation of additional anatomical data. These data can be used to influence the degree of smoothness throughout the image or the location of boundaries or edges in the image.

3. Using Anatomical Images for PET Image Formation and Analysis

There are two distinct ways in which anatomical MR images can be combined with PET data. The first approach is to use the MR to define anatomical regions of interest (ROIs) over which the PET data are then analyzed, either for computing semiquantitative metrics such as the Standardized Uptake Value (SUV) (32) or by fitting a dynamic model to determine pharmacokinetic parameters of interest such as the volume of distribution or binding potential (33). This approach can be taken one step further when the anatomical image is used as the basis to effectively increase the resolution of the PET image, using the anatomical ROI to compensate for partial volume effects, as we describe in Section 3.1. The second approach is to use some facet of the MR image to directly influence the reconstruction of the PET image. The rationale for this is that while anatomical and functional images clearly give very different views on the human body, it is also true that PET images, whether they represent metabolism, blood volume, or receptor binding, will exhibit a spatial morphology that reflects the underlying anatomy. While we cannot be sure of uniform uptake within relatively homogeneous tissue regions, we can be confident that most tracers will exhibit distinct changes in activity as we cross tissue boundaries. Alternatively, we can say that a priori we have no reason to expect smooth variation in tracer uptake across anatomical boundaries, while within homogeneous tissue regions, we are more likely to see smooth variations in uptake, unless there is evidence to the contrary in the PET data itself. Consequently we can use an anatomical prior to influence formation of the PET image by indicating those regions in which, a priori, we are more likely to see more abrupt changes in activity. Importantly, this does not mean that there must be such a change, but rather that changes in these locations are more likely. In Section 3.2 we describe how these ideas can be encoded within an image reconstruction algorithm using Bayesian and related formulations.

3.1 Improving Quantitation through Partial Volume Correction

If we assume accurate calibration and normalization, the reconstructed radiotracer concentration within each voxel differs from its true value because of two main effects: spread of activity into neighboring voxels and spill-over of activity from neighboring voxels. The former effect reduces the measured activity concentration while the latter effect increases it. In addition, the size of PET image voxels is usually a few mms and may contain two or more different tissue types. As a result, the activity concentration in each image voxel is a weighted average of the concentration in each tissue type. For quantitative studies of small structures, such as brain FDG scans of neurodegenerative diseases, this may cause significant errors in data analysis. Meltzer et al (34) implemented a two-compartment method to account for the loss of signal in gray matter (GM) due to the influence of cerebrospinal fluid (CSF). Later a three-compartment method was proposed to correct for the different uptake in GM and white matter (WM) (35). The corrected PET image can be represented as:

$${\lambda }_G(x)\approx \frac{\lambda (x)-c_W(s_W(x)\otimes h(x))}{s_G(x)\otimes h(x)}$$ (5)

where λ(x) is the reconstructed image value in location x, s_W and s_G are the support function of the WM and GM respectively, h(x) is the point spread function and c_W is the (assumed) known concentration of radiotracer in WM. This method assumes the GM concentration has small variation near a mean value, WM concentration is constant and CSF concentration is 0.

In another approach proposed by Rousset et al (36), multiple regions were considered and the regional spread function (RSF) of each calculated. The RSF is then used to compute a regional geometric transfer matrix (GTM) between different regions. The true concentrations of the regions are derived by inverting the GTM and multiplying by the measured regional concentrations.

All partial volume correction methods require segmentation of the MR images and are therefore affected by any segmentation error (37). In addition they assume a piecewise constant activity in the regions surrounding the tissue of interest and tend to be sensitive to noise in the data. The use of these methods has so far been restricted to specific applications, such as correction for the effect of cerebral atrophy (38).

3.2 Anatomically Guided PET Image Reconstruction

Rather than using the anatomical MR image for post correction of partial volume effects, an alternative approach is to use the MR image to constrain the reconstruction directly, effectively trying to incorporate partial volume correction directly into the reconstructed image. As noted above, the most common framework in which this has been done is using the MRF prior.

3.2.1 Markov Random Fields

The MRF is a probabilistic image model with properties that allow one to readily specify the joint distribution (within a scale factor) in terms of local “potentials” that describe the interactions between groups of voxels that are mutual neighbors (39). The joint density has the form of a Gibbs distribution:

$$P(\lambda )=\frac{1}{Z}{e}^{-\beta U(\lambda )}$$ (6)

where Z is a normalizing constant, β is a parameter that determines the degree of smoothness of the image, and U(λ) is the Gibbs energy function, which is formed as the sum:

$$U(\lambda )={\sum }_{c\in ℂ}{V}_c(\lambda )$$ (7)

where V_c(λ) are a set of potential functions, each defined on a clique c ∈ ℂ consisting of one or more voxels all of which are mutual neighbors of each other; here ℂ is the set of all cliques. To complete the definition we need to define a neighborhood system. In 2D images, the neighbors of a voxel could be the 4 or 8 nearest neighbors as illustrated in Fig. 1. Similarly, in 3D, we could define a 6 nearest neighbor, or 26 nearest neighbor system, again illustrated in Fig. 1. As the size of the neighborhood grows, so do the number of possible cliques. For the purposes of this paper we will restrict discussion to a 2D image with an 8 nearest-neighbor system. Extensions to higher dimensions and larger neighborhoods are in principal straightforward, although pose practical problems both in terms of computation cost and in specification of the potential functions and their parameters.

Fig. 1.

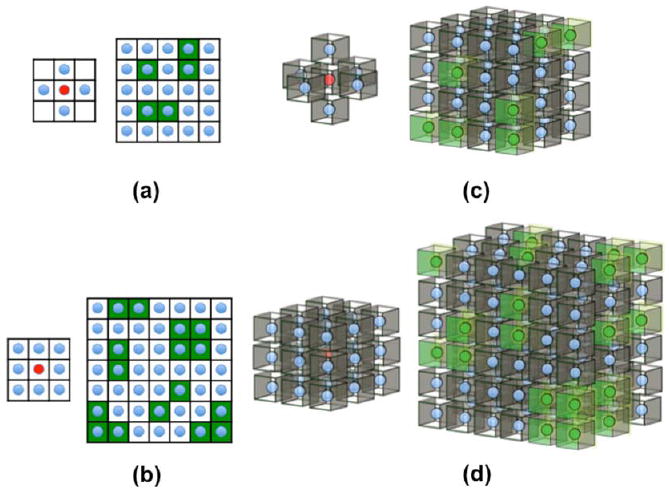
First and second-order neighborhoods and their cliques for Markov random fields: (a) 1^st order 2D neighborhood - the 4 blue voxels at left are the neighbors of the red central voxel; green blocks in the figure at right illustrate cliques of mutual neighbors on which potential functions are defined in eq (7); (b) 2^nd order 2D neighborhood with 8 (blue) neighbors in left figure, green blocks on right show groups of voxels forming cliques with respect to this neighborhood; (c) 1^st order neighborhood in 3D with 6 nearest neighbors and (d) 2^nd order neighborhood with 26 nearest neighbors. In (c) and (d) the groups of green voxels on the right illustrate some of the allowed cliques for their respective neighborhoods.

Let us number the voxels in the image with a single index, i ∈ [1,…. N], and denote the set of neighbors of voxel i as ℕ_i, then for the 8-neighbor system we can write the Gibbs energy function as:

$$U(\lambda )={\sum }_{i=1}^N\varphi ({\lambda }_i)+{\sum }_{i=1}^N{\sum }_{j>i,j\in {\mathbb{N}}_i}\psi ({\lambda }_i,{\lambda }_j)+\mathit{higher\; order\; terms}$$ (8)

where the higher order terms include three or more voxels. The first term on the right hand side allows us to specify properties we may know about individual voxels, but it is the second term that forms the basis for most MRF priors used in tomographic image reconstruction. This term specifies a potential function or penalty on each pair of neighboring voxels. Typically this is done through specification of a weighted function of their difference:

$$\psi ({\lambda }_i,{\lambda }_j)={\beta }_{\mathit{ij}}\gamma ({\lambda }_i-{\lambda }_j)$$ (9)

with the constraint that γ(λ_i − λ_j) ≥ 0 and that the function is monotonically nondecreasing in |λ_i − λ_j|.

Choice of the function γ(λ_i − λ_j) and the associated weights β_ij determine the properties of the prior. The simplest and most widely used is the quadratic penalty: γ(λ_i − λ_j) = (λ_i − λ_j)². When the image has the same value at each voxel, the potential functions and hence the energy function U(λ) are zero and the probability density function $P(\lambda )=\frac{1}{Z}{e}^{-\mathit{\beta U}(\lambda )}$ is at its maximum value. As the difference between voxels increases, so does U(λ), with P(λ) decreasing correspondingly, indicating less likely images. The advantage of this weighting is that it tends to produce the most natural looking images. The disadvantage is that the quadratic penalty between voxel differences attaches very low probability to large changes so that reconstructed images tend to be smooth. A large number of alternative functions have been explored that reduce the penalty for larger differences as illustrated in Fig. 2 (40).

Fig. 2.

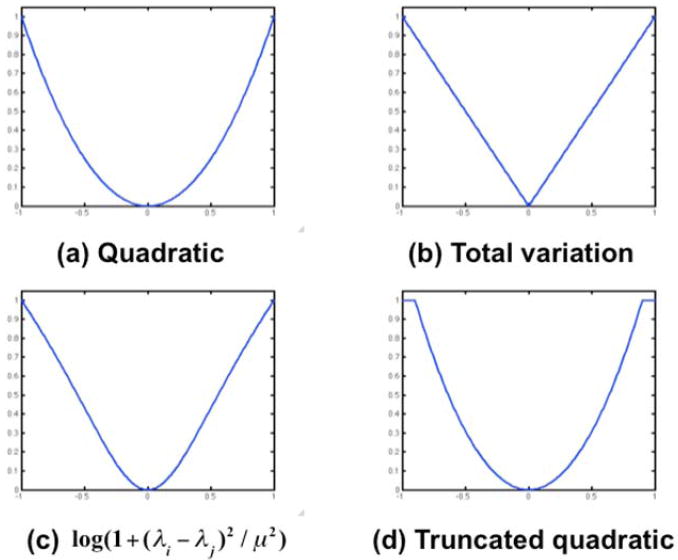
Illustration of different possible choices for the potential function γ(λ_i – λ_j). The quadratic penalty tends to produce globally smoother images; the alternatives attempt to achieve a trade-off between local smoothness and allowing occasional large changes to reflect changes in uptake at organ or lesion boundaries in the PET image.

In all the cases shown in Fig. 2, other than the quadratic penalty, the goal is similar: to attach lower probability to images that are not locally smooth but without over-penalizing occasional large changes that might correspond, for example, to organ boundaries. Interestingly the total variation (TV) prior in Fig. 2b is equivalent to the TV norm that is now commonly used in the context of much of the recent literature on sparse imaging (41).

To complete specification of the prior we need to also specify the smoothing parameters. In the absence of anatomical scans, we would intuitively use the same value of the smoothing parameters β_ij for each voxel pair. In fact for PET data, Fessler and Rogers (42) have shown that this leads to a spatially variant resolution in the image that depends on the Fisher information matrix (FIM), a measure of the information content in the data about the unknown image. By locally adjusting β_ij based on the FIM, we are able to achieve approximately uniform resolution (43) when using the quadratic potential function.

3.2.2 Incorporating Anatomical Boundaries and Regions in MRFs

When we introduce anatomical information we are specifically attempting to achieve a nonuniform resolution since we use anatomy to guide the formation of boundaries in the PET image. In this case we can make the β_ij parameters dependent on the edge strengths in the MR image. Suppose we apply an edge detection operator to the MR image, f, to produce an edge strength map g. Then the simplest approach to using anatomical information to guide formation of the PET image is to set β_ij = F(g_i, g_j) where F(g_i, g_j) is a function whose value is small when the two edge strengths are large (a small penalty for an edge in the PET image) and large when the edge strengths are small (a higher penalty for an edge in the PET image). Specific algorithms will then differ in the manner in which the edge map g is computed, in the choice of the weighting function F(g_i, g_j), and also in the associated choice of the potential function γ(λ_i − λ_j). This process with a quadratic penalty with weights dependent on boundary locations in a segmented volumes is described by (44) and (45). To account for possible misregistration between the anatomical and functional images, some degree of blurring can be applied to the estimated edge maps (44). Bowsher et al (46) avoid using a segmented anatomical information but attach nonzero weight to only those cliques consisting of voxels whose intensities in the anatomical image are sufficiently close.

One can also introduce the anatomical priors through use of a “weak membrane” model in which a quadratic penalty is used within homogeneous regions, but at boundaries no penalty is applied, effectively making the weight F(g_i, g_j) = 0 at these locations and performing no smoothing across anatomical boundaries (47). The use of larger neighborhoods for the MRF allows introduction of the higher order terms in eq (8). In this way analogs of mechanical models can be introduced into the prior where the image reflects the bending of a thin metal plate (47). Anatomical boundary information can then be used to control the bending of this plate by weighting interaction terms in a similar manner to that described above (48). In the limiting case where weights go to zero at boundaries, this leads to the “weak plate” model that allows penalized discontinuities in the PET image across anatomical boundaries (47).

A related approach is to first attach a label C_i to each of the voxels f_i in the MR image through a segmentation process (e.g. in brain images, we can label brain voxels as WM, GM or CSF) and then define weights β_ij = F(c_i, c_j) based on the labels of the two voxels (49, 50). A variation on this framework uses the segmented anatomical image to define different distributions in the prior as a function of tissue type, essentially defining a tissue mixture model (51).

Segmented MR images can also be used in the context of a hierarchical MRF model. In these models, rather than model the PET image intensity itself as a MRF, we model regions in the image using one discrete label for each region or tissue type. The MRF is then defined on this discrete image using a Potts model (52). As with eq (7), the Gibbs energy function is defined on cliques of neighboring voxels in such a way as to encourage formation of contiguous homogeneous regions (53). The PET image is then defined in terms of a PDF conditioned on this underlying segmented model. When anatomical information is available, these can be used to modify the Potts model for the segmented PET image so that it largely follows the underlying morphology but with sufficient freedom to allow the formation of lesions or other structures in the PET image that may not be well defined in the anatomical image.

Compound MRF models are able to explicitly model boundaries in the image. This is achieved by augmenting the image intensity values, λ_i, with a set of binary random variable “edge processes”, ι_ij, representing the presence (ι_ij = 1) or absence (ι_ij = 0) of an edge or boundary between that pair of voxels (31). The compound MRF model includes a neighborhood system consisting of a combination of voxels and edge processes. The potential functions are defined in such a way as to encourage the formation of contiguous regions of similar intensity separated by continuous boundaries formed by connected vertical and horizontal edge processes as illustrated in Fig. 3.

Fig. 3.

Line sites between each pair of image voxels. Three different regions are shown where image voxels are represented with different intensities. Line sites are equal to 1 (solid bars) on the boundaries of the regions and 0 (open bars) elsewhere.

To use this model for incorporation of anatomical information, we used a segmented MR image to define likely locations of boundaries and used these as weights in the Gibbs energy function which had the following form (54):

$$U(\lambda ,l)={\sum }_i{\sum }_{j>1,j\in {\mathbb{N}}_i}\left\{\beta {({\lambda }_i-{\lambda }_j)}^2(1-l_{ij})+\alpha l_{\mathit{ij}}+H(l_{\mathit{ij}})\right\}$$ (10)

where the first term corresponds to a quadratic potential function when the associated line process is off, but is turned off when the edge is present. The second term penalizes the nonzero line sites in the image thus avoiding too many edges. The third term is used to encourage formation of closed and connected boundaries and defined on cliques consisting of two or more line process variables. Incorporation of anatomical information in this context is straightforward by using the location of anatomical boundaries to spatially modulate the weights α to encourage formation of similar boundaries in the PET image (54, 55). Extensions of this approach include methods in which the edge processes are solved for implicitly to reduce computational costs, as described in (56).

Fig. 4 shows this approach applied to simulated brain phantom data from (54). A patient MR image was segmented into four regions: WM, GM, lesion and ventricles. A hot spot was inserted in the left side of the WM to simulate functional edges not present in the MR image. The result clearly shows the benefits of using the anatomical edges including improved gray/white matter contrast and better visibility of the functional lesion.

Fig. 4.

(a): Original MR brain image. (b): Segmentation of (a) into four tissue types. (c): Anatomical boundaries extracted from (b). (d): Computed PET phantom generated from MR template (b). (e): PET reconstruction using filtered backprojection. (f): PET reconstruction using maximum likelihood estimation. (g): PET reconstruction using a simple quaratic MRF model. (h): PET reconstruction using a compound MRF model without anatomical prior (i): PET reconstruction using compound MRI with anatomical prior. Reprinted with permission.54

One of the disadvantages of the line site model is that there is no guarantee that the reconstructed edge sites form continuous boundaries. The use of the Potts MRF model in which the PET image is explicitly segmented avoids this problem, but presents additional computational challenges related to the need to optimize over many discrete variables. An alternative to explicit use of line sites is to instead model continuous boundaries directly. This was done by Cheng-Liao and Qi using a level set function (LSF) to represent the continuous boundaries in the functional image (57). The anatomical image is then used to influence the location of the estimated functional boundaries. In a related approach, Hero et al (58) used B-splines to represent boundaries in the PET image, again using the anatomical image to guide its formation. Another interesting approach is to use the anatomical image to generate an irregular mesh (rather than a uniform voxel grid) on which to reconstruct the PET image (59). In this approach the anatomical image is first segmented. The curves (or surfaces in 3D) representing tissue boundaries, and the regions inside them, are then tessellated so that the mesh reflects the underlying anatomy. Reconstruction of the PET image on this mesh, with local MRF smoothing based on adjacency in the mesh will naturally encourage formation of a PET image that reflects underlying anatomy.

3.2.3 Information Based Methods for Incorporating Anatomical Priors

The methods presented in the previous section almost all rely on boundary or regional information extracted from the anatomical image by segmentation or edge detection. Another approach that avoids this requirement is to maximize an information-based similarity measure between the anatomical and reconstructed PET image. These methods are inspired by the great success found in coregistration of multimodal images based on mutual information (60). The essential idea is that while anatomical and functional images represent different parameters, they are mutually informative: you can infer something about the functional image from the anatomical image, and vice versa. This should in turn be reflected in their joint density function, p(λ, f). Given an image pair λ and f we can estimate this density using the joint histogram. An information measure I(λ, f), such as the Kullback-Leiber (KL) distance, joint entropy or mutual information, can be used to quantify the degree to which p(λ, f), (or its estimate) reflects consistency between the two modalities. Maximization of this metric in combination with the likelihood function for the data therefore leads to a PET image that, in some sense, extracts the most information available from the anatomical image. The methods we review below differ primarily in the choice of this metric.

The general formulation of the inverse problem in this case can be written as:

$$\widehat{\lambda }=\arg {\max }_{\lambda \ge 0}\{\mathit{Ln\; P}(Y\mid \lambda )+\beta I(\lambda ,f)\}$$ (11)

By comparison to eq (4) we see that this is similar to the MAP formulation with the information theoretic measure replacing the role of the log of the prior density.

One of the earliest papers to use this approach (61) used a modified KL distance as a measure of dissimilarity between the two images:

$$I(\lambda ,f)={\sum }_i\left[{\lambda }_i\ln \left(\frac{{\lambda }_i}{f_i}\right)-{\lambda }_i+f_i\right]$$ (12)

To encourage edge formation in the reconstructions the anatomical image was first preprocessed with an edge-preserving filter. This differs from later work in the sense that the images themselves are used as the sample PDFs rather than their histograms. This results in a far simpler computational problem but will of course produce quite different results.

Interpreted in the usual sense, information measures are computed on the joint density p(λ, f). By quantizing the voxel intensities we can estimate this density as p̂(Λ_k, F_l), k = 1,… K, l = 1, … L, equal to the fraction of voxels that have the value λ_i = Λ_k when f_i = F_l. The Parzen window estimate of the joint density, which makes numerical optimization more straightforward and works with fewer voxels, computes a continuous estimate of the joint density as

$$\widehat{p}(\mathrm{\Lambda },F)=\frac{1}{N}{\sum }_i\vartheta (\frac{\mathrm{\Lambda }-{\lambda }_i}{{\sigma }_{\lambda }})\vartheta (\frac{F-f_i}{{\sigma }_f})$$ (13)

where ϑ(.) Is a compact window function whose extent is determined by the parameters σ_λ and σ_f. The Mutual information (MI) between two random variables can be computed as

$$I_{\mathit{MI}}(\lambda ,f)=H(\lambda )+H(f)-H(\lambda ,f)$$ (14)

where the entropy H(λ) and joint-entropy (JE) H(λ, f) are defined as

$$\begin{array}{cc}H(\lambda )=-\int p(\lambda )\log (p(\lambda ))\mathit{d\lambda }& H(X,Y)=-\int p(\lambda ,f)\log (p(\lambda ,f))\mathit{d\lambda df}\end{array}$$ (15)

and can be computed from the estimated PDFs defined above. By substituting the numerical approximation of MI into eq (11) and optimizing it, we can compute the PET image consistent with the data with maximum MI relative to the anatomical image.

Using a phantom simulation data, Nuyts showed that MI-based anatomical priors may introduce bias in the PET image estimates due to the tendency to create separate clusters in the marginal histogram of the PET image (62). By using JE instead of MI (i.e. by ignoring the marginal entropy terms H(λ) and H(f)) he found that this problem can be avoided. In related work, Tang and Rahmim (63) used a JE prior between the intensities of anatomical and functional images and used a one-step-late MAP algorithm for PET image reconstruction. We also found a similar bias issue when comparing MI and JE based priors (64). In (65), a Bayesian joint mixture model was formulated and PET image reconstructed by minimizing a joint mixture energy function including the MI between anatomical and functional class labels. A parametric model was used where the class conditional prior was assumed to have a Gamma distribution.

The information-based measures described so far make the implicit assumption that all voxels are spatially independent. In other words, we would obtain identical MI or JE measures if the anatomical and PET image voxel indices were randomly reordered (provided we retain the same pairing). For this reason, these methods do not directly exploit the spatial structure in the images. In our recent paper we investigated the use of a scale space representation of the image (64). A three-element feature vector at each voxel location was formed by concatenating, for each modality, the original image, the image blurred with a Gaussian kernel and the Laplacian of the blurred image. Fig. 5 shows these scale-space features for a MR brain image. By maximizing the sum of the JEs for each of these three components, the resulting image directly exploits similarities in structural smoothness (through the Gaussian filtered image) and edginess (through the Laplacian of Gaussian image). A related approach from Tang and Rahmim (66) use mutual information with respect to a multi-scale wavelet representation.

Fig. 5.

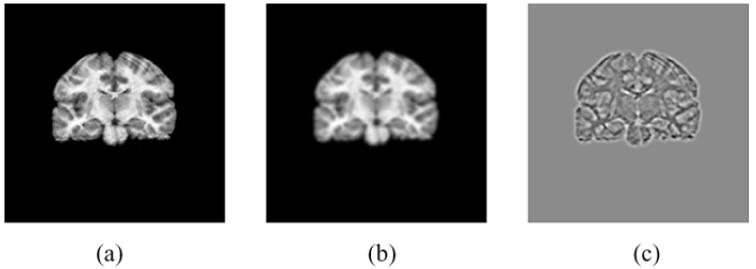
Scale-space features of a coronal slice of an MR image of the brain used for information-based PET image reconstruction with anatomical priors: (a) Original image, (b) image blurred by a Gaussian, and (c) Laplacian of the blurred image in (b). Reprinted with permission.64

Simulation and clinical data show that the MI and JE based priors can improve resolution compared to a simple quadratic MRF prior. Fig. 6 shows the joint PDF of the MR image and the PET image (original and reconstructed using different methods). It can be seen that reconstruction using a JE prior is closer to that for the true PET image than the results either using a standard OSEM-based ML reconstruction or using the MI prior. Fig. 7 shows an application of this approach to reconstruction of a clinical brain scan using F18 Fallypride, a dopamine receptor binding tracer. The JE prior image demonstrates superior definition of subcortical nuclei than obtained using a standard quadratic MRF prior with minimal smoothing, indicating the effect of the anatomical prior in guiding placement of the edges of the caudate and putamen.

Fig. 6.

Joint PDFs of the anatomical image and (a) true PET image, (b) OSEM estimate used for initialization, (c) image reconstructed using MI-intensity prior, (d) Image reconstructed using JE-Intensity prior. Reprinted with permission.64

Fig. 7.

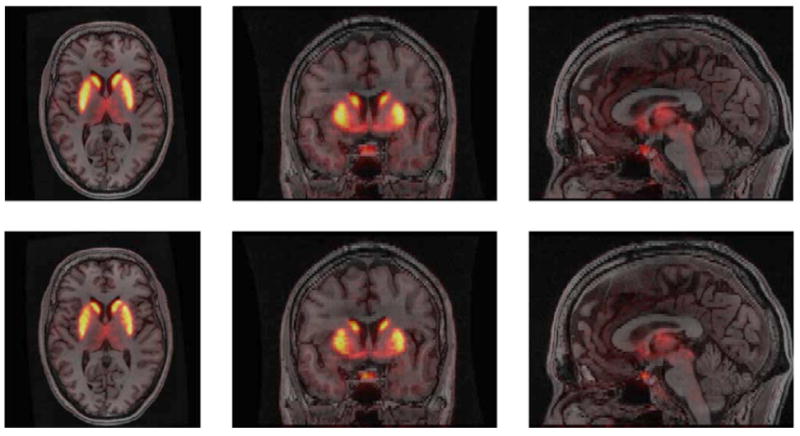
Overlay of PET reconstruction over coregistered MR image for quadratic MRF prior (top) and joint entropy prior (bottom). Reprinted with permission.64

4. Discussion

We have summarized the methods reviewed above in Table 1. Throughout these publications, images reconstructed using anatomical priors have been compared with those reconstructed without. One needs to be careful with these evaluations, because the results may be affected by factors including registration and segmentation error and noise in the MR image. We now consider the performance of the methods in Table 1 as they relate to the two primary tasks for which PET is employed: quantitation and lesion detection.

Table 1.

The approaches reviewed here are summarized in the following table. We indicate the general approach, the form of anatomical information used and whether the method requires segmentation or labeling of the anatomical image prior to use in the reconstruction algorithm.

General Category	Method	Information Used	Anatomical image segmentation	References
Post processing	Two/three compartment	Region	Yes	(34, 35)
	GTM	Region	Yes	(36)
	PML	Region	Yes	(67)
Anatomical prior	Weighted Markov prior	Boundary	Yes	(45, 48)
	Line process	Boundary	Yes	(54-56, 58, 59, 68, 69)
	ALSM	Boundary	Yes	(57)
	Region based prior	Region	Yes	(44, 49-51, 53, 70, 71)
	Bowsher prior	Region	No	(46)
	Cross Entropy	Image intensity	No	(61)
	Mutual information	Image features	No	(62, 64, 65)
	Joint Entropy	Image features	No	(62-64, 66)

4.1 Quantitation

The quantitative accuracy of PET images can be investigated by studying the trade-off between bias (or resolution) and noise properties in reconstructed images. In one of the few papers to compare different approaches to including anatomical priors, Vunckx et al (72) compared three MR-based anatomical priors with EM reconstruction of maximum likelihood images: A-MAP (51), JE-prior (62) and a modified Bowsher-prior (46). The evaluation used a realistic Monte Carlo simulation of a brain with 20 lesions. The parameters for each prior were determined from a preliminary reconstruction using a fast analytical simulator. Quantitative evaluation used a single figure of merit parameter, as well as the bias-noise tradeoff in GM and lesions and the SNR in the lesions. Fig. 8 shows samples of reconstructed images and Fig. 9 shows a bias-noise analysis from a simulated 1 minute FDG brain scan. Overall they found anatomical priors produced significantly better results than ML-EM reconstruction. The Bowsher-prior yielded the best images, while the JE-prior had the worse performance among the anatomical priors and was more sensitive to the reconstruction parameters and the noise in the MR image and PET data.

Fig. 8.

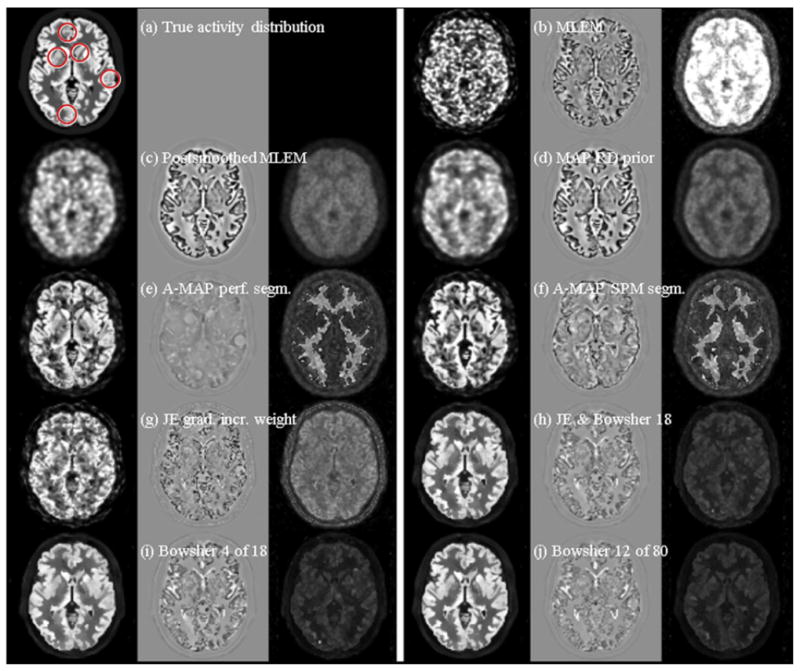
True activity distribution (a) and example reconstruction images (first columns) and the corresponding bias (second columns) and standard deviation images (third columns) of a PET-SORTEO simulated 1-min FDG PET-scan of a brain with hypointense lesions using the simulated noisy MRI. The following reconstruction algorithms were used: (b) MLEM, (c) postsmoothed MLEM (6 mm FWHM), (d) MAP with a quadratic prior, (e) A-MAP using perfectly segmented MRI information, (f) A-MAP using SPM segmented MRI information, (g) JE with gradually increased weight, (h) JE + Bowsher using 4 out of 18 neighbors, (i) Bowsher using 4 out of 18 neighbors, and (j) Bowsher using 12 out of 80 neighbors. Both the bias images and the standard deviation images were multiplied by 3 for visualization reasons. Reprinted with permission.72

Fig. 9.

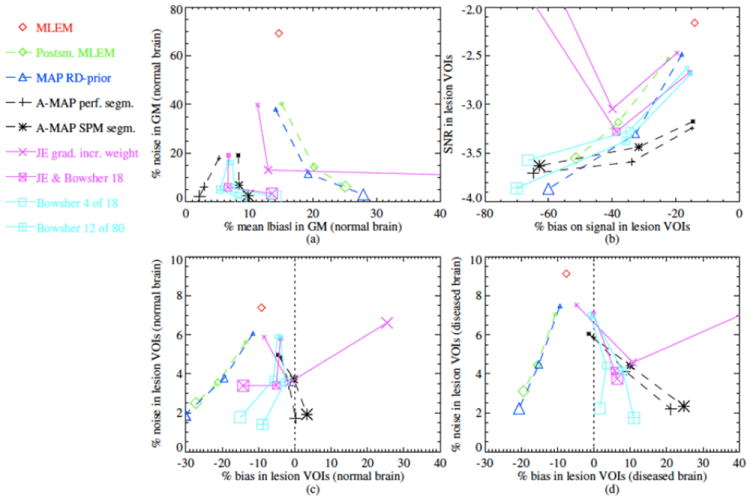
Bias-noise analysis for the reconstructed images in Fig. 8. In (a) the percentage noise in the GM voxels is plotted with respect to the percentage mean absolute bias in these voxels. In (b) the signal-to-noise ratio in the lesion VOIs is plotted with respect to the percentage bias on the signal in the lesion VOIs. In (c) and (d) the percentage noise in the lesion VOIs in the normal brain (c) and in the brain with lesions (d) is plotted with respect to the percentage bias in these VOIs. Reprinted with permission.72

Cheng-Liao and Qi compared their level set method for incorporating anatomical priors with several existing algorithms using simulation data and looked at situations when the anatomical and functional boundaries are not matched (57). The authors concluded that the level set method has better bias-variance performance. Fig. 11 shows the contrast-variance performance from their simulated human phantom data.

Fig. 11.

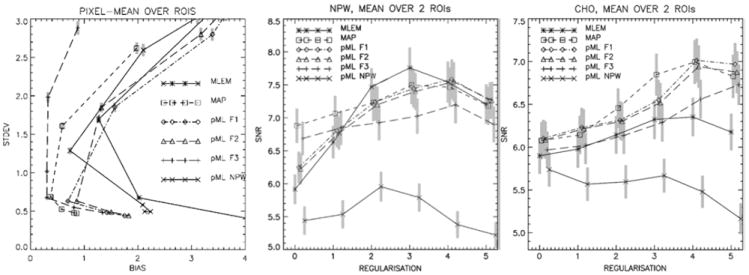
Bias-noise curve (left), SNR for NPW (middle), SNR for CHO (right), averaged over all lesions, as a function of the degree of regularization (0 = minimum; 5 = maximum), using the BRAIN phantom. Reprinted with permission.67

4.2 Detection

Several groups have evaluated the performance of anatomical priors for lesion detection (51, 67, 71, 73-76) using either computer observer or human observers for the evaluation. The most common figure of merit is the area under the receiver operating characteristic (ROC) curve. In general it appears that if the task is to detect lesions with elevated activity, the use of organ boundary does not increase the detection accuracy, while using both organ and lesion boundaries may improve the accuracy, especially when the contrast of activity concentration in lesion and background is high (73, 74, 76). Baete et al (51) compared A-MAP with post-smoothed ML-EM, where the task is detection of hypometabolic regions in brain FDG PET. They calculated the SNR of a non-prewhitening computer observer. A-MAP yields similar SNR as ML-EM with optimal post-smoothing. In (71), similar experiments were done with human observers. The authors found that in contrast to the computer observer result, A-MAP outperforms post-smoothed ML-EM in human observer studies.

Nuyts et al studied the use of anatomical information in lesion detection using simulated phantom data. (67) Two methods were compared. One method uses anatomical priors in MAP reconstruction and the other uses it in post-processing of ML-EM images. The performance was evaluated by computing bias-noise curves and detection performance for non-prewhitened (NPW) and channelized Hotelling (CHO) observers. Results show that post-processing ML-EM images using anatomical information is inferior, unless the noise correlations of the voxels are considered by using a prewhitening filter. The prewhitening filter is not as efficient as MAP with anatomical prior, because it is shift-variant and object dependent. The authors concluded that MAP with anatomical priors is the preferred method. Fig. 11 shows bias vs. variance plots as well as the SNR for the NPW and CHO observers as a function of regularization parameter for this study,

In (75), lesion detectability using anatomical and non-anatomical priors was compared using a CHO. In this case, the authors found no difference in lesion detectability.

5. Limitations and Challenges

We have described the framework for a number of different approaches to incorporating anatomical MR information into PET images and reviewed some of the literature evaluating their performance. It is clear that there is some improvement in quantitation and detection when the anatomical prior provides accurate information about the location of boundaries of lesions or organs in which we want to detect/quantify tracer uptake. As the quality of the MR data deteriorates, or when there is a mismatch between anatomical and functional boundaries, these advantages appear to be largely lost. An important challenge therefore is to ensure that the PET and MR data are well registered or that the methods have robustness to small errors in registration.

One of the potential downsides to using anatomical priors is that we are deliberately making image resolution anisotropic and spatially variant. While this may help compensate for partial volume effects and improve detection or quantitation, it also adds challenges in terms of interpretation since the image reader will not know the true resolution at each location. Analytic methods for estimating the image resolution of MAP estimators (77-79) could be extended to reconstruction using anatomical priors. If successful, the reader could then be provided with a map of the spatially variant resolution, although visual interpretation of this data may still be difficult. A similar approach could also provide useful information about the voxelwise and regional variance and covariance which would be useful for quantitative analysis or computer-observer based detection.

A second related challenge, and possible area for future research, is to apply these approaches to dynamic data. When analyzing dynamic data with kinetic models it is important that the resolution does not vary over time, other time-varying partial volume effects will introduce bias into estimated rate parameters. Consequently, if anatomical priors are to be used for dynamic studies it is important the methods be designed to produce time-invariant spatial resolution for reconstruction of each frame of the study.

In this paper we have focused on the combination of structural MR images with static PET data. We close by noting that both PET and MR are very flexible modalities. PET allows static and dynamic imaging using a broad range of radiotracers. MR has great flexibility not only in the control of tissue contrast, but also in terms of functional imaging (fMRI, dynamic contrast-enhanced imaging, imaging spectroscopy, blood flow, etc). There is therefore the potential for many forms of synergistic combination of PET and MR for which combined image reconstruction and analysis should play an important role in the future.

Fig. 10.

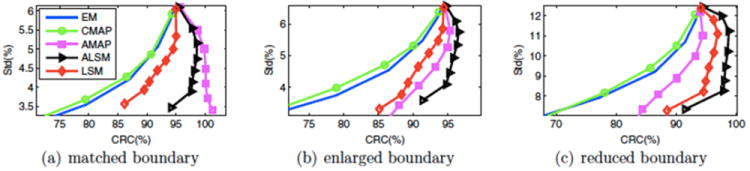
Contrast recover coefficient (CRC) versus standard deviation curves for a human phantom: (a) Matched boundary, (b) enlarged boundary, (c) reduced boundary. Reprinted with permission.57