Mechanistic models of animal migration behaviour – their diversity, structure and use

Abstract

1. Migration is a wide-spread phenomenon in the animal kingdom, including many taxonomic groups and modes of locomotion. Developing an understanding of the proximate and ultimate causes for this behaviour not only addresses fundamental ecological questions but has relevance to many other fields, e.g. in relation to the spread of emerging zoonotic diseases, the proliferation of invasive species, aeronautical safety as well as the conservation of migrants.

2. Theoretical methods can make important contributions to our understanding of migration, by allowing us to integrate findings on this complex behaviour, identify caveats in our understanding and guide future empirical research efforts. Various mechanistic models exist to date but their applications seem to be scattered and far from evenly distributed across taxonomic units.

3. Therefore, we provide an overview of the major mechanistic modelling approaches used in the study of migration behaviour and characterise their fundamental features, assumptions and limitations, and discuss their typical data requirements both for model parameterisation and for scrutinizing model predictions.

4. Furthermore, we review 155 studies that have used mechanistic models to study animal migration and analyse them with regard to the approaches used, focal species and also explore their contribution of advancing current knowledge within six broad migration ecology research themes.

5. This identifies important gaps in our present knowledge, which should be tackled in future research using existing and to-be developed theoretical approaches.

Introduction

Migration is a wide-spread phenomenon in the animal kingdom, occurring in many diverse taxonomic groups ranging from insects, fishes, reptiles to birds and mammals, including all modes of locomotion, in rivers and oceans, on land and through the skies. Understanding this general phenomenon, its proximate and ultimate drivers and determinants, not only touches fundamental ecological questions, but has also relevance to many other fields, e.g. the spread of emerging diseases (Altizer, Bartel & Han 2011), the proliferation of invasive species (e.g. Brochet et al. 2009), aeronautical safety (e.g. Marra et al. 2009) as well as the conservation of migrants (e.g. Wilcove & Wikelski 2008).

Why do animals move? Where to and when? Which factors – local or global – determine the movements? Which physiological, anatomical or behavioural adjustments do animals make before and during migration? What are the fitness and demographic consequences of specific migratory behaviours? These are probably the major questions asked when studying migration (Milner-Gulland, Fryxell & Sinclair 2011). Theoretical methods may substantially contribute to answering them, e.g. via testing alternative assumptions and hypotheses or analysing the response to changing parameter settings (i.e. sensitivity analysis). But they also allow for summarising our present knowledge and thus, identify avenues for focused future research.

Although a variety of migration models exists, their application appears to be scattered and theoretical efforts are far from being evenly distributed across taxonomic units (e.g. Bauer et al. 2009). Furthermore, the recent rapid advances in empirical methods and notably the development of new high-resolution and ultra-light tracking and logging devices (e.g. Stutchbury et al. 2009) have created marvellous datasets on the spatio-temporal distribution of migrants (e.g. compiled in www.movebank.org), allowing for better parameterising and scrutinising of models. Thus, in the wake of these technological advances, we consider it a timely endeavour to promote theoretical frameworks for a causal understanding of animal migrations.

To stimulate the use of modelling techniques, we provide an overview of the existing mechanistic approaches, characterise their general features, assumptions and limitations and data requirements, both for model parameterisation and for scrutinizing model predictions and introduce some applications. Finally, we review the use of mechanistic models across 155 published studies, identify focal taxa and their contribution to present knowledge in six broad research themes within migration ecology, which highlights important knowledge gaps and shows where future work is required.

Delimiting the subject - “migration” and “modelling”

We are concerned with mechanistic (i.e. based on processes underlying migration), mathematical models for the investigation of animal migratory behaviour that aim to increase our understanding of its proximate and ultimate causes (biological and physical) and its consequences.

We define migratory behaviour as being persistent, directional, undistracted by resources that would normally halt it, with distinct departing and arrival behaviours, and energy reallocated to sustain it (cf. Dingle 1996). Therefore, we only include models dealing explicitly with seasonal or life-stage coupled migratory behaviour and exclude models of diel or tidal vertical migration (e.g. Speirs et al. 2002), other non-seasonal within-habitat movements (e.g. Scheibe & Richmond 2002) and also ([meta]-population) studies on dispersal.

Migration may encompass a range of separate behaviours, for which models have been developed, e.g. models of optimal foraging (e.g. Davies, Krebs & West 2012), aerodynamic flight (e.g. McMahon 1989), or fuel use (e.g. Pennycuick & Battley 2003). Rather than addressing these behavioural aspects in isolation, the models we deal with cover bouts of or entire migrations, ideally combining some of the above mentioned behaviours.

The models here reviewed should not be confused with statistical analyses of migration (e.g. Bauer, Gienapp & Madsen 2008), which may also yield predictive models but are not based on (assumed or hypothesised) mechanisms underlying migration (for these see, e.g., Bunnefeld et al. 2011).

The specific modelling approaches

We distinguished the following major modelling approaches: simple analytical models (SAM), game-theoretic models (GT), dynamic optimisation models (also known as stochastic dynamic programming models, SDP), individual-(or agent) based models (IBM), physical transport models (PTM), models based on evolutionary programming (EP) and a few other approaches that fall in none of these categories (see Appendix S1).

Simple analytical models

Structure, assumptions & limitations

SAMs typically consist of a set of (differential) equations that are solved analytically. Predictions are very general, seeking to explain general migration patterns across larger groups, e.g. between species. No distinction is made between individuals, no temporal dynamics included and the environment is typically considered indirectly and very simply, e.g. with a single parameter such as the rate of fuel accumulation for migration.

Data requirements

Only few data are required to parameterise or scrutinise the model but these can be aggregated parameters that are difficult or at least challenging, to determine in the field, e.g. fuel deposition rates.

Applications

Most SAMs in migration research have been straightforward optimality models, first introduced in the pioneering work of Alerstam & Lindström (1990). They predict behaviours that optimize a fitness-relevant currency, such as time, energy or predation risk. By combining relations as to how flight range increases with body stores and the rate at which body stores can be accumulated, they derived a set of predictions on the relationships between maximum and rate of body store accumulation, flight range, predation risk, and staging time at migratory stopover sites under a variety of environmental and migrant-specific conditions.

Modifications of this initial model investigated many facets of migratory behaviour, e.g. how the fuel deposition rate along the migratory route determines the length of migratory steps and the departure fuel loads (Weber & Houston 1997), identified the optimal daily travel schedules - nocturnal, diurnal or a combination (Alerstam 2009); explained migratory detours (Alerstam 2001); or the use of flight mode, i.e. flapping or soaring, in relation to morphological characteristics (Hedenström 1993). Most SAMs have specifically addressed bird migration but the fundamental relation between distance moved and fuel load (the “range equation” in birds) has been extended to animals with other locomotion modes (Hedenström 2003a, Hedenström 2003b) and to identify the energetic and biomechanical constraints for migration of animals with different body sizes (Alexander 2002; Hein, Hou & Gillooly 2012).

Game theoretic models

Structure, assumptions & limitations

Seeking explanations for the co-existence of multiple behavioural strategies, GTs investigate the behaviour of players in strategic situations. Players can be individuals, populations or any relevant organismal unit. The success (fitness) of a player depends both on its own decision and on the choices made by all other players. The aim of a GT is to find the evolutionarily stable strategy (ESS), i.e. the strategy that, if adopted by all members of a population, cannot be invaded under natural selection by another strategy (i.e. the Nash-equilibrium). Central to GT models are pay-off tables that define the costs and benefits of each behavioural alternative, given the behaviour of the other players.

Data requirements

Usually, no specific data are required but the general patterns that the model aims to explain, e.g. in a migration context: which proportion of the population migrates or remains resident under which conditions.

Applications

GTs have mainly addressed the issue of differential migratory strategies within a population; how can different strategies co-exist, e.g. among sex and age groups (e.g. Kaitala, Kaitala & Lundberg 1993; Kokko 2011). The decision to migrate or not can usually only be evaluated when considering competing activities, such as breeding or territory acquisition. For instance, using a GT approach Kokko (1999) addressed the problem an individual migratory bird is facing that needs a breeding territory on the breeding grounds (favoured by early departure from wintering grounds), but also strives for maximizing the chances of successful migration (favoured by later departure). Obviously, in the absence of competition for breeding territories, birds would stay longer in the wintering quarters, with an increasing tendency for an earlier departure from the wintering grounds as competition for breeding territories increases.

Although pure game-theoretic models are relatively rare in migration studies, other modelling approaches, e.g. dynamic optimisation models (see below) can include game-theoretic aspects if for situations when the behaviour of an individual or a group cannot be determined in isolation from others.

Dynamic optimisation models

Structure, assumptions, limitations

SDPs are temporally and spatially explicit. The basic ingredients are state variables, decisions and a currency. State variables represent physiological, morphological or environmental characteristics relevant to the animals’ behaviour, e.g. body reserves, age, immuno-competence. An animal can choose from a set of actions (e.g. migrate or stay); the decision for a particular action depends on the animal’s state and on costs and benefits of this action. For instance, staying on a site allows foraging and, thus, increasing body-stores and a higher chance of a successfully completing migration but potentially increases the animal’s susceptibility to predation. These costs and benefits depend on internal (e.g. flight and foraging costs) and external constraints (e.g. food availability, weather conditions), that may or may not be stochastic. The currency is assumed to be (a correlate of) fitness, e.g. expected reproductive success. SDPs assume that evolution has shaped the behaviour of individuals, i.e. at any point in time the animals make decisions based on their state and the (stochastic) internal and external constraints that ultimately lead to the maximization of the currency. How state variables are translated into the currency is a crucial input to the model, which is called the terminal reward function (e.g. how the animal’s state at the last time step translates into reproductive success).

The optimal behaviour is found using a backward iterative procedure, a technique known as dynamic programming. Important to note here is that SDPs do not require the a priori formulation of trade-offs, i.e. how an animal makes a decision between alternative behaviours, but this is a resultant of the model. Once the optimal behaviour has been calculated, a Monte-Carlo simulation is run following optimal migrants in time, generating individual time-trajectories, which may be influenced by stochastic wind or food conditions. The predictions thus yielded can be compared to and thus, scrutinized by, empirical data of individual migration behaviour.

In their simplest form, SDP models require a minimal number of state variables (e.g. body stores level and location) and internal (e.g. flight costs) and external (e.g. food availability, predation risk) constraints. Computation time increases drastically with the number of state variables and as with any increase in complexity, results become increasingly more difficult to analyse and interpret.

Interactions between individuals (such as effects of resource-depletion or density-dependent decreases in fecundity) and their environment can only be included in a restricted manner. If direct interactions are important, a game-theoretic approach might be necessary, setting strong restrictions to the number of interacting individuals.

The explicit assumption that animals behave optimally under the given conditions implicitly assumes that animals are omniscient about their environment. This may be violated, notably when migrants face novel environmental changes (e.g. as a result of global change processes). On the other hand, this characteristic may also allow for assessing the consequences of a lack of knowledge in a rapidly changing world (e.g. Klaassen et al. 2006).

Elaborate background and methodology can be found in the excellent textbooks of Houston & McNamara (1999) and Clark & Mangel (2000).

Data requirements

For model parameterisation, internal and external constraints (e.g. the costs of locomotion and food availability in space and time) need to be known as well as how these change the values of state variables (e.g. how food availability affects body stores). Model predictions are ideally scrutinized by spatio-temporal explicit data of the population along the migratory route (e.g. count data) or individual migration data from tracking studies.

Applications

SDPs for migration have investigated single journeys, e.g. migration from the wintering to the breeding grounds, and the full annual cycle.

Many single journey SDPs have investigated the influence of conditions on stop-over sites on bird migration behaviour (e.g. Weber, Ens & Houston 1998, Clark & Butler 1999; Farmer & Wiens 1999, Purcell & Brodin 2007, Bauer, Ens & Klaassen 2010), the impact of global changes on stop-over site use (Weber, Houston & Ens 1999, Bauer et al. 2008) but also the managing of migrant populations at lowest economic cost (Klaassen et al. 2008a). Besides birds, SDP models have also investigated the spawning migrations of cod assuming optimal energy allocations (Jørgensen & Fiksen 2006, Jørgensen et al. 2008).

A more complex type of SDPs are annual routine models, which investigate the scheduling of competing life-history activities (e.g. migration, breeding, moult) over the course of a year. Annual routine models not only calculate the optimal behavioural annual routine but also identify how decisions are being translated into fitness via the state variables (terminal reward). Since annual routine models deal with several life-history activities and the selection pressures that shape them, they usually require additional state variables, e.g. including moult requires feather quality to be included as a state variable.

In annual routine models, costs and benefits of particular activities often depend on the behaviour of other animals (density- and/or frequency dependence) and thus, include game-theoretic aspects. Annual routine models have investigated the timing of migration in the context of a bird’s annual routine (McNamara, Welham & Houston 1998) and the timing of moult, migration and breeding (Holmgren & Hedenström 1995; Barta et al. 2008) but also the timing of overwintering migrations in zooplankton (Varpe et al. 2007; Varpe et al. 2009).

Individual-based or agent-based models

Structure, assumptions, limitations

Individual-based or agent-based models (IBM) specify rules for the behaviour of individuals and then follow these individuals through time and space. It is thus assumed that individuals, their actions and interactions with one another and the environment, affect the system as a whole. The properties on the population level naturally follow from the individual behaviours and interactions and thus, deliver mechanistic explanations for emergent system properties.

The fundamental units in these models are individuals (agents), which are characterised by a set of state variables and can chose from a set of actions. The individuals are followed over time and usually also over space. Individuals can interact with one another and with their environment. Consistent individual differences, individual adaptive behaviour, local interactions and random events play an important role. The environment is typically included in an explicit, realistic, detailed manner, e.g. as a grid, where grid-cells represent spatial units of the individuals’ environment and are also characterised by a set of relevant state variables.

IBMs are typically parameter-rich and complex numerical simulation models. A challenge lies in justifying the model assumptions, managing the complexity and uncertainty in model structure and parameters, analysing model results and communicating the model to the scientific community. Strategies have been developed to deal with these particular difficulties to make individual-based modelling more rigorous and comprehensive, such as pattern-oriented modelling to scrutinize model predictions (Grimm et al. 2005) and the “ODD” (Overview, Design concepts, Details) protocol to communicate IBMs (Grimm et al. 2006; Grimm et al. 2010). In pattern-oriented modelling, patterns (i.e. quantitative and qualitative knowledge) observed in empirical studies are assumed to be characteristics of a system and thus, indicators of its essential underlying processes and structures. Hypothesized mechanisms can thus be tested in a model on their potential of reproducing observed patterns (i.e. qualitative and quantitative knowledge). Ideally, a successful model explains multiple patterns at different scales and/or hierarchical levels while keeping model complexity as low as possible.

Excellent general introductions to IBMs can be found in Grimm & Railsback (2005) and Railsback & Grimm (2012).

Data requirements

The empirical knowledge required to parameterise IBMs tends to be (very) large. Relevant information about the individuals has to be compiled; hypotheses about their behaviour, decision-makings, interactions with one another and the environment, etc. have to be incorporated in the parameterisation of the IBM. Additionally, patterns on multiple spatial or temporal scales are required for model validation and scrutinizing its predictions. IBMs thus require expert knowledge on individual behaviours (rules) and the quantification of patterns at a higher level than individuals, e.g. population dynamics, spatial distribution, etc.

Applications

IBMs have become very popular over the past decades and have been applied to many migrating animals and particularly successfully to fish. One remarkable finding was the potential effect of numerical domination of inexperienced individuals leading to the development of new migration routes (Huse, Railsback & Ferno 2002). Huse et al. (2004) also simulated interactive migration patterns of predatory cod (Gadus morhua) and their capelin prey (Mallotus villosus). More applied questions have been addressed using IBMs, such as the effect of fisheries on migration routes or population dynamics (e.g. Jorgensen et al. 2008; O'Callaghan & Gordon 2008).

In birds, research questions included the identification of decision rules for migration routes and schedules (Erni, Liechti & Bruderer 2003; Duriez et al. 2009; van Loon et al. 2011), individual variability in currencies (Vrugt, Van Belle & Bouten 2007), how territory acquisition can shape migratory arrival patters (Kokko et al. 2006), but also applied issues such as the consequences of habitat loss are on the annual cycle and population dynamics (Pettifor et al. 2000).

Physical transport models

Structure, assumptions, limitations

PTMs have been incorporated as sub-models in IBMs or used as particle tracking models on their own. They describe the environment (i.e. the medium in which animals move) in great detail both in space and time. For instance, ocean circulation models describe currents, including wind data, heat fluxes and freshwater exchange (for review of these, see Fossette et al. 2012) and animals with a relatively low movement-speed compared to that of their environment are typically assumed to be transported passively (or observed movements are contrasted with those of passively moving particles). Thus, PTMs generally concentrate on the dynamics of the physical environment but often neglected the movement capabilities of the study organisms.

Data requirements

Enormous data over large spatial scales, with a high spatio-temporal resolution are required to parameterise PTMs. However, many data and models are increasingly freely available (for overview of ocean particle tracking data and models, see Fossette et al. 2012) .

Applications

PTMs have typically been employed for species whose movements are influenced by air flows or currents, such as in insects and many marine animals (e.g. sharks Sleeman et al. 2010, cod (Gadus morhua) larvae Vikebo et al. 2007, or capelin Barbaro et al. 2009). Many of the insect PTMs hindcasted the likely origin of migrating insects (e.g. Otuka et al. 2010).

Some recent PTMs have included biological attributes in the model in addition to physical attributes of the environment, such as active swimming or flying in a persistent direction, and active height/depth selection, and have shown that these active behaviours can make substantial differences to the migratory routes and the success of the migration in even comparatively slow-moving organisms (e.g. Fiksen et al. 2007; Chapman et al. 2010; Chapman et al. 2012; Scott, Marsh & Hays 2012)

Evolutionary programming models

Structure, assumptions & limitations

Evolutionary programming (EP) methods are a group of optimization techniques that include genetic algorithms, evolutionary strategies, genetic programming, and (artificial) neural networks. These techniques use methods analogous to biological principles, e.g. mutations and crossovers (genetic methods), strengthening of preferred pathways (neural networks), and natural selection. EPs typically apply four main steps in the search of a near-optimal solution: First, many potential solutions (i.e., “offspring” in natural selection) are generated, and the success of each solution is quantified (“competition”). Subsequently, the least successful solutions are removed (“death”), and the successful solutions generate (“birth”) related (“mutation”) solutions that may be superior to those of their parents. This cycle may repeat for thousands of generations, with incrementally superior solutions selected, until the solution is sufficiently close to some target, which, e.g., may result from field observations.

Often, EP models are based on IBMs where the behaviour of model individuals is subject to an optimization procedure similar to natural selection. EP methods thus provide a means for studying the evolution of behaviour and the force of selection on behaviour. Additionally, they have also a strong population level- component since they incorporate biological details such as density and frequency dependence, co-evolution, etc.

EP methods are particularly appropriate for optimisation problems that involve large (high-dimensional) state spaces that are simply too large for dynamic programming methods to provide an efficient solution. For example, if there is a high level of environmental uncertainty and unpredictability, then it is difficult to store all environmental states within an SDP. As a consequence of the high complexity of EPs, their parameterisation, tests and analyses may be very arduous.

Data requirements

Similar to IBMs, the data requirements for EPs are considerable. Besides information that is needed in constructing an IBM, additional parameters may be needed to define the selection criteria to drive the evolutionary modelling process.

Applications

There are only a handful of examples where evolutionary models were applied to migration phenomena, e.g. the evolution of wildebeest (Boone, Thirgood & Hopcraft 2006) and fish migration (Giske, Huse & Berntsen 2001), consequences of global environmental changes on the migration of capelin (Huse & Ellingsen 2008). Another EP exercise covering the full life-cycle of fish was conducted by Huse & Giske (1998) investigating a range of hypotheses on how fish find their way.

Reviewing the use of mechanistic migration models

We reviewed 155 mechanistic modelling studies with regard to approach used, focal taxa, and central research questions being addressed (see Table S2 for full list and categorisation).

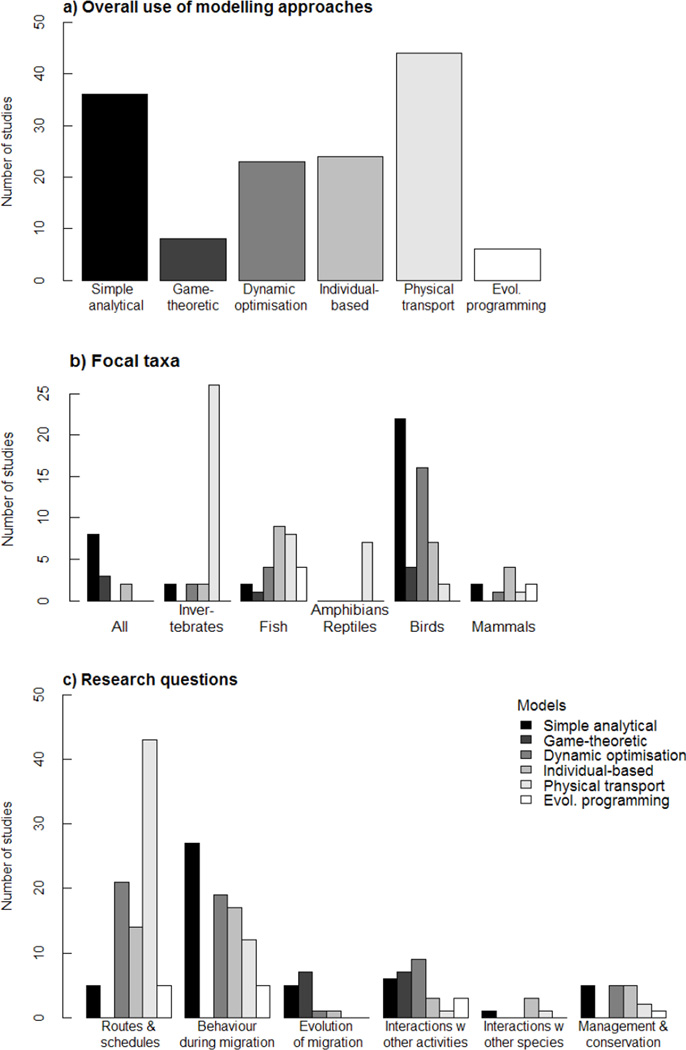
Apart from game-theoretic and evolutionary programming models, all other models were used relatively frequently in migration studies with physical transport and simple analytical models being the most frequently used approaches (Fig. 1a).

Fig. 1.

Overview of the modelling approaches reviewed here, their target organisms and the research questions in the 155 theoretical studies considered here.

There was a striking disparity in the focal taxa with birds being the by far most frequently tackled group, followed by the still frequent insect and fish studies, while reptiles and mammals were represented by only a handful of publications (Fig. 1b). This bias is probably due to the fact that bird migration is so apparent and has long fascinated man. Theoretical studies on insects and fish are likely driven by the strong economic interests of predicting their movements. The poor representation of other taxa might additionally be explained by the difficulties of tracking these animals for prolonged periods of time – be it because they are too small to be followed with current technology or because of their secretive way of life.

The application of the individual modelling approaches to animals of different taxa was highly non-uniform (Fig. 1b). Given their good representation among the studies reviewed, studies on birds and fish showed the largest variety in modelling techniques. In birds, simple analytical and dynamic optimisation models were the most frequently used approaches. Conversely, numerical models seem to be very well represented in fish, where good quantitative predictions of spatio-temporal distributions are an important economic objective for fisheries. Not surprisingly given their small size and reliance on wind patterns for migration there was also a striking bias in insect studies towards physical transport models.

Challenges in Migration Research

Building on the topics suggested by Bowlin et al. (2010), we identified six broad research themes that highlight different facets of migration. Migration routes and timing of migration are aspects that are addressed in almost 90% of all modelling studies, using close to the full variety of techniques (Fig.1c). Most of these models have assisted in identifying crucial environmental variables that determine spatio-temporal variation in migration. Opting for the right behaviour during migration allows migrants to face many challenges during their journeys. It are these decisions, related to finding the way (orientation and navigation), choosing travel speed and altitude/depth, adjusting body morphology and physiology (e.g. organ flexibility, metabolic rates), and engaging in specific social interactions when travelling in groups that are explicitly addressed in approximately 80% of the mechanistic modelling studies, again using a large variety of techniques. Still, key-insights for these questions have undoubtedly been gained with simple analytical models and with the flight range equation in particular (Alerstam & Lindström 1990 and follow-up studies, see Table S2).

Thus, the studies within these first two themes attempted to establish a mechanistic link between migratory movements and ecological or internal factors. This contrasts to Holyoak et al. (2008) who reviewed movement literature at large and found a striking preponderance of descriptive studies. This discrepancy highlights an important corollary of developing a model, namely that a hypothesis on causal relations has to be formulated.

The evolution of migration has importantly been addressed with GT models. These are ideally poised to address questions like why animals choose to migrate at all, why specific subgroups in some species migrate differently from others (e.g. males/females or young/adults)? Explanations include a variety of processes, ranging from the exploitation of temporally available food sources, predation avoidance, escaping diseases and parasites to competition with other species. Although the realm of GT models, simple analytical and other optimality models have importantly assisted in highlighting the possible selective pressures shaping migratory behaviour, notably SAMs have been crucial in scrutinising potential currencies for migration; are animals primarily time- or energy-minimizers, do they optimize other currencies such as predation risk or a combination of several?

Migration is only one of several challenging life-history activities. Its interactions with other (life-history) activities, such as reproduction, moult, shedding or acquisition of territories have so far been addressed in few modelling studies only. Although the importance of carry-over effects (Harrison et al. 2011) is increasingly acknowledged, few techniques, with the exception of annual routine models (Barta et al. 2008) have considered migration and other life-history activities in combination and investigated how activities are traded-off against each other or how performing one activity influences the timing and performance of other activities.

Another research theme that deserves more modelling efforts is interactions with other species. Migrant interact in various ways with other organisms: They can be hosts to pathogens and parasites, transport nutrients, propagules and other organisms (Green & Figuerola 2005), take different ‘roles’ in the communities they visit, e.g. forager, predator or prey. Migrants can change the dynamics of resident communities (e.g. Jefferies, Jano & Abraham 2006) but migrants are similarly affected by processes (biotic and abiotic) in the resident communities, changing the way they travel (e.g. Pomeroy 2006). Surprisingly few studies have investigated the role of parasites and pathogens on migration and the dynamics of diseases in migrating hosts although the importance of understanding this interaction has meanwhile become obvious given the hypothesised role of migratory animals in the spread of zoonotic diseases (Altizer, Bartel & Han 2011).

The conservation and management of migratory animals is high on the agenda as they are assumed to be at particular risk from global change processes (Wilcove & Wikelski 2008). Indeed, many migratory species have shown population declines over the past decades (Sanderson et al. 2006). Given the perceived size of the problem, however, only few models have investigated the (population-dynamical) consequences of climatic and habitat changes along migration routes explicitly.

In contrast to the majority, some migratory species, including many European and North American goose species, do better than ever and reached all-time highs in their population sizes (Van Eerden et al. 2005). This has resulted in conflicts with agriculture calling for efficient management. Protecting and managing migratory species requires a global approach since changes on one site will have effects on (the use of) other sites that are difficult to predict and models can importantly contribute in developing sustainable, efficient and cost-effective actions (Klaassen et al. 2008b).

The above shows that surprisingly few mechanistic modelling studies have addressed a number of topics that otherwise have started to feature prominently on the current research agenda: Trade-offs between migration and other life-history activities are not being fully understood, the interactions between pathogens/ parasites and migrant animals have so far remained largely unexplored although a wealth of epidemiological models exists (but see importance of taking consequences of infections on migratory behaviour into account in Galsworthy et al. 2011) and studies of interactions of migrant animals with other species, their role in community dynamics and ecosystem processes have remained scattered to non-existent. To address these questions existing models could be extended or new types of models developed. For instance, investigating the role of migrants in community and ecosystem dynamics might require linking behaviour-based migration models with ecosystem models. Similarly, incorporating epidemiological details into migration models or extending existing epidemiological models by including the particular characteristics of migrating animals might yield new insights into the spread of diseases. With global changes taking place and public awareness rising, there will also be an increased need for answers to more applied questions in conservation and management. For these, we consider a combination of migration and socio-economic models, incorporating social and economic costs of specific management actions, a fruitful avenue.

What modelling framework to use?

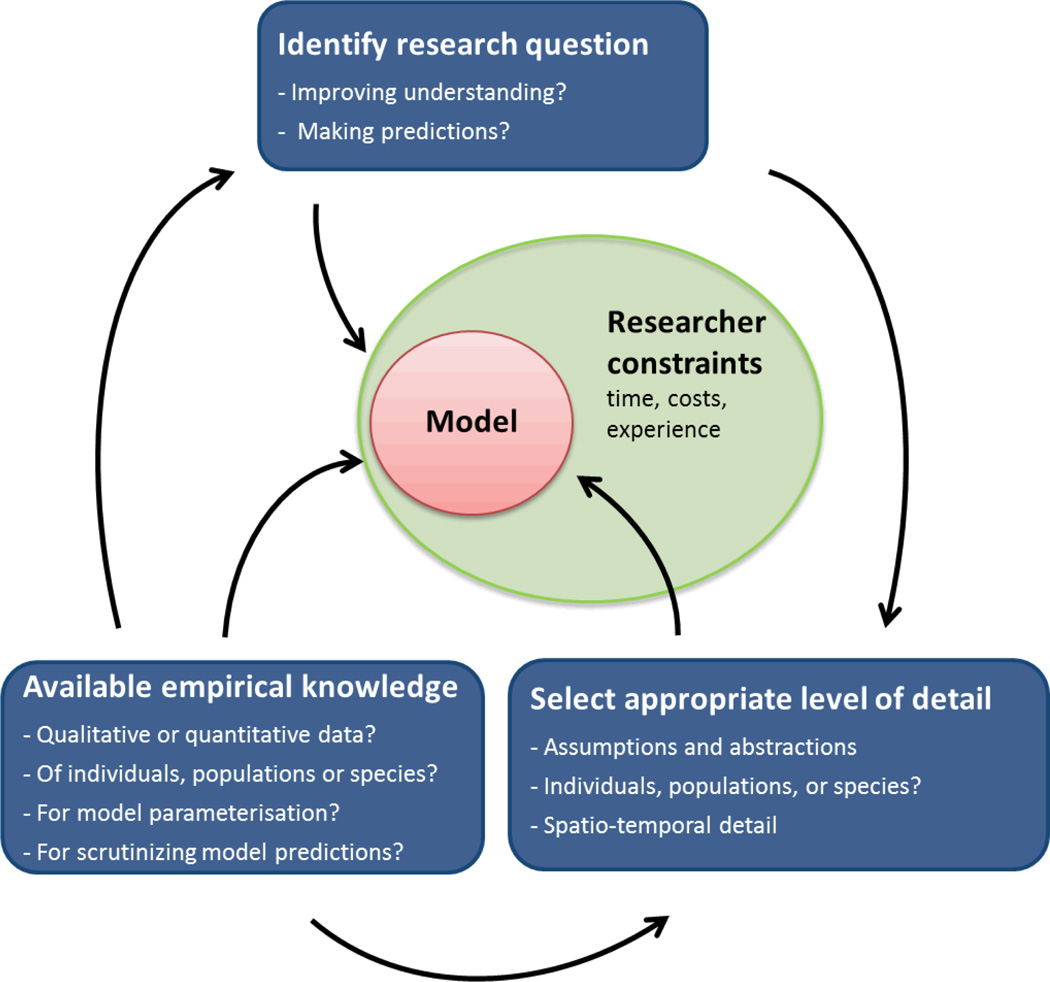
Since modelling approaches are not specifically linked to taxon or question per se (see above), choosing an appropriate modelling approach for a migratory problem is not an easy task and may often entail dilemmas and compromises (Fig. 2, Table 1). It is perhaps needless to say that every modelling method has advantages and drawbacks (e.g. Levins 1966) and that the approach chosen should match the purpose of the study (e.g. Giske, Huse & Berntsen 2001). Particularly, the implicit and explicit assumptions made with each approach should be verified in the specific study system, or alternatively, it should be tested how their violations influence model predictions (see general ecological modelling books, e.g. Grimm & Railsback 2005; Soetaert & Herman 2009). Similarly important is the number of parameters considered, i.e. the degree of complexity, with preference given to a parsimonious model. Unfortunately, no equivalent of measures such as Akaike’s Information Criterion (AIC) exists for simulation models, making rigor in the number of parameters largely subjective. Therefore, it should be explored how an additional parameter adds both to a model’s uncertainty and to its explaining power (sensitivity analysis). However, if, e.g. the purpose of the study is to simulate realistic spatio-temporal distributions, (parameter-rich) approaches that can more readily be linked with observations will be the approach of choice (Giske, Huse & Berntsen 2001), requiring a solid empirical basis for as many parameters as possible. For migrants moving through media with a relatively high velocity of its own, e.g. small airborne or marine species, PTMs involving an explicit and dynamic environment may be crucial to consider, again adding complexity (Chapman et al. 2011).

Fig. 2.

The process of selecting a modelling approach contains three central steps: 1) Identifying the overall aim, which may range from a general understanding of (the mechanisms behind) observed behaviour, its driving forces (proximate factors) or selective pressures (ultimate factors) to the reproduction of observed migration patterns with the aim of making (specific) predictions. 2) Selecting the level of detail required to achieve the aim(s), including the specification of assumptions and simplifications, the choice of organismal level (individuals, populations, or species?) and the representation of space and time (incl. potentially relevant biotic and abiotic environmental variables). 3) Finally, the model requirements should be evaluated in the light of empirical data available, both for the parameterisation of the model and for scrutinizing its predictions.

Importantly, the ultimate model choice is also determined by the researchers’ own familiarity with approaches and constraints such as time and funding.

Table 1.

Schematic summary of the characteristics of the modelling approaches considered, which may assist in identifying the appropriate modelling approach for a specific research problem (see also Fig. 2).

	Simple analytical models (SAM)	Game-theoretic models (GT)	Dynamic optimisation models (SDP)	Individual-based models (incl. Physical transport models) (IBM, PTM)	Evolutionary programming models (EP)
Model questions typically aim at …	explaining general migration patterns, incl. differences between species or populations	explaining (coexistence of) behavioural strategies in groups	identifying optimal (individual) behaviours	explaining & predicting individual behaviour and interactions and resulting population dynamics	explaining & predicting individual behaviour and interactions and resulting population dynamics, additionally includes “evolutionary” selection of optimal behavioural decisions
Parameter richness & complexity*	low	low	medium	medium - high	high
Representation of space (environment)	implicit, simple	none or implicit	explicit, static & simple	explicit, dynamic & detailed	explicit, dynamic & detailed
Temporal dynamics considered?	no	no	yes	yes	yes
Basic organismal unit	any	any	individual	individual	individual
Characterisation of organismal units by	a limited set of variables	their strategy	a set of state variables	a set of state variables	a set of state variables
Behavioural repertoire (migration in context of annual routine or other life-history activities)	restricted; usually looks at specific aspects of migration only	restricted; but includes migration and one or few other competing activities	restricted; typically includes movement & foraging, can detect knock-on effects	rich; can include movement, foraging, reproduction, territory acquisition and many more activities	rich; can include movement, foraging, reproduction, territory acquisition and many more activities
Fundamental tenet	specific currency is optimized, e.g. time, energy or predation-risk	behaviour of specific player depends on behaviour of all others	evolution has shaped behaviour such that it maximises fitness	emergent properties arise from behaviour & interaction of individuals	evolution of individual behaviour towards optimality
Population dynamics	no	no	implicit	explicit; many levels of detail possible	explicit; many levels of detail possible
Empirical data required for model parameterisation	few but possibly challenging parameters	cost & pay-offs of behavioural alternatives	costs of activities, expected fitness as dependent on state variables	set of rules for behaviour of individuals and their energetic consequences	in addition to parameters of “usual” IBM, selection criteria for evolutionary modeling process required
Empirical data required for scrutinizing model predictions	general migration patterns	strategies in populations/ subgroups	individual migration routes & schedules, constraints of activities	individual migration routes & schedules, other population level patterns, e.g. spatial distributions	individual migration routes & schedules, other population level patterns, e.g. spatial distributions

^*This includes the number of parameters and the level of detail with which processes are considered but is also inversely related to the ease with which model output can be understood, interpreted and scrutinized.

In principle, as became clear from our analysis of modelling approaches, all can be used to address a variety of problems; however, each has its field of expertise (Table 1): SAMs should be chosen for questions of specific (confined) behaviours during migration or rather general patterns of migration. Similarly, GTs are of relatively restricted use but can offer very general insights.

Modelling approaches that can more readily be linked to individual tracking data are SDPs and IBMs. Between these two, SDPs offer slightly more generalizable results, incorporate at least one full migration, highlight decision during migration but usually do not include inherent individual differences and interactions between individuals. IBMs do not suffer these limitations and environmental conditions can be included in a highly detailed and dynamic manner, up to every possible resolution and characteristic. Furthermore, the incorporation of empirical knowledge is straightforward. Yet, despite this flexibility and the straightforward methodology of IBMs the number of parameters involved may easily run out of control often reducing a model’s robustness and intelligibility. The next step, EP methods sound very appealing but are extremely time-consuming to develop and test, leaving their development and application in the hands of an adept community.

In addition to the model developments suggested above (see “challenges in migration research”), future efforts could combine the advantages of existing approaches, e.g. between SDP and IBM as in Railsback & Harvey (2012).