Evaluation of measurement error is a fundamental procedure in clinical studies, field surveys, or experimental researches to confirm the reliability of measurements. If we examine oral health status of a patient, the number of caries teeth or degree of periodontal pocket depth need to be similar when an examiner repeated the measuring procedure (intra-examiner reliability) or when two independent examiners repeated the measuring procedure, to guarantee the reliability of measurement. In experimental researches, confirming small measurement error of measuring machines should be a prerequisite to start the main measuring procedure for the study.
1. Measurement error in our daily lives
We meet many situations which might be subject to measurement error in our daily lives. For example, when we measure body weight using a scale displaying kilograms (kg) to one decimal point, we disregard body weight differences less than 0.1 kg. Similarly, when we check time using a hand-watch with two hands indicating hours and minutes, we implicitly recognize there may be errors ranging up to a few minutes. However, generally we don't worry about these possible errors because we know such a small amount of error comprises a relatively small fraction of the quantity measured. In other words, the measurements may still be reliable even under consideration of the small amount of error. The degree of measurement error could be visualized as a ratio of error variability to total variability. Similarly, degree of reliability could be expressed as a ratio of subject variability to total variability.
2. Reliability: Consistency or absolute agreement?
Reliability is defined as the degree to which a measurement technique can secure consistent results upon repeated measuring on the same objects either by multiple raters or test-retest trials by one observer at different time points. It is necessary to differentiate two different kinds of reliability; consistency or absolute agreement. For example, three raters independently evaluate twenty students' applications for a scholarship on a scale of zero to 100. The first rater is especially harsh and the third one is particularly lenient, but each rater scores consistently. There must be differences among the actual scores which the three raters give. If the purpose is ranking applicants and choosing five students, the difference among raters may not make significantly different results if the 'consistency' was maintained during the entire scoring procedure. However if the purpose is to select students who are rated above or below a preset standard absolute score, the scores from the three raters need to be absolutely similar on a mathematical level. Therefore while we want consistency of the evaluation in the former case, we want to achieve 'absolute agreement' in the later case. Difference of purpose is reflected in the procedure used for reliability calculation.
3. Intraclass correlation coefficient (ICC)
Though there are some important reliability measures, such as Dahlberg's error or Kappa statistics, ICC seems to be the most useful. The ICC is a reliability measure we may use to assess either degree of consistency or absolute agreement. ICC is defined as the ratio of variability between subjects to the total variability including subject variability and error variability.
If we evaluate consistency of an outcome measure which was repeatedly measured, the repetition is regarded as a fixed factor which doesn't involve any errors and the following equation may be applied:
| ICC (consistency) = subject variability / (subject variability + measurement error) |
If we evaluate absolute agreement of an outcome measure which was repeatedly measured, the repetition variability needs to be counted because the factor is regarded as a random factor as in the following equation:
| ICC (absolute agreement) = subject variability / (subject variability + variability in repetition + measurement error) |
Reliability based on absolute agreement is always lower than for consistency because a more stringent criterion is applied.
4. ICC for a single observer and multiple observers
If multiple observers assessed subjects, the average of repetition variability and error variability are applied in calculating ICC. Use of average variability results in higher reliability compared to use of any single rater, because the measurement error is averaged out. When k observers were involved, the ICC equations need to be changed as following:
| ICC (consistency, k raters) = subject variability / (subject variability + measurement error/k) |
| ICC (absolute agreement, k raters) = subject variability / [subject variability + (variability in repetition + measurement error) / k] |
5. An Example: evaluation of measurement errors
1) Repeated scores of oral health-related quality of life (OHRQoL)
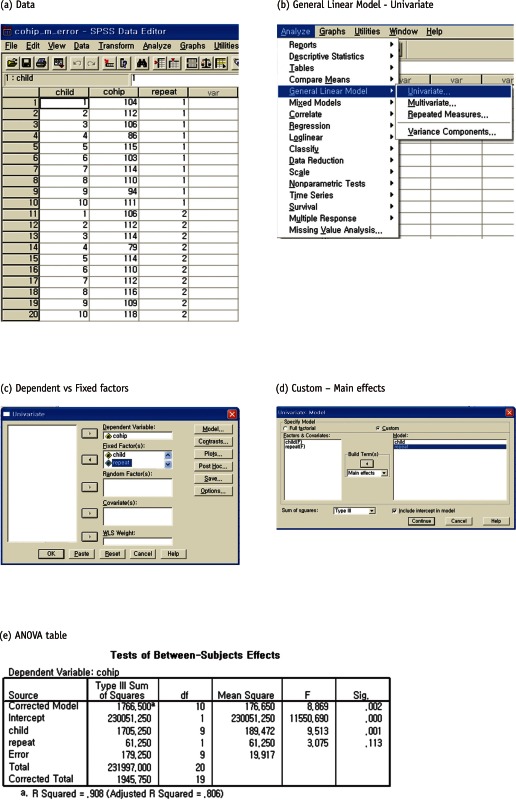
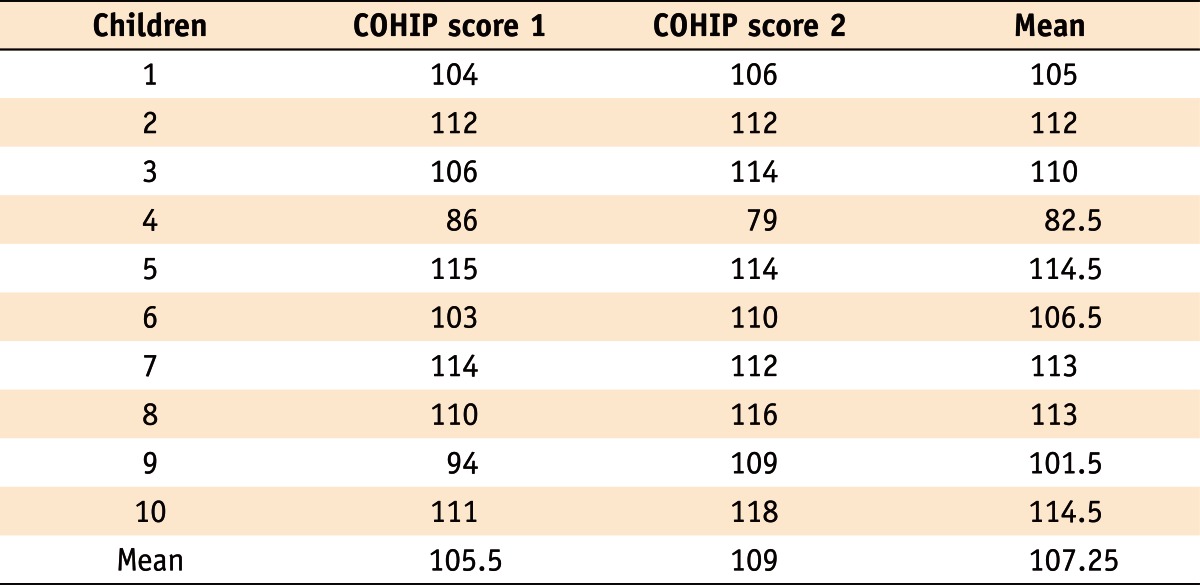
Table 1 displays repeatedly measured scores of the oral health impact profile for children (COHIP), one of the measures for OHRQoL which was obtained among ten 5th-grade school children. The COHIP inventory is a measure ranging from 0 (lowest OHRQoL) to 112 (highest OHRQoL), which assesses level of subjective oral health status by asking questions mainly about oral impacts on daily lives for children. Let's assume that the repeated measurements were obtained by a rater with an appropriate interval to assess test-retest reliability.
Table 1.
Repeatedly measured scores of the oral health impact profile for children (COHIP)
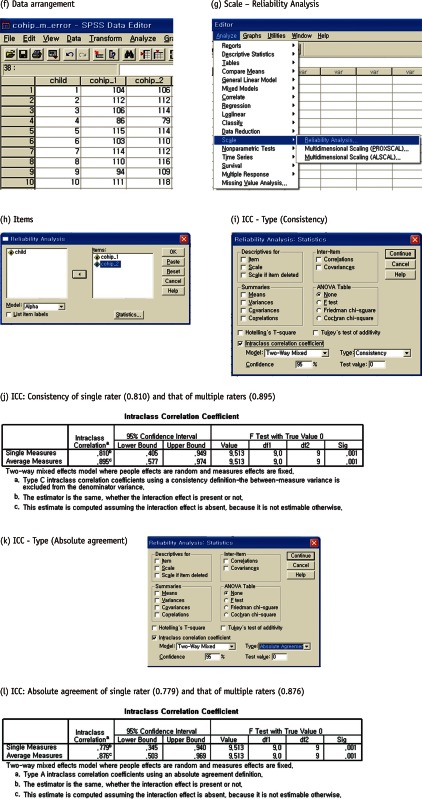
2) Intraclass correlation coefficient (ICC) measuring consistency and absolute agreement
To calculate ICC, we need to obtain subject variability and error variability using a statistical package, such as SPSS, as shown in the following procedures.
From the ANOVA table, we use Mean Square (MS) to calculate variances of subject (σ2 child), repetition (σ2 repet), and error (σ2 error) as following:
| MS (child) = 2 (number of repetition) * σ2child + σ2error = 189.47 |
| MS (repetition) = 10 (number of children) * σ2repet + σ2error = 61.25 |
| MS (error) = σ2error = 19.92 |
From the equations above we obtain the variance among children (σ2 child) as 84.78, and variance of repetition (σ2 repet) as 4.13. Then the ICC measuring consistency may be calculated as the proportion of subject (children) variability among total variability excluding variability of repetition which is regarded as a fixed factor.
| ICC (consistency, single rater) = σ2child / (σ2child + σ2error)= 84.78 / (84.78 + 19.92) = 0.810 |
| ICC (consistency, two raters) = σ2child / (σ2child + σ2error/2)= 84.78 / (84.78 + 19.92 / 2) = 0.895 |
| ICC (absolute agreement, single rater) = σ2children / (σ2child + σ2repet + σ2error) = 84.78 / (84.78 + 4.13 + 19.92) = 0.779 |
| ICC (absolute agreement, two raters) = σ2children / [σ2child + (σ2repet + σ2error) / 2]= 84.78 / [84.78 + (4.13 + 19.9) / 2] = 0.876 |
The same ICC for consistency may be obtained using SPSS, following procedure: