Gait stability in children with cerebral palsy

Abstract

Children with unilateral Cerebral Palsy (CP) have several gait impairments, amongst which impaired gait stability may be one. We tested whether a newly developed stability measure (the foot placement estimator, FPE) which does not require long data series, can be used to asses gait stability in typically developing (TD) children as well as children with CP. In doing so, we tested the FPE’s sensitivity to the assumptions needed to calculate this measure, as well as the ability of the FPE to detect differences in stability between children with CP and TD children, and differences in walking speed.

Participants were asked to walk at two different speeds, while gait kinematics were recorded. From these data, the FPE, as well as the error that violations of assumptions of the FPE could have caused were calculated.

The results showed that children with CP walked with marked instabilities in anterior-posterior and mediolateral directions. Furthermore, errors caused by violations of assumptions in calculation of FPE were only small (~1.5 cm), while effects of walking speed (~20 cm per m/s increase in walking speed) and group (~5cm) were much larger. These results suggest that the FPE may be used to quantify gait stability in TD children and children with CP.

1. Introduction

Children with unilateral Cerebral Palsy (CP) have several gait impairments, amongst which impaired gait stability may be one (Hsue, Miller, & Su, 2009a, 2009b; Iosa, Marro, Paolucci, & Morelli, 2012; Kurz, Arpin, & Corr, 2012; Opheim, Jahnsen, Olsson, & Stanghelle, 2012).

Gait stability may be operationally defined as the ability to maintain gait in the presence of perturbations. In practice, people with lower gait stability are more likely to fall, making gait stability an important functional gait metric.

Recent studies have aimed at quantifying gait stability impairments in children with CP. For instance, Iosa et al. (2012) used variability measures and Kurz et al. (2012) used maximum Floquet multipliers (i.e. a measure derived from dynamical systems theory, that indicated the tendency of small, naturally occuring perturbations to grow or decay per gait cycle) to study gait stability in children with CP. In doing so, both found that children with CP are less stable than healthy controls. Still, accurate calculation of Floquet multipliers (Bruijn, van Dieen, Meijer, & Beek, 2009) and variability measures (Owings & Grabiner, 2003) requires a substantial number of strides. For instance, for Floquet multipliers, 150 strides has been recommended (Bruijn, van Dieen, et al., 2009) and for variability measures 200 strides (Owings & Grabiner, 2003). Such long measurements may be infeasible in a clinical setting. Moreover, recent studies have criticised the relationship between both maximum Floquet multipliers and variability measures and gait stability (Bruijn, Bregman, Meijer, Beek, & van Dieen, 2011; Van Schooten et al., 2011). All in all, Floquet multipliers and variability measures may not be ideal to assess gait stability in a clinical population.

A gait stability measure that requires a minimum number of strides is ideal for clinical gait assessment. One such measure is the recently developed foot placement estimator ([FPE] Millard, McPhee, & Kubica, 2012; Millard, Wight, McPhee, Kubica, & Wang, 2009; Wight, Kubica, & Wang, 2008). The FPE uses an inverted pendulum representation of the participant to calculate where the center-of-pressure (CoP) should be placed with respect to the center of mass (CoM), such that the participant passively transitions to a statically stable standing pose (see figure 1). The FPE requires the measurement of full-body kinematics. Since quantifying arm movements in gait analysis is becoming more common in clinical studies (Bruijn, Meyns, Jonkers, Kaat, & Duysens, 2011; Meyns, Desloovere, et al., 2012; Meyns, Van Gestel, et al., 2012; Meyns et al., 2010, 2011), this no longer poses a practical restriction for clinical practice. The distance between the FPE and the participant’s closest foot (D_FPE) is a direct measure of how far the participant is from a balancing step. This distance is therefore a measure of the participant’s instability.

Figure 1.

(A) The foot placement estimator is calculated by assuming that human gait is pendular, and planar. It calculates the angle at which the leg must be placed so that the pendulum would come to a standstill (i.e., θ̇ in the next step. From the position corresponding to this angle, the error in foot placement (D_FPE) can be calculated. (B) Variables in the calculation of the foot placement estimator X(φ), which is calculated from the leg angle φ. m and Jcom represent body mass and moment of inertia respectively. V⃗ is the CoM velocity vector, consisting of horizontal (Vx) and vertical (Vy) velocities of the CoM, and h is CoM height. Walking man comes from (Muybridge, 2007).

In order to use a simplified representation of the participant’s dynamics, the FPE assumes that (1) leg length (in this context defined as the distance between the CoM and CoP), (2) total body moment-of-inertia, and (3) total body energy (kinetic + potential), remain constant after foot contact. In addition, it is assumed that (4) the total body angular momentum about the new CoP location is conserved during contact. Although these assumptions might seem restrictive, the sensitivity analysis completed in prior studies (Millard et al., 2012; Millard et al., 2009) suggests that these assumptions introduce little error when analyzing healthy adult human walking. It is unknown whether these assumptions are also true for typically developing (TD) children, and more specifically for children with CP. Therefore, the first aim of the current study is to perform a sensitivity analysis of the FPE to these four factors in TD children and children with CP, thereby quantifying the maximal errors in FPE due to assumption violations in these groups.

Absolute errors in a measure become more meaningful in the context of differences that can be expected by experimental manipulations, or group differences. Therefore, we tested if and to what extent gait stability was impaired in children with CP compared to TD children, and how gait stability was affected by walking speed. The latter question is of great interest, since the relationship between gait stability and walking speed has been under debate for some time (Bruijn, van Dieën, Meijer, & Beek, 2009; Dingwell & Marin, 2006; England & Granata, 2007; Hak et al., 2012).

2. Methods

2.1. Participants

A total of 11 children with unilateral CP (age 7.83 ± 2.98 years, weight 23.9 ± 7.6 kg and height 1.22 ± 0.15 m) and 24 typically developing (TD) children (age 9.40 ± 2.16 years, weight 31.7 ± 8.6 kg and height 1.38 ± 0.14 m) participated in the experiment. The children with CP were recruited from the Clinical Movement Analysis Laboratory of the University Hospital Leuven (U.Z. Leuven), were ambulant (without walking aids), diagnosed with the predominantly spastic type of CP, and had sufficient cooperation to follow verbal instructions. Children who underwent Botulinum Toxin-A treatment within the past 6 months, or who previously received lower limb orthopedic surgery, were excluded. TD children were all healthy, with no self-reported problems that could interfere with walking, and no known neurological or musceloskeletal disorders. All experiments were approved by the local ethical committee, and informed written consent was obtained from the parents.

2.2. Procedure

All participants received three-dimensional (3D) kinematic analysis of gait, based on the total body PlugInGait markers configuration (Vicon, Oxford Metrics, Oxford, UK), and performed by an experienced physical therapist. During gait analysis, participants were barefoot, and wore their own shorts. In addition, girls wore a top that did not obscure upper body marker. Participants were asked to walk at a self-selected speed along the 10 meter walkway in a straight line. After three successful trials, the participants were asked to walk as fast as possible (without running) along the walkway. Throughout all trials, kinematics were measured using an infrared video camera system (10 to 15 MX cameras, Vicon, Oxford Metrics, Oxford, UK) sampling at 100 samples/second.

2.3. Calculations

2.3.1. Pre-processing

The marker coordinates were filtered and smoothed using Woltring’s quintic spline routine (Woltring, 1986), implemented in Vicon Workstation software. For all subsequent analyses, custom-made Matlab programmes (The Mathworks, Natick, MA) were used. Segment inertial parameters were calculated using a geometrical model (Zatsiorsky, 2002). Using gait kinematics and inertial parameters, a 15 segment 3D model (feet, shanks, thighs, pelvis, thorax, head, upper arms, lower arms, hands) was constructed, and total body CoM kinematics were calculated. Angular momentum of all segments with respect to the CoM was then calculated, and total body angular momentum was calculated by summing angular momenta over all segments

2.3.2. Basic gait parameters

Foot contact was detected based on the foot marker coordinates, and stride times were obtained by taking the average time difference between subsequent foot contacts. Walking speed was obtained by dividing the time between first and last initial contact over the distance travelled by the CoM during that period. Moreover, to overcome differences in stride times, we calculated single support and double support times for each leg, expressed as percentage of the gait cycle. Step widths were calculated as the distance between the feet at initial contact.

2.3.3. Foot Placement Estimator

The equations for the FPE assume that movements occur in a vertical plane. To be able to handle 3D motion, 3D walking was represented as two dimensional (2D) walking, by creating an instantaneous “plane of progression”. The first axis of this plane of progression was the (global) vertical axis, and the second axis was perpendicular to this vertical axis and to the vector formed by the horizontal component of the participant’s angular momentum about the static ground projection of the CoM (Millard et al., 2012). All quantities necessary for the calculation of the FPE were projected on this plane (Millard et al., 2012). By doing so, calculations became 2D (within the plane of progression). From here on, all quantities referred to are assumed to be their 2D projected versions.

From the total body angular momentum about the CoM, (H_tot), total body angular velocity (θ̇) was calculated as:

$$\stackrel{.}{\theta }=\frac{H_{\mathit{tot}}}{J_{\mathit{com}}}$$

In which J_com is the total body inertia component perpendicular to the projection plane, calculated from segment inertias using the parallel axes theorem (see figure 1B).

The value of the leg angle (φ) that would allow the equivalent inverted pendulum to transition to a statically standing pose was found by solving:

$$0=\frac{{(mh(v_{x}cos(\phi )+v_{y}sin(\phi ))cos(\phi )+J_{\mathit{com}}\stackrel{.}{\theta }{cos}^2(\phi ))}^2}{{mh}^2+J_{\mathit{com}}{cos}^2(\phi )}+2\mathit{mghcos}(\phi )(cos(\phi )-1)$$

Where m was the child’s mass, h was the height of the CoM, v_x and v_y were the horizontal and vertical velocity of the CoM, and g was the gravitational constant (see figure 1B). Trigonometry was used to find the actual foot placement location;

$$X(\phi )=htan(\phi )$$

After X(φ) was calculated, its position was rotated back into the 3D world, to obtain X(φ)_AP and X(φ)_ML, and the distance from X(φ)_AP to the toe marker (in 3D lab space) (D_FPEAP), and from X(φ)_ML to the most lateral point of the foot (in 3D space) (D_FPEML) at initial contact were calculated. If the swing foot covers the FPE, it is possible to come to a standstill without taking another step. If the FPE is outside of the feet (and not between them), at least one more stride is required to come to a standstill. D_FPEAP and D_FPEML thus give an indication of how stable the gait pattern is.

2.3.4. Sensitivity analysis for the FPE

To test the internal validity of the FPE for use in children, we tested the sensitivity of the FPE to changes in leg length (ΔL), moment of inertia (ΔJ), system energy (potential and kinetic energy, Δ(T + V) and angular momentum (ΔHo). This sensitivity was calculated by taking the partial derivative of these variables with respect to X(φ) at initial contact (denoted, $\frac{\delta X(\phi )}{\delta L},\frac{\delta X(\phi )}{\delta J},\frac{\delta X(\phi )}{\delta (T+V)}$ and $\frac{\delta X(\phi )}{\delta Ho}$ respectively (Millard et al., 2012; Millard et al., 2009)). Next, to investigate the potential influences of these sensitivities on actual outcomes, these partial derivatives were multiplied by the maximum differences in any of these variables in the time span from initial contact to mid-stance (denoted ΔL, ΔJ, Δ(T + V), and ΔHo, respectively), thereby obtaining the maximum difference that violations of assumptions may have caused in estimates of X(φ) (denoted εL, εJ, ε(T + V), and εHo respectively). Since angular momentum is only assumed to be constant during initial contact, but may vary freely afterwards, the maximum difference in angular momentum (about the ground projection of the lateral malleolus) around initial contact (from −50 ms to +50ms) was calculated.

In order to give a good insight into how much, and why, the assumptions of violations lead to errors in X(φ), we report the partial derivatives for each variable ( $\frac{\delta X(\phi )}{\delta L},\frac{\delta X(\phi )}{\delta J},\frac{\delta X(\phi )}{\delta (T+V)}$, and $\frac{\delta X(\phi )}{\delta Ho}$), the actual maximum difference in that variable (ΔL, ΔJ, Δ(T + V), and ΔHo), and the error in X(φ) that this difference may have caused (εL, εJ, ε(T + V), and εHo).

2.4. Statistical analysis

For each subject, condition, and variable, the mean of the variable over all steps of all three successful trials was used for further analysis.

Unpaired t-tests were used to test for differences in participant demographics between groups.

We used Generalized Estimation Equations (GEE (Liang & Zeger, 1986; Zeger & Liang, 1986)), which allowed us to test the effects of group, leg, and speed (and their interactions) using actual measured walking speed (in both the self-selected and fast conditions) as a continuous rather than categorical variable. To test effects of condition (self-selected vs. fast) on speed (the continuous variable), we used condition as a categorical variable. In all other analyses, speed was used as a covariate. Since GEE is essentially a regression method, main effects of the categorical repressors (group and leg) may not reflect true main effects whenever an interaction with speed is present. Thus, for effects of group and leg (and their interaction), we report the effects on the estimated marginal means, rather than effects on regression coefficients. Whenever an interaction effect did not reach significance, it was removed from the model.

SPSS 17.0 was used for all statistical analysis, and significance level was set at P<0.05.

3. Results

For one TD child, no full stride was recorded at the highest speed, and data from this child at this condition had to be omitted.

3.1. Participant demographics

Children with CP had a smaller mass (P=0.01) and height (P=0.008) than TD children, but both groups had comparable ages (P=0.09).

3.2. Basic gait parameters

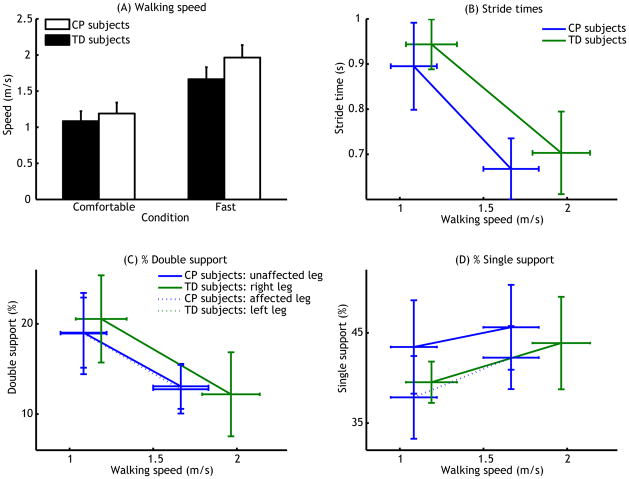
All participants walked faster in the fast walking condition (condition, P<0.001, see Figure 2A). More importantly, children with CP walked slower in both conditions (group, P<0.001), and increased speed less than TD children (condition × group interaction P<0.001).

Figure 2.

(A) Effects of condition (horizontal axis, comfortable vs. fast walking) and group (different bar colours) on walking speed (m/s). (B) Effects of walking speed (m/s, horizontal axis) and group (different lines,) on stride times (s). (C & D) Effects of walking speed (m/s, horizontal axis) and group as well as leg (different lines) on % of the stride cycle in double (C) and single (D) support. Error bars represent standard deviations; Error bars in horizontal direction indicate standard deviation of walking speed.

Stride times decreased with speed (P<0.001, Figure 2B). There was no difference in stride times between children with CP and TD children (P=0.8, see Figure 2B), but stride times decreased less with increasing speed in the TD children (group × speed interaction (P<0.032). Double support (Figure 2C) decreased with increasing speed (P<0.001), but was not different between groups (P=0.057). Single support (Figure 2D) increased with increasing speed (P<0.001). When compared to TD children, children with CP had a similar single support at the affected leg (P=0.37), but an increased single support at the unaffected leg, also when compared to their own affected leg (P<0.001).

3.2. Sensitivity of the FPE in children

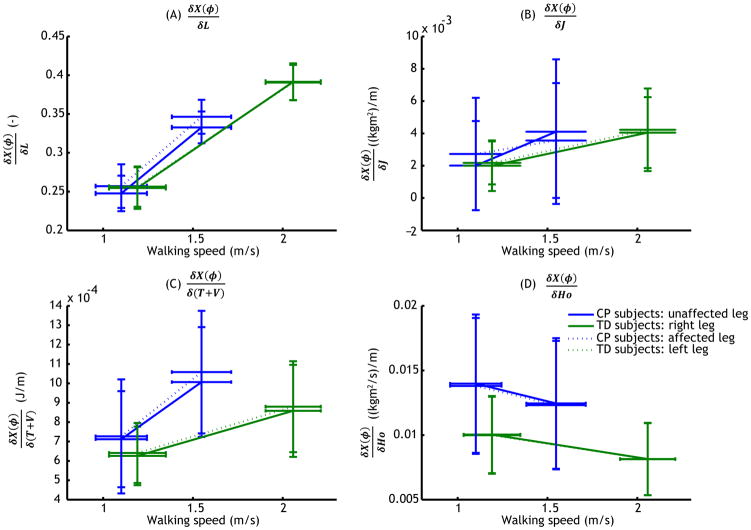
All partial derivatives showed significant effects of walking speed (see figure 3, table 1). Moreover, $\frac{\delta X(\phi )}{\delta L},\frac{\delta X(\phi )}{\delta (T+V)}$ and $\frac{\delta X(\phi )}{\delta Ho}$ showed an effect of group, which for $\frac{\delta X(\phi )}{\delta L}$ and $\frac{\delta X(\phi )}{\delta (T+V)}$ manifested itself as an interaction between group and speed (see table 1).

Figure 3.

Effects of walking speed (m/s, horizontal axis) and group as well as leg (different lines) on (A) $\frac{\delta X(\phi )}{\delta L}$, (B) $\frac{\delta X(\phi )}{\delta J}$ (C) $\frac{\delta X(\phi )}{\delta (T+V)}$ and (D) $\frac{\delta X(\phi )}{\delta Ho}$. Error bars represent standard deviations; Error bars in horizontal direction indicate standard deviation of walking speed.

Table 2.

Statistical significant effects of the different independent variables on ΔL, ΔJ, Δ(T + V), and ΔHo indicated with an asterisk.

	ΔL	ΔJ	Δ(T	ΔHo
Group		*		*
Leg	*		*
Speed	*		*	*
Group × Speed	*
Group × Leg	*		*
Leg × Group
Group × Leg × Speed

Figure 4 represents ΔL, ΔJ, Δ(T + V), which all showed significant effects of group (or significant interactions involving the group effect, see table 2).

Figure 4.

Effects of walking speed (m/s, horizontal axis) and group as well as leg (different lines) on (A) ΔL, (B) ΔJ, (C) Δ(T + V), and (D) ΔHo. Error bars represent standard deviations; Error bars in horizontal direction indicate standard deviation of walking speed.

Table 3.

Statistical significant effects of the different independent variables on εL, εJ, ε(T + V), and εHo, indicated with an asterisk.

	εL	εJ	ε(T	εHo
Group	*
Leg	*		*	*
Speed	*	*	*	*
Group × Speed	*
Group × Leg	*		*	*
Leg × Group
Group × Leg × Speed				*

Figure 5 shows εL, εJ, ε(T + V), and εHo, which represent the effects deviations from the assumptions of the FPE may have on the calculated value of the FPE (see also table 3). With the exception of the assumption that leg length is constant during the stride, the violations of the assumptions led to maximum effects in the order of millimetres. The violation of the assumption of a constant leg length however could lead to a maximum deviation in the FPE of about 1.5 cm at higher walking speeds.

Figure 5.

Effects of walking speed (m/s, horizontal axis) and group as well as leg (different lines) on (A) εL, (B) εJ, (C) ε(T + V) and (D) εHo. Error bars represent standard deviations; Error bars in horizontal direction indicate standard deviation of walking speed.

3.3. Stability differences between groups and effects of speed

Children with CP had a higher D_FPEAP (effect of group, P<0.01), and even more so for higher speeds (group × speed interaction, P<0.01), and for the affected leg (leg and group × leg effects, both P<0.01). These results indicate that in the AP plane, the children with CP were more unstable than TD children. At self-selected speed, both groups covered the FPE with their contacting foot (i.e., 0<D_FPEAP, see figure 6), implying they could have stopped without taking another step. When walking speed increased, all participants had a negative D_FPEAP implying that they were “falling” forward at each step (effect of Speed, P<0.01).

Figure 6.

Effects of walking speed (m/s, horizontal axis) and group as well as leg (different lines) on (A) D_FPEAP and (B) D_FPEML. Error bars represent standard deviations; Error bars in horizontal direction indicate standard deviation of walking speed.

In the mediolateral (ML) plane, all participants placed their feet a few centimetres wider than the FPE position (i.e., positive D_FPEML, see figure 6B). Moreover, statistical analysis showed a significant interaction between group and speed (P<0.01), indicating that D_FPEML decreased with increasing speed for the children with CP, thus indicating decreased stability in the ML plane with increasing walking speed for this group.

4. Discussion & Conclusion

We studied whether the foot placement estimator can be used to assess gait stability in TD children and children with CP. This measure is promising since unlike other frequently used measures, such as Lyapunov exponents (Dingwell & Cusumano, 2000; Sloot et al., 2011; Van Schooten et al., 2011), Floquet multipliers (Hurmuzlu & Basdogan, 1994) and variability measures (Bruijn, Bregman, et al., 2011), which require in the hundreds of strides (Bruijn, van Dieen, et al., 2009; Owings & Grabiner, 2003), the FPE requires only a few strides to assess gait stability. We found that violations to the assumptions of the FPE could be responsible for changes in D_FPE in the order of 1.5 cm, while the effects of group (~ 5 cm for D_FPEAP) and walking speed (~20 cm per m/s walking speed increase for D_FPEAP) were much higher. These findings support the idea that the FPE can be used to assess gait stability in children with CP.

4.1 Sensitivity of FPE in children (with and without CP)

Interestingly for adults, deviations in angular momentum caused the largest errors in D_FPE, while in children, changes in leg length caused the largest error (Millard et al., 2009). This could also be seen in $\frac{\delta X(\phi )}{\delta L}$, which in our study was around 0.4 at the highest walking speed, while (Millard et al., 2009) reported values of −0.077. As a general rule of thumb, it is necessary to calculate the potential errors in estimates of D_FPE, so that insight into the validity of the parameter is achieved.

While errors potentially caused by deviations from assumptions were generally smaller than the effects of walking speed, and of group, it remains to be investigated whether this also warrants the use of the FPE as an individual indicator of gait stability. At present, we did not assess other measures that could be used as an external criterion to correlate D_FPE values to in the children with CP, and thus, we do not know how well it works on an individual level. Still, for comparisons at the group level, our results suggest that the FPE is a valid measure, able to discriminate TD children from children with unilateral CP.

4.2 Deficient gait stability in children with CP

Children with CP walked with marked instabilities, as indicated by a D_FPE that was an order of magnitude larger than the errors that could have been caused by assumptions of the violations of the FPE. This seems in agreement with other literature using different measures, such as variability measures (Iosa et al., 2012), maximum Floquet multipliers (Kurz et al., 2012), and relationships between CoM and CoP (Hsue et al., 2009a, 2009b).

It is interesting to hypothesize on the cause of the more unstable gait in children with CP. It is actually advantageous to place the CoP behind the FPE if coming to a complete stop is undesirable, because it allows the body to retain some of its momentum through the stance phase. This modulation of step placement with respect to the FPE is apparent in running, where the FPE can be so far ahead of the runner’s body that it is impossible to reach it, and thus to stop, in a single step. Children with CP might be stepping further behind the FPE to offset the weak push-off they get from their stance limb (Gage, 2004; van der Krogt, Delp, & Schwartz, 2012; Wiley & Damiano, 1998). Alternatively, children with CP might be stepping further behind the FPE than TD children because they have difficulties taking large steps, due to primary and secondary problems (Gage, 2004). Lastly, due to their impaired motor control, children with CP may be simply unable to control their movements well enough to assure a correct step position. Overall, there may be several reasons why children with CP have a less stable gait pattern. These potential underlying reasons that cause children with CP to have a less stable gait pattern can now be systematically and experimentally studied using the FPE both as a conceptual model and measure of balance.

4.3 Effects of walking speed on gait stability

All in all, it seems that our findings cannot give a definitive answer in the debate on the effects of walking speed on gait stability. Our analysis showed higher values of D_FPEAP with increasing walking speed, indicating less stable walking at higher speeds, even more so for children with CP than for TD children, as indicated by the interaction effect. For D_FPEML, speed effects were less pronounced. The increased D_FPEAP with increasing speed seems in agreement with findings of Dingwell and Marin (2006) and England and Granata (2007), who showed that maximum Lyapunov exponents increased with increasing walking speed (indicating a decreased stability at higher walking speeds). On the other hand, the absence of clear effects of walking speed on D_FPEML is in agreement with findings by Bruijn et al. (2009), who (using maximum Lyapunov exponents) showed similar effects of gait speed on stability. It has been suggested that ML foot placement is more important than AP foot placement (O’connor & Kuo, 2009), which would make ML results more important. Still, further research is required to provide a definitive answer in the debate on the effects of walking speed on gait stability.

4.4 Limitations

The current study had some limitations. Firstly, we applied a geometrical anthropometric model (Zatsiorsky, 2002) that has not been validated for children. Nonetheless, our sensitivity analysis showed that errors in estimating inertia had only limited effects on estimates of D_fpe. Secondly, although we could model speed as a covariate, participants still walked with different stride times. It is unclear how this affects our results, or how this could have been avoided, since our aim was to study natural walking. Lastly, we did not quantify stability using more clinical measures, or using measures that have been shown to be related to fall risk, such as for instance maximum Lyapunov exponents or variability measures. Thus, the external validity of the FPE as a measure of gait stability remains to be tested (Bruijn, Dieën, Meijer, & Beek, Submitted), but it is promising to see that this measure has a good theoretical validity, and was found to be internally valid in the current study.

4.5 Directions for future research

As also mentioned above, and by Bruijn et al. (Submitted), a first step in future research should be to further test the validity of D_FPE in predicting probability of falling. Moreover, a recent study (McAndrew Young, Wilken, & Dingwell, 2012) used the margin of stability (which has similarities to the foot placement estimator concept) to assess gait stability while participants were walking in a destabilizing environment. Their results suggested that quantifying step-to-step changes in margins of stability may be more useful than averaged margins of stability in assessing how individuals control walking stability. Similarly, for the FPE, step-to-step variations in D_FPE could yield extra, meaningful information. Future research may address this idea of both mean values of D_FPE and variations in D_FPE as indicators of dynamic gait stability. The downside of using the variations in D_FPE as (additional) measure of gait stability would of course be that longer gait trials are needed, which may be unwanted in a clinical setting.

Table 1.

Statistical significant effects of the different independent variables on $\frac{\delta X(\phi )}{\delta L},\frac{\delta X(\phi )}{\delta J},\frac{\delta X(\phi )}{\delta (T+V)}$ and $\frac{\delta X(\phi )}{\delta Ho}$, indicated with an asterisk.

	$\frac{\delta X(\phi )}{\delta L}$	$\frac{\delta X(\phi )}{\delta J}$	$\frac{\delta X(\phi )}{\delta (T+V)}$	$\frac{\delta X(\phi )}{\delta Ho}$
Group				*
Leg
Speed	*	*	*	*
Group × Speed	*		*
Group × Leg
Leg × Group
Group × Leg × Speed

Highlights.

• Children with Cerebral Palsy (CP) are assumed to have an unstable gait

• The recently developed foot placement estimator (FPE) may be used to estimate gait stability from short walking trials

• We used the FPE to assess gait stability in typically developing (TD) and CP children, and assessed its validity

• The FPE indicated that children with CP walked more unstable than TD children

• Assumption violations lead to changes in FPE much smaller than effects of pathology, rendering the FPE a useful measure.

Abbreviation/symbol

$\frac{\delta X(\phi )}{\delta (T+V)}$

Partial derivative of X(φ) with respect to changes in system energy

$\frac{\delta X(\phi )}{\delta Ho}$

Partial derivative of X(φ) with respect to changes in total body angular momentum

$\frac{\delta X(\phi )}{\delta J}$

Partial derivative of X(φ) with respect to changes in total body inertia

$\frac{\delta X(\phi )}{\delta L}$

Partial derivative of X(φ) with respect to changes in leg length

θ̇

Total body angular velocity

2D

Two-dimensional

3D

Three-dimensional

AP

Antero-posterior

CoM

Centre of mass position vector

CoP

Centre of pressure vector

CP

Cerebral Palsy

D_FPE

Distance between X(φ) and the foot at initial contact

D_FPEAP

AP distance between X(φ)_AP and toe marker at initial contact

D_FPEML

ML distance between X(φ)_ML and the most lateral foot marker at initial contact

FPE

Foot placement estimator method

g

Gravitational constant

GEE

Generalized Estimation Equations

h

CoM height

H_tot

Total body angular momentum vector

J_CoM

Total body inertia tensor

m

Mass of the subject

ML

Medio-lateral

TD

Typically developing

v_x

Horizontal component of the velocity of the CoM

v_y

Vertical component of the velocity of the CoM

X(φ)_AP

AP position of X(φ) in lab coordinates

X(φ)_ML

ML position of X(φ) in lab coordinates

X(φ)

Position of the foot placement estimator within plane of progression

Δ(T + V)

Change in system energy from initial contact to mid-stance

ΔHo

Change in total body angular momentum from 50 ms before initial contact to 50 ms after initial contact

ΔJ

Change in total body inertia from initial contact to mid-stance

ΔL

Change in leg length from initial contact to mid-stance

ε(T + V)

Potential error in X(φ) due to changes in system energy

εHo

Potential error in X(φ) due to changes in total body angular momentum

εJ

Potential error in X(φ) due to changes in total body inertia

εL

Potential error in X(φ) due to changes in leg length

φ

Leg angle