Efficient Mapping and Geographic Disparities in Breast Cancer Mortality at the County-level by Race and Age in the U.S.

Abstract

This study identified geographic disparities in breast cancer mortality across the U.S. using kriging to overcome unavailability of data because of confidentiality and reliability concerns. A structured additive regression model was used to detect where breast cancer mortality rates were elevated across nine divisions with 3109 U.S. counties during 1982-2004. Our analysis identified at least 25.8% of counties where breast cancer mortality rates were elevated. High-risk counties compared to lower-risk counties had higher relative risks for African American women than for White women. Greater geographic disparities more likely present in African American women and younger women. To sum up, our statistical approach reduced the impact of unavailable data, and identified the number and location of counties with high breast cancer mortality risk by race and age across the United States.

1 INTRODUCTION

Breast cancer consistently ranks as second leading cause of cancer death among women in the U.S. (American Cancer Society, 2012;Lacey et al., 2002). Racial disparities in breast cancer mortality exist (Adams et al., 2011; van Ravesteyn et al., 2011), with African American women having a higher breast cancer mortality rate than White women (American Cancer Society, 2012). Starting in the early 1980s, racial disparities in breast cancer mortality rates have continued to where mortality rates were about 38% higher in African American women than White women in the U.S in 2006 (American Cancer Society, 2009; DeSantis et al., 2008). Reducing disparities is an overarching goal of the Healthy People 2010 (U.S. Department of Health and Human Services, 2010) initiative and of the National Cancer Institute’s (NCI) strategic plan (National Cancer Institute, 2007).

While racial disparities have been investigated extensively, less is known about breast cancer mortality variation in different geographic regions (i.e., geographic disparities), especially among small areas (e.g., counties). Despite the importance of small-area public health practice and research, examination of small-area mortality rates brings new challenges and is often hampered by confidentiality and reliability concerns about releasing data based on few cases or small population size. To alleviate these concerns, breast cancer mortality data is often presented at the state level (e.g., the CDC’s Interactive Cancer Atlas) or metropolitan level (e.g., CDC’s WONDER system) or is suppressed for counties with small number of cases (e.g., NCI’s State Cancer Profiles). As a result, many previous studies have examined geographic disparities by focusing on limited regional areas (e.g., counties in the Surveillance, Epidemiology, and End Results program) or used states as geographic unit (Canto et al., 2001; Grann et al., 2006; Merkin et al., 2002). A recent county-level study described changes in geographic disparities over time (Schootman et al., 2010). Also, studies in Texas showed areas where breast cancer incidence was elevated and how risk factors affected the geographic disparity in incidence (Bambhroliya et al., 2012; Hsu et al., 2006).

Few studies have examined geographic disparities in breast cancer mortality across the entire U.S, but new statistical approaches are now available that can take into account spatial autocorrelations, and can identify where disparities in the risk of disease are most pronounced even when data are based on few cases or small population size (Berke, 2004; Goovaerts, 2005; Haining et al., 1994; Yu et al., 2010). Along with the maturing of techniques for handling spatiotemporal data and with the improvement of software and hardware for complex calculations, there is still a tendency to analyze data which contains risk factors and outcome variables but lacks geographical details (Copeland, 2010).

Thus, the purpose of our analysis was to identify geographic disparities by race and age using population-based breast cancer mortality in all 3109 counties in the contiguous United States, and to use spatial statistics to overcome unavailable data because of confidentiality and reliability concerns. Within the context of prevailing geographic disparities in different races and ages, we examined: 1) the magnitude of geographic disparities in breast cancer mortality across the U.S.; 2) where breast cancer mortality was significantly higher or lower; and 3) the magnitude of the breast cancer mortality risk in high-risk counties.

2 METHODS

2.1 Breast cancer mortality data

Breast cancer mortality data for 1982-2004 were obtained from an individual-level Multiple Cause-of-Death Database from the National Center for Health Statistics (NCHS). The study data were limited to women aged 40 years or older who died of breast cancer as identified by International Classification Diseases codes (Ninth Revision codes 174.0-174.9 or Tenth Revision code C50). Ninety-seven percent of breast cancer deaths occurred in women aged 40 and older (American Cancer Society, 2009). Data about individual women were aggregated to the county level for two race groups (White and African American) and four age levels (40-49 years, 50-59 years, 60-69 years, and 70 or older). Women of other races were not included because of their small number. The county population estimates for different races and age categories from 1982 to 2004 were from the U.S. Census Bureau.

2.2 Study area

Counties in the U.S. are the earliest geographic units of local government since the 17^th century, and have been the main administrative divisions of states. This geographic unit is frequently recorded in large national databases in the U.S., such as the Surveillance Epidemiology, End Result and the National Vital Statistics System. Counties form the building blocks of most states to implement public health policy. We chose county to perform spatial analyses since it is the smallest geographic unit with the social, political, and legal responsibility for providing a broad range of health services in the U.S. (Schootman et al., 2010). The study area contained 3109 counties within the 48 contiguous United States, which can be split into nine Census Bureau-designated regional divisions (Fig 1): New England Division (67 counties), Mid-Atlantic Division (150 counties), East North Central Division (437 counties), West North Central Division (618 counties), South Atlantic Division (590 counties), East South Central Division (364 counties), West South Central Division (470 counties), Mountain Division (280 counties), and Pacific Division (133 counties)(U.S. Bureau of the Census, 2012). During the study period, the average population size across counties varied substantially. Loving County, Texas, had the fewest residents (21.6 persons) and Los Angeles County, California, had the most residents (1,876,480.4 persons). In an average county there were 121,873.4 residents. County boundary data for the 2000 Census were downloaded from the Census Bureau website and converted into a two-dimensional neighborhood weighted matrix for disease mapping and spatial effect estimation. Two counties were defined as neighbors if they shared a common boundary. There were no substantive changes in county boundaries during the study period.

Fig 1.

Locations of the 3109 counties within the nine regional divisions in the United States

2.3 Kriging

After 1989, the Center for Disease Control and Prevention/National Center for Health Statistics announced that the “County of Occurrence” in each death record was coded as 999 for counties with a total population less than 100,000 persons (National Center for Health Statistics, 1989), which means that 2,184 of 3,109 counties (70.3%) were missing in the Multiple Cause-of-Death Database. This situation reduced the available data with county designation to only 75% of all breast cancer deaths during the study period. Because excluding these deaths among low-population counties may lose useful patient information, reduce statistical power, and introduce bias, we used kriging, a method that produces an unbiased linear estimator with minimum uncertainty (Chiles and Delfiner, 1999), to approximate the number of breast cancer deaths in counties with missing data. Suppose the kriged mortality rate of year t at a county c located at s_cis denoted by ẑ(s_c, t), which is the linear combination of observations expressed as $\widehat{Z}(S_c,t)={\sum }_{i=1}^{n_c}{\lambda }_{i,(S_C,t)}Z(S_i,t)$ , where n_c is the number of observation within the county c in year t, and λ_i,(sc,t) is the kriging weight derived from the semivariogram functions, accounting for the spatiotemporal dependence among the observations (Olea, 1999). Note that the location s_c is defined by the latitude and longitude of each county. When the kriged mortality rate ẑ(s_c,t) was obtained, the kriged death count for breast cancer can be calculated by ẑ(s_c,t) multiplying the corresponding population in year t at county c. Kriging was applied to each race and each age level separately. The efficiency of the kriged data was verified by the cross-validation and covariance in the spatial distance and temporal lag, see Appendix A & B. Hispanic women are not included because of overestimation of the observed data.

2.4 Statistical analysis

The structured additive regression (STAR) model (Brezger and Lang, 2006; Fahrmeir and Lang, 2001) estimated the spatial distribution in the yearly breast cancer mortality rate in order to account for temporal autoregressive correlation and spatial autocorrelation among the 3109 counties in the U.S. during 1982-2004. Assume Y_ct is the number of breast cancer deaths in county c=1, 2, …, 3109 at calendar year t=1, 2, …, 23, which follows a Poisson distribution POI(μ_ct). Thus, a STAR model can be constructed by:

$$\log \left({\mu }_{\mathrm{ct}}\right)=\alpha +\mathrm{f}\left(\mathrm{t}\right)+{\mathrm{f}}_{\mathrm{spat}}\left(\mathrm{c}\right)+\text{offset}.$$ (1)

The parameter represents the intercept and the overall average of the log of the expected mortality rate for all counties for all counties. The time smoother f(t), estimated by a cubic B-spline with a second-order random walk prior (Lang and Brezger, 2004), is used to control the temporal autoregressive correlation of breast cancer mortality over the 23-year study period. The spatial function f_spat(c) is the sum of an unstructured spatial function f_spat^u(c) and a structured spatial function f_spat^s(c). The f_spat^u(c) can be regarded as a random intercept fitted by an exchangeable normal prior with mean zero and variance σ_u². The f_spat^s(c) is based on the Markov random fields (Kindermann and Snell, 1980), having a Gaussian prior with mean ${\sum }_{c^{\prime }\in {ϴ}_C}{\mathrm{f}}_{\mathrm{spat}}\left({\mathrm{c}}^{\prime }\right)∕{\mathrm{N}}_{\mathrm{c}}$ f_spat(c’)/N_c and variance σ_s²/N_c, where Θ_c is a set of neighboring counties adjacent to county c, and N_c is the number of neighboring counties in the set Θ_c. Two unknown parameters σ_u² and σ_s² are assumed to have an inverse Gamma distribution IG(a, b) with two known parameters a = b = 0.001. The offset is the log county-level population in each race and each age category from 1982 to 2004.

The estimated spatial effect in each county was the posterior mean obtained from f_spat(c) via Eq.(1). Its posterior distribution determined the 95% credible interval (CI), and its exponentiation calculated the relative risk (RR). The 95% CIs of the 3109 counties were classified into three groups relative to the value zero (the mean of the spatial effect across the United States): (i) high-risk counties, which included counties where their 95% CIs were strictly larger than zero; (ii) low-risk counties, which included counties where their 95% CIs were strictly smaller than zero; and (iii) nonsignificant-risk counties, where their 95% CIs were not significantly higher or lower than zero. These clusters can distinguish the risk status of breast cancer mortality in every county, and the variance of RR can reflect nationwide and division-wide geographic disparities. For the purpose of understanding whether the cluster of high-risk counties due to breast cancer mortality was statistically distinguished from the other counties, an index Z was defined by coding 1 for high-risk counties and 0 for lower-risk counties (i.e., low-risk and nonsignificant-risk counties), and added to Eq.(1):

$$\log \left({\mu }_{\mathrm{ct}}\right)=\alpha +\beta \times \mathrm{Z}+\mathrm{f}\left(\mathrm{t}\right)+{\mathrm{f}}_{\mathrm{spat}}\left(\mathrm{c}\right)+\text{offset}$$ (2)

for calculating the RR of breast cancer mortality in high-risk counties compared to lower-risk counties, where the RR is equal to exp(β). In this step, the model settings and assumptions of Eq.(2) were identical to Eq.(1).

The STAR model was fitted by fully Bayesian inference using Markov Chain Monte Carlo simulation techniques by randomly drawing samples from a fully conditional distribution of unknown parameters conditional on the rest of the parameters and the data (Fahrmeir and Lang, 2001). In total 25,000 iterations were carried out, with the first 5,000 samples used as burn in. Every 20th sample was stored from the remaining 20,000 samples, giving a final sample of 1,000 for use as posterior estimates. Moreover, the estimated variance of spatial function ${\mathcal{C}}_{spat}^2$ was used to quantify the level of geographic disparities, explaining that the county risk of breast cancer mortality is on average about $\left[\exp \right(\sqrt{{\sigma }_{spat}^2})-1]\%$ larger or smaller than the overall breast cancer mortality (Pankratz et al., 2005). The data analysis was implemented using the BayesX 2.01 software package (Brezger et al., 2005). We considered a 95% CI of covariates that did not contain zero as statistically significant.

3 RESULTS

During 1982-2004, the average annual female population aged 40 year or older in the United States was 57,035,121. The average annual number of breast cancer deaths was 40,182.6 during the entire study period. However, the average annual number of breast cancer deaths with valid county codes was dramatically reduced to only 31,592.0 after 1989 because of the lack of available data due to potential confidentiality concerns by the NHCS. Since 1989, the percentage of unavailable data of the total number of breast cancer deaths was 28.3%, ranging from a low of 26.3% in 2004 to a high of 29.5% in 1992. Using kriging, the average of annual breast cancer deaths was 40778.9, which was 1.5% higher than the observed average annual number of breast cancer deaths (Table 1).

Table 1.

Available, unavailable and kriged breast cancer death counts from 1989 to 2004.

	Observed			Kriged†
Year	Total	Available	Unavailable	N1	N2	Δ (%)
1989	40529	28921	11608	12660	41581	2.6
1990	41088	29200	11888	12617	41817	1.8
1991	41208	29324	11884	12675	41999	1.9
1992	40761	28743	12018	12341	41084	0.8
1993	41383	29338	12045	12837	42175	1.9
1994	41293	29889	11404	12139	42028	1.8
1995	41437	29845	11592	12185	42030	1.4
1996	40806	29353	11453	11909	41262	1.1
1997	39684	28547	11137	11574	40121	1.1
1998	39426	28174	11252	11801	39975	1.4
1999	38984	27904	11080	11742	39646	1.7
2000	39678	28295	11383	12020	40315	1.6
2001	39156	28009	11147	11699	39708	1.4
2002	39321	28018	11303	11710	39728	1.0
2003	39390	29039	10351	10878	39917	1.3
2004	38778	28589	10189	10487	39076	0.8

^†N₁ = number of kriged breast cancer deaths; N₂ = total number of breast cancer deaths after kriging; Δ = the percent difference between the total observed breast cancer deaths and the number after kriging,

Table 2 shows the model assessment of eight STAR models by race and age, indicating that all STAR models reached convergence and fit the data well. Variance components show that the structured spatial function had a larger variance than the unstructured spatial function. For White women, the structure spatial variance (σ_s²) reached the highest level at 1.06 for age 40-49 years of age, and decreased to only 0.36 with increasing age, while the structure spatial variance for African American women was relatively stable varying from 0.65 to 0.71 among different age groups. The unstructured spatial variance (σ_u²) was similar for each age group for both races. The proportions of the structured spatial variance of the total spatial variance (ρ) in the eight models showed that the structured spatial variance account for at least 98% of the total variance, suggesting the importance of the spatial function in this study. The spatial variance also implies that geographic disparities of breast cancer mortality for White women decreased from 180.0% to 74.5% with increasing age, while geographic disparities in African American women did not vary by age, ranging from 123.6% to 132.2%.

Table 2.

Model performance for each race and age level, United States 1982-2004.

	White				African American
Age	40-49	50-59	60-69	70+	40-49	50-59	60-69	70+
D(θ)	33874.89	38709.78	40103.15	38129.81	13305.50	12929.37	15334.33	17746.79
pd	92.41	46.62	44.65	51.69	132.60	153.63	133.27	170.91
DIC	33967.30	38756.40	40147.80	38181.50	13438.10	13083.00	15467.60	17917.70
σ u 2	0.001	0.0003	0.0002	0.0001	0.01	0.01	0.01	0.01
σ s 2	1.06	0.77	0.59	0.31	0.65	0.71	0.69	0.67
ρ (%)	99.88	99.97	99.97	99.97	98.21	98.16	98.72	98.92

Abbreviation: D(θ) = posterior mean of the deviance; p_d = effect number of parameters. DIC = deviance information criteria. σ_u² = structured spatial variance; σ_s² = unstructured spatial variance; ρ = proportion of the structured spatial variance in total spatial variance, i.e., σ_s²/(σ_u²+ σ_s²)×100%

We calculated the RR between high-risk counties compared to the other counties (low-risk and nonsignificant-risk) for each race and age group to evaluate the magnitude of the increased breast cancer mortality risk. Table 3 shows that high-risk counties had higher RR for African American women than for White women for each age group. The RR increased for both races with decreasing age. Fig 2 and Fig 3 display where mortality rates were higher by age and race.

Table 3.

Relative risks of breast cancer mortality in high-risk counties compared with the other counties, calculated by Eq.(2). Significance was defined 95% credible interval of the spatial effect in that a county had a strictly positive credible interval.

	White		African American
Age	RR	95% CI	RR	95% CI
40-49	2.03	(1.97, 2.08)	2.54	(2.38, 2.69)
50-59	1.70	(1.68, 1.74)	2.46	(2.33, 2.59)
60-69	1.55	(1.53, 1.57)	2.24	(2.13, 2.36)
70+	1.17	(1.16, 1.18)	1.72	(1.69, 1.75)

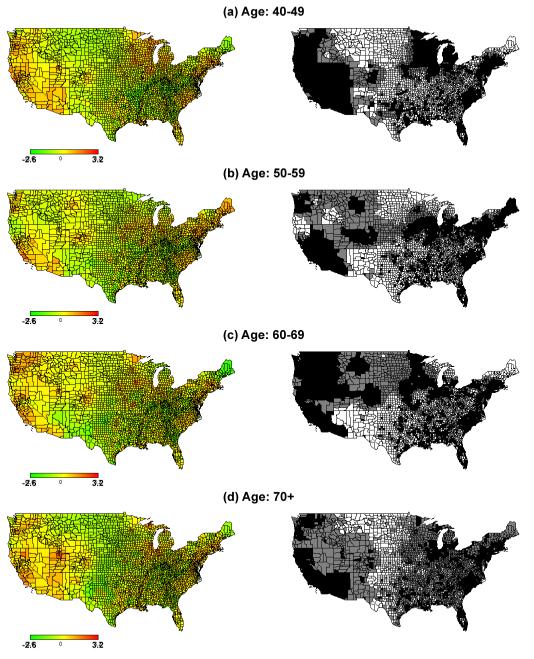
Fig 2.

Maps of the spatial effect (left) with corresponding 95% credible interval (right) for White women’s breast cancer mortality among 3109 U.S. counties. Counties shaded by black color had higher breast cancer mortality rates compared to the national average, while white color had breast cancer mortality rates lower than the national average. Grey counties had breast cancer mortality rates similar to the national average

Fig 3.

Maps of the spatial effect (left) with corresponding 95% credible interval (right) for African American women’s breast cancer mortality among 3109 U.S. counties. Counties shaded by black color had higher breast cancer mortality rates compared to the national average, while white color had breast cancer mortality rates lower than the national average. Grey counties have breast cancer mortality rates similar to the national average

For White women, average RR and geographic variation declined with increasing age among all counties in the United States (Table 4). Higher average RR presented in the New England, Mid Atlantic, East North Central, and Pacific Divisions across all four age groups, also suggesting that greater geographic disparities appeared in these divisions. The highest proportion of counties in these divisions was in the high-risk group, also evidenced by the small spatial variance in these divisions. The Mountain Division had the highest percentage of low-risk counties of any of the nine Divisions. There were five divisions where at least 50 percent of the counties were in the high-risk group for each of the four age groups: New England, Mid Atlantic, East North Central, South Atlantic, and Pacific Divisions. Only for the Mountain Division, at least 50% of the counties were in the low-risk group for all four age levels.

Table 4.

The mean and variance of relative risks for breast cancer mortality calculated by the spatial function in Eq.(1) and the proportion of high-risk, low-risk, and nonsignificant-risk counties for White women in each regional division compared to the mean national level.

Age	Division	N	Mean	Variance	High-risk (%)	Nonsig-risk (%)	Low-risk (%)
40-49	NE	67	2.00	0.17	95.5	0.0	4.5
	MA	150	2.06	0.10	96.7	0.7	2.7
	ENC	437	1.61	0.39	77.8	4.1	18.1
	WNC	618	0.82	0.25	28.5	6.6	64.9
	SA	590	1.34	0.50	59.7	4.2	36.1
	ESC	364	1.14	0.40	50.0	3.9	46.2
	WSC	470	1.01	0.31	44.7	5.5	49.8
	MO	280	0.90	0.27	36.4	5.7	57.9
	PA	133	1.65	0.32	80.5	1.5	18.1
	Total	3109	1.22	0.47	54.0	4.6	41.4
50-59	NE	67	1.64	0.07	95.5	3.0	1.5
	MA	150	1.72	0.03	100.0	0.0	0.0
	ENC	437	1.48	0.12	87.4	1.6	11.0
	WNC	618	0.88	0.20	36.4	5.8	57.8
	SA	590	1.24	0.24	68.1	3.1	28.8
	ESC	364	1.14	0.18	61.5	3.0	35.4
	WSC	470	0.93	0.18	43.6	5.7	50.6
	MO	280	0.79	0.16	32.5	5.4	62.1
	PA	133	1.42	0.14	84.2	2.3	13.5
	Total	3109	1.14	0.25	59.7	3.8	36.5
60-69	NE	67	1.54	0.05	95.5	0.0	4.5
	MA	150	1.54	0.04	97.3	1.3	1.3
	ENC	437	1.41	0.06	93.8	0.9	5.3
	WNC	618	0.97	0.19	49.8	3.4	46.8
	SA	590	1.14	0.13	69.7	2.0	28.3
	ESC	364	1.11	0.13	70.3	2.2	27.5
	WSC	470	0.97	0.14	55.3	3.8	40.9
	MO	280	0.74	0.15	28.6	3.9	67.5
	PA	133	1.29	0.09	85.7	0.8	13.5
	Total	3109	1.11	0.17	65.9	2.5	31.6
70+	NE	67	1.32	0.02	98.5	0.0	1.5
	MA	150	1.29	0.01	100.0	0.0	0.0
	ENC	437	1.21	0.01	97.3	1.1	1.6
	WNC	618	1.06	0.08	74.3	3.7	22.0
	SA	590	1.04	0.05	61.7	13.2	25.1
	ESC	364	1.01	0.03	49.5	16.5	34.1
	WSC	470	0.95	0.06	53.0	8.1	38.9
	MO	280	0.83	0.09	32.1	5.7	62.1
	PA	133	1.07	0.05	78.2	3.8	18.1
	Total	3109	1.05	0.07	67.1	7.2	25.6

Abbreviation: NE = New England; MA = Mid-Atlantic; ENC = East North Central; WNC = West North Central; SA = South Atlantic; ESC = East South Central; WSC = West South Central; MO = Mountain; PA = Pacific Percentages of at least 50.0% are in bold.

The average RRs and the spatial variances were similar across the four age groups for African American women across all U.S. counties (Table 5). Larger average RRs were present for counties in the New England, Middle Atlantic, East North Central, West North Central, Mountain, and Pacific Divisions. The larger spatial variances in these divisions also implied greater geographic disparities than the other divisions. The percentage of high- and low-risk counties for each Division is varied by age group. However, for the Mid Atlantic and Pacific Divisions, at least 50% of the counties were in the high-risk group across all four age groups. For the East South Central and West South Central Divisions, there was a high percentage of low-risk counties across three of the four age groups. Overall, there were at least 25.8% high-risk, 22.9% low-risk, and 19.7% nonsignificant counties for African American women.

Table 5.

The mean and variance of relative risk for breast cancer mortality calculated by the spatial function in Eq.(1) and the proportion of high-risk, low-risk, and nonsignificant-risk counties for African American women in each regional division compared to the mean national level.

Age	Division	N	Mean	Variance	High-risk (%)	Nonsig-risk (%)	Low-risk (%)
40-49	NE	67	1.80	2.29	47.8	6.0	46.3
	MA	150	1.80	1.20	62.7	17.3	20.0
	ENC	437	1.89	1.53	65.7	16.9	17.4
	WNC	618	1.07	0.74	22.2	22.8	55.0
	SA	590	1.26	0.90	37.8	15.9	46.3
	ESC	364	0.76	0.26	17.3	13.5	69.2
	WSC	470	1.01	0.67	24.9	22.8	52.3
	MO	280	1.15	0.47	28.9	36.8	34.3
	PA	133	2.39	1.24	88.7	9.8	1.5
	Total	3109	1.29	1.04	37.0	19.7	43.3
50-59	NE	67	2.43	1.68	79.1	14.9	6.0
	MA	150	2.49	2.13	84.0	12.7	3.3
	ENC	437	1.61	1.92	52.6	29.1	18.3
	WNC	618	1.09	1.11	21.4	35.6	43.0
	SA	590	1.25	0.77	41.2	15.9	42.9
	ESC	364	0.81	0.31	19.0	17.9	63.2
	WSC	470	0.89	0.34	19.6	18.9	61.5
	MO	280	1.19	0.54	29.3	49.6	21.1
	PA	133	1.81	1.75	57.9	28.6	13.5
	Total	3109	1.26	1.17	35.5	25.8	38.7
60-69	NE	67	1.21	1.24	38.8	10.5	50.8
	MA	150	1.74	0.89	64.0	24.0	12.0
	ENC	437	1.35	0.77	44.6	25.4	30.0
	WNC	618	1.27	0.66	36.4	44.8	18.8
	SA	590	1.13	0.59	42.5	11.0	46.4
	ESC	364	0.90	0.30	30.2	10.2	59.6
	WSC	470	0.86	0.31	21.1	15.5	63.4
	MO	280	1.36	0.57	50.7	30.7	18.6
	PA	133	2.66	1.77	93.2	6.0	0.8
	Total	3109	1.24	0.77	40.8	22.5	36.7
70+	NE	67	1.91	1.89	49.3	50.7	0.0
	MA	150	1.83	0.85	63.3	36.7	0.0
	ENC	437	1.73	2.90	39.1	57.9	3.0
	WNC	618	0.75	0.21	5.8	50.0	48.2
	SA	590	1.29	0.60	35.8	45.4	18.8
	ESC	364	0.97	0.31	15.1	59.1	25.8
	WSC	470	1.01	0.40	16.4	53.2	30.4
	MO	280	1.50	1.43	12.9	67.9	19.3
	PA	133	2.12	1.15	66.2	33.8	0.0
	Total	3109	1.26	1.08	25.8	51.3	22.9

Abbreviation: NE = New England; MA = Mid-Atlantic; ENC = East North Central; WNC = West North Central; SA = South Atlantic; ESC = East South Central; WSC = West South Central; MO = Mountain; PA = Pacific; % = row percentage Percentages of at least 50.0% are in bold.

4 DISCUSSION

This nationwide spatiotemporal analysis of breast cancer mortality described the location and magnitude of geographic disparities among African American women and White women by age group, alleviating concerns about confidentiality and reliability of sparse data. Using kriging and the STAR model, we first showed that the relative risk for African American women who lived in high-risk counties was at least 2.5 times higher than for those who lived in lower-risk counties. This disparity was smaller among White women in each age group. Our second finding shows the extent of the geographic disparity in and the location of counties with high breast cancer mortality rates by age group and race. Use of kriging and the STAR model allowed us to identify priority counties by age and race that should be targeted for interventions aimed at reducing breast cancer mortality.

First, the relative risk for African American women who lived in high-risk counties was at least 2.5 times higher than for African American women who lived in lower-risk counties, with younger women showing larger disparity. While the same age pattern was found among White women, the magnitude of this geographic disparity at the county level was lower than among African American women. An advantage of the STAR model is that we were able to estimate the breast cancer mortality rate by age and race for each county, while many previous studies used age-adjusted methods or combined counties with similar elevated risks using statistical clustering methods (Singh et al., 2011; Vinnakota and Lam, 2006). Combining counties makes the implementation of interventions locally more difficult because of the local infrastructure and resources available. Unlike previous studies, we were able to estimate the geographic disparity by age and race, showing that the geographic disparity in breast cancer mortality rates was much larger among African American women than among White women, particularly among women aged 70 or older. Geographic disparities could be up to 1.77 times higher for African American women (132.2%) than among White women (74.5%) at age level 70+. While the spatial disparity declined with increasing age among White women, the spatial disparity remained explicitly vast by age among African American women. This result suggests that there might be opportunities for counties with high breast cancer mortality rates to reduce their rates to levels similar to counties with much lower rates among younger White women and all age groups for African American women. Also, the much larger geographic disparity among African American women relative to White women may suggest a need for additional studies focusing on understanding whether other factors could reduce the differences of breast cancer mortality among different counties.

Our second finding shows the extent of the geographic disparity and the location of counties with high breast cancer mortality rates by age group and race. Our results based on kriging and the STAR model were generally similar to previous studies that have focused on local breast cancer mortality, such as Houston, Dallas and San Antonio for African American women (Tian et al., 2011) and in Gulf Coast Texas for both non-Hispanic Whites and Blacks (Hsu et al., 2004). Regardless of race, areas in the Northeast U.S., such as New York, Philadelphia, and the east coast from Baltimore to Boston, had elevated breast cancer mortality rates (Goovaerts, 2005; Kulldorff et al., 1997). These studies and our results show that specific counties can be identified that have elevated breast cancer mortality rates worthy of further investigations and likely interventions.

Strengths of this study are the combined use of kriging and the STAR model to overcome a large amount of data with unavailable location (county) codes after 1989, taking into account temporal autoregressive and spatial autocorrelation. Kriging has been used in small-area public health research to reduce the influence of missing location data based on few cases and small population size and also to normalize extreme values of mortality rates (Goovaerts, 2005; Kazembe et al., 2007; Oliver et al., 1998). In this study, kriging mainly affected the data for African American women because of small population size in certain counties, although there were several counties where kriging had to estimate data for White women. Our approach using kriging and the STAR model is directly applicable to other geographic units and different diseases where confidentiality and reliability based on sparse data is of concern. With increasing availability of data for small geographic areas, the need for statistical methods such as ours will only increase. In addition to the use of kriging, the STAR model was able to analyze spatiotemporal data, including several covariates and smoothing functions using Markov random fields. Its use has been described in previous studies (Chien and Bangdiwala, 2012; Chiogna and Gaetan, 2010; Kandala et al., 2011; Khatab, 2010; Musio et al., 2010; Serio and Claudia, 2009; Wand et al., 2011). In other words, we used a time smoother and a Markov random field to consider spatiotemporal autocorrelations, and added the county-specific population to the offset in each model to obtain reliable estimates. More importantly, the STAR model in our study not only visualized the spatial pattern of the location of high-risk counties, but also compared the risk of breast cancer mortality based on high-risk, low-risk, and nonsignificant counties. In particular, this criterion can clarify some counties with a RR close to the U.S. average. Taking into account the offset by using the population size in the STAR model can also avoid that counties with extremely large and small population were always classified into the high-risk and low-risk clusters. This allowed us to identify priority counties by age and race that should be targeted for interventions aimed at reducing breast cancer mortality.

There are some limitations to this study. First, kriging techniques have some inherent limitations, such as the linearity of the estimators and the assumption of normality (Yu et al., 2009). Second, the STAR model is limited by our inability to calculate county-specific risk factor estimates for all counties because a model with over 3000 random effects would likely result in overfitting or lack of model convergence. Third, our models did not examine other risk factors, such as county-level socioeconomic status, availability of mammography facilities or primary care physicians, or biological factors (e.g., tumor biomarkers) that might explain reasons for higher risk of breast cancer mortality by race or age, but that was not the purpose of our study. Fourth, results for other races, such as Hispanic, were not included in this study because kriging overestimated the breast cancer mortality rate, which led to unreliable results. Fifth, using the 95% CI to determine significance was not always used in other studies because some studies used the 80% CI (Kandala et al., 2011; Kazembe and Mpeketula, 2010; Kazembe 2009; Kazembe et al., 2008). In certain situations the 80% CI may produce more significant areas leading different results from the 95% CI. Future development of the statistical approach might be to incorporate the temporal variation in addition to the geographic disparity of breast cancer mortality rates and identify priority counties by incorporating the posterior distribution and standard error of the estimates.

The flexibility of the STAR modeling approach provides future opportunities for advanced analyses. For example, more risk factors, such as socioeconomic status and primary care physician ability, can be examined for their nationwide, county-specific, and time-varying impacts by including linear fixed effects, random effects, and varying coefficients in the model, respectively (Chien et al., 2012). In addition, this functionality can be used to evaluate the change of spatial variance in the spatial function for determining which factor can affect geographic disparities among counties. Furthermore, the model for each race or each age level can be integrated in a spatial interactive term in the STAR model to implement spatial comparison among different races and ages (Sauleau et al., 2007).

5 CONCLUSION

In summary, we used kriging and the STAR model to reduce the impact of unavailable data because of confidentiality concerns in an attempt to identify the number and location of counties with high breast cancer mortality risk by race and age across the United States. The RR of breast cancer mortality in high-risk counties was higher in younger women for both races. Geographic disparities of breast cancer mortality were greater in younger African American women.

Highlights.

• We model breast cancer mortality in 3109 U.S. counties from 1982-2004.

• We apply kringing to overcome unavailable data due to confidentiality issue.

• At least 25.8% of counties have elevated breast cancer mortality due to locations.

• The trend of the relative risk elevates for both races with decreasing age.

• Geographic disparities are greater in younger African American woman.

Appendix A

Fig A. Covariances of spatial distance and temporal lag for White women, where blue line is for original data, and red line is for kriging data

Fig B. Covariances of spatial distance and temporal lag for African American women, where blue line is for original data, and red line is for kriging data

Appendix B

Table.

Cross-validation of White and African American women in four age levels

Age	White	African American
40-49	1.95×l0−7	7.98×10−6
50-59	4.03×l0−7	7.46×10−5
60-69	1.44×10−6	2.01×10−3
70+	9.75×10−7	1.03×10−3