Fast Analytical Methods for Macroscopic Electrostatic Models in Biomolecular Simulations

Abstract

We review recent developments of fast analytical methods for macroscopic electrostatic calculations in biological applications, including the Poisson–Boltzmann (PB) and the generalized Born models for electrostatic solvation energy. The focus is on analytical approaches for hybrid solvation models, especially the image charge method for a spherical cavity, and also the generalized Born theory as an approximation to the PB model. This review places much emphasis on the mathematical details behind these methods.

1. Introduction

Over the past few decades, increasingly large-scale simulations of macromolecular systems at the atomic level have been conducted in investigating the structure, function, and properties of biological molecules and their complexes; molecular dynamics (MD) simulation techniques have served as a principal tool [107, 170]. Classical MD simulations using Newton's second law calculate the trajectories of interacting atoms in a system comprising biomolecules and surrounding solvents. This computational method provides detailed information on conformational changes of the biomolecules; thus, macroscopic properties can be accurately obtained by sampling microscopic properties along a sufficiently long trajectory. The forces in MD simulations are generated from atom-atom interactions, which are often given by an empirical potential energy function,

$$E=\sum _{\text{bonds}}{k}_b{(b-b_0)}^2+\sum _{\text{angles}}{k}_{\theta }{(\theta -{\theta }_0)}^2+\sum _{\text{torsions}}{k}_{\omega }\left[\cos \right(n\omega +\gamma )+1]+\sum _{\text{atom pairs}}\left[\left(\frac{A_{\mathit{ij}}}{r_{\mathit{ij}}^{12}}-\frac{B_{\mathit{ij}}}{r_{\mathit{ij}}^6}\right)+\frac{q_i{q}_j}{r_{\mathit{ij}}}\right],$$ (1.1)

where the first three summations are contributions due to, respectively, deviations of bond lengths b from their equilibrium values b₀, deviations of valence angles θ from their equilibrium values θ₀, and torsional potentials from bond rotations (dihedral angles ω with phase shifts γ of the n-fold term). The fourth summation is composed of the van der Waals (vdW) interactions represented by Lennard–Jones 6–12 potentials, and the Coulomb electrostatic interactions. The functional form and parameter set for each type of atom in (1.1) is called a force field, which is derived from experimental observations and quantum mechanical calculations. Popular force fields, such as those in Amber [207, 217], CHARMM [29, 136], GROMACS [193, 87], and OPLS [99], have been developed and widely applied to energy minimization and dynamic simulation of biomolecules. The first three terms and the vdW potential in (1.1) are all short-range interactions that are negligible when interparticle distances are greater than a certain small value. Since there are many efficient methods to treat these short-range interactions, in this paper we will discuss only the calculation of the long-range electrostatic interactions, which is the main challenge in current algorithmic developments and plays an essential role in investigating structure, function, and properties of biopolymers [167, 47, 204, 194, 178, 9, 106, 205, 197].

For a realistic biomolecule model in an aqueous environment, in order to take into account the solvent effects, classical electrostatic models use explicit representations of solvent molecules around the solute and place the solute-solvent system inside a simulation box on which periodic boundary conditions are usually imposed. The periodic conditions represent an open system with infinitely many images of the particles in the box; thus, only the particles in the box are simulated. Acceleration methods such as Ewald [61, 1, 55], particle-mesh Ewald (PME) [44, 60, 55], particle-particle particle-mesh (P3M) [174, 135], and fast multipole methods (FMM) [80, 38, 184, 221] can be employed for electrostatic interactions. However, with explicit solvent models in MD, especially in large-scale simulations, the computational cost of all-atom descriptions is significantly high due to the large size of the simulation box required to minimize artifacts induced by the interactions of unphysical periodic images. For a typical setting for an average protein from the genomic databases with approximately 5500 atoms, an extra 20–30 thousand solvent atoms have to be added to the simulation in order to have a standard 10–12 Å of discrete water molecules surrounding the protein [9, 100]. The computational expense of these “extra” atoms far exceeds that of the protein itself.

Alternatively, continuum electrostatic models for the solvent [69, 63], which model it using a high dielectric continuum medium, are attracting attention. Their advantage is that they can greatly reduce the number of degrees of freedom of the simulated biological system; see Figure 1.1 for the surfaces of a biomolecule. In the continuum models, the solute background is also described by a dielectric medium with a fixed atomic charge distribution, and the system is then governed by the Poisson–Boltzmann (PB) equation, which can be numerically solved for irregular dielectric interfaces between the solute and solvent. Direct numerical solutions in three-dimensional space (3D) or on the biomolecular surface using boundary integral formulations are still expensive; therefore, various accelerated techniques and theoretical approaches have been developed. The generalized Born (GB) theory [182, 17, 151] has been widely accepted as an alternative to the PB theory due to its high efficiency in implementations. The GB method approximates the PB free energy through an analytical pairwise formula, and the numerical solutions of the discretized PB equation thus can be avoided. Due to its simplicity, the GB method has been widely used in MD simulations.

Fig. 1.1.

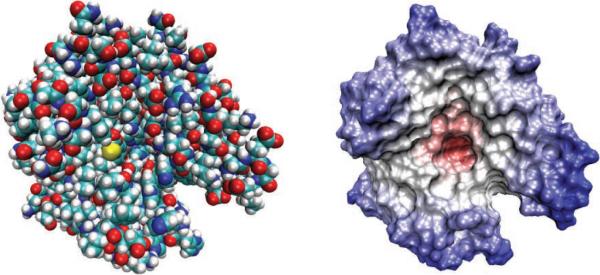
Molecular surfaces of the carbonic anhydrases-II [125]. (Left) The van der Waals (vdW) surface of the domain composed of the sum of overlapping vdW spheres. (Right) The solvent accessible surface (SAS) generated by rolling a small sphere on the vdW surface. In the macroscopic theory, the molecular domain inside the surface is given a low dielectric constant and the enclosed atoms are treated explicitly, while the exterior domain is treated as a homogeneous continuum medium with a higher dielectric constant. Poisson–Boltzmann models often use the SAS to define the molecular boundary, while generalized Born methods usually take the vdW surface.

The analytical method in the continuum solvent framework also includes the hybrid implicit/explicit solvation model [146]; this model includes several water layers close to the solute in a fixed volume, which is often taken to be a spherical cavity surrounded by a continuum solvent. The analytical Kirkwood series expansion [105] is available for solving the PB equation for such a simple geometry.

In this article, we will review recent developments in analytical methods for the electrostatic free energy calculations in the framework of the macroscopic PB continuum solvent representation, since these methods are widely used in MD simulations. We will focus on the GB theory and the hybrid solvation models, in particular, the image charge methods for the reaction field of a dielectric sphere.

2. Poisson–Boltzmann Electrostatic Model for Biomolecular Solvation

The electrostatic force is one of the most important forces in the structure and stability of biomolecules in an aqueous environment [91, 69]. The classical electrostatic theory applies to a medium composed of the solute macromolecule and the surrounding solvent environment. In the classical continuum approach, the solute is described as a region with a low dielectric constant ∊_i, typically ∊_i = 1 ~ 4, and partial charges q_j are assigned to atomic locations r_j, giving a charge density

$$\rho \left(\mathbf{r}\right)=\sum _{j=1}^N{q}_j\delta (\mathbf{r}-{\mathbf{r}}_j),$$ (2.1)

where the partial charges q_j can be computed through quantum mechanical calculations [47] or from molecular mechanics force fields [107], and the atomic locations r_j are taken as the nuclear centers of the atoms inside the solute. The solute boundary Γ is defined by the molecular surface (see Figure 1.1), which is given by either the vdW surface composed of the sum of overlapping vdW spheres or the solvent accessible surface (SAS) generated by rolling a small sphere on the vdW surface [125]. The solvent, occupying the exterior of the solute, is assigned a higher dielectric constant ∊_o ≈ 80 and in general is an ionic liquid with mobile ionic charges n_i(r) for ions of type i, in contrast to the fixed charges inside the solute.

Therefore, the macroscopic potential Φ(r), due to the embedded fixed charges in the solute, the mobile ionic charges in the solvent, and the polarization effects of the solvent from the solute charges, is governed by the Poisson equation

$$-\nabla \cdot ∊\left(\mathbf{r}\right)\nabla \Phi \left(\mathbf{r}\right)=4\pi \left[\rho \right(\mathbf{r})+n(\mathbf{r}\left)\right],$$ (2.2)

where n(r) = Σ_i n_i(r). To complete the model, two interface conditions on Γ for the continuities of the potentials and the normal displacements are required, i.e.,

$$\Phi \left({\mathbf{r}}^{-}\right)=\Phi \left({\mathbf{r}}^{+}\right),{∊}_i\frac{\partial \Phi \left({\mathbf{r}}^{-}\right)}{\partial \mathbf{n}}={∊}_o\frac{\partial \Phi \left({\mathbf{r}}^{+}\right)}{\partial \mathbf{n}}$$ (2.3)

for r ∊ Γ, where r⁻ and r⁺ are, respectively, the inner and outer limits at position r and n is the outward unit normal to the surface of the solute.

The mobile ionic charges will be subject to the influence of the electric field of the solute charges. The ions are assumed to obey the Boltzmann distribution [153], under a potential of mean force (PMF) w_i(r) [88], for the ith type of ions in the solvent,

$$n_i\left(\mathbf{r}\right)=n_i^0\exp (-{\omega }_i(\mathbf{r})∕k_{B}T),$$ (2.4)

where $n_i^0$ is the number density of ions of type i in the bulk solvent in the absence of the solute, T is the temperature, and k_B is the Boltzmann constant.

The negative gradient of the PMF w_i(r) gives the average force on a given ion of type i due to all other charges in the system, and it is defined by a Gibbs average over all other ions and charge configurations, i.e., by a Boltzmann factor weighted integration over the positions of all other ions/charges in the phase space [88]. In the Debye–Hückel theory [48] on electrolyte solutions, it was proposed that the PMF on an ion of type i be approximated by the ion charge multiplied by the macroscopic electrostatic potential Φ(r) of the solute-solvent system,

$${\omega }_i\left(\mathbf{r}\right)=q_i\Phi \left(\mathbf{r}\right);$$ (2.5)

thus, the distribution of the ith type of ion is

$$n_i\left(\mathbf{r}\right)=n_i^0\exp (-q_i\Phi ∕k_{B}T).$$ (2.6)

By substituting (2.6) into (2.2), we obtain a nonlinear PB equation for the electrostatic potential Φ(r) in the solute-solvent system:

$$-\nabla \cdot ∊\left(\mathbf{r}\right)\nabla \Phi \left(\mathbf{r}\right)=4\pi \rho \left(\mathbf{r}\right)+4\pi \sum _i{q}_i{n}_i^0\exp (-q_i\Phi ∕k_{B}T).$$ (2.7)

For an ionic solution containing a 1:1 salt (e.g., NaCl), the PB equation for dimensionless electrostatic potential in the solvent region (ρ(r) = 0 and ∊(r) = ∊_o in this region) can be rewritten [131] as

$$\Delta \Phi \left(\mathbf{r}\right)-{\lambda }^2\sinh \left[\Phi \right(\mathbf{r}\left)\right]=0.$$ (2.8)

In (2.8), λ is called the Debye–Hückel inverse length and is defined by

$$\lambda =\sqrt{\frac{8\pi N_A{e}^{2}I}{1000{∊}_o{k}_{B}T}},$$ (2.9)

where N_A is Avogadro's number, e is the electron charge, and I is the ionic strength of the bulk solution. When the electrostatic field is weak, the hyperbolic sine function can be linearized using a Taylor series expansion, leading to the linearized PB equation [88]:

$$\Delta \Phi \left(\mathbf{r}\right)-{\lambda }^2\Phi \left(\mathbf{r}\right)=0.$$ (2.10)

Although in some biological systems the fundamental assumption of small Φ is not justified, the linearized PB equation has been widely used instead of the nonlinear version in biomolecular applications due to the former's simplicity; its mathematical analysis [114], numerical solutions [131], and dynamics simulations [64] are currently under investigation.

The PB theory in the context of electrostatic solvation energy [47, 91] as described here has been used in various other areas and is known as the Gouy–Chapman theory [77, 34] in electrochemistry, the Debye–Hückel theory [48] in solution chemistry, and the DLVO (Derjaguion–Landau–Verwey–Overbeek) theory [53, 195] in colloidal chemistry. However, it should be emphasized that the nonlinear and linear PBs, which ignore the finite size effect of ions and the ion-ion correlations, are approximations that capture the properties of monovalent ion solutions reasonably well at low salt concentrations, but they fail to deal with mixtures or divalents with reasonable accuracy [16, 62, 21, 22]. Specifically, it has been shown [102] that the PB model fails to predict the charge inversion phenomenon in double layers near charged surfaces [127, 190] and the similar charge-charge attractions of double layers in aqueous electrolyte solutions of divalent ions [88, 103, 141, 166]. Recent efforts have been made to address the ion size effects in [59], which incorporates the finite size effect of ions in solvents and ion channels through an energy variational formulation, and also in [27, 183, 113].

In the framework of the nonlinear PB electrostatic model for the solute-solvent system, the electrostatic energy of the system can be defined by a variational principle for an energy-density functional W_ed [172, 68, 104],

$$W_{\mathit{ed}}=\frac{1}{4\pi }{\int }_{{\mathbb{R}}^3}d\mathbf{r}\left[4\pi \rho \left(\mathbf{r}\right)\Phi \left(\mathbf{r}\right)-{\int }_0^{\Phi \left(\mathbf{r}\right)}S\left(\varphi \right)d\varphi -\frac{∊\left(\mathbf{r}\right)}{2}{\mid \nabla \Phi \left(\mathbf{r}\right)\mid }^2\right],$$ (2.11)

where

$$S\left(\varphi \right)=-4\pi \sum _i{q}_i{n}_i^0\exp (-q_i\varphi ∕k_{B}T).$$ (2.12)

It can be shown that the nonlinear PB equation (2.7) can be obtained as the Euler–Lagrange equation of (2.11).

Using Gauss' law, W_ed can be shown [227] to be equivalent to

$$W_{\mathit{ed}}=\frac{1}{4\pi }{\int }_{{\mathbb{R}}^3}d\mathbf{r}\left[2\pi \rho \left(\mathbf{r}\right)\Phi \left(\mathbf{r}\right)+\frac{1}{2}S\left(\Phi \right(\mathbf{r}\left)\right)\Phi \left(\mathbf{r}\right)-{\int }_0^{\Phi \left(\mathbf{r}\right)}S\left(\varphi \right)d\varphi \right],$$ (2.13)

which can be further simplified for the linearized PB equation (2.10) when S becomes a linear function:

$$W_{\mathit{ed}}=\frac{1}{2}{\int }_{{\mathbb{R}}^3}\rho \left(\mathbf{r}\right)\Phi \left(\mathbf{r}\right)d\mathbf{r}.$$ (2.14)

Moreover, (2.13) is equivalent to the charging energy W_ch of the solute atomic charges from zero values to their full values [227], i.e.,

$$W_{\mathit{ed}}=W_{\mathit{ch}}\equiv {\int }_0^{1}d\eta {\int }_{{\mathbb{R}}^3}d\mathbf{r}\rho \left(\mathbf{r}\right)\Phi (\mathbf{r},\eta ),$$ (2.15)

where Φ(r, η) is the potential of the charging state η (η = 0 is the zero charged state; η = 1 is the fully charged state) obtained by solving (2.7) when ρ(r) is replaced by ηρ(r). Note that for the linearized PB model, Φ(r, η) = ηΦ(r), and thus (2.15) is reduced to (2.14).

In physical chemistry, free energy is one of the most important quantities; it describes the tendencies for a molecular system to associate and react. Being able to calculate the free energy quickly and accurately is of primary importance and is a key goal in algorithm development for computer simulations of molecular systems. In a biomolecular system, the chemical processes usually happen in a solvent environment. One important aspect of these processes is to predict the solvation free energy, ΔG_sol, which corresponds to the free energy associated with the transfer of a solute molecule from a vacuum (gas) phase to a solvent phase. In practical calculations, the solvation energy is most conveniently decomposed into two components, ΔG_pol and ΔG_np, which are referred to as polar and nonpolar solvation energy, respectively [162]. The nonpolar part, usually related to the SAS of the solute, is associated with the first step of the insertion process, where an empty space is created to form the solute cavity to accommodate the solute atoms whose charges have been nullified. The polar solvation energy is the more computationally expensive part in calculating ΔG_sol and represents the bottleneck in dynamic simulations of biomolecules. Depending on whether or not free ions are present in an aqueous solution, the PB or Poisson solvent representation is one of the most important theories used to find ΔG_pol within the framework of continuum electrostatics in inhomogeneous media.

The polar electrostatic solvation energy ΔG_pol results from the polarization of the solvent and redistribution of the mobile ion charges through the polarization reaction field, reflecting the interaction of the solute charges and the polarization in the solvent. As mentioned above, ΔG_pol can also be identified as the difference between the energy needed to charge the solute atomic charge from zero to its full charge value in the ionic solvent environment and that in a reference environment (usually the vacuum or a homogeneous dielectric environment)[148, 172, 227, 69], i.e.,

$$\Delta G_{\mathit{pol}}=W_{\mathit{ch}}\left(\mathit{sol}\right)-W_{\mathit{ch}}\left(\mathit{ref}\right).$$ (2.16)

In the classical Born solvation energy [26] for an ion with an atomic radius a and a charge q immersed in a solvent with a dielectric constant ∊_o, the solvent is polarized by the ion charge producing a reaction field, Φ_rf (r), whose value at the center of the ion is given by (see (3.14) in section 3.1.1)

$${\Phi }_{\mathit{rf}}\left(0\right)=-\frac{q}{a}\left(\frac{1}{{∊}_i}-\frac{1}{{∊}_o}\right),$$ (2.17)

here a dielectric constant ∊_i = 1 is often assigned to the a-sphere containing the ion. The Born solvation energy is then obtained by using (2.14) and (2.16) (see also (2.19)),

$$\Delta G_{\mathit{pol}}=-\frac{1}{2}q{\Phi }_{\mathit{rf}}=-\frac{q^2}{2a}\left(\frac{1}{{∊}_i}-\frac{1}{{∊}_o}\right).$$ (2.18)

For a general solute molecule, (2.7) is solved twice to produce a reaction field Φ_rf, while the dielectric constant ∊(r) is described with a two-constant model, i.e., ∊(r) = ∊_i inside the solute and ∊(r) = ∊_ext for the exterior of the solute. First, the equation is solved with ∊_ext = ∊_o to produce a potential Φ(r) in the solvent environment; second, it is solved with ∊_ext = ∊_i to produce a potential in a reference environment [17], denoted by Φ_ref(r). The difference between these two potentials gives the reaction field Φ_rf = Φ − Φ_ref, which is used to define the electrostatic free energy ΔG_pol through (2.14) and (2.16). To be exact, ΔG_pol is the electrostatic energy needed to transfer the solute from the reference environment to the solvent dielectric [172, 227, 17, 177]:

$$\Delta G_{\mathit{pol}}=-\frac{1}{2}{\int }_{{\mathbb{R}}^3}{\Phi }_{\mathit{rf}}\left(\mathbf{r}\right)\rho \left(\mathbf{r}\right)d\mathbf{r}.$$ (2.19)

In most cases, the exact solution of the reaction field Φ_rf(r) in the PB equation (2.7) is unknown due to the complexity of the equation and the geometric shape of the solute biomolecule. To obtain an approximate solution, various numerical methods have been developed, mostly for the linearized PB equation, including finite difference, finite element, and boundary element methods. Among them the most widely used method is the finite difference method [93, 91, 206, 132, 229], which has been incorporated into popular software for biomolecular electrostatics, such as Amber, CHARMM, DelPhi, and UHBD, due to its simple approach to mesh generalization and refinement using uniform grid divisions. Because of the jump in the dielectric constants on the solute's boundary, it is necessary to accurately define the molecular surface so dielectric values at each grid point can be assigned. The “rolling ball” algorithm [175] usually uses a probe sphere of a particular radius, typically 1.4Å, which rolls over the vdW surface of the biomolecule. The process yields an SAS area, sometimes called the Lee–Richards molecular surface [108]. The domain inside this surface is then considered to be the solute region (as shown in Figure 1.1). A low dielectric constant is assigned to the grid points in this domain and all other grid points are assigned a high dielectric value. Another tricky issue is to assign the charges inside the solute to grids, because they are usually not located at grid sites and are singular, taking the form of a Dirac delta function. To overcome this difficulty, each charge is split up and assigned to the eight nearest grid points. The accuracy of the finite difference method depends on the grid size, the mesh used to sample the irregular interface, and the ability to not merge opposite charges for dipoles at one node. The finite difference method leads to expensive linear algebraic systems with large numbers of degrees of freedom, even with acceleration techniques such as multigrid solvers. Adaptive finite element methods [90, 10, 11] have also been developed to provide local refinement using an error indicator. Multigrid techniques are available for the solution of the resulting linear system, leading to a linear scaling method in both memory and computational complexity [3]. An alternative approximation is based on surface integral representation of the linearized PB equation and leads to boundary element methods [196, 226, 25, 28, 98, 117, 128, 129], which reduce the 3D problem to a 2D problem on the molecular surface. However, some essential difficulties remain, such as the mesh generation over the surface and the treatment of singular integrals. The biggest challenge is that the full matrix produced by the boundary element method requires large storage and large computational time to solve. Recently, progress has been made in speeding up the calculation, in particular, using the FMM [28, 128, 129], the treecode algorithm [115], or other fast direct solvers [81, 5] to achieve a linear-scaling or approximately linear-scaling algorithm in terms of the number of mesh cells.

A complete description of the development of and advances in numerical PB methods can be found in a recent review [131]. However, the numerical solution of the PB equation is still considered too complex for practical MD simulations. The technical problem in force calculations due to the dielectric boundary also remains unsolved. Only moderate progress [191, 130, 133, 156] has been reported for dynamics applications, limited to small biomolecules such as peptides. Several popular analytical models have been introduced for a more economical and simple implementation of the long-range electrostatics computation. These include the GB model and the hybrid explicit/implicit model, both based on the PB theory and reviewed in this paper.

3. Hybrid Solvation Models

The use of the hybrid explicit/implicit model [201, 202, 101, 19, 4, 146, 18] as an alternative to the implicit method is based on the fact that solvent ions and molecules close to the molecular surface have different structural and dynamic properties compared to those in the bulk solvent, and so should be treated explicitly to accurately capture these properties. Recent work has highlighted the failure of the implicit solvent model with prescribed solute surfaces in predicting the correct dependence of binding affinity of a hydrophobic probe particle and two hydrophobic plates on the charge magnitude on the plates [198], and the implicit method needs to be further developed to incorporate the interplay of hydrophobic, dispersion, and electrostatic effects, for example, using a recently developed variational implicit solvent approach [57, 39].

In the hybrid solvation model, the explicit solvent atoms together with the solute are enclosed in a fixed cavity, surrounded by a bulk solvent; i.e., the solvent is split by a dielectric boundary into an explicit part and an implicit part. The simulation system is then composed of two dielectric media. Mathematically, the electrostatic potential is still described by the PB equation, but the charge distribution ρ(r) now includes the explicit ions and water molecules. A typical setting is illustrated in Figure 3.1 with a spherical surface as the dielectric boundary. The number of explicit water molecules can be flexible, and the simulation volume can then be a regular shape such as a sphere or a prolate spheroid for elongated biomolecules. The hybrid methods promise to have advantages of both implicit and explicit methods in at least three aspects. First, the electrostatic interactions can be treated as a pairwise sum using image charge approximation for the reaction field, allowing the use of the FMM. Second, as the hybrid methods treat the bulk water with a reaction field, the artificial periodicity of all explicit methods is avoided. This results in an accurate solution, even if the simulation system is very small. Third, the hybrid methods can treat nonneutral systems [225], for which the explicit methods require some special techniques leading to possible inaccuracy. Since the spherical and prolate spheroidal shapes are often used as the simulation volume in the hybrid methods for which exact solutions can be found, we will review recent progress on this topic.

Fig. 3.1.

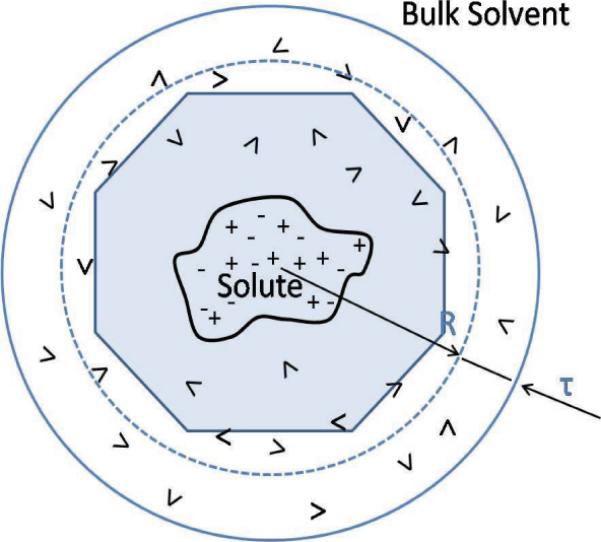
Illustration depicting a typical setting of a hybrid solvation model. The solute and solvent molecules inside the spherical cavity are treated explicitly, while the solvent outside is treated as a homogeneous continuum medium. A buffer layer of thickness τ is used to eliminate the singularity in reaction fields and surface effects due to the jump in the dielectric constants. The space-filling truncated octahedron (TO) box is used to implement the periodic boundary condition treatment of nonelectrostatic interactions.

For simplicity, we define the following notation used throughout this paper:

$$\kappa =\frac{{∊}_i}{{∊}_o},\gamma =\frac{{∊}_i-{∊}_o}{{∊}_i+{∊}_o},\delta =\frac{{∊}_i}{{∊}_i+{∊}_o}.$$ (3.1)

3.1. Exact Solutions of the Linearized Poisson–Boltzmann Equation

3.1.1. Spherical Geometry

Exact solutions of the linearized PB equation are only available for simple geometries such as spheres, ellipsoids, and cylinders. These simple geometries are employed in many of the current methodology developments. Two early theoretical contributions were the Born [26] and Onsager [149] models, which were used to study the solvation effects of the electrostatic component of the free energy. They considered the cases of a single ion and a dipole, respectively, placed at the center of a spherical cavity of radius a surrounded by a dielectric solvent medium. The exact solutions of these two cases can then be found by solving the PB equation. The Born solvation energy (2.18) is the simplest model, successful in dynamics simulations of biomolecules, where a different spherical cavity centered at each atom in the system is used to compute the reaction field by choosing a set of cavity radii, usually from crystal structures [23]. The model is also the starting point of the well-known GB theory which is reviewed in section 4.

The Born and Onsager models are both special cases of the result derived by Kirkwood, who considered an array of fixed charges within a spherical cavity immersed in a dielectric medium. The result is also known as the Tanford–Kirkwood theory [105, 185], which is one of the earliest treatments of electrostatics in biomolecular systems. Despite its simplicity, the model has enjoyed remarkable success in electrostatics calculations of biomolecules in a variety of settings, especially in the context of MD simulations [4, 186, 84].

We consider a spherical cavity Ω of radius a, which contains a set of charges from both the solute and explicit solvent atoms. Outside Ω, the solvent is represented by a continuum medium with a dielectric constant ∊_o. Due to the principle of linear superposition, we consider only the potential induced by a single charge q located at r_s = (r_s, θ_s, ϕ_s) inside a spherical cavity under the spherical coordinate system. Then the potential inside the cavity satisfies

$$-{∊}_i{\nabla }^2\Phi \left(\mathbf{r}\right)=4\pi q\delta (\mathbf{r}-{\mathbf{r}}_s).$$ (3.2)

The equations of Φ outside Ω and boundary conditions are given by (2.3) and (2.10), respectively.

The potential inside the sphere can be written as a sum of two parts,

$$\Phi ={\Phi }_C+{\Phi }_{\mathit{rf}},$$ (3.3)

where ${\Phi }_C=\frac{q}{{∊}_i\mid \mathbf{r}-{\mathbf{r}}_s\mid }$ is the contribution of the Coulombic potential and is the fundamental solution of the Poisson equation, and the reaction potential Φ_rf satisfies the Laplace equation,

$${\nabla }^2{\Phi }_{\mathit{rf}}\left(\mathbf{r}\right)=0.$$ (3.4)

The general solution at any point r of the Laplace equation can be expressed in terms of Legendre polynomials of cos φ, where φ is the angle between r and r_s, i.e.,

$${\Phi }_{\mathit{rf}}\left(\mathbf{r}\right)=\sum _{n=0}^{\infty }{A}_n{r}^n{P}_n\left(\cos \phi \right).$$ (3.5)

Here, cos φ satisfies cos φ = cos θ cos θ_s + sin θ sin θ_s cos(ϕ − ϕ_s). The Coulombic field can be rewritten as an expansion of Legendre polynomials P_n(cos φ). For r > r_s, it is given by

$$\frac{q}{{∊}_i\mid \mathbf{r}-{\mathbf{r}}_s\mid }=\frac{q}{{∊}_i}\sum _{n=0}^{\infty }\frac{r_s^n}{r^{n+1}}{P}_n\left(\cos \phi \right).$$ (3.6)

Meanwhile, outside the cavity, the general solution of the linearized PB equation can be written as a series of Legendre polynomials of cos φ, which takes the form

$$\Phi \left(\mathbf{r}\right)=\sum _{n=0}^{\infty }{B}_n{k}_n\left(\lambda r\right)P_n\left(\cos \phi \right)\text{for}r\ge a,$$ (3.7)

where the function k_n(·) is the modified spherical Hankel function [2], defined by

$$k_n\left(r\right)=\frac{\pi {\mathrm{e}}^{-r}}{2r}\sum _{l=0}^n\frac{(n+l)!}{l!(n-l)!}\frac{1}{{\left(2r\right)}^l}.$$ (3.8)

Now we have represented the potential inside and outside the cavity by two series of Legendre polynomials. The unknown coefficients A_n and B_n are determined by the interface conditions (2.3). By using the orthogonal property of the Legendre polynomials and substituting the formulas in conditions (2.3), we have

$$A_n{a}^n+\frac{q{r}_s^n}{{∊}_i{a}^{n+1}}=B_n{k}_n\left(\lambda a\right),$$ (3.9)

$$n{A}_n{a}^{n-1}-\frac{q}{{∊}_i}\frac{(n+1)r_s^n}{a^{n+2}}=\frac{{∊}_o}{{∊}_i}{B}_n\lambda k_n^{\prime }\left(\lambda a\right).$$ (3.10)

Solving the system of each n ≥ 0 for A_n and B_n yields

$$A_n=\frac{q}{a{∊}_i{r}_K^n}\frac{{∊}_i(n+1)k_n\left(u\right)+{∊}_{o}u{k}_n^{\prime }\left(u\right)}{{∊}_{i}n{k}_n\left(u\right)-{∊}_{o}u{k}_n^{\prime }\left(u\right)},$$ (3.11)

$$B_n=\frac{q{r}_s^n}{{∊}_i{a}^{n+1}}\frac{{∊}_i(2n+1)}{{∊}_{i}n{k}_n\left(u\right)-{∊}_{o}u{k}_n^{\prime }\left(u\right)},$$ (3.12)

with u = λa and r_K = a²/r_s being the radial location of the conventional Kelvin image point (r_K, θ_s, ϕ_s). We thus obtain the reaction field potential inside the cavity as

$${\Phi }_{\mathit{rf}}\left(\mathbf{r}\right)=\frac{q}{a{∊}_i}\sum _{n=0}^{\infty }\frac{r^n}{r_K^n}\frac{{∊}_i(n+1)k_n\left(u\right)+{∊}_{o}u{k}_n^{\prime }\left(u\right)}{{∊}_{i}n{k}_n\left(u\right)-{∊}_{o}u{k}_n^{\prime }\left(u\right)}{P}_n\left(\cos \phi \right).$$ (3.13)

With this exact solution, a straightforward way to calculate the reaction potential is to truncate the infinite series as a finite sum [19]; but this method is usually slow for charges near the spherical surface. More efficient methods are those based on image charge approximations, which will be discussed in section 3.2. For a pure solvent, (3.13) reduces to a simpler formula,

$${\Phi }_{\mathit{rf}}\left(\mathbf{r}\right)=\frac{q}{a{∊}_i}\sum _{n=0}^{\infty }\frac{r_s^n{r}^n}{a^{2n}}\gamma \left(1+\frac{1+\gamma }{1-\gamma +2n}\right)P_n\left(\cos \phi \right),$$ (3.14)

as the parameter u is zero.

3.1.2. Prolate Spheroidal Geometry

In many biological applications, a solute molecule, such as a DNA molecule, may take an elongated geometric shape. The use of a spherical cavity to enclose such a solute may introduce too many explicit water molecules to the simulated system, resulting in a large number of degrees of freedom. In this case, a prolate spheroidal cavity should be employed. The real challenge is then to quickly and accurately calculate the reaction field due to a point charge inside a spheroid.

A straightforward way to solve this problem is by using fast spectral boundary integral methods, tailored to the prolate spheroidal geometry [213]. Exact solutions of similar electrostatic problems were discussed in [160, 123, 124], where a point charge is put outside a dielectric or conducting prolate spheroid. The analytical solution for an ellipsoidal geometry has also been used for free energy calculations for DNA chip design [6]. Recently, Deng [49] systematically studied the exact solution of the reaction field for charges inside a dielectric prolate spheroid surrounded by a bulk solvent with or without ionic effects. Some detail for the pure water case λ = 0 is given below.

Suppose the horizontal and vertical radii of the spheroid are R and L, respectively. Then the domain Ω is

$${\left(\frac{x}{R}\right)}^2+{\left(\frac{y}{R}\right)}^2+{\left(\frac{z}{L}\right)}^2<1$$

in a prolate spheroidal coordinate system (ξ, η, ψ), which can be represented as

$$\begin{array}{cc}\hfill x& =\frac{b}{2}\sqrt{({\xi }^2-1)(1-{\eta }^2)}\cos \psi ,\hfill \\ \hfill y& =\frac{b}{2}\sqrt{({\xi }^2-1)(1-{\eta }^2)}\sin \psi ,\hfill \\ \hfill z& =\frac{b}{2}\xi \eta ,\hfill \end{array}$$ (3.15)

where ξ ∈ [1, ∞), η ∈ [−1, 1], ψ ∈ [0, 2π] are the radial, angular, and azimuthal variables, respectively, the focal distance is $b=2\sqrt{L^2-R^2}$, and the dielectric boundary is defined by ξ = ξ₁ = 2L/b.

Again using the linear superposition principle, we consider only one point charge q located at r_s = (ξ_s, η_s, ψ_s). Similar to the case of a sphere, the solution Φ can be split into two contributions, Φ = Φ_C + Φ_rf, where the Coulomb potential ${\Phi }_C=\frac{q}{{∊}_i\mid \mathbf{r}-{\mathbf{r}}_s\mid }$ is the fundamental solution of the Poisson equation and the reaction field satisfies the Laplace equation ΔΦ_rf(r) = 0.

The solution of the Laplace equation can be obtained by the method of separation of variables in prolate spheroidal coordinates using the basis functions

$$\left\{\begin{array}{c}\hfill \cos m\psi \hfill \\ \hfill \sin m\psi \hfill \end{array}\right\},\left\{\begin{array}{c}\hfill P_n^m\left(\eta \right)\hfill \\ \hfill Q_n^m\left(\eta \right)\hfill \end{array}\right\},\left\{\begin{array}{c}\hfill P_n^m\left(\xi \right)\hfill \\ \hfill Q_n^m\left(\xi \right)\hfill \end{array}\right\},$$ (3.16)

where $P_n^m$ and $Q_n^m$ are the associated Legendre functions of the first and the second kinds [2, 224], respectively. Due to the boundedness of the potentials, Φ_rf inside the cavity and Φ outside can be written as

$${\Phi }_{rf}\left(\mathbf{r}\right)=\frac{q}{b{∊}_i}\sum _{n=0}^{\infty }\sum _{m=0}^n\left[A_{\mathit{mn}}\cos m\right(\psi -{\psi }_s)+B_{\mathit{mn}}\sin m(\psi -{\psi }_s\left)\right]P_n^m\left(\eta \right)P_n^m\left(\xi \right)$$ (3.17)

for r ∈ Ω and

$$\Phi \left(\mathbf{r}\right)=\frac{q}{b{∊}_i}\sum _{n=0}^{\infty }\sum _{m=0}^n\left[C_{\mathit{mn}}\cos m\right(\psi -{\psi }_s)+D_{\mathit{mn}}\sin m(\psi -{\psi }_s\left)\right]P_n^m\left(\eta \right)Q_n^m\left(\xi \right)$$ (3.18)

for $\mathbf{r}\in {\mathbb{R}}^3\Omega$, where a phase shift ψ_s to the azimuthal angle ψ is used without loss of generality. The Coulombic potential has the following expansion [140] under the prolate spherical coordinate system:

$$\frac{q}{{∊}_i\mid \mathbf{r}-{\mathbf{r}}_s\mid }=\frac{q}{b{∊}_i}\sum _{n=0}^{\infty }\sum _{m=0}^n{H}_{\mathit{mn}}\cos m(\psi -{\psi }_s)P_n^m\left({\eta }_s\right)P_n^m\left({\xi }_s\right)Q_n^m\left({\xi }_s\right)$$ (3.19)

for ξ > ξ_s, where the coefficient H_mn is given by

$$H_{\mathit{mn}}=2(2n+1)(2-{\delta }_{m0}){(-1)}^m{\left[\frac{(n-m)!}{(n-m)!}\right]}^2$$

and δ_m0 is the Kronecker delta.

In (3.17)–(3.19), we have expressed the potentials inside and outside the cavity as series in terms of sines, cosines, and the Legendre polynomials where, for each m and n, four unknowns A_mn, B_mn, C_mn, and D_mn are to be determined. These can be solved using the boundary conditions (2.3), which lead to four equations at each m and n of the series due to the orthogonality of the basis functions,

$$\{\begin{array}{cc}\hfill & P_n^m\left({\xi }_1\right)A_{\mathit{mn}}-Q_n^m\left({\xi }_1\right)C_{\mathit{mn}}=-H_{\mathit{mn}}{P}_n^m\left({\eta }_s\right)P_n^m\left({\xi }_s\right)Q_n^m\left({\xi }_1\right),\hfill \\ \hfill & P_n^m\left({\xi }_1\right)B_{\mathit{mn}}-Q_n^m\left({\xi }_1\right)D_{\mathit{mn}}=0,\hfill \\ \hfill & {∊}_i{\widehat{P}}_n^m\left({\xi }_1\right)A_{\mathit{mn}}-{∊}_o{\widehat{Q}}_n^m\left({\xi }_1\right)C_{\mathit{mn}}=-{∊}_i{H}_{\mathit{mn}}{P}_n^m\left({\eta }_s\right)P_n^m\left({\xi }_s\right){\widehat{Q}}_n^m\left({\xi }_1\right),\hfill \\ \hfill & {∊}_i{\widehat{P}}_n^m\left({\xi }_1\right)B_{\mathit{mn}}-{\widehat{Q}}_n^m\left({\xi }_1\right)D_{\mathit{mn}}=0,\hfill \end{array}\phantom{\}}$$ (3.20)

where ${\widehat{P}}_n^m(\cdot )$ and ${\widehat{Q}}_n^m(\cdot )$ are defined by

$${\widehat{P}}_n^m\left({\xi }_1\right)=(n-m+1)P_{n+1}^m\left({\xi }_1\right)-(n+1){\xi }_1{P}_{n+1}^m\left({\xi }_1\right),$$

$${\widehat{Q}}_n^m\left({\xi }_1\right)=(n-m+1)P_{n+1}^m\left({\xi }_1\right)-(n+1){\xi }_1{Q}_{n+1}^m\left({\xi }_1\right).$$

Solving the system of four equations (3.20), we have B_mn = D_mn = 0 and

$$A_{\mathit{mn}}=H_{\mathit{mn}}{P}_n^m\left({\eta }_s\right)P_n^m\left({\xi }_s\right)\frac{({∊}_i-{∊}_o)Q_n^m\left({\xi }_1\right){\widehat{Q}}_n^m\left({\xi }_1\right)}{{∊}_o{P}_n^m\left({\xi }_1\right){\widehat{Q}}_n^m\left({\xi }_1\right)-{∊}_i{Q}_n^m\left({\xi }_1\right){\widehat{P}}_n^m\left({\xi }_1\right)},$$

$$C_{\mathit{mn}}=H_{\mathit{mn}}{P}_n^m\left({\eta }_s\right)P_n^m\left({\xi }_s\right)\frac{\left[P_n^m\left({\xi }_1\right){\widehat{Q}}_n^m\left({\xi }_1\right)-Q_n^m\left({\xi }_1\right){\widehat{P}}_n^m\left({\xi }_1\right)\right]}{{∊}_o{P}_n^m\left({\xi }_1\right){\widehat{Q}}_n^m\left({\xi }_1\right)-{∊}_i{Q}_n^m\left({\xi }_1\right){\widehat{P}}_n^m\left({\xi }_1\right)}.$$

This finally yields the exact solution of the reaction field potential inside the prolate spheroidal cavity:

$${\Phi }_{rf}\left(\mathbf{r}\right)=\frac{q}{b{∊}_i}\sum _{n=0}^{\infty }\sum _{m=0}^n\frac{({∊}_i-{∊}_o)H_{\mathit{mn}}{P}_n^m\left({\eta }_s\right)P_n^m\left({\xi }_s\right)Q_n^m\left({\xi }_1\right){\widehat{Q}}_n^m\left({\xi }_1\right)}{{∊}_o{P}_n^m\left({\xi }_1\right){\widehat{Q}}_n^m\left({\xi }_1\right)-{∊}_i{Q}_n^m\left({\xi }_1\right)-{\widehat{P}}_n^m\left({\xi }_1\right)}\cos m(\psi -{\psi }_s)P_n^m\left(\eta \right)P_n^m\left(\xi \right).$$ (3.21)

Thus, we have derived the exact solution of the Poisson equation inside the prolate spheroidal cavity immersed in a dielectric medium. Extension to an ionic solvent was also discussed in Deng [49], but the solution is cumbersome and is thus not presented here. However, the solution in pure water can be directly applied to the ionic case using the GB method [17], for which there exist efficient treatments to incorporate the ionic effects into the resulting pairwise formulation.

3.2. Image Charge Methods for the Dielectric Sphere

For the case of a spherical cavity, the series representation of the exact solution of the electrostatic potential can reach any desired accuracy, depending on the number of truncating terms of the series. However, the convergence rate is slow, in particular, for charges near the cavity boundary. Finding an effective image charge approximation to the reaction field, which provides simpler analytical expressions, then becomes an important issue for faster and more accurate computational simulations.

We start with the case of the pure solvent, say, (3.14). The reaction field potential given in (3.14) can be reformulated as

$${\Phi }_{rf}\left(\mathbf{r}\right)=\frac{\gamma q}{a{∊}_i}\sum _{n=0}^{\infty }\frac{r_s^n{r}^n}{a^{2n}}{P}_n\left(\cos \phi \right)+\frac{\gamma (1+\gamma )q}{2a{∊}_i}\sum _{n=0}^{\infty }\left(\frac{1}{n+\frac{1-\gamma }{2}}\right)\frac{r_s^n{r}^n}{a^{2n}}{P}_n\left(\cos \phi \right),$$ (3.22)

which can be simplified to the following form, using the Legendre expansion of the distance [2]:

$${\Phi }_{rf}\left(\mathbf{r}\right)=\frac{q_K}{{∊}_i\mid \mathbf{r}-{\mathbf{r}}_K\mid }+{\int }_{r_K}^{\infty }\frac{q^{\text{line}}\left(x\right)}{{∊}_i\mid \mathbf{r}-\mathbf{x}\mid }dx,$$ (3.23)

with

$$q_K=\frac{a\gamma }{r_s}q\text{and}{q}^{\text{line}}\left(x\right)=\frac{\gamma (1+\gamma )}{2}\frac{q}{a}{\left(\frac{r_K}{x}\right)}^{(1-\gamma )∕2},$$

where x = (x, θ_s, ϕ_s). Here, the first term on the right-hand side is seen as the Coulombic potential of a point charge q_K at r_K, known as the Kelvin image charge [140], while the second term is the potential due to a line image charge q^line(x) that extends from the Kelvin image point to infinity along the radial direction.

The exact image charge representation (3.23) was given originally in 1883 by C. Neumann [142] but was little known for around a century. It was rediscovered several times in recent decades in different fields of application, for example, [222, 67, 58, 155, 121, 30, 145]. A recent review by Lindell [147] summarizes in more detail the history of Neumann's image principle.

3.2.1. Single Image Charge Approximation

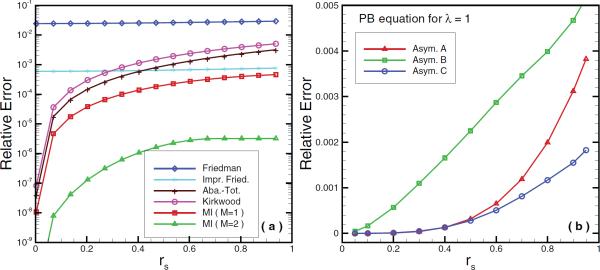
The widely used image methods [71, 1] in computer simulations of biological systems are the approximations of the line image (3.23) at different levels of accuracy. Here we give a brief survey of those methods popularly employed in simulations, from the point of view of how (3.23) is approximated. They include image charge methods of Friedman, Abagyan and Totrov, and Kirkwood. A comparative study of their performance is shown in Figure 3.3(a) and the details can be found in [52].

Fig. 3.3.

Relative errors of image approximations with the source locations. (a) Accuracy performance of Friedman, improved Friedman, Abagyan–Totrov, and Kirkwood image approximations, and multiple image approximations (M = 1 and 2), for the Poisson equation. (b) Accuracy performance of line image approximations to the exact series solution of the PB equation for λ = 1 using different asymptotic formulas, where M = 20 is used in order to discretize the line image with high accuracy to give “exact” values. Asyms. A, B, and C represent formulas (3.33), (3.35), and (3.36), respectively.

Note that for a usual dielectric environment, γ ≈ −1. The coefficient (1 + γ) contained in the line charge q^line(x) is very small. Therefore, the contribution of the Kelvin image in (3.23),

$$V^{\left(0\right)}=\frac{q_K}{{∊}_i\mid \mathbf{r}-{\mathbf{r}}_K\mid },$$ (3.24)

is an approximation to the reaction field with a first order of error O(κ). This is known as Friedman's image approximation [71]. Friedman's image approximation can be improved without much additional computational cost by including a correction term V⁽¹⁾ that approximates the line image in (3.23), leading to the improved Friedman image approximation

$${\Phi }_{rf}\approx V^{\left(0\right)}+V^{\left(1\right)}.$$ (3.25)

To obtain V⁽¹⁾, taking 1 − γ ≈ 2 in the power in the line image, we have

$$q^{\text{line}}\left(x\right)\approx \frac{\gamma (1+\gamma )}{2}\frac{q}{a}\left(\frac{r_K}{x}\right),$$

resulting in an analytic integration of the line image term,

$$V^{\left(1\right)}=\{\begin{array}{c}\frac{\gamma (1+\gamma )}{2{∊}_i}\frac{q}{a\mu }\ln \left(\frac{\sqrt{1-2\mu \cos \tilde{\theta }+{\mu }^2}+\mu -\cos \tilde{\theta }}{1-\cos \tilde{\theta }}\right)\text{for}\cos \tilde{\theta }\ne 1,\hfill \\ -\frac{\gamma (1+\gamma )}{2{∊}_i}\frac{q}{a\mu }\ln (1-\mu )\text{for}\cos \tilde{\theta }\ne 1,\hfill \end{array}\phantom{\}}$$ (3.26)

where μ = rr_s/a² and $\tilde{\theta }=\theta -{\theta }_s$. Friedman's methods have been widely applied to MD or Monte Carlo simulations; see [165, 199] for examples.

As r_s tends to zero, Friedman's image approximation cannot reproduce the Born formula (2.18). To remedy this flaw, Abagyan and Totrov [1] proposed a modified approximation based on Friedman's method. They used a position-independent correction to Friedman's first-order image approximation

$${\Phi }_{rf}\approx V^{\left(0\right)}+\frac{q\gamma }{a{∊}_o},$$ (3.27)

where the correction potential is computed to compensate for the free energy difference at the Born limit [26]. It is clear that the Abagyan–Totrov image method has lower computational cost than the improved Friedman's method, while its accuracy is comparable to the latter. Therefore, this method has been used in a variety of applications [84, 154].

The Kirkwood image approximation [105] slightly changes the charge strength of V⁽⁰⁾ in the Abagyan–Totrov image method, allowing its reaction field energy to reproduce the Born formula. It is expressed by

$$V_{KW}^{\left(0\right)}=\frac{{\tilde{q}}_K}{{∊}_i\mid \mathbf{r}-{\mathbf{r}}_K\mid },\text{with}{\tilde{q}}_K=\frac{{∊}_i-{∊}_o}{{∊}_o}\frac{a}{r_s}q.$$ (3.28)

A correction potential can also be developed to improve the accuracy of the Kirkwood image approximation.

3.2.2. Multiple Image Charge Approximation

The methods discussed above employed by Friedman, Abagyan and Totrov, and Kirkwood all use a single image charge which, with or without a correction, represents a crude approximation to the reaction field. Their accuracy may be limited in some the line applications. Historically, image expression (3.23) is not the starting point when deriving these image methods. Recently, the multiple image method [32] has been developed to provide a high-order accurate approximation. A schematic illustration of the approximation is shown in Figure 3.2. Its basic strategy is to introduce a numerical integration to the line image. Gauss or Gauss–Radau quadrature can be employed to approximate the integral in (3.23) to obtain a series of discrete image charges,

$${\int }_{r_K}^{\infty }\frac{q^{\text{line}}\left(x\right)}{{∊}_i\mid \mathbf{r}-\mathbf{x}\mid }dx\approx \sum _{m=1}^M\frac{q_m}{{∊}_i\mid \mathbf{r}-{\mathbf{x}}_m\mid },$$ (3.29)

where the magnitude and location of the discrete image charges are defined by

$$q_m=\frac{\gamma \kappa }{2}\frac{{\omega }_m{x}_m}{a}q\text{and}{x}_m=r_K{\left(\frac{2}{1-s_m}\right)}^{1+\kappa }.$$ (3.30)

Here, {ω_m, s_m, m = 1, …, M} are the Gauss or Gauss–Radau weights and points defined on the interval [−1, 1] that can be computed by various software packages such as ORTHPOL [74]. Eventually, the multiple image approximation is given by

$${\Phi }_{rf}\left(\mathbf{r}\right)\approx \frac{q_K}{{∊}_i\mid \mathbf{r}-{\mathbf{r}}_K\mid }+\sum _{m=1}^M\frac{q_m}{{∊}_i\mid \mathbf{r}-{\mathbf{x}}_m\mid },$$ (3.31)

which in theory can approximate the reaction field to an arbitrary accuracy by increasing the number, M, of the quadrature points. Figure 3.3(a) illustrates results from different image approximations, where multiple image approximations use M = 1 and M = 2 Gauss quadrature points (discrete images). It can be seen that the error in the multiple image approximations depends on the location of the source charge, and more discrete charges are required when the source charge is near the boundary in order to yield a desired accuracy. However, a small number of image charges is usually sufficient for a good enough accuracy; for example, when r_s/a ≤ 0.9, three or fewer discrete image charges are enough to provide a 0.01% relative error in the reaction field potential. In fact, two image charges provide high accuracy. Moreover, as the first quadrature point x₁ of the Gauss–Radau quadrature is exactly the Kelvin image point r_K, the first point image q₁ and the Kelvin image can be combined into one single image charge. From this point of view, the Gauss–Radau quadrature is a cost-effective approach for real simulations.

Fig. 3.2.

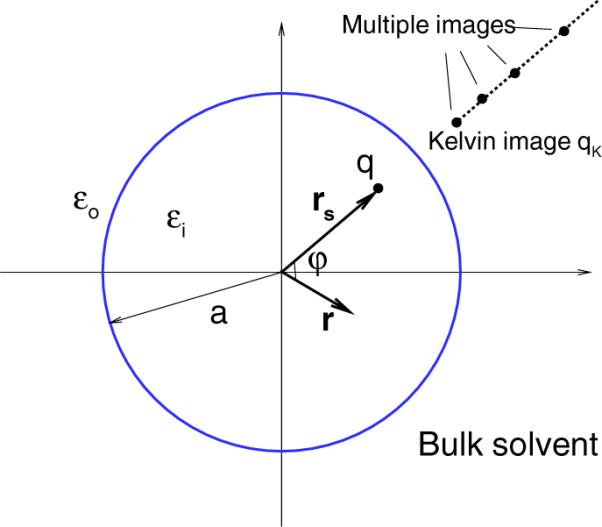
A 2D schematic illustration of the multiple image approximation of the reaction field for a dielectric sphere of radius a embedded in a bulk solvent. A source charge q is located at r_s, and its reaction field at r inside the sphere due to the bulk water is represented by the potential of discrete point image charges on a ray starting from the Kelvin image point along the radial direction of r_s.

The multiple image method evidently speeds up the computation in comparison with the Kirkwood expansion. It is illustrated in [32] that the pairwise sum of the image method without any accelerated technique is 20–30 times faster than the direct series expansion method for the same level of accuracy. Furthermore, once the image charges are generated, the electrostatic interactions among those charges together with the source charges are Coulombic, where the inhomogeneity of the simulating system is removed. The interactions can then be readily handled by the FMM [82, 80, 38, 221]. An order-N algorithm can then be achieved for the system by combining the FMM and the image charge approximation.

3.2.3. Extension to the Poisson–Boltzmann Equation

No exact line image representation of the series solution of the PB equation (3.13) is known, due to the complexity of the special function k_n(u). However, approximate representations have been developed. Let us define a function,

$${\mathcal{S}}_n\left(u\right)=\frac{k_n\left(u\right)}{u{k}_n^{\prime }\left(u\right)};$$

then (3.13) can be rewritten as

$${\Phi }_{rf}\left(\mathbf{r}\right)=\frac{q}{a{∊}_i}\sum _{n=0}^{\infty }\frac{r^n}{r_K^n}\frac{\kappa (n+1){\mathcal{S}}_n\left(u\right)+1}{\kappa {\mathcal{S}}_n\left(u\right)-1}{P}_n\left(\cos \phi \right).$$ (3.32)

Finding an approximate asymptotic approximation to the function ${\mathcal{S}}_n\left(u\right)$ is the key to deriving an accurate image charge expression [50, 51, 216, 215, 209].

Note that the ionic strength is often very low in practical applications. The parameter u = λa can be assumed to be small, say, u < 1, and so a second-order asymptotic formula can be derived [50]:

$${\mathcal{S}}_n\left(u\right)=-\frac{1}{n+1}+O\left(u^2\right).$$ (3.33)

With this formula, the reaction field can be represented by a Kelvin image plus a line image at the first order of accuracy, or at the second order if a position-independent correction potential is added. Higher-order image approximations [51, 216, 209] were developed straightforwardly using higher-order asymptotic representations of ${\mathcal{S}}_n\left(u\right)$. For example, in [51] the following form of the asymptotic formula is used:

$${\mathcal{S}}_n\left(u\right)=-\frac{-(2+u^2)+4n}{(u^2-2)+(2-u^2)n+4n^2}+O\left(u^4\right).$$ (3.34)

This leads to a fourth-order image approximation of the reaction field, composed of a Kelvin image, two line images, and a position-dependent correction term.

Later, a series of different asymptotic formulas were proposed in [215] that remove the requirement u < 1, thanks to the fact that as u → ∞,

$${\mathcal{S}}_n\left(u\right)=-\frac{1}{n+1+u}+O\left(\frac{1}{u^2}\right),$$ (3.35)

$${\mathcal{S}}_n\left(u\right)=-\frac{1}{n+1+\frac{u^2}{1+u}}+O\left(\frac{1}{u^2}\right),$$ (3.36)

and, at the same time, as u → 0,

$${\mathcal{S}}_n\left(u\right)=-\frac{1}{n+1+u}+O\left(u\right),$$ (3.37)

$${\mathcal{S}}_n\left(u\right)=-\frac{1}{n+1+\frac{u^2}{1+u}}+O\left(u^2\right).$$ (3.38)

Substituted into (3.32), the formula (3.35) yields

$${\Phi }_{rf}\left(\mathbf{r}\right)\approx \frac{q_K}{{∊}_i\mid \mathbf{r}-{\mathbf{r}}_K\mid }+{\int }_{r_K}^{\infty }\frac{q_1^{\text{line}}\left(x\right)}{{∊}_i\mid \mathbf{r}-\mathbf{x}\mid }dx,q_1^{\text{line}}\left(x\right)=q\frac{{\delta }_1}{a}{\left(\frac{x}{r_K}\right)}^{-{\sigma }_1},$$ (3.39)

with ${\sigma }_1=\frac{1+u}{1+\kappa }$ and ${\delta }_1=\gamma (1-{\sigma }_1)-\frac{u}{1+\kappa }$, similar to the pure water case. The image expression obtained from the second asymptotic formula (3.36) is similar, except for one more correction term,

$${\Phi }_{rf}\left(\mathbf{r}\right)\approx \frac{q_K}{{∊}_i\mid \mathbf{r}-{\mathbf{r}}_K\mid }+{\int }_{r_K}^{\infty }\frac{q_2^{\text{line}}\left(x\right)}{{∊}_i\mid \mathbf{r}-\mathbf{x}\mid }dx+{\Phi }^{\text{corr}},q_2^{\text{line}}\left(x\right)=q\frac{{\delta }_2}{a}{\left(\frac{x}{r_K}\right)}^{-{\sigma }_2},$$ (3.40)

where ${\sigma }_2=\frac{1+\tilde{u}}{1+\kappa }$, ${\delta }_2=\gamma (1-{\sigma }_2)-\frac{\tilde{u}}{1+\kappa }$, and $\tilde{u}=\frac{u^2}{1+u}$, and the correction is a position-independent constant:

$${\Phi }^{\text{corr}}=\frac{q}{a{∊}_i}\left(\frac{\kappa }{1+u}-\frac{\kappa }{1+\tilde{u}}\right).$$

The discretization of the line images into discrete image charges is the same as that in (3.29). As these line image approximations are accurate for both low and high concentration regions of ionic effects, numerical evidence [215] indicated that they could perform well for the intermediate region, giving a solution of image charge approximations of the reaction field induced by bulk solvent with arbitrary ionic strengths. In Figure 3.3(b), the accuracy performance for λ = 1 is presented, which shows that the line image (3.40) from (3.36) has the smallest error, in particular, when r_s > 0.5.

More recently, the method of least squares fitting was used to find multiple image approximations [157]. It is based on the fact that a line image generally starts from the Kelvin image point to infinity along the radial direction, and thus the locations of the quadrature points (images) can be fixed, resulting in an approximation of the reaction field:

$${\Phi }_{rf}\left(\mathbf{r}\right)\approx \sum _{m=1}^M\frac{q_m}{{∊}_i\mid \mathbf{r}-{\mathbf{x}}_m\mid },$$ (3.41)

with x_m = (x_m, θ_s, ϕ_s) and $x_m=r_K{\left(\frac{2}{1-s_m}\right)}^{1+\kappa }$. Here, the Kelvin image is included in the first image charge due to x₁ = r_K. As the exact series solution exists, the strength of each charge can be found by minimizing the overall error for preset N field points,

$$\text{Err}(q_1,\dots ,q_M)={\sum _{n=1}^N\left({\Phi }_{rf}\left({\mathbf{r}}_n\right)-\sum _{m=1}^M\frac{q_m}{{∊}_i\mid {\mathbf{r}}_n-{\mathbf{x}}_m\mid }\right)}^2.$$ 3.42

Presumably, this method will produce a more accurate result because the analytically based image charge methods lose some accuracy in approximating the series solution by the line image, as verified numerically in [157].

3.3. Analytical Methods for Some Nonspherical Geometries

Historically, image solutions of the Poisson and PB equations have been widely studied for a point charge located in various shapes of dielectric or conducting environments, such as 3D half space, a cylinder, and a 3D wedge; see [180, 37, 36, 144, 143, 41] for examples and [122, 31] for reviews. Here we introduce only a few cases which are useful in biomolecular simulations.

It should be noted that the image charge method of spherical geometry can be directly extended to a point charge located inside a hemispherical cavity over a conducting half space. Such a setting is useful in studying electrostatic interactions between biomolecules and inorganic surfaces, which is of significance in the fields of biomaterial synthesis and fabrication and biotechnologies [24, 75]. Due to the conducting boundary, the reaction field of the source charge q can be represented by an image charge −q at the mirror symmetry of the interface, together with the reaction field of these two charges from the polarization of the sphere.

There are also studies of analytical multipole methods for systems in the presence of multipole proteins represented by spheres [126]. Recently, Yap and Head-Gordon [219] developed a semianalytical PB solver by representing the molecular surface as a collection of spheres, and thus the Kirkwood expansion technique can be applied to solve the surface charges iteratively. Due to its analytical treatment and the advantage of the boundary element method, the semianalytical method performs better than the traditional numerical PB solvers for irregular biomolecules.

For nonspherical geometries, a rectangular volume can also be used in reaction field calculations if its solution can be computed simply. Yang and coworders [218, 7] developed a rectangular image charge method to accurately represent the reaction field of a cubic box of lengths L_x, L_y, and L_z as the explicit cavity Ω. Let the source charge q be located at r_s = (x_s, y_s, z_s) under the Cartesian coordinate system. The electrostatic potential can be described by infinite image charges [218] as

$$\Phi \left(\mathbf{r}\right)=\sum _{l,m,n=-\infty }^{+\infty }\frac{q\gamma \mid l\mid +\mid m\mid +\mid n\mid }{{∊}_i\mid \mathbf{r}-{\mathbf{r}}_{\mathit{lmn}}\mid },$$ (3.43)

with r_lmn = ((−1)^lx_s + lL_x, (−)^my_s + mL_y, (−1)ⁿz_s + nL_z).

Recently, in order to treat biological ion channels with the hybrid solvation model, the image charge method [211, 118] was developed for a source charge inside a finite length cylinder due to the electric polarization of the surrounding inhomogeneous continuum, where the membrane and bulk water are characterized by layers of different dielectric media. An optimization method was used to find the image representation for the cylinder by fitting the exact expression in terms of cylindrical harmonics [41], which was then combined with more images in order to satisfy the boundary conditions at the planar membrane interfaces. The electrostatic interaction problem defined in a complex inhomogeneous system is thus converted into one in a homogeneous free space embedded with discrete charges, which can be solved efficiently by various fast particle-interaction algorithms such as the FMM.

3.4. Discussion of Hybrid Solvation Models

The hybrid models combine both explicit and implicit treatments of the solvent and seek to gain a favorable balance between accuracy and speed. There are two main strategies to treat the explicit-implicit boundary, resulting in two classes of hybrid schemes. The first class is known as the translational reaction field (TRF) method [15, 14, 186, 92], which centers a different spherical cavity at each charge (or group of charges), where the solvation energy is given exactly by the Born formula (2.18). This method allows the use of periodic boundary conditions; thus, the surface effects can be eliminated due to unrestricted movement of water molecules. However, the periodicity requirement of the simulated system limits its accuracy in treating strongly inhomogeneous systems such as proteins.

The second class of hybrid approach is the fixed reaction field (FRF) method [101, 19, 199, 218], also known as the solvation shell approach, which embeds the entire system within a fixed boundary, often spherical in shape, and treats the outside solvent as a dielectric medium. A repulsive potential on the wall, which played an important role in the previous successes of this method, is applied to maintain the explicit molecules inside the boundary. The FRF method is particularly useful for biomolecule solutes, where the Kirkwood series expansion can be used to analytically calculate the reaction field in a spherical cavity, as shown in early studies [101, 19]. Without the limitation of the periodicity, the FRF method greatly reduces the system size by introducing fewer explicit water molecules, in comparison to the lattice-sum methods based on the explicit model. The FMM method with the image charge approximation can provide a linear-scaling calculation of the long-range electrostatic interactions. For homogeneous systems [119], the CPU time to compute electrostatic forces using the FMM based on the hybrid solvation model currently is not faster than that using PME with the explicit solvent model. The reason is threefold: first, the periodic boundary condition is acceptable for homogeneous systems, necessary for the PME, and a small system size is sufficient to provide accurate results; second, the FMM has a large prefactor in the scaling, which is more efficient only for sufficiently large simulation systems; third, in equivalent calculations, the FMM system has more particles which include not only the source charges inside the volume, but also the image charges. However, when the simulation system is extended to include a biomolecule, especially a nonneutral molecule, the PME method has to significantly increase the system size to reduce the effects of the periodic boundary condition, and the savings of the system size with the hybrid solvation model may then be significant.

As the dielectric on the boundary between explicit and implicit solvent is modeled as a sharp transition from ∊_i to ∊_o, singular reaction fields have to be carefully dealt with. A buffer layer [4] of fixed thickness is usually used to remove the unphysical singularities in the reaction field. However, simply increasing the size of the simulation volume does not eliminate unphysical long-range effects which propagate throughout the cavity. A three-layer model [164, 43] with a constant transition layer was used to reduce these effects. Mathematically, the artificial discontinuity in dielectric can be completely eliminated with a smooth transition layer from low to high values. Recently, Qin et al. [157] proposed such a smooth function where the dielectric profile in the buffer zone is selected to satisfy ${\nabla }^2\sqrt{∊\left(r\right)}=0$, leading to an exact solution of the PB equation; thus its image charge approximation can be developed.

Once the reaction field is represented by image charges with an analytical formula, it is straightforward to calculate the electrostatic force on a charge, q_i, by

$$\mathbf{f}\left(\mathbf{r}\right)=-q_i\nabla \Phi \left(\mathbf{r}\right),$$ (3.44)

where the potential Φ(r) is the sum of Coulomb potentials of all image charges and source charges except for the source charge q_i itself. Recently, the multiple image charge representation of the reaction field coupled with the FMM has been incorporated into MD simulations of aqueous solutions under the FRF framework [119, 120], together with a periodic boundary condition using a space filling truncated octahedron (TO) box for nonelectrostatic interactions (see Figure 3.1). Minimal surface effects in MD simulations were seen in this new hybrid solvation model. A major advantage of this FRF method over the lattice-sum methods, considered to be the most accurate electrostatics treatments currently available, is that there is no need to treat electrostatic interactions of periodic images, thus it can be used for electrically nonneutral molecules. After extensive investigations, the method was shown to be in excellent agreement with the PME simulations [44, 60] for sufficiently large simulation boxes. The effect of model parameters, which include the size of the cavity, the number of discrete image charges, and the thickness of the buffer zone, was investigated using the PME simulations as a reference. An optimal set of parameters was then obtained allowing for a faithful representation of many static, structural, dielectric, and dynamic properties of the simulated water and ions, while maintaining manageable computational cost. The novel hybrid solvation model is particularly well suited for computing pKa values in proteins, which are now most frequently calculated by numerically solving the PB equation [205] for charged and neutral versions of ionizable residues, to obtain the reaction field. The advantage of the model is that the reaction field experienced by a solute molecule is directly accessible in the simulation. There is no need to perform any additional calculations. Unlike the PB approach, the method includes the effects of local conformational fluctuations and the discrete nature of water molecules.

Figure 3.4 shows some of the results of recent MD calculations for pure water systems with the hybrid solvation model [119, 120], in comparison to those of the PME method. In Figure 3.4(a), the local particle densities along the diagonal of TO boxes for varying thickness τ of the buffer zone are illustrated, where two image charges M = 2 are used for each source charge. The plot shows that the results of the hybrid model converge as thickness τ increases, and taking τ between 4 ~ 6Å is enough to significantly reduce the surface effects of the spherical cavity. The right-hand side of the figure shows the dielectric constant ε(R) of the pure water, which is a macroscopic property of a material, as a function of the sample radius R in the simulation box. Ideally, the curve of ε(R) is expected to have a plateau starting at some radius and to remain around 80, i.e., the dielectric constant of the bulk water. In the results reported in [119], the plateau values for both M = 1 and 2 are between 70 ~ 80, while the curve of M = 0 falls back to a low dielectric constant of around 24 after an initial increase. In comparison, the plateau value of the PME simulation is 91±10. Therefore, the calculations with the image-charge-based hybrid model produce the correct dielectric constant for the bulk water, consistent with the PME results within allowed statistical variations. Moreover, the data show that the reaction field is essential for maintaining the dielectric property throughout the simulation volume, as emphasized in many previous studies [199]. For a complete description and validation of the hybrid model, please refer to [119]. The hybrid model was also validated for ions solvated in pure water [120].

Fig. 3.4.

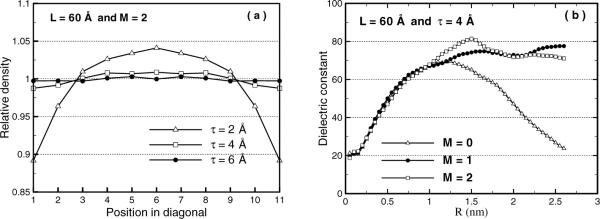
MD results of the hybrid model for varying geometric parameters of the simulation volume, taking PME results as the reference solutions. (a) Relative local particle density along the diagonal of TO boxes with varying buffer layer thicknesses. (b) Dielectric function as a function of sample radius R for increasing image charges.

So far the image-based reaction field method has been successful in reproducing structural and dynamical properties of pure water and ions in pure water, but many issues remain to be investigated. For example, it is yet unknown how to take into account ionic effects [70, 163], which play an important role in biomolecular simulations and are relevant for many problems in organic chemistry and biochemistry. MD simulations based on periodic boundary conditions for those problems may lead to significant artifacts [220]. A boundary integral formulation of biomolecular electrostatics of explicit ions [210] has been proposed under the framework of the PB theory. For the hybrid solvation model discussed above, related issues also include the determination of the number of explicit ions and their positions, for which Monte Carlo simulations [138, 220] can be used to provide an enhanced sampling. Moreover, despite the fact that a spherical cavity is widely used as a simulation volume, the simulation system may be too large because large numbers of water molecules are needed to fill the spherical cavity for some biomolecules, particularly elongated molecules such as DNA. An alternative could be a cuboidal shape, for which the image charge method was developed by Yang, Liaw, and Lim [218]; the method represents the reaction field by a summation of an infinite number of images for each source charge. Many approaches based on irregular simulation cavities have been developed to reduce the number of explicit water molecules. A straightforward strategy to compute the reaction field for an arbitrary geometry is to solve the PB equation directly [94]. The GB approximation, reviewed below, was developed by Lee and coworkers [112, 110]; this approximates the reaction field by a pairwise sum, and a sum-over-spheres approach is used to define the simulation volume. The multigrid approximation [179] was employed to reduce the computational cost of the pairwise summation.

4. Generalized Born Methods

The need for faster computational methods for implicit models in MD simulations has motivated other more efficient alternatives to solving the PB equation numerically. Empirical distance-dependent dielectric models [203, 89, 159, 173, 97] have been widely used in MD simulations. These models take into account the influence of the solvent by using Coulomb's law with the dielectric constant being a function of the interparticle distance, thus providing very fast calculations; however, limited accuracy is unavoidable due to their inability to measure buried and solvent-exposed regions of the solute. The GB theory [40, 182] has been accepted as one of the most successful approaches to producing an accurate approximation to the Poisson result, while still being fast enough to be applied in MD simulations. Here, we present a brief overview of the main purpose and methodology of the GB methods. Interested readers may consult Bashford and Case [17], Feig and Brooks III [64], Onufriev [150, 151], and Chen, Brooks, and Khandogin [35] for more systematic reviews and discussions.

4.1. Generalized Born Formalism

The GB method approximates the solvation free energy by an analytical pairwise sum over the molecular atoms proposed by Still et al. [182]:

$$\Delta G_{\mathit{pol}}=-\frac{1}{2}\left(\frac{1}{{∊}_i}-\frac{1}{{∊}_o}\right)\sum _{i,j}\frac{q_i{q}_j}{f_{\mathit{ij}}},$$ (4.1)

where

$$f_{\mathit{ij}}=\sqrt{r_{\mathit{rj}}^2+R_i{R}_j\exp (-{\mathit{gr}}_{\mathit{ij}}^2∕R_i{R}_j)},$$ (4.2)

g is a positive constant, and R_i is the so-called effective Born radius of atom i, defined through its self-energy by generalizing the Born solvation energy formula (2.18),

$$R_i=-\frac{1}{2}\left(\frac{1}{{∊}_i}-\frac{1}{{∊}_0}\right)\frac{q_i^2}{\Delta G_{\mathit{pol}}^i}.$$ (4.3)

Equation (4.1) is an interpolation between two extreme cases, for which (4.1) is exact, of the interparticle distance: the Born limit (2.18) [26] at small distances (r_ij = 0) and the Coulomb limit at large distances. The ionic effects can be incorporated by simply substituting e^−λr_ij /∊_o for 1/∊_o in the formulation, which also satisfies the limit conditions at the Debye–Hückel level [181]. Here, λ is the inverse Debye–Hückel screening parameter in the linear PB equation (2.10). The inverse of parameter g in (4.1) can be a value from 0.1 to 0.5; 0.25 is used most commonly for historical reasons [182]. The zero limit of g = 0 was suggested by Grycuk [83], resulting in a simpler function $f_{\mathit{ij}}=\sqrt{r_{\mathit{ij}}^2+R_i{R}_j}$. Other variations of Still's pairwise formula (4.2) were also used, such as f_ij = r_ij + 0.5(R_i + R_j) exp[−2r_ij/(R_i + R_j)], which has better performance than the original one for the spherical case [112].

Ideally, the self-energy $\Delta G_{\mathit{pol}}^i$ of atom i in (4.3) would be computed directly from the Poisson equation by setting the atomic charges of all atoms except the atom i itself to zero, leading to the so-called “perfect” effective Born radius [152]. This approach is impractical for an irregular geometry due to its high computational cost, though it can be used as an error measure for other approximate methods. An alternative is to express $\Delta G_{\mathit{pol}}^i$ using an integral formulation [17, 76] over an appropriate volume or surface, which can then be calculated using some fast algorithm based on either grid-based or analytical pairwise implementations. The volume integral formulation takes the form

$$\frac{1}{R_1}={\alpha }_N\doteq {\left(\frac{N-3}{4\pi }{\int }_{\Omega \mathit{ext}}\frac{d\mathbf{r}}{r^N}\right)}^{1∕(N-3)},N\ge 4,$$ (4.4)

or their combinations. In (4.4), the origin of coordinates is at location r_i. For a charge centered at a spherically symmetric cavity, the formulas are all exact, i.e., they can all reproduce the Born radius; but for more complex geometries, deviations may be too large.

4.2. Derivation of Integral Expressions

In the early GB models, the Coulomb field approximation (CFA) [17] was usually employed. The basic assumption of the CFA is that the electric displacement flux D due to charge q_i at r = 0 remains in Coulombic form,

$${\mathbf{D}}_i\approx \frac{q_i\mathbf{r}}{r^3},$$ (4.5)

even when dielectrics vary from ∊_i to ∊_o during the solvation process. Thus, the work of assembling the charge i at its location within the molecule can be approximated by

$$W_i=\frac{1}{2}{\int }_{{\mathbb{R}}^3}(\mathbf{E}\cdot \mathbf{D})\approx \frac{1}{2}{\int }_{{\mathbb{R}}^3}\frac{q_i^2}{∊\left(\mathbf{r}\right)r^4}d\mathbf{r},$$ (4.6)

where the origin is set at the charge location and a linear response D = ∊(r)E is used to define the relation between the electric field E and the displacement flux D. The formula for the work given by (4.6) using E and D is equivalent to the electrostatic solvation energy (2.19) after excluding the infinite self-energy terms associated with point charges (refer to section 4.7 of [96]). The electrostatic free energy of solvation is then obtained by taking the difference in work W_i between the solvent environment ∊_ext = ∊_o and the reference environment ∊_ext = ∊_i of the exterior domain of the molecule,

$$\Delta G_{\mathit{pol}}^i=\frac{1}{2}{\int }_{{\mathbb{R}}^3}\frac{q_i^2}{{∊}_i{r}^4}d\mathbf{r}-\frac{1}{2}{\int }_{{\mathbb{R}}^3}\frac{q_i^2}{∊\left(\mathbf{r}\right)r^4}d\mathbf{r}=-\frac{q_i^2}{2}\left(\frac{1}{{∊}_i}-\frac{1}{{∊}_o}\right){\int }_{{\Omega }_{\mathit{ext}}}\frac{1}{r^4}d\mathbf{r},$$ (4.7)

which leads to an integral expression of (4.4) with N = 4 that approximates the inverse effective Born radius. However, it is widely known that the CFA heavily overestimates the effective Born radii for off-center charges in a spherical solute; a straightforward calculation of the sphere model shows the maximum error can reach a 50% relative error for some atoms near the spherical surface [111, 83].

A rigorous derivation for the spherical cavity in Grycuk [83] gave a simple yet very precise formula, termed the R6 model, which has an error around only 1% with a single integral α₆ and is exact for the conductor limit of the solvent dielectric. For a sphere, the “perfect” effective Born radii can be obtained exactly from the series solution (3.14) of the PB equation by letting r = r_s = r_i,

$$\frac{1}{R_i^{\mathit{PB}}}=\frac{1-\delta }{a(1-p^2)}+\frac{1}{a}\sum _{n=0}^{\infty }\frac{(1-\delta )(1+\gamma )p^{2n}}{1-\gamma +2n},$$ (4.8)

and p = r/a. The coefficient 1 + γ is small, so the effect of the series on the right-hand side can be negligible. The R6 model approximates the series solution of the self-energy by

$$\frac{1}{R_i^{R6}}=\frac{1}{a(1-p^2)}={\alpha }_6,$$ (4.9)

where δ ≈ 0 is also used in order to reproduce the Born radius. The R6 radius is actually equivalent to the Kirkwood image approximation (3.28) for the spherical case, while the integral expression α₆ can be extended to irregular geometries. For complex geometries in realistic biomolecules, the model also achieved a very high accuracy [139, 188, 189, 137], allowing for potentially wide application in MD simulations, though the theoretical reason behind this advantage remains an open problem.

More accurate integral expressions have been created from a combination of several single integrals of (4.4). Early empirically obtained expressions that contain combinations of several α_N terms, such as α₄ and α₅ [111] or α₄ and α₇ [109], were seen to provide good approximations to the “perfect” Born radii. Several other expressions were proposed that contain as many as four integrals [161], formulated over the surface of a solute molecule rather than over its volume. However, these methods are all empirical and include parameters obtained by fitting a set of small proteins. Recently, a theoretical method [214] has been developed to derive optimal combinations of these volume integrals, starting from the spherical case. The basic strategy of the derivation is to derive the series representation of the “perfect” Born radii in terms of a finite volume integral:

$$\frac{1}{R_i^{\mathit{PB}}}\approx (1-\delta ){\alpha }_6+\sum _{n=4}^s{c}_n{\alpha }_n\left(p\right).$$ (4.10)

As expressed in (4.8), $1∕R_i^{\mathrm{PB}}$ is a polynomial series of p. And α_n(p) can be integrated out to show the dependence on p, as

$${\alpha }_4\left(p\right)=\frac{1}{2a}\left(\frac{1}{1-p^2}+\frac{1}{2p}\log \frac{1+p}{1-p}\right)$$ (4.11)

and, for n ≥ 5,

$$\begin{array}{cc}\hfill & {\alpha }_n\left(p\right)=\frac{1}{a(1-p^2)}{\left[2\right(n-2\left)\right(n-4\left)p\right]}^{-\frac{1}{n-3}}\hfill \\ \hfill & \times {\left[{(1+p)}^{n-3}\right(n-3-p)-{(1-p)}^{n-3}(n-3+p\left)\right]}^{\frac{1}{n-3}}.\hfill \end{array}$$ (4.12)

The coefficients in (4.10) can be then determined by the method of undetermined coefficients by truncating high-order terms of pⁿ for an arbitrary combination of specified integrals. The combination of only two integrals of α₆ and α₄ can provide a very accurate approximation to the “perfect” radius, where the inverse radius is given by

$${\alpha }_6^{\text{corr}}=(1-\delta )\left[\frac{6(1+\gamma )}{(1-\gamma )(3-\gamma )}{\alpha }_4-\frac{8\gamma }{(1-\gamma )(3-\gamma )}{\alpha }_6\right].$$ (4.13)

Since γ ≈ −1, the α₆ term in (4.13) is a dominant term, thus (4.13) is actually the R6 model with a CFA correction.

4.3. Incorporation of Varying Dielectric Effects

Historically, GB models were designed for a typical dielectric environment with solute dielectric of ∊_i = 1 and solvent dielectric around 80. These models may be problematic for varying dielectrics in applications of such as free energy transfer of a solute between two solvents or MD simulations of supercritical water [42], where the solvent dielectric can be very small. Feig, Im and Brooks [65] proposed an empirical formula using a dielectric-dependent combination of two volume integrals α₄ and α₇, expressed as

$$\frac{1}{R_i}=\frac{1}{C_0{\alpha }_4+C_1\left(\frac{3{∊}_o}{3{∊}_o+2{∊}_i}\right){\alpha }_7}+D+\frac{E}{{∊}_o+1},$$ (4.14)

where optimized parameters are given by C₀ = 0.3255, C₁ = 1.085, D = −0.14, and E = −0.15. Wojciechowski and Lesyng [208] developed a modified R6 model with a volume of a noninteger power,

$$\frac{1}{R_i}={\left(\frac{N-3}{4\pi }{\int }_{{\Omega }_{\mathit{ext}}}\frac{d\mathbf{r}}{r^n}\right)}^{1∕(N-3)},N=\frac{4.32}{{(\kappa +0.33)}^{0.3}},$$ (4.15)

which incorporates the varying dielectric into the power N and reduces to the R6 model for the standard dielectric environment ∊_i = 1. Wojciechowski and Lesyng's formula gives an even better approximation to the reference PB solutions. Sigalov and coworkers [177, 176, 151] developed an efficient analytical extension, accounting for the dielectrics of the solute and solvent, from the exact Kirkwood's series solution to reproduce the Born radii, applicable for arbitrary geometric shapes. More recently, the combination formula (4.13) was proposed to incorporate the effect of dielectric environments; this formula is extremely precise for sphere-like shapes and also very accurate for arbitrary geometries after introducing a correction parameter. Recently, Still's equation was treated by introducing a scaling formula [177, 187] in order to incorporate the dependence of dielectrics.

4.4. Calculations of Integral Expressions for Effective Born Radii

The GB methods have been widely studied in the last two decades owing to their easy applicability and fast performance in MD simulations [17, 66, 64, 35]. However, the calculation of the effective Born radius represented by the volume integrals, a key quantity in the GB theory, remains a major challenge. A straightforward way to construct the Born radii solver is to use the methods based on 3D grids or 2D molecular surfaces, which are known to be accurate but not fast enough for large macromolecular dynamic simulations. The available methods include volume integration of the molecule based on a cubic grid [168], or surface integral [76, 161, 8], or quadrature techniques from density functional theory [111]. We will review in some detail an FFT accelerated grid-based method [33, 171] and a pairwise approximation approach [72, 73].

4.4.1. An FFT-Based Acceleration Method

Recently, a grid-based method using the FFT was proposed in [33] to provide an O(N log N) algorithm for the effective Born radii. Here, N is the number of grid sites in the 3D space. Although it is straightforward to extend the method to arbitrary volume integrals (for example, [171]), we describe the basic idea from the CFA as in [33].

The idea of the FFT-based method is to rewrite the exterior integral as a combination of three contributions,

$$\frac{1}{R_i}=\frac{1}{4\pi }{\int }_{{\mathbb{R}}^3}G(\mathbf{r}-{\mathbf{r}}_i)d\mathbf{r}-\frac{1}{4\pi }{\int }_{{\Omega }_{\mathit{in}}}G(\mathbf{r}-{\mathbf{r}}_i)d\mathbf{r}+\frac{1}{4\pi }{\int }_{B_i}\left[\frac{1}{{\mid \mathbf{r}-{\mathbf{r}}_i\mid }^4}-G(\mathbf{r}-{\mathbf{r}}_i)\right]d\mathbf{r},$$ (4.16)

where the singular kernel $\frac{1}{{\mid \mathbf{r}-{\mathbf{r}}_i\mid }^4}$ is modified by a window smoothed function G(r) within a sphere S_i of radius a centered at r_i. As a result, the volume integral within Ω_in is without singularity. The radius a is usually taken to be a relatively large number so that the integrand can be sufficiently smooth, though it may cause a portion B_i of the sphere S_i to protrude outside Ω_in for an atom close to the boundary. In (4.16), the integrand G(r) is defined by

$$G\left(\mathbf{r}\right)=\{\begin{array}{cc}{W}_a^n\left(r\right)\hfill & \text{for}r\le a,\hfill \\ \frac{1}{r^4}\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$ (4.17)

and $W_a^n\left(r\right)$ is a function yielding the nth order derivative continuity of G(r) at r = a; for example,

$$W_a^1\left(r\right)=-\frac{2}{a^6}{r}^2+\frac{3}{a^4},$$

$$W_a^2\left(r\right)=\frac{3}{a^8}{r}^4-\frac{8}{a^6}{r}^2+\frac{6}{a^4},$$

$$W_a^3\left(r\right)=-\frac{4}{a^{10}}{r}^6+\frac{15}{a^8}{r}^4-\frac{20}{a^6}{r}^2+\frac{10}{a^4}.$$

The first term in (4.16) is composed of an integral of the window function within the sphere S_i and an integral of 1/r⁴ outside the sphere. Both integrals can be integrated exactly. The third contribution in (4.16) can be approximated by an analytical formula assuming that domain B_i is small and can be approximated by a spherical cap. Therefore, the only time-consuming contribution in (4.16) is the second integral defined on the molecular domain Ω_in, which can be calculated by the FFT as follows.

As the dielectric boundary is fixed, the second term in the inverse effective Born radius formula (4.16), denoted by I(r), is actually a scalar function defined on the whole domain,

$$I\left(\mathbf{r}\right)=\frac{1}{4\pi }{\int }_{{\Omega }_{\mathit{in}}}G(\mathbf{r}-{\mathbf{r}}^{\prime })d{\mathbf{r}}^{\prime }.$$ (4.18)

If the scalar function R⁻¹(r) is calculated on a 3D grid, the atomic Born radius of each atom can be obtained explicitly by a simple interpolation from the nearby data on the lattice sites surrounding the atom. Now, the function I(r) can be rewritten as an integral over the full space,

$$I\left(r\right)=\frac{1}{4\pi }{\int }_{{\mathbb{R}}^3}G(\mathbf{r}-{\mathbf{r}}^{\prime })f\left({\mathbf{r}}^{\prime }\right)d{\mathbf{r}}^{\prime }=\frac{1}{4\pi }G\ast f\left(\mathbf{r}\right),$$ (4.19)

where f(r) is the indicator function of the molecular volume that takes 1 for r inside the volume and zero, otherwise. Thus, the convolution of functions G and f can be evaluated using the Fourier transform. Furthermore, as function G is defined explicitly on a regular domain, its Fourier transform can be obtained analytically. In addition, to speed up the convergence when calculating the frequency spectral of the indicator function f, a smoothing technique can be used to reduce the sharp discontinuity on the molecular boundary; this technique was also used in other GB methods [95], or the finite difference PB solver [93].

The FFT approach is a grid-based method and is thus not suitable for straightforward force calculations of MD simulations due to the lack of Born radii derivatives with respect to charge locations. However, since the effective Born radii are computed on grid sites, these derivatives can be simply constructed from difference formulas. The construction of the Born radii derivatives is also a necessary step in implementing the treecode algorithm, as shown recently in [212], to reduce the computational cost from quadratic to linear complexity for pairwise charge-charge interactions.

4.4.2. Pairwise Descreening Approximation

Other than the grid-based approaches, many methods have been developed to approximate the integral as a sum of overlapping spheres [85, 158, 54] of Gaussians [169, 72, 79] (see Figure 1.1 for a molecular surface composed of overlapping vdW spheres), such as the analytical pairwise descreening approximation, which is very fast because the spherical integrals centered at each atom are easily computed; however, accuracy may be lost due to the difficulty in compensating for the overlap region of spheres. Because the effective Born radii are given analytically, the force calculation can be easily obtained by a differentiation; see, for example, [72]. Let us discuss how the analytical pairwise approximation is achieved.

In the pairwise descreening approximation, suppose the volume is composed of a set of atomic spheres A_j with vdW radius a_j; the volume integral in (4.4) is approximated by a pairwise sum of integrals,

$$\frac{1}{R_i^{N-3}}=\frac{1}{a_i^{N-3}}-\frac{N-3}{4\pi }\sum _{j\ne i}{Q}_{\mathit{ji}},$$ (4.20)

where

$$Q_{\mathit{ji}}={\int }_{A_j{A}_i}\frac{d\mathbf{r}}{{\mid \mathbf{r}-{\mathbf{r}}_i\mid }^N}$$ (4.21)

is an analytically solvable integral. However, a straightforward summation of each spherical integral overstates the molecular region due to the possible overlap of atomic spheres, leading to a significant overestimation of the effective Born radius. To treat the overlap regions, scaling factors s_ji are introduced to reduce the influence of the descreening, giving the following modified form of (4.20):

$$\frac{1}{R_i^{N-3}}=\frac{1}{a_i^{N-3}}-\frac{N-3}{4\pi }\sum _{j\ne i}{s}_{\mathit{ji}}{Q}_{\mathit{ji}}.$$ (4.22)

A number of strategies [85, 72, 86, 56, 192] have been developed to calculate the scaling factors, each one depending on a different approximation of the overlap regions, and we now introduce one of them [72] in detail. An accurate definition of the overlap regions starts from the inclusion-exclusion principle (also known as the Poincaré formula or the sieve principle) in combinatorics:

$$V=\sum _i{V}_i-\sum _{i<j}{V}_{\mathit{ij}}+\sum _{i<j<k}{V}_{\mathit{ijk}}+\cdots ,$$ (4.23)

where $V_i=\frac{4\pi }{3}{a}_i^3$ is the spherical volume of atom i and V_ij and V_ijk are, respectively, second- and third-order intersection volumes. In Gallicchio and Levy [72], the self-volume ${\tilde{V}}_i$ of atom i is defined by

$${\tilde{V}}_i=V_i-\frac{1}{2}\sum _j{V}_{\mathit{ijk}}+\frac{1}{3}\sum _{j<k}{V}_{\mathit{ijk}}+\cdots ,$$ (4.24)

so that $V={\sum }_i{\tilde{V}}_i$, resulting in $s_i={\tilde{V}}_i∕V_i$, the ratio between the self-volume and the spherical volume of atom i, which is a measure of the molecule volume. The scaling factor s_ji is approximately calculated by adding back a correction to the ratio s_j to yield

$$s_{\mathit{ji}}\approx s_j+\frac{1}{2}\frac{V_{\mathit{ij}}}{V_j},$$ (4.25)

which satisfies the consistent condition, s_ji = 1, when no other atoms intersect atom j. However, exact calculations of high-order intersection volumes are expensive, so an approximate algorithm developed by Grant and Pickup [78] was used, in which the volume of each atom is described by a Gaussian density function,

$${\rho }_i\left(\mathbf{r}\right)=\frac{4\pi }{3}{\left(\frac{\mu }{\pi }\right)}^{3∕2}{e}^{c_i{(\mathbf{r}-{\mathbf{r}}_i)}^2},$$ (4.26)

where $c_i=\frac{\mu }{a_i^2}$ and μ is a dimensionless parameter. The overlap volume of atoms i₁, …, i_m can then be approximated by the integral of the product of their density functions, which can be evaluated analytically as

$$\begin{array}{cc}\hfill & V_{i_1},\dots ,i_m\approx {\int }_{{\mathbb{R}}^3}d\mathbf{r}{\rho }_{i_1}\left(\mathbf{r}\right)\cdots {\rho }_{i_m}\left(\mathbf{r}\right)\hfill \\ \hfill & ={\left[\frac{4\pi }{3}{\left(\frac{\mu }{\pi }\right)}^{3∕2}\right]}^m{\left(\frac{\pi }{C}\right)}^{\frac{3}{2}}\exp \left(-\frac{1}{C}\sum _{p=1}^m\sum _{q=p+1}^m{c}_{i_p}{c}_{i_q}{r}_{i_p,i_q}^2\right),\hfill \end{array}$$ (4.27)

where

$$C=\sum _{p=1}^m{C}_{i_p}.$$ (4.28)

The parameter μ was set to be 2.227, which was accurate in reproducing the molecule volume [78]. Recently, Tjong and Zhou [188] used a pairwise approximation based on the R6 model and obtained a parameterized model, called GBr⁶, which reproduces the PB solvation energy with an accuracy of about 0.6% in unsigned relative errors; it can also reproduce the nonlinear PB energy by introducing more empirical parameters [189].

5. Conclusions and Perspectives

We have surveyed fast analytical methods for electrostatic interactions with focus on two important classes of macroscopic solvation models: hybrid explicit/implicit reaction field models and implicit GB models. To conclude and give a perspective on future research, it may be useful to briefly highlight the hierarchy of approximate models.

When we start a realistic molecular simulation, an important issue is to find an effective model suitable to our problem, drawn from the hierarchical structure of approximations, that will achieve a balance between speed and desired accuracy. As is well known, a straightforward choice if computing power is adequate is an all-atom solvent model with a large enough simulation box, which will produce accurate results. However, given the increase in system size and complexity, the demand on computer facilities increases exponentially. A tradeoff between speed and accuracy has to be achieved. Implicit solvent models are successful in reducing the degrees of freedom by using a continuum model to treat the solvent molecules as a homogeneous medium, though at the expense of accuracy.

Implicit solvent models provide an estimation of the mean influence that the solvent exerts on a solute, and have become an attractive tool to treat long-range electrostatic interactions. They are particularly superior in the calculation of solvation free energies because the solvent molecules are taken into account macroscopically. An attractive feature of using the PB method lies in it ability to compute pKa values of amino acid side chains of proteins when the charge state of the system is often changed during a simulation.

However, the large cost of numerically solving the PB equation limits its application in dynamics simulations, so simplified implicit models have been developed. Empirical distance-dependent dielectric models [203, 89, 159, 173, 97] have been used to produce long-range pairwise Coulombic interactions in the inhomogeneous environment. The models with a distance parameter successfully simulate problems without high accuracy requirements, but they are usually not accurate enough to study many useful physical and chemical properties of the simulated system due to their inability to distinguish buried and solvent exposed regions of the molecule. Other simplified models include induced multipole models [46, 45], dielectric screening models [134, 116], and surface-based models [200].

With the continuous development of both methodology and algorithms for implicit models, the GB model has become the primary choice of implicit model in biomolecular simulations due to its favorable accuracy and computational efficiency, allowing analytical calculations of electrostatic solvation energies and forces, and it achieves successful reproduction of the numerical PB solution. Although the GB model has been commonly used in MD simulations due to its efficiency, the intrinsic limitations of continuum solvent models remain; in particular, the continuum model breaks down at small length scales where the size of the solvent molecule becomes nonnegligible [228]. Growing evidence has shown that the common description with a sharp dielectric boundary to separate the solute and solvent mediums is not well justified [20]. It was also reported that the continuum models fail to describe the formation of a salt bridge between oppositely charged amino acids in proteins [223, 20]. It is clear that it is necessary to treat explicitly some parts of the solvent at the atomic scale, for example, those water molecules close to the protein surface.

There are many issues yet to be addressed in regard to more accurate and rapid treatments of macroscopic electrostatics. For the GB methods, although mathematical tools have been used to construct more accurate formulations and design more powerful algorithms, many questions remain to be answered before a better understanding of various integral expressions is achieved. Attempts [12, 13] have been made to explain how different GB models improve the accuracy; however, a systematic understanding of the GB methods is still an open question. In particular, a theoretical interpretation of the pairwise sum of the energy formula is still needed. Another important topic is the fast computation of the pair energies. For larger biomolecular systems, the cost of the pairwise sum could be a bottleneck and an accurate linear-scaling algorithm is required.

Hybrid explicit/implicit models are promising ways to take into account the influence of water molecules near the solute surface, while performing dynamics simulations at a reduced cost. More importantly, the number of water molecules can be flexible, thus regular cavities, often of spherical shape, are used and electrostatic interactions are obtained analytically, as described in this article. It should be noted that, although the hybrid models have been shown to be successful in modeling short peptides, successful application to bigger and more complicated systems remains to be carried out. In principle, the hybrid solvation model can be extended to any geometry with analytical representation of the reaction field. In some applications, such as ion channels, a cylindrical explicit region is preferred, and thus accurate analytical methods are needed in this setting.