The authors present a framework, developed in an introductory physics for life sciences majors course, for analyzing interdisciplinary tasks. This framework will be useful for both curriculum designers and education researchers seeking to understand how integrated science curricula can be designed to support interdisciplinary learning objectives.
Abstract
The national conversation around undergraduate science instruction is calling for increased interdisciplinarity. As these calls increase, there is a need to consider the learning objectives of interdisciplinary science courses and how to design curricula to support those objectives. We present a framework that can help support interdisciplinary design research. We developed this framework in an introductory physics for life sciences majors (IPLS) course for which we designed a series of interdisciplinary tasks that bridge physics and biology. We illustrate how this framework can be used to describe the variation in the nature and degree of interdisciplinary interaction in tasks, to aid in redesigning tasks to better align with interdisciplinary learning objectives, and finally, to articulate design conjectures that posit how different characteristics of these tasks might support or impede interdisciplinary learning objectives. This framework will be useful for both curriculum designers and education researchers seeking to understand, in more concrete terms, what interdisciplinary learning means and how integrated science curricula can be designed to support interdisciplinary learning objectives.
INTRODUCTION
The national conversation about the need for interdisciplinary science education has been growing steadily. As reflected in national reports (National Research Council, 2003; American Association for the Advancement of Science [AAAS], 2010; Association of American Medical Colleges–Howard Hughes Medical Institute [AAMC–HHMI], 2009), as well as in the articles in this special issue, biology education has been at the center of this conversation. The general consensus is that preparing undergraduate biology students for the increasingly interdisciplinary nature of biological research and healthcare professions requires a shift from a fragmented to a more-integrated introductory science curriculum. Integrated courses are expected to go beyond teaching the content of a single discipline to support interdisciplinary learning objectives. For example, the AAMC–HHMI (2009) report emphasizes the need for interdisciplinary curricula that help students develop a broad set of scientific competencies combining conceptual understanding, skills and reasoning strategies, and attitudes from across disciplines.
How to operationalize interdisciplinary learning objectives in practice remains largely underspecified. What, concretely, does interdisciplinary learning look like, what specific features of learning environments can support this kind of learning, and how do we know whether interdisciplinary learning has occurred? To realize the aims of interdisciplinary science education, it will be important to be more systematic about how we describe and assess interdisciplinary learning (Stevens et al., 2005).
One way forward is to approach the problem from the perspective of educational design research (Brown, 1992; Cobb et al., 2003; Collins et al., 2004). Design research is an iterative process that involves making hypotheses that specify how particular features of learning environments can support intended learning objectives and then investigating to what extent those objectives are met. This information is then used to refine initial design hypotheses and inform subsequent cycles of design and implementation. Design research can support both pragmatic and theoretical ends; over time, it can help practitioners bring learning objectives and learning outcomes into better alignment and lead to a deeper understanding of the mechanisms of learning.
In the context of interdisciplinary education, design research can help address theoretical questions about what interdisciplinary learning means and what interdisciplinary learning looks like, as well as pragmatic concerns about how to design learning environments and evaluate the learning outcomes that emerge from those environments. Because interdisciplinary courses are relatively new, very little research specific to interdisciplinary learning objectives has been done (cf. Ivanitskaya et al., 2002).
At the University of Maryland, we are in the early stages of designing and researching an introductory physics for life sciences majors (IPLS) course as part of the HHMI National Experiment in Undergraduate Science Education (NEXUS) project.1 Our team consists of an interdisciplinary collaboration among disciplinary experts in physics, biology, and chemistry and education researchers. The initial design of the course was guided by extensive discussions and negotiations among the members of this team about how to support the broad goal of making introductory physics more relevant and engaging for life sciences students (e.g., Redish and Cooke, 2013). This initially meant reorganizing the content to reflect topics relevant to biology (e.g., switching the emphasis of thermodynamics toward microscopic phenomena, such as random motion and diffusion, including other nontraditional physics topics, such as fluid dynamics and chemical bonds), and explicitly attempting to support the development of basic scientific competencies described in the Scientific Foundations for Future Physicians (AAMC–HHMI, 2009) and Vision and Change (AAAS, 2010) reports.
In 2011–2012, we piloted 1 yr of the new IPLS course. As part of our research effort, we undertook a reflective analysis focusing on the interdisciplinary tasks (including homework, in-class, and small-group problems) that were designed to bridge physics and biology. In reflecting on these tasks, we noticed variation in the nature and degree of interaction between the disciplines. We also observed differences in the ways in which students responded to these tasks. This prompted us to conduct a more systematic analysis of the tasks we had designed as a step toward refining our initial learning objectives and developing concrete design conjectures about how to support these objectives.
In this paper, we present a theoretical framework that has helped us describe this variation and has allowed us to begin to articulate a set of initial design conjectures that posit how different characteristics of these tasks might support or impede interdisciplinary learning objectives. This framework will be useful for both curriculum designers and education researchers seeking to understand, in more concrete terms, how integrated science courses can support interdisciplinary learning.
We first present the theoretical framework and then apply it to illustrative tasks drawn from our examination of the IPLS course. Next, we present an analysis of how the framework can aid in redesigning tasks to better align with interdisciplinary learning objectives. Finally, we return to discussing how our analysis leads to a set of design conjectures that link the degree of interdisciplinary interaction to interdisciplinary learning objectives for students, and we propose an emerging set of research questions to be addressed by education researchers working in interdisciplinary contexts.
What Are the Learning Objectives of Interdisciplinary Education?
To begin, we must first attempt to define our goals for interdisciplinary science education. We articulate four interdisciplinary learning objectives reflected in the national conversation and identified by our interdisciplinary research team as particularly important in our evolving work.
Developing Deeper Levels of Conceptual Coherence.
One objective of increased integration in science instruction is to help students develop deeper and more coherent conceptual frameworks. Fragmented courses are likely to support fragmented understanding (e.g., Redish et al., 1998; diSessa, 2002; Sternberg, 2003). For example, students are likely to emerge from current training with an understanding of potential and kinetic energy as ideas that belong in physics class, chemical and electrochemical energy as ideas that belong in chemistry, and metabolic energy as an idea that belongs in biology (Dreyfus et al., 2013b). The problem this creates is that students’ understanding of energy is not just fragmented across disciplinary lines, but that students hold potentially inconsistent ideas about what energy means or how it behaves in different contexts. Students with a robust, coherent understanding of energy would be able to move between different disciplinary conceptualizations of energy and recognize when one (or more) conceptualizations would be more productive to the problem at hand. To see evidence of a robust, coherent understanding of energy, it would be insufficient to demonstrate reasoning successfully about kinetic and potential energy in macroscopic scenarios (typical of introductory physics) in one setting and reasoning successfully about the use of ATP to accomplish biological work (canonic for introductory biology) in another setting. A coherent conceptual understanding of energy would include an understanding of the relationships among different forms of energy (such as potential energy, bond energy, and ATP) and the development of a framework for understanding how energy is transformed among systems of different kinds (Dreyfus et al., 2013a). A robust coherent understanding would allow students to move among these ways of reasoning, seek connections across them, understand when to bring certain ideas to bear on a problem, and relate various disciplinary conceptualizations.
In general, increased coherence at the introductory level can potentially help students see connections among scientific ideas that they would typically encounter in separate courses and build more robust conceptual frameworks for reasoning about a range of phenomena.
Developing a Varied Set of Scientific Reasoning Strategies.
Scientists across disciplines have at their disposal a powerful set of practices for reasoning about the world. These include, for example, developing conceptual and mathematical models, working with a variety of representational systems, and engaging in scientific argumentation (e.g., Nersessian, 1999, 2002; Dunbar, 2000; Wong and Hodson, 2009). The specific reasoning strategies that scientists routinely employ will reflect differences in underlying epistemological aims and commitments and can differ greatly both within and between disciplinary subcultures (Knorr-Cetina, 1999). However, differences in what counts as good reasoning in different disciplines can be exaggerated in instructional settings (Stevens et al., 2005; Redish and Cooke, 2013). Without opportunities to examine how and when these strategies are used in different disciplines, students can potentially compartmentalize their expectations about what kinds of reasoning are appropriate in different courses. For example, classroom experiences can perpetuate the belief that reasoning with equations is a strategy that belongs in physics (and not biology; e.g., Hall, 2013) or that conceptual explanation is a strategy to be used in biology (and not physics; e.g., Watkins et al., 2012).
Interdisciplinary classrooms can provide opportunities to examine disciplinary differences in how these strategies are enacted and to highlight opportunities for synergy. For example, Bialek and Botstein (2004) argue that
There are commonalities of the mathematical structures that summarize our understanding of seemingly disparate topics. Classical mechanics presents a model of the world's dynamics based (in the introductory account) on simple differential equations, but chemical kinetics and even the dynamics of populations provide models of the same general form. (p. 789)
To be clear, Bialek and Botstein are not simply suggesting that students develop the general ability to solve differential equations, but rather that they develop the expertise to leverage this particular mathematical tool in a variety of disciplinary contexts.
When reasoning about complex scientific problems, students should be able to draw on a variety of reasoning strategies, both qualitative and quantitative. Interdisciplinary courses can provide opportunities for students to develop this kind of scientific procedural knowledge. This objective suggests that interdisciplinary courses can potentially expand the repertoire of reasoning strategies students have available for making sense of a range of scientific phenomena and begin to help students understand how and when to use these strategies.
Metacognition and Adaptive Interdisciplinary Expertise.
Interdisciplinary courses have the potential to support metacognitive learning objectives, including the ability to know when and how to use different concepts and reasoning strategies. These kinds of learning objectives are what distinguish routine from adaptive expertise (Hatano and Inagaki, 1986). A routine expert can effectively and consistently solve problems of a particular type. An adaptive expert can do this as well, but also has an understanding of the meaning and purpose of the problem-solving strategy. This is because adaptive expertise involves the coordinated use of conceptual and procedural knowledge; the adaptive expert uses his or her understanding of the conceptual context in order to make an informed decision about the relevance and utility of a particular strategy. It is a much more flexible and often creative form of reasoning that allows this sort of expert to select appropriate courses of action, modify those actions if they turn out to not satisfy his or her intention, and possibly even invent new strategies in the face of novel problems. This idea is similar to what Ford and Forman (2006) have described as a “grasp of practice.” The basic goal is for science students to develop the ability to reflect on and take ownership of their own scientific reasoning rather than simply go through the motions of more typical algorithmic problem solving.
Hatano and Inagaki (1986) describe three features of learning environments that are likely to support this kind of learning objective. The first is that learners are given some flexibility and choice in the problems they are asked to solve. The second is that these problems are intrinsically motivating to students. Third, a necessary but not sufficient condition for development of adaptive expertise is that students perceive the learning environment as valuing understanding why a particular approach works rather than just focusing on getting to a particular answer. If students are not given opportunities to practice key features of adaptive expertise or if the qualities of adaptive expertise are not valued, they are unlikely to develop it in those contexts.
Interdisciplinary courses may be particularly well suited to support this sort of learning goal, because when two or more disciplines are brought into interaction, disciplinary choices that are typically implicit can be brought out as objects of critical reflection. Students can be explicitly asked to reflect on the level of conceptual detail that is necessary for making sense of a particular problem, the relevance of the assumptions embedded in particular approaches, and the trade-offs inherent in different strategies.
Shifting Student Attitudes and Expectations about the Disciplines.
Finally, interdisciplinary education can potentially help students develop an interest in and appreciation for disciplines outside of their chosen major. For biology students, this tends to mean overcoming a perceived resistance to quantitative approaches commonly associated with physics and engineering disciplines (e.g., Bialek and Botstein, 2004; Gross et al., 2004; Watkins et al., 2012). The extent to which and the reasons why students hold these negative attitudes about other disciplines is not well-researched. Nevertheless, both anecdotal accounts and case studies suggest that these attitudes are real for at least some students (Hall et al., 2011, 2013; Watkins et al., 2012).
Students’ attitudes about learning science are likely to reflect some interaction between epistemological and affective dimensions (Gupta et al., 2010). That is, students’ expectations about what counts as science learning and what science instruction should look like, as well as prior experiences with other disciplines, both positive and negative, can influence how they respond to interdisciplinary integration. The desired interdisciplinary learning outcome is to support positive attitudes about the utility of integrated instruction by both broadening students’ expectations about what counts as biology to include knowledge and techniques from other disciplines and supporting the development of more positive affective responses to the inclusion of this material.
Actively designing curricula with epistemological messages in mind has been shown to be effective in supporting shifts in students’ expectations and attitudes (e.g., Redish and Hammer, 2009).
Why Focus on Task-Level Analysis and Design?
Learning environments are complex systems. Design research aims to understand how the complex interactions among various aspects of the learning environment (e.g., patterns of discourse, classroom norms, available tools and resources, as well as the specific tasks and problems students are asked to solve) influence student learning (Cobb et al. 2003). In this work, we take a relatively narrow approach to design research by focusing on curricular tasks. While we acknowledge that other aspects of the learning environment are likely to be important, focusing on the level of particular curricular tasks can be a productive starting point for several reasons. First, in many ways, the activities we ask students to engage in, the problems we ask them to solve, and what we ask them to attend to will be central to what students learn. It is well recognized that student activity, rather than what is said in lecture, is the locus of learning (e.g., Hake, 1998; Bransford et al., 2000; Knight and Wood, 2005).
Second, task design is a practical level of granularity for education research. It is much easier to begin by designing tasks than by trying to imagine how to enact learning objectives across an entire course. Once an understanding of how particular tasks support particular learning objectives is reached, these tasks can be sequenced and arranged to support a full course. Furthermore, task-level design is a practical starting point for collecting student data. By observing how students interact with tasks, we can begin to link particular features of tasks to observed learning outcomes. And by examining how different groups of students interact with the same task, we can begin to understand how robust particular task features are for supporting these outcomes. We can begin to conjecture, on the task level, how particular task features might impact learning and then explore these by changing these features and observing how students respond.
Finally, tasks are likely to be the level at which widespread dissemination of curricula is ultimately realized. For this reason, it is crucial to understand the relationship between specific features of tasks and learning outcomes. Thus, while we acknowledge that how students engage in tasks will ultimately depend on a more complex set of factors, unpacking how particular features of the tasks we assign students relate to expected learning outcomes is an important first step.
Design research is an iterative process, and in our work, we are at the early stages of this process. This paper articulates a theoretical framework for analyzing interdisciplinary tasks and informing their redesign. We do so by drawing on theoretical work combined with our practical experience as an interdisciplinary team of curriculum designers and researchers. We see this as a first step within a broader design–research study aimed at understanding how our interdisciplinary learning environment is influencing student learning. Our primary objective in sharing this early-stage analysis is to draw attention to variations we have detected in the nature and degree of interaction among disciplines in interdisciplinary tasks. We also explore the implications of this variation in light of particular interdisciplinary learning objectives.
THEORETICAL FRAMEWORK
Before we move on to discussing the specific physics course in which our work is situated, we introduce a theoretical framework that has helped guide our work and thinking about the nature of interdisciplinary tasks and how variations in these tasks might support or impede the learning objectives listed above.
Paxson's (1996) article, “Modes of Interaction Between Disciplines,” is a theoretical analysis of interaction between disciplines. Paxson's focus is cognitive and epistemological, that is, he is concerned with the development of knowledge and decisions about how particular kinds of knowledge are negotiated when different disciplines are brought into interaction with one another. Consistent with Paxson, we consider disciplines to be constituted of canonical methodological techniques, conceptual frameworks, representations, reasoning strategies/practices, epistemological commitments, assumptions, and specific problems or aims. In an interaction between disciplines, one (or multiple) of these constitutive elements moves from one discipline to another with a variety of possible ramifications. Paxson's perspective on the nature and degree of possible interactions between disciplines is described in the following paragraphs.
One of Paxson's primary objectives is to account for the amount of impact disciplines have on one another. His central premise is that when two disciplines are brought into contact with each other, the nature and depth of that interaction has consequences for the outcome of that interaction in terms of scientific progress. In his analysis, Paxson draws primarily on interactions among expert researchers in different disciplines. He presents an ordered list of interactions along the dimension of increasing impact. When two disciplines impact each other, there is some meaningful exchange of ideas, techniques, or perspectives such that the disciplines emerge from this interaction changed in some way.
At the bottom of this list (at the lowest level) are exchanges of essentially no impact, in which two disciplines are brought into contact to solve some problem, but neither discipline changes or grows. One example Paxson gives is of a multidisciplinary team addressing the needs of a patient in a hospital. Each member of the team contributes to solving the problem by bringing his or her own individual expertise to bear, but the team members do not interact substantially with one another. The team accomplishes the treatment of the patient, but in doing so, none of the team members are significantly impacted by the expertise of the others. In this interaction, no new ideas, techniques, or questions are developed. At this lowest level of interaction, there is an absence of impact, and therefore no real cognitive or epistemological significance for the disciplines involved.
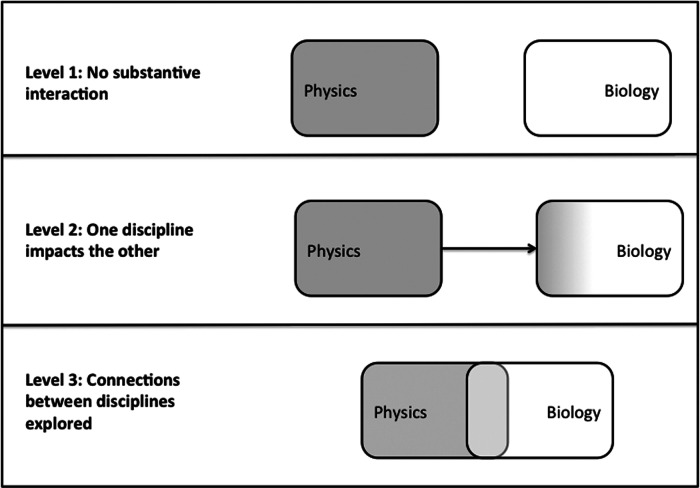
Moving up the list, Paxson then describes four additional levels of interaction that range from relatively low-level impact to high-level impact. We slightly modified this framework, collapsing the four levels into three, which we use to explore interactions between physics and biology in an IPLS course (Figure 1).
Figure 1.
A modified version of Paxson's (1996) framework for interdisciplinary levels for use specifically with physics and biology.
Our version of Paxson's framework has been modified to reflect our aim of designing interdisciplinary tasks for students. Paxson's levels of interaction between disciplines relate to the potential for such interactions to result in scientific progress. In our framework, we use “interaction between the disciplines” to refer to the potential to support interdisciplinary learning objectives. The levels in the framework are intended to capture significant qualitative differences in the ways that disciplines are interacting that are consequential for student learning.
Features of Level 1 Tasks: Superficial Interaction
Level 1 tasks describe those that have a relatively low level of interaction between disciplines. These correspond most closely to Paxson's level 1, which he describes as cases in which one discipline simply begins to “take notice” of the other discipline. In some ways, it is easiest to identify this level of interaction by what it does not do: there is no substantive exchange of ideas between the disciplines, no insights are shared, and there is no reflection on the disciplines themselves (Figure 1).
Features of Level 2 Tasks: One Discipline Impacts the Other
The tasks we identified as level 2 share features with Paxson's level 2 in that there is an increase in interaction among the disciplines. Specifically, in level 2 tasks, one discipline impacts or modifies a second in some substantial way. For example, the methodological techniques or conceptual framework of one discipline is applied to the other in a way that leads to a deeper understanding or a transformation in the practices of the second discipline. Level 2 tasks share with level 1 an imbalance in the direction of this interaction; in this type of interaction, the primary discipline remains largely unaffected, and only the secondary discipline is modified.
Features of Level 3 Tasks: Exploring Connections Between the Disciplines
We collapsed Paxson's levels of 3 and 4 into our level 3, which represents a purposeful, substantive, and bidirectional interaction between disciplines (Figure 1). One way this might occur is by bringing different conceptual frameworks of each discipline to bear on a problem and explicitly examining why these frameworks differ and where they overlap. The result of such interaction is that there is the potential for a deeper understanding of each framework. A second way for two disciplines to overlap could also occur through examination of the epistemological commitments of each discipline, for example, by comparing the methodological choices or assumptions made by each discipline. When the choices made by each discipline are brought into interaction in this manner, an opportunity to critically examine them is created. This is perhaps the defining feature of a level 3 interaction—neither disciplinary perspective is simply taken as unproblematic; rather, both are explicitly examined, so the purpose and limitations of each approach can be illuminated by the comparison.
Our objective is to use Paxson's framework to explore the implications for interdisciplinary education. Paxson asserts that “general education should provide students not only experience and practice in bringing different disciplines into interaction, but in doing so on many levels” (p. 81). In this paper, we illustrate what these different levels of interaction can look like by presenting an analysis of tasks drawn from a physics course for biology majors. We then explore the implications of this variation for student learning and interdisciplinary education more broadly.
METHODS
Course Context
The context of this work was the pilot year of IPLS. The course departs from the traditional introductory physics structure in encouraging students to draw connections between biology, chemistry, and physics. Biology and chemistry are both prerequisites for this course, which facilitates students’ drawing these connections. Furthermore, the course deviates from the traditional topics covered in introductory physics, spending significantly more time on the concepts of energy and thermodynamics because these topics are central to phenomena in chemistry and biology.
Structurally, the course ran as a typical introductory physics course, with three 50-min lectures per week, accompanied by one 110-min lab meeting and one 50-min discussion section. The discussion sections were designed as intensive, collaborative, problem-solving environments in which students worked on tasks that bridged biological, chemical, and physical concepts. Homework was assigned weekly, and students were strongly encouraged to work together to complete the extensive problem sets. Homework assignments ranged from traditional calculation-focused problems, to narrative descriptive essays, to complex Excel computations. The instructor administered short multiple-choice, multiple-response quizzes weekly, two exams during the semester, and a final exam at the end of the term.
Task Analysis
Our analysis of course tasks began as an informal discussion among our research and curriculum development team based on both our experiences attempting to design interdisciplinary tasks and our observations of students’ performance on and reactions to these tasks. We examined students’ written performance on select homework and exam problems. We also conducted analyses of videos and transcripts of students reasoning in group problem-solving settings and of individual interviews designed to probe students’ understanding of and reactions to the course. In research team discussions, we noted that there was variation both in the ways in which interdisciplinarity was introduced in tasks and in students’ reactions to those tasks. This prompted us to attempt to describe this variation more systematically, and it was at this point that drawing on Paxson's framework became useful.
In formalizing our analysis, we defined “task” as any problem or question that students were asked to solve or reason about. In the context of this course, tasks included written homework assignments, problems assigned during group problem-solving sessions, and exam questions. Our course context also included sets of in-class clicker questions and weekly quizzes, but for practical purposes of keeping the number of tasks manageable, these were not considered in our analysis.
We began our analysis by choosing a small number of interdisciplinary tasks and operationalizing Paxson's concept of “impact” by asking a series of questions about the degree to which each discipline (physics and biology) was represented in the task as written:
What is the phenomenological context of this task?
What question or aim is being addressed in this problem?
What set of conceptual ideas are students expected to engage with in this task?
What reasoning strategies are students expected to engage with in this task?
We then used the answers to these questions to reflect back on the central question from Paxson's framework: In what ways are the disciplines interacting in this task and how deeply? These questions aligned well with the articulated objectives for interdisciplinary education in the sense that they brought to the forefront the conceptual ideas and reasoning strategies with which the task prompted students to engage. Foregrounding these ideas allowed for examining the extent to which the tasks were meeting the stated learning objectives. We repeated this analysis over a range of tasks until we felt we had a framework that could capture the variety of different tasks students encountered in this course. However, it was not our intention to be able to fit every task neatly into a specific category. It was more important that the framework allowed us to reflect on the task as initially designed and consider what aspects of that task could be described as interdisciplinary. It is from this perspective of supporting the initial stages of design research that we present our findings.
FINDINGS
In presenting our findings, we have chosen to focus on a few illustrative examples of tasks developed in our course. These tasks were chosen for their potential to illustrate key differences in degree of interdisciplinary interaction and not necessarily because they are exemplary.
Example of Level 1 Task
In our analysis, we placed tasks in this category when the interdisciplinary nature of the task was at a superficial level, which often meant that there was an imbalance in the interaction between the disciplines. In the context of a physics for life sciences course, this meant that the conceptual focus of the problem lay wholly within the domain of physics, while the biological aspects of the problem were largely incidental. The biology only provided the backdrop for the problem, but the biological features of that context were not relevant or necessary to the solving of the problem. As a result, the conceptual and epistemological concerns of the primary discipline (in this case physics) were taken as given, while concerns authentic to the second discipline (biology) were largely absent from such tasks.
We identified several tasks of this type in the first iteration course, the majority of which were either on exams or in homework problems. The one we present here appeared on a semester exam.
The fish buoyancy problem (Figure 2) asks students to reason about buoyant force on fish using Archimedes’ principle: The buoyant force is equal to the weight of the displaced water. Given that each of the three fish are the same volume, they each displace the same amount of water and therefore experience the same buoyant force. This is a level 1 problem, because the fish function only to indicate that buoyant forces can potentially have significance for organisms, but the fact that the objects in this problem are fish is irrelevant to finding the solution. An isomorphic problem that simply referred to three blocks would have an identical solution, because the only ideas needed to solve this problem concern volume and density of the displaced fluid. While this problem nods to a possible connection between ideas about buoyancy and aquatic organisms, the relationship is not explored in this version of the problem. The implications of buoyancy for biological systems are not taken up in this problem—no biological ideas are explored, extended, or modified.
Figure 2.
Fish buoyancy problem.
Examples of Level 2 Tasks
In the context of our task analysis, we conceptualized level 2 tasks as those in which some specific conceptual framework or reasoning strategy from one discipline was applied to the other (Figure 1). This might mean applying a technique that is common in physics (e.g., dimensional analysis) in a biological context. It could also mean applying a conceptual framework from physics to a biological context, either via analogy or to “unpack” the physics underlying some biological phenomenon. In both cases, there is the potential for some meaningful reasoning about biology to emerge from this interaction.
However, the primacy of the disciplinary perspective of physics is maintained. Core concepts or epistemological commitments of biology are not explicitly brought in or examined in such tasks. Physics sets the rules for how to solve such problems. Furthermore, the appropriateness of the application of physics to biology is not considered as an object for critical analysis. The assumption underlying these tasks is that one discipline (physics) has something to offer the other (biology).
The first example illustrates a level 2 task in which the physics underlying some biological phenomenon is unpacked. This homework problem examines the physics of pressure and flow as a means of understanding arteriosclerosis (Figure 3). We categorized this problem as level 2, because it begins with a phenomenon from a biological context—the pathology of arteriosclerosis—and then leads students through a series of questions aimed at unpacking the physical principles that underlie this disease. This intention is stated explicitly in the framing of the problem itself: “Let's see what physics can tell us about coronary arteriosclerosis and its consequences.” The main ideas at play in this problem have to do with flow, which students are expected to calculate using the Hagen-Poiseuille (HP) equation (J = Δp/Z, where Δp is the pressure drop and Z is the resistance, which is inversely proportional to the cross-sectional area). Working through the calculation, students are meant to see that occlusion can lead to decreased blood flow (Figure 3, part B) and that this, in turn, can result in increased pressure on the arterial walls, because the body is attempting to keep flow constant (Figure 3, part C). In Figure 3, part D, the increase in pressure drop is converted into a blood pressure number, so the pressure increase can be related to a relevant medical parameter.
Figure 3.
Arteriosclerosis homework problem.
Again, the reason we have classified this task as level 2 is that the physics framework is used to help students make sense of the relationship between plaque buildup in arteries and changes in blood pressure. The physics model of flow is meant to help deepen students’ understanding of the biological phenomenon by exploring the physical mechanisms that lead from occlusion to an increase in pressure on the arterial walls.
Thus, both the initial context and the ultimate implications of the solution to this problem are biological in nature.
The directionality of this problem from a simple physics model to the implications for the biological system further helped us classify it as level 2. What prevents this problem from being classified at a higher level is a lack of an explicit examination of the physics principles and their applicability to the biological system: Is this model an appropriate starting point for reasoning about arteries? What assumptions does this model make about the biological system? Are these assumptions valid? While this model may indeed be a good starting point for reasoning about arteries, the task itself does not ask students to consider these questions. It proceeds from an assumption that the physics ideas are relevant.
A second example illustrates a different way in which a task can be considered level 2: through the application of reasoning strategies or problem-solving techniques that are common in one discipline to a question or problem from the other. In this example, students are expected to use symbolic and graphical analytical strategies to understand the consequences of variation in growth parameters for earthworm survival (Figure 4). This problem is framed initially as one that is directly applicable to a biological aim—to understand the relationship between organismal structure and function. In this case, how does the shape of an earthworm influence its ability to distribute oxygen through its body tissues? The analytical strategy is one that is not commonly encountered in introductory biology courses. This problem can be considered level 2, because it makes use of a set of strategies more common to physics courses to make progress in understanding a biological pattern.
Figure 4.
Earthworm task.
The problem asks students to model an earthworm as a cylinder (Figure 4, parts A and B) and then to express the relationship between various size parameters and the oxygen absorption rate symbolically (Figure 4, part C). This symbolic expression can be used to explore the relationships between size and oxygen use in the worm. This is first explored graphically (Figure 4, parts D.1 and D.2), which allows for the visualization of how oxygen absorption and oxygen use would vary as the length and width of the worm varied—a technique that allows for the prediction of the optimal dimensions of a worm. Then, in (Figure 4, part D.3, students are asked to translate between the graphs and a symbolic representation of the cross-over point of the oxygen absorption and use curves. This analysis leads to the conclusion that is it the radius not the length of the worm that should constrain worm size.
In this problem, the kinds of mathematical reasoning moves that are often developed in the context of physics are leveraged to make meaning of a biological scenario. The idea that organisms respond to trade-offs in the environment is a familiar one from biology courses, and this problem gives students a way to systematically explore how size parameters trade off against the organism's ability to absorb and distribute oxygen to its cells. It also presents a general set of strategies that could be applied to other problems that involve making predictions about optimality by examining relationships among different parameters.
In both examples, the features that make the task level 2 include the directional application of some concepts or reasoning strategies from physics applied to a biological context (Figure 1). And this application leads to a legitimate progress in making sense of the biology. But in neither of these examples is this application of physics to biology examined in detail, and in neither case does the biology have a reciprocal impact on the physics, as will be the case for level 3 tasks.
Examples of Level 3 Tasks
The IPLS tasks we identified as level 3 brought together a set of ideas from physics and a set of ideas from biology and asked students to make sense of this interaction. Ideas from physics were not privileged by default. Rather, students were asked to consider both the differences and possible areas of overlap between physics and biology. The hallmark of level 3 tasks is this interaction, which impacts both disciplines. The bidirectionality both allowed students to shift or deepen their biological understanding and, at the same time, by taking the biological context seriously, the traditional presentation of the physics content had to be reconsidered. Some of the features of the standard physics approach, both conceptual and procedural, were drawn out and examined.
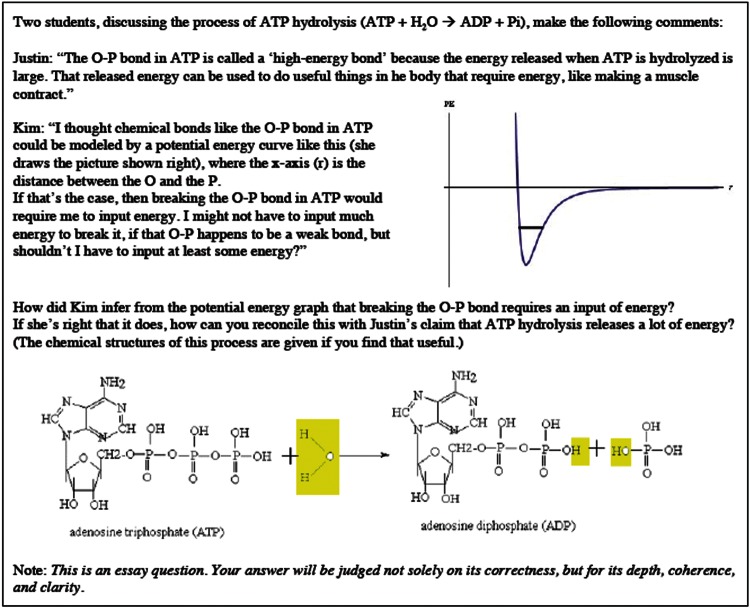
The first example is an essay question developed after we interviewed several students about their understanding of ATP as a “high-energy” molecule (see also Dreyfus et al., 2013a). We noticed that students were struggling to see how to make sense of thinking of ATP as containing a high-energy bond, while at the same time thinking about bonding as a
process that requires energy. The result was an essay question designed to probe students’ understanding of ATP (Figure 5).
Figure 5.
Essay question: Reconciling ideas about ATP and energy.
What makes this a level 3 task is that it explicitly brings two frameworks into interaction and asks students to make sense of the similarities and differences between them. The perspective represented by Justin is one that students will be familiar with from introductory biology, wherein the concept of ATP as an energy carrier is particularly useful. In that context, it is common to conceptualize ATP hydrolysis as an energy-liberating process in which the breaking of the relatively unstable O-P bond in the ATP helps explain the net release of energy from the overall reaction. It is for this reason that the bond is sometimes referred to as “high-energy” in biological contexts. Kim's statement introduces ideas from physics as an alternative lens to understand the chemical reaction. Her analysis focuses on the energetics of bonding, which provides a useful way to understand why breaking a bond requires an input of energy to move two atoms from a bound state with low potential energy to an unbound state with higher potential energy. The energy graph is included as a way to visualize the relationship between bound state and energy.
Several features of this task prompted us to classify it as level 3. First, it introduces students to two possible ways, one of which is more common in biology and the other of which is more common in physics, to conceptualize processes involving a net release of energy and asks them to make sense of the relationship between these two frameworks. Second, neither framework is privileged as correct by default. Finally, students are explicitly asked to consider each argument and to provide a justification for the utility of one or both frameworks. Instead of asking students to choose an answer that is “right” they are asked to “reconcile” the two frameworks. This is intended to signal to students that they need to do more than choose the correct answer from physics; they need to examine whether the biological and physical frameworks can make sense together.
The second level 3 task we present, like the worm problem, introduces the idea of using a simple model to reason about a biological phenomenon. The task explores the meaning of modeling a cell membrane as a capacitor (Figure 6).
Figure 6.
Membrane capacitance problem.
What makes this task level 3 is that it explicitly asks students to both reason with a simplified model and to consider the relevance of the model to the biological system. In Figure 6, part A, students are asked to reason with a simplified model to visualize what the electric field and the electrostatic potential both inside and outside the membrane would look like. Part B in Figure 6 introduces a revised model that builds back in some relevant biological detail by replacing the empty space in the first model with a constant dielectric and asks students to reason through how this change to the model would influence the system. Finally, in Figure 6, parts C and D, students are asked to reflect on the modeling approach and to examine the extent to which the simplifications made by the models are reasonable.
Both the ATP essay question and the membrane-modeling problem exemplify the degree of interaction of a level 3 task. In each, disciplinary perspectives from both physics and biology are represented, and each of those perspectives is modified by its interaction with the other. The ATP task problematizes the default conceptions about bond energy in the context of ATP hydrolysis from both physics and biology, while the membrane task asks students to consider the arguments for and against using a simple analogical model from physics to reason about a biological system.
We reiterate that these tasks were drawn from an initial run of this class and are in no way finished. Our intention is to present them as a way to help draw out and describe some of the different ways in which disciplines can interact in interdisciplinary tasks, not because we expect others to take these particular tasks as exemplary of any of these levels. To further make this point, we next present an example of how we have used this framework as a reflective tool to inform the design and revision of a specific task.
Using the Framework to Inform Task Revision
The utility of this framework lies not so much in its ability to characterize tasks, but as a tool that can help guide task creation and revision. As design research is focused on moving through an iterative process, we describe in this section how attending to this framework has helped us both reflect on the process and make intentional changes to increase the degree of interdisciplinary interaction in a task in the service of supporting the interdisciplinary learning objectives described above. In this stage of design research, we begin with the assumption that modifications to both particular prompts within a task and the general manner in which the task is framed for students can have significant impact on the degree to which core interdisciplinary learning objectives are met.
The problems and question prompts we examine in this section all take place in the same phenomenological context. Starting from the phenomenon has been a logical place to initiate task creation, and as a design team, we often found it productive to begin by identifying an interesting context in which we could see the potential for interaction between physics and biology. In principle, a wide range of phenomena have potential relevance to multiple disciplines. In this course, we have explored a range of scales from molecular to cellular to organismal and have drawn on questions from a range of biological subdisciplines, including cell biology, ecology, evolution, and medicine. Some conceptual contexts are richer than others in their capacity to elicit interesting interdisciplinary discussions, but we have found that the phenomenon itself does not necessarily predict the depth of interdisciplinarity of the resulting task. Instead, it has been careful attention to the questions that emerge from this context and to the conceptual frameworks and reasoning strategies that are relevant to answering those questions that have helped us integrate disciplinary perspectives in deeper and more meaningful ways.
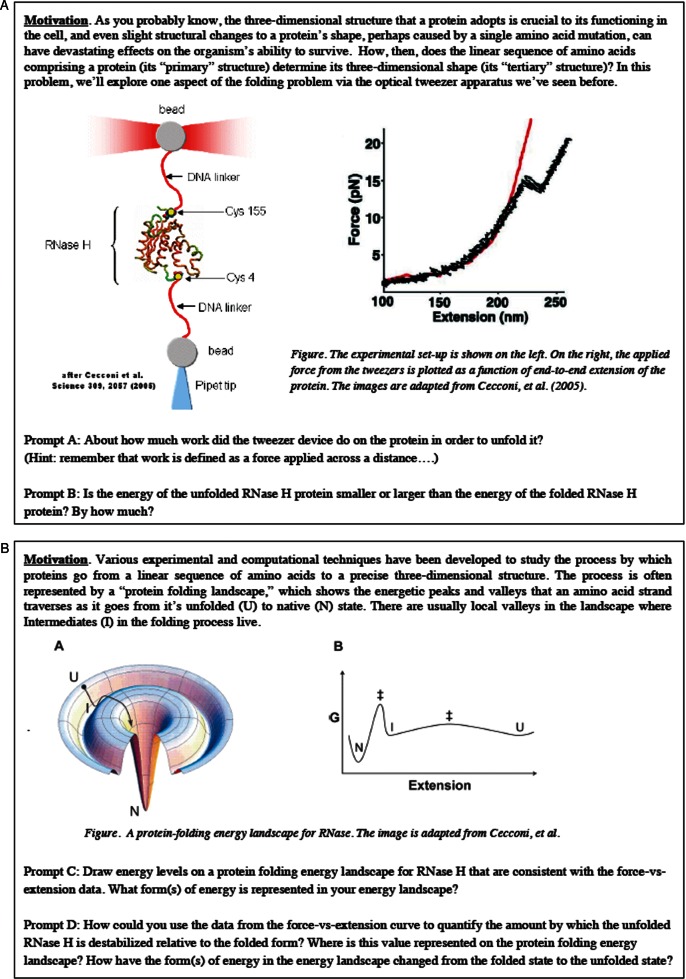
The phenomenon examined in this section is drawn from cutting-edge biophysics research and is therefore one that we felt would have substantial potential to support interdisciplinary learning objectives. The scenario we started from was an experimental apparatus in which a single protein molecule is connected via two DNA “handles” to polystyrene beads, one of which was trapped in the focus of a laser. This so-called optical tweezer arrangement (Figure 7A) is a powerful technique for exploring biophysical phenomena at the level of individual molecules and has been used extensively to study the mechanics of molecular machines (Bustamante, 2004), as well as thermodynamic and kinetic details of the protein-folding pathway (Cecconi et al., 2005). Moving the laser's focus results in the bead trapped in that focus moving as well, and the protein to which the bead is attached can be stretched, twisted, and manipulated with considerable precision. In this series of examples, we consider the case in which the distance between the two beads is steadily increased until, at a particular tension force, the protein unfolds, and the distance between the beads suddenly increases. The data from such a stretch are often represented in a force-versus-extension curve, as shown in Figure 7A. In the following sections, we present a series of prompts drawn from this example to illustrate how the same context can be used to support a range of interdisciplinary interactions.
Figure 7.
(A) Selected elements of the original protein-unfolding task. (B) Selected elements of the revised protein-unfolding task.
Starting at Level 1: Finding the Physics in a Biological Context.
In an initial iteration of task design, the experimental context was used as a backdrop against which students could engage with the work–energy theorem. Students first read some background on the experimental setup, which suggested that this apparatus could be used to gain insight about protein folding. The reason for framing the task in this way was to motivate students to acknowledge the biological authenticity of the exercise. Our students had heard of the protein-folding problem and were aware of its significance in biology, and we as instructors were aware of the use of the optical tweezers technology in single-molecule biophysics labs that were studying protein folding. We hoped to leverage this awareness on the part of our students to make the work–energy theorem seem meaningful and biologically interesting and to encourage broader use of a general physical principle in a microscale biological setting.
Then, students were presented with the graph in Figure 7A and asked to use it to calculate the amount of work required to unfold the protein, as shown in prompt A:
Prompt A: About how much work did the tweezer device do on the protein in order to unfold it? (Hint: remember that work is defined as a force applied across a distance…)
The work–energy theorem provides a way of relating changes in motion to ideas about force. It does so by introducing the idea that the work (force applied over some distance) done by all forces acting on a system is equivalent to the change in kinetic energy of that system, a measure of how much an object moves. This relationship can be used to calculate how much force is required to change the motion of an object by a particular amount. For students to calculate the work done by the tweezers in this prompt, they need only understand work as a force over a distance. In this case, the force provided by the tweezer apparatus is represented on the y-axis and the distance over which the force acts is represented on the x-axis as an increase in extension of the protein molecule. The work done by the tweezers during the unfolding process is therefore the area under the force-versus-extension curve over the portion of the plot where the unfolding occurs.
Typical of level 1, this question is situated in a phenomenological context that appears biological (it involves a protein), but does not substantively engage with biological ideas. The protein-folding backdrop was meant to be motivational, but the actual calculation of the work required to unfold the protein was in no direct or obvious way connected to the broader and richly complex protein-folding problem.
A second prompt asks students to consider the implications of the work done on the total energy of the protein:
Prompt B: Is the energy of the unfolded RNase H protein smaller or larger than the energy of the folded RNase H protein? By how much?
In this second prompt, students are meant to see that the force applied to unfold the protein constitutes work done, and therefore, a positive change in energy from the folded to unfolded states. However, it does not ask the students to consider where this energy goes, that is, it does not ask the students to decide whether the energy goes into the motion of the protein or some other structural change. It is possible to reason through this problem without thinking about the biology very much at all and without thinking carefully about the specific energy changes that result from the applied force. Thus, despite the potential richness of the context, the initial version of this task did not include very much interdisciplinary interaction.
Moving Toward Level 3: Examining the Relationship Between the Biology and the Physics.
In an effort to create a more deeply integrated task, we decided to bring in a more explicitly biological frame and consider how this frame interacted with the ideas foregrounded by the work–energy relationship. An important question that the interdisciplinary team of collaborators asked about the task was this: What are the biologically interesting question(s) and discussions that can emerge from this context and how do those questions interact with the physics ideas we have identified?
In answering this question, we were in part motivated by how our students responded to the initial version of this task. We observed a group of students reasoning through prompt B (Figure 7A) and noticed that some students spontaneously brought in ideas about energy and protein stability from their chemistry and biology courses. For example, Anya, faced with the question of whether the energy in the unfolded RNase H protein is smaller or larger than the energy of the folded RNase H protein, brings in the idea that stable states for proteins are more likely to occur and are therefore more favorable than other states. She reasons:
Anya2: They are asking us if the energy is the same. If we actually thought of a protein, and the energy of the folded and unfolded, you’d hope the folded is somehow favorable energetically speaking.
Anya: I’m just thinking. I think that the unfolded product is going to be higher energy. ’Cause if anything[,] the folded, the only way it folded in the first place is that somehow folding is favorable at one point.
In this short excerpt, Anya uses reasoning about protein stability to come to the conclusion that the unfolded protein must have higher energy than the folded protein, because the folded state is more likely, and therefore is the more stable one with lower energy.
This observation helped us restructure the task such that it would explicitly support an examination of the interaction between ideas about energy and protein stability and the relationship between work and energy. In service of this aim, we brought in a new representation (the protein-folding energy landscape in Figure 7B) that helped focus the task on an important question in biology: What does it mean for a protein to be in a stable state? That protein folding results in a decrease in the free energy of the protein and its surroundings is a concept that students are likely to be familiar with from biology. The diagram is meant to bring in this prior knowledge and draw students’ attention to this idea of protein stability. Our intention was then to help students build a connection between ideas related to the energetic stability of proteins and the work–energy theorem. This intention is reflected in the two prompts below:
Prompt C: Draw energy levels on a protein-folding energy landscape for RNase H that are consistent with the force-vs-extension data (shown in Figure 7A). What form(s) of energy is represented in your energy landscape?
Prompt D: How could you use the data in the force-vs-extension curve (Figure 7A) to quantify the amount by which the unfolded RNase H is destabilized relative to the folded form? Where is this value represented on the protein-folding energy landscape? How have the form(s) of energy in the energy landscape changed from the folded state to the unfolded state?
The use of the work–energy relationship is intended to inform the students’ understanding of protein biology. To say that a protein is in a “stable” energy state means that, in order to move it out of this state, energy would need to be added by doing work on the molecule. Bringing the biological context of protein energy landscapes and protein stability into contact with the physics in the problem may also enhance the students’ understanding of the work–energy relationship. As we mentioned above, the ability of external work to cause a change in an object's kinetic energy is often the only context in which work is explored in traditional introductory physics problems. However, in this task, students encounter a situation in which the work done on the protein does not impact the translational motion, but rather the shape, and therefore the stability, of the protein. Because the internal structure of a biological molecule is crucial to its functioning in a way that may not be true for a nonbiological system (particularly for systems typically explored in a standard introductory physics problem), it is perhaps more apparent in this context than in traditional physics contexts that structural changes must be considered. The work done on the protein changes the protein from a more stable (folded) to a less stable (unfolded) form. Focusing the task on protein stability forces students to consider relationships among forms of energy that they might not typically encounter in a traditional work–energy physics task, thus providing the students an opportunity to refine their ideas about the relationship between work and energy.
The full revised task asks the students to reconcile three distinct representations of the protein-folding process: 1) the physical picture of what the protein and DNA handles look like at any particular moment, 2) the energy landscape (energy-vs-reaction coordinate) as the protein folds/unfolds, and 3) the force-versus-extension curve. By prompting the students to move between these representations repeatedly, the new version calls upon reasoning strategies that cross disciplinary boundaries. The revised task seeks to build the sort of multirepresentational competency that is important in both physics and biology.
Reflection on the process of designing and revising this task revealed the following: Finding an interesting and potentially motivating interdisciplinary context was a logical place to start, but such a choice does not by itself ensure that the reasoning that students will do in this context will be interdisciplinary. To support increased interaction between the disciplines, we considered questions/concerns/aims authentic to each discipline. That is, we asked: What are the features of this context that each discipline might try to elucidate? The aim of making sense of the relationships among force, distance, work, and energy is legitimate in the context of physics, while understanding the idea that folded proteins are somehow more stable than unfolded proteins is an authentic biological concern. Focusing on these aims helped us identify the relevant conceptual frameworks from each discipline and look for places where they could potentially overlap. Finally, this process allows students to be critical of ideas typically taken for granted by each discipline in isolation, for example, the idea that the work–energy theorem is only useful for relating work to motion or the idea that the stability of a folded protein can be taken as a given without careful consideration of the factors that determine stability.
DISCUSSION AND IMPLICATIONS
In the preceding sections, we presented a framework for describing differences in the nature and depth of interdisciplinary interaction embedded in a task prompt and illustrated how it could be used to inform task design and revision. We now articulate how these differences in the nature and depth of interdisciplinary interaction within a task can have implications for the task's potential to support or impede various interdisciplinary learning objectives. We present the alignment between tasks and learning objectives as design conjectures that expose important research questions about student learning to be pursued in future work. We share specific student responses to previously introduced tasks to elucidate the factors that deserve further investigation, and we conclude by arguing for the inclusion of level 3 tasks in interdisciplinary courses based on their unique potential to address particular learning objectives that we highly value.
Connecting Task Levels and Interdisciplinary Learning Objectives
One of the main uses of the framework we have outlined is as a means for analyzing how the degree of interdisciplinarity of a task relates to intended learning objectives of interdisciplinary education. We see important differences in the potential for each level to support different interdisciplinary learning objectives. This, of course, does not mean that any particular task will result in learning for all or even some students. Nevertheless, this framework can help curricula designers and educators reflect on the interdisciplinary learning objectives they have for their students and to make intentional choices that align task design with those intended objectives. It can also help researchers make explicit hypotheses about how tasks can support interdisciplinary learning that can be opened to empirical investigation.
Level 1 Tasks Offer Limited Opportunities to Support Interdisciplinary Learning Objectives.
We hypothesize that level 1 tasks, because they involve concepts and reasoning primarily associated with one discipline and only limited attention to a second discipline, are limited in their ability to support most interdisciplinary learning objectives. While these tasks point to phenomena that have the potential to be explored by multiple disciplines, they do not explore specific questions, aims, or conceptual frameworks that span the disciplines. For example, the fish buoyancy problem (Figure 2) does not explore how buoyant force is relevant for aquatic organisms. It is possible that students might begin to make some of these connections for themselves, but the tasks do not explicitly support such bridging.
Nevertheless, level 1 tasks, because they at least point to a possible connection between the disciplines, could function to begin to help students develop an appreciation or at least open-mindedness about cross-disciplinary relevance. By situating physics problems in biological contexts, students might begin to see physics as a discipline that is in some way relevant to biology. Encountering a variety of problems like this could help students see that there exist a broad range of phenomena for which ideas from more than one discipline could have potential relevance.
Alternatively, level 1 tasks may work against other interdisciplinary learning objectives, such as conceptual coherence. Students may see biology in the tasks, but see this biology as a superficial “hook” that does not bear any relation to the reasoning expected in the task. Students may feel the extensive prior knowledge they may have about the biological scenario is not being leveraged in these tasks, particularly if the tasks do not justify or ask students to justify why ignoring particular contextual features of the scenario is appropriate for the problem at hand. In this way, level 1 tasks could communicate that the biology in the task is something to be ignored and gets in the way of physics sense-making. This could prevent students from developing conceptual coherence and contribute to negative affect if students feel frustration at seeing the biology as an extra distraction.
There are some indications from our own course that level 1 tasks can, in fact, promote negative feelings about the relevance of connections between the disciplines. Consider the following quote from a student interview in which Camille was reflecting on the exam that contained the fish buoyancy problem:
Interviewer: Did you feel like in this physics test there was very much biology?
Camille: Uh, definitely not in this one (points to fish buoyancy problem in Figure 2). I mean [the instructor] even said it in class, he's like, I thought you guys would get tripped up on the fish problem because you would think about like their fish bladders and stuff, I don't know. But because we are in a physics class we just automatically think physics. When I thought about this I didn't think of them as fish, I just thought of them as A and B and C, like the little blocks that we have been seeing the whole time.
I think all of us have had so many problems where it's like physics problems, and we have the blocks floating and just think about the blocks themselves. Because if you think about it as a fish you might get caught up in the fact that it has an air bladders and like the fact that they are different shapes and sizes and stuff, but if you just think of it like that [as blocks] it makes it a lot simpler.
From her response, it is clear that this student did not see the inclusion of fish as relevant to the problem. Instead, she describes how she actively ignored the biological context and simply thought of the fish as blocks, so she could concentrate on solving the physics problem. Framed in this way, the potential to make connection to the biology seems more like a distraction than a place to see the value or relevance of interdisciplinarity.
Despite the limited potential to support interdisciplinary learning objectives, there are still good reasons that instructors might want to include level 1 tasks in IPLS courses. These tasks can help students develop basic physics ideas that are both important in their own right and may also be necessary precursors from which to build up to more complex interdisciplinary problems. Furthermore, if interdisciplinary tasks at this more superficial level are embedded in the context of an entire course that also includes tasks that engage students with higher levels of interdisciplinary connection, they may be less likely to trigger negative attitudes about relevance.
Level 2 Tasks Begin to Support Interdisciplinary Learning Objectives.
We hypothesize that level 2 tasks, because they explore the implications of applying ideas and techniques from one discipline to another, have a greater potential to support a range of interdisciplinary learning. For example, the arteriosclerosis problem (Figure 3) has the potential to help students build connections between the idea of “blood pressure” from a medical context and the concept of “pressure drop” from the HP model, thereby extending and deepening their understanding of blood pressure and how it is related to the size of the arterial opening. It can also introduce students to the importance of quantifying such relationships. The r4 relationship from the HP model shows why one might consider “small” arterial clogging can have catastrophic effects.
The earthworm problem (Figure 4) presents an opportunity for students to develop reasoning strategies applicable to both disciplines. Strategies such as dimensional analysis, solving systems of equations, phase–space analysis, and reasoning from graphical representations have been well integrated into physics training, and while these strategies are increasingly common among expert biologists, they are still relatively rare for undergraduate biology students. Level 2 tasks that emphasize the utility of such strategies in biological contexts have the potential to extend the repertoire of strategies students are able and willing to bring to problem solving across a range of disciplinary contexts. If students begin to see similar strategies applied in different contexts, they may begin to see the general utility of these techniques rather than viewing them as confined to particular courses or disciplines.
Further, if students encounter increased conceptual coherence and are able to see the relevance of interdisciplinary reasoning strategies, we might also expect to see more favorable shifts in their attitudes toward interdisciplinary integration. Explicitly asking students to explore the ways in which physics can be applied to biological contexts may lead students to see the utility of integrating disciplines. For these reasons, level 2 tasks play an important role in IPLS and similar courses, and tasks like these seem to be fairly common in courses of this type.
However, the authenticity of the interdisciplinary interaction of such tasks is potentially limited by the unidirectionality of the impact. Level 2 tasks can give the impression that the ideas and concerns from one discipline are being imposed upon the other. Because care has not been taken to make clear why this connection is truly relevant to the second discipline, it is possible that students might still feel dismissive of such tasks. If physics is viewed as something that can be applied to biology but does not address concerns that have originated from within biology, this may reduce the perceived authenticity of such tasks for students.
Ultimately, how a student interprets the authenticity of a task will be the result of an interaction between the task itself, the larger course context, and his or her prior experiences.
Students are likely to enter courses with a range of different expectations and attitudes about the utility of interdisciplinary reasoning. For those who have strong negative attitudes about the utility of integrating ideas and techniques, simply showing that a set of ideas from one discipline can be applied to the other may not be enough. These students might need to see more examples of tasks in which this integration is driven by an important question or idea from within biology or in which the connections between the physics and biology are more explicitly examined and reflected upon.
Level 3 Tasks Support a Range of Interdisciplinary Learning Objectives.
We hypothesize that level 3 tasks can potentially support many of the important learning objectives of interdisciplinary science instruction. First, they can provide opportunities for students to meaningfully connect their conceptual frameworks. This potential is evident in the ATP essay question (Figure 5), which takes two ideas that are typically segregated by course and asks students to connect them. Doing so creates the possibility of bridging ideas about ATP as somehow storing energy with an understanding of the energetics of bonds. The aim is that students emerge from such a task with a more coherent framework for thinking about energy by linking together ideas about ATP hydrolysis as a reaction that releases energy with an understanding of the energetics of bond breakage and energy release.
In addition, this task creates opportunities for students to reflect on the nature and utility of the different conceptual frameworks they encounter in their different science courses. In the ATP essay, students have the opportunity to consider how to reconcile two seemingly different ways of reasoning about the bonds in ATP (see Dreyfus et al., 2013a, for a further discussion of this reconciliation). Asking students to do this potentially encourages them to begin to develop an appreciation for why these frameworks seem different in the first place. Instead of positioning disciplines as presenting conflicting information, level 3 tasks can create opportunities for students to develop a deeper understanding of areas of overlap and areas of disunity. This kind of understanding of scientific knowledge is integral to adaptive expertise. An adaptive expert has an understanding of the importance of context and can make decisions about what conceptual framework will help him or her make the most progress as opposed to reasoning within the default framework of a single discipline.
Second, level 3 tasks can help students develop and see the broad utility of scientific reasoning strategies and problem-solving techniques. The membrane capacitance task (Figure 6) introduces students to some basic ideas about scientific modeling as a decision-making process. Rather than presenting a model as the default, it presents modeling as a strategy of making choices about what assumptions and simplifications are appropriate, and at least begins to invite students to participate in this decision-making process. Consider, for example, some of the responses students gave to part D of the membrane problem (Figure 6), which asked them to reflect on whether the capacitor is a “reasonable starting point” for a membrane:
Student A: Yes, because our membranes are filled with fluid, not empty space. If we models cells with solely empty space one wouldn't be able to see the true complexity of an electric field and the interactions with the environment.
Student B: Sure, the membrane is “reasonably” infinite especially because the membrane is spherical (no edge effects) and the membrane will be made of some material with a dielectric.
Student C: Yes, if nothing else it introduces the ideas of capacitance and charge separation, concepts on which things like the Nernst potential across neuronic membranes are built.
In these responses, students are offering their justification for whether a capacitor is a good model of a cell membrane and pointing to specific reasons from the biological context to support their claims. Student A argues that the model that includes the dielectric more accurately reflects the complexity of the biological phenomenon. Student B addresses the assumption that a membrane can be modeled as an infinite sheet and concludes that this is legitimate due to the sphericity of the membrane. And Student C uses this question to reflect on how this model connects to more complex models relevant to nerve cell signaling. The prompt itself is short and is not the main focus of the problem, and so it is not particularly well designed to elicit students’ ideas about modeling. Nevertheless, even these brief answers reveal the potential for tasks of this type to scaffold students’ adaptive expertise around modeling at the interface of physics and biology.
A follow-up interview with Fatima, conducted after this exam, provides a more extended look at one student's reasoning about this problem:
Fatima: Oh, I said it's reasonable because um nothing is really—there is no empty space in the body. It's going to be essentially just water or different ionic concentrations. So you are not really explaining the complexity with just modeling it with empty space. You need to at least put some fluid inside.
Interviewer: When you go to think about whether or not that model is reasonable, what are the kinds of things you think about there?
Fatima: Um. Well I guess in terms of the membrane, I immediately went to the cellular aspect of things and just like what exists in the body or what is in between cells and how are they like changing in terms of … how the cells are interacting with the environment and like just trying to keep it simple. But you also need to incorporate some of the more complex aspects, which I mean filling it with something with a constant dielectric constant, um isn't that complicated, but just thinking about it in terms of that so that once you do get to more complicated models you are not just like, oh there is only one—like you have the two sheets of charge and then there is nothing else going on, which is very misleading I think.
The student, reflecting on her response, demonstrates a sophisticated process of comparing the situation she is intended to be modeling with the simplified model. She observes that there is not empty space in the body and uses this as a justification for making the choice to include a dielectric in the capacitor instead of a vacuum (empty space). She also demonstrates the ability to reflect on the broader context of modeling, acknowledging that models can incorporate different levels of complexity, and that if one were investigating a more complicated model, this simplification would be particularly problematic.
We can imagine level 3 tasks that do a better job of supporting this kind of expertise by asking students to make and justify modeling decisions and to explicitly consider how and when different disciplines would make different kinds of modeling choices. Asking students to participate in the process of making decisions about developing models makes the choices and assumptions of the disciplines more transparent and invites a critical analysis of the simplifications.
Our expectation is that tasks in which students are given the opportunity to compare, contrast, and explore the utility of alternative frameworks, as well as take responsibility for making and justifying choices about their own reasoning, have the potential to support metacognitive learning goals. Once again, it is the capacity for level 3 tasks to support this kind of metacognitive reflection that is part of what it means to be an adaptive expert.
Open Questions for Interdisciplinary Design Research
In the above discussion, we presented a series of conjectures about the potential of tasks designed at each of these three levels to support different interdisciplinary learning objectives. Within the context of design research, these conjectures suggest testable research questions that can guide education research focused on interdisciplinary learning. We list below some possible ways to translate the design conjectures we have articulated into more specific research questions that we plan to investigate. Our hope is that other researchers interested in supporting interdisciplinary learning will find these useful as well.
- In what ways do tasks of different levels support conceptual coherence?
- To what extent do level 1 tasks work against interdisciplinary conceptual coherence learning objectives—supporting a “silo-ing” of conceptual resources based on disciplinary domains? How might this effect vary in different course contexts?
- Do level 3 tasks increase students’ willingness to bring in and reconcile ideas from a range of disciplinary perspectives?
- In what ways do tasks support the development of scientific reasoning strategies?
- Do level 2 or level 3 tasks promote development of competencies/reasoning strategies that are important across multiple disciplines? How many tasks like this must students encounter in the context of a course?
- Do level 3 tasks help students develop the ability to make, justify, and challenge different approaches for reasoning about a problem?
- In what ways do tasks at different levels support the development of an appreciation of or open-mindedness about the relevance of one discipline for another?
- Do students see the “biological backdrops” of level 1 tasks as superficial, bearing no importance on the reasoning that is expected?
- Do students perceive level 1 tasks as suggesting their extensive prior knowledge about these biological phenomena is not useful for reasoning (without justification)?
- Does engagement with level 2 or level 3 tasks positively shift students’ attitudes and expectations about interdisciplinarity?
- In what ways can tasks be designed to support the development of adaptive expertise?
- Can level 3 tasks help students learn to function like adaptive experts? If so, what particular features of such tasks are important? And how often must students encounter these kinds of tasks?
Answering these questions will require researchers to intentionally design tasks so they align with particular learning objectives and to develop ways of measuring whether those objectives have been met. While we do not address the issue of assessment in this paper, in our experience, understanding the nuances of how a task can or cannot support a particular learning objective must begin with detailed qualitative analysis of students working through the task. Only when we have a qualitative description of how students are likely to engage with a particular task can we begin to develop more quantitative instruments to assess its success (e.g., Dreyfus et al., 2013a). In design research, understanding how task features and learning outcomes might be aligned is a necessary precursor to developing more standardized measures. More qualitative work describing how students respond to interdisciplinary tasks of different types is needed to move our understanding of interdisciplinary learning forward.
CONCLUSIONS
A Vision for a More Integrated Science Education Instruction at the Undergraduate Level
We are caught between demands to transcend the boundaries and perspectives of the separate disciplines, in order to obtain more complete understanding, and demands to ground inquiry in the disciplines…. This is the locus of interdisciplinary study, but it is caught uncomfortably between these two conflicting demands, unwilling to concede wholly to either. Both the impetus and resistance to interdisciplinarity will be with us for the foreseeable future. (Paxson, 1996, p. 80)
Our analysis of interdisciplinary tasks in this IPLS course has helped us see the potential value of increased integration in introductory science curricula. As Paxson noted, we must balance the goal of transcending disciplinary boundaries with the goal of grounding experiences in disciplinary practices. Design research, with its focus on bringing learning objectives and learning outcomes into better alignment, is particularly well-suited to attending to this balance. As we have demonstrated throughout this paper, even at this early stage in design research, attending to the interdisciplinary nature of tasks has given us insight into how features of these tasks support or impede our stated learning objectives. It seems important that students appreciate the variety of conceptual frameworks and reasoning strategies that scientists have at their disposal and recognize that decisions about how and when to use these are choices that vary with context rather than default properties of disciplines.
For students planning to pursue careers in science, these lessons are potentially even more important. The typical undergraduate science experience rarely provides students with the opportunity to understand the significance (or lack of significance) of disciplinary differences. In some cases, these differences are useful and represent the different epistemological orientations of the disciplines. In other cases, the distinction is artificial. That introductory biology courses have historically not included quantitative techniques, while introductory physics courses have tended to avoid the complexities inherent in “real” systems, does not necessarily reflect a lack of utility of these approaches in either of these disciplines. Thus, we would do well to prepare both future physicists and future biologists to be able to recognize those contexts in which a particular set of ideas or reasoning techniques will help them make intellectual progress. That is, one of the important roles for interdisciplinary education efforts is to help students develop the kind of flexible adaptive expertise that will prepare students to solve a range of complex problems and work with scientists trained from a variety of perspectives as is increasingly becoming the case in cutting-edge research fields. Increasingly, training future scientists to reason like adaptive, as opposed to routine, experts is an important goal of science education.
If we take this goal seriously, then we need to put more effort into designing tasks intended to help students develop this sort of expertise. We also need to increase our research efforts around interdisciplinary education to explore whether and in what ways we are able to support this kind of learning. The framework we have presented can support both of these aims of design research. It can be used as a tool to help educators and curriculum designers reflect on the alignment between interdisciplinary learning objectives and the tasks they have designed. It can also help researchers articulate and ultimately test hypotheses about how particular tasks can support or impede interdisciplinary learning. Ultimately, this combination of intentional design, theory development, and empirical testing can help advance the goal of a more integrated and interdisciplinary introductory science curriculum.
ACKNOWLEDGMENTS
We thank Ben Dreyfus and Arnaldo Vaz for valuable contributions to the thinking represented in this article. We appreciate the contribution of Joe Redish, the instructor of the course in this paper, and Todd Cooke, who contributed to the designing of many of these tasks. We are particularly grateful to the Biology Education Research Group at the University of Maryland for their help in conceptualizing the interdisciplinary framework presented here. We also thank the University of Maryland Physics Education Research Group for their valuable feedback on the arguments presented in this paper. Finally, we thank two anonymous reviewers whose insightful suggestions improved the clarity of the manuscript. This material is based on work supported by the National Science Foundation (NSF) under a Graduate Research Fellowship (DGE 0750616) and NSF-TUES DUE 11-22818. This work is also supported by an HHMI NEXUS grant. Any opinions, findings, and conclusions or recommendations expressed in this publication are those of the author(s) and do not necessarily reflect the views of the NSF or the HHMI.
2All student names are pseudonyms.
This research involved human subjects, and was approved in advance by the University of Maryland Institutional Review Board, protocol #11-0431.
REFERENCES
- American Association for the Advancement of Science 2010. Vision and Change in Undergraduate Biology Education: A Call to Action.
- Association of American Medical Colleges–Howard Hughes Medical Institute . Scientific Foundations for Future Physicians: Report of the AAMC–HHMI Committee. Washington, DC: AAMC; 2009. [Google Scholar]
- Bialek W, Botstein D. Introductory science and mathematics education for 21st-century biologists. Science. 2004;303:788–790. doi: 10.1126/science.1095480. [DOI] [PubMed] [Google Scholar]
- Bransford JD, Brown AL, Cocking RR. How People Learn: Brain, Mind, Experience, and School, expanded edition. Washington, DC: National Academies Press; 2000. [Google Scholar]
- Brown AL. Design experiments: theoretical and methodological challenges in creating complex interventions in classroom settings. J Learn Sci. 1992;2:141–178. [Google Scholar]
- Bustamante C. Of torques, forces, and protein machines. Protein Sci. 2004;13:3061–3065. doi: 10.1110/ps.041064504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cecconi C, Shank EA, Bustamante C, Marqusee S. Direct observation of the three-state folding of a single protein molecule. Science. 2005;309:2057–2060. doi: 10.1126/science.1116702. [DOI] [PubMed] [Google Scholar]
- Cobb P, Confrey J, DiSessa AA, Lehrer R, Schauble L. Design experiments in educational research. Educ Res. 2003;32:9–13. [Google Scholar]
- Collins A, Joseph D, Bielaczyc K. Design research: theoretical and methodological issues. J Learn Sci. 2004;13:15–42. [Google Scholar]
- diSessa AA. Why “conceptual ecology” is a good idea. In: Limon M, Mason L, editors. Reconsidering Conceptual Change: Issues in Theory and Practice. Boston: Kluwer Academic; 2002. pp. 29–60. [Google Scholar]
- Dreyfus BW, Geller BD, Sawtelle V, Svoboda J, Turpen C, Redish EF. Students’ interdisciplinary reasoning about “high energy bonds” and ATP. In: 2012 Physics Education Research Conference, AIP Conference Proceedings, vol. 1513, New York: AIP. 2013a:122–125. [Google Scholar]
- Dreyfus BW, Redish EF, Watkins J. Students’ views of macroscopic and microscopic energy in physics and biology. In: 2012 Physics Education Research Conference, AIP Conference Proceedings, vol. 1513, New York: AIP. 2013b:179–182. [Google Scholar]
- Dunbar K. How scientists think in the real world: implications for science education. J Appl Dev Psychol. 2000;21:49–58. [Google Scholar]
- Ford MJ, Forman EA. Redefining disciplinary learning in classroom contexts. Rev Res Educ. 2006;30:1–32. [Google Scholar]
- Gross LJ, Brent R, Hoy R. Points of view: the interface of mathematics and biology. Cell Biol Educ. 2004;3:85–92. [Google Scholar]
- Gupta A, Danielak BA, Elby A. Understanding students’ difficulties in terms of coupled epistemological and affective dynamics. In: Proceedings of the 2010 IEEE Frontiers in Education Conference, Red Hook, NY: Curran Associates. 2010:S3G-1–S3G-6. [Google Scholar]
- Hake RR. Interactive-engagement versus traditional methods: a six-thousand-student survey of mechanics test data for introductory physics courses. Am J Phys. 1998;66:64–74. [Google Scholar]
- Hall KL. Examining the effects of students classroom expectations on undergraduate biology course reform. Dissertation, University of Maryland, College Park. 2013 [Google Scholar]
- Hall KL, Watkins JE, Coffey JE, Cooke TJ, Redish EF. Examining the impact of student expectations on undergraduate biology education reform. 2011 Paper presented at the American Educational Research Association National Meeting, held April 2011 in New Orleans, LA. [Google Scholar]
- Hatano G, Inagaki K. Two courses of expertise. In: Stevenson HW, Azuma H, Hakuta K, editors. Child Development and Education in Japan. New York: Freeman; 1986. pp. 262–272. [Google Scholar]
- Ivanitskaya L, Clark D, Montgomery G, Primeau R. Interdisciplinary learning: Process and outcomes. Innov High Educ. 2002;27:95–112. [Google Scholar]
- Knight JK, Wood WB. Teaching more by lecturing less. Cell Biol Educ. 2005;4:298–310. doi: 10.1187/05-06-0082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knorr-Cetina K. Epistemic Cultures: How the Sciences Make Knowledge. Cambridge, MA: Harvard University Press; 1999. [Google Scholar]
- National Research Council. BIO2010: Transforming Undergraduate Biology Education for Future Research Biologists. Washington, DC: National Academies Press; 2003. [PubMed] [Google Scholar]
- Nersessian NJ. Model-based reasoning in conceptual change. In: Magnani L, Nersessian N, Thagard P, editors. Model-Based Reasoning in Scientific Discovery. New York: Kluwer Academic/Plenum; 1999. pp. 5–22. [Google Scholar]
- Nersessian NJ. The cognitive basis of model-based reasoning. In: Carruthers P, Stich S, Siegal M, editors. The Cognitive Basis of Science. Cambridge, UK: Cambridge University Press; 2002. pp. 133–153. [Google Scholar]
- Paxson TD. Modes of interaction between disciplines. J Gen Educ. 1996;45:79–94. [Google Scholar]
- Redish EF, Cooke TJ. Learning each other's ropes: negotiating interdisciplinary authenticity. CBE Life Sci Educ. 2013;12:175–186. doi: 10.1187/cbe.12-09-0147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redish EF, Hammer D. Reinventing college physics for biologists: explicating an epistemological curriculum. Am J Phys. 2009;77:629. [Google Scholar]
- Redish EF, Saul JM, Steinberg RN. Student expectations in introductory physics. Am J Phys. 1998;66:212–224. [Google Scholar]
- Sternberg R. What is an “expert student”? Educ Res. 2003;32:5–9. [Google Scholar]
- Stevens R, Wineburg S, Herrenkohl L, Bell P. Comparative understanding of school subjects: past, present, and future. Rev Educ Res. 2005;75:125–157. [Google Scholar]
- Watkins J, Coffey JE, Redish EF, Cooke TJ. Disciplinary authenticity: enriching the reforms of introductory physics courses for life-science students. Phys Rev ST Phys Educ Res. 2012;8:010112. [Google Scholar]
- Wong SL, Hodson D. From the horse's mouth: what scientists say about scientific investigation and scientific knowledge. Sci Educ. 2009;93:109–130. [Google Scholar]