Equivalent Intrinsic Noise, Sampling Efficiency, and Contrast Sensitivity in Patients With Retinitis Pigmentosa

Abstract

Purpose.

To determine the relationships among equivalent intrinsic noise (N_eq), sampling efficiency, and contrast sensitivity (CS) in patients with retinitis pigmentosa (RP), where N_eq is an estimate of the amount of noise within the visual pathway and sampling efficiency represents the subject's ability to use stimulus information optimally.

Methods.

Participants included 10 patients with RP aged 10 to 54 years, who had visual acuities of 20/40 or better, and 10 visually normal control subjects aged 22 to 65 years. CS was measured for 2-cycles-per-degree Gabor patch targets presented in the absence of noise (CS₀) and in five levels of noise spectral density. Data were fit with a standard linear amplifier model, which provided estimates of N_eq and sampling efficiency.

Results.

CS₀ for the patients ranged from normal to as much as a factor of 3 below the lower limit of normal. All 10 patients had abnormally high N_eq, including two patients with normal CS₀. In comparison, only two patients had lower-than-normal sampling efficiency, and these two patients also had below-normal CS₀. Log CS₀ for the patients was correlated significantly with log N_eq (r = −0.80, P < 0.05), but not with log efficiency (r = 0.54, P = 0.11).

Conclusions.

Low CS was associated with elevated intrinsic noise in this group of RP patients, but even patients with normal CS had elevated noise levels. The results suggest that CS measurement in both the presence and absence of luminance noise can provide important information about visual dysfunction in RP patients.

This study demonstrated that patients with retinitis pigmentosa have abnormally high levels of equivalent intrinsic noise, which are correlated significantly with their contrast sensitivity losses.

Introduction

Retinitis pigmentosa (RP) refers to a heterogeneous group of inherited retinal diseases characterized functionally by night blindness, visual field restrictions, and abnormalities in the electroretinogram.¹ The functional abnormalities are typically most pronounced in the peripheral visual field, but foveal function can also be affected, manifested clinically as a reduction in visual acuity.^2–4 Additionally, patients with RP can have low foveal contrast sensitivity (CS),^5–7 which is typically correlated significantly with their visual acuity^8,9 and visual field areas.⁸

A number of potential explanations for the deficits in foveal function in RP patients have been investigated and discounted, including a reduced quantal catch (the “dark glasses” model), spatial sampling irregularities due to photoreceptor dropout, and elevated intrinsic blur due to a loss of high spatial frequency analyzers.^7,10,11 A possible explanation for the low foveal CS in patients with RP that has not yet been evaluated is an abnormally high level of noise within the visual system. It has been proposed, for example, that most retinal diseases impair visual function by increasing the level of noise within the visual pathway.¹² Nevertheless, a study of four patients with age-related macular degeneration who had low CS found that only one patient had an abnormally high level of internal noise.¹³ Therefore, the extent to which elevated internal noise accounts for the abnormal CS of RP patients remains unclear.

The amount of noise within the visual pathway can be evaluated using the “equivalent input noise method.” According to this approach, CS measurements are made in the presence and absence of additive white luminance noise. The data are then analyzed within the context of a model of human performance in noise. A commonly used model is the linear amplifier model (LAM), which factors performance into two independent components: (1) equivalent intrinsic noise, which is an estimate of the amount of noise within the visual pathway; and (2) sampling efficiency, which represents the subject's ability to make use of stimulus information relative to an ideal observer.¹⁴ The present study used the equivalent input noise approach and the LAM to investigate the relationships among equivalent intrinsic noise, sampling efficiency, and CS in patients with RP.

Methods

Subjects

Ten patients with RP (three males and seven females, aged 10–54 years) participated in the study. No patient had an atrophic-appearing macular lesion or more than a minimal cataract in the tested eye, based on clinical examination. The Table gives the patients' ages, inheritance patterns, logarithm of the minimum angle of resolution (logMAR) visual acuities, Pelli-Robson letter contrast sensitivities, and horizontal diameters of the visual field (VF) obtained with a Goldmann II/4e target. The characteristics given in the Table are for the tested eye, which was selected at random, but the fellow eye had similar characteristics. VF diameter was correlated significantly with logMAR visual acuity (r = −0.84, P < 0.05), consistent with previous research,⁸ but there was no significant correlation between VF diameter and Pelli-Robson letter contrast sensitivity (r = 0.19, P = 0.63). By optical coherence tomography (OCT), six patients had a normal macula, two patients (nos. 8 and 10) had extrafoveal patchy losses of the inner segment ellipsoid region, and two patients (nos. 1 and 6) had slight extrafoveal microcystic changes, but none of the 10 patients had an epiretinal macular membrane.

Table.

Subject Characteristics

AD, autosomal dominant; AR, autosomal recessive; ISO, isolated; USH2, Usher syndrome type II; VA, visual acuity; P-R CS, Pelli-Robson letter contrast sensitivity; VF, visual field horizontal width using a Goldmann II/4e target.

Values of equivalent intrinsic noise and sampling efficiency from the patients with RP were compared with those of 10 visually normal control subjects, aged 22 to 65 years, who had best corrected visual acuities that were 0.04 logMAR or better and normal Pelli-Robson letter CS. The mean age of the control subjects was not significantly different from that of the patients (t = 1.03, P = 0.32). The study conformed to the tenets of the Declaration of Helsinki and the experiments were approved by an institutional review board at the University of Illinois at Chicago. Written informed consent was obtained from each subject prior to testing.

Stimuli and Instrumentation

The instrumentation has been described in detail elsewhere.¹⁵ In brief, stimuli were generated by a Macintosh G4 computer and were displayed on an NEC monitor (FE2111SB) with a screen resolution of 1280 × 1024 and an 85-Hz refresh rate, driven by a video card with 10-bit digital to analog resolution (ATI Radeon 9000 Pro; Advanced Micro Devices, Sunnyvale, CA). The monitor, which was the only source of illumination in the room, was viewed monocularly through a phoropter with the subject's best refractive correction. A 3.0-mm artificial pupil mounted on the eyepiece of the phoropter was used to control the retinal illuminance. The luminance values of the display were derived from a linearized lookup table, which was calibrated with a photometer (Minolta LS 110; Konica Minolta, Tokyo, Japan). The temporal characteristics of the display were confirmed using an oscilloscope and photocell. The experiments were written in a numerical computing environment (MATLAB; MathWorks, Natick, MA) using the Psychophysics Toolbox extensions.¹⁶

The test stimulus was a 2-cycle-per-degree Gabor patch (i.e., Gaussian-windowed sinusoidal grating), subtending 1.7°. Letter optotypes, which are broad-band in spatial frequency content, can complicate the interpretation of contrast sensitivity measurements,¹⁷ so frequency-limited Gabor patch stimuli were used to ensure that the same spatial frequency information mediated contrast sensitivity for the patients and the controls at all levels of external noise. The Gabor patch was presented in sine phase either in the center of a uniform field with a luminance of 50 cd/m² or in the center of a noise field of the same mean luminance. The contrast (C) of the Gabor patch was defined as Weber contrast:

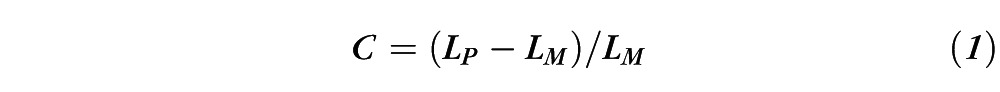where L_P was the peak luminance of the Gabor patch in cosine phase and L_M was its mean luminance.

The noise field, which covered an area that was approximately 1.5 times larger than the Gabor patch, consisted of independently generated square checks with luminances drawn randomly from a uniform distribution. Each noise check subtended 0.083° by 0.083°, which corresponds to six noise checks per cycle of the Gabor patch, a value consistent with that used by others.¹² The check duration was 0.012 seconds (1 video frame). The noise spectral density (N) ranged from 0 to 1 × 10⁻⁵ deg²/s in 0.5 log unit steps and was computed as the product of the noise check area, check duration, and the root mean square contrast of the noise check squared.¹⁸

As illustrated in Figure 1, the target duration was 106 ms and the total noise duration was 318 ms. The target onset was delayed relative to the noise onset by 106 ms and the duration of the noise that preceded the target was equal to the noise duration following the target offset. This type of asynchronous presentation is used commonly in studies of equivalent intrinsic noise.^{12,15,18–21}

Figure 1. .

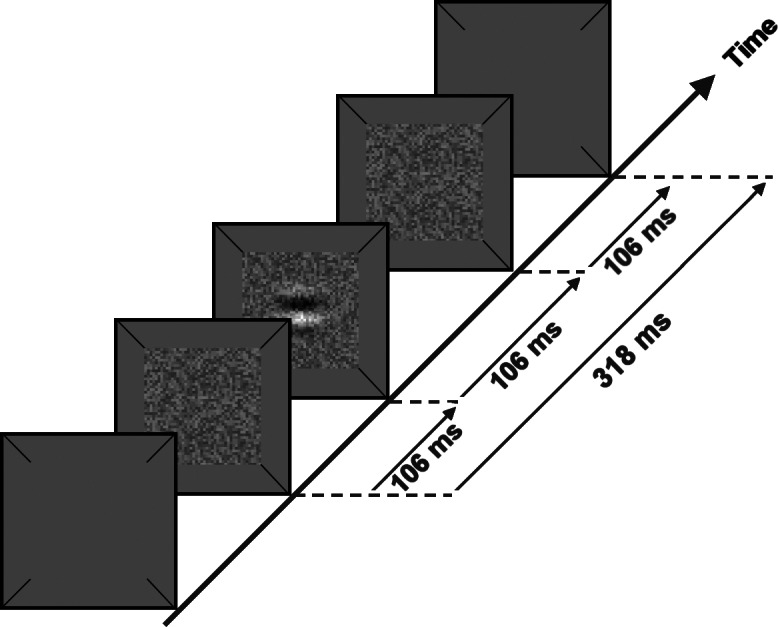
Schematic illustration of the temporal sequence of stimulus presentation in which a target of 106-ms duration was added to luminance noise of 318-ms total duration, with 106 ms of noise preceding and following the target presentation.

Procedure

Prior to all measurements, the pupil of the tested eye was dilated with 2.5% phenylephrine hydrochloride and the display was viewed through the 3-mm artificial pupil. A 30-second period of adaptation to a uniform field preceded each session, and a brief warning tone signaled the start of each stimulus presentation. The subject's task was to judge the orientation of the Gabor patch, which was randomly displayed either horizontally or vertically on each trial. No feedback was given. Contrast threshold was measured using the QUEST adaptive staircase procedure,²² with 40 trials per condition and a targeted value of 82% correct. For each subject, contrast threshold was measured in the absence of noise and in the presence of each of the five external noise levels (N) with the order of conditions randomized.

Analysis

Data were analyzed using the LAM as follows. First, contrast threshold measurements were converted to log threshold signal energy (E_t), which was computed as the integral over space and time of the squared signal function.¹⁸ Next, log E_t was plotted as a function of log N and the data were fit with the following equation¹⁴:

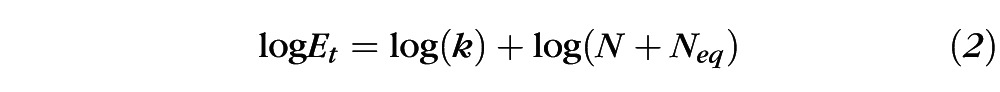where k and N_eq are free parameters that were adjusted to minimize the mean squared error between the data and the fit. Equivalent intrinsic noise (N_eq) is given directly by Equation 2 and sampling efficiency (J) is reciprocally related to k of Equation 2 according to the relationship:

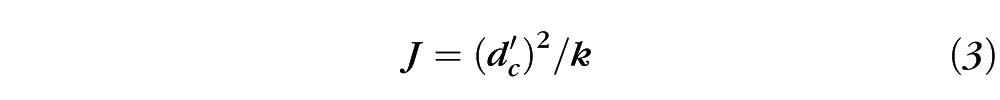where d′_c is the criterion level of detectability, which was 1.29 in the present study.²³

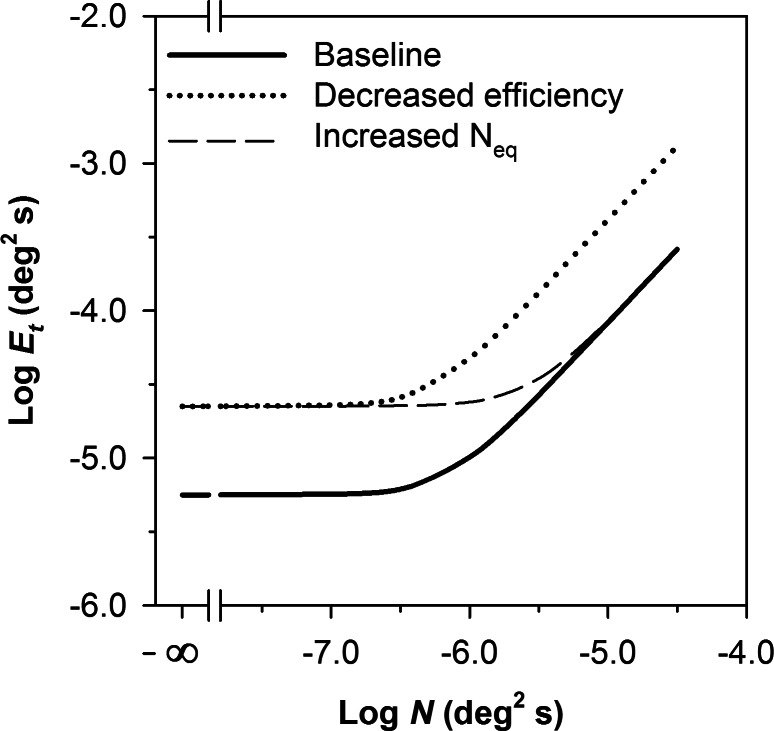
Figure 2 illustrates the shape of the function given by Equation 2 on log-log coordinates. At low levels of N relative to N_eq, log E_t is independent of log N and the slope of the function is 0. When N is substantially greater than the N_eq, log E_t increases in proportion to log N. The dashed curve in Figure 2 represents the effect of a 4-fold elevation in N_eq relative to the baseline (solid curve). The increase in N_eq shifts the curve upward and to the right by equal amounts, so that log E_t is elevated for low values of log N, but there is no elevation of log E_t for high values of log N. The dotted curve in Figure 2 represents a 4-fold reduction in efficiency. The decrease in efficiency shifts the curve uniformly upward, so that log E_t is elevated equally for all values of log N.

Figure 2. .

Functions generated by the LAM showing a baseline (solid line), a 4-fold elevation in N_eq (dashed line), and a 4-fold reduction in sampling efficiency (dotted line).

Results

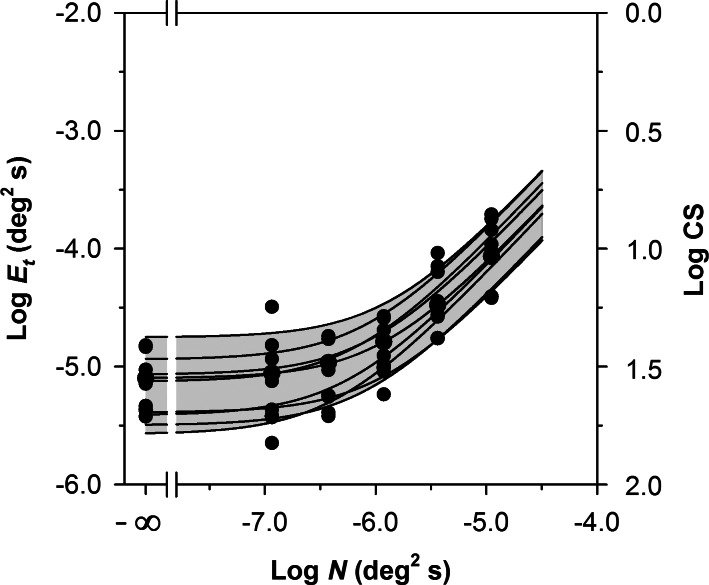
Figure 3 presents log E_t as a function of log N for the 10 control subjects. The log CS equivalents of the log E_t values are shown on the right y-axis. The curves represent the least-squares best fit of Equation 2 to each subject's data. These functions provided a good fit (the mean and standard deviation of the R² values for the 10 control subjects were 0.93 and 0.05, respectively). The functions showed approximately uniform vertical shifts, which correspond primarily to differences in sampling efficiency among the control subjects (cf. the dotted curve in Fig. 2). The gray region, which represents the range of normal, was derived by first determining the maximum and minimum values of E_t for each value of N for the 10 control subjects. The data that define the maximum and minimum values were then fit with Equation 2 to generate the range of normal shown in Figure 3.

Figure 3. .

Log E_t as a function of log N for the 10 normally-sighted control subjects. The log CS equivalents of the log E_t values are given on the right y-axis. The curves represent the least-squares best fits of Equation 2 to the data of each individual control subject. The gray region represents the normal range, as defined in the text.

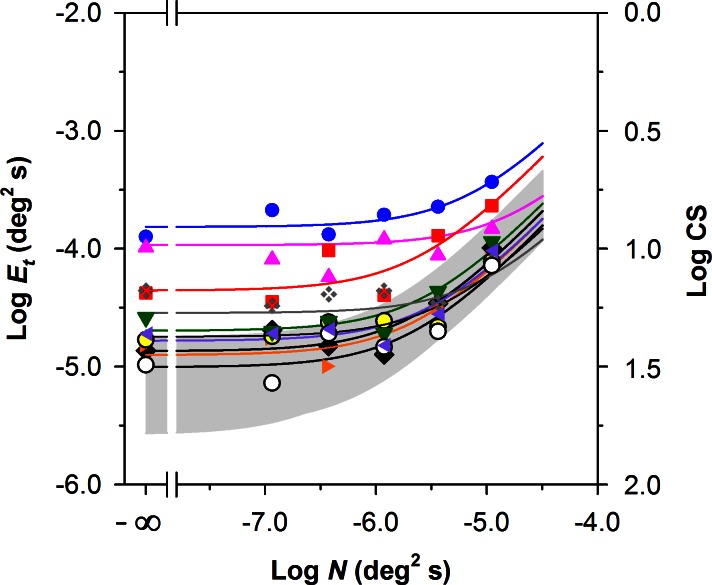
Figure 4 presents log E_t as a function of log N for the 10 patients compared with the range of normal (gray region), which is replotted from Figure 3. The symbols representing the individual patients correspond to those given in the Table. The curves are the least-squares best fits of Equation 2 to the data for the individual RP patients. These functions provided a good fit to the data (the mean and standard deviation of the R² values for the RP patients were 0.78 and 0.14, respectively). The values of E_t measured in the absence of noise (i.e., E_t0, corresponding to the leftmost points in Fig. 4) were above the upper limit of normal for seven patients. However, only two patients had values of E_t measured in the highest level of noise (i.e., rightmost points in Fig. 4) that were above normal. Thus, the functions for the patients tended to converge at the highest noise level. Qualitatively, the pattern of results for the patients is most similar to elevated N_eq (cf. the dashed curve in Fig. 2).

Figure 4. .

Log E_t as a function of log N for the 10 patients with RP compared with the normal range for the 10 control subjects (gray region). The log CS equivalents of the log E_t values are given on the right y-axis. The curves represent the least-squares best fits of Equation 2 to the data of each patient with RP, with symbols corresponding to those shown in the Table.

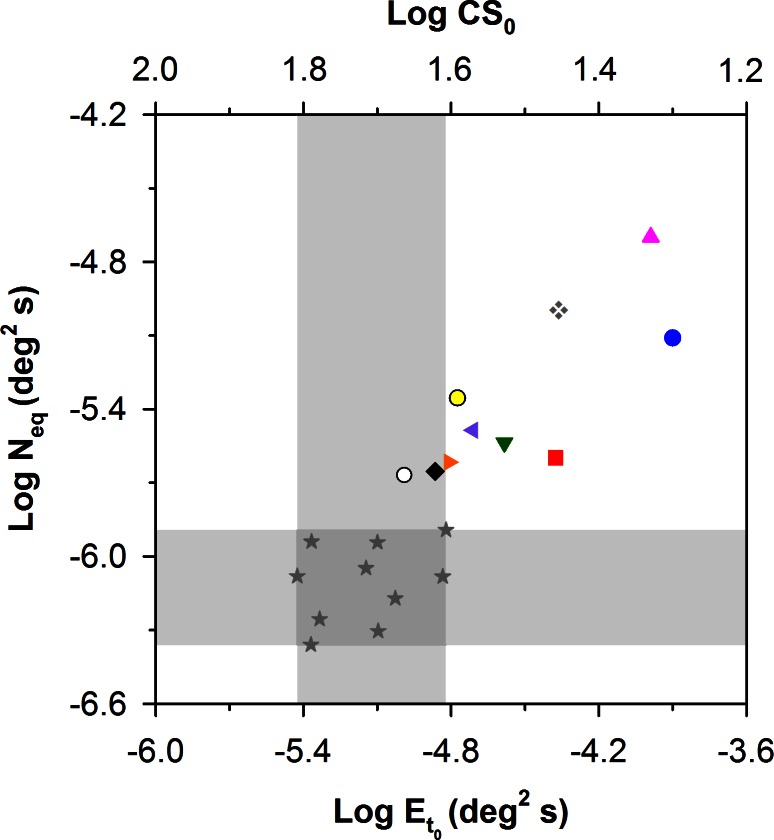
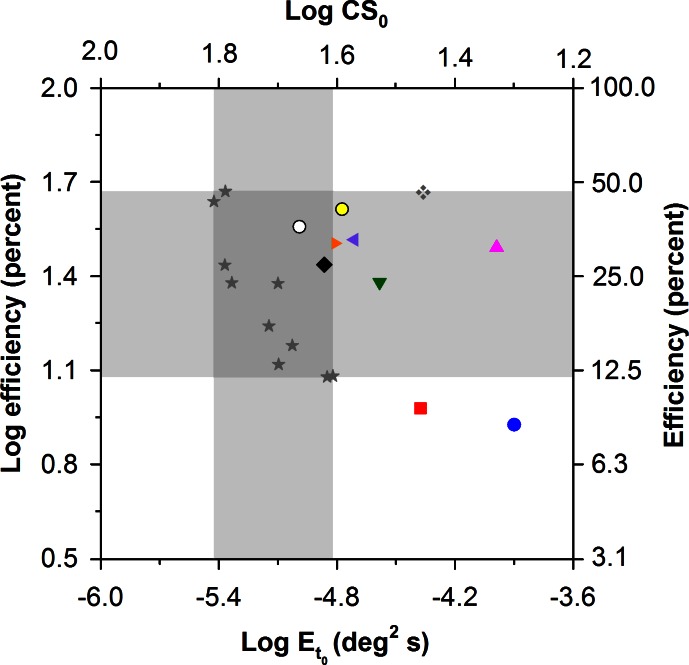
To confirm this qualitative assessment, the values of N_eq and efficiency that were derived from the LAM were plotted as a function of E_t0 in Figures 5 and 6, respectively. Figure 5 shows log N_eq versus log E_t0 for the 10 patients and 10 control subjects. The upper x-axis gives the log CS₀ equivalents of the log E_t0 values. The vertical and horizontal gray regions demarcate the normal range of log E_t0 and log N_eq, respectively. Two patients had log E_t0 values (and log CS₀ values) that were within the range of normal. The remaining eight patients had values of log E_t0 that were elevated by as much as 0.92 log units (approximately a factor of 8) above the upper limit of normal, corresponding to reductions of CS₀ by as much as approximately a factor of 3. The values of log N_eq, were above the range of normal for all 10 patients, and there was a statistically significant difference in log N_eq between the patients and controls (t = −6.32, P < 0.05). Log N_eq and log E_t0 were correlated significantly for the RP patients (r = −0.80, P < 0.05), but not for the control subjects (r = 0.34, P = 0.34). This is consistent with the observation that the individual functions for the patients with RP shown in Figure 4 were shifted primarily upward and rightward by equal amounts, whereas this was not the case for the control subjects (Fig. 3). There was also a statistically significant correlation between log N_eq and visual field diameter (r = −0.69, P < 0.05), such that patients with more restricted fields, representing greater disease progression, had higher values of log N_eq.

Figure 5. .

Log N_eq versus log E_t0 for the 10 patients with RP and 10 control subjects (stars), with patient symbols corresponding to those of the Table. The gray regions demarcate the normal ranges of log N_eq (horizontal region) and E_t0 (vertical region). The log CS₀ equivalents (i.e., CS in the absence of noise) of the log E_t0 values are given on the top x-axis.

Figure 6. .

Log sampling efficiency versus log E_t0 for the 10 patients with RP and the 10 control subjects (stars), with patient symbols corresponding to those of the Table. The gray regions demarcate the normal ranges of log efficiency (horizontal region) and E_t0 (vertical region). The log CS₀ equivalents (i.e., CS in the absence of noise) of the log E_t0 values are given on the top x-axis; the linear values corresponding to log efficiency are given on the right y-axis.

Figure 6 plots log efficiency as a function of log E_t0 for the 10 patients and 10 control subjects. The vertical and horizontal gray regions demarcate the normal ranges of E_t0 and sampling efficiency, respectively. The efficiency values for all but two of the patients fell within the normal range, and the efficiency reductions in these two patients (nos. 8 and 9) were less than 4% below the lower range of normal. These two patients also had elevated values of E_t0 (0.92 and 0.45 log units above the upper limit of normal, respectively), as well as reduced visual acuity and highly constricted visual fields (Table). Two other patients (nos. 5 and 10) had relatively large elevations in log E_t0, but log efficiency that was within the normal range. These two patients also had poor visual acuity (Table). Mean log efficiency for the patients was not significantly different from that of the controls (t = −0.82, P = 0.42). There was no significant correlation between log efficiency and log E_t0 for the patients (r = 0.54, P = 0.11), but the correlation was statistically significant for the controls (r = 0.77, P < 0.05). The significant correlation for the control subjects is consistent with the overall upward shifts of their functions shown in Figure 3.

Discussion

It has been proposed that most retinal diseases impair contrast sensitivity by increasing the level of noise within the visual pathway rather than by reducing sampling efficiency.¹² This study evaluated this proposal in patients with RP by measuring CS, N_eq, and sampling efficiency in these patients. All RP patients in our sample had a value of N_eq that was greater than normal, but sampling efficiency was generally within normal limits. This pattern of elevated N_eq with normal sampling efficiency produces a CS reduction in the absence of external noise, but normal CS in the presence of a high level of external noise. The findings of elevated N_eq with normal sampling efficiency suggest that high levels of noise within the visual system may, at least in part, limit CS in patients with RP, in agreement with a previous proposal.¹²

Although the source of the above-normal N_eq is presently uncertain, there are a number of potential explanations. For example, elevated N_eq in our patients with RP could be due to cell death, dysfunction, or the retinal remodeling that has been demonstrated in patients with retinal degenerative disease and in animal models of retinal degeneration.²⁴ Increases in N_eq could also be related to inner retina dysfunction (e.g., abnormal ganglion cell function due to a loss of photoreceptor input), an intriguing possibility in light of recent evidence for ganglion cell hyperactivity in rd1 and rd10 mouse models of retinal degeneration.²⁵ However, the relative contribution of these potential sources of noise to N_eq elevations in patients with RP requires further investigation.

Elevations in N_eq are typically thought to reflect increased levels of neural noise within the visual system. Nevertheless, elevated values of N_eq have been reported in patients with optical defects due to cataracts^13,26 and senescent optical changes.^27,28 The elevated N_eq for patients with optical defects is due to the fact that contrast threshold is determined by the ratio of target contrast to noise contrast (i.e., the signal-to-noise ratio). Optical attenuation affects target contrast and noise contrast equally, leaving the ratio unchanged. Thus, log E_t for patients with optical defects is elevated only for low values of log N, similar to the pattern for RP patients (as shown in Fig. 4). However, it seems unlikely that optical defects would account for the elevated levels of N_eq in our patients with RP. These patients had minimal or no cataract, were optically corrected to minimize low-order aberrations, and viewed the stimuli through a 3-mm artificial pupil that minimized both low- and high-order aberrations. Therefore, it seems more likely that the higher levels of N_eq observed in our patients with RP are related to neural rather than to optical sources.

The present study measured CS in the presence of asynchronous dynamic noise, which has been shown previously to bias visual processing toward the parvocellular (PC) visual pathway.¹⁹ The use of static noise, on the other hand (whether synchronous or asynchronous), appears to bias visual processing toward the magnocellular (MC) visual pathway.¹⁹ However, it is unlikely that the use of a noise paradigm that biased processing toward the MC pathway would significantly alter the conclusions of the present study. Previous work has shown that the CS deficits of patients with RP are similar for conditions that are biased toward the MC or the PC pathway when measured with grating targets.⁷ Nevertheless, it would be worthwhile to verify this conclusion by using temporal sequences of target and noise presentation and forms of luminance noise that are designed to target either the MC or the PC pathway in patients with RP.

In conclusion, our results indicate that an increased level of intrinsic noise within the visual pathway is a major determinant of CS impairments in RP patients, but even patients with normal CS can have increased equivalent intrinsic noise. Thus, CS measurement in both the presence and absence of luminance noise can provide important information about visual dysfunction in patients with RP that cannot be obtained from noise-free CS measurements alone. Furthermore, CS measurements made in the presence and absence of external noise might be of use as an outcome measure in future treatment trials and for assessing macular dysfunction in patients with RP.