Standardized Nomenclature, Symbols, and Units for Bone Histomorphometry: A 2012 Update of the Report of the ASBMR Histomorphometry Nomenclature Committee

Introduction

Before publication of the original version of this report in 1987, practitioners of bone histomorphometry communicated with each other in a variety of arcane languages, which in general were unintelligible to those outside the field. The need for standardization of nomenclature had been recognized for many years,⁽¹⁾ during which there had been much talk but no action. To satisfy this need, B Lawrence Riggs (ASBMR President, 1985 to 1986) asked A Michael Parfitt to convene an ASBMR committee to develop a new and unified system of terminology, suitable for adoption by the Journal of Bone and Mineral Research (JBMR) as part of its Instructions to Authors. The resulting recommendations were published in 1987⁽²⁾ and were quickly adopted not only by JBMR but also by all respected journals in the bone field. The recommendations improved markedly the ability of histomorphometrists to communicate with each other and with nonhistomorphometrists, leading to a broader understanding and appreciation of histomorphometric data.

In 2012, 25 years after the development of the standardized nomenclature system, Thomas L Clemens (Editor in Chief of JBMR) felt that it was time to revise and update the recommendations. The original committee was reconvened by David W Dempster, who appointed one new member, Juliet E Compston. The original document was circulated to the committee members and was extensively revised according to their current recommendations. The key revisions include omission of terminology used before 1987, recommendations regarding the parameters and technical information that should be included in all histomorphometry articles, recommendations on how to handle dynamic parameters of bone formation in settings of low bone turnover, and updating of references.

Preliminary Definitions

It is generally agreed that a bone is an individual organ of the skeletal system, but the term ‘‘bone’’ has at least three meanings. The first is mineralized bone matrix excluding osteoid; this usage conforms rigorously to the definition of bone as a hard tissue. Osteoid is bone matrix that will be (but is not yet) mineralized, and is sometimes referred to as pre-bone. The second meaning of ‘‘bone,’’ and the one we have adopted, is bone matrix, whether mineralized or not, ie, including both mineralized bone and osteoid. The third meaning of ‘‘bone’’ is a tissue including bone marrow and other soft tissue, as well as bone as just defined. We refer to the combination of bone and associated soft tissue or marrow as ‘‘bone tissue.’’ ‘‘Tissue’’ is defined⁽³⁾ as ‘‘an aggregation of similarly specialized cells united in the performance of a particular function.’’ In this sense, bone, bone marrow, and the contents of osteonal canals are certainly not the same tissue, but in a more general sense, most textbooks of histology recognize only four fundamental tissues—epithelium, nerve, muscle, and connective tissue⁽⁴⁾—of which the last-named includes bone and all its accompanying nonmineralized tissue.

In current clinical and radiologic parlance, ‘‘trabecular’’ and ‘‘cortical’’ refer to contrasting structural types of bone. But ‘‘trabecular’’ does not appear in any standard textbook of anatomy or histology as a name for a type of bone; rather, ‘‘spongy’’ or ‘‘cancellous’’ is used. ‘‘Spongiosa’’ (primary or secondary) is best restricted to the stages of endochondral ossification; ‘‘cancellous’’ is most commonly used in textbooks^(4,5) and is the term we have chosen. We retain the noun ‘‘trabecula’’ and its associated adjective ‘‘trabecular’’ to refer to an individual structural element of cancellous bone, in accordance with current practice in histology,⁽⁴⁾ pathology,⁽⁶⁾ and biomechanics.⁽⁷⁾ Etymologically, a trabecula is a beam or rod, and in young people plates rather than rods are the predominant structural elements, both in the spine⁽⁸⁾ and in the ilium,⁽⁹⁾ but no convenient alternative is available. The size, shape, and orientation of trabeculae (as just defined) vary considerably between different types of cancellous bone.^(9,10)

‘‘Density’’ is a frequent source of confusion in discussions about bone. We propose that the term should be restricted as far as possible to its primary meaning in physics of mass per unit volume,^(11,12) with a subsidiary meaning analogous to population density, which is applied mainly to cells. This precludes the use of ‘‘density’’ in its stereologic sense, as will be discussed later. Corresponding to the definitions given earlier, the volume to which mass is referred can be of mineralized bone, bone, bone tissue (cortical or cancellous), or a whole bone. Mineralized bone density is slightly less than true bone density, which excludes the volume of osteocyte lacunae and canaliculi.⁽¹¹⁾ This volume is small and generally ignored; lacunar volume can be readily measured,⁽¹³⁾ but canalicular volume is inaccessible to light microscopy. Bone density reflects the volumetric proportion of osteoid; bone matrix volume, excluding lacunar and canalicular volume, has been referred to as absolute bone volume.⁽¹⁴⁾ Bone tissue density reflects the volumetric proportion of soft tissue, or porosity. Whole bone density, often referred to as apparent bone density, reflects the volumetric proportions of cortical bone tissue, cancellous bone tissue, and diaphyseal marrow within a bone, the organ volume of which is usually measured by Archimedes’ principle.⁽¹⁵⁾

‘‘Osteoblast’’ is defined differently in the clinical and experimental literature. In young, rapidly growing small animals, most bone surfaces are undergoing either resorption or formation and virtually all cells on the surface are either osteoclasts or osteoblasts,⁽¹⁶⁾ but in the adult human, most bone surfaces are quiescent with respect to bone remodeling. We refer to the flat cells that cover quiescent internal (nonperiosteal) bone surfaces as lining cells and restrict the term ‘‘osteoblast’’ to cells that are making bone matrix currently or with only temporary interruption, rather than including all surface cells that are not osteoclasts.⁽¹⁶⁾ Lining cells are of osteoblast lineage and are thought to have osteogenic potential.⁽¹⁷⁾ The term ‘‘osteoclast’’ is restricted to bone-resorbing cells containing lysosomes and tartrate-resistant acid phosphatase; they are usually multinucleated, although some osteoclast profiles may have only one or no nucleus. Criteria for identification of osteoblasts and osteoclasts, whether morphologic or histochemical,^(18,19) should always be stated or referenced.

Dimensional Extrapolation and Stereology

A two-dimensional histological section displays profiles of three-dimensional structures. Four types of primary measurement can be made on these profiles—area, length (usually of a perimeter or boundary), distance between points or between lines, and number.⁽²⁰⁾ Some histomorphometrists report all results only in these two-dimensional terms because the assumptions needed for extrapolation to three dimensions may be difficult to justify and because the diagnostic significance of the measurements or the statistical significance of an experimental result are not affected. For these limited objectives, this is a reasonable view, but bone cannot be fully understood unless conceived in three-dimensional terms. In every other branch of science that uses microscopy as an investigative tool, the ultimate goal is to understand three-dimensional reality by the application of stereology, which is the relevant mathematical discipline.^(20–22) We believe that this also should be the goal of bone histomorphometry. Accurate three-dimensional data are necessary for proper comparison between species, between bones, and between different types of bone, for input into finite element models of bone strength, for realistic estimation of radiation burdens, and for many aspects of bone physiology, such as the calculation of diffusion distances and the measurement of individual cell work.

But as a practical matter, it is unrealistic to insist on universal adoption of a three-dimensional format. All stereologic theorems require that sampling be random and unbiased, a condition only rarely fulfilled in bone histomorphometry; the closest feasible approach is to rotate the cylindrical bone sample randomly around its longitudinal axis before embedding.^(20,23) In the past, the use of a hemispherical grid^(20–22) in the ocular lens was a convenient way of ensuring randomness of test line orientation, but even this cannot compensate for sampling bias introduced at an earlier stage. With the exception of the conversion of area fractions to volume fractions, most stereologic theorems also require that the structure be isotropic, meaning that a perpendicular to any element of surface has an equal likelihood of pointing in any direction in space.^(20,24) Although not true for all cancellous bone, in the ilium there is only moderate deviation from isotropy, and stereologic theorems may be used with acceptable error.^(24,25) But it is more accurate to apply the theory of vertical sections; a cycloid test grid is required, which is incompatible with the use of a digitizer,^(23,26) but there is no other way of obtaining truly unbiased estimates. Because Haversian canals generally do not deviate from the long axis by more than 10°, stereologic problems in diaphyseal cortical bone are minimal, but investigation of the correct stereologic approach to iliac cortical bone has not been done.

Accordingly, we recommend that everyone reporting histomorphometric data should select one of two options: either present all results strictly and consistently in two dimensions, using the terms perimeter (for length), area, and width (for distance), or (as favored by the committee) present only the corresponding three-dimensional results using the terms surface, volume, and thickness; with the latter option, an explanation is needed for each type of measurement of exactly how it was derived from the primary two-dimensional measurement, as described later. A mixture of two- and three-dimensional terms should not be used in the same article. The only exception is number, the fourth type of primary measurement, for which there is no convenient way of extrapolating to three dimensions without making assumptions concerning the three-dimensional shape of the objects counted.^(21,22) Direct enumeration of number in three dimensions is possible if the same object can be identified in serial sections of known thickness and separation,⁽²⁷⁾ but this method has not yet been applied to bone. Topological properties such as connectivity also cannot be determined from two-dimensional sections.⁽²⁸⁾

The original committee chose not to adopt the terminology of the International Society of Stereology, as was suggested at the First International Workshop on Bone Morphometry.⁽²⁹⁾ Stereologists use the term ‘‘density’’ in a very general sense to identify any measurement referred to some defined containing volume,^(21,22) so that fractional volume is ‘‘volume density’’ (V_v) and surface area per unit volume is ‘‘surface density’’ (S_v). Although the unification of scientific terminology is desirable in the long term, the practical disadvantage of using ‘‘density’’ in two different senses outweighs the theoretical advantage. Nevertheless, all investigators wishing to remain at the cutting edge of bone histomorphometry will need to be thoroughly familiar with the terminologic conventions of stereology because many important methodologic articles applicable to bone are published in the Journal of Microscopy, which is the official journal of the International Society of Stereology.^(26–28)

The Importance of Referents

Primary two-dimensional measurements of perimeter, area, and number are indices of the amount of tissue examined and can be compared between subjects only when related to a common referent, which will be some clearly defined area or perimeter within the section. Absolute perimeter length and absolute area in two dimensions have no corresponding absolute surface area and absolute volume in three dimensions, but it is convenient to refer to perimeters as surfaces and to areas as volumes if the appropriate referent is clear from the context. Primary two-dimensional measurements of width (and corresponding three-dimensional thicknesses) and mean profile areas of individual structures have meaning in isolation and are the only type that do not require a referent. Different referents serve different purposes and lead to different interpretations, so that use of multiple referents is unavoidable, and it is important to clearly distinguish between them.⁽³⁰⁾ Commonly used referents include tissue volume (TV), bone volume (BV), bone surface (BS), and osteoid surface (OS) and their corresponding two-dimensional areas or perimeters. With explicit identification of the referent, the use of ‘‘relative’’ as a qualifying term becomes redundant.

The volume of the cylindrical biopsy core is not commonly used as a referent at present but is needed for comparison with physical methods of measuring bone density,⁽³¹⁾ for comparing the absolute amounts of cortical and cancellous bone lost because of aging or disease,⁽³¹⁾ for determining the contributions of different types of bone and different surfaces to various histological indices, such as amount of osteoid and surface extent of osteoblasts,⁽³²⁾ and for examining in detail the relationships between histological and biochemical indices of whole-body bone remodeling.⁽³²⁾ Use of the core volume (CV) as a referent provides the closest approach possible from an iliac biopsy to the in vivo level of organization corresponding to bone as an organ. An intact, full-thickness transiliac biopsy can be regarded as representative of the entire bone^(18,33) because the length of the cylindrical biopsy core perpendicular to the external surface depends mainly on the width of the iliac bone at the site of sampling. Cortical thickness can be measured with a vertical biopsy through the iliac crest,⁽⁵⁾ but the proportions of cortical and cancellous tissue in the bone cannot be measured. However, with either type of biopsy, the results can be weighted by the proportions of cortical and cancellous bone tissue in the entire skeleton.⁽³⁴⁾ The same principle can be applied to rib biopsies and to long bone cross sections by using the whole area enclosed by the periosteum as the referent.

Lexicon of Bone Histomorphometry

The recommended individual terms are listed in Table 1 in alphabetical order of their abbreviations or symbols. Several general comments are in order. First, like a dictionary, the lexicon is intended to be consulted, rather than memorized. Second, the use of abbreviations is always discretionary, never compulsory. Although designed mainly to save time or space, there is a more subtle reason for abbreviations, as for other symbols. Words frequently carry unwanted implications from their use in other contexts, but confusion is less likely with symbols that can be approached with fewer preconceptions.⁽¹⁾ Nevertheless, our purpose is not to encourage or discourage the use of abbreviations and symbols but to ensure that the same ones are used by everybody. To this end, we have made the lexicon comprehensive to anticipate future needs and forestall the introduction of new abbreviations with different meanings. We have included metals frequently identified in bone (with their usual elemental abbreviations) and terms commonly used in quantitative microscopy and stereology, as well as terms for all the major structural features of bone and of bones and for some important concepts of bone physiology. Terms with unfamiliar meanings are explained and defined in relation to their use.

Table 1.

Abbreviations and Symbols of Terms Used in Bone Histomorphometry

A	Apposition(al)
Ad	Adipocytea
Ab	Absolute
Ac	Activation
Aj	Adjusted
Al	Aluminum
Ar	Area (2D)b
a	Activ(e)(ity)
B	Bone
BMU	Basic multicellular unit
Bd	Boundary (2D)b
C	Core
Ca	Canal(icula)(r)
Cd	Corrected
Ce	Cell
Cg	Cartilage
Cm	Cement
Cn	Cancellous
Cp	Cytoplasm(ic)
Ct	Cort(ex)(ical)
Cy	Cycle
D	Dimension(al)
De	Depth
Dg	Degenera(tive)(tion)
Dm	Diameter
Dn	Density
Do	Domain
Dp	Diaphys(is)(eal)
Dt	Delta
d	Doublec
E	Ero(ded)(sion)
Ec	Endocortical
En	Envelope
Ep	Epiphys(is)(eal)
Es	Endost(eal)d(eum)
Ex	External
F	Formatione
Fa	Fat(ty)
Fb	Fibro(sis)(us)
Fe	Iron
Fr	Front
f	Frequency
G	Grow(th)(ing)
H	Haversian
Hm	Hematopoietic
Hp	Hypertrophic
Ht	Height
Hz	Horizontal
H	Hit
I	Interfacef (3D)b
Ia	Intra
Ic	Intercept
Il	Initial
In	Internal
Ir	Inter
Is	Instantaneous
It	Interstitial
I	Intersection
L	Label(led)
Lc	Lacuna(r)g
Le	Length
Li	Lining
Lm	Lamella(r)
Ln	Line
Lo	Longitudinal
L	Lag
M	Mineral(iz)(ing)(ation)
Ma	Marrow
Md	Mineralized
Me	Medullary
Ml	Modeling
Mo	Mononucle(ar)(ated)
Mp	Metaphys(is)(eal)
Mu	Multinucle(ar)(ated)
Mx	Matrix
M	Maturation
N	Number of profiles or structures
N	Number of sampling unitsh
Nc	Nucle(us)(ar)
Nd	Node
O	Osteoid
Ob	Osteoblast(ic)
Oc	Osteoclast(ic)
On	Osteon(al)
Ot	Osteocyt(e)(ic)
P	Period
Pf	Profile
Pl	Plate
Pm	Perimeter (2D)b
Po	Por(e)(ous)(osity)
Ps	Periost(eal)(eum)
Pt	Point
Q	Quiescent
R	Rate
Rd	Radi(al)(us)
Rf	Referen(ce)(t)
Rm	Remodeling
Rs	Resorptione
Rv	Reversal
S	Surface (3D)b
Sa	Sample
Se	Section
Sg	Sigma
Sm	Seam
Sn	Spongiosa
Sp	Separation
St	Structur(e)(al)
S	Single
T	Tissue
Tb	Trabecula(r)i
Th	Thickness (3D)b
Tm	Termin(al)(us)
Tr	Transitional
Tt	Total
T	Time
U	Unit
V	Volume (3D)b
Vd	Void
Vk	Volkmann
Vt	Vertical
W	Wall
Wi	Width (2D)b
Wo	Woven
y	Year
Z	Zone

Note: For further definitions and explanations, see text.

^aIncluded here and in Table 3 because of the rekindled interest in assessing adipocyte parameters in the marrow space of iliac crest bone biopsies and the shared progenitor cell with osteoblasts.

^b2D or 3D refers to the format in which data are reported, not the dimensions of an individual quantity.

^cAlso day, but context should eliminate ambiguity.

^dEndocortical + cancellous.

^eAs a process, not as a morphologic feature.

^fBetween osteoid and mineralized bone.

^gIf unqualified, osteocytic, not Howship’s.

^hFor example, subjects, sites, sections, etc.

ⁱAn individual structure, not a type of tissue.

With one exception, the abbreviations and symbols in Table 1 consist of only two letters; ‘‘BMU’’ (basic multicellular unit) is retained because it is important and widely used and lacks a suitable alternative. The most commonly used descriptive terms are given a single capital letter. Other terms have an additional lowercase letter, chosen in many cases to emphasize the second or later syllable and usually avoiding the second letter of the word abbreviated by the single capital letter. Single lowercase letters are used for terms that are in some sense related to time, for the primary data of classical grid counting (hit and intersection), and for n in its usual statistical sense. When used in combination, double-letter abbreviations should be demarcated by a period; in the absence of periods, each letter is to be construed as an individual abbreviation. In this way, any combination of abbreviations can be unambiguously deciphered without having to determine which terms are included in the lexicon.

The Nomenclature System

Bone histomorphometry can be applied to many types of material, but the most common are sections of cylindrical biopsy samples of iliac bone obtained from human subjects and sections of long bones obtained from experimental animals. For orientation, we first present the terminology for describing these sections.

Description of section

‘‘Core’’ (C) refers to the entire biopsy specimen (Fig. 1). For transiliac biopsies, the distance between external (Ex) and internal (In) periosteum is termed ‘‘width’’ (Wi) because it is related to the thickness of the iliac bone at the biopsy site; for vertical biopsies through the iliac crest, the term ‘‘length’’ (Le) is more appropriate. Core width is subdivided into cortical (Ct) widths and cancellous (Cn) width; for transiliac biopsies, measurements on the two cortices (including their width) are usually pooled, but it is possible to keep track of their identity and examine them separately. In this case, the two cortices are generally distinguished by their width (thick versus thin). Identification of the inner and outer cortex would require that one be marked in some way (eg, by ink or cotton thread) at the time of the biopsy, but this is seldom done. The outer cortex generally has more attached fibrous and muscle tissue than the inner cortex. The other dimension of the core is referred to as ‘‘diameter’’ (Dm), although only sections through the central axis of the cylinder have the same diameter as the trephine; the more accurate term ‘‘chord length’’ is too cumbersome. If the axis of the transiliac core is oblique to the plane of the ilium, its dimensions are apparently changed (Fig. 2). It is convenient to define core diameter as mean ‘‘periosteal length’’ (external and internal) regardless of obliquity because true values for cortical and cancellous width corrected for obliquity are then given by the relationships between length and area set out in the legend to Fig. 2.^(31,35)

Fig. 1.

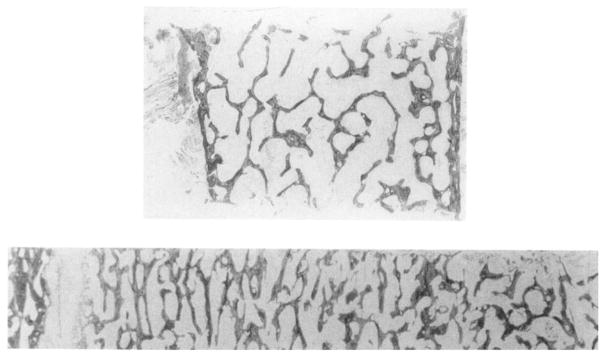
Sections of representative bone biopsies from different sites. Upper: transiliac (outer cortex on left). Lower: vertical (iliac crest on left). Supplied by H Malluche; transiliac biopsy reproduced from Malluche and Faugere⁽⁵⁾ with permission.

Fig. 2.

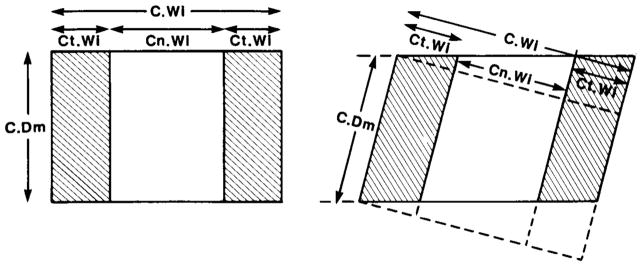
Diagram of sections through cylindrical biopsy core of ilium. Direction of trephine perpendicular on left, oblique on right. C.Wi = core width; C.Dm = core diameter; Ct.Wi = cortical width; Cn.Wi = cancellous width. Relationships to areas: C.Ar = core (or section) area = C.Dm*C.Wi; Ct.Ar = cortical area = C.Dm*Ct.Wi; Cn.Ar = cancellous area = C.Dm*Cn.Wi. Provided the inner and outer periosteum do not depart seriously from parallelism and their mean length is used for C.Dm, these relationships remain true for the oblique section because the areas enclosed by the interrupted and solid lines are equal.⁽³⁵⁾ Consequently, the relationships can be used to estimate C.Wi, Ct.Wi, and Cn.Wi without measuring the angle of obliquity.

For long bone cross sections (Fig. 3), bone diameter (B.Dm) is similarly subdivided into two cortical widths and either cancellous diameter (Cn.Dm) for metaphyseal (Mp) cross sections, or marrow diameter (Ma.Dm) for diaphyseal (Dp) cross sections. The relationships between these diameters and bone area, cortical area, and cancellous or marrow area depends on the precise geometry of the cross section. For biomechanical purposes, such measurements may be needed at multiple locations in relation to the in vivo orientation. For both iliac and long bone sections, it is necessary for certain purposes to recognize a transitional zone (Tr.Z) lying between cortical and cancellous bone tissue and intermediate in geometrical and topological features.⁽³⁶⁾ This zone is not indicated in Figs. 2 or 3 because methods of defining its boundaries are not yet fully developed. A threshold-based algorithm has recently been used to address this problem in high-resolution peripheral quantitative computed tomography (pQCT) images.^(37,38) This may be applicable to iliac crest bone biopsy samples, but this has not yet been tested. For all bones, all interior surfaces in contact with bone marrow are referred to as endosteal (Es) and are subdivided into cancellous bone surface and endocortical (Ec) surface; the latter is the inner boundary of the cortex. Demarcation between these components is subject to large observer error⁽³⁹⁾ unless made in accordance with some well-defined rule⁽⁴⁰⁾ and will also depend on whether the transitional zone is measured separately. Interior surfaces not in contact with bone marrow are generally referred to as cortical (Ct), with optional qualification as ‘‘intra’’ (In); the cortical surface can also be referred to as the Haversian canal (H.Ca) or osteonal canal (On.Ca) surface.

Fig. 3.

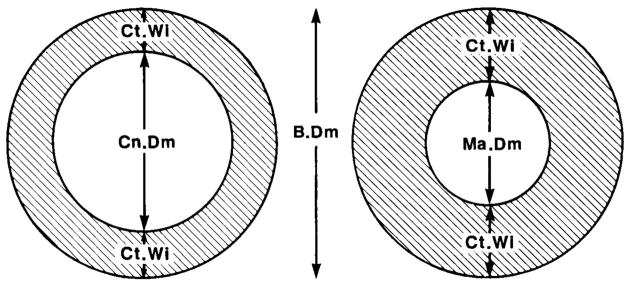
Diagram of cross sections through the shaft of a long bone; metaphyseal region is on the left, and diaphyseal region is on the right. For clarity, the cancellous bone of the metaphysis is not shown. B.Dm = bone diameter; Ct.Wi = cortical width; Cn.Dm = cancellous diameter; Ma.Dm = marrow diameter.

Standard format

The following standard and universally applicable method for reporting all data should be used: Source–Measurement/Referent. Note that the complete elimination of ambiguity applies to punctuation as well as to terminology; the dash (–) and slash (/) are used only as illustrated and periods are used only as described earlier. ‘‘Source’’ refers to the structure on which the measurement was made, whether this was a particular surface or a particular type of tissue. Most of the commonly used sources have already been defined (Table 2); many others are definable by using the lexicon (Table 1). If measurements are restricted to some subdivision of a source, such as the outer portion of a cortex⁽⁴¹⁾ or the central zone of cancellous tissue,⁽³³⁾ the same symbol can be used, but the appropriate qualification should be made in the description of methods. For measurements made on the entire section, the source is identified as ‘‘total’’ (Tt). Usually it will not be necessary to specify the source each time a particular quantity is referred to—if only one source is used in an article, it need only be mentioned once. If several sources are included, their names can be used as subheadings for presentation of results in tables or text, and in most cases will need to be repeated only if measurements from several sources are discussed together, such that confusion between them is possible. For some measurements, such as trabecular thickness, only one source is possible and its specification is redundant.

Table 2.

Sources and Referents in Bone Histomorphometry

Sources		Referents
Name	Abb.	Name	Abb.
Total core	Tt	Bone surface	BS
Cortical bone tissue	Ct	Bone volume	BV
Cancellous bone tissue	Cn	Tissue volume	TV
Endocortical surface	Ec	Core volume	CV
Periosteal surface	Ps	Osteoid surface	OS
Transitional zone	Tr.Z	Bone interface	BI
Diaphyseal bone	Dp	Eroded surface	ES
Metaphyseal bone	Mp	Mineralized surface	Md.S
Epiphyseal bone	Ep	Osteoblast surface	Ob.S
Medullary bone	Me	Osteoclast surface	Oc.S

Abb. = abbreviation.

Those listed will cover most situations in both human and nonhuman studies, but neither list is exhaustive. Combinations of source terms may be needed, such as Dp.Ec for diaphyseal bone, endocortical surface.

The need for referents was described earlier. The most commonly used referents have already been defined and are listed in Table 2, but the relationships between them need further explanation, as follows (OV is used here as an example of the variable in the numerator; the asterisk is the most typographically convenient symbol for multiplication):

$$\begin{array}{l}\text{OV}/{\text{BS}}^{\ast }\text{BS}/\text{BV}=\text{OV}/\text{BV}\\ \text{OV}/{\text{BS}}^{\ast }\text{BS}/\text{TV}=\text{OV}/\text{TV}=\text{OV}/{\text{BV}}^{\ast }\text{BV}/\text{TV}\\ \text{OV}/{\text{BS}}^{\ast }\text{BS}/\text{CV}=\text{OV}/\text{CV}=\text{OV}/{\text{BV}}^{\ast }\text{BV}/\text{CV}\end{array}$$

The three surface/volume ratios and the two volume/volume ratios are the key quantities needed to convert from one referent to another.⁽³⁰⁾ BS/BV is equivalent to S/V in stereologic terminology, and BS/TV and BS/CV are equivalent to S_v (surface density) in stereologic terminology. These ratios are derived from the corresponding two-dimensional perimeter/area ratios—B.Pm/B.Ar, B.Pm/T.Ar, and B.Pm/C.Ar—by multiplying either by 4/π (1.273), which is correct for isotropic structures,^(20–22) or by 1.2, which has been experimentally determined for human iliac cancellous bone.⁽²⁵⁾ The ratios increase with microscopic resolution, so that the magnification must always be stated and preferably standardized.⁽⁴²⁾ BV/TV and BV/CV correspond to V_v (volume density) in stereologic terminology and are numerically identical with the corresponding area/area ratios B.Ar/T.Ar and B.Ar/C.Ar.^(20–22)

For some purposes, a subdivision of the bone surface is needed as a referent (Table 2). Osteoblast surface (Ob.S) and mineralizing surface (MS) are often related to osteoid surface (/OS). Osteoclasts usually avoid osteoid, and it can be useful to relate osteoclasts to the mineralized surface (/Md.S), previously called nonosteoid surface,⁽⁴³⁾ as an alternative to the more usual referents bone surface and eroded surface (/ES). Various kinetic indices of bone formation can be related to the osteoblast surface (/Ob.S) or to the number of osteoblast profiles (/N.Ob), as well as to osteoid surface or bone surface.⁽³⁰⁾ Finally, it may be appropriate to use the interface between mineralized bone and osteoid, or bone interface, as a referent (/Bl) for the length of tetracycline label or of positive aluminum staining because the interface is where these features are located. In many cases, as when only one referent is used for each measurement, the referent need only be specified once and not repeated each time the measurement is mentioned. If more than one referent is used, measurements with the same referent can be grouped together to avoid repetition.

Primary measurements

These are listed together with abbreviations in both 3D and 2D form in Table 3. Many have already been defined but some need additional explanation.

Table 3.

Primary Measurements in Bone Histomorphometry

		Abbreviations
Type of measurement	Name of measurement	3D	2D
Area	Bone volumea	BV	B.Ar
	Osteoid volume	OV	O.Ar
	Mineralized volume	Md.V	Md.Ar
	Void volume	Vd.V	Vd.Ar
	Marrow volume	Ma.V	Ma.Ar
	Fibrosis volume	Fb.V	Fb.Ar
	Canal volumeb	Ca.V	Ca.Ar
	Cell volumeb,c	Ce.V	Ce.Ar
	Cytoplasmic volumeb,d	Cy.V	Cy.Ar
	Nuclear volumeb,d	Nc.V	Nc.Ar
Length	Bone interfacee	BI	B.Bd
	Bone surfacef	BS	B.Pm
	Osteoid surface	OS	O.Pm
	Eroded surface	ES	E.Pm
	Quiescent surfaceg	QS	Q.Pm
	Mineralized surfaceh	Md.S	Md.Pm
	Osteoblast surface	Ob.S	Ob.Pm
	Single-labeled surfacei	sLS	sL.Pm
	Double-labeled surfacei	dLS	dL.Pm
	Osteoclast surface	Oc.S	Oc.Pm
	Reversal surfacej	Rv.S	Rv.Pm
Distancek	Cortical thicknessl	Ct.Th	Ct.Wi
	Wall thickness	W.Th	W.Wi
	Mineralized thickness	Md.Th	Md.Wi
	Osteoid thickness	O.Th	O.Wi
	Label thickness	L.Th	L.Wi
	Trabecular thicknessm	Tb.Th	Tb.Wi
	Interstitial thickness	It.Th	It.Wi
	Trabecular diametern	Tb.Dm	—o
	Canal radius	Ca.Rd	—o
	Cell heightc	Ce.Ht	—o
	Nuclear heightd	Nc.Ht	—o
	Erosion depth	E.De	—o
Numberp	Osteoblast number	—	N.Ob
	Osteoclast number	—	N.Oc
	Osteocyte number	—	N.Ot
	Adipocyte number	—	N.Ad
	Nuclear numberd	—	N.Nc
	Canal number	—	N.Ca
	Seam number	—	N.Sm
	Erosion number	—	NE
	Profile number	—	N.Pf

^aArea in 2D.

^bPotential confusion between tissue aggregates and individual structures; see text.

^cSpecify cell type if needed, eg, Oc.V or Oc.Ar.

^dQualify by cell type if needed, eg, Oc.Nc.V.

^eBoundary in 2D.

^fPerimeter in 2D.

^gBS – (OS + ES).

^hES + QS.

ⁱAlternative terms are single- (or double-) labeled interface (sLI, dLI).

^jES – Oc.S.

^kBetween points or lines.

^lWidth in 2D; for the cortex, width and thickness are numerically equal, but for other measurements, thickness = width divided by 4/π or by 1.2.

^mAssumes that trabeculae are thin plates;(54) = 2/(BS/BV).

ⁿAssumes that trabeculae are cylindrical rods;(58) = 4/(BS/BV).

^oNo unique corresponding term in 2D.

^pNo 3D equivalent by standard methods; with appropriate referent could be referred to as density. For further details, see text.

Area measurements

‘‘Mineralized volume’’ is used for simplicity instead of mineralized bone volume and is given by (bone volume – osteoid volume). Osteoid may need to be qualified as lamellar, OV(Lm), or as woven, OV(Wo). Note the distinction in the lexicon between M, which refers to a process, and Md, which refers to a state: for convenience, all tetracycline-based measurements are considered with the kinetic indices discussed earlier. ‘‘Void’’ is a general term applicable to all tissue that is not bone⁽⁴⁴⁾ and includes marrow in cancellous bone and Haversian and Volkmann canals in cortical bone. For both types of tissue, porosity (Po) = void volume/tissue volume.

Problems can arise with area measurements on individual profiles, such as cells or cortical canals. The profiles can be treated as an aggregate of tissue, indicated by use of the appropriate referent. For example, Ce.V/TV is the total area of all cell profiles referred to the total area of tissue and expressed in 3D terms. The profiles can also be treated as individual structures, indicated by absence of a referent; eg, Ca.Ar is the mean area of individual canal profiles. If confusion is still possible, the term could be qualified as total (Tt) or mean (x̄). Mean areas in 2D cannot be extrapolated to mean volumes in 3D unless the structures are counted in 3D.⁽²⁷⁾ Assuming cylindrical geometry, mean canal area can be used to estimate canal radius (Ca.Rd), but it is preferable to measure this directly, as described later.

Perimeter measurements

Osteoid seams do not end abruptly so that some minimum width should be specified for measurement of osteoid surface (OS). We avoid the terms formation (or forming) surface and resorption (or resorbing) surface because the implications of current activity may be erroneous, and for the same reason we avoid the qualification ‘‘active.’’ Eroded surface (ES) is synonymous with crenated or lacunar surface and comprises the osteoclast surface (Oc.S) and the reversal surface (Rv.S); individual erosions can also be classified as osteoclast positive, ES(Oc + ), or osteoclast negative, ES(Oc−). Some mononuclear cells probably resorb bone,⁽⁴⁵⁾ and better methods are needed for identifying and classifying the nonosteoclast cells on the eroded surface or reversal cells. Quiescent surface (QS) is synonymous with resting or inactive surface; the term implies that remodeling activity will return at some future time. The thin layer of unmineralized connective tissue lying beneath the flat lining cells on quiescent surfaces should not be referred to as osteoid.⁽⁴⁶⁾ It is possible that some eroded surface covered by flat lining cells should be counted as quiescent surface rather than as reversal surface.

Distance measurements

In principle, all distance measurements can be obtained in two ways—either by direct measurement at multiple locations or by indirect calculation from measurements of area and perimeter. The direct method is more precise and can provide a frequency distribution and a standard deviation as well as a mean value but requires that measurement sites be randomly selected.⁽⁴⁷⁾ The indirect method is less laborious and less subject to sampling bias. The direct method is usually used for wall thickness, distance between labels, and cell and nuclear dimensions, and the indirect method is usually used for trabecular thickness (plate model), diameter (rod model), and separation. Both methods are widely used for osteoid thickness and cortical thickness. The direct method is essential for reconstructing the remodeling sequence from the relationships between individual measurement values at particular locations and instantaneous values at particular times during the remodeling cycle.^(45,48) The mean value determined by either method in an individual must be distinguished from the mean value in a group of subjects.

Mineralized thickness is the distance from the cement line to the interface between bone and osteoid.⁽⁴⁸⁾ It is used in remodeling sequence reconstruction⁽⁴⁵⁾ and in characterizing different types of abnormal osteoid seam, and defining different stages of severity in osteomalacia;⁽⁴⁹⁾ the mean value should be close to the difference between wall thickness and osteoid thickness. Label thickness is measured on an individual label; it has been used in the rat for calculation of the rate of initial mineral accumulation⁽⁵⁰⁾ and in human subjects as an index of treatment response in renal osteodystrophy.⁽⁵¹⁾ Interstitial thickness (It.Th) is the mean distance between cement lines on opposite sides of a trabecula, usually calculated as Tb.Th-2*W.Th for the plate model.⁽⁵²⁾ Canal radius is an index of bone loss from the cortical surface, but too little is known of the internal geometry of iliac cortical bone to decide the most stereologically correct method of measurement. On the reasonable but unproven assumption that elliptical profiles are the result of oblique sections through cylindrical canals, direct measurements can be restricted to the short axes of the ellipses.⁽⁵³⁾

Number measurements

Most of these are self-explanatory, but restriction to 2D and invariable need for a referent must be reemphasized. In most cases, the referent will be an area or perimeter, but number of nuclei can also be expressed per cell; eg, N.Nc/Oc is the mean number of nuclear profiles per osteoclast profile. Profile number without qualification refers to isolated bone profiles in cancellous bone tissue, a quantity that increases with age as connectivity declines and then decreases as some remaining structures are completely removed. Nodes are branch points and termini are endpoints in a trabecular network that has been skeletonized to facilitate examination of its topological properties.⁽⁵⁵⁾ The ratio of nodes to termini (Nd/Tm) in a section is an index of spatial connectivity.⁽⁵⁶⁾

Derived indices

These can be either structural or kinetic (Table 4). Many of the calculations are based on assumptions that are reasonable but not rigorously established, and individual investigators may decide to use all, some, or none of the indices that we have selected.

Table 4.

Derived Indices in Bone Histomorphometry

Type of index	Name of indexa	Abbreviationa	Formulab
Structural	Trabecular number	Tb.N	(BV/TV)/Tb.Thc
	Trabecular separation	Tb.Sp	(1/Tb.N) – Tb.Thc
	Trabecular width	Tb.Wi	(BV/TV)/Tb.N
Kinetic	Mineralizing surfaced	MS	(dLS + sLS/2)/BSe
	Mineral apposition rate	MAR	Ir.L.Th/Ir.L.t
	Adjusted apposition ratef	Aj.AR	MAR* (MS/OS)
	Osteoid apposition rate	OAR	sameg
	Mineral formation rated	MFR	MAR* (MS/BS)
	Bone formation rated	BFR	sameg
	Bone resorption rated	BRs.R	see text
	Mineralization lag time	Mlt	O.Th/Aj. AR
	Osteoid maturation time	Omt	O.Th/MARh
	Formation period	FP	W.Th/Aj.AR
	Resorption period	Rs.P	FP* (Oc.S/OS)h
	Reversal period	Rv.P	FP* (ES – Oc.S)/OS
	Remodeling periodi	Rm.P	FP* (ES + OS)/OS
	BMU life span (sigma)	Sg (or σ)	see text
	Quiescent period	QP	FP* (QS/OS)
	Total periodj	Tt.P	FP* (BS/OS)
	Activation frequencyk	Ac.f	(1/Tt.P)

^aName and abbreviation are the same whether 2D or 3D expression used, except for mineralizing surface.

^bFor 3D expression, in applying these formulae, it is essential to keep track of units throughout the calculations.

^cFor parallel plate model, see text for rod model.

^dReferent must be specified; /BS is used in formula.

^eOther methods of measurement and calculation can be used (see text).

^fTime averaged over osteoid seam life span.

^gMean value given by preceding quantity in steady state and in absence of osteomalacia.

^hFor a more accurate method, see Eriksen.(45)

ⁱRs.P + Rv.P + FP.

^jRm.P + QP.

^kl/Tt.P.

Structural indices

Trabecular number (or density) is usually calculated with dimensions Length⁻¹ (in specifying dimensions, length and time are usually abbreviated L and T, but these have other meanings in the lexicon) according to the parallel plate model as (BV/TV)/Tb.Th, which is numerically equal to one-half of BS/TV for cancellous bone.⁽⁵⁷⁾ With the alternative cylindrical rod model,⁽⁵⁸⁾ Tb.N is given with dimensions Length⁻¹ by (4/π* BV/TV)^0.5/Tb.Dm. To maintain consistency between the alternative models, this is preferred to the corresponding squared value with dimensions Length⁻². It should be noted that there is ambiguity in the term trabecular number, which has been measured using a different method by others.⁽⁵⁹⁾ By the ASBMR definition, trabecular number goes down with estrogen deficiency, whereas with the alternate definition,⁽⁵⁹⁾ it goes up. Trabecular separation, defined as the distance between edges rather than between midpoints, is calculated according to the parallel plate model as Tb.Th* (TV/BV–l), or as (1/Tb.N)–Tb.Th. This quantity when multiplied by π/2 is an estimate of the mean distance across marrow cavities.^(20,24) According to the cylindrical rod model, and assuming a parallel rectangular lattice, trabecular separation is given by Tb.Dm* ((π/4*TV/BV)^0.5–1) but cannot be related in any simple way to the size of the marrow cavities. Trabecular spacing, defined as the distance between midpoints, is given by 1/Tb.N, and can also be measured directly.⁽⁶⁰⁾

Mineralizing surface

The extent of surface active in mineralization at a particular time is given by the total extent of the labeled surface resulting from label administration at that time. The total extent of double label plus half the extent of single label is equivalent to the mean of the separately measured first label length (L1) and second label length (L2), thus following the normal scientific procedure of taking the mean of two separate observations when they are available. Use of the neutral term mineralizing surface (MS) or mineralizing interface (MI) allows a choice between the mean of the two labels, the second label alone (because it is closer in time to the biopsy), the total label (if only one label was given), in vitro tetracycline staining,⁽⁶¹⁾ histochemical identification of the mineralization front,⁽⁴³⁾ or autoradiography after radiocalcium administration. Whatever the choice, the specification and validation of the method and of the exact conditions of measurement are the responsibility of the investigator and should be clearly stated. MS can be expressed in relation to a variety of referents (Table 2); MS/OS is equivalent to the fraction of osteoid seam life span during which mineralization occurs. It should be noted that length of individual labels varies depending on the fluorochrome. Parfitt and colleagues⁽⁶²⁾ showed that demethylchlortetracycline labels were significantly longer than oxytetracycline labels, regardless of the order in which they were administered. This should be taken into account in the calculation of MS/BS and BFR, and it is particularly important to do so when a quadruple labeling protocol is used to assess longitudinal changes in bone formation rate in a single biopsy.^(63,64)

Apposition rates

Mineral apposition rate (MAR) is the distance between the midpoints⁽³⁰⁾ or between the corresponding edges⁽⁶⁵⁾ of two consecutive labels, divided by the time between the midpoints of the labeling periods. Both the number of sites available for measurement and the mean value of the measurement may vary with the length of the labeling interval,^(30,65) which must always be stated and preferably standardized. We avoid the terms calcification rate and mineralization rate because they may lead to confusion between mineral apposition and mineral accumulation⁽⁶⁶⁾ and are often used in radiocalcium kinetics to refer to the whole body bone formation rate. There is no convenient way of distinguishing between the two-dimensional and three-dimensional quantities by different names, so that if the latter is chosen, it is important that the dimensional extrapolation factor be used consistently. Adjusted apposition rate (Aj.AR) is calculated as MAR*MS/OS, and represents either the mineral apposition rate or the bone formation rate averaged over the entire osteoid surface.^(66,67) It is analogous to the osteon radial closure rate⁽⁶⁸⁾ and is synonymous with effective apposition rate,⁽⁶⁹⁾ corrected apposition rate,⁽⁷⁰⁾ formation velocity,⁽⁷¹⁾ and ‘‘bone formation rate—BMU level—surface referent,’’⁽⁶⁷⁾ but none of these alternative names is satisfactory.

The concept is important because in a steady state and in the absence of osteomalacia the adjusted apposition rate is the best estimate available from a biopsy of the mean rate of osteoid (or matrix) apposition. Under these conditions, the rates of formation of mineralized bone and of bone matrix, time-averaged over the osteoid seam life span, including periods of activity and inactivity, are identical even though their instantaneous values are systematically out of step,⁽⁶⁶⁾ and the term osteoid apposition rate (OAR) may be used. We refer to these quantities (Aj.Ar and OAR) as apposition rates rather than as formation rates to maintain the distinction that an apposition rate has meaning at a point on the surface, whereas a formation rate has meaning only in relation to some aggregate of tissue, either surface or volume. An apposition rate represents in some sense the activity of a team of osteoblasts, but a formation rate is influenced by the rate of remodeling activation and so depends on the number of osteoblast teams as well as on their activity. The team rather than the single cell is emphasized as the conceptual unit because the activity of the team depends on the number of its members as well as on their individual productivity.

Formation and resorption rates

Mineral formation rate (MFR) is the volume of mineralized bone formed per unit time, calculated as the product of mineral apposition rate and mineralizing surface as defined earlier. If this term could be misinterpreted as relating to the physical chemistry of mineralization, the more precise term mineralized bone formation rate (Md.BFR) can be used. In a steady state and in the absence of osteomalacia the mineral formation rate is identical with the bone formation rate (BFR), and except when the distinction is important, the latter and more familiar term should be used. There is a bone formation rate corresponding to each possible referent for mineralizing surface: /OS, /BS, /BV, /TV, and /CV. Bone formation rate calculated using the osteoid surface referent is numerically identical to the adjusted apposition rate, as explained earlier. Expressing bone formation rate per unit of bone surface (BFR/BS) seems most logical when considering hormonal effects on bone remodeling.⁽³²⁾ Bone formation rate per unit of bone volume (BFR/BV) is equivalent to the bone turnover rate, which determines bone age and various age-dependent properties of bone.⁽⁶⁶⁾ Bone formation rate per unit of tissue volume (BFR/TV) seems most logical when considering biochemical markers of bone remodeling because the entire tissue is perfused and contributes its products to the circulation.⁽³²⁾ The significance of the core volume referent was discussed earlier.

Bone resorption rate (BRs.R) cannot be measured directly by histomorphometry but can be estimated indirectly as the bone formation rate increased or decreased by an assumed or measured rate of change of bone volume, provided that all terms are expressed in relation to the same referent.^(30,72,73) Previous gains or losses of bone from a surface can be estimated by comparing trabecular thickness and number, cortical thickness, and osteonal canal radius with mean values in age-matched control subjects, but it cannot be assumed that bone formation persisted at the current rate throughout the time over which these changes occurred. Because the rate of bone loss rarely exceeds 10% of the rate of bone turnover, under most circumstances the error from assuming that resorption and formation rates are equal is less than the error of measurement, but it is more accurate to assume that mineralized volume changes in proportion to some local or whole body measurement of bone mineral.⁽⁷³⁾ An alternative is to use sequential biopsies to estimate the change in bone volume,⁽³⁰⁾ which is satisfactory for a group of adequate size but subject to substantial error from sampling variation in a single subject. However it is estimated, BRs.R can be expressed in relation to a variety of different referents, including osteoclast number.⁽⁷³⁾

Timing of mineralization

Mineralization lag time (Mlt) is the mean time interval between deposition and mineralization of any infinitesimal volume of matrix, averaged over the entire life span of the osteoid seam, and is given by O.Th/Aj.AR. The concept is important in the understanding of osteomalacia and the control of osteoid volume because it can be demonstrated that OV/BV = BFR/BV*Mlt,⁽⁴⁹⁾ corresponding respectively to the birth rate and life span of individual moieties of osteoid.⁽⁶⁶⁾ Osteomalacia has been defined as O.Th > 12.5 mcm (corrected for obliquity) and Mlt > 100 days.^(5,49) Mlt must be distinguished from osteoid maturation time (Omt), which is the mean time interval between the onset of matrix deposition and the onset of mineralization at each bone-forming site. The name implies that the delay results from extracellular modification of the matrix, such as collagen cross-linking.⁽⁶⁶⁾ In the growing rat, Mlt and Omt are identical, but in human subjects Omt is usually shorter and never longer than Mlt. Omt can be estimated as O.Th/MAR, and has also been referred to as direct rather than indirect Mlt,⁽⁷⁴⁾ but it is more accurate to measure Omt by remodeling sequence reconstruction.⁽⁴⁵⁾ Omt provides less insight into the mechanisms of osteoid accumulation than Mlt, but it may be more convenient for diagnostic use because, unlike Mlt, it is always normal in osteoporosis.⁽⁴⁹⁾ Techniques that can be readily applied to embedded biopsy samples, such as microradiography, backscattered electron imaging, and fourier transform infrared spectroscopy, yield important information about the degree of secondary mineralization, which can be correlated with static and dynamic indices of bone formation.^(75–77)

Remodeling cycle duration and its subdivisions

Formation period (FP) is the mean time required to rebuild a new bone structural unit (B.St.U) or osteon from the cement line back to the bone surface at a single location, and is given by W.Th/Aj.AR. It includes so-called downtime or offtime⁽⁶⁸⁾ or whatever other mechanism contributes to the difference between osteoid surface and mineralizing surface that cannot be attributed to label escape,⁽⁶²⁾ and so can be qualified as active, FP(a + ), given by W.Th/MAR, or inactive, FP(a−), given by W.Th/Aj.AR* (OS/MS-l), or FP-FP(a + ). One example of a mechanism that could contribute to a difference between osteoid surface and mineralizing surface is the presence of thin osteoid seams during the terminal period of bone formation when MAR is too low to allow detectable separation of labels or deposition of sufficient amount of tetracycline to allow its visualization.⁽⁷⁸⁾ FP(a + ) has also been referred to as osteoblast life span.⁽⁷⁹⁾ FP is the key quantity needed for calculation of all other temporal subdivisions of the remodeling sequence. In a steady state, fractions of space are equivalent to fractions of time,⁽⁶⁶⁾ so that xP = xS/OS*FP, where x is any remodeling state other than formation, including osteoclastic resorption, reversal, and quiescence (Table 4), but these calculations will reflect the uncertainty in classifying reversal cells.^(45,65) Osteoclasts are motile and their area of activity probably extends beyond their current contact area⁽⁶⁶⁾ and in principle the osteoclast domain (Oc.Dm) determined by scanning electron microscopy⁽⁸⁰⁾ could be used to calculate RP.

The sum of the resorption, reversal, and formation periods is the remodeling period (Rm.P), which is the average total duration of a single cycle of bone remodeling at any point on a bone surface. Rm.P is substantially shorter (by a factor of 2 or 3) than the total duration of bone remodeling activity that follows a single event of activation, because once initiated, the remodeling process moves for a variable distance across the bone surface or through the bone.⁽⁶⁶⁾ For example, many cortical osteons are much longer than a single cortical BMU, including both cutting and closing cones,⁽⁶⁶⁾ and the three-dimensional extent of many trabecular osteons is much larger than the extent of a single erosion or a single osteoid seam.⁽⁸⁾ Although not commonly recognized, it is this extended period⁽⁶⁶⁾ that is the true BMU life span (or sigma) needed for attainment of a new steady state after any pathogenic process or therapeutic intervention.⁽⁶⁸⁾ As it is still used and appears frequently in key reference material, σ remains an acceptable symbol for this crucially important concept; however, Sg is an alternative that avoids the inconvenience and outmoded use of Greek letters.

Activation interval and frequency

The sum of the remodeling period and the quiescent period (QP) is the total period (Tt.P), which is the average time interval between the initiation of two successive remodeling cycles at the same point on the surface.^(45,66) The reciprocal of Tt.P is the activation frequency (Ac.f), which is the probability that a new cycle of remodeling will occur at any point on the surface by the event of activation.^(45,66) Ac.f can also theoretically be calculated in the more traditional manner as the birth rate of remodeling sites of assumed or measured mean area,⁽⁶⁶⁾ and expressed in relation to the various volume referents in Table 2. However, the caveat here is that current technology does not permit measurement of the remodeling site area, particularly in cancellous bone. It can be shown that Ac.f*W.Th = BFR/BS, which is reasonable because W.Th can be regarded as the average amount of bone formed per activation event.

Assessment of dynamic parameters when remodeling rates are low

When methods were first developed for assessment of tetracycline-based parameters of bone formation, states of low remodeling rate were rarely encountered in human iliac crest bone biopsies, except in specific disease states. However, with the advent and widespread use of potent antiresorptive agents, biopsies are now frequently encountered in which turnover rates are so low that there are no labels or only single labels in cancellous and/or cortical bone.⁽⁸¹⁾ One potential reason for lack of labels is that the tetracycline was not taken or properly or efficiently absorbed. This can sometimes be ruled out by the presence of labels in another biopsy compartment, eg, in the cortex or on the endocortical surface. The suspicion that a paucity of labels truly represents a low turnover rate can be supported by low values for static parameters of bone formation, such as osteoid surface or osteoblast number. Reduced tetracycline uptake presents a problem for the reporting and interpretation of the data and requires a uniform approach. In situations where there are no labels in an adequate sampling area, we recommend that MAR be recorded as a missing datum and that the number of such samples in a treatment group be clearly stated in the results section of the article. In this situation, it is appropriate to record a value of zero for MS/BS and to include these samples in the calculation of group means for MS/BS. In biopsies where only single labels or too few double labels are present to measure MAR reliably, MS/BS can be measured and reported in the usual way. MAR can be recorded as a missing value or one has the option of assigning (imputing) a minimum value to MAR. Two such values have been determined empirically: 0.3 mcm/d,⁽⁸²⁾ or 0.1 mcm/d,⁽⁸³⁾ based on either the lowest measurable average value for MAR in the first case or the lowest measured value in the second. The lowest measured value for MAR in the laboratory where the analysis is performed could also be used. Alternatively, if double labels are present in another envelope of the biopsy, say within the cortex, the measured value for MAR in that envelope can be used or one could use the average value for MAR for the cohort to which the subject belongs. In any of these approaches, if MAR is expressed in three dimensions, the appropriate correction factor should be applied (see above). The advantage of assigning a value to MAR when only single labels are present is that a larger number of samples can be used to calculate group means for MAR and parameters derived from it, such as BFR, with the caveat that group means for MAR and the derived parameters may be biased upwards, whereas exclusion of such samples will have the opposite effect. The key recommendation here is that all articles clearly state the numbers of samples in a group with double labels, the number with only single labels, and the number without labels and the method of dealing with single labels. Another option is to present the results using both methods.^(84,85) Some authors have applied extended search protocols to hunt for labels throughout the biopsy.^(84,86) Although this allows a statement to be made on the proportion of biopsies in a treatment group that have labels, it does not change the quantitative data and the extra effort may be disproportional to the additional information obtained. If labels are low or absent in an adequate sampling area, it is likely that they will be low or absent in the rest of the biopsy. The presence or absence of single and double labels should be described separately for cortical and cancellous bone.⁽⁸⁷⁾ The above recommendations for estimating and reporting MAR would also apply in the rare situations in which only one tetracycline label is administered.

Units and dimensions

Two primary units of length, micrometer (mcm) and millimeter (mm), and two primary units of time, day (d) and year (y), should be used, with the choice depending on convenience, consistency, and the principle of providing the most important information in front of rather than after the decimal point. Dimensions are useful for checking equations and derivations⁽⁸⁸⁾ and for indicating the similarities between some quantities expressed in different units. For surface/surface and volume/volume ratios, we prefer percentages rather than decimal fractions; in this case, the percent sign can be used to combine the referent and unit (eg, OS%BS instead of OS/BS(%)). If abbreviations are not used for these ratios, the names can be simplified by writing the type of measurement only once (eg, osteoid/bone [surface]). We avoid units such as mm²/cm² because their magnitude changes with transition from two to three dimensions (eg, 1 mm²/cm² = 10 mm³/cm³). Such units also do not conform to the SI⁽⁸⁹⁾ and make it more difficult to perceive that the quantity is dimensionless. All section dimensions should be expressed in mm, all primary perimeter and area measurements in mm or mm², and all surface/volume ratios in mm²/mm³ (Length⁻¹). Thickness measurements should be expressed in mcm, with mm as an alternative for cortical thickness. Apposition rates should be expressed as mcm/d (Length⁻Time⁻¹) and formation rates with volume referent as %/y (Time⁻¹). Times and periods should be expressed in days or years as most appropriate and activation frequency in /y (Time⁻¹).

Summary of Nomenclature System and Recommended Parameters

We recognize that many who perform bone histomorphometry or interpret its results will on most occasions need to use only a small proportion of the foregoing material. Accordingly, we provide here a summary of its most important features, but this is not intended to stand on its own without reference to the main body of the article. We also provide a list of parameters that preferentially should be included in all histomorphometry studies.

Definitions

All acceptable terms are listed in Table 1; only the most basic are discussed here. The term ‘‘bone’’ refers to bone matrix whether mineralized or not and ‘‘bone tissue’’ refers to bone as defined with its associated marrow or other soft tissue. Bone tissue is usually either cortical or cancellous; the junction between them, which is the inner border of the cortex, is referred to as ‘‘endocortical surface.’’ A trabecula is an individual structural element of cancellous bone tissue, whether plate-like or rod-like in form. The term ‘‘osteoid’’ refers to unmineralized bone matrix that in the normal course of events will become fully mineralized, and does not include the thin layer of permanently unmineralized collagen-containing connective tissue that lies beneath bone lining cells on all quiescent surfaces. The junction between osteoid and mineralized bone is referred to as the ‘‘bone interface’’ or, more precisely, ‘‘osteoidbone interface.’’

The term ‘‘osteoblast’’ is restricted to cells that are assumed to be currently making bone and does not refer to all cells with osteogenic potential. The qualifications ‘‘active’’ and ‘‘inactive’’ are not used; ‘‘inactive osteoblasts’’ are called ‘‘lining cells.’’ Terms that embody assumptions, such as ‘‘formation (or forming) surface’’ and ‘‘resorption (or resorbing) surface,’’ are avoided. Instead, the purely descriptive terms ‘‘osteoid surface’’ and ‘‘eroded surface’’ are used. The extent of currently active mineralization is referred to as ‘‘mineralizing surface’’ (or interface) regardless of how it is estimated. The method used for its determination must be specified and justified. A cylindrical biopsy specimen from the ilium, whether transverse or vertical, is referred to as a ‘‘core,’’ and the term ‘‘total’’ is generally used only when measurements are made on the entire core.

General principles

Dimensional expression

There must be consistent use of only two-dimensional or only three-dimensional terminology and units throughout the same article or the same report. Primary measurements are referred to as area, perimeter, and width if expressed in two dimensions and as volume, surface (or interface), and thickness if expressed in three dimensions (Table 1). Number, the fourth type of primary measurement, can be expressed three-dimensionally only if serial sections are examined. If three-dimensional expression is used, the method of calculation should be exactly specified and its underlying assumptions carefully considered.

Stereology

The terminology and symbols of the International Society of Stereology will not be used. Consequently, the term ‘‘density’’ retains its primary meaning in physics of mass per unit volume. However, this in no way diminishes the importance of stereologic theory for proper sampling, measurement, and dimensional extrapolation.

Referents

An absolute area, perimeter, or number measurement is useful only as an index of the amount of tissue examined, for which acceptable minimum values should be specified (see below); the term ‘‘absolute’’ is not used in any other sense. Of the four types of primary measurement, only width (or thickness) can be interpreted without a referent, which will normally be some defined and measured area (or volume) or perimeter (or surface) in the section. Because several referents are possible for virtually all measurements, the chosen referent must always be specified consistently and explicitly; when this is done, terms such as ‘‘ratio’’ and ‘‘relative’’ are redundant and should not be used. If only one referent is used, or if measurements with the same referent are grouped together, the referent may need to be mentioned only once, but it must be repeated each time if there is any possibility of confusion.

Abbreviations

These consist of the first letters in the same order as the words in the name, without superscripts or subscripts. Each symbol component has only one meaning, as specified in Table 1, and no latitude in the choice of abbreviations is allowed. Single capital letters are used for the most frequent terms, a capital letter and an additional lowercase letter for less frequent terms, and a single lowercase letter for terms that are in some sense related to time. Double letter abbreviations must be demarcated by periods; in the absence of periods, each letter is to be construed as a separate abbreviation.

Standard format

The same format is used for all measurements: Source –Measurement/Referent. The source is the type of structure or region within a sample on which the measurement was made and will most commonly be cortical bone tissue (Ct), cancellous bone tissue (Cn), endocortical surface (Ec), or total biopsy core (Tt), but many other sources are in occasional use (Table 2) or can be defined using the lexicon (Table 1). Circumstances in which the source can be omitted from the name are detailed in the body of the text. Current practice is inconsistent in this respect; even when measurements have only been made on cancellous bone tissue, the source is almost always mentioned for some measurements (eg, trabecular bone volume) and frequently omitted for others (eg, osteoid volume and surface). The need for and the rules pertaining to referents were given earlier. The most commonly used referents are tissue volume (TV), bone volume (BV), bone surface (BS), osteoid surface (OS), and bone interface (BI), but many other referents can be defined for particular purposes (Table 2). The principal referents are related by the surface to volume ratios BS/BV (S/V in stereologic terminology) and BS/TV (S_v in stereologic terminology).

Adequate tissue sampling and recommended measurements

For human iliac crest biopsies, we recommend a Bordier/Rochester type trephine with an internal diameter of at least 7.5 mm (5 mm for pediatric samples). Useful qualitative and quantitative information can be obtained with smaller bore trephines and with vertical rather than horizontal biopsies, but the number of variables that can be reliably quantified is more limited.^(5,90) The minimum acceptable tissue area to be sampled is 30 mm² and the minimum acceptable bone perimeter is 60 mm. We recommend that sections be collected from at least two, and, preferably, three regions within the biopsy starting at about halfway through the core and separated by approximately 300 mcm. Short core widths (Fig. 2) may require additional sampling to achieve the minimum acceptable tissue area and bone perimeter. The number of sections and the tissue area and bone perimeter measured should be reported in all publications. The committee recommends that a minimum of five double labels be used to measure MAR. If necessary MAR can be estimated with fewer double labels, but in that case the lowest number of double labels used to estimate MAR in a group of subjects should be stated.

Table 5 gives a list of measurements that, where practical and appropriate, should be performed and reported in all histomorphometry studies,⁽⁸¹⁾ together with their abbreviations and units. Note that the recommended units are based on two units for length (mcm and mm) and two units for time (day and year), and that percent is preferred for dimensionless ratios. It is conventional to distinguish between static and dynamic measurements, the former not requiring tetracycline labeling, but it is perhaps more important to distinguish between primary measurements (Table 3) and derived indices (Table 4). By primary measurement is meant not the absolute raw data, but the use of no more manipulation of the raw data than is needed to express them in terms of a referent or to divide by a constant such as the time interval between labels. Derived indices require more complex arithmetical manipulation and usually rest on one or more assumptions that should always be made clear. Derived indices should not be reported without the primary measurements from which they are derived.

Table 5.

Terminology, Abbreviations, and Units for Recommended Primary Measurements and Derived Indices in Cancellous Bone Tissue

Parametera,b	Abbreviation	Units
Tissue areac	T.Ar	mm2
Bone areac	B.Ar	mm2
Bone perimeterc	B.Pm	mcm
Bone volume	BV/TVd	%
Wall thickness	W.Th	mcm
Osteoid surface	OS/BS	%
Osteoid volume	OV/BV	%
Osteoblast surface	Ob.S/BSe	%
Osteoblast number	N.Ob/BS	/mm
Osteoid thickness	O.Th	mcm
Eroded surface	ES/BS	%
Osteoclast surface	Oc.S/BSf	%
Osteoclast number	N.Oc/T.Ag	/mm2
Bone surface	BS/TV	mm2/mm3
Double-labeled surface	dLS/BS	%
Single-labeled surface	sLS/BS	%
Mineralizing surface	MS/BS	%
Mineralizing surface	MS/OS	%
Mineral apposition rate	MAR	mcm/d
Adjusted apposition rate	Aj.AR	mcm/d
Mineralization lag time	Mlt	D
Osteoid maturation time	Omt	D
Activation frequency	Ac.F	N/y
Cortical thickness	Ct.Th	mcm
Cortical porosity	Ct.Po	%
Bone formation rate	BFR/BS	mcm3/mcm2/d
Bone formation rateh	BFR/BV	%/y

^aMeasurement name only; need for inclusion of source and/or referent in name varies with context, as discussed in text.

^bThree-dimensional expression except where otherwise stated.

^cShould always be included to allow the reader to assess adequacy of tissue sampling. Should be expressed as a range (minimum – maximum) for the samples analyzed.

^dThe full name and abbreviation would be cancellous bone volume/ tissue volume (Cn-BV/TV).

^eOS is another frequently used referent.

^fES sometimes used as an additional referent.

^gBone perimeter is an alternative referent; note that expression must be 2D, not 3D.

^hEquivalent to rate of bone turnover.