Intravascular contrast agent T₂* relaxivity in brain tissue

Abstract

Dynamic, susceptibility-weighted, contrast-enhanced (DSC) MRI perfusion measurements depend on estimating intravascular contrast agent (CA) concentration (C) from signal intensity changes in $T_2^{\ast }$-weighted images after bolus injection. Generally, linearity is assumed between relaxation and C, but previous studies have shown that compartmentalization of CA and secondary magnetic field perturbations generate deviations from linearity. Physical phantoms using bulk blood have been used to empirically determine the relationship between relaxation rate and C in large vessels. However, the relaxivity of CA in the microvasculature is not easily measured since constructing appropriate phantoms is difficult. Instead, theoretical relaxivity models have been developed. In this study we empirically tested a non-linear expression based on the static dephasing regime (SDR) and a linear approximation. Signal-time curves in white matter (WM) and grey matter (GM) were converted to concentration-time curves (CTCs) using both expressions. Parameters for both the linear and non-linear formulations were adjusted to give the best agreement between cerebral blood volumes (CBV) calculated from the WM and arterial CTCs in a group of normal subjects scanned at 3T. The optimized parameters were used to calculate blood volume in WM and GM in healthy subjects scanned at 3T and in meningioma patients scanned at 1.5T. Results from this study show the non-linear SDR formulation gives an acceptable functional form for tissue relaxivity, giving reliable CBV estimates at different field strengths and echo times.

Introduction

Dynamic, susceptibility-weighted, contrast-enhanced (DSC) MRI is used to characterize perfusion in many neurological conditions including brain ischemia (1–2), multiple sclerosis (1) and brain tumors (3–4). A series of T₂*-weighted images is acquired before, during and after an injection of an intravascular contrast agent (CA). From signal changes occurring during bolus passage, different analyses can be applied to yield estimates of absolute cerebral blood flow (CBF) and volume (CBV) (5–6) or relative CBV (rCBV) (7). Regardless of the analysis, the essential first step is to convert changes in signal to estimates of blood CA concentration, C.

If T₁ effects are neglected, the signal, S, in a DSC MRI experiment is given by

$$S=S_{pre}\text{exp}(-\Lambda (C\left)\right)$$ [1]

where S_pre is the signal before contrast injection and Λ(C) is a function describing signal loss due to the presence of CA in the vasculature. (It should be noted Λ(C) is a unitless function).

In general, CA concentration corresponding to a particular signal is estimated by first calculating signal log ratios, λ

$$\lambda =-\ln \left(\frac{S}{S_{pre}}\right)$$ [2]

and applying the inverse of Λ(C) either analytically or by means of a lookup table:

$$C={\Lambda }^{-1}({\Lambda }_0+\lambda ).$$ [3]

In most studies a linear relationship between C and relaxation rate is assumed so that

$$\Lambda =rC{T}_E$$ [4]

where r is the CA relaxivity constant. However, studies have demonstrated that this linear relationship, while valid in simple solutions, may fail in more structured media and thus can lead to systematic errors in C quantification in vivo (8–9). Worse, relaxivity is generally dependent on both magnetic field and echo time so that DSC results are protocol dependent and cannot be meaningfully compared across studies. For example, the optimal rCBV cutoff for distinguishing low and high grade gliomas has been reported as anywhere between 1.5 and 5.6 (4,10–13).

The exact expression for relaxivity depends on the compartmentalization of CA in different tissue types (8,14–20). Studies of gadopentetate dimeglumine (Gd-DTPA) in bulk blood (and hence large vessels) have found a quadratic relaxivity so that (17,20–22)

$$\Lambda =(pC+q{C}^2)T_E$$ [5]

where p and q are constants.

However, tissue microvasculature is difficult to replicate in a physical phantom and in vivo calibration measurements are difficult to perform. For these reasons, researchers have resorted to theoretical models and Monte Carlo simulations to determine tissue CA relaxivity (14–15,18,23). Two theoretical limiting cases of $T_2^{\ast }$ relaxivity have been described: the static dephasing regime (SDR) and the diffusion narrowing regime (DNR). In the latter, the signal dephasing time is long enough for molecular diffusion to average out phase shifts caused by different magnetic moments (24). DNR holds when the diffusion length of a water proton is much greater than the characteristic distance describing the distribution of contrast agent in tissue. Conversely, the SDR holds when diffusion lengths are small.

The SDR, first formulated by Yablonskiy and Haacke (25) for randomly oriented cylinders, is divided into short and long dephasing time regimes:

$$\Lambda =\{\begin{array}{cc}0.3\zeta {\left(\omega T_E\right)}^2\hfill & \omega T_E\le 1.5\hfill \\ \zeta (\omega T_E-1)\hfill & \omega T_E\ge 1.5\hfill \end{array}\phantom{\}}$$ [6]

where

$$\omega =\eta \pi \gamma ({\chi }_0+kC)B_0,$$ [7]

ς is the tissue vascular fraction, η is a constant that depends on the geometry of the vasculature network, γ is the gyromagnetic ratio, B₀ is the external magnetic field, χ₀ is the magnetic susceptibility due to deoxygenated red blood cells, and k is a coefficient relating susceptibility to Gd-DTPA concentration.

Yablonskiy and Haacke also give an interpolation formula valid over all T_Es (25):

$$\Lambda =\zeta \frac{1}{3}{\int }_0^1(2+u)\sqrt{1-u}\frac{1-J_0\left(\underset{2}{\overset{3}{}}\omega T_{E}u\right)}{u^2}du,$$ [8]

where J₀ is the zeroth order Bessel function and we have included a simplified form for ω in the second form of the equation.

A later study by Kjølby et al. using Monte Carlo and suggested that a linear relationship is adequate to describe relaxivity for T_E > 10 ms when using double-dose contrast (23). However, a more recent simulation study (26) suggests a non-linear relationship is more accurate for single dose.

The purpose of this study was to determine a functional form for Λ that allows reliable estimates of C in WM and GM at different field strengths and echo times. To this end, we compared the full (Eq. [8]) and linear approximation (the long T_E approximation of Eq. [6]) of the SDR model. Constants in these equations can be estimated theoretically (23,25) but depend on factors such as vessel geometry, etc., that are not accurately known. We therefore assumed ω = rCB₀ for the linear model and determined empirically the value of r that gave the best agreement between tissue and arterial bolus curves in control subjects. Similarly, we assumed that ω = (a + bC)B₀ for the full SDR model and found best agreement values of a and b. However, during development we observed that the procedure was very insensitive to the a term giving similarly good fits and similar b values (within about 2%) when it was constrained to be zero. This lack of sensitivity can be explained by the shape of the calibration curve (Fig. 3). Altering the value of the constant term shifts the relaxivity curve along the concentration axis close to the origin. Because the slope of the curve is close to zero at that point, the change in relaxivity is very small. Our final results were therefore derived with a set to zero. (Note that although this also gives a linear relationship between C and ω, Λ is non-linear with C.)

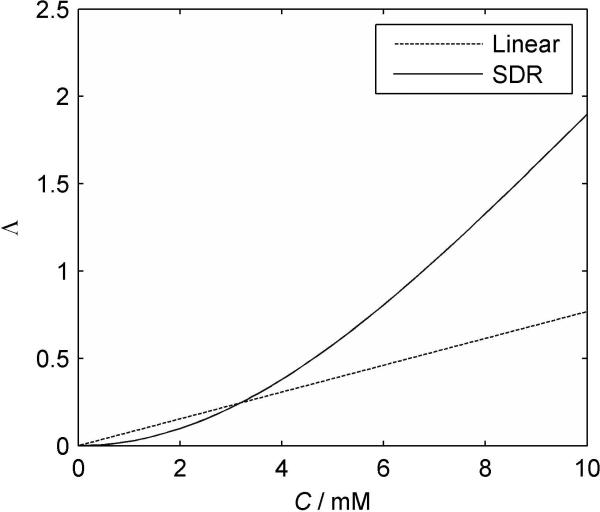
FIG. 3.

Plots of Λ vs. C in blood for the optimized linear (dashed) and SDR (solid) formulations (B₀ = 3T; T_E = 32ms).

The empirically determined values of r and b were then validated in WM and GM at different field strengths and echo times in a different set of subjects.

Experimental

Patient and Imaging Data

This retrospective study was approved by our Institutional Review Board. Data were obtained from 5 meningioma patients scanned at 1.5T who had undergone DSC MRI as part of their standard clinical examination and 10 healthy subjects who had been scanned at 3T. A series of 60 T₂*-weighted single-shot EPI images were acquired from each subject at one second intervals during injection of a standard dose of Gd-DTPA (0.1 mmol/kg) at a rate of 5 ml/sec followed by a 20 ml bolus of saline also at 5 ml/sec. Imaging parameters at 1.5T were: T_E = 40 ms: T_R = 1000 ms, field of view, 228 × 228 mm²; 7 slices; section thickness, 5 mm; matrix, 128 × 128; in-plane voxel size, 1.78 × 1.78 mm²; flip angle, 90° and at 3T were: T_R = 1000 ms, T_E = 32 ms, field of view, 230 × 230 mm²; 12 slices; section thickness, 3 mm; matrix, 128 × 128; in-plane voxel size, 1.79 × 1.79 mm²; flip angle, 30°.

Analysis

All software was written in-house in IDL (ITT Visual Information Solutions, Boulder, CO) and Matlab (Mathworks, Natick, MA).

Subject data were divided into two groups: 5 sets at 3T were used to determine the optimum coefficients in the linear and SDR formulations; 10 test sets were used to test the accuracy of those coefficients.

Optimization Data

WM signals were measured in regions of interest (ROIs) of approximately 10 pixels in the frontal lobes. Arterial pixels were automatically selected using the criterion described by Rempp et al. (5). Selected pixels were ordered by fractional signal drop and the first ten pixels which did not exhibit signal saturation and phase cancellation were averaged.

A basic tenet of DSC MRI is that, in the absence of leakage, the area under the bolus portion of the plasma concentration-time curve (CTC) is equal at all points in the vasculature. The area under the tissue CTC is therefore proportional to the vascular fraction (or blood volume), ς. Hence, if we know the area, A_A, under the bolus estimated in large vessels, we can predict the area under the bolus in white matter, ${\widehat{A}}_{WM}$, using literature values of white matter ς, and taking into account the different hematocrits found in small and large vessels so that

$${\widehat{A}}_{WM}=\zeta \frac{1-H_{SV}}{1-H_{LV}}{A}_A$$ [9]

where ς is the vascular fraction in white matter. In this study we assumed: ς = 0.025 (27); H_LV = 0.4 (28); and H_SV = 0.28 (29).

To find A_A, arterial signals were first converted to estimates of log ratio, λ_A (Eq. [2]) then converted to arterial contrast agent concentration, C_A, using the empirically derived quadratic calibration curves, Eq. [5], with constants p and q those found in bulk blood with 40% Hct (17,21): 1.5T, p = 7.2 s⁻¹mM⁻¹, q = 0.74 s⁻¹mM⁻²; 3T, p = 0.49 s⁻¹mM⁻¹, q = 2.61 s⁻¹mM⁻².

To smooth out noise and simplify calculation of the bolus area, C_A, was modeled by an analytic bolus shape function. The most commonly used bolus shape function is the gamma variate function

$$\mathrm{g}(t:y_{\max },t_{\max },\alpha )=y_{\max }{t}^{\prime \alpha }\exp \left(\alpha \right(1-t^{\prime }\left)\right)$$ [10]

where

$$t^{\prime }=\frac{(t-t_0)}{(t_{\max }-t_0)},$$ [11]

t₀ is the start of the bolus, t_max is the time when the bolus is at maximum height, y_max is the maximum height and α is a decay parameter. (This is the modified form of the gamma variate function introduced by Madsen (30) which is more robust for least squares fitting.) However, the gamma variate does not describe recirculation well. We therefore use a model called the single compartment recirculation (SCR) model (31):

$$C\left(t\right)=g\left(t\right)+\kappa {\int }_0^{t}g\left(\tau \right)d\tau$$ [12]

where κ is a constant less than one (usually about 0.04). This equation is composed of the gamma variate given in Eq. [10] and an integral term that describes recirculating contrast. There is some theoretical justification for this model (32) and, empirically, it describes the data well.

The bolus per se is represented by the gamma variate portion of Eq. [12], so that A_A is given by

$$A_A=\int \mathrm{g}(t:y_{\max },t_{\max },\alpha )dt=y_{\max }{\left(\frac{t_{\max }}{\alpha }\right)}^{\alpha +1}\Gamma (\alpha +1)$$ (13)

where Γ is the gamma function.

White matter concentrations were also modeled by the SCR (Eq. [12]). In general, t₀, t_max and α will be different in WM and arteries due to delay and dispersion. However, the area under the bolus is set to equal to the predicted value, ${\widehat{A}}_{WM}$ (Eq. [9]), which constrains the value of y_max. Similarly κ will be equal to the arterial value since the post-bolus concentration is equal in all vessels (33). This constrained model for white matter concentration is converted to log ratio values using the linear or non-linear formulations and fitted to measured values with t₀, t_max, α and b as free parameters.

In summary, the process proceeds as follows:

1. Measure arterial signal and convert to log ratio estimates, λ_A.

2. Model arterial concentration, C_A and fit to the SCR model with t₀, t_max, y_max, α and κ as free parameters.

3. Calculate the area under the arterial bolus, A_A, and calculate the predicted area under the white matter bolus, ${\widehat{A}}_{WM}$.

4. Measure WM signal and convert to log ratio estimates, λ_WM.

   1. Model WM concentration, C_WM, by the SCR model, convert to log ratio with either the linear or non-linear formulations and fit to λ_WM with κ equal to that found in arteries, y_max constrained to give bolus area $A_{WM}^{\prime }$ and t₀, t_max, α, and b as free parameters.

The derived parameters r (Eq. [4]) and b are the coefficients that give the best agreement between estimated and fitted concentration curves assuming linear and non-linear relaxivities. Uncertainties in r and b were calculated by scaling the formal 1-sigma errors (calculated from the covariance matrix) to the square root of the summed squared residuals divided by the degrees of freedom.

This procedure was carried out on 3T WM data from the five training subjects. (It should be noted that B₀ is equal to 2.89T on our nominally 3T systems.) To obtain the best global estimates all fits were conducted simultaneously with different values of SCR parameters for each data set but a single value of b for all sets.

Test Data

WM and arterial signals were measured as before and GM measurements were taken from the caudate nucleus. The empirically optimized Λ calibration curves were used to calculate estimates of bolus area, ${\widehat{A}}_{WM}$ and ${\widehat{A}}_{GM}$ using Eq. [9] and the fractional error in relative to literature values was calculated

$$FE=\frac{A-\widehat{A}}{\widehat{A}}\times 100\%.$$ [14]

Since CBV is proportional to the bolus area under the tissue curve, the FE in the bolus area is equivalent to the FE in CBV. Single pixel signal measurements were also made in WM and GM to determine how reproducible CBV measurements in noisy data.

As a further test, WM and GM CTCs were directly compared. WM and GM ROIs are sufficiently close that we would expect little differential delay or dispersion between the two. The only difference should then be in amplitude. Specifically the GM curve should be larger by a factorς_GM/ς_WM = 3.8/2.5 = 1.52 (27). The GM CTC values were therefore divided by 1.52 and compared with WM CTCs for both linear and non-linear formulations.

RESULTS

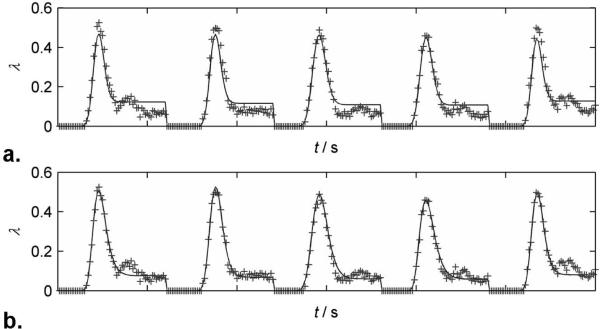
Fig. 1 shows a typical $T_2^{\ast }$- weighted EPI image at 3T and the positions of the WM and GM ROIs and pixels. Fig. 2 shows measured (+) and fitted log ratio (λ) white matter curves in the optimization sets (B₀ = 3T; T_E = 32ms) for both linear (Fig. 2a) and non-linear formulations (Fig. 2b). Data from all patients have been concatenated. The linear formulation clearly underestimates the bolus peak and width and overestimates the recirculation portion (tail) of the curves, while the non-linear formulation yields an excellent fit.

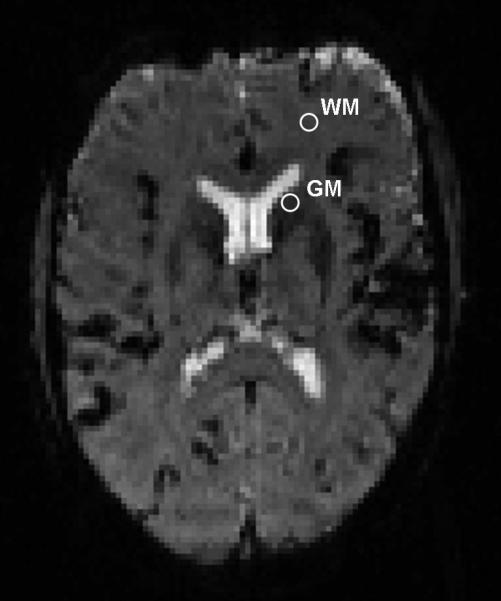
FIG. 1.

$T_2^{\ast }$-weighted DSC MRI image acquired at 3T. Region of interests and single pixels were drawn to measure signal intensities in, WM, normal appearing white matter; and GM, caudate nucleus.

FIG. 2.

Plots of measured (+) and fitted values of log ratio, λ. Each plot is the concatenation of 5 data sets at 3T, T_E = 32ms. a) Linear formulation. b) Non-linear formulation.

Final optimum coefficients and uncertainty in estimated parameters were r = 28.9 ± 0.48 s^-1T^-1mM^-1 and b = 114.4 ± 0.84 s^-1T^-1mM^-1. Fig. 3 shows the two blood calibration curves for WM, B₀ = 3T and T_E = 32ms.

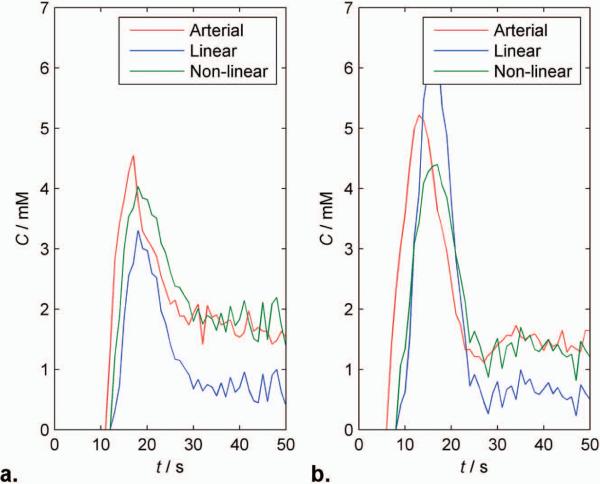
Fig. 4 shows calculated blood CTCs derived from arteries (red) and WM in control patients using the linear (blue) and non-linear (green) formulations in typical test patients at 1.5T and 3T (Fig. 4a and b), respectively (tissue CTCs were normalized by ς to give blood CTCs). At both field strengths, the arterial curve starts before and is narrower, with higher peak height than the SDR WM curves, consistent with delay and dispersion between brain and artery. The heights of the arterial and non-linear curves are very similar in the recirculation phase, after complete bolus dissipation. With the linear formulation, the 1.5T WM curve appears to somewhat underestimate concentration during both bolus and recirculation phases, at 3T the linear formulation markedly underestimates concentration during both phase. Similar effects are seen in fits used to determine b (Fig. 2a). This suggests that finding a single value of b for the linear formulation that reliably describes relaxivity at different field strengths and echo times is difficult.

FIG. 4.

Plots of estimated blood contrast agent concentration from a single patient at a) 1.5T and b) 3T. The concentration estimates were obtained from signals in arteries (red line), white matter using the linear (blue line) and non-linear (green line) formulations. The arterial and white matter concentrations calculated using the non-linear formulation is in excellent agreement when considering delay and dispersion.

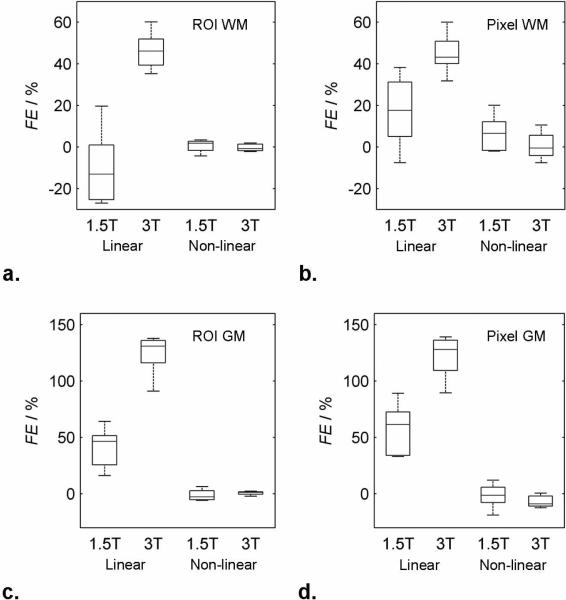
Fig. 5 gives box and whisker plots of fractional errors of measured CBV (i.e. A) from the test data at both 1.5 and 3T and for both linear and non-linear formulations taking ROI and single pixel measurements in WM (Fig. 5a–b) and GM (Fig. 5c–d) and in Table 1. With the non-linear model all values are very close to literature values and the variance is relatively small. The linear model produces a marked bias and large variance in all measurments Results from the individual voxels are noisier than those from the ROIs (as would be expected), but are otherwise similar to the ROI results.

FIG. 5.

Box and whisker plots of fractional error in ROI and single pixel measurements in white matter (a and b) and grey matter (c and d) CBV estimates obtained using the linear and non-linear formulations at 1.5T and 3T. In each box, the central line represents the median of measurements in five test patients, the upper and lower boundaries of the box represent the upper and lower quartiles and the whiskers represents the range.

Table 1.

Fractional error in white and grey matter CBV estimates (%) relative to literature values by the linear and non-linear equations at 1.5 and 3T for both ROI and single voxel measurements.

		1.5T		3T
		ROI	Voxel	ROI	Voxel
WM	Linear	−10.1% ± 18.8	17.2% ± 17.7	46.2% ± 9.4	45.1% ± 10.2
	Non-linear	0.5% ± 3.1	6.5% ± 9.1	−0.3% ± 1.8	0.7% ± 6.9
GM	Linear	40.7% ± 18.6	57.0% ± 23.6	123.9% ± 19.1	121.5% ± 20.0
	Non-linear	−1.1% ± 5.1	−1.6% ± 11.4	0.7% ± 1.8	−6.7% ± 5.5

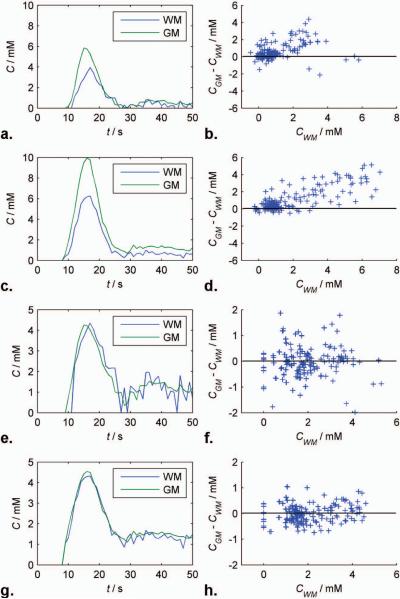
Blood CTCs calculated using linear and non-linear formulations in WM (blue) and GM (green) from a single test patient are shown at 1.5T (Figs. 6a and e) and 3T (Figs. 6c and g), respectively. The remarkable agreement between the two tissue curves at both field strengths suggests that the non-linear SDR formulation is an excellent functional form for brain tissue relaxivity. Differences between scaled GM and WM curves from the beginning of the bolus to 30 seconds after are plotted against WM concentration over all test patients at using linear and non-linear formulations at 1.5T (Fig. 6b and f) and 3T (Fig. 6d and f), respectively. The linear formulation appears to systematically overestimate GM concentration and high concentrations. By contrast, there appears to be no systematic bias to concentration estimates obtained with the non-linear SDR form.

FIG. 6.

Blood concentration-time curves in WM (blue) and GM (green) from a single test patient calculated using linear and non-linear formulations at 1.5T (Figs. 6a and e) and 3T (Figs. 6c and g), respectively. Differences between scaled GM and WM curves from the beginning of the bolus to 30 seconds after are plotted against WM concentration over all test patients at using linear and non-linear formulations at 1.5T (Fig. 6b and f) and 3T (Fig. 6d and f), respectively.

DISCUSSION

Estimating contrast agent concentration from changes in relaxation rate is the essential first step in making contrast-based MRI perfusion measurements. Without an accurate relationship, absolute quantification of perfusion parameters is impossible. Furthermore, because relaxivity in tissues may be a complex function of contrast agent concentration, field strength and echo time (i.e., it is not necessarily a simple linear function), an accurate comparison of results between sites using different imaging protocols is challenging. Although the theory of relaxivity is quite well established it consists of a number of different regimes and it is sometimes unclear which is applicable in practice. We believe that this study represents the first attempt to compare different functional forms for relaxivity – a linear approximation and a non-linear interpolation formula – empirically.

It is clear from Figs. 2 and 3 that the linear approximation underestimates high values of concentration and overestimates low values. Difficulty in reconciling the over- and underestimates with the measured data will contribute to the errors in accuracy seen in Fig. 5, and it seems likely may also contribute to the poor precision. All patients underwent the same injection protocol, if a different injection rate were used or if patients had variable cardiac output, we would expect to see greater errors. Finally, the apparently systematic difference in errors at 1.5 and 3T suggest that a single linear relaxivity constant cannot adequately describe relaxivity at different field strengths or echo times.

The results using the linear function suggest that the correct function should have an increasing slope. That is relaxation rate must change relatively slowly with concentration at low concentration and faster at high concentration. The non-linear formulation is therefore of the more appropriate form (Fig. 3) and gives excellent agreement between: 1) experimental and fitted curves (Fig. 2); 2) arterial and WM derived blood CTCs (Fig. 4) after considering dispersion; 3) CBV values for WM and GM (Fig. 5); 4) WM and GM CTCs (Fig. 6). The agreement appears equally good at the two field strengths and echo times suggesting that the formulation should hold good for a variety of different imaging protocols.

The very low values of fractional error seen with the non-linear model in Fig. 5 are partially because the calibration method used here forces measured values towards the assumed, literature value. (I.e., fractional error is relative to the assumed value not to the true value which is unknown.) However, calibration coefficients were derived from white matter measurements and then applied to grey matter in test subjects. Agreement with literature values of grey matter (which had not been used in the calibration) were nonetheless excellent. Furthermore, the same calibration procedure was used to obtain optimum linear coefficients which still produced an apparent bias in estimates, once again confirming that a linear model is inadequate for describing relaxivity. The systematic overestimation of CBV at 3T relative to 1.5T emphasizes the problems in finding a single linear relaxation relationship that fits multiple field strengths.

The bias in the linear results is due to the inability of linear expression to adequately track the bolus portion of the curve (Fig. 4).

Calibration values were calculated on the basis of PET literature values of WM blood volume, the gold standard. The low fractional error in WM test estimates relative to the same literature values seen in Fig. 5 might therefore be expected. However, GM literature values were not used in the calibration procedure, only in testing, and therefore cannot explain the low fractional error in these estimates. Furthermore, the same literature values of WM were used to obtain the linear calibration curves which nonetheless demonstrate large biases. Furthermore, the low variance of these estimates at both field strengths suggests that even if not accurate they should at least be consistent across field strengths and echo times. Note also, that although it is not often made explicit, the use of literature values of brain blood volumes is universal. Since the relaxivity of contrast in brain microvasculature is unknown, but much greater than that in arteries, it is necessary to introduce a calibration factor to obtain realistic estimates of CBV.

The values for the coefficient b can be found theoretically using Eq. [7]; γ = 2.675·10⁸ rad·s⁻¹T⁻¹, k = 0.027 ppm·mM⁻¹ (34), b is 30 for isotropically distributed vessels (η = (4/3)π (25)) and 45 for vessels perpendicular to the external magnetic field (η = 2π (35)). This compares quite well with the optimum value of 28.9 found for the linear formulation, but is very far from the optimum of 114.4 found for the non-linear formulation. There are number of possible explanations for this. First, Hct and oxygen extraction fraction (OEF) levels vary depending on age, gender and medical conditions and treatment. However, although a rather large effect is seen in the empirical studies of whole blood (21–22,36), it is much reduced when plasma concentration is considered. That is, the relaxivity of X moles of CA per ml of plasma is very similar regardless of Hct or OEF. Since our calibration procedure (Eq. [9]) takes Hct explicitly into account, the effect on our results will be small. Second, the SDR formula is based on modeling the vasculature as infinitely long straight cylinders, which is an idealization that may introduce errors into theoretical estimates. However, it again seems unlikely that these errors will be sufficient to explain the discrepancy. The most likely explanation may lie in inaccuracies in the interpolation formula, Eq. [8]. Although the formula is reliable at low and high concentrations, and is of a reasonable functional form, its accuracy is unknown at intermediate concentrations. The slope of the linear asymptote of Eq. [6] may critically affect the curvature of the interpolation section. Since the brain parenchyma concentrations on which our calibration is based fall into this intermediate range, our results will be biased towards finding good agreement in this range at the expense of accuracy at high concentrations. Support for the hypothesis that the form of the interpolation determines the empirical optimum of b is given by our finding that the alternative interpolation formula of Kiselev (18) gives a very different optimum (~220, even farther from the theoretical value). Better agreement may therefore be found with alternative interpolation formulae. Nonetheless, the empirically optimum value of b used with Eq. [8] gives excellent agreement over the range of concentrations found in normal brain with standard doses of contrast. Furthermore, the success of our calibration values in predicting grey matter CBV suggests applicability when vascular density is moderately increased. However, these values should be used with caution at very high values of C where the linear range applies. Moreover, in areas where vessel density is greatly increased, the effects of diffusional narrowing may begin to invalidate Eq. [6].

The close agreement between between grey and white matter measurements seen in Fig. 6 suggests that the static dephasing regime is adequate to describe relaxivity in normal tissue and therefore that diffusional narrowing (37) is negligible in these circumstances.

There are a number of limitations in this study. 1) We did not attempt to measure Hct or OEF. 2) The empirically determined bulk blood relaxivity curves used in this study were created using a different Gd chelating agent, Optimark gadoversetamide (Gd-DTPA-BMEA), than that used in our study. However calibration curves obtained at 1.5T using different compounds show only small differences. 3) We have considered only Gd contrast agents. Different calibration values are likely to be found with other paramagnetic agents or superparamagnetic agents (e.g., ultra-small, superparamagnetic iron oxide particles). 4) Our control subjects at 1.5T were meningioma patients. Although it would have been preferable to use healthy subjects, it proved difficult to recruit subjects given concerns over nephrogenic systemic fibrosis. However, meningiomas are extra-axial tumors that do not infiltrate into normal brain, and there is no reason to suppose they substantially alter the vasculature. This is confirmed by our finding that CBV estimates in these patients agree with values obtained in controls at 3T. 5) It would have been preferable to obtain our calibration values of WM blood volume by direct measurements of our subjects using the gold standard of PET. We cannot therefore claim that our results in Fig. 5 are accurate but merely consistent with expected values. 6) Finally, this calibration was based on estimates of the arterial input function. This is notoriously difficult to estimate due to partial volume effects. To some extent the procedure presented here is self-correcting in that the coefficients are chosen to give the expected, literature values. That is, if the area under the AIF were reduced by a factor α, then the empirical coefficients r and b would be increased by a similar factor to generate the expected CBV value. (Note, however, that in the non-linear case this would also produce distortions in the CTC. That none are seen in Figs. 4 and 6 provides evidence that AIF partial volume effects were small in this study.) Provided partial volume effects in our subjects were typical, it should not affect the consistency across protocols (rather than precision) of results obtained with these calibration values. Furthermore, the small variance in measured results suggests that AIFs were, in practice, relatively reproducible from patient to patient. This may be because we took particular care to exclude pixels where “spiky” boluses or saturation suggested phase cancellation due to partial volume effects.

In conclusion, we have derived a calibration curve that gives consistent estimates of contrast agent concentration from measured relaxivity changes in white matter and grey matter at different values of T_E and B₀ and which should be applicable in a wide range of conditions. The function has the same functional form as the non-linear interpolation formula of Yablonskiy and Haacke (Eq. [8]) with ω = 114.4 CB₀. Linear approximations are not adequate to describe relaxivity in brain parenchyma. To our knowledge, this study represents the first attempt to confirm any theoretical form of $T_2^{\ast }$ relaxivity in tissue experimentally and the first to provide a reliable expression for relaxivity in the brain.

Glossary

SDR

Static dephasing regime

None

CA

Contrast agent

None

CTC

Concentration-time curve

None

α

Decay parameter in gamma variate function

None

γ

Gyromagnetic ratio

MHzT⁻¹

η

Vascular fraction geometry constant

None

κ

SCR model recirculation constant

None

Λ

Function describing the loss of signal in the presence of vascular paramagnetic ions

None

λ

Measured log ratio of signal

None

ς

Vascular fraction

%

χ

Magnetic susceptibility due to contrast

ppm

χ₀

Susceptibility difference between deoxygenated and oxygenated blood cells

ppm

ω

Angular frequency

rad/s⁻¹

A

Area under the bolus

None

b

Constant describing the susceptibility of microvasculature due to contrast agent

s⁻¹T⁻¹mM⁻¹

C

Contrast agent concentration mM

Hct, H

Hematocrit

%

k

Coefficient relating to contrast agent concentration to susceptibility

ppm·mM⁻¹

p

Linear coefficient in bulk blood relaxivity

s⁻¹mM⁻¹

q

Quadratic coefficient in bulk blood relaxivity

s⁻¹mM⁻²

r

Contrast agent relaxivity constant

s⁻¹mM⁻¹

S

Signal

None

S_pre

Signal before contrast agent injection

None

t₀

Start of the bolus

s

t_max

Time when bolus is at maximum height

s

y_max

Maximum height of bolus

mM

FE

Fractional Error

%

CBV

Cerebral blood volume

mL per 100g tissue