Precise, reproducible measurements of liver iron concentration (LIC) are critical for the early diagnosis, treatment and follow-up of patients with primary or secondary iron overload. Magnetic resonance imaging (MRI), which exploits the paramagnetic properties of iron, has gained acceptance as a noninvasive and accurate tool for LIC assessment. Two different techniques have been described: methods measuring signal intensity ratio between liver and muscles (Gandon, et al 2004), and relaxometry methods measuring absolute R2 (St Pierre, et al 2005) or R2* (Wood, et al 2005) values, which increase proportionally to iron concentration. The gradient-echo R2* technique is most widely used in clinical practice (Anderson, et al 2001, Hankins, et al 2009, Meloni, et al 2011, Wood, et al 2005), because it is faster and easier than R2 acquisition.
R2* values can be converted to underlying tissue iron concentration, using appropriate calibration curves. The first calibration curve was proposed by Anderson et al (2001) and later updated by Garbowski et al (2009). This methodology has been implemented in a popular analysis software named “ThalassaemiaTools”, a CMRtools (Cardiovascular Imaging Solutions Ltd, London, UK) plug-in. A second calibration curve was proposed (Wood et al 2005) and later confirmed (Hankins et al 2009), but it demonstrated a 15% lower scaling coefficient between R2* and LIC.
The two R2* analysis methods differ in the size of analysed region of interest (ROI) and the model used to fit the signal decay at different echo times. A systematic comparison of R2* and LIC values obtained with the two methodologies has never been reported. This study aimed to detect the potential differences in R2* values obtained with different post-processing approaches and to explore whether the detected differences would be corrected when converted into LIC values.
Single- and multi-centre patient cohorts were used. The single-centre cohort included 45 patients (25 males, 16.4±10.2 years) scanned at the Children’s Hospital of Los Angeles (CHLA). The multi-centre cohort (N=47; 19 females, 28.1±8.9 years) was baseline data from a phase II clinical trial of the iron chelator FBS0701 and was included to obtain higher generalizability
The study was approved by the CHLA Committee for the Protection of Human Subjects and the institutional review boards of all participating hospitals.
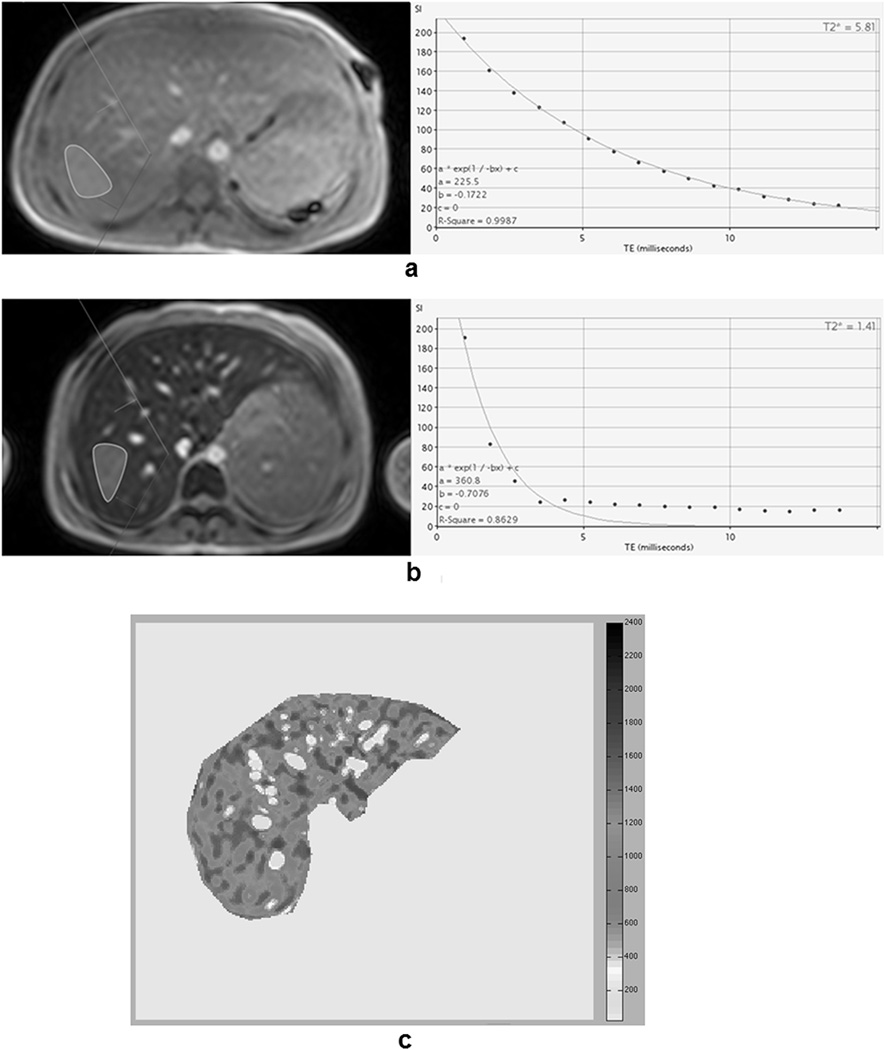
With the ThalassaemiaTools, a ROI was defined in an area of homogeneous liver tissue. All pixels were averaged together and fit to a single-exponential model. Later echo times were manually excluded from the fit in images where iron-mediated signal loss was high (Figures 1a–1b). R2* values (=1000/T2*) were converted into LIC by (Garbowski, et al 2009):
| [Equation 1] |
Figure 1.
a) and b) Screenshot of CMRtools software (region of interest definition in the left and signal decay fitting in the right) for a patient with moderate iron overload and for a patient with severe iron overload, respectively. For the patient with severe iron overload, the single-exponential model was not able to compensate the signal offset. In order to obtain an optimal fitting (R-square > 0.99), the last echo times (TEs) were excluded by de-selecting them. The final T2* was 1.05 ms, corresponding to a R2* of 952.4 Hz and a liver iron concentration (LIC) of 29.3 mg/g/dw. c) R2* map obtained with the Wood’s approach for the same patient in Figure 1b. The mean R2* for this distribution was 1087.9 Hz, corresponding to a LIC of 29.5 mg/g/dw.
In our laboratory R2* measurements were performed using a custom-written software. The ROI included the entire liver profile in the slice, excluding the major hilar vessels. The signal in each pixel was fit to an exponential-plus-constant model, producing a R2* map (Figure 1c). The mean was calculated (R2*Wood). LIC values (LICWood) were calculated as:
| [Equation 2] |
R2* assessment, by either method, is limited to LIC<40 mg/g because rapid signal decay precludes adequate characterization of the relaxation curve for higher iron concentrations.
In order to compare the two approaches linear regression analysis and Bland-Altman technique were used.
The results are indicated in Table I and Supplemental Figures 1, 2.
Table 1.
Comparison between R2*Wood and R2*Pennell values and between LICWood and LICPennell values for the two cohorts of patients. LIC values are expressed also in µmol/g/dw, calculated from values expressed in mg/g/dw.
| Values | Regression Analysis | Bland Altman | ||||
|---|---|---|---|---|---|---|
| Mean ± standard deviation [range] |
Slope | Intercept | R- squared |
Mean difference | Limits | |
| Single-centre cohort | ||||||
|
R2*Wood vs R2*Pennell |
422.3±445.6 Hz [29.7–1344.9 Hz] vs 367.5±380.6 Hz [28.1–1219.5 Hz] |
1.16±0.02 | −3.99±12.72 Hz | 0.982 | 54.7 Hz | −113.3 to 222.8 Hz |
|
LICWood vs LICPennell |
10.9±11.3 mg/g/dw [0.9–34.4 mg/g/dw] vs 11.7±11.4 mg/g/dw [1.5–37.3 mg/g/dw] |
0.98±0.02 | −0.59±0.33 mg/g/dw | 0.991 | −0.8 mg/g/dw | −3.8 to 2.2 mg/g/dw |
|
LICWood vs LICPennell |
195.6±202.6 µmol/g/dw [17.1–615.1 µmol/g/dw] vs 209.9±204 µmol/g/dw [27.6–667.4 µmol/g/dw] |
0.98±0.02 | −10.54±5.97 µmol /g/dw | 0.991 | −14.3 µmol /g/dw | −68.6 to 40.0 µmol /g/dw |
| Multi-centre cohort | ||||||
|
R2*Wood vs R2*Pennell |
499.8±314.2 Hz [64.2–1237.6 Hz] vs 440.4 ± 256.1Hz [62.2–1087.0 Hz] |
1.21± 0.02 | – 32.07±16.31 Hz | 0.969 | 59.5 Hz | −90.8 to 209.7 Hz |
|
LICWood vs LICPennell |
12.9±7.9 mg/g/dw [1.8–31.6 mg/g/dw] vs 13.9±7.7 mg/g/dw [2.5–33.3 mg/g/dw] |
1.02±0.03 | −1.33±0.43 mg/g/dw | 0.969 | −1.0 mg/g/dw | −3.8 to 1.8 mg/g/dw |
|
LICWood vs LICPennell |
230.9±142.9 µmol/g/dw [32.8–566.3 µmol/g/dw] vs 249.0±137.5 µmol/g/dw [45.9–596.2 µmol/g/dw] |
1.02±0.03 | −23.82±7.71 µmol /g/dw | 0.969 | −18.2 µmol /g/dw | −67.7 to 31.4 µmol /g/dw |
For both the cohorts the relationship between R2*Wood and R2*Pennell values was well described by a line. Results were unbiased for R2*<300 Hz, but large systematic differences in R2* appeared at higher values, with the exponential-plus-constant fits averaging ~20% higher. For the single-centre cohort the mean difference (± standard deviation) was 54.7±85.7 Hz (95% confidence intervals [CI], 28.9–80.5 Hz), corresponding to a percentage R2* difference of 9.1±11.8%. Individually, 41 patients (93%) had R2*Wood>R2*Pennell value. For the multi-centre cohort the mean difference was 59.5±76.7 Hz (95%CI, 36.9–81.9 Hz), corresponding to a relative difference of 8.5±13.8%.
When the technique-appropriate calibration curves were used, this bias effectively disappeared, producing excellent agreement between the two approaches. For the single-centre cohort the mean difference was −0.8±1.5 mg/g/dry weight (dw) (95%CI, −1.3 to −0.3 mg/g/dw). Individual LIC estimates had 95%CI from −3.8 to 2.2 mg/g/dw. For the multi-centre cohort the mean difference was −1.0±1.4 mg/g/dw (95%CI, −1.4 to −0.6 mg/g/dw), indicating a small, systematic bias. Individual LIC estimates had 95%CI of −3.8 to 1.8 mg/g/dw.
There is ongoing discussion as to which of the two decay models most closely describes the true tissue relaxation. By simulation (true value known), the key determinant is whether there is any other signal contribution besides iron. If there is any background signal from non-iron containing tissue, the exponential-plus-constant model is more accurate (Positano, et al 2009). If there is no signal contribution from bile, blood or fat, the truncated exponential is more appropriate (Beaumont, et al 2009).
Given that the two approaches sample the liver differently, one could potentially attribute the observed R2* differences to systematic gradients in iron distribution with proximity to the hilum. This was demonstrated to be untrue (McCarville, et al 2010, Positano, et al 2009).
The 0.8–1 mg/g residual bias between the two LIC estimates is clinically irrelevant at higher values, but could be important when assessing the risk of over chelation. Some of the bias is evident from inspection of Equations 1 and 2; the calibration curves have a 0.5 mg/g difference in y-intercept. To ensure good extrapolation into normal iron levels, the y-intercept in Equation 2 was constrained such that the calibration curve passes through the middle of the normal range (Wood, et al 2005), while Equation 1 was not. To illustrate the potential consequences of this difference, R2* values in healthy volunteers are typically reported to be 30–40 Hz. Equation 2 predicts LIC values of 1.0–1.2 mg/g and Equation 1 predicts LIC values of 1.4–1.6 mg/g. Practitioners who use Equation 1 should know that “normal” LIC corresponds to a value around 1.5 mg/g and base their therapeutic judgments about that set-point.
In conclusion, both signal decay models yield clinically-acceptable estimates of LIC if the ROI’s are drawn correctly and the proper calibration curve is applied to correct for systematic differences in R2* estimation. Proper choice of technique at any given institution will depend on software availability and training. However, in the literature, R2* values should be converted into LIC values using the appropriate calibration curve to facilitate comparisons across studies.
Supplementary Material
ACKNOWLEDGMENTS
This work was supported by a grant from the National Institutes of Health, National Heart Lung and Blood Institute (1 RO1 HL075592-01A1), the Center for Disease Control (1 U01 DD000309-1), the National Center for Research Resources, Children’s Hospital Los Angeles General Clinical Research Center (RR00043-43) and FerroKin BioSciences as sponsor of the study.
We thank all patients for their cooperation.
Footnotes
AUTHORSHIP CONTRIBUTIONS
AM analysed the images, performed the statistical analysis and wrote the manuscript. HR, AJ, AP and ML contributed to the interpretation of the results. JCW conceived the study and was involved in writing the manuscript.
COMPETING INTERESTS
The authors declare no competing interests.
REFERENCES
- Anderson LJ, Holden S, Davis B, Prescott E, Charrier CC, Bunce NH, Firmin DN, Wonke B, Porter J, Walker JM, Pennell DJ. Cardiovascular T2-star (T2*) magnetic resonance for the early diagnosis of myocardial iron overload. European Heart Journal. 2001;22:2171–2179. doi: 10.1053/euhj.2001.2822. [DOI] [PubMed] [Google Scholar]
- Beaumont M, Odame I, Babyn PS, Vidarsson L, Kirby-Allen M, Cheng HL. Accurate liver T2 measurement of iron overload: a simulations investigation and in vivo study. Journal of Magnetic Resonance Imaging. 2009;30:313–320. doi: 10.1002/jmri.21835. [DOI] [PubMed] [Google Scholar]
- Gandon Y, Olivie D, Guyader D, Aube C, Oberti F, Sebille V, Deugnier Y. Non-invasive assessment of hepatic iron stores by MRI. Lancet. 2004;363:357–362. doi: 10.1016/S0140-6736(04)15436-6. [DOI] [PubMed] [Google Scholar]
- Garbowski MJ, Carpenter JP, Smith G, Pennell DJ, Porter JB. Calibration of Improved T2* Method for the Estimation of Liver Iron Concentration in Transfusional Iron Overload. Blood (ASH Annual Meeting Abstracts) 2009;114:791. abstract 2004. [Google Scholar]
- Hankins JS, McCarville MB, Loeffler RB, Smeltzer MP, Onciu M, Hoffer FA, Li CS, Wang WC, Ware RE, Hillenbrand CM. R2* magnetic resonance imaging of the liver in patients with iron overload. Blood. 2009;113:4853–4855. doi: 10.1182/blood-2008-12-191643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarville MB, Hillenbrand CM, Loeffler RB, Smeltzer MP, Song R, Li CS, Hankins JS. Comparison of whole liver and small region-of-interest measurements of MRI liver R2* in children with iron overload. Pediatric Radiology. 2010;40:1360–1367. doi: 10.1007/s00247-010-1596-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meloni A, Luciani A, Positano V, De Marchi D, Valeri G, Restaino G, Cracolici E, Caruso V, Dell'amico MC, Favilli B, Lombardi M, Pepe A. Single region of interest versus multislice T2* MRI approach for the quantification of hepatic iron overload. Journal of Magnetic Resonance Imaging. 2011;33:348–355. doi: 10.1002/jmri.22417. [DOI] [PubMed] [Google Scholar]
- Positano V, Salani B, Pepe A, Santarelli MF, De Marchi D, Ramazzotti A, Favilli B, Cracolici E, Midiri M, Cianciulli P, Lombardi M, Landini L. Improved T2* assessment in liver iron overload by magnetic resonance imaging. Magnetic Resonance Imaging. 2009;27:188–197. doi: 10.1016/j.mri.2008.06.004. [DOI] [PubMed] [Google Scholar]
- St Pierre TG, Clark PR, Chua-anusorn W, Fleming AJ, Jeffrey GP, Olynyk JK, Pootrakul P, Robins E, Lindeman R. Noninvasive measurement and imaging of liver iron concentrations using proton magnetic resonance. Blood. 2005;105:855–861. doi: 10.1182/blood-2004-01-0177. [DOI] [PubMed] [Google Scholar]
- Wood JC, Enriquez C, Ghugre N, Tyzka JM, Carson S, Nelson MD, Coates TD. MRI R2 and R2* mapping accurately estimates hepatic iron concentration in transfusion-dependent thalassemia and sickle cell disease patients. Blood. 2005;106:1460–1465. doi: 10.1182/blood-2004-10-3982. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.