Abstract
Here we describe an easily implemented protocol based on sparse MR acquisition and a scrambled ‘music’ auditory stimulus that allows for reliable measurement of functional activity within the medial geniculate body (MGB, the primary auditory thalamic nucleus) in individual subjects. We find that our method is equally accurate and reliable as previously developed structural methods, and offers significantly more accuracy in identifying the MGB than group based methods. We also find that lateralization and binaural summation within the MGB resembles that found in auditory cortex.
Keywords: medial geniculate body, auditory cortex, functional magnetic resonance imaging
Introduction
Compared to vision, a great deal of auditory processing occurs sub-cortically, within areas such the brainstem, midbrain, and thalamus (Ehret and Romand, 1997, Jones, 2003). The medial geniculate body (MGB) plays a key role in this pathway. As well as providing a thalamic relay between the inferior colliculus (IC) and the auditory cortex (AC), subregions of the MGB are involved in multiple ascending and descending auditory and multisensory pathways (see Winer et al., 2005, for a review). One difficulty in neuroimaging the human MGB is that it has proved quite difficult to reliably identify, either structurally or functionally, within individual subjects.
Individual thalamic nuclei are not distinctively revealed in typical T1- or T2- weighted structural scans. Devlin et al. (2006) described two methods for identifying the MGB anatomically in individual subjects: high-resolution proton density weighted scanning optimized for sub-cortical grey-white contrast, and tractography based on diffusion weighted imaging scans. Both methods can identify the MGB with reasonably reliability, but remain technically challenging. More recently, susceptibility weighted imaging (Haacke et al., 2009) has been proposed, but not yet validated, as a method of identifying the MGB. However SWI acquisition and analyses are challenging to implement.
When relying on functional data to localize a given area, there is a continuum of possible approaches, ranging from using a separate condition as a functional localizer to predetermine the area of interest at one extreme, to carrying out whole brain analyses for the contrast of interest and identifying focal activity in an appropriate region as MGN responses (see Friston and Henson, 2006, Friston et al., 2006, Saxe et al., 2006, for a discussion of the strengths and weaknesses of these two approaches across different paradigms).
However, to date, there is no validated technique for functionally localizing the MGB, and as a result most (though not all Noesselt et al., 2010) papers examining MGB responses have relied heavily on group averaged responses to identify the MGB (Giraud et al., 2000, Griffiths et al., 2001, Krumbholz et al., 2005). This has been the case even when individual subject responses were of interest and an individual functional localizer ROI approach might therefore have been more optimal (von Kriegstein et al., 2008, Diaz et al., 2012). As described in more detail below, when comparing results across individuals using a group ROI, if a generous group ROI is chosen, then responses within individual subjects are likely to be averaged across an ROI that contains a high proportion of noise voxels. On the other hand, a more stringent choice of group ROI has the potential to underestimate MGB responses within individuals whose MGB falls outside the group ROI.
There are a number of potential reasons why functionally identifying the MGB may have proved so difficult. First, subcortical structures located near the brain stem can suffer from pulsatile motion effects. Factoring out these pulsatile motion effects using cardiac gating has been shown to improve signal to noise, but not sufficiently to allow for reliable imaging of the MGB within individuals (Guimaraes et al., 1998). However, BOLD modulation within the neighboring LGN can be can be imaged reliably without the need for cardiac gating (Wunderlich et al., 2005, Schneider and Kastner, 2009). Second, the MGB is small, with a volume of approximately 90 mm3 in humans (5 mm wide, 4 mm deep, and 4-5 mm long, Winer, 1984). However visual responses within subdivisions (Schneider et al., 2004, Haynes et al., 2005) of the neighboring lateral geniculate nucleus have been measured. Thus is seems likely that neither cardiac motion nor the small size of the MGB fully explain why it is so difficult to obtain reliable individual responses within the MGB.
Another possibility is that MGB responses to commonly used experimental stimuli, such as simple tones, noises, or dynamic spectral ripples, might be relatively small, especially compared to the strong acoustic transients generated by environmental scanner noise. In non-human primates, MGB neurons are responsive to natural and artificial sounds that vary along a diverse range of spectral and temporal feature dimensions (Symmes et al., 1980, Allon and Yeshurun, 1985, Bartlett and Wang, 2011). Moreover, the MGB has been demonstrated to show strong responses to complex speech-like stimuli (von Kriegstein et al., 2008, Diaz et al., 2012). Here we examined whether clearer responses within the MGB might be elicited by using stimuli containing spectrotemporally complex features (such as transients, broadband content, tonal elements and a low degree of predictability) while minimizing the effects of scanner noise by using sparse imaging.
Three experiments were carried out: in Experiment 1 we measured responses in the MGB to scrambled music in a passive listening task. In Experiment 2 we measured responses in the MGB to scrambled music while subjects carried out a one-back task where they had to identify when a music segment was consecutively repeated multiple times. In Experiment 3 we measured responses in the MGB while subjects passively listened to a dynamic ripple stimulus. These experiments demonstrate that a complex stimulus (scrambled music) containing complex elements (transients, broadband content, tonal elements and a low degree of predictability) can reliably identify the MGB within individuals when combined with a sparse acquisition protocol.
Methods
Participants
A total of 11 young adults (4 males; 1 left-handed; 27.4 ± 4.7 years old) participated across all three experiments. Nine subjects carried out Experiment 1 (passive listening), nine subjects carried out Experiment 2 (1-back task): there was an overlap of 7 subjects between Experiments 1 and 2. The order of experiments was counterbalanced for subjects who participated in Experiments 1 and 2. Four of the subjects who participated in Experiment 1 also carried out Experiment 3 (dynamic ripple).
All participants reported normal hearing and no history of neurological or psychiatric illness. Written and informed consent was obtained from all participants prior to the experiment, following procedures approved by the Institutional Review Board of the University of Washington Human Subjects Division of the University of Washington.
Auditory stimuli
Auditory stimuli were delivered via MRI-compatible stereo headphones (Sensimetrics S14, Malden MA) and sound intensity was adjusted to each individual participants’ comfort level. The intensity in the binaural condition was scaled by -6 dB in each ear relative to the monaural case to equate the total sound amplitude across monaural and binaural conditions. Equating the amplitudes in this way reduces differences in loudness across conditions, but unfortunately did not allow us to measure binaural interactions.
Scrambled music
For both Experiment 1 and Experiment 2, auditory stimuli consisted of scrambled musical segments extract from popular music including “God shuffled his feet” (Crash Test Dummies), “Will o’ the wisp” (Miles Davis), and “Saeta” (Miles Davis). Miles Davis tracks consisted of music only, both Crash Test Dummies tracks contained lyrics. For each scan, only one sound file (i.e., one song) was used, and the order of the files was kept the same for all participants. Overall sound levels were scaled to equate amplitude across three songs. Scrambling was done by reading song files into MATLAB (Mathworks, MA), subdividing these files into 900ms segments, and then presenting these 900ms segments in a scrambled order. Each 8s stimulus presentation interval consisted of 8 randomly selected 900ms segments, separated by 100ms silent intervals, presented either monaurally or to both ears.
Dynamic ripple
For Experiment 3, the auditory stimulus was dynamic ripple, a spectrally and temporally modulated complex broadband stimulus that has been used to study BOLD responses in auditory cortex (Langers et al., 2003, Schonwiesner and Zatorre, 2009). Following Lanting et al. (2008), we used a dynamic-ripple stimulus that consisted of temporally and spectrally modulated noise, with a frequency range of 125-8000 Hz, a spectral modulation density of one cycle per octave, a temporal modulation frequency of two cycles per second, and a modulation-amplitude of 80%. This dynamic-ripple stimulus was presented both binaurally or monaurally in a single session, using analogous methods as for the passive scrambled music experiment (Experiment 1).
Procedure
All participants were instructed to close their eyes and pay attention to the auditory stimulus. In Experiment 1 and Experiment 3 there was no task (mimicking the passive localizer stimuli traditionally used to identify the LGN, Schneider and Kastner, 2009). In Experiment 2, we included a one-back task, where participants were required to press the response button when they detected a consecutively repeated 900-ms segment. Such repetitions occurred randomly, 3-4 times during each scan.
During a stimulus presentation interval, scrambled musical segments were delivered either to both ears (binaural condition), to the right ear (monaural right condition), or to the left ear (monaural left condition). The monaural right condition is described as the contralateral condition for regions in the left hemisphere and as the ipsilateral condition for regions in the right hemisphere, and vice versa for the monaural left condition. We also included a 4th condition in which no sound was delivered during the stimulus presentation interval (silence condition). Conditions were presented in a fixed order (binaural, monaural right, monaural left, and silence) across all experiments. Each condition was repeated 8 times in a scan for a total of 32 8s auditory stimulus presentation intervals (each followed by 2s MR acquisition). Each scan therefore lasted for 320s (10 s × 4 conditions × 8 reps). Each subject carried out six scans, which resulted in a total of 48 repetitions per condition over the course of scanning for each of the three experiments.
MRI scanning
Blood oxygenation-level dependent (BOLD) functional imaging was performed with a 3T Philips system at the University of Washington Diagnostic Imaging Sciences Center (DISC). The scan protocol consisted of 2.75 × 2.75 × 3 mm voxels; repetition time, 10 s; echo time, 16.5 ms; flip angle, 76°; field of view, 220 × 220; 32 transverse slices. Three-dimensional (3D) anatomical images were acquired at 1×1×1mm resolution using a T1-weighted MPRAGE (magnetization-prepared rapid gradient echo) sequence.
A sparse echo planar imaging pulse sequence was used so that stimulus presentation was uninterrupted by acoustic MRI scanner noise (Hall et al., 1999). 2s volume acquisitions were preceded by a 8s delay period during which there was no scanner noise and the auditory stimuli were delivered (Figure 1). Because of a hemodynamic delay of about ~4-5 s to peak response within auditory cortex (Jancke et al., 1999, Inan et al., 2004), each volume acquisition measures BOLD response to stimulation during the middle of the stimulus presentation period, with relatively little contribution from the acoustic scanner noise of the previous acquisition. It is worth noting that the longer delay between acquisitions (which allows for more time to restore magnetic equilibrium) results in a higher signal-to-noise ratio for each individual acquisition, which partially but not entirely compensates for the reduced number of acquisitions (Hall et al., 1999).
Figure 1.
Sparse echo planar imaging pulse sequence used to minimize the contribution of MRI scanner noise. 8s of auditory stimulus (Binaural, Right and Left monaural, and Silence) were interspersed with 2s volume acquisitions.
fMRI data analysis
Data were analyzed using BrainVoyager QX (Version 2.3, Brain Innovation, Maastricht, the Netherlands) and MATLAB (Mathworks, MA). Prior to statistical analysis, the functional data underwent standard preprocessing steps that included 3D motion correction (trilinear/sinc interpolation), linear trend removal, and high-pass filtering to remove nonlinear low frequency drifts using a standard GLM approach implemented within BrainVoyager. The chosen method for high pass filtering was the GLM approach using a Fourier basis set consisting of 2 cycles of sines/cosines as predictors for lower frequencies (BrainVoyager Users Guide: Temporal High Pass Filtering). No spatial smoothing was applied to functional data. Both anatomical and functional data were transformed and up-sampled into Talairach space (Talairach and Tournoux, 1988) at 1×1×1mm resolution.
A combination of anatomical (the expected location and size of the MGB) and functional criteria were used to define the MGB in each individual subjects. We defined each subject's MGB as including approximately 100 contiguous voxels (at 1×1×1 anatomical resolution: 110 ± 20 in Experiment 1 and 103 ± 24 in Experiment 2) that significantly activated for any of the three non-silent conditions in the expected anatomical location (Naidich et al., 2009). Significance values were based on the ‘goodness of fit’ of a full 3 factor (binaural, monaural right, and monaural left) fixed effects general linear model. The use of a fit value based on the full 3 factor model ensured that the selection of MGB voxels was not biased towards or against any condition. Unsurprisingly, the significance level of activation varied across individual subjects, but was never less than p<0.05, uncorrected.
Group MGBs for both Experiment 1 and Experiment 2 were defined using fixed effects thresholds of p(bonf) < 0.05, p(bonf) < 0.01 and q(FDR) <0.001 (multiple comparison correction using the false discovery rate statistic, this threshold is less stringent than p(bonf)<0.05, Genovese et al., 2002).We also defined group MGBs using random effects thresholds of p < 0.01, p < 0.005, and p < 0.001.
Auditory cortex ROIs were defined for each participant for each of the three experiments using a cluster centered on Heschl's gyrus (“HG”) with maximum spread range (the spatial extent in three dimensions around the selected center) of 5 1×1×1mm voxels. This resulted in a cluster that consisted of a maximum of 125 voxels that surrounded the most highly activated voxel in Heschl's gyrus.
Beta weights were then estimated for all experimental conditions within these ROIs in Brain Voyager using a fixed effects standard generalized linear model. Further custom analyses were carried out using custom software written in MATLAB (Mathworks, MA).
Results
Across Experiment 1 (Scrambled music passive listening) and 2 (Scrambled music 1-back task), we were able to functionally localize MGB in both left and right hemispheres within 9 of our 11 participants, Figures 2 and 3 and Table 1. The two participants in whom we failed to localize MGB within both hemispheres (one subject from Experiment 1, the other from Experiment 2) had permanent stainless-steel dental retainers. Though stainless steels in dentures and braces are known to produce MRI artifacts in the facial region (New et al., 1983, Hinshaw et al., 1988) it has not yet been reported that orthodontic retainers reduce the detectability of sub-cortical activation. Data from these two participants were not included in further analyses.
Figure 2.
Individually localized MGB for the 8 (of 9) subjects for whom we were able to successfully identify the MGN in Experiment 1 (Passive listening). Average Talairach coordinates of individually defined functionally localized MGB are shown in Table 1.
Figure 3.
Individually localized MGB for the 8 (of 9) subjects for whom we were able to successfully localized in Experiment 2 (1-back task).
Table 1.
Average Talairach coordinates of functionally localized MGB
| Subject | x | y | z | Number of Voxels | x | y | z | Number of Voxels |
|---|---|---|---|---|---|---|---|---|
| RH |
LH |
|||||||
| Exp. 1 Passive Listening | ||||||||
| S01 | 14 | -26 | -4 | 71 | -16 | -25 | -6 | 98 |
| S02 | 15 | -26 | -5 | 106 | -16 | -25 | -4 | 91 |
| S03 | 12 | -27 | -6 | 134 | -17 | -25 | -5 | 131 |
| S04 | 11 | -27 | -9 | 118 | -16 | -30 | -7 | 118 |
| S05 | 16 | -23 | -7 | 106 | -18 | -24 | -7 | 138 |
| S06 | 10 | -25 | -4 | 98 | -16 | -25 | -3 | 97 |
| S07 | 13 | -25 | -6 | 138 | -14 | -25 | -6 | 123 |
| S08 | 14 | -25 | -5 | 109 | -18 | -26 | -6 | 82 |
| Exp. 2 1-Back Task | ||||||||
| S01 | 14 | -26 | -4 | 53 | -15 | -25 | -6 | 101 |
| S02 | 14 | -28 | -7 | 88 | -15 | -29 | -7 | 127 |
| S03 | 14 | -24 | -6 | 119 | -16 | -23 | -7 | 58 |
| S04 | 15 | -27 | -6 | 105 | -16 | -27 | -5 | 118 |
| S05 | 14 | -24 | -5 | 96 | -15 | -24 | -13 | 125 |
| S06 | 11 | -26 | -6 | 126 | -17 | -23 | -7 | 120 |
| S07 | 13 | -24 | -6 | 133 | -14 | -24 | -6 | 93 |
| S09 | 14 | -24 | -6 | 100 | -16 | -23 | -6 | 92 |
Experiment 1: Passive listening
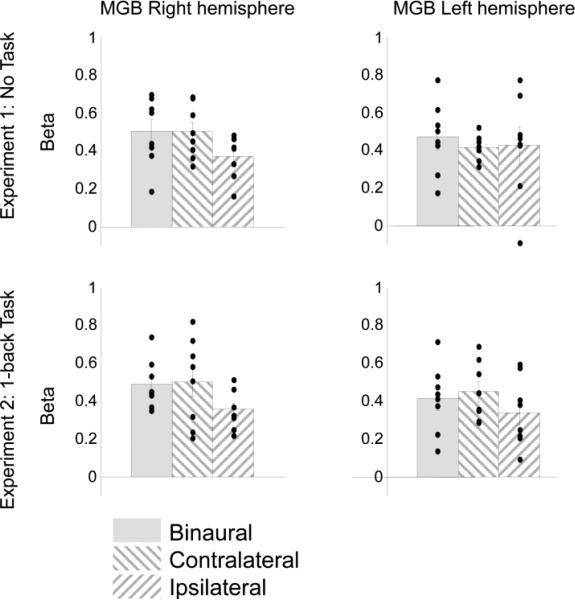
Bilateral MGBs were localized in 8 of 9 participants (Talairach coordinates, mean ± SD, right: x 13±2, y -26±1, z 6±2, size 110±21; left: x -16±1, y -26±2, z -6±1, size 110±20; see Figure 2 and Table 1 for the Talairach location for subjects in whom the MGB was successfully defined). Condition-related Beta weights (averaged across all the voxels in the ROI) were then estimated from individually localized MGB (Figure 4, upper panels) and HG ROIs (Figure 5, upper panels).
Figure 4.
Average MGB activation for Binaural, Contralateral and Ipsilateral stimulation averaged across subjects, shown for both left and right MGB in Experiment 1 (Passive listening, upper panels, n = 8) and Experiment 2 (1-back task, lower panels, n = 8). Black dots represent individual subjects and error bars represent the standard error across subjects.
Figure 5.
Average HG activation for Binaural, Contralateral and Ipsilateral stimulation averaged across subjects, shown for both left and right HG in Experiment 1 (Passive listening, upper panels, n = 8) and Experiment 2 (1-back task, lower panels, n = 8). Black dots represent individual subjects and error bars represent the standard error across subjects.
A 3-way repeated measures ANOVA was used to test the difference between areas (HG vs. MGB), between hemispheres (left vs. right), and among auditory stimulation conditions (Binaural, Contralateral, Ipsilateral). There was a main effect of area (F(1, 7) = 316.26, p < 0.0001), with higher activation found in the HG than in the MGB. There was no main effect of hemisphere (F(1, 7) = 3.21, ns), though there was a trend for the interaction between hemisphere and area (F(1, 7) = 5.18, p = 0.057). This is most likely driven by higher overall activation in the left HG ROI then in the right HG ROI, as shown in Figure 5 (upper panels).
The main effect of stimulation condition was highly significant (F(2, 14) = 23.98, p < 0.0001). Duncan's multiple range test showed Binaural and Contralateral activation to be significantly higher than Ipsilateral activation (ps < 0.05). These differences across conditions were more evident in the HG than in MGB, which resulted in a significant interaction between area and condition (F(2, 14) = 4.92, p < 0.03). There was no significant difference in activation level between Bilateral and Contralateral stimulation conditions.
Neither the two-way interaction between hemisphere and condition, nor the three-way interaction among area, hemisphere, and condition reached significance.
Experiment 2: 1-back task
Bilateral MGBs were localized in 8 of 9 participants (right: x 13±1, y -25±2, z 6±1, size 103±25; left: x -15±1, y -25±2, z -7±2, size 105±23; see Figure 3 and Table 1 for the Talairach location for subjects in whom the MGB was successfully defined). Condition-related Beta weights were estimated from individually localized MGBs (Figure 4, lower panels) and HG ROIs (Figure 5, lower panels).
A 3-way repeated measures ANOVA was used to test the difference between areas (HG vs. MGB), between hemispheres (left vs. right), and among auditory stimulation conditions (Binaural, Contralateral, Ipsilateral). Similar to Experiment 1, there was a main effect of area (F(1, 7) = 113.76, p < 0.0001), with higher activation found in the HG than in the MGB. There was no main effect of hemisphere (F(1, 7) = 1.68, ns), and no significant interaction between hemisphere and area (F(1, 7) = 3.11, ns).
The main effect of condition was again highly significant (F(2, 14) = 47.24, p < 0.0001). Duncan's multiple range test showed Binaural and Contralateral activation to be significantly higher than Ipsilateral activation (ps < 0.05). There was again no significant difference in activation level between Bilateral and Contralateral stimulation conditions. There was a trend for a significant interaction between area and auditory stimulation condition (F(2, 14) = 3.5, p = 0.059). The activation differences between Binaural/Contralateral and Ipsilateral conditions were larger in the HG than in the MGB ROIs.
Again, neither the two-way interaction between hemisphere and condition, nor the three-way interaction among area, hemisphere, and condition reached significance.
Comparison between Passive listening (Exp. 1) and the 1-back task (Exp. 2)
To investigate the effect of task, we compared the Beta weights across the seven participants who took part in both experiments. A 3-way repeated measures ANOVA was performed separately for each brain region of interest, with task (passive vs. 1-back task), hemisphere (left vs. right), and condition (Binaural, Contralateral, Ipsilateral) as factors.
In MGB, we found no main effect of either task (F(1, 6) = 0.53, ns) or hemisphere (F(1, 6) = 0.9, ns). As shown in Figure 4, the overall magnitude of MGB activation was comparable between the two experiments and the two hemispheres. There was once again a main effect of condition (F(2, 12) = 0.78, p <0.01), with higher activation in the Binaural and Contralateral conditions than in the Ipsilateral condition revealed by Duncan's multiple range test (ps < 0.05). No two-way or three-way interaction reached significance.
Similar results were found in the HG, where similar activation was found between two experiments (F(1, 6) = 2.06, ns) and between the two hemispheres (F(1, 6) = 2.8, ns). The main effect of condition (F(2, 12) = 24.99, p <0.0001) was similarly driven by higher Binaural/Contralateral activation than Ipsilateral activation (ps < 0.05).
Experiment 3: Dynamic ripple
We found little or no activation to the dynamic ripple stimulus within the MGB in any of the four subjects tested with this stimulus. Using the dynamic ripple stimulus, no voxels were identified as belonging to the MGB in either hemisphere for any of these four subjects, even at a more liberal threshold of p=0.05 (uncorrected for multiple comparisons). In contrast, for all four of these subjects the MGB could be reliably identified using the scrambled music stimulus: collapsing across left and right hemisphere, the mean number of voxels identified as belonging to either left or right MGB (using a more stringent threshold of q(FDR) < 0.05) for the scrambled music stimulus was 168 voxels, with a range of 65-387.
We also found that dynamic ripples induced weaker BOLD responses in auditory cortex. To compare the effectiveness of stimulus in eliciting BOLD responses in HG, we joined the HG ROIs created using passive listening to scrambled music (Experiment 1) and dynamic ripple (Experiment 3). Beta weights within this combined HG ROI were then estimated for each of the four subjects who took part in both experiments. A 3-way repeated measures ANOVA with stimuli (scrambled music vs. dynamic ripples), hemisphere (left vs. right), and condition (Binaural, Contralateral, Ipsilateral) as factors found that stronger activation was elicited by scrambled music (F(1, 3) = 15.39, p < 0.03). Similar activation was found between the two hemispheres (F(1, 3) = 1.44, ns). There was a trend for effect of condition (F(2, 6) = 4.79, p =0.057), mostly driven by higher Binaural than Ipsilateral activation (p < 0.05). There were no significant two-way or three-way interactions.
Lateralization
The lateralization of monaurally driven activity within left and right MGB and HG is examined in Figure 6. The leftmost panels show lateralization as a vector sum. In these vector plots, Contralateral beta values are represented as a 90 degree (upward) vector and Ipsilateral beta values as a 0 degree (rightward) vector. The vector sum of these two responses represents lateralization. Equal responses to Contralateral and Ipsilateral stimuli would result in a 45 degree vector.
Figure 6.
Lateralization within the MGB (upper panels) and HG (lower panels) in Experiment 1 (Passive listening, n = 8) and Experiment 2 (1-back task, n = 8). Leftmost panels show data plotted using polar co-ordinates. Contralateral responses are represented as a 90 degree (upward) vector and Ipsilateral responses as a 0 degree (rightward) vector. The radius represents Beta values. Dashed hemicircles represent Beta values of 1 (MGB) and 1 and 2 (HG). Data for each subject are shown with thin grey lines. The group average is shown with a thick black line, and the 45 degree angle (representing equal responses to Contralateral and Ipsilateral stimulation) is shown with a black dashed line. Significance values represent the circular statistic one-sample 1-tailed t-test testing whether the vector angle representing subjects’ responses was significantly greater than 45 degrees – i.e. whether responses across subjects were significantly stronger for Contralateral than Ipsilateral stimulation, *** p<0.001, ** p<0.01, * p<0.05. Rightmost panels: Here these same data are re-plotted using Lateralization Index=(Contralateral-Ipsilateral)/(Contralateral+Ipsilateral). Group means are shown with grey bars. Black dots represent individual data points. Note that the apparent outlier point did not meet criteria for any standard method of outlier removal.
We examined lateralization (as represented by the vector angle) separately for each experiment using a two way circular statistic ANOVA (Harrison, 1988, Berens, 2009) (ROI × hemisphere) and found no main effect of either ROI (Experiment 1: F(1, 1) = 0.68., ns; Experiment 2: F(1, 1) = 0.42., ns) or hemisphere (Experiment 1: F(1, 1) = 0.56, ns; Experiment 2: F(1, 1) = 0.75, ns), with no significant interactions. A two-way circular statistics ANOVA (task × ROI, collapsed across hemispheres) similarly found no main effect (both F(1, 1) < 1, ns) or interactions. Nor did individual circular t-tests reveal any significant difference in lateralization across corresponding MGB and HG ROIs (e.g. between right hemisphere MGB and HG for the Passive listening condition), or as a function of task for a given ROI (e.g. between the Passive listening and 1-Back conditions within right hemisphere MGB).
The rightmost panels of Figure 6 show these same data re-plotted using a lateralization index, as used in a previous study (Schonwiesner et al., 2007): Lateralization Index = (Contralateral-Ipsilateral)/(Contralateral+Ipsilateral). This index has previously been used to measure lateralization in auditory areas. As discussed further below, this lateralization index has two disadvantages when applied to BOLD responses, first, it does not differentiate between high selectivity values caused by weak versus negative ipsilateral responses and second it is susceptible to producing very large lateralization estimates when the normalization term is close to zero or can take negative values (Simmons et al., 2007). For example, in the case of left MGB in Experiment 1 a data point showing a weakly negative ipsilateral response (probably due to noise) results in extremely high lateralization values. More generally, subjects with weak overall activation tend to inflate lateralization index values, for reasons described more fully below.
Accuracy of our method compared to current structural methods
Although approaches like susceptibility weighted imaging offer some promise (Haacke et al., 2009), currently the only two validated methods of identifying the MGB within individuals are (1) high density proton density imaging optimized for subcortical grey–white contrast, and (2) probabilistic tractography on diffusion-weighted imaging data, which can be used to automatically segment the medial and lateral geniculate nuclei from surrounding structures based on their distinctive patterns of connectivity to the rest of the brain (Devlin et al., 2006).
We compared the accuracy of our functional method to that reported by Devlin et al. using the center of mass (CoM) metric reported in their paper. As seen in Figure 7, Euclidian distances were non-significantly different across our two estimates (Exp.1 Passive listening and Exp. 2 1-back task) than across the two estimates of Devlin et al. (2006) (proton density and tractography). Distances between individual estimates of MGB location and either Talairach co-ordinates (Talairach and Tournoux, 1988) or the probabilistic map of the MGB described by Rademacher et al. (2001) were also similar for our method and that of Devlin et al. (2006).
Figure 7.
A comparison of methods for defining the MGB. Left and right MGB are treated as separate data points. Each bar represents mean Euclidian distance between the estimated centers of mass (CoM) of two different estimates of MGB location. Red bars show the Euclidian distance between estimates of MGB location across our two tasks (Passive listening and 1-back task, diagonal stripes) or distances across Devlin's two methods (2006) (proton density and tractography, vertical and horizontal stripes). Yellow bars show Euclidian distances between individually estimated MGB CoMs and Talairach co-ordinates (Talairach and Tournoux, 1988). Blue bars show Euclidian distances between individually estimated MGB CoMs and the probabilistic map of the MGB of Rademacher et al (2001). Standard deviations rather than standard errors are shown because the data for Devlin et al. is based on 10 hemispheres (5 subjects × 2 hemispheres) while our data are based on 14 hemispheres.
Accuracy of our method compared to Group-averaging techniques
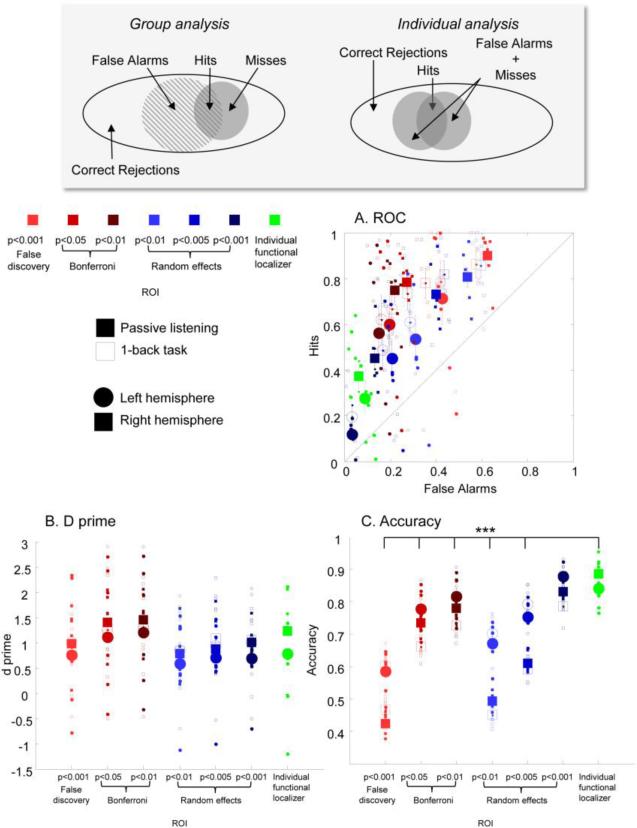
If variability in the location of the MGB across individuals was smaller than variability across scanning sessions, then using a group MGB might be preferable to using individually defined MGB. Figure 8 compares accuracy in identifying the MGB using group based vs. individual ROI techniques. We compared the accuracy of individually defined ROIs to three fixed effects group-averaged MGB (thresholds of q(FDR) < 0.001, p(bonf) < 0.05, and p(bonf) < 0.01) and three random effects ROIs (thresholds of p < 0.01, p < 0.005, and p < 0.001)
Figure 8.
The accuracy of identification of the MGB using a group based approach as compared to identification across sessions within individual subjects. The shaded inset panel shows how components of the confusion matrix are defined in the case of group and individual analysis. Panel A shows a traditional ROC curve. Large symbols represent group averages and small symbols represent individual data points. Vertical and horizontal lines (often smaller than symbols size) represent standard errors of the mean. Panel B shows d prime values across group and individual ROIs. Panel C shows accuracy (the proportion of true results, i.e., “Hits” + “Correct rejections”). Significance values are shown from individual uncorrected two-tailed Wilcoxon rank sum tests comparing group ROIs to the individual functional localizer approach, *** p<0.001.
Unsurprisingly, fixed effectsgroup-averaged MGB were much larger than individually-defined MGB. Median numbers of voxels (collapsed across tasks and hemispheres) for the fixed effects group-averaged MGB were: p(bonf) < 0.01= 208 voxels; p(bonf) < 0.05 =256 voxels; and q(FDR) < 0.01 = 456 voxels respectively. Median numbers of voxels (collapsed across tasks and hemispheres) for the random effects group-averaged MGB were: p < 0.01 = 316 voxels; p < 0.005 = 199 voxels; and p < 0.001 = 48 voxels respectively. The median number of voxels within individually-defined MGB (collapsed across tasks, hemispheres and subjects) was 91 voxels.
The traditional way to measure a binary classifier system is through the confusion matrix, which describes the proportions “Hits”, “Misses”, “False Alarms” and “Correct Rejections”, as shown in the shaded inset panel of Figure 8. In the case of the group-averaged MGB “Hits” were defined as the number of voxels that belonged to both the group-averaged MGB and that individual's individually defined MGB (defined during the same Experiment, note this leads to a slight circularity in ROI selection since the group average includes that individuals’ data, which advantages the group-averaged approach). “Misses” were defined as voxels within the individually defined MGB that were not within the group-averaged MGB. “False alarms” were defined as voxels within the group-averaged MGB that were not within the individually defined MGB. “Correct Rejections” were defined as voxels that were defined as belonging to any of the group ROIs that were not within the individually defined MGB.
In the case of the individually-defined ROI approach “Hits” were defined as the number of voxels that were defined as belonging to that individual's MGN in both Experiment 1 and 2 (for the sake of this analysis we assumed that the task-differences between Experiment 1 and 2 should make no difference in the identified location of the MGB). “Misses” and “False Alarms” were combined, and were defined as half the number of voxels that were defined as belonging to the MGB in only one of the two Experiments. “Correct Rejections” were defined as voxels that were defined as belonging to any of the group ROIs that were not within the individually defined MGB (once again, data were collapsed across Experiments 1 and 2).
Data shown in Figure 8 are collapsed across individuals, hemisphere and tasks. Panel A shows the receiving operator characteristic (ROC) curve which describes the relative proportion of correct identification of voxels within the MGB (“Hits”) as compared to the proportion of falsely identified voxels (“False Alarms”). Unsurprisingly, as the threshold for the group-averaged MGB becomes less stringent there are more “Hits” but this comes at the cost of an increasing number of “False Alarms”.
Because ROIs based on individual functional localizers tended to be much smaller than the group ROIs there was a smaller proportion of “Hits” for the individually defined functional localizer than for all but the most stringent (the random effects ROI defined at p < 0.001) of the group ROIs (uncorrected Wilcoxon rank sum test, ps<0.001). However, the individually-defined approach also resulted in significantly fewer “False Alarms” than all but one of the group-averaged MGB (ps < 0.001; uncorrected Wilcoxon rank sum tests), with the exception once again being the random effects ROI defined at p < 0.001.
Thus, while group-based methods tended to identify a high proportion of the voxels that fall within the MGB, this came at a cost – far more ‘noise’ voxels are included within most group MGB ROI. Critically, it is this ratio of signal to noise voxels that is likely to be critical for data quality when measuring responses within the MGB.
Panel B shows estimated d prime values across group and individual ROIs (based on standard assumptions of normality). Wilcoxon rank sum tests showed no significant difference (p > 0.05) in d prime between the individual functional localizers and any of the group ROIs.
Panel C shows accuracy (the proportion of true results (“Hits” + “Correct rejections”) across the population of responses. The individually-defined approach was significantly more accurate than all but one of the 6 group ROI approaches, and showed similar accuracy to the random effects ROI defined at p < 0.001. It is worth noting that while the ability to successfully categorize voxels as belonging to the MGB was similar using an individual functional localizer and a random effects ROI defined at a stringent significance level (p < 0.001), one advantage of the individual ROI approach is that it results in significantly larger ROIs (the mean ROI size was 91 voxels for individually defined ROIs as compared to 48 voxels in the random effects ROI defined at p < 0.001), and therefore offers increased power when measuring BOLD responses in separate experimental conditions.
Discussion
Comparisons between the three experiments
It has previously been shown that the amount of attentional modulation within the MGB depends on whether or not the task involves attending to ‘speech like’ elements (von Kriegstein et al., 2008, Diaz et al., 2012) – a finding very consistent with our hypothesis that MGB responds preferentially to more complex ‘speech-like’ structure. We did not see a difference in the amount of activation with the MGB across Experiment 1 (Passive listening) and Experiment 2 (1-back task). However, the lack of a difference between the task and no-task condition in our study could easily be related to the salient and ever-changing stimulus used in this study – even when the subjects were not actively engaged in the task, features of the stimuli likely provided strong exogenuous cuing of attention. As a consequence, our conditions do not allow us to make strong claims about the presence (or absence) of task-dependent attentional effects in the MGB.
We did see a large difference in the amount of activation elicited by scrambled music vs. dynamic ripple stimuli. Well-controlled spectrotemporally complex sounds, such as dynamic ripple (Kowalski et al., 1996a, b) have been used in a variety of previous studies to characterize the spectrotemporal receptive fields in the MGB of anesthetized cat (Miller et al., 2002) and to elicit fMRI activation in human auditory cortex (Langers et al., 2003, Schonwiesner and Zatorre, 2009) and inferior temporal cortex (Chandrasekaran et al., 2012a). Dynamic ripples represent some of the spectro-temporal complexity of ecologically relevant sounds, whereas at the same time satisfying the formal requirements for deriving receptive fields (Klein et al., 2006, Schonwiesner and Zatorre, 2009).
However, compared to dynamic ripple, our scrambled music localizer contains a variety of complex features present in speech, such as transients, tonal elements, and a low degree of predictability (Griffiths et al., 2001, Gill et al., 2008) that have been shown to modulate auditory responses, even within subcortical areas (von Kriegstein et al., 2008, Hornickel et al., 2011, Chandrasekaran et al., 2012b). Our finding that scrambled music was much more effective than dynamic ripple for reliably eliciting robust functional responses within individually defined MGB suggests that MGB is highly selective for these more complex stimulus properties (von Kriegstein et al., 2008, Diaz et al., 2012) and/or shows a high degree of adaptation or repetition suppression for predictable stimuli (Dubnov, 2006, Gill et al., 2008). Because our scrambled music localizer differed from the dynamic ripple stimulus in terms of both complexity and predictability/repetitiveness, it remains unclear which of these qualities are critical for eliciting robust responses within the MGB.
Lateralization
Our goal in these experiments was primarily to develop and validate a method by which functional responses could be measured within individuals within the MGB. However our results also contribute to a literature examining lateralization in subcortical and cortical auditory structures.
We represented lateralization using a vector approach, inspired by traditional measures of color selectivity (Lennie et al., 1990). Conceptually, the vector approach assumes that contralateral and ipsilateral responses are driven by independent (rather than opponent) mechanisms, and that selectivity can be characterized as the vector sum along Contralateral and Ipsilateral dimensions, with the angle representing the degree of selectivity and the length representing overall responsiveness. One advantage of this vector sum approach over normalized indices is that the angle of the vector differentiates between lateralization due to weak as compared to negative BOLD responses.
A second advantage of the vector approach is that normalized indices are mathematically inappropriate under conditions where responses can be negative or the normalization term can potentially take zero values. One reason for concern that has been previously described, is that any negative values in the normalization term will artificially inflate lateralization estimates (Simmons et al., 2007). Another is that such indices become highly nonlinear as the normalization term approach zero. Thus, noise can easily inflate selectivity values when responses are small, or when responses can be negative as well as positive. Thus the vector approach is more robust than normalization indices, especially when comparing lateralization across areas or across subjects that differ either in their mean BOLD response or in their signal to noise ratio.
In this study, while we consistently saw larger responses to contralateral as compared to ipsilateral stimuli, we saw no evidence of any hemispheric specialization for the particular stimuli that we used. This may be because the stimuli which we used contained a combination of auditory-noise, music-like and speech-like features. A series of studies have suggested that auditory noise (Devlin et al., 2003) and ‘speech like’ stimuli containing fast temporal modulations may be preferentially processed in left auditory structures (Zatorre and Belin, 2001, Schonwiesner et al., 2007), while musical stimuli, spatial or motion information may be preferentially processed in the right hemisphere (Zatorre et al., 2002, Krumbholz et al., 2005), though this lateralization may depend on context (Brechmann and Scheich, 2005, Shtyrov et al., 2005, Schonwiesner et al., 2007).
Comparisons to other methods of identifying the MGB
We compared our method to that of Devlin et al. (2006) in two ways. First we calculated Euclidian distances between the centers of mass of MGB identified within individuals using both our 1-back task and passive listening conditions, and compared these distances to those obtained across individual estimates of the MGB obtained using proton density imaging or tractography, as reported by Devlin et al (2006). Second we calculated Euclidian distances to the centers of mass of the MGB, as reported by two atlases (Talairach and Tournoux, 1988, Rademacher et al., 2001). Our method performed comparably to that of Devlin's et al. (2006) using both measures. We believe, given that it shows similar accuracy, that our method has four significant methodological advantages. First, our approach is marginally simpler in terms of scanning parameters in that it uses a relatively standard functional scanning protocol. This is not a major advantage over the method described by Devlin et al. (2006), since proton density scans and diffusion scans are also relatively easily to implement. However our method is currently significantly easier to implement than non-standard protocols like susceptibility weighted imaging (Haacke et al., 2009), which has also been proposed (though not yet validated) as a potential method for estimating the location of the MGB. Second, our method is simple in terms ofcross-scan alignment. Precise alignment of small structures between anatomical, fMRI and (in particular) diffusion space requires care, due to distortions of the B0 field. Given that one common use for our method is likely to be identifying an MGB ROI within which to measure BOLD activity in subsequent experimental manipulations, the use of a functional protocol to identify the MGB minimizes the issue of having to correct for different distortions across scans. Third, the analysis methods required of our method are trivial to implement, and are included within all major fMRI analysis packages. The same is true of identification using proton density imaging. However identification based on connectivity patterns is not at all computationally trivial to implement, and is not implemented in most publically distributed software packages. Finally, our method is relatively free from experimenter bias. While the extent of activity can vary considerably across subjects a single threshold parameter is the only free variable across subjects, and if one preferred a criterion free method, one could fix the size of the MGB (e.g. to 100mm3) and adjust threshold accordingly. In contrast, both the proton density method and the tractography methods described by Devlin require hand-drawing the MGB, a process that is not only time consuming but also requires large amounts of experimenter experience. All three raters in the Devlin et al. paper were authors, and there was still significant inter-experimenter variability. While in theory automated segmentation might be possible using proton density images, this extension of the method has not yet been validated.
Conclusions
In summary, within those with normal auditory systems our method identifies the functional MGB with equal accuracy and reliability as the current standard (Devlin et al., 2006), and for most laboratories, will be considerably easier to implement. However it is worth noting that our functional method and Devlin's structural methods are not measuring exactly the same thing. Our method finds the brain region that shows BOLD responses as a result of activity within the MGB. Due to blurring of the vasculature and the low resolution of fMRI, this region is likely to extend outside structural MGB, and is likely to be larger in individuals with stronger MGB activity, regardless of the structural size of the MGB. As such, our method is best suited for identifying a region of interest within which to measure BOLD activity in subsequent experimental manipulations or across subject populations. In contrast the method used by Devlin's et al. (2006) measures the extent of the structural MGB. As such their method is more appropriate for examining structural differences across subject groups.
Highlights.
We describe fMRI protocol for reliably localizing human MGB in individual subjects
The method employs sparse MR acquisition and a scrambled ‘music’ auditory stimulus
Our method is equally accurate and reliable as structural methods
Our method offers more accuracy in identifying MGB than group based methods
Lateralization within the MGB resembles that found in primary auditory cortex
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Allon N, Yeshurun Y. Functional organization of the medial geniculate body's subdivisions of the awake squirrel monkey. Brain Res. 1985;360:75–82. doi: 10.1016/0006-8993(85)91222-3. [DOI] [PubMed] [Google Scholar]
- Bartlett EL, Wang X. Correlation of neural response properties with auditory thalamus subdivisions in the awake marmoset. J Neurophysiol. 2011;105:2647–2667. doi: 10.1152/jn.00238.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berens P. CircStat: A MATLAB Toolbox for Circular Statistics. Journal of Statistical Software. 2009;31 [Google Scholar]
- Brechmann A, Scheich H. Hemispheric shifts of sound representation in auditory cortex with conceptual listening. Cereb Cortex. 2005;15:578–587. doi: 10.1093/cercor/bhh159. [DOI] [PubMed] [Google Scholar]
- Chandrasekaran B, Koslov S, Luther E, D. R . High-resolution imaging reveals tonotopic organization in human auditory midbrain. CNS Chicago; 2012a. [Google Scholar]
- Chandrasekaran B, Kraus N, Wong PC. Human inferior colliculus activity relates to individual differences in spoken language learning. J Neurophysiol. 2012b;107:1325–1336. doi: 10.1152/jn.00923.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devlin JT, Raley J, Tunbridge E, Lanary K, Floyer-Lea A, Narain C, Cohen I, Behrens T, Jezzard P, Matthews PM, Moore DR. Functional asymmetry for auditory processing in human primary auditory cortex. J Neurosci. 2003;23:11516–11522. doi: 10.1523/JNEUROSCI.23-37-11516.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devlin JT, Sillery EL, Hall DA, Hobden P, Behrens TE, Nunes RG, Clare S, Matthews PM, Moore DR, Johansen-Berg H. Reliable identification of the auditory thalamus using multi-modal structural analyses. Neuroimage. 2006;30:1112–1120. doi: 10.1016/j.neuroimage.2005.11.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diaz B, Hintz F, Kiebel SJ, von Kriegstein K. Dysfunction of the auditory thalamus in developmental dyslexia. Proc Natl Acad Sci U S A. 2012 doi: 10.1073/pnas.1119828109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubnov S. Spectral anticipations. Computer Music Journal. 2006;30:63–83. [Google Scholar]
- Ehret G, Romand R. The central auditory system. Oxford University Press; New York: 1997. [Google Scholar]
- Friston KJ, Henson RN. Commentary on: Divide and conquer; a defence of functional localisers. Neuroimage. 2006;30 doi: 10.1016/j.neuroimage.2005.08.012. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Rotshtein P, Geng JJ, Sterzer P, Henson RN. A critique of functional localisers. Neuroimage. 2006;30 doi: 10.1016/j.neuroimage.2005.08.012. [DOI] [PubMed] [Google Scholar]
- Genovese CR, Lazar NA, Nichols T. Thresholding of statistical maps in functional neuroimaging using the false discovery rate. Neuroimage. 2002;15:870–878. doi: 10.1006/nimg.2001.1037. [DOI] [PubMed] [Google Scholar]
- Gill P, Woolley SM, Fremouw T, Theunissen FE. What's that sound? Auditory area CLM encodes stimulus surprise, not intensity or intensity changes. J Neurophysiol. 2008;99:2809–2820. doi: 10.1152/jn.01270.2007. [DOI] [PubMed] [Google Scholar]
- Giraud AL, Lorenzi C, Ashburner J, Wable J, Johnsrude I, Frackowiak R, Kleinschmidt A. Representation of the temporal envelope of sounds in the human brain. J Neurophysiol. 2000;84:1588–1598. doi: 10.1152/jn.2000.84.3.1588. [DOI] [PubMed] [Google Scholar]
- Griffiths TD, Uppenkamp S, Johnsrude I, Josephs O, Patterson RD. Encoding of the temporal regularity of sound in the human brainstem. Nat Neurosci. 2001;4:633–637. doi: 10.1038/88459. [DOI] [PubMed] [Google Scholar]
- Guimaraes AR, Melcher JR, Talavage TM, Baker JR, Ledden P, Rosen BR, Kiang NY, Fullerton BC, Weisskoff RM. Imaging subcortical auditory activity in humans. Hum Brain Mapp. 1998;6:33–41. doi: 10.1002/(SICI)1097-0193(1998)6:1<33::AID-HBM3>3.0.CO;2-M. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haacke EM, Mittal S, Wu Z, Neelavalli J, Cheng YC. Susceptibility-weighted imaging: technical aspects and clinical applications, part 1. AJNR Am J Neuroradiol. 2009;30:19–30. doi: 10.3174/ajnr.A1400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall DA, Haggard MP, Akeroyd MA, Palmer AR, Summerfield AQ, Elliott MR, Gurney EM, Bowtell RW. “Sparse” temporal sampling in auditory fMRI. Hum Brain Mapp. 1999;7:213–223. doi: 10.1002/(SICI)1097-0193(1999)7:3<213::AID-HBM5>3.0.CO;2-N. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrison DaK, G. K. The development of analysis of variance for circular data. Journal of applied statistics. 1988;15:197–223. [Google Scholar]
- Haynes J-D, Deichmann R, Rees G. Eye-specific effects of binocular rivalry in the human lateral geniculate nucleus. Nature. 2005;438:496–499. doi: 10.1038/nature04169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinshaw DB, Jr., Holshouser BA, Engstrom HI, Tjan AH, Christiansen EL, Catelli WF. Dental material artifacts on MR images. Radiology. 1988;166:777–779. doi: 10.1148/radiology.166.3.3340777. [DOI] [PubMed] [Google Scholar]
- Hornickel J, Chandrasekaran B, Zecker S, Kraus N. Auditory brainstem measures predict reading and speech-in-noise perception in school-aged children. Behav Brain Res. 2011;216:597–605. doi: 10.1016/j.bbr.2010.08.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inan S, Mitchell T, Song A, Bizzell J, Belger A. Hemodynamic correlates of stimulus repetition in the visual and auditory cortices: an fMRI study. NeuroImage. 2004;21:886–893. doi: 10.1016/j.neuroimage.2003.10.029. [DOI] [PubMed] [Google Scholar]
- Jancke L, Buchanan T, Lutz K, Specht K, Mirzazade S, Shah NJ. The time course of the BOLD response in the human auditory cortex to acoustic stimuli of different duration. Brain Res Cogn Brain Res. 1999;8:117–124. doi: 10.1016/s0926-6410(99)00012-9. [DOI] [PubMed] [Google Scholar]
- Jones EG. Chemically defined parallel pathways in the monkey auditory system. Ann N Y Acad Sci. 2003;999:218–233. doi: 10.1196/annals.1284.033. [DOI] [PubMed] [Google Scholar]
- Klein DJ, Simon JZ, Depireux DA, Shamma SA. Stimulus-invariant processing and spectrotemporal reverse correlation in primary auditory cortex. Journal of computational neuroscience. 2006;20:111–136. doi: 10.1007/s10827-005-3589-4. [DOI] [PubMed] [Google Scholar]
- Kowalski N, Depireux DA, Shamma SA. Analysis of dynamic spectra in ferret primary auditory cortex. I. Characteristics of single-unit responses to moving ripple spectra. J Neurophysiol. 1996a;76:3503–3523. doi: 10.1152/jn.1996.76.5.3503. [DOI] [PubMed] [Google Scholar]
- Kowalski N, Depireux DA, Shamma SA. Analysis of dynamic spectra in ferret primary auditory cortex. II. Prediction of unit responses to arbitrary dynamic spectra. J Neurophysiol. 1996b;76:3524–3534. doi: 10.1152/jn.1996.76.5.3524. [DOI] [PubMed] [Google Scholar]
- Krumbholz K, Schonwiesner M, Rubsamen R, Zilles K, Fink GR, von Cramon DY. Hierarchical processing of sound location and motion in the human brainstem and planum temporale. Eur J Neurosci. 2005;21:230–238. doi: 10.1111/j.1460-9568.2004.03836.x. [DOI] [PubMed] [Google Scholar]
- Langers DR, Backes WH, van Dijk P. Spectrotemporal features of the auditory cortex: the activation in response to dynamic ripples. Neuroimage. 2003;20:265–275. doi: 10.1016/s1053-8119(03)00258-1. [DOI] [PubMed] [Google Scholar]
- Lanting CP, De Kleine E, Bartels H, Van Dijk P. Functional imaging of unilateral tinnitus using fMRI. Acta Otolaryngol. 2008;128:415–421. doi: 10.1080/00016480701793743. [DOI] [PubMed] [Google Scholar]
- Lennie P, Krauskopf J, Sclar G. Chromatic mechanisms in striate cortex of macaque. J Neurosci. 1990;10:649–669. doi: 10.1523/JNEUROSCI.10-02-00649.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller LM, Escabi MA, Read HL, Schreiner CE. Spectrotemporal receptive fields in the lemniscal auditory thalamus and cortex. J Neurophysiol. 2002;87:516–527. doi: 10.1152/jn.00395.2001. [DOI] [PubMed] [Google Scholar]
- Naidich TP, Duvernoy HM, Delman BN, Sorensen AG, Kollias SS, Haacke EM. Duvernoy's atlas of the human brain stem and cerebellum : high-field MRI : surface anatomy, internal structure, vascularization and 3D sectional anatomy. Springer; New York: 2009. [Google Scholar]
- New PF, Rosen BR, Brady TJ, Buonanno FS, Kistler JP, Burt CT, Hinshaw WS, Newhouse JH, Pohost GM, Taveras JM. Potential hazards and artifacts of ferromagnetic and nonferromagnetic surgical and dental materials and devices in nuclear magnetic resonance imaging. Radiology. 1983;147:139–148. doi: 10.1148/radiology.147.1.6828719. [DOI] [PubMed] [Google Scholar]
- Noesselt T, Tyll S, Boehler CN, Budinger EH, H-J, Driver J. Sound-induced enhancement of low-intensity vision: multisensory iInfluences on human sensory-specific cortices and thalamic bodies relate to perceptual enhancement of Visual detection sensitivity. J Neurosci. 2010;30:13609–13623. doi: 10.1523/JNEUROSCI.4524-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rademacher J, Morosan P, Schormann T, Schleicher A, Werner C, Freund HJ, Zilles K. Probabilistic mapping and volume measurement of human primary auditory cortex. Neuroimage. 2001;13:669–683. doi: 10.1006/nimg.2000.0714. [DOI] [PubMed] [Google Scholar]
- Saxe R, Brett M, Kanwisher N. Divide and conquer: a defense of functional localizers. Neuroimage. 2006;30:1088–1096. doi: 10.1016/j.neuroimage.2005.12.062. [DOI] [PubMed] [Google Scholar]
- Schneider KA, Kastner S. Effects of sustained spatial attention in the human lateral geniculate nucleus and superior colliculus. J Neurosci. 2009;29:1784–1795. doi: 10.1523/JNEUROSCI.4452-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider KA, Richter MC, Kastner S. Retinotopic organization and functional subdivisions of the human lateral geniculate nucleus: a high-resolution functional magnetic resonance imaging study. J Neurosci. 2004;24:8975–8985. doi: 10.1523/JNEUROSCI.2413-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schonwiesner M, Krumbholz K, Rubsamen R, Fink GR, von Cramon DY. Hemispheric asymmetry for auditory processing in the human auditory brain stem, thalamus, and cortex. Cereb Cortex. 2007;17:492–499. doi: 10.1093/cercor/bhj165. [DOI] [PubMed] [Google Scholar]
- Schonwiesner M, Zatorre RJ. Spectro-temporal modulation transfer function of single voxels in the human auditory cortex measured with high-resolution fMRI. Proc Natl Acad Sci U S A. 2009;106:14611–14616. doi: 10.1073/pnas.0907682106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shtyrov Y, Pihko E, Pulvermuller F. Determinants of dominance: is language laterality explained by physical or linguistic features of speech? Neuroimage. 2005;27:37–47. doi: 10.1016/j.neuroimage.2005.02.003. [DOI] [PubMed] [Google Scholar]
- Simmons WK, Bellgowan PS, Martin A. Measuring selectivity in fMRI data. Nat Neurosci. 2007;10:4–5. doi: 10.1038/nn0107-4. [DOI] [PubMed] [Google Scholar]
- Symmes D, Alexander GE, Newman JD. Neural processing of vocalizations and artificial stimuli in the medial geniculate body of squirrel monkey. Hear Res. 1980;3:133–146. doi: 10.1016/0378-5955(80)90041-6. [DOI] [PubMed] [Google Scholar]
- Talairach J, Tournoux P. Co-Planar Stereotaxic Atlas of the Human Brain. Thieme Medical Publishers; New York: 1988. [Google Scholar]
- von Kriegstein K, Patterson RD, Griffiths TD. Task-dependent modulation of medial geniculate body is behaviorally relevant for speech recognition. Curr Biol. 2008;18:1855–1859. doi: 10.1016/j.cub.2008.10.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winer JA. The human medial geniculate body. Hear Res. 1984;15:225–247. doi: 10.1016/0378-5955(84)90031-5. [DOI] [PubMed] [Google Scholar]
- Winer JA, Miller LM, Lee CC, Schreiner CE. Auditory thalamocortical transformation: structure and function. Trends Neurosci. 2005;28:255–263. doi: 10.1016/j.tins.2005.03.009. [DOI] [PubMed] [Google Scholar]
- Wunderlich K, Schneider KA, Kastner S. Neural correlates of binocular rivalry in the human lateral geniculate nucleus. Nat Neurosci. 2005;8:1595–1602. doi: 10.1038/nn1554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatorre RJ, Belin P. Spectral and temporal processing in human auditory cortex. Cereb Cortex. 2001;11:946–953. doi: 10.1093/cercor/11.10.946. [DOI] [PubMed] [Google Scholar]
- Zatorre RJ, Belin P, Penhune VB. Structure and function of auditory cortex: music and speech. Trends Cogn Sci. 2002;6:37–46. doi: 10.1016/s1364-6613(00)01816-7. [DOI] [PubMed] [Google Scholar]