Evaluation of Vaccine-induced Antibody Responses: Impact of New Technologies

Abstract

Host response to vaccination has historically been evaluated based on a change in antibody titer that compares the post-vaccination titer to the pre-vaccination titer. A four-fold or greater increase in antigen-specific antibody has been interpreted to indicate an increase in antibody production in response to vaccination. New technologies, such as the bead-based assays, provide investigators and clinicians with precise antibody levels (reported as concentration per mL) in ranges below and above those previously available through standard assays such as ELISA. Evaluations of bead assay data to determine host response to vaccination using fold change and absolute change, witha general linear models used to calculate adjusted statistics, present very different pictures of the antibody response when pre-vaccination antibody levels are low. Absolute changes in bead assay values, although not a standard computation, appears to more accurately reflect the host response to vaccination for those individuals with extremely low pre-vaccination antibody levels. Conversely, for these same individuals, fold change may be very high while post-vaccination antibodies do not achieve seroprotective levels. Absolute change provides an alternate method to characterize host response to vaccination, especially when pre-vaccination levels are very low, and may be useful in studies designed to determine associations between host genotypes and response to vaccination.

Introduction

Analyses of immunologic responses to vaccines are complicated by previous exposure to relevant antigens and pre-existing antibody levels. Measures such as fold change (FC; the ratio of the final to the pre-vaccination value) or percentage change in antibody levels have traditionally been used to quantify response to vaccines, but each has drawbacks that make interpretation of results difficult, both immunologically and mathematically [1—2]. Several authors have discussed methodologies to address problems in the assessment of vaccine immunogenicity in populations with seropositive individuals prior to vaccination [1, 3—4]. Some have noted that pre-existing antibody titers significantly affect response to vaccines [3, 5—11]. Numerous measures of pre-post change have been considered [2—3, 12—13], especially when seropositive individuals comprise a substantial portion of the pre-vaccination sample [1].

The Population Genetics Analysis Program (PopGen) investigated genetic determinants of vaccine immunogenicity in an Indian population using a vaccine to Salmonella typhi [14]. Because 45% of participants demonstrated pre-vaccination typhoid antibody levels that were considered seroprotective as revealed by the bead assay [15], we examine different methods of computing immunogenicity to quantify antibody production while also accounting for pre-vaccination immunity. We demonstrate that data analyses using different methods to calculate the response to vaccination may dramatically affect the outcome measure and that when researchers select a method to calculate response to vaccination, they must carefully consider the question(s) being asked.

Methods

PopGen Population

In a stratified random sampling design, 997 participants receiving vaccine to S. typhi were recruited from eight strata (two age groups: 6-to-25 years and >25 years; both genders; and two ethnic groups: Hindu and Muslim) [14—15]. The research design entailed a longitudinal assessment of vaccination response in a large ethnic population recruited from several wards in Kolkata, India. Typhoid infections are endemic in this population, comprising primarily Hindu lower caste groups and their Muslim counterparts. Persons with typhoid infections in the previous 12 months were excluded. Blood was collected from all participants at baseline (just before vaccination) and 3 days and 28 days post-vaccination. This report focuses on the baseline and Day 28 results. Data from this study are included in the National Institute of Allergy and Infectious Diseases ImmPort repository (immport.niaid.nih.gov/).

Bead Assay to Assess Antibody Levels

A new laboratory assay—a bead-based immunoassay of anti-Vi IgG—was developed for this project [15]. Assays were performed for 997 study participants, but two sera did not yield Day 28 bead assay values and four yielded Day 28 values that were below Day 0 values, so 991 are included in the present analyses. Approximately 45% of the pre-vaccination population was seropositive. Assay data used in the current study was obtained from IMMPORT (https://immport.niaid.nih.gov).

Statistical Methods

We provide the change statistics (both fold (FC) and absolute (AC)) as unadjusted statistics and as adjusted statistics per Beyer et al. [1]. We do not discuss another commonly used statistic, the relative percent increase, because it completely correlates with FC as it is FC minus 1, expressed as a percentage.

First we define z_0,i and z_28,i to be the Day 0 (pre-vaccination) and Day 28 (post-vaccination) assay results for the i^th participant, respectively. Then, if x_0,i = log₁₀ (z_0,i), the mean x_0,i is:

$${\overline{x}}_0=\frac{{\sum }_{i=1}^n{x}_{0,i}}{n}$$ (1)

Finally, we define δ_i to be the log-transformed Day 0 value for the i^th participant centered about the mean for all participants as:

$${\delta }_i=x_{0,i}-{\overline{x}}_0$$ (2)

Unadjusted FC

The relative increase, i.e., FC, in antibody levels is given by: z

$${\phi }_i=\frac{z_{28,i}}{z_{0,i}}$$ (3)

FC adjusted for Day 0

For general linear models that adjust for Day 0, we use the log of the FC for the i^th participant:

$${log}_{10}\left({\phi }_i\right)={log}_{10}\left(\frac{z_{28,i}}{z_{0,i}}\right)={log}_{10}\left(z_{28,i}\right)-{log}_{10}\left(z_{0,i}\right)$$ (4)

We adjust for Day 0 levels using the following linear model similar to Beyer et al.[1]:

$${log}_{10}\left({\phi }_i\right)={\beta }_0+{\beta }_1{\delta }_i+{\epsilon }_i$$ (5)

where β₀ and β₁ are parameters estimated from our data and ε_i are the residuals, representing the variation in log₁₀(FC) that is unexplained by log₁₀(Day 0). [In all models we utilize the independent variable δ_i, rather than the log₁₀(Day 0) levels. However, this does not affect the slope of the linear relationship, only the intercept.]

At the value δ_i = 0, the adjusted FC values are equal to:

$${log}_{10}{\left({\phi }_i\right)}^{\text{A}}={\widehat{\beta }}_0+{\epsilon }_i$$ (6)

In other words, the residual, ε_i, is directly proportional to the adjusted FC.

Unadjusted AC

An estimate of the quantity of antibody produced in response to vaccination is computed from the AC in the bead assay (untransformed):

$${\mathrm{\Delta }}_i=z_{28,i}-z_{0,i}$$ (7)

AC adjusted for Day 0

For statistical modeling, we compute log₁₀(Δ_i), the log of the absolute difference in bead assay. The AC has a meaningful interpretation (estimate of antibody produced), but the distribution of values is not Gaussian. We transform these values for all subsequent analyses. We adjust for Day 0 levels, similar to FC adjustment above:

$${log}_{10}\left({\mathrm{\Delta }}_i\right)={\alpha }_0+{\alpha }_1{\delta }_i+{\omega }_i$$ (8)

where α₀ and α₁ are parameters estimated from our data and ω_i are the residuals, representing the variation in log₁₀(AC) that is unexplained by log₁₀(Day 0). Therefore, the adjusted values for AC are computed at δ_i = 0 by:

$${log}_{10}{\left({\mathrm{\Delta }}_i\right)}^{\text{A}}={\widehat{\alpha }}_0+{\omega }_i$$ (9)

Consequently, the residual, ω_i, is directly proportional to the adjusted AC.

Relationship between FC and AC

At any value for Day 0, we may express both FC and AC as linear functions of the mean-centered level δ_i (equations 5 and 8, respectively). By solving equation 8 for δ_i and substituting into equation 5, we have a linear relationship between log₁₀(FC) and log₁₀(AC):

$${log}_{10}\left({\phi }_i\right)={\beta }_0-\frac{{\beta }_1}{{\alpha }_1}{\alpha }_0+\frac{{\beta }_1}{{\alpha }_1}{log}_{10}\left({\mathrm{\Delta }}_i\right)+{\epsilon }_i-\frac{{\beta }_1}{{\alpha }_1}{\omega }_i$$ (10)

The rescaled residual term:

$${\epsilon }_i-\frac{{\beta }_1}{{\alpha }_1}{\omega }_i$$ (11)

is a weighted (or rescaled) difference between the two residuals. Substituting in from equations 6 and 9, note that this rescaled residual difference is proportional to the difference in the two adjusted statistics:

$${\epsilon }_i-\frac{{\beta }_1}{{\alpha }_1}{\omega }_i={log}_{10}{\left({\phi }_i\right)}^{\text{A}}-\frac{{\beta }_1}{{\alpha }_1}{log}_{10}{\left({\mathrm{\Delta }}_i\right)}^{\text{A}}-\text{constant}$$ (12)

where the constant is a function of the α₀, α₁, β₀, and β₁. We refer to the variable in 11 as the rescaled residual and explore this term in the results below. We used SAS statistical software to conduct all statistical analyses and calculated Pearson’s correlations coefficients.

Results

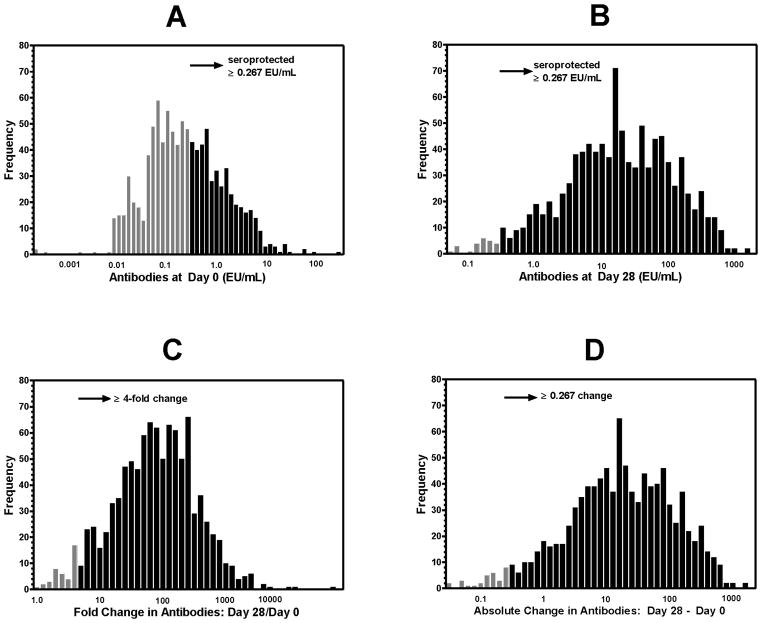
Figure 1A and B illustrate the distributions of Day 0 and Day 28 bead assay results. In the PopGen population, 45% of individuals were seroprotected at Day 0 (Figure 1A), according to Staats et al. [15] criteria (value ≥ 0.267 EU/mL). Most individuals (98%) attained a Day 28 level that exceeds the seroprotection cutoff (Figure 1B). Figure 1C displays the distribution of FC (unadjusted for Day 0 levels), and Figure 1D illustrates the distribution of AC (unadjusted for Day 0). Although the AC score, i.e., antibody production (see Figure 1D), is not a typical computation in vaccine immunogenicity assessment, we include it among possible outcomes to express response to vaccine. (Values for Day 0, Day 28, unadjusted and adjusted FC and AC, and the rescaled residuals for selected participants are given in Appendix I.)

Figure 1.

Distributions of bead assay antibodies. (A) Pre-vaccination anti-Vi serum IgG levels (Day 0). (B) Post-vaccination anti-Vi serum IgG levels (Day 28). In (A) and (B), dark bars indicate levels at or above the seroprotective level of 0.267 EU/mL per Staats et al. (2010). (C) Distribution of fold change (Day 28/Day 0) in bead assay antibodies. Dark bars indicate at least 4-fold change from Day 0 levels. (D) Distribution of absolute change (Day 28 – Day 0) in bead assay antibodies. Dark bars indicate absolute changes >0.267 EU/mL.

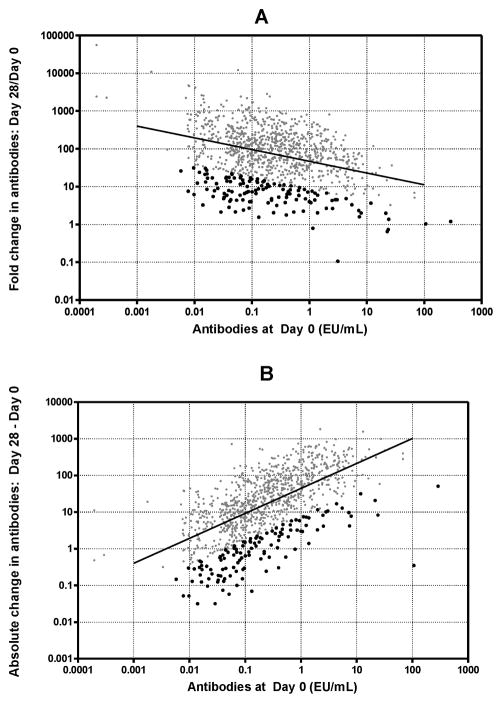
Because a large percentage was seropositive at baseline, the use of unadjusted FC is problematic [1], so we looked at adjusted values. Table 1 shows the measures of antibody levels and response, both unadjusted and adjusted for pre-vaccination levels. It is immediately apparent, as expected, that the adjustment does change the variance, but the means for the entire distribution of FC or AC are not altered. Table 2 provides parameter estimates and statistics related to the adjustment regressions for FC and AC. Although unadjusted FC appears to account for Day 0 (i.e., Day 0 is used in the computation of the ratio), a correlation still exists between log₁₀(FC) and log₁₀(Day 0) (see Table 2; test for no effect of Day 0 p < 0.001; see Figure 2A; correlation (r)= −0.35; dark dots are discussed below). FC remains influenced negatively by baseline levels, i.e., higher baseline levels predict lower FC. Conversely, AC is positively correlated with Day 0 (see Table 2; test for no effect of Day 0 p < 0.001); Figure 2B; r = 0.63; red dots are discussed below), demonstrating that much of the variation in AC is explained by Day 0. However, unlike FC, higher Day 0 levels predict greater change in AC. The residuals (which are proportional to the adjusted FC and AC) from both models that adjust for Day 0, are not correlated with Day 0 (r ≈ 0.0, p > 0.99).

Table 1.

Measures of antibody levels and response, unadjusted and adjusted for pre-vaccination (Day 0) levels (N= 991 participants)

Measurea	Mean (SD)
	Estimates Unadjusted for Day 0	Estimates Adjusted for log10(Day 0)
log10 (Day 0)	−0.641 (0.792)	—
log10 (Day 28)	1.233 (0.833)	1.233 (0.617)
log10 (Day 28/Day 0)	1.874 (0.660)	1.874 (0.617)
log10 (Day 28 – Day 0)	1.210 (0.850)	1.210 (0.658)

^alog₁₀ (Day 28/Day 0) is the log₁₀(fold change) and log₁₀ (Day 28 – Day 0) is the log₁₀(absolute change).

Table 2.

Regression models of log₁₀(fold change) and log₁₀(absolute change) on log₁₀(Day 0)^a

Regression Model Parameters and Statistics	log10(fold change)	log10(absolute change)
Intercept (SE)	1.874 (0.020)	1.210 (0.021)
Slope (SE)	−0.294 (0.025)	0.680 (0.026)
p-value (no effect of Day 0)	<0.001	< 0.001
Pearson’s r (correlation)	−0.353	0.634

^aEach model is a linear regression of the outcome statistic on the mean-centered log₁₀(Day 0) value (δ, where δ = log₁₀(Day 0) − mean of log₁₀(Day 0) values): Outcome = Intercept + Slope * δ. Parameter estimates and measures of variability are based on 991 samples.

Figure 2.

Pre-vaccination anti-Vi serum IgG versus unadjusted change statistics. (A) Fold change (Day 28/Day 0) versus Day 0 antibody levels. Correlation between log₁₀ (fold change) and pre-vaccination levels = −0.35; p < 0.001) suggests that fold change is negatively dependent on pre-vaccination levels. Dark dots indicate lowest residual values (using log₁₀ values in model). (B) Absolute change (Day 28 - Day 0) versus Day 0 antibody levels. Correlation between log₁₀ (absolute difference) and pre-vaccination levels (r = 0.63; p < 0.001) suggests that absolute change is positively dependent on pre-vaccination levels. Dark dots indicate lowest residual values (using log₁₀ values in model).

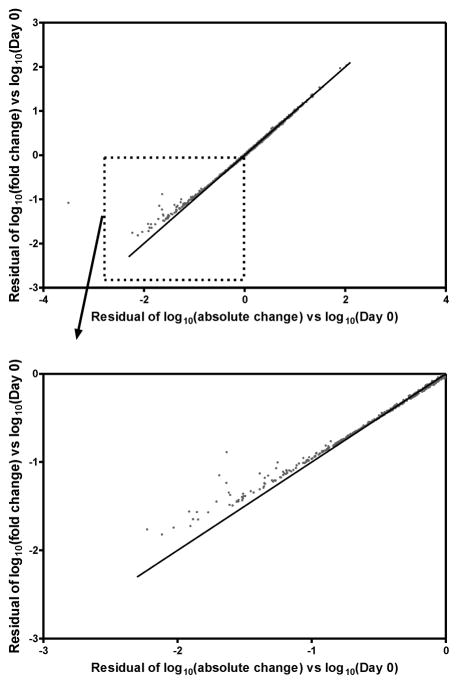
Because AC is not a standard computation for immunologic investigations, we investigated its association with unadjusted FC (r = 0.494; p < 0.001). Further, when the residuals from the regression models (equations 5 and 8), which are proportional to the adjusted FC and adjusted AC, are plotted against each other (Figure 3), the values are linearly related for most of the range. That is, with a simple linear equation, one statistic (e.g., the adjusted AC) almost completely predicts the value of the other adjusted statistic for most of the sample. However, when the residuals (or adjusted statistics) are very low (that is, a log value less than −1.0, as illustrated in Figure 3B), there is a departure from the linear relationship, indicating that within this range, adjusted values for FC and AC diverge. In Figure 2, the results corresponding to this range of divergent results are highlighted in as dark dots. It can be seen that, for both FC and AC, these are the most negatively deviant values from what is expected based on Day 0.

Figure 3.

Residuals for Day 0 adjusted models: log₁₀(fold change) model versus log₁₀(absolute change) model. (A) All data points. Note that for the majority of values, the two residual values are very similar, only diverging from the line of equality at very low values (e.g., less than −1.0). (B) Subset of data points with residuals less than 0.

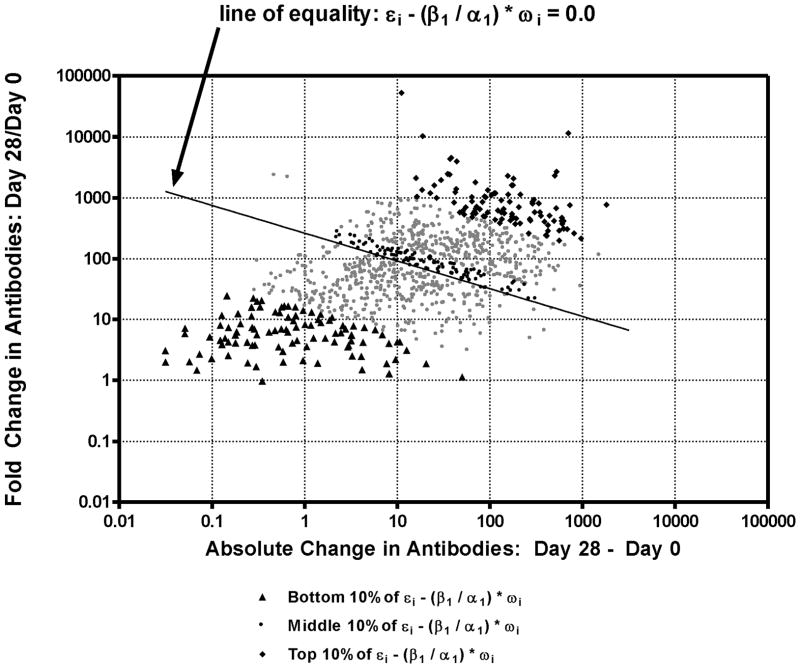
To explore this divergence, we look at the rescaled residual, which is a measure of the weighted difference between the adjusted statistics (see equation 12). The rescaled residual in this sample ranges from −2.738 to 2.904. We then identified the most negative and most positive rescaled residuals. These are the participants with the greatest differences between the adjusted FC and adjusted AC (i.e., when the pre-vaccination levels were taken into account). In Figure 4, we show the unadjusted FC and AC of all of the participants, highlighting the participants with the largest negative rescaled residual in dark traingles and with the largest positive rescaled residuals in dark diamonds. Of the 99 rescaled residuals that are the most extreme and negative (Appendix I, first 99 records), all subjects exhibited a FC > 4 (or log₁₀(4) > 0.602). However, 23 of these subjects did not achieve seroprotection (bead assay ≥ 0.267 EU/mL) at Day 28.

Figure 4.

Fold change in bead assay antibodies (Day 28/Day 0) vs absolute change in bead assay antibodies (Day 28 - Day 0). Different ranges of the rescaled residual values ( ${\epsilon }_i-\frac{{\beta }_1}{{\alpha }_1}{\omega }_i$) are highlighted by dark symbols. Dark triangles: bottom 10% of values and most divergent meanings for FC and AC; dark diamonds: top 10% of values; dark circles: values closest to zero (middle of the distribution). (Data for results with dark symbols are given in Appendix.)

To evaluate how these measures behaved to predict seroprotection, we looked at the 549 participants whose antibodies on Day 0 were below seroprotective levels. Although by Day 28, a majority had attained seroprotective levels, 23 had not. Of these, 16 had an FC greater than 4 (false positive rate of 70%). The false positive rate is even higher for those 117 individuals with Day 0 levels less than 1/10 the seroprotective cutoff, i.e., less than 0.026. Of these participants, 10 had not attained seroprotective levels by Day 28; however, 9 of those participants had FC greater than 4 (false positive rate of 90%).

As expected, all 23 participants with Day 28 levels below the seroprotection level had AC levels less than 0.267.

Discussion

Vaccine immunogenicity as measured by vaccine-specific antibody responses is often quantified according to the magnitude of the FC. Seroconversion (e.g., 4-fold FC) is a relevant outcome in a mostly naive population but may be deceptive in a population with prior exposure to relevant antigens. Senn [12] discusses the merits and disadvantages of change scores compared to the ANCOVA (adjustment) approach, but the goal of his discussion was methodology that produces unbiased estimates for treatment comparisons. Our focus on the differences between FC and AC was motivated by our observation of several extremely small changes in antibody levels between Day 0 and Day 28 in some individuals, and instances in which the FC statistic indicated dramatic changes in antibodies, but the Day 28 antibody levels were well below the seroprotective level. Bead assay measured anti-Vi IgG levels ranged from 0.0002 EU/mL (several orders of magnitude less than the seropositive cutoff) to above 1500 EU/mL.

Most laboratories that provide antibody-titer measures do not report values below or above certain cutoffs, e.g., influenza titers are not reported below 1:10 or above 1:1280[8]. In the data analyzed here, the antibody responses were measured using a sensitive bead-based assay that provides antibody responses comparable to ELISA assay results. However, the bead-based assay has superior signal-to-noise ratios for the entire range of the standard curve (0.0001 to 1 EU/ml). When some subjects have pre-vaccination antibody levels less than one-quarter of the seropositivity level, the challenge for interpreting response to vaccination is that FC values of 4 do not necessarily indicate seroconversion or seroprotection. The issue is more pronounced when much smaller antibody levels, for instance on the order of 10⁻¹ and 10⁻² the seroprotective level, are reliably assessed and identified in the pre-vaccination population. In the extreme, a FC of greater than10 might be observed, but the individual will not be seroprotected.

The definitions of both FC and AC statistics are meant to correct for pre-vaccination Day 0 antibody titers, by dividing or subtracting the Day 0 titer, respectively. However, both FC and AC are significantly correlated with pre-vaccination Day 0 antibody titers in our partially seropositive population (Pearson’s correlation coefficient = −0.35 and 0.67, respectively). When the FC and AC statistics were then further adjusted for pre-vaccination levels by applying linear regression on Day 0 levels, the two adjusted statistics were highly correlated and tracked each other for most of the population. That is, the magnitude of the regression residuals, which are proportional to adjusted FC and AC, were strongly correlated for most of the individuals in the sample. However, there was a noticeable deviation for some of the sample. The rescaled residual was a useful statistic to identify individuals for whom the adjusted FC and adjusted AC differed. Individuals with the lowest rescaled residuals tended to have very low pre-vaccination antibody titers (Figure 4, values listed in Appendix I). When the individuals with the largest negative rescaled residuals were plotted, almost 70% had FC scores of 4 or greater, indicating seroconversion, but almost 25% did not have Day 28 antibody levels indicating seroprotection (at least 0.267 EU/mL). When examined further, most of these individuals who were inappropriately identified as seroconverters had very low levels of pre-vaccination antibodies.

Several recommendations can be derived from these analyses. First, use of FC or AC is largely interchangeable for most of the population. Second, for those individuals with very low pre-vaccination levels, AC, rather than FC (unadjusted or adjusted), is a more appropriate statistic to evaluate response to vaccination. When the antibody levels are reported at a level on the same order of magnitude as the seroprotective level, either FC or AC can be used. Although AC is not a standard computation, in studies that use sensitive assays to measure antibody levels, it appears to more accurately reflect the immune response.

FC as a measure of response to intervention has been questioned in other settings, such as controlled trials. The use of ANCOVA to adjust FC has been advocated because FC is statistically inefficient, thereby often lacking power to detect changes [16—17], and ANCOVA can deal with conditional bias [12].

There are several possible limitations to our study. First, these comparisons and analyses have only been conducted on one population with one polysaccharide antigen vaccine thought to be T-cell independent. Replication in other studies is important. Second, a high proportion of the pre-vaccination population in our study was seroprotected, and an even higher proportion was likely to have had prior exposure. No data were available to determine if a proportion of the seronegative population had prior exposure. Consequently, it would be important to conduct a similar comparison of the serological variables in seronegative populations.

As laboratory tools continue to improve and we extend the range of accurate measurement, we need to look carefully at the interpretation of statistics that are commonly used to evaluate the success of treatment. In some cases, we will find that deceptively simple statistics that purport to be generalizable have limited use in individuals with outlying pre-treatment characteristics.

With an increasing number of studies aimed at identifying host genetic factors that correlate with host response to vaccination, often by grouping subjects into “high” and “low” responder groups [18], it is important to classify subjects accurately as high or low responders. Our results demonstrate that calculations of FC and AC can yield different classifications of low or high responders, and this classification may influence which host genes are identified as controlling response to vaccination.

Highlights.

• We use several measures of immunogenicity to evaluate typhoid vaccine response.

• We used a bead assay to precisely quantitate antibody levels, even for low values.

• Very large fold-changes for low pre-vaccine levels do not reflect seroprotection.

• Absolute-change is alternative measure when pre-vaccine levels are very low.