Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Sep 1.
Published in final edited form as: Neuroimage. 2013 Apr 10;78:210–216. doi: 10.1016/j.neuroimage.2013.03.074

Mapping average axon diameters in porcine spinal cord white matter and rat corpus callosum using d-PFG MRI

ME Komlosh a,b, E Özarslan a,b,c, M J Lizak d, I Horkayne-Szakaly e, R Z Freidlin f, F Horkay a, P J Basser a
PMCID: PMC3672372  NIHMSID: NIHMS449738  PMID: 23583426

Abstract

Knowledge of microstructural features of nerve fascicles, such as axon diameter, is crucial for understanding normal function in the central and peripheral nervous systems as well as assessing changes due to pathologies. In this study double-pulsed field gradient (d-PFG) filtered MRI was used to map the average axon diameter (AAD) in porcine spinal cord, which was then compared to AADs measured with optical microscopy of the same specimen, as a way to further validate this MRI method. A novel 3D acquisition scheme was then used to obtain AADs in each voxel of a coronal slice of rat brain corpus callosum. AAD measurements were also acquired using optical microscopy performed on histological sections and validated using a novel MRI glass capillary array phantom.

Keywords: MRI, average axon diameter, AAD, pulsed-field gradient, PFG, double wave vector, double, d-PFG, dPFG

1. Introduction

The central nervous system (CNS) white matter consists of fascicles containing long bundles of myelinated axons, which serve as pathways to transfer impulses between regions within the brain, and from the cortex to other parts of the body and back (Kandel, Schwartz et al. 2000). Each fascicle comprises axons with a distribution of diameters whose range can vary significantly. Since the diameter of a myelinated axon is linearly related to conduction velocity (Hursh 1939; Tasaki, Ishii et al. 1943), axon diameter helps determine the amount of information transferred along a pathway (Pajevic, Assaf et al. 2008; Perge, Niven et al. 2012; Pajevic and Basser 2013). Neuroanatomically, one finds axons in the spinal cord somatotopically organized into distinct clusters characterized by different average diameters and diameter distributions, which enable them to perform different functions. The ability to detect axon diameter non-invasively on a voxel-by-voxel basis in the spinal cord and in other white matter pathways would improve our understanding of both the normal function of the nervous system and many pathologies that may affect and be affected by changes in microstructure. This information might also provide valuable insights about the course of normal and abnormal development and changes that can occur in aging and degeneration. Of particular interest is following possible subtle pathological changes, which may occur in Traumatic Brain Injury (TBI), and may be too small to detect using conventional diffusion MRI or other imaging methods.

Prior to the development of MRI-based methods, histological analysis was the only means for measuring axon diameters. Histological methods, however, require extracting tissue specimens, usually after sacrifice, and then fixing, sectioning, staining, and viewing with an optical or electron microscope. The microscopic resolution necessary to see individual axons inherently limits the field of view (FOV), requiring one to stitch together different swatches of tissue images to construct a quilt or cross-section of a large tissue structure, such as the spinal cord, or a brain white matter pathway.

CHARMED (Assaf, Freidlin et al. 2004) and AxCaliber (Assaf, Blumenfeld-Katzir et al. 2008; Barazany, Basser et al. 2009) MRI were developed, in part, to overcome the inherent deficiencies of conventional histological analysis of white matter structure and architecture. These in vivo MRI methods use concepts of porous media NMR combined with MRI to measure, respectively, the apparent axon diameter and the axon diameter distribution (ADD) within nerve fascicles voxel by voxel. While the voxel resolution of MRI is on the order of millimeters, the MR signal is sensitized to the microscopic diffusive or random motion of water molecules, and to the size and shape of confining compartments that contain intra-axonal water, which are on the order of microns.

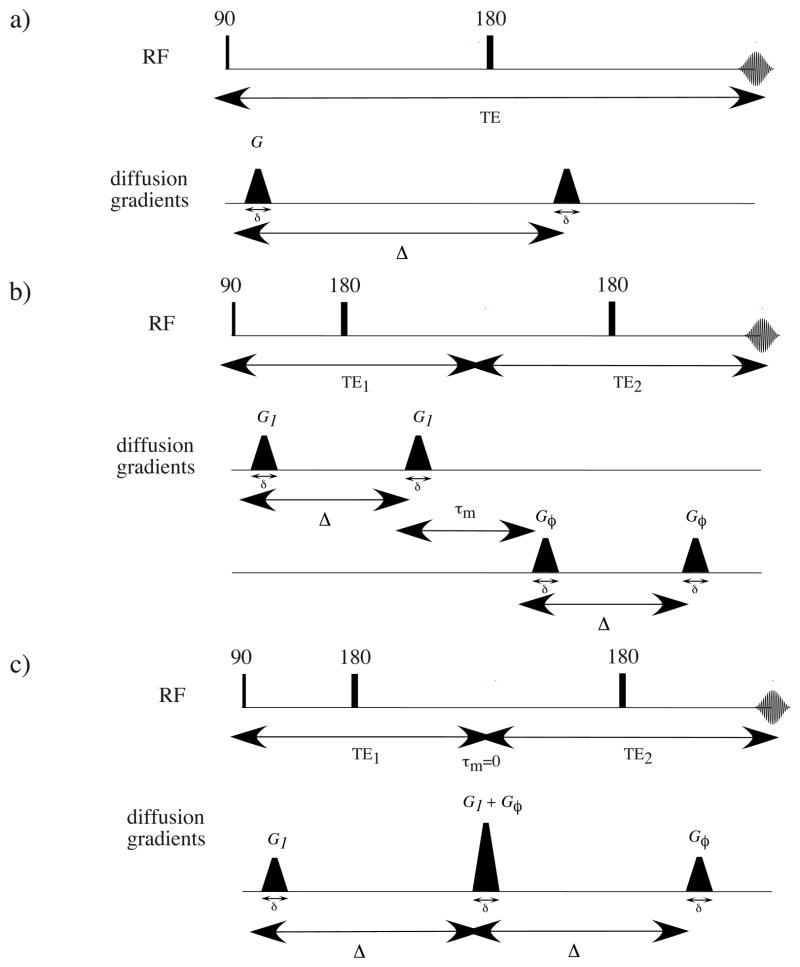
Both CHARMED and AxCaliber MRI employ a single pair of Stejskal-Tanner (Stejskal and Tanner 1965) pulsed-field gradients (PFG) to measure the water proton spins’ motion (Figure 1a). The lengthscale that they probe is characterized by the wave vector q = γGδ/(2π) (where γ is the magnetogyric ratio, G is the magnetic field gradient strength, and δ is the duration of the PFG), separated by a diffusion time, Δ. These methods can detect microscopic net displacements of the tissue’s water. In these methods the resulting signal attenuations can be correlated with the spins’ 3D mean squared net displacement, which can be used to infer the size of pores and confining boundaries. In the case of CNS white matter, which consists of long aligned axons that crudely resemble micro-capillaries, water diffusion is anisotropic; movement is assumed to be free along the principal fiber axis and restricted perpendicular to it (Moseley, Cohen et al. 1990; Basser, Mattiello et al. 1994; Pierpaoli, Jezzard et al. 1996).

Figure 1.

Figure 1

Open in a new tab

The pulse sequences: a) single-PFG, b) double-PFG (d-PFG), c) d-PFG with τm = 0, the pulse sequence used in this study.

In principle, for highly uniform aligned axons having a narrow ADD, an effective way to measure the average pore diameter would be from the position of the first diffraction peak in a diffusion-diffraction experiment (Callaghan, Coy et al. 1991; Callaghan 1996). However, these peaks arise only when the ADD is very narrow and the angle between the axis of the fibers and the direction of the applied diffusion sensitizing gradient is close to 90° (Avram, Assaf et al. 2004). Any small deviation of the applied gradient vector from orthogonality with respect to the fiber axis causes these peaks to disappear. Moreover, there is an inverse relationship between the pore or axon diameter and the q value needed to probe it using the single PFG MRI experiment, so extremely strong gradients are required (Ong, Wright et al. 2008) to measure an axon diameter in white matter, which are on the order of a few microns. Such gradients are an order of magnitude stronger than what is currently available on conventional clinical scanners, making such measurements infeasible at this time (Basser 2002).

Another approach to measuring pore diameter is to use the double Pulsed Field Gradient (d-PFG) NMR method (Mitra 1995; Cheng and Cory 1999; Özarslan and Basser 2008) (Figure 1b). Inherently, d-PFG MRI requires smaller gradients than the single PFG methods described above. The d-PFG MRI employs two pairs (rather than one) of Stejskal-Tanner PFG blocks separated by a mixing time, τm. The resulting signal loss is related to the correlation between net displacements during the two diffusion times rather than the net displacements themselves. With the addition of a second displacement dimension, numerous microstructural details can now be revealed, particularly as a function of τm. For long τm insight into microscopic (Komlosh, Horkay et al. 2007; Komlosh, Lizak et al. 2008; Lawrenz and Finsterbusch 2011) and compartment shape anisotropy (Cheng and Cory 1999; Özarslan 2009; Shemesh, Özarslan et al. 2012) can be gleaned, while for a negligibly short τm (Figure 1c) (when τm = 0, the second pulse of the first PFG block overlaps with the first pulse of the second PFG block) the average pore diameter (Koch and Finsterbusch 2008; Weber, Ziener et al. 2009; Komlosh, Özarslan et al. 2011) can be obtained.

In this study we mapped the average axon diameters (AAD) voxel by voxel in an axial section of porcine spinal cord white matter using d-PFG MRI. For the first time the AAD obtained in spinal cord using d-PFG MRI was compared to the AAD obtained with optical microscopy of the same specimen, as a way to further validate this method. A novel 3D acquisition scheme was then used to obtain the AAD in each voxel of a coronal slice of rat brain corpus callosum.

2. Materials and Methods

2.1 Specimen preparation and MRI protocol

2.1.1 Spinal cord

A porcine spinal cord was excised and put immediately in a 4% formalin solution. Prior to performing MRI experiments a portion of the spine was saved for subsequent histology studies while the rest was rehydrated with phosphate buffered saline (PBS) for MRI. The rehydrated spine was immersed in perfluoropolyether (Fomblin LC/8, Solvay Solexis, Italy) and inserted into a 10 mm Shigemi tube (Shigemi Inc., Japan) with a plunger matched to the susceptibility of water. The tube was placed in a 14T vertical-bore Bruker AVANCE III MRI scanner equipped with a micro2.5 gradient system powered by GREAT 60 gradient amplifiers with a nominal gradient strength of 24.65 mT m−1 Amp−1.

2.1.1.1 Acquisition scheme and MRI protocol

Since the spinal cord white matter consists of long aligned fibers with known orientation (free axis and restricted plane), the spinal cord specimen could be placed in the magnet so that its long axis is aligned with the main magnetic field. For such samples whose axis of free diffusion can be aligned with the main magnetic field, a circular two-dimensional (Figure 2a) d-PFG gradient sampling scheme can be applied. The gradients of the first PFG NMR block are fixed along the x-axis, perpendicular to the fiber’s free diffusion axis (z), while the orientation of the gradients in the second block is varied by an angle φ from the x-axis between 0 and 2π within the x-y plane.

Figure 2.

Figure 2

Open in a new tab

The d-PFG MRI acquisition schemes that were used in this study: a) 2D—for the spinal cord and b) 3D—for the rat corpus callosum.

The PFG NMR parameters were: δ = 3.15 ms, Δ = 60 ms, and G was varied between 0 and 664 mT m−1. The MRI parameters were: TR/TE = 3500/6.54 ms, FOV = 10.5 mm, matrix size = 128×128, spatial resolution = 82 μm2, and slice thickness = 3.6 mm. Prior to the d-PFG MRI experiment a diffusion tensor imaging (DTI) (Basser, Mattiello et al. 1994; Pierpaoli, Jezzard et al. 1996) protocol was applied to verify/establish the spine’s orientation. The DTI parameters were: δ = 3 ms, Δ = 50 ms, 24 diffusion direction orientations with b-values of 100 and 1000 s mm−2, TR/TE = 3500/57.3 ms, FOV = 10.5 mm, matrix size = 128×128, spatial resolution = 82 μm2, and slice thickness = 3.6 mm.

2.1.2 Rat corpus callosum

A perfused rat brain was excised and placed in 4% paraformaldehyde (PFA) for 24 hours and then rehydrated in phosphate buffered saline (PBS). The brain was immersed in perfluoropolyether (Fomblin LC/8, Solvay Solexis, Italy) and inserted into a 30 mm Falcon tube (Becton Dickinson, NJ) with an Ultem (Ensinger, UK) plunger and bottom that is susceptibility-matched to water to eliminate susceptibility artifacts at the tube-plunger interface. The tube was placed in a 7T vertical bore Bruker DRX MRI scanner equipped with a micro2.5 gradient system with a nominal gradient strength of 24.65 mT m−1 Amp−1 and GREAT 60 gradient amplifiers.

2.1.2.1 Acquisition scheme and MRI protocol

Unlike the spinal cord white matter, the brain white matter fibers do change orientation from voxel to voxel. Thus, the 2D circular gradient sampling scheme that was used on the spinal cord specimen could no longer be used to acquire this d-PFG MRI data. To obtain the AAD for a fiber bundle with an arbitrary or variable orientation, a 3D gradient sampling scheme should be used (Figure 2b). The one employed in this study was designed not to bias any one direction over another by sampling 66 d-PFG-weighted MRIs spread over 3 shells (Sloane 2000). The outermost shell (G1 = G2 = 591.6 mT/m) consisted of images with 11 distinct orientations of G1 sampling the hemisphere uniformly. For each of these 11 directions three separate images were acquired with φ = 0, π/2 and π resulting in 11×3 = 33 acquisitions. Similarly, the second shell consisted of 6×3 = 18 points with G = 443.7 mT m−1 and the inner shell consisted of 3×3 = 9 points with G = 221.85 mT m−1. The number of orientations in each shell was determined by taking into account the angular contrast and the predicted signal to noise ratio (SNR). To improve the radial sampling resolution, six images were taken with G ranging from 0 to 591.6 mT m−1 with d-PFG NMR blocks with an orientation of φ = π.

The PFG NMR parameters were: δ = 3.15 ms, Δ = 30 ms. The MRI parameters were: TR/TE = 3500/6.12 ms, FOV = 17 mm, matrix size = 100×100, spatial resolution = 170×170 μm2, and slice thickness = 1 mm.

An independent DTI protocol was also used to verify the brain white matter fiber orientation. The DTI parameters were: δ = 3 ms, Δ = 30 ms, 6 diffusion direction orientations with b-values of 100 and 21 diffusion directions with b-values of 1600 s mm−2, TR/TE = 3500/37.1 ms.

When the angle between the two d-PFG blocks is π the middle gradient pulse vanishes, which results in a single PFG experiment where the diffusion time is now doubled. Consequently, the corpus callosum fiber orientation can potentially be obtained from these experiments as well, and the DTI experiment performed prior to the d-PFG acquisition can be omitted. We used a subset of twenty conventional diffusion weighted experiments taken from the d-PFG acquisition to examine it.

2.1.3 Phantom validation

In order to assess the accuracy of the 3D sampling scheme, we acquired d-PFG MRI data on a glass capillary array (GCA) MRI phantom (Komlosh, Özarslan et al. 2011) using both 2D and 3D sampling schemes. The GCA phantom consists of a 13 mm wafer, 0.5 mm thick with a parallel pack of fused capillary tubes of 5μm nominal pore diameter filled with water. The d-PFG NMR parameters were identical in both experiments: δ = 3.15ms, Δ = 75ms, and G was varied between 0 and 664 mT m−1. The MRI parameters were: TR/TE = 5000/14 ms, FOV=17 mm, matrix size = 128×128, spatial resolution = 133 × 133 × 500 μm3. The 2D and 3D sampling schemes followed the same pattern as the spinal cord and rat brain corpus callosum respectively.

2.2 Modeling and analysis

Analysis of the white matter d-PFG MRI signal data involved the use of a matrix operator formalism to predict E(q,φ) for restricted diffusion in a cylinder i.e., the intra-axonal compartment. The fitted model employs bi-compartmental diffusion, which arises from the restricted signal within the axons and the free water within the extracellular matrix (ECM), assuming no exchange between the two compartments. The model takes into account all experimental parameters including the use of a “fat” rather than an infinitesimally short gradient pulse. A more complete description of this modeling framework is contained in the following papers (Robertson 1966; Grebenkov 2007; Özarslan, Shemesh et al. 2009; Shemesh, Özarslan et al. 2009; Özarslan, Komlosh et al. 2011).

2.3 Histology

Small sections of the spine were fixed in 3% glutaraldehyde, post-fixed in osmium tetroxide, and embedded in plastic (Finck 1960; Freeman and Spurlock 1962). One-micron thick sections were stained with toluidine blue and were scanned with an Olympus BX51 light microscope with a resolution of 0.23×0.23 μm2. The AAD was obtained using NIH ImageJ (Bethesda, MD).

To compare the AAD measured by both methods, a k-means segmentation analysis was performed on the AAD maps obtained from the d-PFG MRI experiments.

3. Results

3.2 Spinal cord

The results from the independent DTI acquisition performed on the spinal cord specimen are shown in Figure 3. Figure 3a and b show the DTI-derived direction-encoded color (DEC) and the fractional anisotropy (FA) maps, respectively. The DEC maps show a uniform orientation of white matter aligned with the B0 field. The FA map shows a fairly uniform level of high diffusion anisotropy in white matter, and an expected reduction in FA in the “butterfly”-shaped gray matter region. Neither map shows any significant variation within the white matter regions. Therefore, for this specimen and its placement in the magnet, a d-PFG 2D MRI sampling scheme is appropriate to see whether it can detect any regional variations within white matter.

Figure 3.

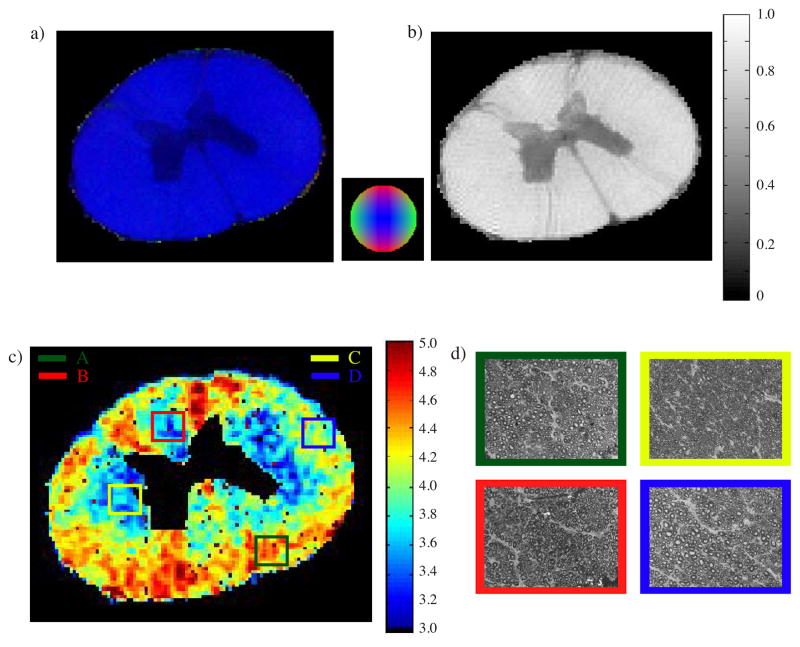
Figure 3

Open in a new tab

a) DEC and b) FA maps of spinal cord obtained from DTI using δ = 3 ms, Δ = 50 ms with b-values of 100 and 1000 s-mm−2. c) Average axon diameter map obtained from d-PFG MRI data using δ = 3.15 ms, Δ = 60 ms, and G = 0 – 664 mT m−1. d) Toluidine blue light microscope images corresponding to the marked ROIs.

Figure 3c shows the AAD map calculated from the d-PFG filtered MRI experiments. AADs are estimated to be between 3 and 5 μm. Figure 3d shows the Toluidine blue sections that were taken from the ROIs marked in Figure 3c.

AADs were obtained from histology. Table 1 contains the AAD data obtained from the histological slices shown in Figure 3d and from the corresponding regions of the spinal cord using the ROIs shown in Figure 3c.

Table 1.

Average axon diameter (AAD) and the standard deviation for the ROIs marked in Figure 6a. The AAD obtained from multiple Toluidine blue histological sections were taken from the marked ROI. The d-PFG AADs were obtained from similar ROI’s in the d-PFG map.

ROI AAD histology (μm) AAD d-PFG map (μm)
A 4.53 ± 2.0 4.5 ± 0.2
B 2.67 ± 2.1 3.4 ± 0.3
C 3.92 ± 1.4 3.6 ± 0.4
D 4.42 ± 1.9 4.2 ± 0.3
Open in a new tab

Figure 4 shows results obtained from the same specimen using a d-PFG-filtered MRI experiment. Figure 4a shows the raw non-diffusion weighted d-PFG-filtered MRI. The image appears free of hardware artifacts with a high SNR of 37.5. Figure 4b, and c show the raw d-PFG MRIs for the same specimen with gradients of 597 mT m−1 acquired with collinear and perpendicular gradient blocks (i.e., φ = 0 and π, respectively). Due to the particular alignment of the fibers that allows a 2D circular sampling scheme, the difference between the two images is very pronounced.

Figure 4.

Figure 4

Open in a new tab

d-PFG MRI images of the spinal cord using δ = 3.15 ms, Δ = 60 ms a) G = 0 and b) and c) G = 597.6 mT m−1 for φ = 0 and π.

3.2 GCA phantom

Figure 5a and b show the pore diameter map of the GCA—a proxy for the AAD—obtained using the 2D and 3D acquisition schemes, respectively. A Region of Interest (ROI) analysis of the maps yielded an AAD of 4.88 ± 0.04 μm and 4.7 ± 0.3 μm for the 2D and 3D acquisition schemes, respectively.

Figure 5.

Figure 5

Open in a new tab

Average pore diameter map obtained from the GCA using d-PFG MRI data, with δ = 3.15 ms, Δ = 75 ms, and G = 0 – 664 mT m−1. a) 2D and b) 3D acquisition scheme.

3.3 Rat corpus callosum

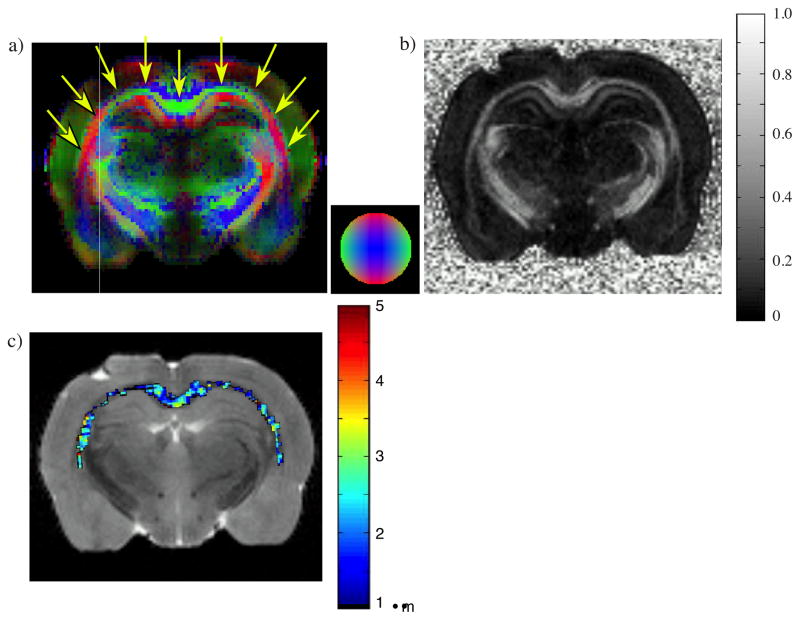
Figure 6a and b show the DEC and FA maps calculated from the DTI data obtained on a coronal slice of rat brain (arrows mark the corpus callosum). The corpus callosum is very visible in these images. The variation in color in the DEC map in the corpus callosum clearly shows the change in fiber orientation of this structure within the image plane.

Figure 6.

Figure 6

Open in a new tab

a) DEC and b) FA maps of a coronal slice of fixed rat brain obtained from DTI using δ = 3 ms, Δ = 30 ms with b-values of 100 and 1600 s-mm−2 c) AAD map for the corpus callosum obtained from d-PFG data, using δ = 3.15 ms, Δ = 30 ms, and G = 0 – 591.6 mT m−1, with DTI employed overlay a T2-weighted image.

Figure 6c shows the corresponding AAD map in the corpus callosum obtained from the 3D d-PFG MRI experiment. The fiber orientation was first obtained from the DTI experiment prior to the d-PFG MRI acquisition and the signal attenuation perpendicular to the eigenvector associated with the largest eigenvalue—the purported fiber direction (Basser, Biophys J. 1994)—was used to estimate the axon diameter. The FA map in Figure 6b appears fairly homogeneous as expected from a coronal slice of the corpus callosum while the AADs ranged between 1 and 3 μm with a mean AAD of 1.5 μm.

Figure 7a shows a DEC map obtained from the d-PFG MRI experiments. Even though the map is noisy and inferior in quality to the same map obtained by DTI, the corpus callosum (marked with arrows) is well defined. The resulting AAD map (Figure 7b) looks remarkably similar to the one in Figure 6c with the same mean diameter of 1.5 μm.

Figure 7.

Figure 7

Open in a new tab

a) DEC map obtained from the 3D d-PFG MRI experiment. b) AAD map obtained from d-PFG data where the DTI was not employed overlay a T2 image.

4. Discussion

The spinal cord AAD map, obtained from the d-PFG MRI experiments clearly shows variations in white matter microstructure that are not visible in the corresponding DTI-derived maps. The d-PFG MRI AAD maps agree well with and follow the known anatomy of the spinal cord where the various regions of the cross section can be identified (Snell 2001). The AAD map obtained from the d-PFG MRI experiments also agrees very well with the corresponding AADs obtained from our own histological analysis of corresponding ROIs.

For specimens that can be aligned in the magnet (such as the spinal cord) a 2D d-PFG MRI sampling scheme is suitable. N.B. determining the orientation of the sample is crucial for the success of the d-PFG analysis and a DTI experiment is recommended to measure fiber orientation prior to the 2D d-PFG MRI. However, for tissues where the fiber orientation may vary from voxel to voxel, such as in the corpus callosum, a 3D d-PFG MRI acquisition scheme should be used where the gradient orientations are distributed over various shells. The high degree of similarity of the pore diameter maps and values obtained in the GCA using the 2D and 3D acquisition schemes validate the use of the 3D spherical d-PFG MRI acquisition. We also anticipate that similar type of phantom will be useful in validating new in vivo methods for measuring AAD distributions within the brain using quad and other multiple PFG MRI methods, such as were recently demonstrated in(Avram, Özarslan et al. 2012).

The AAD map of the rat corpus callosum follows the known anatomy of the rat brain (Kruger, Saporta et al. 1995), and yields the expected distribution of AADs (Barazany, Basser et al. 2009). The 3D d-PFG MRI acquisition contains enough single diffusion weighted images to obtain a reasonably high-quality fiber orientation map using DTI because each time the angle between the successive PFG blocks is π, the middle gradient pulses vanish, resulting in a single PFG experiment with twice the diffusion time. Therefore, a separate DTI experiment is no longer needed in this case and the acquisition time can be reduced.

5. Conclusions

The d-PFG MRI is a new tool for revealing the underlying microstructure of axons in the PNS and CNS. Assuming a simple bi-compartmental model, with no a priori assumptions about the axon diameter distribution, one can obtain an AAD map. As a result, this method has the potential to characterize features or changes in brain structure from genetic manipulations (knock-in or knock out models), neurotrauma, degenerative diseases or disorders (such as MS or ALS), and cognitive or behavioral disorders where a neuroanatomical substrate may be suspected or neuroanatomic sequelae occur, even if these cannot be detected by current MRI methods. We have presented d-PFG MRI acquisition scheme appropriate for studying tissues with known a priori axonal orientation and for making this measurement in the brain and other tissues where the axon orientation is not known a priori and can be assumed to change from voxel to voxel.

4. Highlights.

  • Double pulsed field gradient (d-PFG) MRI was used to study nerve microstructure.

  • Average axon diameter (AAD) map was obtained in fixed porcine spinal cord.

  • MRI findings were verified with optical microscopy.

  • Novel 3D d-PFG acquisition scheme was tested in rat brain.

  • AAD map was obtained in rat corpus callosum.

Acknowledgments

MK and EÖ were supported by funds from the CNRM and Henry Jackson Foundation. EÖ was supported in part by NIH R01MH074794. PJB and FH were supported by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development, NIH. RZF was supported by the Center for Information Technology, NIH. We are grateful to Mr. R. R. Clevenger, Mr. T. J. Hunt, Mrs. Joni Taylor, Ms. G. J. Zywicke, Mr. A. D. Zetts, Mrs. K. Keeran, Mr. S. M. Kozlov, and Mr. K. R. Jeffries, from LAMS, NHLBI, and Dr. M. D. Budde from the Department of Neurosurgery, Medical College of Wisconsin for obtaining the specimens. We would also like to thank Dr. Doug Morris from the NMRF/NINDS for assistance with the instrumentation.

Footnotes

Reviewer Suggestions

  1. Jürgen Fisterbusch, J.Finsterbusch@uke.uni-hamburg.de, Department of system neuroscience, Hamburg University, One of the leading scientists in the field of multiple scattering MRI
  2. Daniel Topgaard, daniel.topgaard@fkem1.lu.se, Knowledge in the field diffusion acquisition and modeling methods including d-PFG, Division of Physical Chemistry, Lund University
  3. Silvia Capuani, silvia.capuani@roma1.infn.it, Department of physics, University of Roma La Sapienza, Knowledge in the field anomalous diffusion and biological porous media
  4. Frederick Bernd Laun, f.laun@dkfz.de, German Cancer Research Center, Heidelberg University, Knowledge in the field of diffusion methods acquisition and modeling

References

  1. Assaf Y, Blumenfeld-Katzir T, et al. AxCaliber: a method for measuring axon diameter distribution from diffusion MRI. Magn Reson Med. 2008;59:1347–1354. doi: 10.1002/mrm.21577. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Assaf Y, Freidlin RZ, et al. New modeling and experimental framework to characterize hindered and restricted water diffusion in brain white matter. Magn Reson Med. 2004;52:965–978. doi: 10.1002/mrm.20274. [DOI] [PubMed] [Google Scholar]
  3. Avram AV, Özarslan E, et al. In vivo detection of microscopic anisotropy using quadruple pulsed-field gradient 2 (qPFG) diffusion MRI on a clinical scanner. NeuroImage. 2012 doi: 10.1016/j.neuroimage.2012.08.048. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Avram L, Assaf Y, et al. The effect of rotational angle and experimental parameters on the diffraction patterns and micro-structural information obtained from q-space diffusion NMR: implication for diffusion in white matter fibers. J Magn Reson. 2004;169:30–38. doi: 10.1016/j.jmr.2004.03.020. [DOI] [PubMed] [Google Scholar]
  5. Barazany D, Basser PJ, et al. In vivo measurement of axon diameter distribution in the corpus callosum of rat brain. Brain. 2009;132:1210–1220. doi: 10.1093/brain/awp042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Basser PJ. Relationships Between Diffusion Tensor and q-Space MR. Magn Reson Med. 2002;47:392–397. doi: 10.1002/mrm.10052. [DOI] [PubMed] [Google Scholar]
  7. Basser PJ, Mattiello J, et al. MR diffusion tensor spectroscopy and imaging. Biophys J. 1994;66:259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Callaghan PT. NMR imaging, NMR diffraction and applications of pulsed gradient spin echoes in porous media. Magn Reson Imaging. 1996;14:701–709. doi: 10.1016/s0730-725x(96)00152-x. [DOI] [PubMed] [Google Scholar]
  9. Callaghan PT, Coy A, et al. Diffraction-like effects in NMR diffusion studies of fluids in porus solids. Nature. 1991;351:467–351. [Google Scholar]
  10. Cheng Y, Cory DG. Multiple scattering by NMR. J Am Chem Soc. 1999;121:7935–7936. [Google Scholar]
  11. Finck H. Epoxy resins in electron microscopy. J Biophys Biochem Cytol. 1960;7:27–30. doi: 10.1083/jcb.7.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Freeman JA, Spurlock BO. A new epoxy embedment for electron microscopy. J Cell Biol. 1962;13:437–443. doi: 10.1083/jcb.13.3.437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Grebenkov DS. NMR survey of reflected Brownian motion. Rev Mod Phys. 2007;79:1077–1137. [Google Scholar]
  14. Hursh JB. The properties of growing nerve fibers. Am J Physiol. 1939;127:140–153. [Google Scholar]
  15. Kandel ER, Schwartz JH, et al. Principle of neural science. New York: McGraw-Hill; 2000. [Google Scholar]
  16. Koch MA, Finsterbusch J. Compartment size estimation with double wave vector diffusion-weighted imaging. Magn Reson Med. 2008;60:90–101. doi: 10.1002/mrm.21514. [DOI] [PubMed] [Google Scholar]
  17. Komlosh ME, Horkay F, et al. Detection of microscopic anisotropy in gray matter and in novel tissue phantom using double Pulsed Gradient Spin Echo MR. J Magn Reson. 2007;189:38–45. doi: 10.1016/j.jmr.2007.07.003. [DOI] [PubMed] [Google Scholar]
  18. Komlosh ME, Lizak MJ, et al. Observation of microscopic diffusion anisotropy in the spinal cord using double-pulsed gradient spin echo MRI. Magn Reson Med. 2008;59:803–809. doi: 10.1002/mrm.21528. [DOI] [PubMed] [Google Scholar]
  19. Komlosh ME, Özarslan E, et al. Pore diameter mapping using double pulse-field gradient MRI and its validation using a novel glass capillary array phantom. J Magn Reson. 2011;208:1168–1177. doi: 10.1016/j.jmr.2010.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Kruger L, Saporta S, et al. Photographic atlas of the rat brain. Cambridge: Cambridge university press; 1995. [Google Scholar]
  21. Lawrenz M, Finsterbusch J. Detection of microscopic diffusion anisotropy on a whole-body MR system with double wave vector imaging. Magn Reson Med. 2011;66:1405–1415. doi: 10.1002/mrm.22934. [DOI] [PubMed] [Google Scholar]
  22. Mitra PP. Multiple wave-vector extension of the NMR pulsed-field-gradient spin-echo diffusion measurement. Phys Rev B. 1995;51:15074–15078. doi: 10.1103/physrevb.51.15074. [DOI] [PubMed] [Google Scholar]
  23. Moseley ME, Cohen Y, et al. Diffusion-weighted MR imaging of anisotropic cat central nervous system. Radiology. 1990;176:439–445. doi: 10.1148/radiology.176.2.2367658. [DOI] [PubMed] [Google Scholar]
  24. Ong HH, Wright AC, et al. Indirect measurement of regional axon diameter in excised mouse spinal cord with q-space imaging: simulation and experimental studies. NeuroImage. 2008;40:1619–1632. doi: 10.1016/j.neuroimage.2008.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Özarslan E. Compartment shape anisotropy (CSA) revealed by double pulsed field gradient MR. J Magn Reson. 2009;199:56–67. doi: 10.1016/j.jmr.2009.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Özarslan E, Basser PJ. Microscopic anisotropy revealed by NMR double pulsed field gradient experiments with arbitrary timing parameters. J Chem Phys. 2008;128:154511. doi: 10.1063/1.2905765. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Özarslan E, Komlosh ME, et al. Double pulsed field gradient (double-PFG) MR imaging (MR) as a means to measure the size of plant cells. Magn Reson Chem. 2011;49(Suppl 1):S79–84. doi: 10.1002/mrc.2797. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Özarslan E, Shemesh N, et al. A general framework to quantify the effect of restricted diffusion on the NMR signal with applications to double pulsed field gradient NMR experiments. J Chem Phys. 2009;130:104702. doi: 10.1063/1.3082078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Pajevic S, Assaf Y, et al. Neuroscience. Washington, DC: 2008. An optimum principle predicts skewed and heavy-tailed distributions of axon diameter in white matter fascicles. [Google Scholar]
  30. Pajevic S, Basser PJ. An optimum principle predicts the distribution of axon diameters in normal white matter. PLoS One. 2013 doi: 10.1371/journal.pone.0054095. PONE-D-12-20642R20642. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Perge JA, Niven JE, et al. Why do axon differ in caliber? J Neurosci. 2012;32:626–638. doi: 10.1523/JNEUROSCI.4254-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Pierpaoli C, Jezzard P, et al. Diffusion tensor MR imaging of the human brain. Radiology. 1996;201:637–648. doi: 10.1148/radiology.201.3.8939209. [DOI] [PubMed] [Google Scholar]
  33. Robertson B. Spin-echo decay of spins diffusing in a bounded region. Phys Rev. 1966;151:273–277. [Google Scholar]
  34. Shemesh N, Özarslan E, et al. Observation of restricted diffusion in the presence of a free diffusion compartment: single- and double- PFG experiments. J Magn Reson. 2009;200:214–225. doi: 10.1016/j.jmr.2009.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Shemesh N, Özarslan E, et al. Accurate nonivasive measurement of cell size and compartmental shape anisotropy in yeast cells using double-pulsed field gradient MR. NMR Biomed. 2012;25:236–246. doi: 10.1002/nbm.1737. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Sloane NJA. Spherical codes. 2000 from http://www2.research.att.com/~njas/packings/
  37. Snell RS. Clinical neuroanatomy for medical students. Baltimore: Lippincott Williams & Wilkins; 2001. [Google Scholar]
  38. Stejskal EO, Tanner JE. Spin diffusion measurement: spin echo in the presence of time-dependent field gradient. J Chem Phys. 1965;42:288–292. [Google Scholar]
  39. Tasaki I, Ishii K, et al. On the relation between the conduction-rate, the fiber-diameter and the internodal distance of the medullated nerve fiber. Jpn J Med Sci III, Biophysics. 1943;9:189–199. [Google Scholar]
  40. Weber T, Ziener CH, et al. Measurements of apparent cell radii using a multiple wave vector diffusion experiment. Magn Reson Med. 2009;61:1001–1006. doi: 10.1002/mrm.21848. [DOI] [PubMed] [Google Scholar]

RESOURCES