Identifying functional bases for multidimensional neural computations

Abstract

Current dimensionality reduction methods can identify relevant subspaces for neural computations, but do not favor one basis over the other within the relevant subspace. Finding the appropriate basis can further simplify the description of the nonlinear computation with respect to the relevant variables, making it easier to elucidate the underlying neural computation and make hypotheses about the neural circuitry giving rise to the observed responses. Part of the problem is that, although some of the dimensionality reduction methods can identify many of the relevant dimensions, it is usually difficult to map out and/or interpret the nonlinear transformation with respect to more than a few relevant dimensions simultaneously without some simplifying assumptions. While recent approaches make it possible to create predictive models based on many relevant dimensions simultaneously, there still remains the need to relate such predictive models to the mechanistic descriptions of the operation of underlying neural circuitry. Here we demonstrate that transforming to a basis within the relevant subspace where the neural computation is best described by a given nonlinear function often makes it easier to interpret the computation and describe it with a small number of parameters. We refer to the corresponding basis as the functional basis, and illustrate the utility of such transformation in the context of logical OR and logical AND functions. We show that although dimensionality reduction methods such as spike-triggered covariance are able to find a relevant subspace, they often produce dimensions that are difficult to interpret and do not correspond to a functional basis. The functional features can be found using a maximum likelihood approach. The results are illustrated using simulated neurons and recordings from retinal ganglion cells. The resulting features are uniquely defined, non-orthogonal, and make it easier to relate computational and mechanistic models to each other.

1 Introduction

A central challenge in the study of sensory processing neurons lies in discerning the features of a given stimulus that influence spiking behavior. It has become apparent in recent years that many neurons are selective for more than one stimulus feature (Atencio et al., 2008; Cantrell et al., 2010; Chen et al., 2007; Fairhall et al., 2006; Felsen et al., 2005; Fox et al., 2010; Hong et al., 2007; Horwitz et al., 2005, 2007; Kim et al., 2011; Maravall et al., 2007; Rust et al., 2005; Sincich et al., 2009; Touryan et al., 2002), sometimes as many as a dozen, leading to highly nonlinear and potentially very complex input/output relationships. Dimensionality reduction methods, such as spike-triggered covariance (STC) and its extensions (Bialek and de Ruyter van Steveninck, 2005; de Ruyter van Steveninck and Bialek, 1988; Paninski, 2003; Park and Pillow, 2011; Pillow and Simoncelli, 2006; Schwartz et al., 2002, 2006) or maximally informative dimensions (MID) and its extensions (Fitzgerald et al., 2011a; Rajan and Bialek, 2012; Sharpee et al., 2004), are able to produce linear subspaces which are relevant to the spiking activity of a neuron according to some metric (e.g. changes in stimulus covariance caused by spiking or mutual information). However, these and other dimensionality reduction methods specify features not uniquely, but up to a linear combination of them. Often, the results are presented in terms of orthogonal bases. Such orthogonal representations make it difficult to infer the corresponding neural computation that often involve a set of overlapping stimulus features, as in many types of motion computations (Gollisch and Meister, 2010). Here we show that for certain types of computations the relevant subspace produced by these methods contains extractable information about the functional neural circuitry involved in sensory processing.

The STC or MID subspaces are defined by a set of basis vectors which are often interpreted as the stimulus ‘features’ encoded by a neuron. However, it may be more appropriate to say that the features are defined by a functional basis, which spans the same subspace. The functional basis is a set of features that best accounts for the observed nonlinearities in the neural response using a pre-defined function. While the STC and MID bases certainly have a meaning in terms of their respective metrics, they might not coincide with the functional basis, which one may hope will yield insights into the underlying neural circuitry and may be amenable to interpretation. For example, the functional basis may be non-orthogonal, which cannot be matched by orthogonal STC bases. It is possible to order dimensions according to how much information they capture (Pillow and Simoncelli, 2006), but the resultant features also often come out to be orthogonal. In addition, the functional basis may help achieve a more concise description of the nonlinear gain function that describes how the neural spiking probability varies with stimulus components along the features. The nonlinear gain function together with the set of stimulus features forms the so-called linear-nonlinear (LN) model of the neural response (Chichilnisky, 2001; de Boer and Kuyper, 1968; Meister and Berry, 1999; Schwartz et al., 2006; Victor and Shapley, 1980).

Here we explore the boolean operations corresponding to logical OR and logical AND computations, which are thought to describe the computations of some real neurons, such as those that contribute to translation invariance (Riesenhuber and Poggio, 1999; Serre et al., 2007), various types of motion computation (Gollisch and Meister, 2010), build selectivity to increasingly complex stimulus features (Barlow and Levick, 1965) or implement coincidence detection (Carr and Konishi, 1988). We show that operations of this kind have clearly defined functional bases. The functional bases may span the same subspace as STC basis, yet they allow for easier interpretation of the neural computation and the likely neural architecture underlying it. We describe a way to extract the functional feature set from the STC basis and demonstrate the method on several biologically inspired stimulated neurons as well as recordings of salamander retinal ganglion cells.

1.1 Functional bases

Consider a neuron encoding a D dimensional stimulus S. The neural response y is binary (when considered in a small time window), with y = 0 meaning the cell is silent and y = 1 meaning the cell spikes. The instantaneous firing rate of such a neuron is proportional to P(y = 1|S), the conditional probability of a spike. The neuron is said to be selective for n features of the stimulus if P(y = 1|S) = f(x₁, x₂, …, x_n), where x_i = S · v_i is the projection of the stimulus onto a vector v_i. The collection of vectors {v_i} represents the stimulus features for which the neuron is selective.

1.1 Non-orthogonal feature sets

For neurons beyond the sensory transduction stage, the features {v_i} are determined by the relevant stimulus features of afferent neurons, and are in general not orthogonal. For example, a retinal ganglion cell may combine inputs from several bipolar cells that have overlapping receptive fields (Asari and Meister, 2012; Cohen and Sterling, 1991). The STC analysis would typically yield the sum and difference between the bipolar cells receptive fields, as schematically illustrated in Figures 1 and 5. Although the neural response function f can be defined in terms of any linearly independent basis formed from a linear combination of the feature vectors, we are interested in finding a basis that is more closely related to its biological function. Many types of functions can be described using logical operations. Therefore, in this work we focus on finding representations of f that make such logical descriptions explicit, and refer to the corresponding basis as the functional basis.

Figure 1.

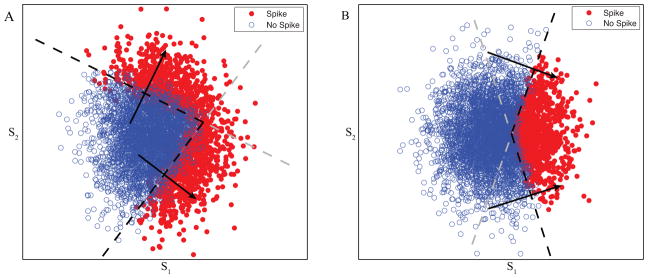
Computations in two dimensions with non-orthogonal features. Each dot represents a high dimensional stimulus that has been projected onto this relevant subspace with axes s₁ and s₂ recovered by STC method. The red dots are stimuli for which y = 1 and the blue circles are those for which y = 0. Both logical OR (A) and logical AND operations (B) with two non-orthogonal features v₁ and v₂ are defined by two thresholds (dashed lines) which lie perpendicular to the feature directions. In the case of logical OR, any stimulus above either threshold causes a spike (corrupted by Gaussian noise), whereas for a logical AND function stimuli must be above all thresholds to elicit spikes. In both panels the parts of the thresholds that determine spiking behavior are shown in black and the irrelevant parts in gray. Note that logical OR nonlinearity leads to the “crescent-shape” distribution of spike-eliciting inputs that are common in sensory systems (Fairhall et al., 2006).

Figure 5.

Logical OR model of a simulated retinal ganglion cell. Each of the 9 blob-like features (A) represents the receptive fields of individual bipolar cells feeding into a retinal ganglion cell. Shown in (B) is the maximum likelihood OR functional basis and in (C) is the STC basis.

As an example, consider a neuron selective for a set of features {v₁, v₂.., v_n}, using a noisy logical OR operation

$$f(x_1,x_2,\dots ,x_n)=\{\begin{array}{ll}1,\hfill & \text{if}{x}_i+{\eta }_i\ge {\theta }_i\text{for}\mathbf{any}i\in \{1,2,\mathrm{..},n\}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (1)

where η_i is Gaussian noise added to x_i and θ_i is the spiking threshold along dimension v_i. A particular instance of this type of neuron is shown in Fig. 1A for n = 2. In this figure, open blue dots represent stimuli for which y = 0 and the red dots represent stimuli for which y = 1, separated by the thresholds (dashed lines) along the dimensions v₁ and v₂.

The horizontal s₁ and vertical s₂ axes of the plot form the basis that a method like STC or MID might recover (in this case they actually correspond to STC dimensions), but a more natural choice of basis is given by v₁ and v₂. These features v₁ and v₂ have a simple meaning in the computation performed by the cell, cf. Eq. (1). By comparison, the nonlinear gain function would require a more complex description in terms of s₁ and s₂, e.g. the threshold value along s₁ dimension depends on the value of s₂. In a general case the description of the nonlinear gain function along a set of n axes requires a large number of parameters, such as $N_{\text{bins}}^n$ values where N_bins is the number of bins along each of the dimensions.

This leads to the “curse of dimensionality” that makes it difficult to map out and/or describe the nonlinear computation at a conceptual level with respect to more than a few relevant dimensions (although recent computational approaches (Park et al., 2011) make it possible to build predictive models with respect to many dimensions simultaneously). The transformation to the functional basis provides a way to model the nonlinear gain function with a small number of parameters, such as the threshold θ_i, scale and noise magnitude along each of the axes in the functional basis. The number of parameters increases linearly with the number of relevant dimensions, and not exponentially as in the case of nonparametric descriptions.

Another computation relevant to biology is the logical AND operation, described by

$$f(x_1,x_2,\dots ,x_n)=\{\begin{array}{ll}1,\hfill & \text{if}{x}_i+{\eta }_i\ge {\theta }_i\text{for}\mathbf{all}i\in \{1,2,\mathrm{..},n\}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (2)

An example of this function is shown in Fig. 1B for n = 2. Again, the features defined by the threshold directions are not orthogonal and therefore could not be found using STC.

We note that the fact that the neural response function depends on n features (as in Eqs. (1) and (2)) does not exclude the possibility that the relevant subspace will have a lower dimensionality d < n. This will happen when the n features are linearly dependent. For instance, a boolean function can have n planar thresholds in a d dimensional relevant subspace where n > d. However in practice it is unlikely that different inputs to a neuron will have linearly dependent stimulus features. For example, if there are three presynaptic neurons, it is unlikely that each one of them is not sensitive to at least partly novel aspects of the stimulus.

1.2 Finding the functional bases for boolean computations

The features encoded by the different pathways in a neural circuit are confined to a subspace in the high dimensional stimulus space. Therefore, finding a functional basis can be simplified by first extracting this subspace using existing dimensionality reduction methods such as STC. Once that subspace is determined, an analytical function representing the boolean OR and AND operations can be fit to identify a set of functional features.

1.1 Dimensionality reduction

The STC method is designed to work with Gaussian stimuli, and as such, we draw samples S(t) for t = 1, 2, …, T from a D dimensional zero mean normal distribution (0, C_prior), where C_prior is the covariance matrix. Applying Eq. (1) with n features produces a model cell spike train {y(t)}, which can be used to calculate the spike-triggered covariance C_spike, defined by the elements

$$C_{\text{spike}}(i,j)=\frac{1}{T}\sum _{t=1}^{T}y(t)S_i(t)S_j(t)-\frac{1}{T^2}\sum _{t=1}^{T}y(t)S_i(t)\sum _{t=1}^{T}y(t)S_j(t).$$ (3)

The change in covariance caused by spiking is ΔC = C_spike − C_prior. By diagonalizing ΔC we obtain the dimensions along which the covariance is altered by the neural response. These can be identified by the eigenvectors that have nonzero eigenvalues. This procedure is valid for uncorrelated and/or spherically symmetric stimuli (Bialek and de Ruyter van Steveninck, 2005; Chichilnisky, 2001; Samengo and Gollisch, 2012; Schwartz et al., 2006). Other methods can be used to find the relevant subspace for more complex stimuli (Fitzgerald et al., 2011a; Park and Pillow, 2011; Sharpee et al., 2004). Here we focus on uncorrelated stimuli, because this work is devoted to finding a specific basis within the relevant subspace, and not the subspace itself.

The accuracy with which the relevant subspace is found can be quantified using an overlap metric (Rowekamp and Sharpee, 2011) with respect to the subspace spanned by the features used by the model:

$$\mathcal{O}=\frac{\sqrt[d]{\mid \text{Det}({UV}^T)\mid }}{\sqrt[2d]{\mid \text{Det}(U{U}^T)\mid }\sqrt[2d]{\mid \text{Det}(V{V}^T)\mid }},$$ (4)

where U and V are d × D matrices whose rows are the normalized eigenvectors {u_i} and features {v_i}, respectively. This metric is bounded between 0 and 1, with 0 meaning the two subspaces have no overlap and 1 meaning they are identical, and gives us a way to evaluate our confidence in the dimensionality reduction step. Note that if the number of features {v_i} is larger than the dimensionality d of the relevant subspace, one can still choose d features that span that space to compute the overlap.

1.2 Maximum likelihood models

Given this reduced space, we wish to find the functional basis by looking for linear combinations of the vectors u_i that best approximate a logical OR or logical AND computation. Such functions have the general form

$$P_{\text{OR}}(y=1\mid \mathbf{S})=1-\prod _{\alpha =1}^n[1-g(U^T{\mathbf{A}}_{\alpha }·\mathbf{S})],$$ (5)

$$P_{\text{AND}}(y=1\mid \mathbf{S})=\prod _{\alpha =1}^{n}g(U^T{\mathbf{A}}_{\alpha }·\mathbf{S}),$$ (6)

where each A_α is a d dimensional vector that describes the components of αth axes of the functional basis within the STC basis. The function g(U^T A_α · S) is some threshold-like function that describes the spike probability along the direction of the αth functional feature of the computation.

To make progress, we must choose a specific functional form of g(U^T A_α · S). An obvious choice is the logistic function g_α = 1/(1 + exp(a_α + U^T A_α · S)), where a_α determines the location of the transition from silence to spiking. This choice of g is able to handle noise in the computation, as well as different thresholds along different features. It is also analytically quite tractable and has an information theoretic interpretation as the least biased response function (Fitzgerald et al., 2011b) consistent with encoding of a linear component along the functional feature.

The parameters {A_α} and {a_α} can be found by maximizing the log likelihood. For a logical OR, this is

$$L_{\text{OR}}=\sum _{t=1}^N\left[y(t)log\left(1-\prod _{\alpha =1}^n\frac{1}{1+e^{-a_{\alpha }-{\mathbf{F}}_{\alpha }·\mathbf{S}(t)}}\right)-(1-y(t))\sum _{\alpha =1}^{n}log(1+e^{-a_{\alpha }-{\mathbf{F}}_{\alpha }·\mathbf{S}(t)})\right],$$ (7)

where F_α = U^T A_α are the functional basis vectors. Note that the functional basis vectors are not normalized to length 1. This optimization problem can be implemented using a straightforward conjugate gradient algorithm. In the end, the parameters {a_α} that determine the threshold positions are unimportant if all that is desired is an estimate of the functional basis. The typical run time for the algorithm with 200,000 stimulus frames each of which had 256 pixels is around 5 minutes on a 3.2 Ghz desktop computer. Convergence time increases linearly with data set size and the number of basis vectors fit, and was not affected by the signal-to-noise ratio of the dataset. The code is publicly available at http://cnl-t.salk.edu/Code/.

2 Results

2.1 Model cells

Three model cells were created to test whether maximizing Eq. (7) is able to recover the functional basis vectors. In all cases 200,000 stimulus samples were created from a uncorrelated Gaussian distribution, with S_i ∈ {0, …, 255} representing the ith pixel intensity of an image. The response models were chosen to be logical OR functions, defined in the same manner as Eq. (1). The thresholds along each feature direction were set to the same value within a given model. The Gaussian noise was added to the projections in such a way that the overall probability of a spike was between 0.2 and 0.4 for all models. The STC subspace in all cases had an overlap 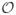> 0.95, indicating a very good recovery of the model subspaces.

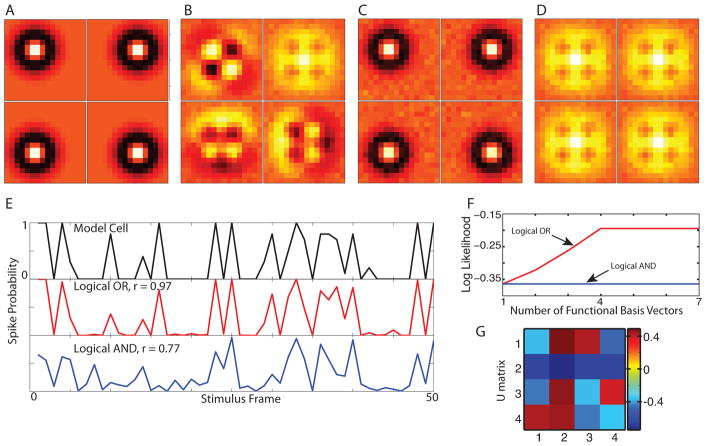
The first model considered is an example of a translationally invariant feature detector, shown in Fig. 2A. The functional basis vectors are 4 shifted versions of a center-surround feature, located in the four corners of the image. These features overlap and are not orthogonal and therefore the STC basis, shown in Fig. 2B, is formed from linear combinations of these features. The logical OR functional dimensions make the computation performed by the cell difficult to interpret in the STC basis. The maximum likelihood OR solution for the functional basis with four features is shown in Fig. 2C, and matches quite well with the true features.

Figure 2.

Translationally invariant model cell. The computation performed by the model is a logical OR operation on a center-surround feature, shifted to the four corners of the receptive field (A). The STC basis (B) and the maximum likelihood OR functional basis (C) both span the same space, but are much different in their appearance and interpretation. A maximum likelihood AND fit (D) finds four identical features, which does not match any of the model features. (E) Comparing the model spike probabilities generated from repeated presentations of a stimulus sequence to the predicted spike probabilities shows the logical OR fit outperforms the logical AND fit significantly, with correlation coefficients of r = 0.97 and r = 0.77 respectively. (F) The average log likelihood per time bin for logical AND and OR models with different number of functional basis vectors. (G) The transformation matrix from the STC to the functional bases (here, each vector was normalized to length one for presentation purposes).

We also fit a maximum likelihood AND function to the STC basis for comparison. The outcome for the logical AND functional basis is shown in Fig. 2D. Each of the four features is very nearly identical, indicating that the optimal solution for a logical AND is in fact not a logical AND at all, but rather a logistic function along a single dimension. This qualitative observation is quantified below.

The performance of these fits can be evaluated by comparing the predicted spike probability as a function of the stimulus to that obtained from the true model cell upon repeated presentations of a group of stimuli. This is shown in Fig. 2E for a 50 frame section of a 200,000 frame stimulus presented 10 times to the model cell. The spike probability obtained from the model (top panel) matches very well with the maximum likelihood logical OR (middle panel) and has a correlation coefficient of r = 0.97 across all 200,000 frames. The maximum likelihood logical AND, on the other hand, has a poorer performance, with r = 0.77. This comparison provides a way to determine how much like an OR or AND operation is the computation performed by a real cell.

If one assumed no a priori about knowledge of the number of features in this example, one can determine the optimal number of features to fit by performing a maximum log likelihood calculation for a given number of features included into the model, cf. Fig. 2F. In the case of the logical OR, the log likelihood increases as the number of features are added up to four. When the number of features is increased beyond four (which is the correct number for this model), no further increases in log likelihood are observed. This happens because extra features are either noise-like and have such large thresholds associated with them that they do not affect the spiking, or they reproduce one of the earlier features. In the case of the logical AND function, the log likelihood does not increase as additional features are added into the model, because all of the features are roughly the same. Thus, finding the number of features where the log likelihood saturates provides a way to determine the correct number of features for a given model. The choice of a particular model structure, such as the logical AND or logical OR model can be made according to which models yields larger log likelihood.

As another example of an invariant computation, we tested a rotationally invariant model, shown in Fig. 3. The model is selective for a curved feature at 8 different orientations (Fig. 3A). Using STC, the 8 dimensional subspace was recovered, Fig. 3B, but had little resemblance to the functional feature set. The maximum likelihood estimate shown in Fig. 3C, however, clearly recovers the functional basis.

Figure 3.

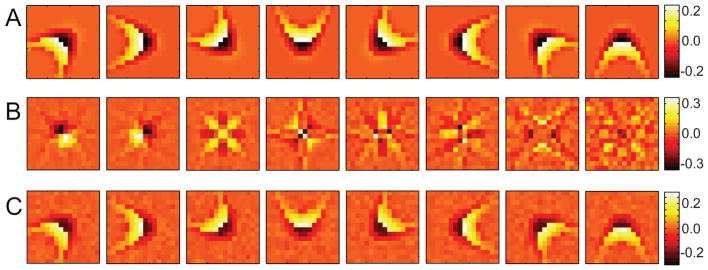
Rotationally invariant model cell. The computation performed by the model is a logical OR operation on a curved feature. The functional basis of the model (A) is defined by rotating the feature to 8 different orientations. The STC basis is shown in panel (B) and the maximum likelihood functional basis in panel (C). The presentation order of the features in (C) was chosen to match the corresponding features of the model logical OR.

Up to this point we have been fitting maximum likelihood functions with n_ML = n_model and considered the case with no overcompleteness where n_model equals the dimensionality d of the relevant subspace. However, the number of features is not known a priori and therefore n_ML may be varied to find the best fit. An example of this is shown in Fig. 4 using the rotationally invariant model cell. The functional basis for n_ML = 7, Fig. 4, recovers 6 of the features very well while the 7th feature is a linear combination of the last two with one orientation dominant over the other. For n_ML = 9, Fig. 4B, recovers all 8 features well while the 9th is mostly redundant with some slight overfitting to the noise in the neural computation. The redundant dimensions are associated with large threshold values such that they seldom contribute to the model spiking.

Figure 4.

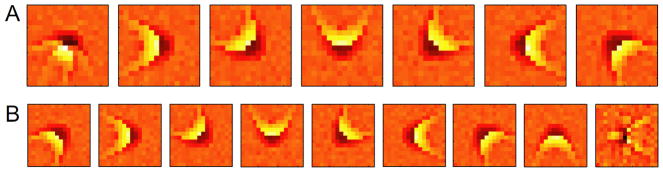
Changing the number of functional features. A maximum likelihood OR fit with n_ML = 7 (A) and n_ML = 9 (B). With n_ML < n_model, some of the features appear as linear combinations of the true features, whereas for n_ML > n_model, some of the features are redundant and begin to fit the noise in the computation. The threshold values along those features is so large that they seldom contribute to the model spiking.

The value of the functional basis model in finding invariant dimensions is that no prior assumption is made about the type of invariance. By comparison, the recent method of maximally informative invariant dimensions (MIID) requires one to specify the type of invariance prior to doing the analysis (Eickenberg et al., 2012; Vintch et al., 2012). The MIID method also imposes a constraint that all of the features are identical except for shift in position or change in angle. Thus, functional basis and invariant methods approach the problem of characterizing neural feature selectivity with invariance from two different perspectives and in principle find the same dimensions if the assumptions made are congruent with the neural computation. Which method is most appropriate for analysis depends on what prior knowledge one has about the system and the degree to which invariance is exact.

To illustrate how the functional basis model can tackle a non-invariant case, we apply it to an example model cell with features that are not shifted or rotated copies of each other. Here, we considered computation inspired by properties of retinal ganglion cells, cf. Fig. 5. This cell encodes 9 blob-like features (Fig. 5A) which could represent the receptive fields of individual bipolar cells (Cohen and Sterling, 1991), and therefore the model could be interpreted as a logical OR retinal ganglion cell. Again the STC basis, shown in Fig. 5C, makes it difficult to interpret the feature selectivity of this model neuron. At the same time, the maximum likelihood OR linear combination of those vectors, shown in Fig. 5B, matches well with the model features. Thus, one of the main advantages of using functional basis representation is that it can characterize the neural computation in cases where the invariance type is not known a priori or invariance is not exact.

2.2 Application to retinal ganglion cell recordings

We now illustrate how the approach works for characterizing encoding of retinal ganglion cells (RGCs) in the salamander retina probed with uncorrelated stimuli. The white noise stimulus consisted of binary checks forming frames with 40 × 40 pixels. The stimulus had 137,145 frames at a rate of 60 Hz. There were a total of 53 cells in the dataset with a wide range of activity from 118 to 30,908 total spikes (median 5,453 spikes). The dataset was collected as part of a previous study and the electrophysiological methods are described there (Marre et al., 2012). As with the model cells, the first step of the analysis was to find the relevant subspace. We decided to focus on the spatial profile of the neurons as a way of illustrating the potential of this method for reconstructing receptive field properties of neurons (or parts of the neural circuit) that are presynaptic to ganglion cells. In the case of retinal ganglion cells, one might hope that the functional bases would then describe receptive fields of bipolar cells feeding into a given ganglion cell or nonlinear pieces within the dendritic computation of the ganglion cell (Soodak et al., 1991). To take into account temporal integration properties of RGCs, we computed the spatiotemporal spike-triggered average (STA) for each neuron (de Boer and Kuyper, 1968). We then performed the singular value decomposition (Press et al., 1992) of the spatiotemporal STA and took the first principal temporal vector as the estimate of the neuron’s temporal kernel. Applying this filter to stimuli yields a set of spatial patterns that can then be associated with the measured neural responses. Subsequent analyses were carried out on 16 × 16 patches of these temporally filtered spatial-only stimuli. The patches were centered at the location of the maximum of the STA of a given neuron. To find the relevant subspace, STC analysis was performed and the relevant vectors were determined by comparing the resulting eigenvalue distribution with the eigenvalue distribution of a series of spike trains whose association with stimuli was broken. The association between stimuli and responses was broken by shifting the spike train forward by various amounts, with a minimal amount of the shift. The advantages of this procedure compared to shuffling spike trains is that preserves all of the higher-order structure in the spike train in addition to the average spike rate (Bialek and de Ruyter van Steveninck, 2005). In our case, the minimal amount of shift was set to 100 frames. The STC analysis was then performed on 40 of such shifted spike trains and the eigenvalue distributions from these analyses were combined. The eigenvalues from the measured (unshifted) spike train/stimuli pairs were considered as significant if they lay outside the bounds of the eigenvalue distribution obtained with shifted spike trains. Of the 53 cells, 30 neurons had more than one relevant stimulus feature and therefore of interest for further investigation using functional bases. The number of spikes available for these cells ranged between 192 to 21,894 (median 5,426). For the example cell, which produced 8389 spikes, the STC method yielded four significant dimensions, cf. Fig. 6A. The STC dimensions have commonly observed spatial profiles, with the dominant feature being uniphasic and the secondary, tertiary, and quaternary feature containing two or more subregions of opposite polarity, similar to what was found in the primary visual cortex (Rust et al., 2005).

Figure 6.

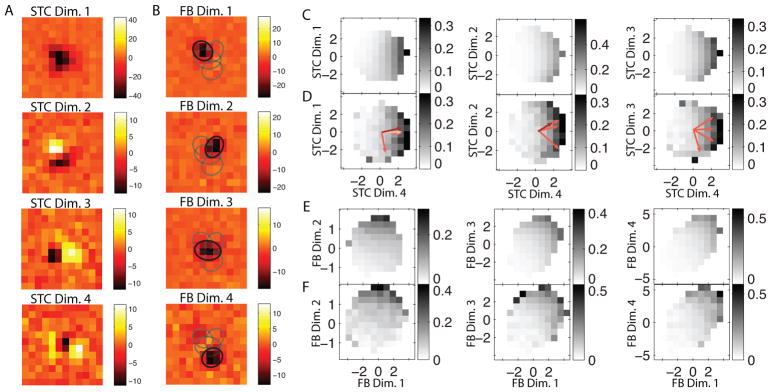
An example RGC stimulated by white noise. The STC basis (A) is rotated according the logical OR functional basis method to produce the functional basis (B). The relevant image features are plotted relative to the average standard deviation per pixel. Unlike the STC basis, the image features in the functional basis are localized. To show the relative positioning of functional basis features relatively to the neuron’s receptive field, we fit these features with two-dimensional Gaussians. Ellipses show one standard deviation contours from Gaussian fits to the four functional basis features. Black ellipses correspond the functional basis feature with which they are overlayed, gray ellipses correspond to the other three functional basis features. We show the two-dimensional nonlinearity predicted (see Eq. 9) by the functional basis method (C) together with the empirically determined nonlinearity from the spiking data (D) in the STC basis. The predicted nonlinearity (E) also closely matches the empirical nonlinearity (F) when plotted in the functional basis projection space.

To find the functional basis for this example neuron, we fit both the logical OR and AND model. In this case, we focus the presentation of results on the logical OR model, which accounted better for the responses of this cell than the logical AND model. First, the data set was split into four sections, as in the jackknife method (Efron and Tibshirani, 1998). By excluding one section for use as a test set to evaluate model performance while the other three sections were used as training sets to fit the model, we had four data sets with which to make a comparison of the functional models. Since the individual test sets have different information contents, the log likelihoods cannot be directly compared. Rather, we computed a normalized log likelihood difference to compare models A and B:

$$\mathrm{\Delta }{L}_{A,B}=\frac{L_A-L_B}{\mid L_A\mid +\mid L_B\mid },$$ (8)

where L_A and L_B are the log likelihoods of model A and B, respectively, computed according to Eq. (7). If the mean log likelihood difference across all test sets, 〈ΔL_A,B〉, was significantly greater than 0, then model A was regarded to be the better model. [The errors were computed using the jackknife method (Efron and Tibshirani, 1998) by scaling the standard error of the mean by t − 1, where t is the number of test datasets, to take into account that the training datasets are not independent.] For the example RGC neuron, the mean log likelihood difference ΔL_OR,AND = 0.0026 ± 0.0001. Comparing logical OR and logical AND to the LN model with nonparametric nonlinearity yielded values ΔL_OR,LN = 0.5454 ± 0.006 and ΔL_AND,LN = 0.5436 ± 0.006, respectively. This shows that for the example cell, logical OR and logical AND both perform better than the non-parametric LN model in making predictions but the logical OR function is a better functional basis model than the logical AND. We note that increasing the number of functional bases did not increase the log likelihood of the logical OR model (logical OR model with respect to five features yielded the log likelihood difference ΔL_OR5;OR4 = −0.0042 ± 0.0285). The features of the functional basis corresponding to the logical OR model are shown in Fig. 6B. Unlike the STC dimensions in panel A, all of the components of the logical OR model in panel B are spatially localized and describe sensitivity to decrements in light intensity in neighboring but displaced parts of the visual field. These dimensions may correspond to the receptive fields of bipolar cells feeding into this RGCs. The expected number of bipolar inputs is ~ 10 (Cohen and Sterling, 1991). Although this is somewhat greater than the four features we observe here, the number of bipolar inputs is known to vary depending on eccentricity, ganglion cell type, and species. It is also possible that the functional basis dimensions we observe here correspond to nonlinear subunits within the dendritic fields of RGCs, as has been discussed for cells in the cat (Soodak et al., 1991) where 2 – 4 subunits were observed. In any case, the subunits that we observe here are physiologically plausible and provide a way to describe functionally separate inputs to a given RGC.

One may also compare this approach to methods that characterize inputs by specifying that relevant features are the same up to position invariance, as in the MIID method. On one hand, MIID method can allow one to potentially obtain more precise estimates of relevant features by pooling measurements from different parts of the visual field. On the other hand, one might be interested in the variability observed at different spatial positions. In particular, for the example cell we are considering the four functional bases features are not exact copies of each shifted to different positions. To determine how important was to consider the individuality of different functional bases dimensions, we compared log-likelihood of the functional basis logical OR model with that of models built on nine identical features shifted by one pixel from the peak of STA, respectively. The log likelihood difference of the invariant dimension model and the log likelihood logical OR model averaged across test sets for the example cell was ΔL_OR,MIID = 0.8710 ± 0.0011. [We also tried the translation invariant model with larger shifts from the STA peak, but these yielded even worse predictive power.] Thus, in this case the functional basis transformation yielded much better predictive power compared to the model where features are constrained to have the same profile shifted to different positions in the visual field.

Similar results were obtained across the population of 30 cells with multidimensional relevant subspaces. The number of relevant dimensions per neuron varied from two to four, with 15 cells having two features, 9 cells having three relevant features, and 6 cells having four relevant STC features. All but two of these cells were best fit by the logical OR functional basis model when compared to the logical AND model (Fig. 7A). No cell was better fit by the LN model than the functional basis model (Fig. 7B). In fact, both functional basis models performed better than the non-parametric LN model for every cell. In all cases, the log likelihood saturated when the number of functional basis features chosen was equal to the number of STC basis vectors. Using the same procedure described in the previous paragraph, MIID was applied and compared to the logical OR model. No cells were better described by invariant dimensions compared to functional bases representation (Fig. 7C).

Figure 7.

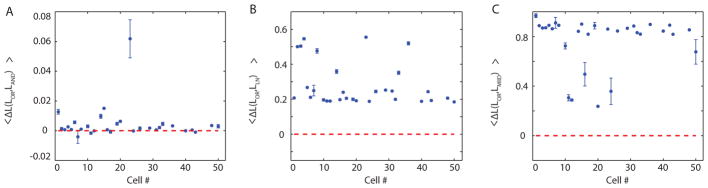
The difference in log likelihoods of the logical OR model against the logical OR model (A), LN model (B), and MIID (C) are plotted across the population of cells. The dashed line marks the threshold value at zero corresponding to the cross-over between the models that are being compared for the ability to predict the neural responses. The logical OR model outperformed the logical AND model and the non-parametric LN models for the majority of neurons.

The transformation to the functional basis can also be helpful for the interpretation of the nonlinear response function. For the example neuron in Fig. 6D, the two-dimensional nonlinear firing rate function,

$$P(y=1\mid x_i,x_j)=\sum _{k\ne i,j}{\langle P(y=1\mid x_1,x_2,\dots ,x_d)\rangle }_{x_k},$$ (9)

with respect to STC dimensions s_i and s_j has a characteristic “crescent-like” shape, which is one of the types of nonlinearities previously reported in RGCs (Fairhall et al., 2006). The logical OR provides a natural way to explain the occurrence of crescent-like nonlinearities as arising from a sensitivity to similar but not identical features each of which can trigger the neural response. Such nonlinearities are common in both visual (Fairhall et al., 2006; Rust et al., 2005) and auditory (Sharpee et al., 2011) systems. It is noteworthy that the nonlinearity of the model neuron built according the logical OR in Fig. 1 has also crescent shape. Returning to the example retinal neuron, we observe that the crescent shape of the nonlinearity observed in the STC basis (panels C,D) is unfolded by the transformation to the functional basis (panels E, F), as it should have been. Furthermore, the measured nonlinearities (panels D and F) are closely reproduced by the nonlinearities predicted by the model (panels C and E) in both the STC and functional bases.

3 Discussion

The concept of feature extraction using a linear subspace has found much success in the analysis of sensory processing neurons. However, simply discovering the relevant subspace is not necessarily the end of the story if the goal is to gain insights into the neural circuitry responsible for the processing of sensory information.

Dimensionality reduction methods such as STC or MID identify the relevant subspace by finding a basis that captures significant changes in the stimulus covariance due to spiking or large amounts of the mutual information. Despite the meaning inherent in these bases, the resulting features are not necessarily the easiest to interpret in terms of functional computations. This is because standard dimensionality reduction methods describe the neural input/output function using an orthogonal bases whereas the relevant features of afferent inputs to a given neuron are often non-orthogonal. On the other hand, dimensionality reduction methods for characterizing neural feature that are explicitly based on assumptions of invariance (Eickenberg et al., 2012; Vintch et al., 2012) can account for non-orthogonal features, but cannot capture individually in the receptive field subunits, which is also an important part of neural representation (Gauthier et al., 2009; Liu et al., 2009). The functional basis representation provides a compromise in that it does not impose a relationship between the relevant stimulus features, e.g. they do not have to be shifted or scaled copies of each other. At the same time, searching for functional basis representations that correspond to biologically relevant nonlinearities, such as logical OR and AND nonlinearities (Riesenhuber and Poggio, 1999; Serre et al., 2007), allows one to determine types of invariance pertinent to the responses of a given neuron instead of imposing them a priori.

The results obtained by standard dimensionality reduction techniques and the functional basis methods are related in that they share the same relevant stimulus subspace, differing only in the choice of basis within that subspace. However, finding a functional basis representation is not dependent on dimensionality reduction methods such as STC or MID. In principle, a maximum likelihood model of a logical OR or AND response function with n features could be fit in the full D dimensional stimulus space. The appropriate number n of significant features can be determined by maximizing the log likelihood with respect to the number of features just as was done in the reduced subspace. Performing the computation on the full stimulus space can be, however, a computationally daunting task. Thus, the search for the functional basis can be performed effectively and in a much more timely manner within the reduced subspace.

Although we have only considered two specific computational forms, the idea of finding a functional basis may be extended to other types of functions if simplifying features can be suitably defined. There are, however, many computations for which the functional basis is impossible to define without detailed knowledge of the underlying circuitry. For instance, a radially symmetric function in two dimensions, such as in the energy model of a complex cell in area V1 of the visual cortex (Adelson and Bergen, 1985; Rust et al., 2005), is equally well described by any choice of basis. Even in this case however one can take advantage of the deviations from the true radial symmetry that characterize a particular complex cell under consideration to find the number of threshold-like units that can best account for its responses. Another example is when irregularities within the retinal circuitry can help separate individual inputs to a given RGC (Field et al., 2010; Liu et al., 2009; Soo et al., 2011). In summary, finding a functional basis can help bridge the divide between low-dimensional descriptions of neural responses and the underlying neural circuitry.