New Organelles by Gene Duplication in a Biophysical Model of Eukaryote Endomembrane Evolution

Abstract

Extant eukaryotic cells have a dynamic traffic network that consists of diverse membrane-bound organelles exchanging matter via vesicles. This endomembrane system arose and diversified during a period characterized by massive expansions of gene families involved in trafficking after the acquisition of a mitochondrial endosymbiont by a prokaryotic host cell >1.8 billion years ago. Here we investigate the mechanistic link between gene duplication and the emergence of new nonendosymbiotic organelles, using a minimal biophysical model of traffic. Our model incorporates membrane-bound compartments, coat proteins and adaptors that drive vesicles to bud and segregate cargo from source compartments, and SNARE proteins and associated factors that cause vesicles to fuse into specific destination compartments. In simulations, arbitrary numbers of compartments with heterogeneous initial compositions segregate into a few compositionally distinct subsets that we term organelles. The global structure of the traffic system (i.e., the number, composition, and connectivity of organelles) is determined completely by local molecular interactions. On evolutionary timescales, duplication of the budding and fusion machinery followed by loss of cross-interactions leads to the emergence of new organelles, with increased molecular specificity being necessary to maintain larger organellar repertoires. These results clarify potential modes of early eukaryotic evolution as well as more recent eukaryotic diversification.

Introduction

The stark distinction between prokaryotes and eukaryotes is a striking and surprising feature of cellular life. All extant eukaryotes share a large number of defining traits, such as mitochondria, active cytoskeletons, deformable membranes, vesicular traffic, and intracellular compartments (1). The eukaryotic cell plan emerged in the fossil record ∼1.8 billion years ago (GYA), and cells representing major extant eukaryote groups were evident by 1.3 GYA (2). Calibrated molecular phylogeny suggests that the most recent ancestor of all extant eukaryotes (the last eukaryotic common ancestor [LECA]) dates to ∼1.5 GYA (3), although other estimates place LECA more recently (4,5). What is clear is that LECA was already a sophisticated unicellular organism, possessing the complex molecular and phenotypic traits shared by all extant eukaryotic supergroups (6,7). The absence of intermediate forms bridging the prokaryote/eukaryote divide makes it challenging to reconstruct eukaryote evolution before LECA. There is a general consensus that mitochondrial endosymbiosis was a defining step in the origin of eukaryotes, and the nature of the host cell and the timing of this event relative to the emergence of other eukaryotic traits remain active areas of research (8). It has been argued that the mitochondrion was acquired by phagocytic cells that already possessed eukaryote-specific traits (1,4), but recent phylogenetic analyses instead support a prokaryotic archaebacterial host (9). Bioenergetic considerations suggest that the acquisition of mitochondria was a watershed event, setting the stage for the subsequent evolution of eukaryote-specific traits facilitated by a greatly expanded protein repertoire (10). At some point in this process, a recognizably eukaryotic cell with a functional vesicle-traffic apparatus must have emerged. Here we explore the evolutionary period leading from this proto-eukaryote to LECA, during which time the system of intracellular traffic and compartmentalization developed into its present form.

The eukaryotic endomembrane system consists of various organelles, such as the endoplasmic reticulum (ER), Golgi apparatus, endosomes, lysosomes, and plasma membrane, that exchange matter through vesicle-mediated traffic. (Throughout the text we will consistently use the term “organelle” to refer to nonendosymbiotic organelles that belong to the endomembrane system, rather than to symbiotic organelles such as mitochondria and plastids.) The traffic system exists in a dynamic steady state in which the sizes and compositions of the organelles remain approximately constant over time even though each organelle is receiving foreign material and losing its own (11). Eukaryotic cells can regain their internal organization after perturbations, so the structure of the endomembrane system is at least partly encoded by local molecular interactions (12–14). Cell-biological investigations have identified a suite of molecules that coordinate to set up and maintain the endomembrane system. Rab GTPases encode compartmental identity and have been implicated in nearly every step of vesicle-mediated traffic, including vesicle budding, uncoating, motility, and specific fusion (15–18). These GTP/GDP-binding proteins cycle between the cytoplasm (in their GDP-bound inactive state) and the membrane (in their GTP-bound active state). When a Rab is membrane bound and active, it can in turn regulate a large number of downstream effector proteins with diverse functions. Coat proteins such as clathrin, COP I, and COP II initiate vesicle formation by locally deforming the organelle membrane, and concentrate or deplete specific cargo molecules via adaptor-mediated interactions (19–23). Vesicles bud off from source compartments and can be transported to their destinations by motor proteins running on cytoskeletal tracks (23). The soluble NSF attachment protein receptor (SNARE) family of proteins are integral membrane proteins that occur in pairs (24,25): when a v-SNARE on a vesicle meets a specific partner t-SNARE on the target compartment, the two coil together, driving the membranes to fuse with one another. Molecules that regulate SNARE activity provide additional layers of specificity (26). After fusion occurs, the SNAREs are dissociated by N-ethylmaleimide-sensitive fusion protein (NSF) utilizing the energy of ATP hydrolysis, resetting the system for another round of vesicle budding and fusion.

Phyletic distributions suggest that LECA possessed all of the traffic-related protein families necessary to support a sophisticated endomembrane system (27). All extant eukaryotic cells express several paralogous Rabs, coats, and SNAREs—protein families that are essentially absent in prokaryotes. These paralogs arose during multiple pre-LECA gene family expansions, and different members of paralogous gene families tend to be associated with a specific subset of organelles or pathways of transport (28–33). These observations form the basis of a hypothesis proposed by Dacks and Field (27) and Dacks et al. (34) to explain how new organelles arose on the evolutionary branch leading to LECA subsequent to mitochondrial endosymbiosis. The hypothesis can be split into two parts, one mechanistic and one evolutionary: First, a given organelle is essentially determined by the budding and fusion machinery, which dictates how it exchanges matter with the rest of the system. Second, a new organelle can be generated by the duplication of the budding and fusion molecules associated with an existing organelle, and their subsequent divergence into specifically interacting subsets. Thus, an initially simple traffic system would become more complex as new organelles were added through the paralogous expansion of Rabs, coats, SNAREs, and other gene families involved in budding and fusion.

Here we explore the Dacks-Field evolutionary hypothesis using a biophysical model of eukaryotic endomembrane traffic. It is essential to formalize the hypothesis in mathematical terms so that we can examine the implications of constraints at multiple levels, i.e., physical constraints that place limits on membrane transport and the efficiency and specificity of molecular interactions, and biological constraints that require that at every step of evolution a functional traffic system must persist. Previous investigators have modeled endomembrane traffic using a variety of mathematical approaches (35–39). Our own model is detailed enough to include the machinery of vesicle budding and fusion, and general enough to allow complex, multicompartment steady states. We interrogate the model using simulations as well as bifurcation analyses, and find that the duplication of budding and fusion molecules can indeed give rise to new organelles, as long as molecular interactions obey certain minimum limits of specificity. Thus, the Dacks-Field hypothesis, which was originally posed in qualitative terms based only on phylogenetic signals of gene family expansion, is essentially compatible with our biophysical understanding of the present-day traffic machinery. This fits with the idea that the traffic molecules and their rules of interaction achieved their present form long before LECA and the emergence of the standard eukaryotic cell plan (27). If this is true, the same evolutionary forces that gave rise to LECA probably also contributed to the subsequent diversification of the eukaryotic supergroups, and might continue to operate in extant organisms.

Materials and Methods

The traffic model

The traffic model (Fig. 1) is realized as a system of ordinary differential equations describing how the sizes and compositions of membrane-bound compartments change with time. The components of this model are N_S types of SNAREs, N_C types of coats, and M preexisting compartments (we only discuss cases in which M > N_C, N_S). Throughout the text, we use Greek indices to denote SNARE types (α, β = 1, …, N_S) or coat types (γ = 1, …, N_C), and Roman indices to indicate compartments (i, j = 1, …, M). Each compartment is described by its size and SNARE composition:

• $w^0$ = constant size (membrane area) of a single vesicle

• $w^j$ = variable size (membrane area) of compartment j

• $x_{\alpha }^j$ = number of molecules of SNARE α on compartment j

with

$$w^{tot}=\sum _{j=1}^M{w}^j,x_{\alpha }^{tot}=\sum _{j=1}^M{x}_{\alpha }^j$$ (1)

Figure 1.

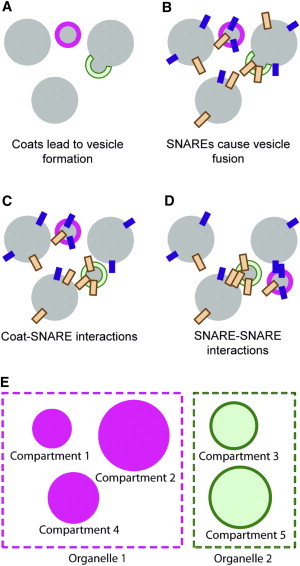
Traffic model. (A) N_C different coat types that lead to the formation of N_C types of vesicles, budding from preexisting compartments. In the figure, we label the two coat types using solid or outlined annuli. (B) N_S different types of SNAREs that cause vesicle fusion. In the figure, we label the two SNARE types using solid or outlined rectangles. (C) Coat-SNARE interactions: the coat type of a vesicle determines how much of each SNARE is packaged into that vesicle (${\theta }_{\alpha \gamma }$ = affinity of coat γ for SNARE α). From the figure, we might conclude that the solid coat has a high affinity for the solid SNARE, and the outlined coat has a high affinity for the outlined SNARE. (D) SNARE-SNARE interactions determine the rates of fusion of vesicles into compartments (${\varphi }_{\alpha \beta }$ = affinity of SNARE α for SNARE β). From the figure, we might conclude that each SNARE has a high affinity only for its own type. (E) We use the word “compartment” to mean a physically distinct membrane-enclosed bag (solid or outlined discs, indicating different chemical compositions). We use the word “organelle” to mean a set of compartments that all have the same composition at steady state (boxes).

Vesicles are assumed to fuse to their destination compartments nearly instantaneously after their formation, so the total membrane area and total SNARE amounts, $w^{tot}$ and $x_{\alpha }^{tot}$, are obtained by summing over compartments alone. Coat proteins cause vesicles to bud off compartments; therefore, there are N_C types of vesicles corresponding to the N_C coat types. We assume for simplicity that coat proteins of each type are available in equal amounts, so the rate of budding of any type of vesicle depends only on the size of the source compartment. We assume a power-law dependence: the rate of budding of γ-coated vesicles from compartment j, in units of membrane area per unit time, is given by

$$R_{\gamma }^j=\lambda {\left(w^j\right)}^{\mu }$$ (2)

The parameter λ has dimensions of membrane area to the power 1-μ per unit time. The dimensionless exponent μ describes the dependence of the budding rate on compartment size: the case μ = 0 gives vesicle budding independently of the source compartment size, as when coat proteins are rate limiting; the case μ = 1 is the mass-action situation in which the budding rate is proportional to the available source area; and other values of the exponent can be used to capture curvature-dependent budding rates.

SNARE proteins are themselves a variety of cargo. A vesicle packages all of the SNAREs present on the source compartment, but to different extents depending on the affinity of its coat and associated adaptors for each SNARE. We assume that the concentration of a SNARE on a vesicle is a constant multiple of its concentration on the source compartment. Let the amount of SNARE α on γ-coated vesicles from compartment j be $x_{\alpha \gamma }^j$. We then have

$$\left(\frac{x_{\alpha \gamma }^j}{w^0}\right)={\theta }_{\alpha \gamma }\left(\frac{x_{\alpha }^j}{w^j}\right)$$ (3)

where ${\theta }_{\alpha \gamma }$ is the dimensionless parameter describing the affinity of coat γfor SNARE α. Because cargo packaging is an energy-dependent process, there are no thermodynamic constraints on $\theta$ (40). The value ${\theta }_{\alpha \gamma }$ = 1 represents the special case in which budding vesicles of type γ sample SNARE α directly from the source compartment; higher or lower values, respectively, will produce vesicles enriched or depleted in SNAREs.

The fusion of vesicles into target compartments is mediated by the pairing of SNAREs, modulated by associated factors such as Rabs and tethers. The probability that a vesicle will fuse into a compartment is assumed to depend on the specificity with which the SNAREs on the vesicle interact with the SNAREs on the target, and on the product of the vesicular and compartmental SNARE concentrations. The rate at which γ-coated vesicles from compartment j fuse into compartment i is obtained by a weighted sum over all possible SNARE pairs:

$$\begin{array}{c}{r}_{\gamma }^{i\leftarrow j}=\rho {\left[\sum _{\alpha ,\beta =1}^{N_S}{\varphi }_{\alpha \beta }\left(\frac{x_{\alpha \gamma }^j}{w^0}\right)\left(\frac{x_{\beta }^i}{w^i}\right)\right]}^n{\left(w^i\right)}^{\upsilon }\\ =\rho {\left[\sum _{\alpha ,\beta =1}^{N_S}{\varphi }_{\alpha \beta }{\theta }_{\alpha \gamma }\left(\frac{x_{\alpha }^j}{w^j}\right)\left(\frac{x_{\beta }^i}{w^i}\right)\right]}^n{\left(w^i\right)}^{\upsilon }\end{array}$$ (4)

where ρ is a scale factor whose value we will later determine. The parameter ${\varphi }_{\alpha \beta }$ captures the affinity of interaction between SNAREs α and β. We do not explicitly incorporate pairs of v- and t-SNAREs; however, v/t-like pairing of SNAREs can be modeled by an appropriate choice of ${\varphi }_{\alpha \beta }$. There is experimental evidence that SNARE-mediated membrane fusion is a cooperative, nonlinear process (41,42); the exponent n describes the extent of SNARE cooperativity. The specific form of Eq. 4—summing over all possible SNARE pairs and taking the nth power afterwards—is chosen so that having two distinct SNAREs that interact identically with all other components of the model is equivalent to having only one SNARE, but doubled in amount. Finally, the rate of fusion depends on the size of the target compartment, as described by the term ${\left(w^i\right)}^{\upsilon }$.

The exponents μ and ν describe how vesicle budding and fusion rates scale with compartment size. Setting μ = ν = 1 implies that budding and fusion rates should scale linearly with area. This is equivalent to assuming that each infinitesimal patch of membrane on a compartment can be treated as an independent unit whose likelihood of giving rise to a vesicle or fusing with one depends only on its local composition, and not on the size of the compartment on which it resides. Setting either μ or ν different from one assumes that a tiny patch of membrane can sense the compartment size. In real cells, it is plausible that the rates of surface processes such as vesicle budding and fusion increase with the compartment surface area in a nonlinear fashion, given the existence of membrane-curvature-sensing proteins (43,44) and their involvement in the vesicle-trafficking machinery (45–47).

We assume that vesicles fuse into compartments almost as soon as they form, that is, vesicles exist for a period much shorter than the timescale in which source compartments change composition. Using a simple one-species model of vesicular transport, Dmitrieff and Sens (39) showed that a finite-fusion-time version of this model can be mapped onto a simpler instantaneous fusion version. Our assumption of instantaneous vesicle fusion implies that the total rate of budding of γ-coated vesicles from one compartment (Eq. 2) is equal to the sum of their rates of fusion to all target compartments (including the source):

$$R_{\gamma }^j=\sum _{k=1}^M{r}_{\gamma }^{k\leftarrow j}=\rho \sum _{k=1}^M{\left[\sum _{\alpha ,\beta =1}^{N_S}{\varphi }_{\alpha \beta }{\theta }_{\alpha \gamma }\left(\frac{x_{\alpha }^j}{w^j}\right)\left(\frac{x_{\beta }^k}{w^k}\right)\right]}^n{\left(w^k\right)}^{\upsilon }$$ (5)

This sets the value of the factor ρ. Combining Eqs. 2, 4, 5, we obtain

$$r_{\gamma }^{i\leftarrow j}=\lambda {\left(w^j\right)}^{\mu }\frac{{\left[\sum _{\alpha ,\beta =1}^{N_S}{\varphi }_{\alpha \beta }{\theta }_{\alpha \gamma }\left(\frac{x_{\alpha }^j}{w^j}\right)\left(\frac{x_{\beta }^i}{w^i}\right)\right]}^n{\left(w^i\right)}^{\upsilon }}{\sum _{k=1}^M{\left[\sum _{\alpha ,\beta =1}^{N_S}{\varphi }_{\alpha \beta }{\theta }_{\alpha \gamma }\left(\frac{x_{\alpha }^j}{w^j}\right)\left(\frac{x_{\beta }^k}{w^k}\right)\right]}^n{\left(w^k\right)}^{\upsilon }}$$ (6)

Finally, the rates of change of compartment sizes and SNARE amounts are given by conservation laws:

$$\begin{array}{c}\frac{d{w}^j}{dt}=\sum _{i=1}^M\sum _{\gamma =1}^{N_C}\left(r_{\gamma }^{j\leftarrow i}-r_{\gamma }^{i\leftarrow j}\right)\\ \frac{d{x}_{\alpha }^j}{dt}=\sum _{i=1}^M\sum _{\gamma =1}^{N_C}\left(r_{\gamma }^{j\leftarrow i}{\theta }_{\alpha \gamma }\left(\frac{x_{\alpha }^i}{w^i}\right)-r_{\gamma }^{i\leftarrow j}{\theta }_{\alpha \gamma }\left(\frac{x_{\alpha }^j}{w^j}\right)\right)\end{array}$$ (7)

Equations 6 and 7 capture the complete content of our model.

Parameter values

For convenience, we take the number of coat and SNARE types to be equal (N_C = N_S = N), although the model can accommodate more general scenarios. We choose the units of time so that λ = 1, the units of membrane surface area so that $w^{tot}$ = 1, and the units of amounts of each type of SNARE so that $x_{\alpha }^{tot}$ = 1. The exponents are generally held fixed at the values μ = 1.1, ν = 1, and n = 2, unless otherwise mentioned. The remaining key parameters of our model are the coat-SNARE specificity matrix θ and the SNARE-SNARE specificity matrix ϕ. The fixed points of this system are invariant to rescaling θ, but their stabilities are not; in the present analysis, we restrict our attention to matrices θ with maximal value unity. Finally, the system is invariant to rescaling ϕ, which only appears in the numerator and denominator of Eq. 6; we scale ϕ so its maximal value is unity.

Bifurcation analysis

Consider an N coat, N SNARE, N compartment version of the model in which θ and ϕ are of the forms given in Eq. 8. Suppose all compartments are equally sized and there is a one-to-one map between each compartment i and its dominant SNARE α(i). For each i, the amount of SNARE α(i) on compartment i is y₀, with the remaining (1 − y₀) being distributed uniformly among the remaining compartments. Because all interaction parameters are completely symmetric, there is nothing to break the symmetry of this initial state. As the system evolves with time, it will stay on the line $w^i=1/N$, $x_{\alpha \left(i\right)}^i=y\left(t\right)$, $x_{\alpha \left(i\right)}^{j\ne i}=\left(1-y\left(t\right)\right)/\left(N-1\right)$, for all i. This line is therefore a one-dimensional (1D) dynamical system described by the dynamical variable y, whose time evolution is given by some function $dy/dt=f(y,\delta ,\epsilon )$. For a given δ and ε, when f is plotted against y (see Fig. 4, A–H), we will have fixed points whenever f = 0. The stability of any fixed point is determined from the local slope of the graph: $\partial f/\partial y$. Bifurcations (i.e., the emergence or loss of stable fixed points) occur where f and $\partial f/\partial y$ vanish simultaneously. This 1D dynamical system contains both the one-organelle (y = 1/N, all compartments identical) and N-organelle (y > 1/N, all compartments distinct) fixed points. We numerically analyze the emergence and stability of the 1D fixed points in δ-ε space, and verify by simulations that this correctly gives the stability of the fixed points of the full dynamical system.

Figure 4.

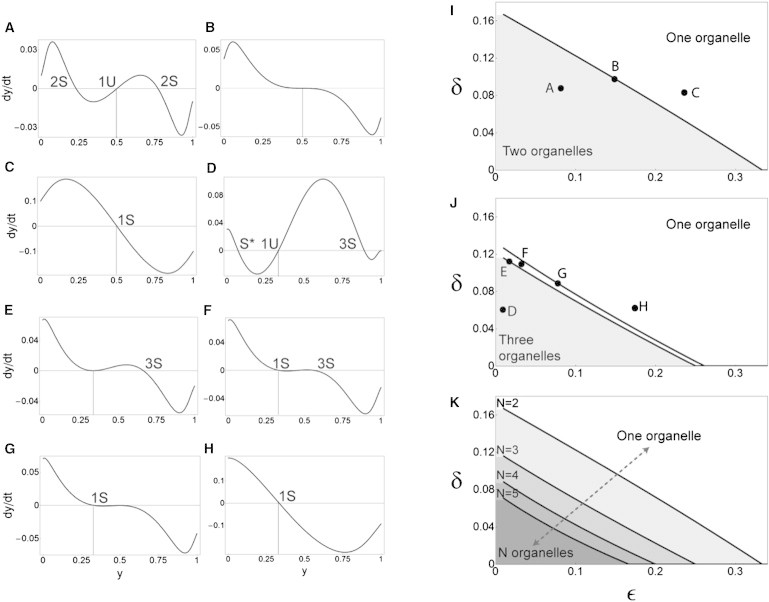
Larger organellar repertoires require greater molecular interaction specificity. We consider the N compartment, N coat, N SNARE case. The parameters δ and ε capture the strengths of cross-interactions: the lower their value, the higher the degree of molecular specificity. We restrict our attention to the 1D dynamical subsystem, in which compartments are equally sized and each compartment is labeled by a unique dominant SNARE whose amount is y(t). Time evolution is given by $dy/dt=f\left(y,\delta ,\epsilon \right)$. (A–H) Graphs of dy/dt versus y corresponding to different points in δ-ε space. These graphs tell us about the existence of fixed points (where the graph crosses zero) and their stability (crossings with negative slope are stable and those with positive slope are unstable). The one-organelle fixed point is the uniform case in which y = 1/N (vertical dotted lines); it always exists but can be stable (1S) or unstable (1U). The N-organelle fixed point is the case in which dominant SNAREs emerge, so y > 1/N; it is always stable whenever it does exist (2S and 3S). Note that stability within the 1D subsystem is necessary but not sufficient for stability within the full system; for example, we never observe the subdominant fixed point y < 1/N (S^*) in simulations. (A–C) N = 2. (D–H) N = 3. (I) For N = 2, we find a boundary that separates δ-ε space into two-organelle (shaded) and one-organelle (white) regions. The corresponding graphs of dy/dt are symmetric around y = 0.5, preventing more complex bifurcations. (J) For N ≥3 there are no symmetry constraints, so we find two bifurcation boundaries. In the shaded region bounded by the lower curve, we see only three-organelle behavior. Between the two curves, both one-organelle and three-organelle behaviors are stable, so the outcome depends on initial conditions, and across the upper curve we see only one-organelle behavior. (K) For N = 2, 3, 4, and 5, we show the curves that bound the shaded regions of always-N-organelle behavior. We see that as N increases, this region shrinks toward the origin.

Simulations

All simulations and calculations were done in Wolfram Mathematica 7.0. Numerical solutions of ordinary differential equations were obtained using the function NDSolve. Roots of functions for the bifurcation analysis were determined numerically using the function FindRoot.

Results

Ingredients of the traffic model

The pioneering model of two coats and two SNARES developed by Heinrich and Rapoport (35) reaches a steady state in which two initially similar compartments become distinct in composition—enriched in different SNAREs and sending out vesicles with different coats. This result is interpreted as the two compartments becoming distinct organelles. Our model is similar in spirit to the Heinrich-Rapoport model but has three distinguishing features: First, we treat physically distinct compartments and chemically distinct organelles differently, which allows us to separate the effects of biochemistry from those of available membranes. Second, we explicitly formulate the model using network equations with arbitrary numbers of proteins of each molecular variety, which allows us to study large systems with complex topologies. Third, we treat molecular interactions as parameters that can vary, for example, over evolutionary timescales.

The model pertains only to local molecular mechanisms of budding and fusion, and is formulated in biologically realistic terms supported by experimental evidence (Fig. 1, A–D; see “The traffic model” above). The traffic system consists of single-membrane-bound compartments. We do not explicitly include the de novo synthesis of new compartments, but this is implicit in our assumption that the number of compartments always exceeds the number of available coat and SNARE types. Coat proteins of different types (a shorthand that includes associated factors such as Rabs and adaptors) cause these compartments to give rise to vesicles of different compositions (19–23), and SNAREs (a shorthand that includes associated factors such as Rabs and tethers) on compartment and vesicle membranes specifically pair up to drive fusion (24–26). Because we are specifically interested in exploring the Dacks-Field evolutionary scenario, we focus on the budding and fusion machinery and ignore additional complexities such as cytoskeletal transport and transport via tubules. In the simple two-compartment case, over all parameter values we tested, our model produced results qualitatively similar to those obtained with the Heinrich-Rapoport model. This suggests that the results we describe below arise from broad biological considerations rather than from specific details of the model’s formulation.

Compartments segregate into compositionally distinct organelles

We studied the behavior of this model through numerical simulations (see “Simulations” above). For many forms of the specificity matrices θ and ϕ, and a variety of initial conditions, we find that the system approaches a steady state. If the genotype includes multiple varieties of coats and SNAREs, this steady state typically comprises many compositionally distinct compartments that can be sorted into subsets: compartments within one subset have identical compositions, and compartments in different subsets have distinct compositions. We refer to all compartments within a subset as being part of the same organelle (Fig. 1 E). In our formulation, as in most previously studied traffic models (36–38) (but not in Heinrich and Rapoport (35)), some degree of SNARE cooperativity (corresponding to n > 1) is necessary to obtain stable, nonidentical organelles (Fig. 2, A and B).

Figure 2.

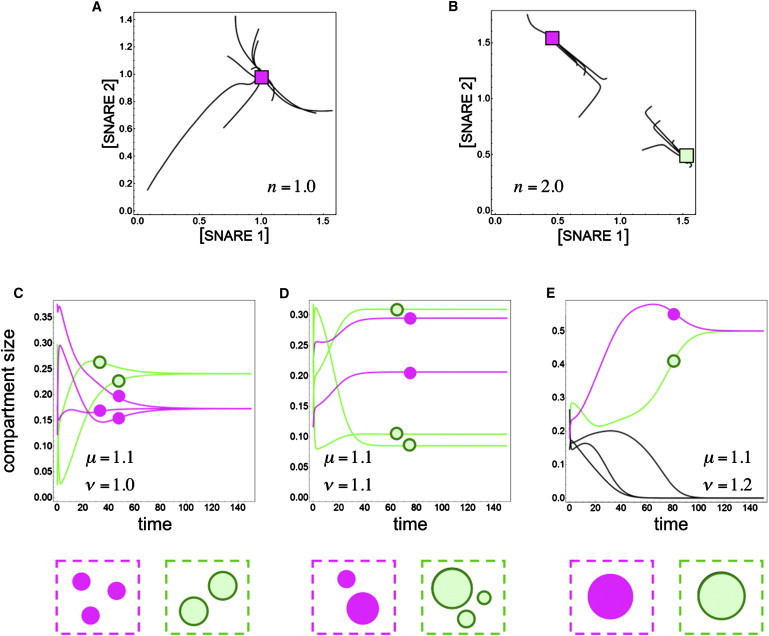
Compartments segregate into distinct organelles. Each panel of this figure shows the result of simulations starting from random initial conditions, with two coats, two SNAREs, and either five or 10 compartments. The interaction matrices θ and ϕ are of the form given in Eq. 8, and the off-diagonal matrix elements are set to δ = ε = 0.1. (A and B) Trajectories of compartments in SNARE concentration space. Each panel shows a single run in which 10 compartments change their compositions over time by exchanging matter with one another. (A) In the absence of SNARE cooperativity (n = 1), all compartments collapse to a single composition with high amounts of both SNAREs. This is a one-organelle steady state. (B) When SNARE cooperativity is included (n = 2), some compartments converge to a point with high SNARE 1 and low SNARE 2, while the rest converge to a symmetrically placed point with high SNARE 2 and low SNARE 1. This is a two-organelle steady state. (C–E) The sizes of a five-compartment system are shown as a function of time. The curve corresponding to a compartment is labeled (solid or outlined dots) according to which organelle it eventually becomes a part of. The two final organelles are nearly equally sized, but their distribution over the available compartments varies. (C) μ > ν: three compartments (solid) end up equally sized and make organelle 1; the two other compartments (outlined) end up equally sized and make organelle 2. (D) μ = ν: two compartments (solid) end up as organelle 1, and three compartments (outlined) end up as organelle 2. The two organelles are equally sized, but the compartments have arbitrary sizes. (E) μ < ν: one compartment (solid) ends up as organelle 1, and another (outlined) ends up as organelle 2. The other three (black) shrink to nothing and are not part of any organelle in steady state.

The manner in which the mass of an organelle is distributed among the compartments it is composed of depends on the relationship between the budding and fusion exponents μ and ν. If μ > ν (budding rates increase faster with surface area than do fusion rates), a compartment that is very large will give rise to many vesicles but will not receive as many in return, so it will tend shrink; conversely, small compartments will tend to grow. The result at steady state is that each organelle is made up of several equally sized compartments (Fig. 2 C). If μ < ν, a large compartment will attract more vesicles than it loses, so it will grow at the expense of smaller compartments. At steady state, each organelle will be made up of a single large compartment, with all other compartments shrinking and eventually disappearing (Fig. 2 E). In the degenerate case of μ = ν, organelles are made up of several compartments of arbitrary sizes (Fig. 2 D). These dynamics are reminiscent of the switch between multiple small compartments and a single large compartment seen in organelles such as the Golgi or late endosomes under a variety of perturbations (48,49).

The number of distinct organelles depends only on specific molecular interactions

As long as the number M of compartments is larger than the number N of coats and SNAREs, we find that the number of organelles (i.e., the number of distinct compartment compositions at steady state) depends only on the interaction matrices θ and ϕ. Fig. 3 shows the results of simulations with four different sets of parameters, with either 10 or 20 initial compartments. The corresponding values for θ and ϕ have simple biological interpretations (Fig. 3 A). In Fig. 3, B–D, each coat has one preferred SNARE that it packages better than it does all the others, and each SNARE has a high affinity for its own type and a low one for all the others, so two SNAREs of the same type make a good pair to cause fusion. If the preferences of coats for SNAREs (or SNAREs for SNAREs) are not very specific (Fig. 3 B), all compartments become identical in composition, and the number of organelles is one. However, if these preferences are sharp enough (Fig. 3, C and D), the number of organelles formed is the same as the number N of coats and SNAREs, and each organelle is given its identity by one dominant SNARE type.

Figure 3.

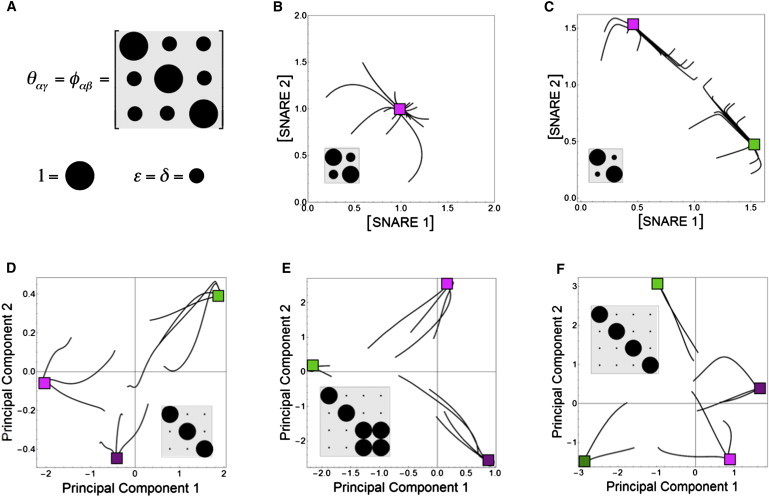
Gene duplication and divergence lead to the formation of new organelles. Each panel shows the results of simulations starting from random initial conditions. The trajectories of all the compartments from a single simulation run are plotted together in (a subspace of) the space of SNARE concentrations. Several of these trajectories converge onto a single point (colored square), indicating that several compartments have acquired the same composition and are now part of the same organelle. (A) The interaction matrices θ and ϕ are equal to one another and of the form given in Eq. 8: diagonal elements are equal to one, and off-diagonal elements are given by δ = ε < 1. These matrices are depicted pictorially, with each entry represented by a disc of proportional area. (B) Two coats, two SNAREs, and 15 compartments, with δ = ε = 0.3. In this case, coat and SNARE interactions are nonspecific. All compartments converge to the same point, resulting in a one-organelle steady state. (C) Two coats, two SNAREs, and 20 compartments, with δ = ε = 0.1. Interactions are now sufficiently specific. As in Fig. 2B, some compartments converge to a high SNARE 1 and low SNARE 2 composition, while the rest converge to a high SNARE 2 and low SNARE 1 composition, resulting in a two-organelle steady state. (D–F) To represent simulation results for higher numbers of coats and SNAREs, we perform a principal components analysis on the final compartment SNARE concentrations, and show trajectories in the space of the first two principal components. (D) Three coats, three SNARES, and 10 compartments, with δ = ε = 0.01. We obtain a three-organelle steady state. (E) We start with the same system as in Fig. 3D, but now duplicate one set of coats and SNARES to generate a four-coat, four-SNARE system. All off-diagonal elements are still δ = ε = 0.01, except for a two-by-two block whose elements are all equal to one, since the new protein copies behave identically to the originals. We still obtain a three-organelle steady state. (F) Four coats, four SNARES, and 10 compartments. We start with the same system as in Fig. 3E, but now we suppress all off-diagonal terms to δ = ε = 0.01 due to the divergence of the duplicate protein copies. This produces a four-organelle steady state.

Gene duplication and loss of cross-interactions can lead to the formation of new organelles

We next examine what happens when gene duplication changes the underlying genotype. A system with three coats and SNAREs with no cross-interactions has a steady state comprising three organelles (Fig. 3 D). Suppose now that one entire molecular set (coats, SNAREs, and all associated factors) is duplicated. In the resulting matrices, although there are four coats and SNAREs, the new protein copies have the same interactions as the old ones, so the number of truly distinct coats and SNAREs is only three. Indeed, we see that only three organelles are formed in steady state (Fig. 3 E). However, if the off-diagonal cross-interaction terms between new and old protein copies are reduced, with all else being held constant, the system switches to a four-organelle state (Fig. 3 F). Thus, the duplication of budding and fusion machinery can be seen as the driving force behind the emergence of new organelles.

Larger organellar repertoires require increased molecular interaction specificity

Gene duplication followed by divergence typically results in a state with a larger organelle number, but this is not always the case. The emergence of new organelles appears to be contingent on the degree of specificity of all the molecules in the system, not just of the duplicated protein copies. To understand this parameter dependence, we performed a bifurcation analysis on a reduced highly symmetric subsystem in which the number of compartments is equal to the number N of coats and SNAREs (see “Bifurcation analysis” above). Suppose the matrices θ and ϕ are of the forms

$${\theta }_{\alpha \gamma }=\{\begin{array}{cc}1,& \alpha =\gamma \\ \delta ,& \alpha \ne \gamma \end{array},{\varphi }_{\alpha \beta }=\{\begin{array}{cc}1,& \alpha =\beta \\ \epsilon ,& \alpha \ne \beta \end{array}$$ (8)

where δ and ε are dimensionless parameters with values between zero and one. As shown in Fig. 3, when δ and ε are small enough, N distinct organelles emerge (Fig. 3, C and D). However, when these parameters are closer to one (meaning that the coats do not discriminate much among the SNAREs, and the SNAREs do not discriminate among themselves), all compartments become identical in composition and the number of organelles is one (Fig. 3 B). For N = 2, 3, 4, and 5, we used a bifurcation analysis (Fig. 4, A–H; see Materials and Methods) to map out the regions of the δ-ε space that give rise to the N-organelle and one-organelle behaviors. For N = 2 (Fig. 4 I), we find a curve in δ-ε space across which N-organelle fixed points appear and the one-organelle fixed point simultaneously becomes unstable. For N ≥ 3 (Fig. 4 J), we find two curves: first, N-organelle fixed points appear but the one-organelle fixed point is still stable; second (as we approach the origin), the one-organelle fixed point becomes unstable. In the region between these two curves, the outcome depends on initial conditions. For increasing N, we can examine the size of the parameter region in δ-ε space that generates N-organelle behavior (Fig. 4 K). We find that as N increases, this region shrinks: δ and ε are both required to be smaller for N-organelle behavior to arise, although decreased specificity along one axis (say, of coat-SNARE interactions) can be compensated for, to a point, by increased specificity along the other axis (say, SNARE-SNARE interactions). In general, greater interaction specificities are required, across all the molecules in the system, to maintain a larger repertoire of distinct organelles.

Discussion

Our goal in this work was to assess the plausibility of the Dacks-Field hypothesis about pre-LECA eukaryote evolution, on the basis of molecular and functional constraints; that is, we sought to perform a biophysical analysis rather than an evolutionary analysis. We inserted all of the evolutionary ingredients (gene duplication and divergence) by hand to capture essential features of the known phylogeny of Rabs, coats, and SNAREs (34). This approach glosses over a variety of complications. For example, we assume that coats, SNAREs, and all their associated factors are encoded by individual genes, ignoring the issue of multimeric proteins and interacting complexes with potentially overlapping subunits. What is represented as a single duplication event in our analysis corresponds to multiple underlying duplication and divergence events. Understanding the frequency with which such a series of rare events might occur would require a detailed population-genetic analysis—one that includes effects of population size, selection, underlying mutation, recombination rates, and so on. Such an analysis is not only technically complex but requires a deep understanding of ancient conditions and selection pressures. However, we are not asking for the likelihood that some series of gene duplication events might occur—we want to check, given that some series of events did occur, whether their claimed effects on intracellular organization are consistent with known biophysical constraints. The Dacks-Field hypothesis is extremely specific: it posits that duplication and coevolution of the machinery underlying vesicle budding and fusion were sufficient by themselves to generate new organelles. This is falsifiable. It is possible, for example, that organelle numbers were determined by templating from parent to daughter cells, or that they arose through active cytoskeletal processes, or that they depended on having distinct endosymbiont genomes. What we do find is precisely what the basic qualitative form of the hypothesis predicts, with two important additions. First, we place quantitative limits on the degree of molecular specificity required to maintain a functional endomembrane system. Second, we show that specificity must increase across the entire system to support larger organellar repertoires. Indeed, many layers of specificity are built into present-day endomembrane systems (50). It is possible that unrelated selective pressures could have favored increased specificities in the short term, setting the stage for organellar diversification in the long term (51).

The acquisition of mitochondria was necessary but not sufficient for the emergence and diversification of the endomembrane system. The endosymbionts provided the energy to support a vast expansion in gene families (10), but this does not in itself explain the very structured type of gene duplication and divergence required by our model. If we start with an initial set of interacting proteins (some set of Rabs, coats, and SNARES), all of these proteins must duplicate, the resulting pairs of initially identical proteins must break up into two subsets, and members of each subset must coevolve to maintain interactions among themselves while at the same time suppressing interactions with the other subset. Hybridization parsimoniously accounts for the emergence of multiple weakly interacting protein subsets (Fig. 5, A and B). Hybridizations between moderately diverged single-celled eukaryotes are relatively common in high-density populations (52), and endosymbiotic associations among eukaryotes may promote hybridization between more diverged varieties (53). There is another, more subtle route that leads to the desired result, one that can only operate in compartmentalized cells. Whole-genome duplication can produce multiple, simultaneous gene duplications (Fig. 5 C), but we must still account for the subsequent loss of cross-interactions. In the hybridization scenario, the precursor protein sets are segregated into two distinct cells. By analogy, after a whole-genome duplication and a few mutations in targeting sequences, precursor protein sets might become segregated into distinct compartments, a process termed neolocalization (54). Subsequent coevolution would tend to suppress cross-interactions, although some form of selection would be required to maintain within-set interactions (Fig. 5 D). This retargeting scenario opens up the following interesting possibility: a cell with many existing compartments is more likely to achieve multiple weakly interacting protein subsets. Conversely, we have shown how duplicate protein subsets of Rabs, coats, and SNAREs can generate new compartments. This virtuous cycle may have triggered an accelerated phase of pre-LECA eukaryote evolution, resulting in the prokaryote/eukaryote divide we observe among extant organisms.

Figure 5.

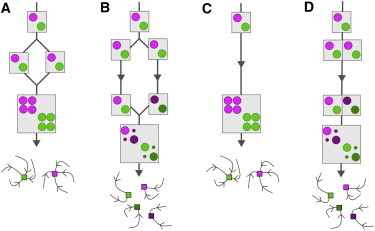
Evolutionary scenarios for the simultaneous duplication and divergence of multiple genes. We start with a cell that contains two distinct weakly interacting sets of coats and SNAREs (represented by pictorial matrices, as in Fig. 4), and therefore have two distinct organelles (represented as schematic compartment trajectories in compositional space). (A and B) Hybridization scenarios. (A) If two identical daughter cells of a single mother fuse, the new protein copies will be identical to the old copies, so the interaction matrix will have two blocks. The result is a two-organelle steady state. (B) If the daughter cells are allowed to diverge over evolutionary timescales, protein complexes within a single lineage will coevolve, but will tend to lose interactions with protein complexes in the other lineage. If these diverged cells eventually fuse, their interactions will have the correct diagonal form. The result is a four-organelle steady state. (C and D) Neolocalization scenarios. (C) We start with a whole-genome duplication in which a cell fails to segregate a newly replicated genome. As in Fig. 5A, the new protein copies are identical to the old copies and the interaction matrix has two blocks. The new copies are constrained from diverging, because they are still confronted with their old interaction partners. The result is a two-organelle steady state. (D) Now we imagine that some of the new protein copies are retargeted to a different compartment of the cell and therefore never see their old partners. If these neolocalized proteins somehow contribute to fitness, they will maintain interactions among themselves, but cross-interactions with partners in other compartments will tend to be lost. If the four protein sets are eventually retargeted to the same compartment, their combined interaction matrix will have the correct diagonal form. The result is a four-organelle steady state.

Conclusions

Given the patchy fossil record of unicellular organisms, the study of pre-LECA eukaryote evolution has so far been restricted to phylogenetic analyses and comparative genomics. Mathematical models of the endomembrane system can supplement these bioinformatic tools, providing a powerful means to falsify evolutionary hypotheses or evaluate their plausibility.

The emergence of stable nonidentical compartments seems to be a universal feature of endomembrane traffic models (35–39). We, too, find that initially heterogeneous compartments sort themselves into subsets whose members have identical compositions, and each such subset embodies a distinct organelle. The surprising result is that the number of organelles depends only on specific molecular interactions in a highly predictable manner, and not on the number of preexisting compartments or the initial state. Although we discovered this property in the context of a certain mathematical formulation, we imagine it occurs quite generally among a broad class of self-organized traffic models. Taking this further, we suggest that it is likely to be a verifiable property of real present-day cells. Crucially, this robust mapping from molecular genotype to compartmental phenotype paves the way for forces acting at the genetic level to drive changes in intracellular organization. Thus, the present-day structure of cells contains clues about the evolutionary processes through which they arose, processes that have continued to operate over billions of years.