Kinesin-8 Is a Low-Force Motor Protein with a Weakly Bound Slip State

Abstract

During the cell cycle, kinesin-8s control the length of microtubules by interacting with their plus ends. To reach these ends, the motors have to be able to take many steps without dissociating. However, the underlying mechanism for this high processivity and how stepping is affected by force are unclear. Here, we tracked the motion of yeast (Kip3) and human (Kif18A) kinesin-8s with high precision under varying loads using optical tweezers. Surprisingly, both kinesin-8 motors were much weaker compared with other kinesins. Furthermore, we discovered a force-induced stick-slip motion: the motor frequently slipped, recovered from this state, and then resumed normal stepping motility without detaching from the microtubule. The low forces are consistent with kinesin-8s being regulators of microtubule dynamics rather than cargo transporters. The weakly bound slip state, reminiscent of a molecular safety leash, may be an adaptation for high processivity.

Introduction

Control of microtubule length is crucial to chromosome alignment during mitosis (1–3). Recently, it was shown that members of the kinesin-8 motor family regulate the dynamics of microtubules. The budding yeast kinesin-8, Kip3, acts cooperatively to mediate length-dependent microtubule depolymerization (4–7). Human kinesin-8, Kif18A, also antagonizes microtubule growth, though the mechanism is still unclear (3,8–10). To modulate microtubule dynamics, it is essential for these motors to reach the microtubule plus ends. Kinesin-8s are highly processive motor proteins. Their run length is ∼10 μm (4,11–13), which is the longest observed for microtubule-related motor proteins. This high processivity of kinesin-8s was recently shown to be due in part to a second microtubule-binding domain in the nonmotor domain, which increases the run lengths up to fourfold (11–13). This facilitates plus-end localization (13–15), which is important for the microtubule-regulating activities (11,12). However, even without the additional microtubule-binding domain, the run lengths of truncated kinesin-8s are still up to ∼4 μm and at least twice that of kinesin-1 (16).

To better understand the stepping mechanism of this kinesin class, in particular its high processivity, we precisely tracked in vitro the ATP-dependent translocation of kinesin-8 motors subjected to both hindering and assisting load forces using optical tweezers. We found that kinesin-8 is a slow, low-force motor. Interestingly, we discovered that even in the presence of ATP, kinesin-8 can enter a weakly bound state that manifests itself in the form of slippage events under hindering or assisting loads. This weakly bound state has similarities to the weakly bound ADP state in which Kip3 diffuses on the microtubule lattice in the absence of force and slips in the presence of force (17). Weakly bound or frictional states (17) are important for force generation by muscle myosin (18), the collective properties of molecular motors (19), and the efficient search of target sites via one-dimensional diffusion in the case of DNA enzymes (20) and microtubule-associated proteins (21–24). We argue that in kinesin-8, the weakly bound state may contribute to the motor’s high processivity.

Materials and Methods

Kinesin-8 expression and purification

The motor proteins 6xHis-Kip3-eGFP (abbreviated as Kip3 in the text), full-length 6xHis-Kif18A-eGFP (Kif18A), and 6xHis-Kif18AT777-eGFP truncated after amino acid 777 (Kif18AT777) were expressed in Sf+ cells (Bac-to-Bac expression system; Invitrogen, Paisley, UK). Proteins were purified by cation exchange chromatography (Kip3 only) followed by metal-chelating chromatography as described previously (4,8). The motor Kip3-eGFP-6xHis with a 6xHis tag at the tail (Kip3-HT) was expressed in Sf+ cells (Protein Facility, Max Plank Institute of Molecular Cell Biology and Genetics (MPI-CBG), Dresden, Germany) and purified by metal-chelating chromatography on Ni-NTA agarose beads (Qiagen, Hilden, Germany).

Sample preparation and assay

Flow-cell construction and immobilization of GMPCPP microtubules were performed as described in Bormuth et al. (25) except that the Pluronic F-127 incubation time was increased to 20 min. The channels were rinsed with 20 μl motility solution with kinesin-8-functionalized microspheres (see below) for the optical trapping experiments. The motility solution consisted of BRB80 (80 mM PIPES/KOH pH 6.9, 1 mM MgCl₂, 1 mM EGTA) with 112.5 mM KCl, 0.1 mg/ml casein, 1 mM Mg-ATP, and an antifade cocktail (0.5% β-mercaptoethanol, 20 mM glucose, 20 μg/ml glucose oxidase, 8 μg/ml catalase). The measurements were performed at 24.5°C. In the optical tweezers apparatus, microtubules were visualized by differential interference contrast (DIC) employing a light-emitting diode (LED-DIC) (26).

Microsphere preparation

We functionalized carboxylated polystyrene microspheres (PC03N/6487, 590 nm; Bangs Laboratories, Fishers, IN) using carbodiimide coupling. Carboxyl groups were activated by using EDC (1-ethyl-3-[3-dimethylaminopropyl]-carbodiimide hydrochloride) and sulfo-NHS (N-hydroxysulfosuccinimide). The activated carboxyl groups on the microsphere surface reacted with amine groups of the polyethylene-glycol spacer molecules (PEGs, 3 kDa,≈23 nm contour length; Rapp Polymere, Tübingen, Germany). The carboxyl groups at the other end of the PEGs were activated by a second carbodiimide reaction identical to the first activation. The enhanced green fluorescent protein (EGFP) antibodies (Antibody Facility, MPI-CBG, Dresden, Germany) reacted with the activated carboxyl groups of the PEGs. These functionalized, reactive PEGs were used in combination with nonreactive methylated PEGs (1:10, 2 kDa; Rapp Polymere). The microspheres were stored in phosphate-buffered saline and used for 3 weeks. Before each experiment, kinesin-8 was incubated with the prepared microspheres for 7 min at room temperature. The EGFP at the tail of the kinesin-8 bound to the EGFP antibody at the end of the PEGs.

Single-molecule conditions with preserved motor functionality

Single-molecule conditions were optimized according to a statistical analysis of the probability of interaction of motor-coated microspheres with immobilized microtubules (27). This probability as a function of the motor-to-microsphere ratio followed Poisson statistics. All measurements were done at a low motor-to-microsphere ratio, such that only one out of four microspheres (25%) showed motility. Assuming Poisson statistics and taking into account the geometry of the microsphere–microtubule interaction, at least 95% of the interactions were due to single molecules. To test whether the coupling of kinesin-8 to the microsphere affected the functionality of the motor, we compared the average speed of free motors with that of motors attached to microspheres (with the optical trap switched off). We measured the former by tracking single, fluorescently labeled motor molecules moving along immobilized microtubules in total internal reflection fluorescence (TIRF) measurements (4,11,17) and the latter by tracking motor-driven microspheres in DIC time-lapse images. The microsphere speeds were 45 ± 2 nm/s, based on $N=10$ microspheres for Kip3, 42 ± 7 nm/s ($N=4$) for Kip3-HT, 162 ± 10 nm/s ($N=6$) for Kif18A, and 173 ± 11 nm/s ($N=4$) for Kif18AT777. Within the error margins, these speeds were consistent with the TIRF measurements (4,11,17) and confirmed the functionality of the motor when attached to a microsphere.

Optical tweezers setup

The measurements were performed in a single-beam optical tweezers. The setup and calibration procedures are described in detail elsewhere (17,25,26,28,29). Briefly, a 1.5 W Nd:YVO₄ laser (1064 nm) was expanded and coupled into an inverted microscope with a 100×/1.3 NA oil-immersion objective. Signals were recorded in three dimensions with a position-sensitive photodiode in the back-focal plane. Time traces were recorded with 20 kHz with an alias-free analog-to-digital converter.

Trapping experiments

All measurements were done with approximately the same trap stiffness, $\kappa =0.04$ pN/nm. For the constant-force mode, the trapping laser was moved with a piezo-mirror relative to the sample with an update rate of 200 Hz. This movement was such that the microsphere displacement $\text{Δ}x$ out of the trap center (see inset in Fig. 1) was kept on average constant. By keeping this displacement constant, we ensured that the force $F_{\text{trap}}=\kappa \text{Δ}x$ was also constant. Overall, we analyzed the motion of 26, 6, 11, and 6 different single Kip3, Kip3-HT, Kif18A, and Kif18AT777 molecules, respectively. For all Kip3 and Kif18A molecules, we applied different forces ranging from $-5$ to $+5$ pN and $-2.5$ to $+2.5$ pN, respectively. For each force, we used on average 30 independent traces, excluding slip events (see below), and fitted lines to intervals of 1 s. We averaged the resulting slopes and plotted the corresponding mean velocity. Slip events (see below) were software-detected when the amplitude of force spikes exceeded a threshold of 4 and ≈6 standard deviations (SDs) of the unfiltered and 400 Hz boxcar-filtered force noise, respectively. Control experiments with rat kinesin-1 (rK430-eGFP-6xHis) under the same conditions, except that no KCL was added, did not show any slip events. Furthermore, as expected (30), the kinesin-1 motors moved at ≈800 nm/s and stalled at ≈6 pN.

Figure 1.

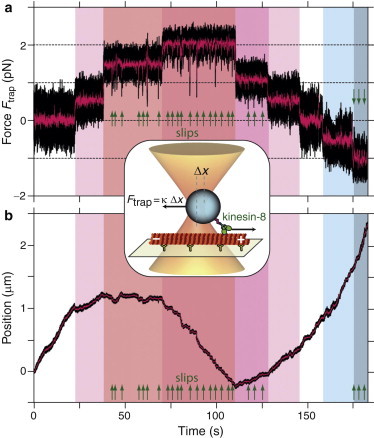
Typical trace of a single Kip3 motor. Inset: Schematic of the experiment (not to scale). A kinesin-8-coated microsphere is trapped by a focused laser near an immobilized microtubule. The motor moves on the microtubule and displaces the microsphere from the trap center by $\text{Δ}x$. In the constant-force mode, the laser follows the protein movement with a constant force $F_{trap}=\kappa \text{Δ}x$, where κ is the trap stiffness. (a) Time trace of the load force acting on the microsphere. Hindering or opposing load forces, defined as positive (red shaded regions), are directed toward the microtubule minus end; assisting load forces (blue shaded) are directed toward the microtubule plus end. The spikes (large ones marked by arrows (25 out of 64)) indicate slip events (see text). (b) Time trace of the corresponding position (boxcar filtered to 2 kHz (black line) and 100 Hz (magenta line)).

Results

Kinesin-8s are slow and weak motors

To determine how the translocation of the kinesin-8 motors was affected by load, we tracked the position of single-motor-powered microspheres as a function of time while applying controlled, constant loads with the optical tweezers (Fig. 1, inset; see Materials and Methods). Due to the high processivity of kinesin-8, we could apply a large range of both hindering and assisting forces during a single run of a single molecule (Fig. 1 a). We defined a hindering force as positive (red shaded in Fig. 1) and an assisting force as negative (blue shaded). The example trace of position versus time (Fig. 1 b) shows that already for small hindering forces of ≲1 pN, the microsphere slowed down and eventually stalled. For higher hindering loads, the motor moved backward. For assisting loads, the movement was accelerated.

To quantify the motor movement, we determined the average speed for the different forces by linear regressions of the position traces (Fig. 2; see Materials and Methods). We observed a zero-force speed of 42 ± 4 nm/s and 130 ± 42 nm/s for Kip3 and Kif18A, respectively (inset in Fig. 2; mean ± SE if not noted otherwise). These speeds were consistent with those determined for motor-driven microspheres tracked with the optical trap turned off (see Materials and Methods) or free motors tracked by TIRF measurements (4,11,17). We measured a stall force, where the mean speed of the motor was zero, of 1.11 ± 0.07 pN and 0.76 ± 0.06 pN for Kip3 and Kif18A, respectively. Whereas Kip3 had a nearly linear force-velocity relation over the measured force range, the Kif18A relation showed a strong increase in velocity as the assisting force was increased. In comparison with conventional kinesin-1 (30,31), both kinesin-8s were much slower and weaker.

Figure 2.

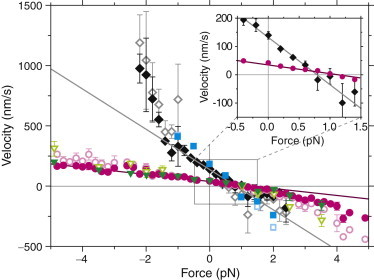
Force-velocity relation. Velocity of Kip3 (magenta circles), Kip3-HT (green triangles), Kif18A (black diamonds), and Kif18AT777 (cyan squares) is shown as a function of force (positive is a hindering load force and negative is an assisting load force; mean ± SE). Open symbols include slip events resulting in up to 2.5× faster velocities. Inset: Zoom of the positive quadrant showing the zero-force velocity and stall force. Solid lines are linear fits to the data shown in the inset and extrapolated beyond.

Kinesin-8s take 8 nm steps

During the regular, ATP-driven mechanochemical cycle, the kinesin-8s took ≈8 nm steps (Fig. 3). A zoom into the position traces of Fig. 1 b for Kip3 revealed individual discrete steps with a size consistent with the 8.2 nm spacing between tubulin dimers (32) (Fig. 3 a). Thus, stepping was as expected for a kinesin (33).

Figure 3.

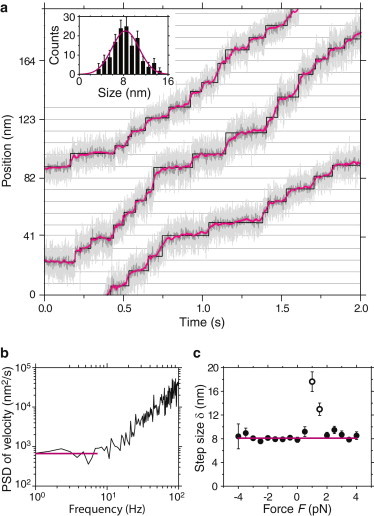
Steps (8 nm) of a single Kip3 motor. (a) Zoom of typical position traces recorded with −1.5 pN assisting load force, showing 41 detected steps (raw data (light grey line); boxcar filtered to 400 Hz (dark grey line) and 100 Hz (magenta line); step detector (black line) (17)). Inset: Histogram of step sizes with a mean of 8.3 ± 0.2 nm ($N=139$) based on a Gaussian fit (magenta line). (b) Example fluctuation analysis (− power spectral density (PSD)) of position traces for Kip3 recorded with zero load force. The plateau at low frequencies (magenta line) indicates that the microsphere moved in a stepwise manner. (c) Step size δ (●) as a function of load force. Step sizes at 1.0 pN and 1.5 pN (○) were excluded from the average (magenta line).

To objectively determine the step size, not only for selected traces and without using a step-finding algorithm, we performed a fluctuation analysis based on a velocity power spectrum method (17,34). An example fluctuation power spectrum for Kip3 calculated from data recorded at zero-load force is shown in Fig. 3 b. With the average plateau value $p=2\upsilon \delta$ (magenta line) and the zero-force velocity $\upsilon =42$ nm/s, the step size δ in this example was 7.9 ± 0.5 nm. The average step size determined in this manner for all Kip3 position traces, excluding slip events, as a function of force is plotted in Fig. 3 c. For traces measured near the stall force, we expected an overestimated step size because of backward steps (35). The weighted average, excluding data points around the stall force, resulted in a step size of 8.1 ± 0.2 nm ($N=62$; Fig. 3 c). This value is again consistent with the 8.2 nm spacing of tubulin dimers. A fluctuation analysis for Kif18A was also consistent with this spacing.

The motors exhibit stick-slip motion under load

Close inspection of the time traces revealed that both kinesin-8 motors frequently slipped for a very short time along the microtubule in the direction of the applied force (arrows in Fig. 1, close-up view in Fig. 4). During a slip, the microsphere moved with a fast and almost constant velocity (Fig. 4 b). Because these events were faster than the response time of the constant-force feedback, we could automatically detect slip events by a sudden drop in force (Fig. 4 a and spikes in Fig. 1 indicated by arrows; see Materials and Methods). For each slip event, we determined the average force $F_{\text{mean}}$ during a slip, the duration τ_s, and distance x_s that the motor slipped, as illustrated by the green lines in Fig. 4 a and b.

Figure 4.

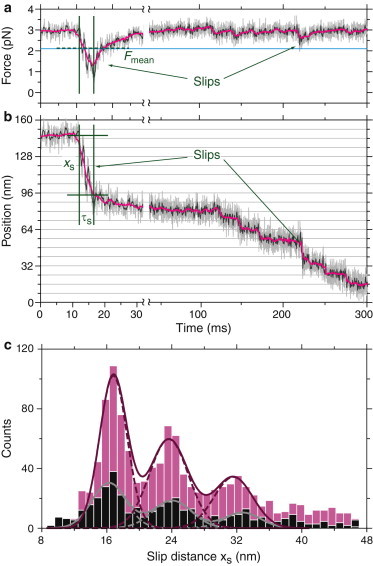
Slip events. (a and b) Typical slip events and backward steps of a Kip3 motor under a 3 pN hindering force. (a) Time trace of force (raw data (light grey line), boxcar filtered to 400 Hz (dark grey line) and 100 Hz (magenta line)). The start and end of the large slip event are marked with green lines. The dashed green line shows the mean force $F_{\text{mean}}$ during that slip. The threshold force for detecting slips in the raw data is marked with a blue horizontal line. (b) Time trace of microsphere position. We determined the slip time τ_s and distance x_s based on the rise time of the force spike. After a slip, kinesin-8 made regular 8 nm (here, backward) steps. (c) Histogram of slip distance x_s of all observed slip events (Kip3 (magenta bars): 1402 events, Kif18A (black bars): 475 events). The mean of the Gaussian fits was 16.5 ± 0.2, 23.6 ± 0.3, and 31.9 ± 0.2 nm for Kip3 (magenta line), and 16.0 ± 0.3, 24.1 ± 0.2, and 32.4 ± 0.6 nm for Kif18A (grey line), corresponding to multiples of ≈8 nm. Slips of 8 nm cannot be distinguished from 8 nm steps and therefore could not be detected.

Independently of force, for both kinesin-8 motors the slip distance was a multiple of ≈8 nm (Fig. 4 c), although we could not resolve individual 8-nm steps during a slip. After each slip, the motor resumed taking its regular ≈8 nm steps (Fig. 4 b).

To gain further insight into the slip state and how it might be related to the regular mechanochemical cycle, we analyzed how the slip parameters (slip distance, time, frequency, and slip velocity) depended on force. The slip distance increased with the hindering or assisting load force (Fig. 5 a). However, the slip time remained constant (Fig. 5 b) and thus was independent of force. For Kip3, the slip time differed significantly depending on the pulling direction (5.4 ± 0.1 ms ($N=9$) and 7.4 ± 0.1 ms ($N=8$) for hindering and assisting load, respectively (magenta closed versus open circles in Fig. 5, b and c). Furthermore, the distribution of slip times was not a simple exponential (Fig. 5 c), as would be expected for a process with a single, rate-limiting step. Instead, the distribution was best fit by a γ distribution with a shape parameter of ≈5 irrespective of the slip length, suggesting that multiple biochemical steps and/or pathways exist during a slip event (36). The number of detected slip events per second (slip frequency) increased with force (Fig. 5 d). This slip frequency corresponds to the transition rate to the slip state. The transition rate from the slip state is the inverse of the slip time (∼160 s⁻¹ and 50 s⁻¹ for Kip3 and Kif18A, respectively). The time between slip events (approximately the reciprocal slip frequency) is the mini-run time in which the motor runs in its regular stepping cycle (Fig. 5 e). We distinguish this time from the total time that kinesin-8s spend during their processive motility, which is on the order of minutes. The (mini-) run time $t_{\text{run}}$ decreased with force (Fig. 5 e). Using the Arrhenius theory, an exponential fit to the data,

$$t_{\text{run}}\left(F\right)=t_{\text{run}}^0\text{exp}\left[\frac{-x_0\left|F\right|}{k_{\text{B}}T}\right],$$ (1)

allowed us to estimate a zero-force run time of $t_{\text{run}}^0=2.7\pm 0.4$ s and a characteristic distance of $x_0=2.1\pm 0.3$ nm, where $k_{\text{B}}$ is the Boltzmann constant and T is the absolute temperature. Based on the slip time and distance, the mean slip speed ${\upsilon }_s=x_s/{\tau }_s$ as a function of the mean force $F_{\text{mean}}$ (Fig. 5 f) revealed very fast movements of the microsphere of up to 9.6 μm/s and 4.1 μm/s for Kip3 and Kif18A, respectively.

Figure 5.

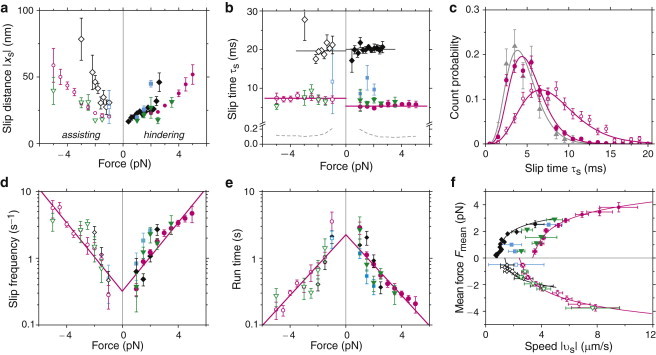
Slip parameters: (a) slip distance x_s, (b) slip time τ_s (solid lines: weighted average), (d) slip frequency (solid lines: fits with Eq. 1), and (e) run time (solid lines: fits with Eq. 1) as a function of force at slip start (hindering forces: Kip3 (red closed circles), Kip3-HT (green downward triangles), Kif18A (black diamonds), and Kif18AT777 (blue squares); open symbols correspond to assisting forces, respectively). (b) The mean slip time was 20.1 ± 0.3 ms and 19.2 ± 0.4 ms for Kif18A, and 5.4 ± 0.1 ms and 7.4 ± 0.1 ms for Kip3, for hindering and assisting load forces, respectively. Relaxation time (- - -) in the trap ${\tau }_{\text{trap}}$. Note the break in the time axis. (c) Histograms for Kip3 slip times. Hindering (red closed circles) and assisting (red open circles) forces were best fit by a γ distribution with a shape parameter of 5.0 ± 0.6 and 4.2 ± 0.4, respectively. Subset of hindering-load slip events (grey upward triangles) with distances of 16 ± 3 nm and a shape parameter of 5.7 ± 0.8. (f) Mean force as a function of slip velocity (the inverse plot was fitted with Eq. 2).

Slips occur when the motor is in a weakly bound state

We do not believe that the slips are due to a short detachment of the motor from the microtubule. During such a detachment, the optical tweezers would pull the microsphere toward the trap center. How long it would take for such a detached and free microsphere to move the observed slip distances would depend on the applied force, the displacement from the trap center, the trap stiffness, and the drag coefficient of the microsphere (see Appendix A). For our parameters, this relaxation time in the trap ${\tau }_{\text{trap}}<0.3$ ms (dashed gray line in Fig. 5 b) was much faster compared with all slip times τ_s, which also differed for the two motors and, for Kip3, also for the pulling directions. Correspondingly, the relaxation speed $x_s/{\tau }_{\text{trap}}$ of a free microsphere would be at least 60 μm/s and 30 μm/s in the case of Kip3 and Kif18A, respectively—much faster than the observed values (Fig. 5 f). Therefore, the motors could not be detached and consequently must have remained in contact with the microtubule. Nor do we believe that slips are due to multiple motors on a microsphere. After a force-dependent detachment of one motor, the microsphere would be expected to relax very quickly to the position of another motor. Also, we did not observe nonspecific interactions of microspheres with the surface when placed next to a microtubule, or of nonmotor-coated microspheres on microtubules (see also Bormuth et al. (17)). Hence, our results indicate that slips occur when the motor is in a weakly bound state.

Importantly, we also observed slipping for the truncated Kif18AT777 motor (blue squares in Figs. 2 and 5; see Materials and Methods) that lacked the microtubule-binding tail domain. Thus, the processivity-enhancing tail domain is not the origin of slipping for Kif18A. Furthermore, we observed slipping for the Kip3-HT motor (green triangle in Figs. 2 and 5; see Materials and Methods), where the C-terminal His-tag is at the tail, which is attached to the microsphere, and not close to the motor domain. Therefore, the His-tag is not the origin of slipping. Instead, slipping is a property of either the motor domain or a region between the motor domain and the microtubule-binding tail domain.

The slipping model supports a weakly bound state

To quantitatively compare the mean load force during a slip with the friction force measured in the presence of ADP (17), we developed an analytical stepping model (see Appendix B). Based on our previous measurements (17), we model the slip state by weakly bound contacts of both kinesin heads to the microtubule at discrete binding sites. The rupture of these contacts or bonds leads to energy dissipation, which can be quantified by a frictional drag coefficient. According to a fit of the model to the data (solid lines in Fig. 5 f, fit parameters listed in Appendix B, Table 1), the binding-site distance was $\delta \approx 8$ nm, suggesting that the motor binds to the same binding sites during slipping and ATP-driven motion. For Kip3, the frictional drag coefficient γ of the weakly bound slip state (Table 1) was comparable (∼3× higher) to the one measured in the presence of ADP but was still much smaller (at least 10×) than that obtained in the nucleotide-free state (17). The analysis revealed an offset in velocity (Fig. 5 f) that was unexpected for biased diffusion in a weakly bound state (17). We account for this offset as being due to a failure to detect events with less than two net steps in the direction of load. This value of the minimal number of steps per slip event is reasonable because 1), in any slip event there is always one more spatial step compared with the number of dwell times; and 2), our spatial resolution to detect slip events was limited by the short duration (Fig. 5 b) and comparatively low load forces. The latter point means that we cannot resolve (back-) steps during a slip event and cannot distinguish an 8-nm slip from a normal 8-nm step. For example, we miss slip events with one forward and one backward step. When this detection limitation was included, the model described the data in Fig. 5 f very well (see also Appendix B).

Table 1.

Parameters of Eq. 2 fitted to the data of Fig. 5f

	δ	${\upsilon }_0$	γ	ε	${\upsilon }_{\text{offset}}^{+}$	${\upsilon }_{\text{offset}}^{-}$	${\chi }_{red}^2$
	(nm)	(nm/s)	(μNs/m)	(nm)	(μm/s)	(μm/s)
Kip3	7.5 ± 0.7	185 ± 53	3.0 ± 0.9	0.1 ± 0.1	3.5 ± 0.1	2.5 ± 0.1	0.7
Kif18A	13 ± 3	64 ± 39	4.9 ± 3.2	0.9 ± 0.3	0.9 ± 0.1	1.4 ± 0.2	1.2

Errors are mean ± SE. The reduced χ²-value ${\chi }_{red}^2$ is the χ²-value divided by the degrees of freedom.

Slip frequency is independent of ADP concentration

To find out more about the state in which kinesin-8s start to slip, we investigated the nucleotide dependence of the slip time and frequency (Fig. 6) for Kip3. For kinesin-1 (37) and kinesin-5 (38), an increase in the detachment rate was reported when ADP was added to the motility solution. However, when we added ADP, we did not observe a significant increase in the slip frequency (Fig. 6 b). One effect of ADP was that it caused the asymmetry in slip times for hindering and assisting loads to disappear (Fig. 6 a). We also did not observe any asymmetry for the Kip3-HT motor (Fig. 5 b). The origin of the asymmetry and why it differs under different conditions is not known.

Figure 6.

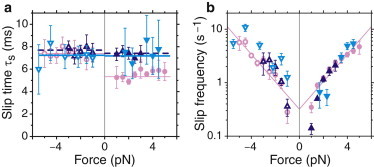
Slip parameters for Kip3 with additional ADP. (a) Slip time τ_s and (b) slip frequency as a function of force at slip start. Added ADP concentration for hindering forces: (light magenta circles) 0 mM (the same data as in Fig. 5b and d serve as a reference), (dark blue upward triangles) 0.01 mM, (light blue downward triangles) 1 mM; open symbols correspond to assisting forces, respectively. Solid lines in a are weighted averages, and in b they are fits of Eq. 1.

Discussion

Our measurements show that both kinesin-8s are slow and weak motor proteins. Although other kinesins have been shown to be slow (39,40), a stall force of ≲1 pN is much smaller than that reported for any other mechanically characterized kinesin (kinesin-1: 5–6 pN (30); kinesin-2: ≈4 pN (41); dimerized kinesin-3: ≈6 pN (42); kinesin-5: ≈5–7 pN (39); and kinesin-7: 6 pN (40)). This finding is not consistent with kinesin-8 being a transport motor, because even small cytoplasmic obstructions are likely to stall the motor or switch it into a slip state.

The strong force dependence (i.e., the low stall force) of the kinesin-8 motors may be caused by several mechanisms. For example, the distance to the transition state for the next step might be large (and positive), such that a hindering force has a strong slowing effect. This position of the transition state, for instance, could be due to the large neck linker of Kip3 (43). Another possibility is that the low force is due to entry into the slip state: the motor does not have enough time to walk against a high force before the next slip event occurs. However, we do not favor such a mechanism, because we do not see many forward steps in between slip events at forces above the stall force (e.g., in Fig. 1 b at 2 pN).

We discovered another feature of kinesin-8s: during ATP-driven motion, the motors can slip under load on the microtubule without detaching. Rather than a continuous run of several microns, kinesin-8 runs are made up of a concatenation of short runs (mini-runs with an associated mini-run time) interrupted by brief slips on the microtubule. Although these slips can be easily observed under loads, they are more difficult to detect under unloaded conditions.

At zero force, does kinesin-8 switch between a processive and diffusive mode? In the absence of load, such mode switching has been reported for kinesin-5 (23,44–46) and kinesin-1 (47). Biasing such a diffusive or weakly bound state by a load (17) should be equivalent to our slip state. For kinesin-5, the slip state may enable load sharing between multiple motors and limit the maximum load on cross-linked microtubules in the mitotic spindle (48). For kinesin-8, our extrapolation of the run time between slip events to zero force (Fig. 5 e) suggests that Kip3 switches approximately every 3 s to the slip state in the absence of load. In contrast, the motor’s 10 μm run length corresponds to a total run time of ∼240 s (≈100 s for the tail mutant (12)), implying frequent switches to the slip mode. However, since the duration of a slip event, τ_s, is much smaller than the expected diffusive stepping time ($\tau ={\delta }^2\gamma /\left(k_{\text{B}}T\right)\approx 25$ ms), Kip3 would only take a random 8-nm step in ∼20% ($\approx 1-\text{exp}\left[-{\tau }_s/\tau \right]$) of the slip events at zero force. Therefore, such events would be indistinguishable from a regular step.

To gain insight into the slip state, we analyzed how the slip speed depended on the mean load force between the motor and the microtubule during slips. Based on this analysis, the distance between binding sites during a slip is 8 nm, consistent with binding at the canonical motor-microtubule strong-binding sites, for which there is only one per tubulin dimer. The distance is not consistent with binding to the negatively charged E-hooks (49), for which there is one binding site per tubulin monomer (i.e., every 4 nm). This finding is consistent with our previous work (17). Therefore, we favor a slipping model in which both heads bind weakly to the canonical binding sites. Because the Kif18A and Kip3 motors sustained forces during slip events up to 3 pN and 5 pN, respectively, we believe that at least one head is always (weakly) bound to the microtubule. Because hand-over-hand stepping is well established for kinesins (50), we hypothesize that kinesin-8 also steps like this while slipping. It is interesting that the 8-nm periodicity of slip distances can be observed even though there is a long and complex linkage between the motor domains and the microsphere (the stalk and tail of kinesin-8, the GFP tag, the antibody, and the PEG coupling to the microsphere). This indicates that there is sufficient time to tauten the linkages after the return to the strongly bound state. However, we do not know whether the dynamical properties of the linkage (e.g., its bending and twisting) play a role in the kinetic properties of slipping, such as the slip time or frequency.

Because the ATP and nucleotide-free states presumably are strongly bound states, in analogy to kinesin-1 (51), we attribute the increased frictional drag coefficient during a slip, which is intermediate between that of ADP and no nucleotide, to one head being in the ADP-P_i state (Fig. 7). For kinesin-1 and kinesin-14, this state was suggested to have ∼3-fold and ∼5-fold higher microtubule affinity, respectively, compared with the ADP state (51). As motivated in the last paragraph, we reason that the other head should also be in a weakly bound state. If ATP is hydrolyzed before ADP is dissociated from the other head (in Fig. 7 between states 2 and 3) (37,50), then one head will be in the ADP-P_i and the other in the ADP state (state 5s). The different nucleotides in the heads may explain the directional asymmetry in the slip time: depending on whether the ADP- or ADP-P_i-bound head detaches first, the slip times may differ. The difference in slip times may also be due to the microtubule polarity, the motor’s directionality, or the His-tag close to the motor domain. Another possibility for entering into the slip mode would be that ADP instead of ATP binds to the nucleotide-free head of state 1 (dashed magenta line in Fig. 7). In this case, both heads would be in an ADP-bound state, where slippage occurs (17). Because this is an additional path for entering the slip mode, we would expect an increase in slip frequency with additional ADP in the motility solution. However, experiments with additional ADP in the motility solution (Fig. 6) showed that this alternative is unlikely to occur. With both heads weakly bound, the motor is off the main pathway (its regular, ATP-driven mechanochemical cycle, in which the heads alternate between strongly and weakly bound states; Fig. 7).

Figure 7.

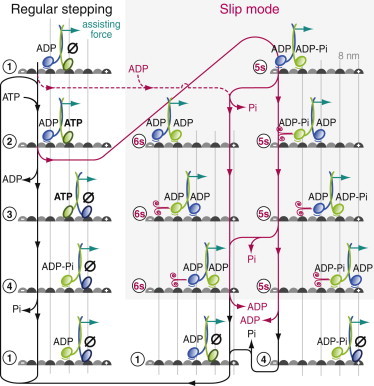
Model for the regular stepping and slip mode of kinesin-8 dimers. The states of the regular stepping and slip pathway are connected by black and magenta lines, respectively. The two heads of kinesin are color-coded (blue and green) and nucleotide states are indicated. Weakly bound states are marked with a line between the motor domain and the microtubule. Fast slip movement is indicated by the magenta curled symbol. An assisting load force is applied to the motor. Several pathways are shown (more are possible). For hindering load forces, an analogous diagram can be drawn.

Our data are consistent with an interpretation that the motor slipped multiple steps per nucleotide. Because ATP-driven stepping is slow and no ADP was added to the solution, the multiple steps during the short-lived slip events (Fig. 5 b) are likely to proceed without exchange of the nucleotides, though it is possible that they are associated with the release of phosphate (Fig. 7). The absence of nucleotide exchange would imply that the slip distance divided by the step size gives a direct measure of the number of steps that the motor can take per nucleotide in a weakly bound state. For Kip3, this number was 3.5 ± 0.1 for hindering and 4.2 ± 0.1 for assisting forces. Termination of a slip event or sticking should occur when one motor head releases its nucleotide to switch to a strongly bound state. Because the slip time was independent of force (Fig. 5 b), we favor the notion that this nucleotide release occurs on the nonload-bearing head, in case of assisting load forces, the front head (Fig. 7).

In summary, for kinesin-1 (37) and kinesin-5 dimers (38), the weakly bound ADP state may correspond to the one in which the motor detaches from the microtubule. For kinesin-8, the weakly bound slip state may have been strengthened such that it acts as a molecular safety leash for kinesin-8, enabling the concatenation of several (mini-) run lengths. This leash, in addition to the tail-microtubule-binding domain, may enable the very high processivity of the motor to regulate the dynamics of microtubules at their plus ends.

Appendix A: Relaxation of a Free Microsphere in the Trap

To rule out the possibility that slip events are short periods of motor detachment from the microtubule, we calculated the relaxation time of a free microsphere. During constant-force measurements, the microsphere is displaced from the trap center on average a distance of $\text{Δ}x=F_{\text{trap}}/\kappa$, where $F_{\text{trap}}$ is the trap force and κ is the trap stiffness (Fig. 1, inset). If the motor detaches, the trap will pull the microsphere toward the position $\text{Δ}x=0$, corresponding to zero force. The time required to move the distance equal to the slip distance x_s at a certain trap force can be calculated from the equation of motion ${\gamma }_{0}dx/dt+\kappa x=0$, where x is the position in the trap and ${\gamma }_0$ is the surface-distance-dependent hydrodynamic drag coefficient of the microsphere (28). The relaxation time in the trap is then given by ${\tau }_{\text{trap}}=-\left({\gamma }_0/\kappa \right)\text{ln}\left(1-\kappa x_s/F_{\text{trap}}\right)<0.3$ ms for Kip3 (Fig. 5 b, dashed ray line) and <0.6 ms for Kif18A (calculation not shown). This time is much smaller than the observed slip times and thus rules out a short motor detachment.

Appendix B: The Slipping Model Quantitatively Accounts for the Force-Dependent Slip Velocity

Our analytical slip-state model is based on our previous measurements (17). In the model, both kinesin heads form weakly bound contacts to the microtubule at discrete binding sites spaced a distance δ apart. The slip speed is then given by

$$\left|{\upsilon }_s\right|=\left|\frac{x_s}{{\tau }_s}\right|=\delta \left|k_{+}-k_{-}\right|+{\upsilon }_{\text{offset}}^{\pm }=\left|{\upsilon }_{+}-{\upsilon }_{-}\right|+{\upsilon }_{\text{offset}}^{\pm }$$ (2)

where $k_{\pm }$ are the effective forward and backward stepping rates, and ${\upsilon }_{\text{offset}}^{\pm }$ is an offset that depends on the direction of slipping and arises, in part, from our ability to resolve only the beginning and ending of the slip events (see main text and below). The model assumes that the forward and backward slip speed ${\upsilon }_{\pm }$ depends in an Arrhenius-type fashion on force:

$${\upsilon }_{\pm }={\upsilon }_0\text{exp}\left[\pm \frac{F_{\text{mean}}\left(\frac{1}{2}\delta \pm \epsilon \right)}{k_{B}T}\right].$$ (3)

The zero-force velocity ${\upsilon }_0=\delta k_0$ is determined by the step size and zero-force stepping rate $k_0$. Here, we have assumed a single, rate-limiting barrier with an asymmetric position characterized by the parameter ε (17). In this case, the sum of the distances to the transition state in the forward and backward directions is equal to the binding-site spacing δ. For $F_{\text{mean}}\left(1/2\delta \pm \epsilon \right)\ll k_{B}T$, a linearized force-velocity relation $\left|F_{\text{mean}}\right|=\gamma \left(\left|{\upsilon }_s\right|-{\upsilon }_{\text{offset}}^{\pm }\right)$ results in the frictional drag coefficient $\gamma =\left(k_{B}T\right)/\left(\delta {\upsilon }_0\right)$.

A fit of Eq. 2 to the Kip3 and Kif18A force-velocity data (Fig. 5 f) resulted in the parameters listed in Table 1. The step sizes agreed within 2 standard errors (SEs) with the expected ≈8 nm step size. The stepping rates ($k_0={\upsilon }_0/\delta$) were ∼23 s⁻¹ and 8 s⁻¹ for Kip3 and Kif18A, respectively, using $\delta =8.2$ nm. Note that these rates need to be added to the rate resulting from the velocity offset. Therefore, the total stepping rate during a slip event is much higher (roughly 80× and 10×) compared with the ATP-driven stepping rate of ∼5 s⁻¹ and 16 s⁻¹ for Kip3 and Kif18A, respectively. Based on the fit parameters δ and ${\upsilon }_0$, and the above-mentioned formula for γ, the frictional drag coefficient was 3.0 ± 0.9 μNs/m and 4.9 ± 3.2 μNs/m for Kip3 and Kif18A, respectively. For Kif18A, the interaction potential may be slightly asymmetric, whereas for Kip3 the asymmetry parameter was not significantly different from zero. The velocity offset, ${\upsilon }_{\text{offset}}$ (from Fig. 5 f and Table 1) for Kip3 was 3.5 ± 0.1 μm/s and 2.5 ± 0.1 μm/s for hindering and assisting load forces, respectively (compared with 0.9 ± 0.1 μm/s and 1.4 ± 0.2 μm/s, respectively, for Kif18A). This offset multiplied by the slip time and normalized to the distance between binding sites results in the number of missed steps: $\left({\upsilon }_{\text{offset}}{\tau }_s\right)/\delta =2.2\pm 0.2$, where we averaged over loading directions and motors. This value of the minimal number of steps means that we can only detect slip events with two net steps in the direction of load (see main text).