Tracking Image Correlation: Combining Single-Particle Tracking and Image Correlation

Abstract

The interactions and coordination of biomolecules are crucial for most cellular functions. The observation of protein interactions in live cells may provide a better understanding of the underlying mechanisms. After fluorescent labeling of the interacting partners and live-cell microscopy, the colocalization is generally analyzed by quantitative global methods. Recent studies have addressed questions regarding the individual colocalization of moving biomolecules, usually by using single-particle tracking (SPT) and comparing the fluorescent intensities in both color channels. Here, we introduce a new method that combines SPT and correlation methods to obtain a dynamical 3D colocalization analysis along single trajectories of dual-colored particles. After 3D tracking, the colocalization is computed at each particle’s position via the local 3D image cross correlation of the two detection channels. For every particle analyzed, the output consists of the 3D trajectory, the time-resolved 3D colocalization information, and the fluorescence intensity in both channels. In addition, the cross-correlation analysis shows the 3D relative movement of the two fluorescent labels with an accuracy of 30 nm. We apply this method to the tracking of viral fusion events in live cells and demonstrate its capacity to obtain the time-resolved colocalization status of single particles in dense and noisy environments.

Introduction

The ideal way to understand the function of a protein is to follow it while it performs its function and observe its interactions with other cellular components. With the development of various labeling strategies, it is possible to label biomolecules with different fluorophores and simultaneously investigate their interaction. Up to now, two different approaches have been employed to identify the colocalization areas. The most common method is based on the visual observation of the overlay image with the appropriate look-up tables for the two different channels. A classical representation is to image one channel in red and the other one in green so that the colocalizing pixels appear in yellow. This method has the advantage of maintaining the spatial information, but the dynamics information is lost and the interpretation of the data is only qualitative and subject to bias. A second class of analysis methods has emerged in the last few decades to allow a quantitative measure of colocalization. Most of them are based on statistical analysis of the pixel intensity distributions and/or calculation of the correlation coefficients (1–5). Hence, the colocalization is calculated in a global manner over the whole image even though a preliminary segmentation of the image can be computed to concentrate on the interesting objects. The main advantage of this class of methods is that the analysis is quantitative, with the results often given as a percentage of colocalization over the whole frame. Additionally, the colocalization analysis can be conducted frame by frame on time-lapse experiments (4,6) and therefore provides a dynamical, quantitative colocalization measurement. More recently, new strategies have been developed to analyze the colocalization particle-wise. The general approach is to locate the fluorescent particles in both channels and measure their interdistance or quantify their overlap (7–9). A threshold is needed to determine the colocalization or noncolocalization status particle-wise, and a global colocalization percentage over the whole image is calculated. Although this class of quantitative methods is powerful, it fails to dissect the fate of individual particles in a heterogeneously colocalizing background.

Another family of very sensitive methods for detecting colocalization that relies on dynamic information is fluorescence fluctuation spectroscopy. The first such method, fluorescence cross-correlation spectroscopy (FCCS) (10,11), determines whether two particles of interest travel together or not through the observation volume of a confocal microscope. Because FCCS is a single-molecule approach, it has the advantage of capturing short-lived states; however, it does not provide the history of interactions for a single molecule or a cellular map of the interactions. A number of image analysis methods have emerged over the past few years (e.g., image correlation spectroscopy (ICS) (12), spatiotemporal ICS (STICS) (13), particle ICS (PICS) (14), and raster ICS (RICS) (15)) that combine the approaches of imaging and correlation analysis. In particular, the correlative motion of two labeled proteins can be addressed as in FCCS and a low-resolution map of the proteins interactions can be obtained by running the analysis in a set of small regions of interest (ROIs) (16,17). However, here again, the colocalization of individual particles is not detectable.

In contrast, in the case of single-particle tracking (SPT), the interactions of a tracked particle can be followed along its journey in the cell. This is of particular interest when one is looking for a gain or loss of colocalization over time for nonsynchronized particles. Up to now, the colocalization analysis of the trajectories has been limited mainly to a simple comparison of the fluorescence intensities in the different color channels (18–20). Hence, efficient detection of changes in colocalization requires a high signal/noise ratio, whereas minimization of photobleaching requires use of the minimum signal/noise ratio allowable for the desired measurement. In addition, the analysis of the trajectories in an unbiased manner requires one to define a global threshold of the fluorescence intensity to determine whether signals are colocalized, which is a delicate matter when different particles have different intensities. Taken together with the possible cross talk between the different channels, these difficulties make it hazardous to rely on only the fluorescence intensity to determine colocalization. Ideally, one would like to combine both SPT and correlation methods. Recently, Vercauteren et al. (21) introduced a novel dynamic colocalization algorithm based on SPT and trajectory correlation to include the temporal information. This leads to better colocalization performance compared with pixel- and object-based methods, but is achieved at the cost of temporal resolution and provides only global colocalization information. Except for this recent work, there is a gap between the correlative or quantitative approaches and the SPT approaches. Here, we describe a new method, called tracking image correlation (TrIC), that computes a colocalization analysis on single particles along their trajectory based on local image cross correlation. We show that the TrIC technique provides a reliable dynamical colocalization analysis at the single-particle scale and, as an additional output, yields the relative position between the particles in the two color channels with an accuracy in our case of 30 nm. To test the validity of the method, we tracked single dual-colored foamy viruses (FVs) and followed their release into the cytosol, thereby gaining dynamic information about the fusion process.

Materials and Methods

Fluorescent beads

As a positive control, multicolored fluorescent beads (190 nm, Ultra Rainbow; Spherotech) were tracked in glycerol. For a negative control, amino beads (Polymer NH2, 0.53 μm; Kisker Biotech, Steinfurt, Germany) were stained with Atto565 NHS-ester (ATTO-TEC, Siegen, Germany) and tracked in glycerol. The conditions (laser intensity and viscosity) were chosen to mimic the fluorescence intensity and mobility of viral particles in the context of live cells.

Cells and viruses

A human cervical HeLa cell line was cultivated in Dulbecco’s modified Eagle’s medium (Gibco, Life Technologies) supplemented with 10% heat-inactivated fetal bovine serum. One day before measurements were obtained, HeLa cells were seeded at a density of 1 × 10⁴ cells/well in eight-chamber slides (Lab-Tek, Scotts Valley, CA). Prior to virus incubation, the cell culture medium was replaced by Dulbecco’s PBS supplemented with calcium and magnesium (DPBS) and the cells were cooled to ∼10°C (5 min). The viruses were then allowed to bind to HeLa cells by incubation for an additional 10 min at ∼10°C. Subsequently, the cells were rinsed with DPBS and the imaging was started immediately after the cells were warmed to 37°C. The dual-colored FVs (Gag-GFP and mCherry-Env) were prepared as described previously (22).

Spinning-disk confocal microscopy

Live-cell and in vitro experiments were conducted on a spinning-disk confocal microscope system (Revolution system; Andor Technology, Belfast, UK) consisting of a Nikon base (TE2000E; Nikon, Tokyo, Japan) and a spinning-disk unit (CSU10; Yokogawa) with a Nikon 100× oil immersion objective (NA 1.49). The detection path was equipped with an Optosplit II (Cairn Research Ltd., Faversham, UK) for dual-color detection, a filter set for enhanced green fluorescent protein (eGFP) and mCherry (BS562, HC525/50, and ET605/70; AHF Analysentechnik AG, Tübingen, Germany), and a DU-897 Ixon EMCCD camera (Andor Technology). In addition, a triple-band dichroic beam splitter was used to separate laser excitation from fluorescence emission (Di01-T405/488/568/647; Semrock, Rochester, NY). The excitation was controlled with an acousto-optic tunable filter (Gooch & Housego, Ilminster, UK). Movies were recorded over 20 min with an exposure time of 130 ms/frame/plane. Then 15–25 z positions spaced by 300 nm were acquired per z-stack, resulting in an interval time of ∼3–5 s between z-stacks.

Image processing

To achieve high precision in the colocalization and relative distance determination of two differently colored particles, one must correct any optical aberrations. A spatial correction can be conducted on every frame of the movie, but this leads to artifacts in the fluorescence intensity. To avoid any manipulation of the original data, we kept the original frames unchanged and corrected only the particle’s coordinates. To determine the mapping between the different channels, we used the pinholes of the nonspinning Nipkow disk as a regular array of bright spots. The positions of the pinholes were determined in the two channels by a two-dimensional (2D) Gaussian fit, and a polynomial transformation was used for mapping of the two channels. We transformed the coordinates in the tracking channel using this mapping to obtain the corresponding positions in the second channel. The colocalization analysis and the fluorescence intensity calculation were achieved by using these transformed coordinates in the second channel. All of the analysis was programmed with MATLAB (The MathWorks, Natick, MA).

Results and Discussion

3D tracking

To achieve single-particle colocalization analysis along a track, one must evaluate the colocalization locally. Therefore, the first step in analyzing the colocalization at the single-particle level is to track the particle of interest. This tracking step is independent of the subsequent colocalization analysis and can be performed in different ways. Due to the density of the virus particles in our live-cell experiments, it was difficult to obtain automatic tracks reliably. Therefore, we used manual tracking. We first made a 2D projection of the 3D movie. We obtained the 2D trajectories by clicking on the particle of interest in each frame, followed by a 2D Gaussian fit for refinement. Thus, only a rough initial tracking was needed. From a ROI centered on the tracked particle, we took the maximum intensity in each z-plane to create an intensity profile in z. We then fit the z profile with a 1D Gaussian to determine the position of the particle in z. The particle’s fluorescence intensity was calculated as the mean intensity in a disk of radius 2 pixels centered on the tracked particle on the 2D projected stack (maximal intensity projection). We then background-corrected the intensity by retrieving the mean intensity of the remaining pixels in the 9 × 9 pixels frame centered on the particle.

The positioning accuracy is limited by the number of photons collected from the particle per image and by the background intensity. These factors depend on several other factors, such as the imaging system, the frame rate, the brightness of the particles, and the autofluorescent environment. For fluorescent viruses in living cells, we typically achieved tracking accuracies of 30 nm in x-y and 40 nm in z, with a 130 ms exposure per frame and 3–5 s per stack.

Single-particle 3D colocalization

Once the 3D trajectory has been obtained, the problem is reduced to a local colocalization question at the position of the particle. A 3D ROI centered on the tracked particle is defined in every frame stack according to the particle’s 3D coordinates (Fig. 1 A). To determine the presence and colocalization of a similar particle in the second channel, we compute the 3D spatial cross correlation of the two respective ROIs, delimited by a 21 × 21 pixels box in x-y and the full stack in z. The ROI in the plane must be chosen to be larger in size than the particle, to keep the information about the particle’s shape. However, the optimum ROI should contain only the particle of interest. When the ROI is too large and other independent particles appear in the ROI, artifacts may occur in the analysis. The coordinates used in the second channel are corrected for optical distortion and spatial shift (see Materials and Methods). Because the fluorescence and background intensities may differ between the two channels, we first subtract the average value of each stack of images, 〈I₁〉 and 〈I₂〉, to correlate only the fluctuations. The images are further normalized with their standard deviation (SD) to obtain normalized images δI′₁ and δI′₂ as follows:

$$\delta I_1^{\prime }=\frac{I_1-\langle I_1\rangle }{{\left(\langle {\left(I_1-\langle I_1\rangle \right)}^2\rangle \right)}^{1/2}}\text{and}\delta I_2^{\prime }=\frac{I_2-\langle I_2\rangle }{{\left(\langle {\left(I_2-\langle I_2\rangle \right)}^2\rangle \right)}^{1/2}}$$ (1)

The method is independent of the normalization method one chooses. In this case, we choose to normalize to the SD to yield a value that is between zero and one (one for autocorrelation). In addition, the cross-correlation amplitude is then independent of the average image intensities in both channels. This normalization is advantageous because the TrIC method was developed for single-particle analysis, where the absolute value of the intensity-normalized cross-correlation function is not relevant. The 3D cross-correlation function, defined by

$$\left(\delta I_1^{\prime }\otimes \delta I_2^{\prime }\right)\left(\xi ,\upsilon ,\zeta \right)=\sum _{x,y,z}\delta I_1^{\prime }\left(x,y,z\right)\times \delta I_2^{\prime }\left(x+\xi ,y+\upsilon ,z+\zeta \right),$$ (2)

is then calculated by a 3D fast Fourier transform according to the cross-correlation theorem (23). Per definition, the result is restricted to values between zero and one.

Figure 1.

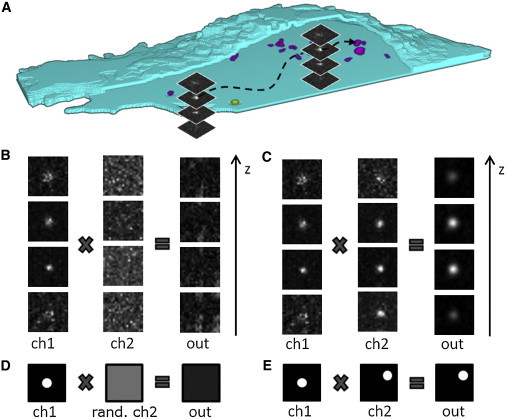
TrIC analysis. (A) Viruses are tracked in 3D as they enter living cells. Along the trajectory, a 21 × 21 pixels² area around the particle of interest is compared to the corresponding region in the second channel via a 3D image cross-correlation analysis. (B) When only background noise is present in the second channel, the result is a 3D stack of images with low intensities and no clear peak. (C) When a single particle is also present in the second channel, the output stack shows a well-defined peak with high intensity. (D) To define a threshold for colocalization that takes into account the intensity of the input channels, the signal in the second channel is randomized and the cross correlation is computed for each time point. (E) When the particle is visible in both channels, the position of the peak of the image cross-correlation function reflects exactly the relative position between the peaks in the first and second channels.

The result of the cross correlation between two 3D stacks of images is a stack with the same dimensions as the inputs. The intensity distribution in this output stack reflects the correlation between the two original stacks of images. As we track the particle of interest, there is always a particle present in the first channel. When there is no particle visible in the second channel, the cross-correlation output shows only noise (Fig. 1 B). On the contrary, if a particle is also visible at the same position in the second channel, a sharp peak is present in the output stack (Fig. 1 C). In every output stack, we measure the maximal value as well as the 3D position of the peak, which is determined with an accuracy of 30 nm in the x-y plane and 40 nm in z by 2D and 1D Gaussian fitting. Hence, for each stack, the analysis provides the correlation amplitude and its position, that is to say, information regarding whether a colocalizing signal is present or absent in the second channel and the corresponding distance between them when a signal is present.

In a noisy environment, a colocalization analysis does not yield a digit value of one or zero but something in between. The background pixels in the vicinity of the tracked particle do not correlate, which decreases the overall correlation value. As a consequence, the amplitude of the correlation function can only be equal to one in the case of autocorrelation function. Similarly, a pair of independent noisy images always shows a random correlation, which renders the correlation amplitude strictly positive. The amplitude of this random correlation depends on the pixels’ intensity distribution and is therefore different for every pair of frames. To determine the colocalization status accurately, we define a threshold for the correlation amplitude computed from a customized negative control for every track. To obtain this no-colocalization correlation amplitude, we randomize the 3D ROI from the second channel before the calculation (Fig. 1 D). Thus, the negative control takes into account the local fluorescence intensity statistics for each frame of the movie. The threshold is then defined as the value of the negative control, averaged using a rolling window (30 s), plus three times its SD determined from the same window. This negative control gives a basal value for the cross-correlation maximum. Hence, a correlation amplitude lower than this threshold may result from random colocalization and should not be taken as a positive colocalization.

The presence of a fluorescent particle at the same position in both channels results in a high value of the cross-correlation maximum and a well-defined position of the peak. The maximum’s position in the output stack reflects the exact relative position between the particles that are visible in the two channels. When the two particles are located at the same position in each channel (Fig. 1 C), the peak is centered in the ROI, and when the two particles are not exactly at the same position (Fig. 1 E), the peak of the 3D image cross correlation is also shifted. To obtain a reliable and accurate relative position between the particles in the two channels, we perform a registration mapping of the two channels to correct for all optical distortions (see Materials and Methods). The calculation is accomplished for every time point along the trajectory and the results are plotted over time to allow determination of the colocalization status in a time-resolved manner. In the case of a colocalization signal in the second channel, the correlation amplitude stays above the threshold and the position of the maximum, i.e., the relative position is close to the center. In the opposite case, where there is no colocalizing signal, the correlation amplitude is low and the relative position takes on random values.

Because noise does not correlate, the cross-correlation calculation has the advantage that it filters out the background noise and shows a higher sensitivity to colocalization than a mere comparison of the fluorescence intensities. In addition, the image cross correlation reflects also the correlation in the object’s shape in the two channels. If the same shape is present in both channels, the peak in the cross-correlation image will be sharper. The calculation presented in this work can also be done in 2D, but the full 3D analysis presented here is more robust. Taking into account the volume around the particle of interest and not just a 2D projection decreases the risk of false-positive colocalization due to another fluorescent particle crossing the ROI in another z-plane. The TrIC method yields not only the colocalization status of the particle along its trajectory via the cross-correlation maximal value but also the relative position between the two fluorescent markers, provided they both remain within the ROI. Hence, tracking information is simultaneously obtained in the second channel through the cross-correlation calculation. This information can be used as an additional hint for colocalization. As discussed further below, the relative position of the two markers may also give additional biologically relevant information.

Because the first step of the method is the tracking of a single fluorescent particle, one can worry about the effect of the tracking accuracy on the colocalization determination. However, as long as the particle remains entirely in the ROI, an off-center position has practically no effect on the cross-correlation output, and the particle still contributes to the cross correlation. The relative-position determination is also not affected because it depends purely on the shift between the particle’s position in the two channels and not on the absolute position of the ROI. Therefore, the relative positioning accuracy depends only on the signal/noise ratio in the cross-correlation output, which in turn is related to the signal/noise ratio in the original images. The interpretation of the results presented so far assumes that there is only one particle in the volume of interest. If a second particle is present in the ROI and is brighter than the particle of interest, then the cross correlation will show the position relative to this brighter particle. Therefore, the size of the ROI has to be carefully chosen to minimize this probability. Typically, a second independently moving particle does not remain long in the ROI, and one can easily detect such events by looking at the fluorescence intensity, the cross-correlation value, and the position, which makes them easy to discard.

Validation using fluorescent beads

To first validate our approach using a positive control, we tracked multicolored fluorescent beads (diameter of 190 nm) diffusing in a glycerol solution. Fig. 2 A shows the 3D trajectory of a representative track recorded over 9 min, during which time the particle has diffused several micrometers in the three directions. The results of the complete analysis with the TrIC method are shown in Fig. 2 B. In both channels, the background-corrected fluorescence intensity slowly decreases over time due to photobleaching (Fig. 2 B, i). The instantaneous velocity of the bead reflects its Brownian motion in solution (Fig. 2 B, ii). The two lower panels of Fig. 2 B (iii and iv) show the outputs of the cross-correlation calculation: the correlation amplitude and the relative distance, i.e., the cross-correlation maximum’s position. Along the trajectory of this diffusing dual-colored particle, the correlation amplitude remains close to 0.4 (blue line and dots in panel iii), which is largely above the threshold value (gray line) calculated as explained previously from the randomized control (black line). The maximum achievable correlation value is one and would only be obtained for an autocorrelation function. In a real experiment, the background around the particle is different in the two channels and decreases the overall correlation value. An effect of the photobleaching is observable on the correlation amplitude, which decreases slightly over time. However, the correlation signal is less noisy and less sensitive to photobleaching (with a SD of 10% of the average value in this example) than the background-corrected fluorescence intensity (which has a SD of 18% of the average value in the green channel in this example). The relative distance between the two signals is <100 nm for the entire trajectory (panel iv). The experimental accuracy is limited by the uncertainty of the relative position of the two signals in all three dimensions (30 nm in x and y, and 40 nm in z), which corresponds to a total uncertainty of ∼60 nm. In addition, the z-stack is collected over 3–5 s and motion of the particle will increase the uncertainty of the calculation. Hence, 100 nm represents the experimental accuracy of the method under the current conditions.

Figure 2.

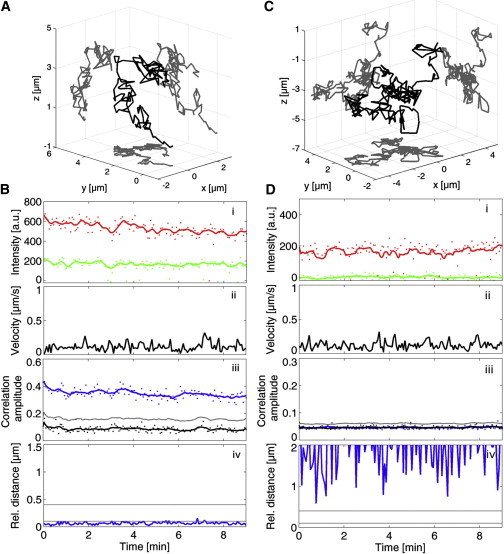
TrIC analysis of dual-colored and single-colored fluorescent beads. (A) 3D trajectory of a dual-colored fluorescent microsphere diffusing in a glycerol/water mixture. (B) Corresponding TrIC analysis showing (i) the fluorescent intensity in both detection channels, (ii) the instantaneous velocity along the track, (iii) the correlation amplitude, and (iv) the relative positions between the two labels. For this positive control, the correlation amplitude remains clearly over the threshold (gray) and the randomized control (black). The relative distance between the particles in the two channels remains below 100 nm, reflecting the resolution of the system. (C) 3D trajectory of a single-colored microsphere in a glycerol/water mixture. (D) Corresponding TrIC analysis for a single-colored microsphere. The correlation amplitude (blue) overlays the randomized control (black) and remains below the threshold (gray) (iii). The relative distance takes random values (iv).

We then conducted the same experiment with single-colored beads (530 nm diameter) to create a negative control in which no colocalization is present. Fig. 2 C shows the 3D trajectory of a single-colored microbead tracked in the red channel over 9 min. As expected, the background-corrected fluorescent intensity is close to zero in the green channel. Along the trajectory, the correlation amplitude (blue line and dots in Fig. 2 D, iii) remains lower than the running threshold (gray) at the same level as the ongoing negative control calculated from the randomized second channel (black line and dots). Since there is no colocalization, i.e., no particle visible in the second channel, the relative distance is random and not meaningful (Fig. 2 D, iv).

The results of these two experiments on fluorescent beads verify the principle of the TrIC analysis for bright particles in a very low background environment. However, the method is principally intended for the study of biological particles in live cells, which are known to be autofluorescent, making fluorescent microscopy, SPT, and colocalization analyses more difficult. To further test the TrIC analysis under such conditions, we tracked dual-colored viruses as they infected living cells.

Investigating the fusion of FVs in live-cell experiments using TrIC

FV is a member of the retrovirus family (24), which is nonpathogenic and thus promising for gene transfer. During the infection process of FVs, the capsid is released from the viral envelope through the fusion of the viral membrane with a host cell membrane. To investigate the entry process, we fluorescently labeled two different proteins of the FV: the capsid protein, Gag, which was fused to eGFP, and the glycoprotein, Env, which was fused to mCherry (22). Thus, the virus particles are dual-colored at the beginning of the infection and the colocalization of the two fluorescent labels is expected to be lost upon fusion. Because the fusion event is not synchronized between viruses, a global colocalization analysis can only provide an overall timescale for fusion, whereas a single-particle analysis such as TrIC provides the distribution of the events that can observed using SPT.

We first validated the TrIC method on modified viruses: a dual-colored, fusion-incompetent FV for the positive colocalization control and a single-colored FV for the negative-colocalization control (Fig. 3). The fusion-incompetent virus is double-labeled, as explained above, but is unable to undergo fusion. The virus is therefore expected to remain dual-colored during its entire journey inside the cell. Fig. 3 A shows the 3D trajectory of such a fusion-incompetent virus tracked over 7 min inside a living cell. The trajectory is confined to an area of a couple of square micrometers in the plane and ∼1 μm along the vertical axis. As expected, the fluorescence intensities stay clearly above zero during the complete trajectory, although the signal becomes noisier toward the end of the movie (Fig. 3 B, i). This is confirmed by the TrIC analysis, which shows a correlation amplitude above the threshold throughout the entire movie (Fig. 3 B, iii). Because the signal/noise ratio is lower than in Fig. 2 B, the correlation amplitude is also reduced (0.12 on average in Fig. 3 B and 0.35 in Fig. 2 B) but never reaches the basal value determined from the randomized channel 2 (in black). The relative distance between the two labels stays below 100 nm (lower gray line in Fig. 3 B, iv), which is within the experimental accuracy of the method as discussed above. As tracking becomes more difficult toward the end of this track due to strong fluctuations in the fluorescence intensities, the calculated relative distance also becomes less accurate.

Figure 3.

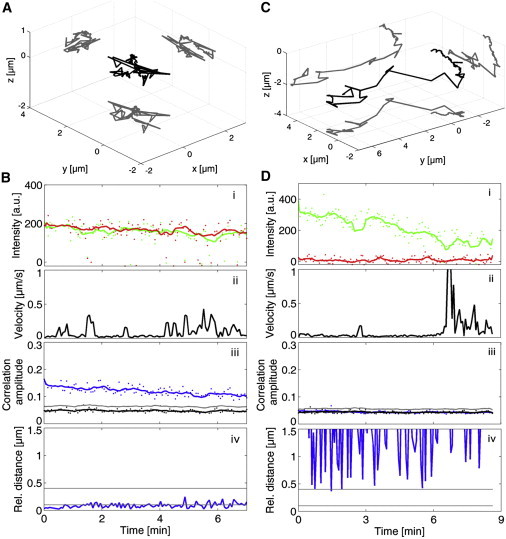
TrIC analysis on dual-colored (Gag-eGFP and mCherry-Env) and single-colored (Gag-eGFP) FV particles. (A) 3D trajectory of a fusion-incompetent, dual-colored virus within a live HeLa cell. (B) The corresponding TrIC analysis showing (i) the fluorescent intensity in both detection channels (ii) the instantaneous velocity along the track, (iii) the correlation amplitude, and (iv) the relative positions between the two labels. The correlation amplitude (blue, iii) remains higher than the threshold (gray) throughout the movie, although its value is lower than for the bead controls. The relative position stays below or close to 100 nm, but is noisier compared with the measurements on fluorescent beads. (C) 3D trajectory of a single-colored virus in a live cell. (D) The corresponding TrIC analysis. Despite the lower signal/noise ratio and decreasing fluorescence intensity (i), the correlation amplitude (blue, iii) always remains below the threshold (gray). The relative position shows high and random values (iv), which are meaningless in this case. The instantaneous velocity determined from the trajectories is plotted with time in panels B, ii, and D, ii.

We then tested the TrIC analysis on a single-colored virus that was labeled only with eGFP fused to the capsid proteins. A representative trajectory for a virus is presented in Fig. 3 C. The virus was initially resting on the cell membrane and then was taken up by the cell, as seen from the peak in the instantaneous velocity (Fig. 3 D, ii). The eGFP fluorescence depends on its close surroundings and is known to be quenched at acidic pH, which can happen in cellular compartments such as late endosomes. In this example, the fluorescence intensity in the green channel (eGFP) looks unstable and decreases over the duration of the track (9 min; Fig. 3 D, i). On the contrary, the correlation amplitude (in blue, Fig. 3 D, iii) is constant, overlaying the automatic negative control very well (in black) and thus remaining below the threshold for colocalization (gray line). Because there is no colocalization, the relative distance is random and meaningless (Fig. 3 D, iv).

Entry and fusion of dual-colored FVs

The above experiments on modified viruses verify the capability of the TrIC analysis to discriminate between dual- and single-colored particles in the cellular context. However, the aim of the TrIC method is to provide a dynamical colocalization analysis during a trajectory. Hence, we measured dual-colored, fusion-competent FVs as they entered live HeLa cells.

The fusion-competent FV particles were labeled with mCherry-Env and Gag-eGFP. Upon fusion, the envelope will detach from the capsid and the fluorescent labels are expected to separate. Fig. 4 shows the complete analysis of a representative FV fusion event. The 3D trajectory of this particular track is shown in Fig. 4 A as 2D projections on the differential interference contrast image of the cell. The track began with the virus at the border of the cell wobbling with a relatively low velocity (<0.2 μm/s; Fig. 4 B, ii). The virus was then transported toward the cell center with instantaneous velocities up to 0.95 μm/s. The background-corrected fluorescence intensity (Fig. 4 B, i) in the tracking channel (Gag-eGFP) shows a smooth decay, whereas the fluorescence intensity in the second channel fluctuates (SD/mean = 39%) before it shrinks, and remains close to zero until the end of the track. This sudden disappearance of the red signal is the first indication of a fusion event in which the capsid (tracked in the green channel) separates from the envelope (red channel). To obtain a clearer signature of the putative fusion event, we conducted a TrIC analysis (see Movie S1 in the Supporting Material). The correlation amplitude (Fig. 4 B, iii) is less noisy and significantly higher than the background compared with the red fluorescence intensity. It shows a clear step down crossing the threshold line (in gray) at 7.5 min. Concomitantly, the relative distance between the green and red signals (Fig. 4 B, iv) suddenly increases to values higher than 1.5 μm, revealing that the red signal left the ROI used for the calculation. In this example, the loss of colocalization happens faster than the temporal resolution, as is clearly visible in the plot of the relative distance where no time averaging is performed. The TrIC analysis firmly confirms the fusion events and gives the precise fusion time through the observation of two different pieces of information: the correlation amplitude and the relative distance. Additionally, the 3D relative movement of the green signal compared to the red one (i.e., of the capsid compared with the envelope) is also provided. This 3D relative trajectory (Fig. 4 C) shows that the green and red signals do not exactly overlay, but rather move around each other, with the relative distance between their center of mass being on average 392 nm before the fusion (Fig. 4 B, iv). This is significantly higher than the relative distance of ∼100 nm in the dual-colored viral control (Fig. 3 B).

Figure 4.

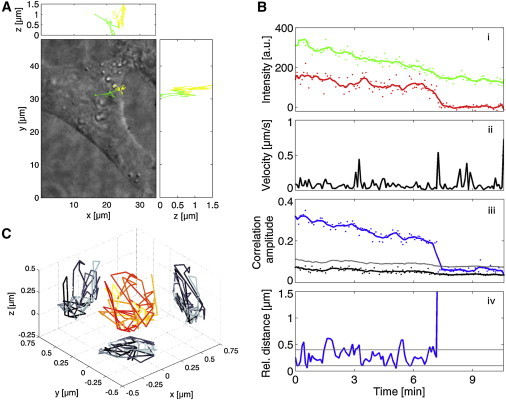
Real-time viral fusion in live cells. (A) 3D trajectory of a fusion-competent, dual-colored FV particle (Gag-eGFP and mCherry-Env) projected on a bright-field image of the cell. The trajectory is shown in yellow when both labels are present and in green after fusion has occurred. (B) TrIC analysis of the FV fusion event. (i) The fluorescence intensity of Gag-eGFP and mCherry-Env is shown as a function of time. The green (Gag-eGFP) fluorescence intensity decreases continuously, whereas the red (mCherry-Env) intensity fluctuates strongly before decreasing to the background level. (ii) The instantaneous velocity determined from the trajectory is plotted with time. (iii) The correlation amplitude (blue) is first smooth and clearly above the threshold. (iv) At time 7.5 min, the correlation amplitude drops below the threshold value and an increase of the relative distance is simultaneously observed. This is the signature of the separation of the two fluorescent labels (here, the fusion of the virus). Before fusion occurs, the relative distance fluctuates between 100 nm and 500 nm. (C) The 3D relative trajectory of the Env-labeled envelop with respect to the Gag-capsid shows movement in the order of hundreds of nanometers between the two labels before the completion of the fusion process. The slow decrease of the correlation amplitude before fusion is a result of the decrease in fluorescence intensity due to photobleaching.

The example track shown in Fig. 4 has a relatively high signal/noise ratio, which makes the fusion event already visible on the fluorescence intensity traces. We also tried the TrIC method on a more difficult track (Fig. 5 A) in which the fluorescence intensity was very low in the second (red) channel, which made the colocalization status impossible to determine without further analysis (Fig. 5 B, i). In this case, the combination of the correlation amplitude, the automatic threshold, and the relative position of the two labels gave a definite answer regarding the colocalization status and the time point of fusion (Fig. 5 B). Here, the loss of the colocalization occurs over a 3 min period (from 4–7 min), during which there is a slow increase in the relative distance from 400 nm to 1.5 μm (Fig. 5 B, iv, and C). Hence, we obtain detailed insight into how the signals separate and we can directly monitor the kinetics of the dissociation process.

Figure 5.

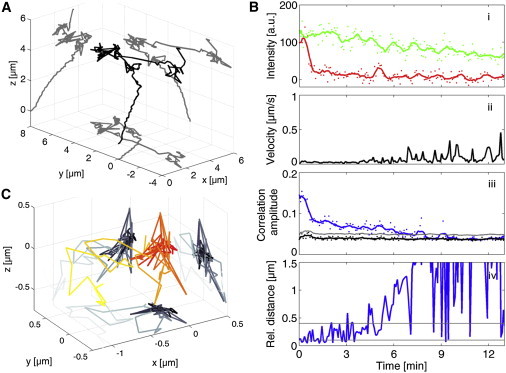
TrIC analysis on a trace with a low signal/noise ratio. (A) 3D trajectory of an FV particle. (B) The corresponding TrIC analysis. (i) The fluorescence intensities of Gag-eGFP and mCherry-Env are shown as a function of time. The red fluorescence intensity is so low that it is impossible to conclude whether fusion has occurred. (ii) The instantaneous velocity determined from the trajectory is plotted with time. The peaks in the plot show that the virus has been taken up by the cell. (iii) The correlation amplitude is above the threshold until ∼7 min and then overlays the automatic negative control. (iv) The relative distance shows a clear colocalization until 4–6 min, when the signals clearly separate. After 7 min, the red particle leaves the ROI used for cross correlation. Due to the very low fluorescence intensity, the resolution for the position of the correlation maximum is poor. (C) Relative trajectory of the Env-labeled envelope with respect to the Gag-capsid during the fusion event.

In the last part of this work, we proved that the TrIC method is capable of determining the colocalization status of a single particle in live-cell experiments and thereby indicating the fusion time of individual retroviruses. The method was shown to be efficient for low signal/noise tracks in which the mere observation of the fluorescence intensities is not conclusive. In addition to the colocalization status along the track of single particles, the TrIC method provides the relative motion between the center of mass of the two fluorescent labels with an accuracy of ∼100 nm. More generally, there is no specific requirement regarding the technique used to acquire the data—the TrIC method is suitable for any type of movie (2D/3D, confocal/TIRF/widefield, etc.). In addition, the TrIC method works regardless of the size or the brightness of the object; the only requirement is that the particle can be detected and tracked.

Conclusions

To detect rare events or interactions of moving particles, such as viral fusion, a single-particle, dynamical colocalization analysis is required. So far, such experiments have been based mainly on the fluorescence intensity, a method that is subject to bias. Here we present a new method, called TrIC, that combines SPT and local image cross correlation. TrIC provides better sensitivity and an automatically defined threshold to precisely and without bias assess the time point of the color separation, when present. Combined with the 3D trajectory, this analysis makes it possible to detect the gain or loss of colocalization events with respect to the environment (e.g., within a cell). In addition, the relative position between the two labels is obtained with an accuracy of better than 50 nm, showing the possible spatial interplay between both labeled components. We first tested the method on fluorescent beads in vitro. We then performed live-cell experiments with single-colored and fusion-incompetent dual-colored viruses to test the principle in the high-background environment of living cells. Finally, we tracked dual-colored viruses during their uptake in live cells and were able to observe viral fusion. This type of event, which is rare and not synchronized, is very difficult to detect with global quantitative colocalization methods. We were able to show that this new colocalization method is well suited for difficult environments (e.g., live cells) and rare events (e.g., viral fusion). In addition, we postulate that the relative position between the two labels given by the TrIC method yields information about the kinetics of the fusion process and can shed light on the separation process of such events. The method is therefore of great interest for various biological applications, such as endosome trafficking and drug delivery.