Automatic Correction of Intensity Nonuniformity from Sparseness of Gradient Distribution in Medical Images

Abstract

We propose to use the sparseness property of the gradient probability distribution to estimate the intensity nonuniformity in medical images, resulting in two novel automatic methods: a non-parametric method and a parametric method. Our methods are easy to implement because they both solve an iteratively re-weighted least squares problem. They are remarkably accurate as shown by our experiments on images of different imaged objects and from different imaging modalities.

1 Introduction

Intensity nonuniformity is an artifact in medical images, perceived as a smooth variation of intensities across the image. It is also referred to as intensity inhomogeneity, shading or bias field. This artifact can be produced by different imaging modalities, such as magnetic resonance (MR) imaging, computer tomography (CT), X-ray, ultrasound, and transmission electron microscopy (TEM), etc. Although intensity inhomogeneity may not be noticeable to human observer, it can degrade many medical image analysis methods like segmentation, registration, and feature extraction, etc.

There exist different kinds of methods to correct the intensity nonuniformity in medical images. In the recent detailed review [1], they are classified into filtering based methods to remove image contents unrelated to the nonuniformity, surface fitting based methods based on the intensities of major tissues or the image gradients [2], segmentation based methods performed by iterating on the two processes of image segmentation and bias field’s fitting [3,4], and image intensity histogram based methods through maximizing the high frequency of the image intensity distribution or minimizing the image entropy [5,6], etc.

In this paper, we propose to apply the sparseness property of the gradient probability distribution in medical images to the automatic estimation of the bias field. The sparse distribution is typically characterized by a high kurtosis and two heavy tails. From this prior knowledge, we obtain a non-parametric method and a parametric method. The two methods are simple to implement. They both work by solving an iteratively re-weighted least squares (IRLS) problem. In each iteration, only a linear equations system needs to be solved. The two novel methods are also remarkably accurate, as shown by our results on simulated and real MR brain images, real CT lung images, and real TEM rabbit retina images.

2 Sparseness of Image Gradient Distribution

Recent research has shown that images of real-world scenes obey a sparse probability distribution in their gradients [7,8]. This sparseness property is extremely robust and characterized with a high kurtosis and two heavy tails in the gradient distribution. It stems from the assumption on the image that adjacent pixels have similar intensities unless separated by edges, i.e. the widely known piecewise constancy property of image.

This sparse distribution can be modeled with different ways, e.g. the exponential function [8], as expressed below

$$p(x)=e^{-{\mid x\mid }^{\alpha }}$$ (1)

where the parameter α < 1 and can be fit from the gradient histogram.

We compute the image gradient histogram with the optimal bin size computed by the method in [9], and then use it to fit α in Eq. (1) with the maximum likelihood [10].

3 Methods

We use this sparseness property of gradient distribution in medical images to estimate the bias field in order to correct the intensity nonuniformity. To be concise, we provide the explanations of the 2D image case. However, the modifications to the 3D volume are straightforward.

3.1 Problem Definition

Considering the noise free case, a given 2D medical image Z is the product of the intensity nonuniformity free image I and a bias field B, as expressed below

$$Z(i,j)=I(i,j)B(i,j),$$ (2)

where (i, j) index pixel in the image, and if M and N represent the total numbers of rows and columns, respectively, we have 1 ≤ i ≤ M and 1 ≤ j ≤ N.

In the process of correcting the intensity nonuniformity, our goal is to estimate B in Eq. (2) for each pixel. This is a classic ill-posed problem because the number of unknowns (I and B) is twice the number of equations. To make it solvable, we need to add constraints on both I and B.

Instead of computing B directly, we solve for its logarithm as in [8]. Let 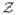= ln Z, 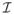= ln I, and = ln B. Then, we have

$$\mathcal{Z}(i,j)=\mathcal{I}(i,j)+\mathcal{B}(i,j).$$ (3)

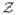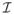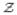We denote the gradients of , , and for each pixel (i, j) by ψ(i, j), ψ 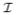(i, j), and ψ 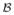(i, j), respectively. Then,

$${\psi }^{\mathcal{Z}}(i,j)={\psi }^{\mathcal{I}}(i,j)+{\psi }^{\mathcal{B}}(i,j).$$ (4)

Given an image 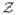with the intensity nonuniformity, we find a maximum a posteriori (MAP) solution to . Using Bayes’ rule, this amounts to solving the optimization problem

$$\mathcal{B}=arg\underset{\mathcal{B}}{max}P(\mathcal{B}\mid \mathcal{Z})\propto arg\underset{\mathcal{B}}{max}P(\mathcal{Z}\mid \mathcal{B})P(\mathcal{B}).$$ (5)

Different specifications of 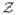P( | ) and P( ) in Eq. (5) may lead to different algorithms to solve the bias field . The conditional probability P( 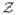| ) can be determined by some prior knowledge on the nonuniformity free image 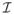= 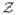− , while P( ) can be set from some prior information on the field .

To compute P( 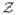| ), we impose the sparseness prior of the image gradient distribution explained in Eq. (1) on 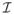as below

$$P(\mathcal{Z}\mid \mathcal{B})=P({\psi }^{\mathcal{I}})=e^{-{\mid {\psi }^{\mathcal{I}}\mid }^{\alpha }},\alpha <1.$$ (6)

From Eq. (4), we have

$${\psi }^{\mathcal{I}}(i,j)={\psi }^{\mathcal{Z}}(i,j)-{\psi }^{\mathcal{B}}(i,j).$$ (7)

Substituting Eq. (7) into Eq. (6), yields

$$P(\mathcal{Z}\mid \mathcal{B})=e^{-{\sum }_{(i,j)}{\mid {\psi }^{\mathcal{Z}}(i,j)-{\psi }^{\mathcal{B}}(i,j)\mid }^{\alpha }}.$$ (8)

To determine P( ), there are basically two ways: non-parametric method and parametric method. Non-parametric method does not assume any model on and estimate for each pixel while enforcing spatially local smoothness. P( ) can be expressed explicitly by values based on the smoothness constraints. Parametric method represents with some model functions and estimate the parameters of the model. P( ) is represented by the parameters of the model through enforcing some prior constraints on the model, or is eliminated when no prior constraint is necessary in the model.

3.2 Non-parametric Method

We impose a smoothness prior over :

$$P(\mathcal{B})=e^{-{\lambda }_s{\sum }_{(i,j)}\left({\mathcal{B}}_{xx}{(i,j)}^2+{\mathcal{B}}_{yy}{(i,j)}^2\right)},$$ (9)

where λ_s is a parameter (e.g. 0.8) determining how smooth the resulting will be, and 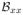(i, j) and 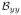(i, j) are the second order derivatives at pixel (i, j) along the horizontal direction and vertical direction, respectively.

The maximization of Eq. (5) becomes the the minimization of the below object function

$$\mathcal{O}=\sum _{(i,j)}{\mid {\psi }^{\mathcal{Z}}(i,j)-{\psi }^{\mathcal{B}}(i,j)\mid }^{\alpha }+{\lambda }_s\left(\sum _{(i,j)}{\mathcal{B}}_{xx}{(i,j)}^2+\sum _{(i,j)}{\mathcal{B}}_{yy}{(i,j)}^2\right).$$ (10)

The minimization of Eq. (10) does not have a closed-form solution because the exponent α in the first term is less than one as mentioned in Eq. (1). To solve it, most nonlinear optimization techniques [11] can be directly applied, however, they would be very time-consuming and easy to be trapped into a local minimum considering the large number of unknowns in Eq. (10) (it equals to the number of pixels). In order to get a good solution in less time to this minimization problem, we employ the iteratively re-weighted least squares (IRLS) technique [12,8]. IRLS poses the optimization as a sequence of standard least squares problems, each using a weight factor based on the solution of the previous iteration. Specifically, at the kth iteration, the energy function using the new weight can be written as

$$\mathcal{O}=\sum _{(i,j)}{w}_k(i,j){\left({\psi }^{\mathcal{Z}}(i,j)-{\psi }^{\mathcal{B}}(i,j)\right)}^2+{\lambda }_s\left(\sum _{(i,j)}{\mathcal{B}}_{xx}{(i,j)}^2+\sum _{(i,j)}{\mathcal{B}}_{yy}{(i,j)}^2\right),$$ (11)

where weight w_k (i, j) is computed in terms of the optimal 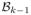from the last iteration as

$$\begin{array}{l}{w}_k(i,j)=e^{-S_1}(1-e^{-S_2}),\\ S_1=\mid {\psi }^{\mathcal{Z}}(i,j)-{\psi }^{{\mathcal{B}}_{k-1}}(i,j)\mid ,S_2=\alpha {(S_1)}^{\alpha -1}\end{array}$$ (12)

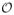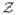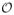It is easy to see that minimizing in Eq. (11) is to make the gradient of equal to the gradient of at each pixel while enforcing spatially local smoothness on . However, it is well known that this kind of problem has no unique solution because adding a constant value on will not influence value. To tackle it, we add another constraint as shown in the new object function below

$$\mathcal{O}={\sum }_{(i,j)}{w}_k(i,j){\left({\psi }^{\mathcal{Z}}(i,j)-{\psi }^{\mathcal{B}}(i,j)\right)}^2+{\lambda }_s\left({\sum }_{(i,j)}{\mathcal{B}}_{xx}{(i,j)}^2+{\sum }_{(i,j)}{\mathcal{B}}_{yy}{(i,j)}^2\right)+\epsilon {\sum }_{(i,j)}\mathcal{B}{(i,j)}^2,$$ (13)

where ε is a very small value, e.g. 0.00001. This constraint makes as small as possible (i.e. B as close to 1 as possible), leading to a unique solution.

The object function in Eq. (13) is a standard least-squares problem. We can always obtain a closed-form optimal solution by solving a linear equations system. Details of the solution can be found in the supplementary file.

In our experiments, we initialize (i, j) = 0 (i.e. B(i, j) = 1) for all pixels (i, j), and find that it suffices to iterate three or four times to obtain satisfactory results. We also observed that the re-computed weights at each iteration k are higher at pixels whose gradients in 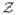are more similar to the ones in the estimated 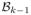. Thus, the solution is biased towards smoother regions whose gradients are relatively smaller. Fig. 1 shows the weights recovered at the final iteration for an MR image.

Fig. 1.

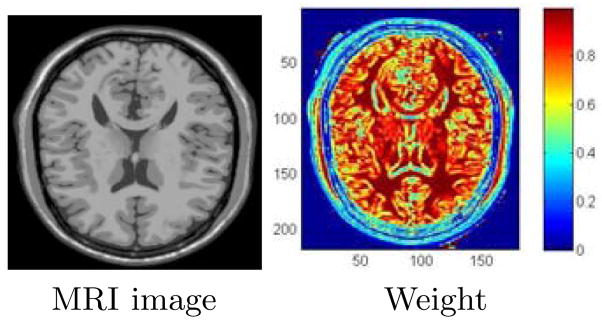
Computed weights (Eq. (13)) in the non-parametric method after the 3rd iteration of the IRLS algorithm, shown by color coding with the spectrum in the color bar (right).

3.3 Parametric Method

Different models are suitable to represent the nonuniformity field , considering its smoothly changing property, like the cubic B-splines [5], thin-plate splines, and the the bivariate polynomial, etc. We choose the bivariate polynomial for its efficiency shown by [2], for which the model in degree D (e.g. 4) is

$$\mathcal{B}(i,j)=\sum _{t=0}^D\sum _{l=0}^t{a}_{t-l,l}{x}_{(i,j)}^{t-l}{y}_{(i,j)}^l$$ (14)

where {a_t−l,l} are parameters determining the polynomial, and x_(i,j) and y_(i,j) are the values of pixel (i, j) on the x-axis and y-axis, respectively. Note that the number of elements in {a_t−l,l} is (D + 1)(D + 2)/2.

We apply the IRLS scheme used in the non-parametric method to estimating model parameters in the parametric method. Considering the fact that the model in Eq. (14) already incorporates the spatial smoothness on , the smoothness constraints on values can be eliminated. The object function in each iteration of the IRLS is then written as

$$\mathcal{O}=\sum _{(i,j)}{w}_k(i,j){\left({\psi }^{\mathcal{Z}}(i,j)-{\psi }^{\mathcal{B}}(i,j)\right)}^2+\epsilon \sum _{t=0}^D\sum _{l=0}^t{a}_{t-l,l}^2$$ (15)

where we add the regularization on {a_t−l,l} in order to get a unique solution as explained in Eq. (13), and the weights w_k (i, j) are computed with Eq. (12).

The object function in Eq. (15) is also a standard least-squares problem relative to {a_t−l,l}, and its minimization also has a closed-form solution by solving a linear equations system. It can be seen from the fact that gradient on is linear to {a_t−l,l}. More details of the solution can be found in the supplementary file. In our experiments, we initialize {a_t−l,l} to zero, and it suffices for three or four times to obtain satisfactory results.

The proposed non-parametric and parametric methods are both easy to implement and run fast. The two methods iterate only three or four times on solving a weighted least square problem with the IRLS technique. The weighted least square problem is solved by resolving a linear equations system for which the solution can be represented by some operations of matrices. We note that the operations of sparse matrices are needed for solving Eq. (13).

4 Results

To implement our algorithms, the matrix operations in Eq. (13) were performed with the TAUCS¹, a library of sparse linear solvers.

We provide both quantitative evaluations with simulated data sets and visual evaluations with real data sets on our algorithms. For all experiments, we use α = 0.71 in the sparse distribution model (Eq. (1)), that was estimated from 84 MR human brain images and 45 CT human lung images. These images were chosen to be free of the intensity nonuniformity guaranteed by visual inspections. In addition, we run our algorithms on a lower resolution image down-sampled from the given image and then reconstruct the resulting bias field to the original size by interpolation, as in [5]. In the experiments, the gradients along the two axis for 2D image and the three axes for 3D volume are all used.

4.1 Quantitative Evaluation

We test our algorithms on the 3D MR volumes obtained from the BrainWeb Simulated Brain Database², for which the ground truth of the bias field is known. The Root Mean Squared Error (RMSE) between the estimation and the ground truth is computed. The results of our algorithms are compared with the widely used N3 [5], AFCM [3], and EM based method [4].

The simulated data sets are obtained with the following settings: T1, T2 and PD modalities, slice thickness of 1 mm, 0%, 3% and 7% noise levels, and 20% and 40% intensity nonuniformity levels. As a preprocessing, the extra-cranial tissues were removed from all 3D volumes according to the ground-truth memberships of the tissues provided on the BrainWeb website. In order to get data sets with more severer intensity nonuniformity effects, we constructed the 60% intensity nonuniformity level by linearly scaling the range values of the ground truth to 0.70 … 1.30 as explained on the website, and then enforcing it on the volumes download with the different noise levels and with 0% intensity nonuniformity. Before computing the RMSE statistics, the multiplicative factor [5] is removed from the resulting bias field by minimizing the mean square distance between the result and the ground truth. Therefore, only the shape differences account for the errors.

We found that the chosen methods all perform very similarly on different imaging modalities. Therefore, we averaged the RMSE statistics over the three modalities. From the results shown in Fig. 2, we can see that our methods can improve the estimation accuracies relative to the standard methods. Moreover, our methods seem more robust to noise. Compared between the two new methods, the parametric method resists noise better but may produce larger errors when the nonuniformity is very severer. It is because a severer bias field may go beyond the representation ability of the model in Eq. (14).

Fig. 2.

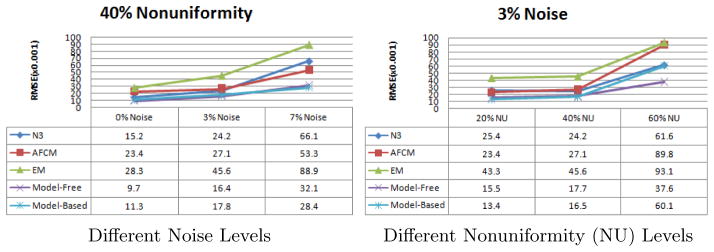
The statistics of Root Mean Squared Error (RMSE) in estimation of the bias field in the simulated MR brain data sets at different levels of noise and nonuniformity

4.2 Visual Evaluation

We also run our algorithms on real data: 9 MR brain volumes, 2 TEM images from the rabbit retina, and 5 CT lung volumes, for which the intensity nonuniformity artifacts can be visually perceived. Due to the lacking of the ground truth of the bias fields, we evaluate the results by visual inspections through observing the intensity profile on selected lines.

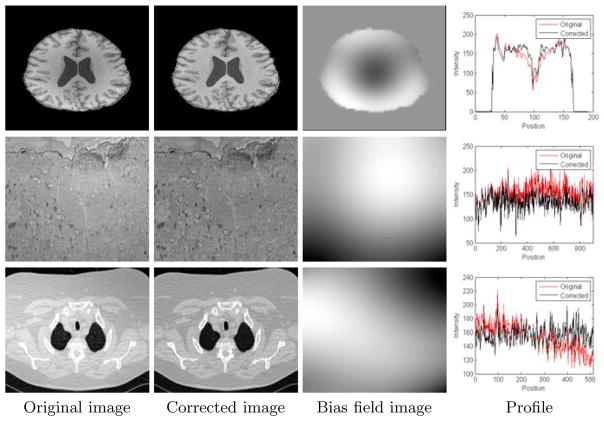
We found that both of our two new methods can efficiently correct the bias field in images from different modalities and of different imaged objects, resulting in flatter profiles. We put some results by the non-parametric method in Fig. 3.

Fig. 3.

Corrections of the bias field by our non-parametric method on one MR brain image (up), one TEM image (middle) from rabbit retina, and one CT lung image (down). The profiles are drawn on a horizontal line of the image.

5 Conclusion and Future Work

Based on the sparseness of the gradient distribution in medical images, we proposed a non-parametric approach and a parametric approach for the automatic correction of the intensity nonuniformity. They are easy to implement and remarkably accurate. Similar strategy has already been used successfully vignetting correction in [8].

Considering the fact that the sparseness property can be treated as a robust prior knowledge of an ideal image or even an ideal deformation field, our paper may also inspire several more works following the line of using this property in medical image inpainting, image segmentation, and image registration.