The effect of population structure on the rate of evolution

Abstract

Ecological factors exert a range of effects on the dynamics of the evolutionary process. A particularly marked effect comes from population structure, which can affect the probability that new mutations reach fixation. Our interest is in population structures, such as those depicted by ‘star graphs’, that amplify the effects of selection by further increasing the fixation probability of advantageous mutants and decreasing the fixation probability of disadvantageous mutants. The fact that star graphs increase the fixation probability of beneficial mutations has lead to the conclusion that evolution proceeds more rapidly in star-structured populations, compared with mixed (unstructured) populations. Here, we show that the effects of population structure on the rate of evolution are more complex and subtle than previously recognized and draw attention to the importance of fixation time. By comparing population structures that amplify selection with other population structures, both analytically and numerically, we show that evolution can slow down substantially even in populations where selection is amplified.

1. Introduction

The rate of evolution measures how quickly new traits can be established in a population. Typically, this is a function of three factors: mutation rate, population size and the fixation probability of new mutations [1–3], but there is increasing recognition that ecological influences, such as population structure [4,5] and the number of competing beneficial mutations [6–10] contribute additional layers of complexity.

The effect of population structure can be particularly strong. This is evident from theoretical studies of evolution on graphs, which show that fixation probability can be enhanced in certain spatially structured populations, compared with unstructured (i.e. well-mixed) populations. Within the category of structured populations, some spatial arrangements, for example, those referred to as ‘stars’, can significantly amplify the effects of selection [4]. This means that in populations with such structures, the fixation probability of beneficial mutations is greater than in unstructured populations of the same size, whereas the fixation probability of deleterious mutations is smaller than in equally sized unstructured populations. Given that a beneficial mutation has a higher likelihood of fixation in a star-structured population, it follows that the rate of evolution will be more rapid in populations with star structures [4].

Only spatially structured populations with specific structures show amplifying effects. Indeed, for the large class of population structures in which every individual has the same probability of replacement by an offspring from a neighbouring node, fixation probability is unaffected by population structure, as proved in the isothermal theorem [4]. This implies that there are many population structures where the rate of evolution ought not to differ between structured and unstructured populations.

The effect of population structure on the rate of evolution is of more than just academic interest. Evolution is often used in both directed and non-directed experiments to achieve particular endpoints, for example, in biotechnology [11,12]. Drawing upon graph theory, a selection experiment that aimed to deliver a catalytically efficient enzyme would have a greater chance of success in a star-structured population. Given opportunities provided by robot-driven manipulations, a selection experiment performed on a ‘super-star’ could be theoretically guaranteed to deliver to the experimenter the most efficient possible solution [4]. Population structures that amplify selection therefore have the potential to open new avenues of research.

Here, motivated by the need to understand the ecological context of evolutionary change more fully, we explore the dynamics of evolution in finite populations on different structures. While computational graph theorists have examined many subtleties pertaining to deme structure [4,13–20], and for frequency-dependent selection in particular [5,21–26], the broader issue of fixation probability and its relationship to the rate of evolution has received little attention.

Focusing first on star-structured populations we show that, whereas the fixation probability is amplified in such populations, the rate at which beneficial mutations go to fixation is significantly retarded, compared with well-mixed populations. We present a transparent and robust mathematical approximation that draws attention to underlying complexities and the role of relevant ecological factors. We also provide numerical examples for the rate of evolution in a lattice structure population in one- and two-dimensions. In both cases, we show that the fixation probability is not affected by the population structure, but the fixation time is. We argue that four primary factors are required in order to predict the rate of evolution: mutation rate, population size, the fixation probability of new mutations and time to fixation. Only under conditions where the mutation rate is vanishingly small can the influence of the fixation time, mediated by population structure, be neglected.

2. Background

The reference case for evolutionary dynamics on graphs is well-mixed populations: changes in fixation probability and fixation time are typically compared with corresponding quantities in unstructured populations. Moreover, the Moran process in well-mixed populations can be studied in great detail by analytical approaches [2,3,27–29].

Many population structures do not differ from the Moran process in well-mixed populations in terms of the fixation probability. An ingenious proof that all population structures in which all individuals have the same probability to be replaced by a neighbour, the so-called isothermal theorem, can be found in Lieberman et al. [4]. The same authors show that fixation probabilities can be very different from well-mixed populations in more complex graphs. The range of graph structures considered here is shown in figure 1.

Figure 1.

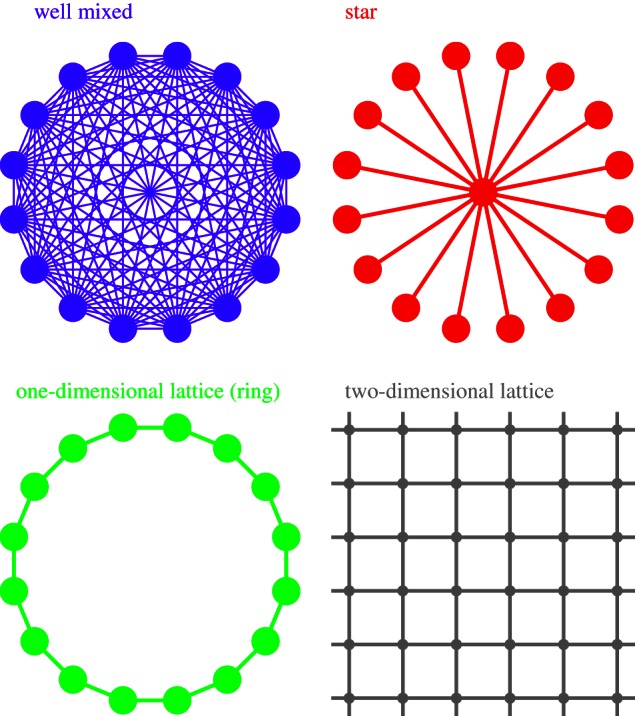
Representation of the four population structures considered in this study. Periodic boundary conditions are assumed for the two-dimensional lattice.

Population structures that increase the fixation probabilities of advantageous mutants, but decrease the fixation probabilities of disadvantageous mutants, are called amplifiers of selection. Similarly, population structures that decrease the fixation probabilities of advantageous mutants, but increase the fixation probabilities of disadvantageous mutants, are called suppressors of selection [4,30].

While fixation probability has been explored in detail on various graphs, the time taken for mutations to proceed to fixation has received considerably less attention. Numerical analyses have shown that the time to the fixation of a mutant is typically greater in population structures that amplify the intensity of selection, relative to well-mixed populations [4,15,18,24]. For special structures such as rings (one-dimensional lattices with periodic boundary conditions) and stars, interesting analytical results have been obtained [17].

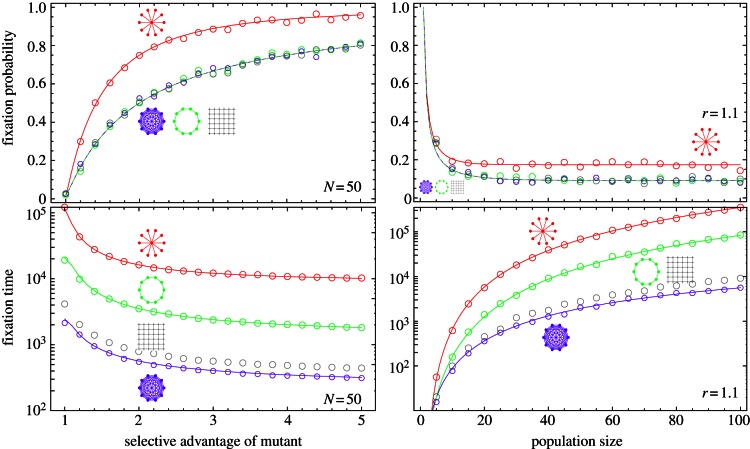
However, basing the idea that amplifying selection increases the rate of evolution entirely on fixation probabilities is problematic. Figure 2 illustrates that while a star-structured population increases the fixation probabilities of advantageous mutants, this process can take much longer compared with the same process in a well-mixed population.

Figure 2.

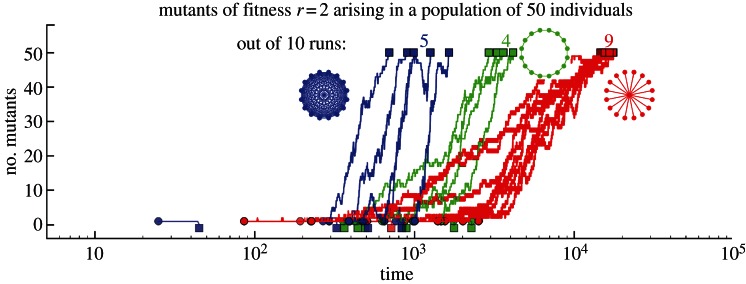
Typical trajectories (10 independent runs) for a population size of N = 50 for mutants with a twofold fitness advantage, r = 2. In the well-mixed population, the mutant goes to fixation 50% of the time. This is identical for the ring-structured population, but it rises to 75% in the star. The time to fixation, on the other hand, is substantially longer for structured populations: for the star, it takes approximately N times as long for either fixation or extinction (filled squares represent the times where a trajectory has reached either extinction or fixation of the mutants, filled circles show the points where new mutants arise).

Previously, it has been argued that strong amplification of selection requires large graphs and thus fixation times increase rapidly [4]. However, because the fixation times scale with the population size differently for well-mixed populations and graphs, this increase in fixation times becomes even more pronounced.

3. Fixation probabilities and fixation times

Let us first recall some properties of general birth–death processes, as this forms the basis for our analytical considerations. In these processes, only transitions to the neighbouring states are possible, which means in our case that the number of mutants changes at most by one. For arbitrary birth–death processes, there are exact expressions for the probability and time to fixation [3,27,31,32]. We denote T^±(j) for the probability to go from j to j ± 1 mutants in a single time step (we always assume that j = 0 and j = N are absorbing, T^±(0) = T^±(N) = 0, and that all other transitions are possible). The probability to go from l mutants to fixation (i.e. to N mutants) is given by

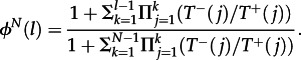3.1

The average time that this process takes starting from a single mutant is given by

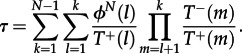3.2

Many other quantities can be computed for such a process, for example, the average time the process spends in each state before it reaches a boundary or the moments of the distribution of fixation times [2,27,33,34]. We also consider the probability that there are ever K mutants in the system, ϕ^K(1). For any birth–death process, this is obtained by making the state with K mutants absorbing, which leads to

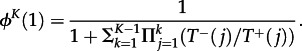3.3

Another quantity that we consider is the average time spent in a state, the so-called sojourn time. As this is straightforward to compute but somewhat technical, we refer to the literature for the concrete equations [27,33,34].

These equations can be used directly for the well-mixed population and the ring. The gist of our approximations for the star-structured population is to map the dynamics onto a birth–death process, such that we can use the same equations as above.

(a). Well-mixed populations

As a reference case, we consider a Moran process in a well-mixed population. The probability to select one out of j mutants with fitness r for reproduction (at random, but proportional to fitness) and a wild-type for death (at random) is given by

3.4

whereas the probability that a wild-type reproduces and replaces a mutant is given by

3.5

Because T⁻(j)/T⁺(j) = 1/r, the fixation probability simply becomes

3.6

a result well known from population genetics [1,2].

(b). Ring (one-dimensional lattice)

For the one-dimensional lattice, exact analytical results are possible, because there will always be a connected cluster of mutants. The probability to increase the number of mutants from j to j + 1 is given by

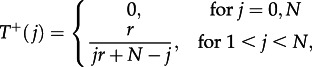3.7

whereas the probability to decrease the number of mutants from j to j – 1 is

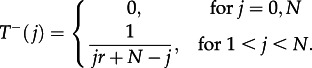3.8

Note that T⁻(j)/T⁺(j) = 1/r for all 0 < j < N. This implies that the fixation probability is the same as for the well-mixed population and that the probability to reach a certain number of states is not affected by this population structure. However, the average time to fixation does not depend on this ratio alone, but also on T⁺(j). Because T⁺(j) is typically of the order of 1/N and thus smaller than in a well-mixed population, fixation will take longer on this population structure. The exact values can be obtained from equation (3.2).

(c). Star-structured population

In Lieberman et al. [4], it has been shown that star-structured populations (figure 1) have a fixation probability which is given by the corresponding fixation probability of the well-mixed population equation (3.6), except that the fitness of the mutant r is replaced by r². This implies that the star is an amplifier of selection. The average fixation time for this population structure has been calculated exactly by Broom & Rychtár [17]. Here, we provide an alternative approximation which is easier to handle, because it allows mapping the dynamics that take place on the star to a birth–death process. This allows calculation of sojourn times and similar quantities based on the same approximation.

The transition probabilities necessary to change the number of mutant nodes can be separated into two cases. If the central node is not occupied by a mutant and there are j mutants in the leaf nodes, then the probability to increase the number of mutant leaf nodes from j to j + 1 is 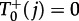(we denote the state of the central node by a lower index), because the wild-type nodes can only receive wild-type offspring from the central node. The probability to decrease j to j − 1, 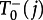, is the probability to choose the central node for reproduction times the probability that the offspring is placed in a mutant leaf node,

3.9

If there is a mutant in the central node, then the number of mutant leaf nodes cannot decrease, 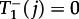, because they are only connected to the central mutant node. The probability that the mutant in the central node can place an offspring in a wild-type leaf node is

3.10

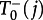and 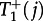are at most of the order of N^–1. In well-mixed populations (equations (3.4) and (3.5)), they are of the order of N⁰, which already implies that the fixation process on the star will be of the order of N⁻¹ slower than in a well-mixed population. The probabilities to switch the central node are given by

3.11

and

3.12

and these are of the order of N⁰ at most. Thus, for large N, the central node switches much faster than all other nodes. We can use this separation of time scales and assume that the central node is always in equilibrium to calculate the transition probabilities of an approximated birth–death process as an average (weighted by the relative probability that the central node is in the respective states),

3.13

and

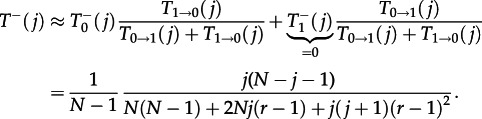3.14

Again, these quantitates are of the order of N⁻¹ smaller than the corresponding values in well-mixed populations. The ratio between the two transition probabilities, which determines the probability of fixation, is T⁻(j)/T⁺(j) = 1/r² here, whereas we obtain 1/r for a well-mixed population. This implies an amplification of selection on the star structure compared with the well-mixed population. For the fixation probability of a single mutant, we obtain

3.15

This is exactly the result given by Lieberman et al. [4]

Note that we have effectively reduced the population size by one, treating the central node separately. This must be taken into account when we look at fixation probability or fixation time based on the full equations (3.1) and (3.2). Figures 2 and 3 compare this approximation with numerical simulations, confirming the validity of our approximation.

Figure 3.

The probability (top) and the time (bottom) to fixation of a single mutant in different population structures depending on the fitness of the mutant (left) and the population size (right). Lines represent analytical results, symbols are computer simulations. The star increases the fixation probability (top) and also the fixation time (bottom) compared with the well-mixed population. The one-dimensional lattice (or ring) and the two-dimensional lattice lead to the same fixation probabilities as the well-mixed population, but they both increase the fixation time.

However, for the probability to ever reach K mutants, our approximation fails when K is small. Instead, the probability to ever reach K = 2 is

3.16

The probability ϕ³(1) can be obtained in a similar way. For the probability to reach more than three mutants, we can take the following approximation: in the term for the probability to reach K nodes, we use our approximation for the transition probabilities for all terms up to K – 2, but for the K – 1 term, we use the probability to increase the hub node rather than the approximated probability, which yields

3.17

Figures 3 and 4 illustrate that this approximation works very well for K ≥ 3.

Figure 4.

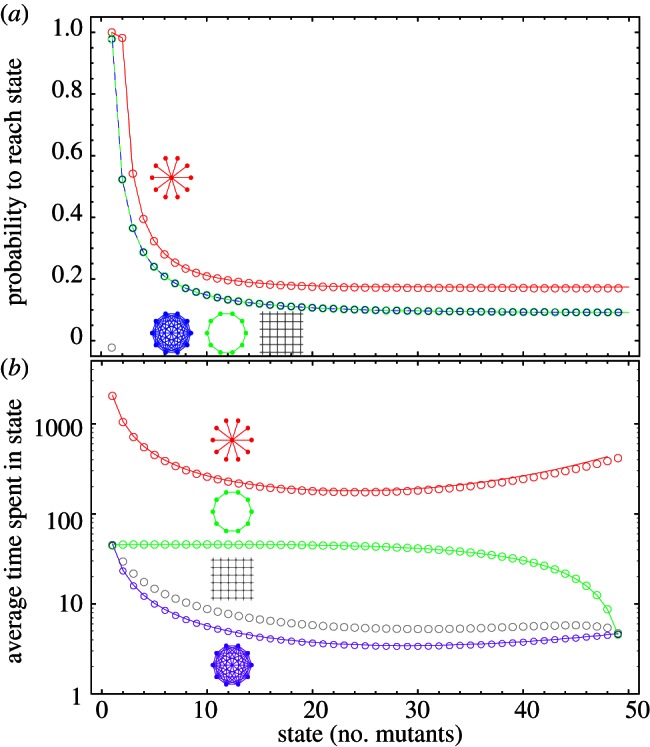
(a) The probability that the process starting from a single mutant ever reaches a certain number of mutants (state). Symbols are simulations, lines represent analytical results. For the star, different approximations are used for K ≤ 3 and K ≥ 3. On a star, there will be a second mutant with a very high probability, but the probability to reach three mutants drops substantially. (b) Average unconditional sojourn in a state with a certain number of mutants, i.e. the average time spend in this state before the mutant is either lost or takes over (r = 1.1, N = 50, simulation averages over 100 000 realizations).

(d). Two-dimensional lattice

For two-dimensional lattices, an initially connected cluster of mutants can break up during the process, which does not allow simple analytical considerations anymore. However, we include numerical results for this population structure in our comparisons, see figures 3 and 4.

Moreover, the fixation probability in such systems is still the same as in a well-mixed population, as a consequence of the isothermal theorem [4].

4. The effective rate of evolution

The rate of evolution is typically considered a function of the fixation probability, but not of fixation time. The underlying assumption is that the waiting time until a successful mutant appears is much larger than the time it takes for this mutant to sweep through the population. As illustrated in figure 2, although the time for a successful mutant to emerge is much smaller in a star graph, the time until the new mutant has reached fixation is substantially longer. Is it still meaningful to argue that the star graph has a higher rate of evolution in light of this illustration? We propose to consider the effective rate of evolution instead, which is the average of the rate of the appearance of a successful mutant and the rate of fixation of the mutant.

The average rate of rate-limited processes is the harmonic mean of the rates. In our case, there are two processes involved: the process until a successful mutant arises and the process of its fixation. The rate of appearance of new successful mutations is given by Nμϕ(1). The time for fixation is τ and thus the corresponding rate is τ⁻¹. Hence, the effective rate of evolution ρ should be

4.1

For μ → 0, this reduces to the usual rate of evolution, ρ = μNϕ^N(1). This simpler result is also a good approximation whenever 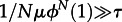or, equivalently, 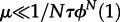. If new types fixate from ‘standing genetic variation’ instead (large μ), the process is limited by τ only (but in that case, mutant clones will typically no longer be independent, because several mutants start their way to fixation simultaneously).

For illustration, let us focus on neutral evolution. In a well-mixed population, we have ϕ^N(1) = N⁻¹ as well as τ = N(N − 1) for neutral evolution. Thus, the rate of evolution is

4.2

Usually, only the first term is considered to be of interest: the neutral rate of evolution equals the mutation rate. The second term is only relevant for sufficiently large μ, μ ≈ N⁻². On a star, we still have the same fixation probability under neutral evolution, but τ ≈ N(N − 1)², leading to

4.3

In this case, the usual approximation will fail for 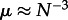, i.e. for much smaller μ than in a well-mixed population. Under selection, the issue becomes even more crucial, because the rate at which successful mutants appear increases: with larger fixation probabilities, the first term in the denominator of equation (4.1) decreases, increasing the influence of the second term (which also decreases with selection). This illustrates that the assumption of small mutation rates is a much more restrictive requirement in structured populations compared with unstructured populations.

5. Discussion

The rate of evolution is typically deduced from three factors: mutation rate, population size and the fixation probability of new mutations. Analyses here show that a fourth factor, namely the time for new mutations to fix, typically requires consideration when populations are structured.

Time to fixation is influenced by population structure, although its effects are complex and at times counterintuitive. Although fixation time and fixation probability arise from the same quantities they are not directly linked. This is most apparent when comparing well-mixed populations to structured populations with isothermal properties (i.e. a population where the probability of being replaced is identical at every position). For both well-mixed and isothermal structured populations, fixation probability is identical. However, the time to fixation can be strikingly different (figure 2).

An intuitive explanation appeals to the fact that transition probabilities are strongly affected by local population structure. In well-mixed populations, there is always the possibility that the number of mutants changes—this happens when the mutant is chosen for either birth, or death. By contrast, in structured populations, the number of mutants can only increase when a mutant at the boundary between mutant and wild-type domains is chosen for birth (and results in replacement of a wild-type individual)—most changes replace an individual by an identical individual from a neighbour within the same domain and thus have no effect on the frequency of the mutant. Given that the probability of a state change in well-mixed populations is usually greater than in structured populations, it follows that the time to fixation is faster in the former.

Decreasing transition probabilities by a factor slows down population dynamics, leading to an increase in the fixation time. However, this decrease in transition probability has no effect on the probability of fixation. In general, the probability of fixation (in structured and unstructured environments) is solely determined by the ratio of two probabilities: the probability to increase the number of mutants in each state and the probability to decrease the number of mutants. Changing both probabilities by a factor leaves their ratio unaffected and thus the probability of fixation remains the same.

The same reasoning holds for all isothermal population structures, for which this ratio—and hence the fixation probability—is exactly the same as in the well-mixed population. Examples for such structures include the ring and the lattice discussed here, but also many other regular population structures.

The issue becomes much more subtle for population structures that affect both the fixation probability and the fixation time. For example, the star structure affects the ratio of transition probabilities and this leads to a higher fixation probability for advantageous mutants. Such structures have been termed amplifiers of selection, because they increase the probability of fixation for mutants with the same selective advantage compared with well-mixed populations. This implies that it takes less time for an advantageous mutant to go to fixation. However, the process of fixation can take substantially longer in star-structured populations compared with well-mixed populations. Thus, the time for new mutations to fix can be much longer in a star-structured population (which amplifies selection) compared with a population structure that does not amplify selection, compare figure 2. The increase in fixation time counteracts the amplifying effects of the star.

Considerations of the rate of evolution are typically based on the assumption that mutations arise in succession. When mutation rates rise above a certain threshold, it is likely that different mutants will be simultaneously propagating in a population, and hence clonal interference may also play a role in the rate of evolution [7]. We have shown that, for a given mutation rate, population structure can substantially affect this threshold. For example, in a star-structured population, clonal interference will play a role for mutation rates that would generate negligible interference in a mixed population of the same size. Specifically, for neutral evolution in a well-mixed population, clonal interference becomes a factor if the mutation rate becomes significant compared with N⁻². For neutral evolution on the star, mutants take much longer to spread and hence the likelihood of multiple simultaneous mutants is higher. As a result, clonal interference arises when the mutation rate becomes significant compared with only N⁻³, that is, at a threshold which is a factor of N times smaller than it would be if the population were freely mixing.

In summary, we have shown that the time for new mutations to go to fixation needs to be included in considerations of the rate of evolution. Fixation probability and fixation time both depend on the same quantities but one does not follow from the other. In a star-structured population, the two work in opposition, such that the probability that a new mutation sweeps in is high, but the time taken to sweep is long. The net effect on the rate of evolution is a combination of both these effects.