Effects of the infectious period distribution on predicted transitions in childhood disease dynamics

Abstract

The population dynamics of infectious diseases occasionally undergo rapid qualitative changes, such as transitions from annual to biennial cycles or to irregular dynamics. Previous work, based on the standard seasonally forced ‘susceptible–exposed–infectious–removed’ (SEIR) model has found that transitions in the dynamics of many childhood diseases result from bifurcations induced by slow changes in birth and vaccination rates. However, the standard SEIR formulation assumes that the stage durations (latent and infectious periods) are exponentially distributed, whereas real distributions are narrower and centred around the mean. Much recent work has indicated that realistically distributed stage durations strongly affect the dynamical structure of seasonally forced epidemic models. We investigate whether inferences drawn from previous analyses of transitions in patterns of measles dynamics are robust to the shapes of the stage duration distributions. As an illustrative example, we analyse measles dynamics in New York City from 1928 to 1972. We find that with a fixed mean infectious period in the susceptible–infectious–removed (SIR) model, the dynamical structure and predicted transitions vary substantially as a function of the shape of the infectious period distribution. By contrast, with fixed mean latent and infectious periods in the SEIR model, the shapes of the stage duration distributions have a less dramatic effect on model dynamical structure and predicted transitions. All these results can be understood more easily by considering the distribution of the disease generation time as opposed to the distributions of individual disease stages. Numerical bifurcation analysis reveals that for a given mean generation time the dynamics of the SIR and SEIR models for measles are nearly equivalent and are insensitive to the shapes of the disease stage distributions.

1. Introduction

Mathematical modelling has proven to be an extremely powerful tool for understanding epidemiological patterns and predicting how demographic changes and control measures influence infectious disease dynamics [1–3]. The most commonly used framework for modelling transmission dynamics involves dividing the population into compartments based on disease status and using ordinary differential equations (ODEs) to specify flows between the compartments. For diseases that confer permanent immunity, the simplest case is the SIR model [1,4], in which the compartments represent susceptible, infectious and removed individuals, while the SEIR model also includes an exposed compartment, containing individuals who are in a latent stage (infected but not yet infectious). These simple models implicitly assume that the time an individual spends in each disease stage (e.g. latent or infectious) is drawn from exponential distributions [2,5], which are unlike real distributions of disease stage durations.

The dynamical effects of exponential versus more realistic distributions of stage durations have been explored extensively in the literature [6–12], which has revealed that changing the shapes of these distributions while keeping their means fixed can have a large impact on predicted dynamics. Consequently, it is important to re-evaluate any inferences drawn about real data from models that assume exponentially distributed stage durations. In this paper, we study the dynamics of a family of SIR and SEIR models with stage duration distributions that range from exponential, to realistically bell-shaped, to fixed. We investigate how the shapes of latent and infectious period distributions affect our predictions concerning epidemiological transitions (e.g. from annual to biennial epidemic cycles) and compare our results with conclusions previously made based on exponentially distributed models [13–15]. As an illustrative example, we apply our analysis to measles epidemics in New York City from 1928 to 1972.

1.1. The shapes of real distributions of disease stage durations

Many authors have estimated infectious period distributions by fitting standard probability distributions (e.g. normal [16–18], log-normal [19,20], gamma [9,21] or fixed [16,17]) to empirical data. For transmission modelling, a gamma distribution with an integer shape parameter—also known as an Erlang distribution—is strongly preferred on theoretical grounds: the Erlang distribution is equivalent to a sequence of independent and identically distributed exponential distributions [6,22–24], so compartmental transmission models with Erlang-distributed stage durations can be expressed as ODEs (as opposed to the integro-differential equations required to express compartmental models with arbitrarily distributed stage durations).

The Erlang distribution with shape parameter n and scale parameter nγ, Erlang (n, nγ), has probability density

1.1

The mean is 1/γ and the variance is 1/nγ².

The Erlang distribution is more restricted in shape than the general gamma distribution, but it is sufficiently flexible to provide a good approximation of realistic stage duration distributions. Figure 1 shows the probability density function of the Erlang distribution with mean 1/γ = 13 days (vertical line) and various shape parameters (n = 1, 2, 3, 5, 8, 20, 100).

Figure 1.

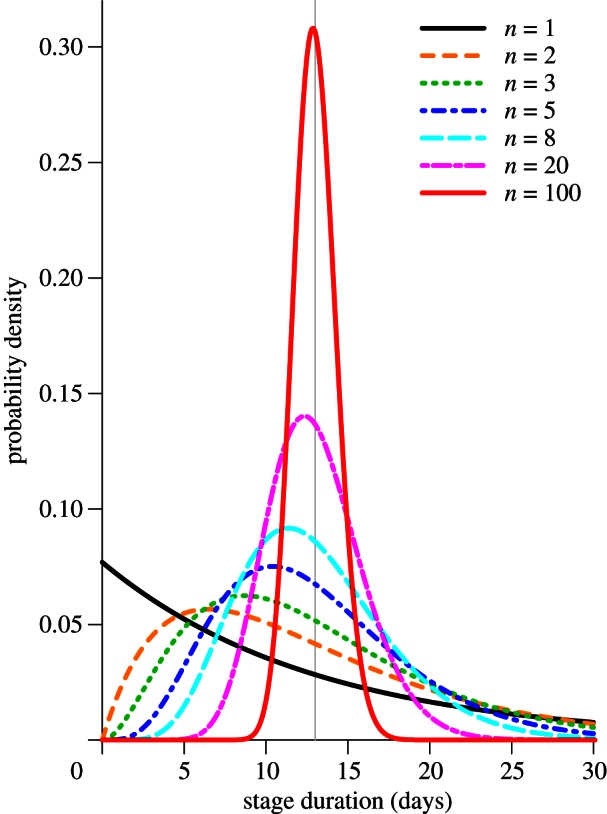
Probability density functions for several Erlang distributions with the same mean (13 days, marked with a vertical grey line) but different shape parameter n (see equation (1.1)). The most extreme cases are the exponential distribution (n = 1) and the Dirac delta distribution (n → ∞). (Online version in colour.)

We write SIⁿR and SE^mIⁿR to refer to the Erlang-distributed SIR and SEIR models, where m and n refer to the shape parameters of the latent and infectious period distributions, respectively. Thus, SI¹R (n = 1) and SE¹I¹R (m = 1, n = 1) denote the standard SIR and SEIR models with exponentially distributed latent and infectious periods. Estimated values of n and m can be inferred from appropriate clinical data and vary widely for different infectious diseases, for example, m = 2, n = 3 for SARS and m = 20, n = 20 for measles [9].

1.2. The Erlang-distributed epidemic models

In our analysis, we use standard Erlang-distributed SIR (equation (1.2)) and SEIR models [6,8–10,23,24].

1.2a

1.2b

1.2c

1.2d

Here, S, I and R are the numbers of susceptible, infectious and recovered (immune) individuals in the population. μ, β and γ are the rates of per capita death, transmission and recovery, respectively. μ quantifies death from ‘natural causes’ (disease-induced mortality is assumed to be negligible). β is the rate at which contacts between susceptible and infectious individuals cause new infections (per susceptible per infected). The term νN₀ denotes the number of births per unit time, where N₀ is the population size at a particular ‘anchor time’ t₀ and ν represents births per capita at time t₀, but not at other times (see also §§2.1 and 2.2 and electronic supplementary material, section ‘Models’). This term is particularly important, because secular changes in this birth rate can induce dynamical transitions [3,13–15]. In our formulation, the birth term (νN₀) is different from the birth term in typical SIR-based model formulation, which assumes that births balance deaths with birth rate being μN. We estimate νN₀ based on demographic data and do not assume that it scales with population size (e.g. we do not assume that the birth rate is μN).

In equation (1.2), the infectious stage is broken up into a sequence of n substages, each exponentially distributed with mean 1/(nγ). The full infectious period distribution is the Erlang distribution with shape parameter n and scale parameter nγ, Erlang(n, nγ).

Transmission of childhood diseases such as measles is strongly influenced by seasonal changes in contact rates among children [13,25]. We assume that the transmission rate varies sinusoidally over the course of a year,

1.3

where 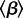is the mean transmission rate and α is the amplitude of seasonal forcing. (See the electronic supplementary material, section ‘Models’.)

A fundamental characteristic of an infectious disease is its basic reproduction number, which is the mean number of susceptible individuals infected by one infectious individual in a completely susceptible population [1]. Formally defining and interpreting 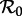in the presence of periodic forcing of parameters requires considerable mathematical care [26,27]; however, what is important for our purposes here is that the threshold for disease spread is determined by the more easily defined basic reproduction number for the time-averaged system [28]—i.e. the autonomous system in which β(t) is replaced by 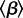—and this is what we shall always mean when referring to ‘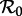’. Thus, 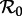is the product of the mean transmission rate 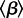(cf. equation (1.3)) and the mean duration of infectiousness T_inf, and an epidemic can occur only if 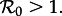The exact expression for T_inf for Erlang-distributed models is cumbersome (see the electronic supplementary material, section ‘Models’) but for typical respiratory infections—for which the duration of infection is much shorter than the average host lifetime 1/μ—it is always true that T_inf ≈ 1/γ and hence

1.4

The first factor here (νN₀/μ) does not normally appear in formulae for 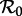because it is typically assumed that births balance deaths, and the population size is often absorbed into the transmission rate β (see the ‘Models’ section of the electronic supplementary material for a more formal discussion of this point). We assume that ν changes slowly enough that it can be regarded as constant for the purposes of defining 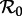at a given time.

Detailed descriptions of the SIⁿR and SE^mIⁿR models can be found in the electronic supplementary material, section ‘Models’.

1.3. Dynamics of epidemic models with Erlang-distributed stage durations

In the past 20 years, the SIⁿR and SE^mIⁿR models—and other more general models—have received a great deal of attention. Equilibrium stability analyses have been conducted on ‘unforced’ models that assume constant contact rates [6,7,29–32], and bifurcation analyses have been conducted on ‘forced’ models in which contact rates vary seasonally [6–12,33]. Lloyd [7] found that the biennial pattern observed in the SI¹R model is reproduced by the SIⁿR model but with much weaker seasonality. Nguyen & Rohani [10] found that complex dynamics of whooping cough could be understood based on the multiple coexisting attractors of an SE¹I⁵R model, whereas the simple SE¹I¹R model with the same mean latent and infectious periods always predicts an asymptotically annual cycle. Wearing et al. [9] argued that the traditional assumptions of exponentially distributed latent and infectious periods may lead to underestimation of the basic reproduction number, 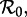and hence to underestimation of the levels of control required to curtail an epidemic.

The primary theme of recent work on SIⁿR and SE^mIⁿR models has been that the shapes of stage duration distributions can significantly affect the qualitative dynamics of infectious diseases. Given this, it is important to re-examine previous work that has attempted to explain observed disease dynamics based on SI¹R or SE¹I¹R models, and determine whether the conclusions of these previous studies remain valid when the analyses are repeated using models with more realistically distributed stage durations. Our particular focus in this paper is on epidemiological transition analysis, by which we mean predicting qualitative changes in epidemic dynamics induced by demographic and behavioural changes in the host population [3,13,15]. As an illustrative example, we analyse measles incidence in New York City for the period 1928–1972, which was first investigated by London & Yorke [25,34] and has been the subject of numerous studies over the past 40 years [13,15,35,36]. We also investigate whether the dynamics of a given SE^mIⁿR model can be approximated with an SIⁿR model.

We begin by describing the method of transition analysis in §2. In §3, we apply transition analysis, based on SIⁿR and SE^mIⁿR models, to measles dynamics in New York City from 1928 to 1972. We consider the role of the distribution of the disease generation time (as opposed to the latent and infectious periods) in §4 and summarize our results in §5.

2. Predicting epidemiological transitions

Many infectious disease time series display occasional, rapid changes in qualitative dynamics, such as transitions from annual to biennial cycles or to irregular dynamics [1,35]. Previous work has shown that these transitions appear to be driven by demographic and behavioural changes that induce bifurcations in the SE¹I¹R model [3,13,15]. We would like to know whether the qualitative inferences made previously based on the SE¹I¹R model remain valid when the analysis is repeated with more realistic SE^mIⁿR models.

Earn et al. [13] used the SE¹I¹R model to show that knowing the changes in birth and vaccination rates—or, more generally, changes in the rate at which susceptible individuals are recruited into the population—it is possible to predict the occurrence of bifurcations that change the period of epidemic cycles. We briefly revisit that argument here in the more general context of the SIⁿR model.

2.1. Theoretical motivation for transition analysis

In equation (1.2a), the factor ν was formulated as the birth rate but can be thought of more generally as the susceptible recruitment rate. Suppose that this rate changes to ν′, which might occur because the birth rate has changed or because we have begun to vaccinate a proportion p of the population (in which case ν′ = ν(1 − p)). To understand the dynamical effect of this change from ν to ν′, consider the following simple change of variables:

2.1

If we insert these expressions in equation (1.2) and solve the equations for the primed variables we obtain, for example,

2.2

That is, the equations for the primed variables are identical to the original equations (with the original susceptible recruitment term ν), but with the transmission rate changed from β to βν′/ν. Thus, the dynamical effect of a change in susceptible recruitment by a given factor is identical to the dynamical effect of changing the transmission rate by exactly that factor,

2.3

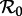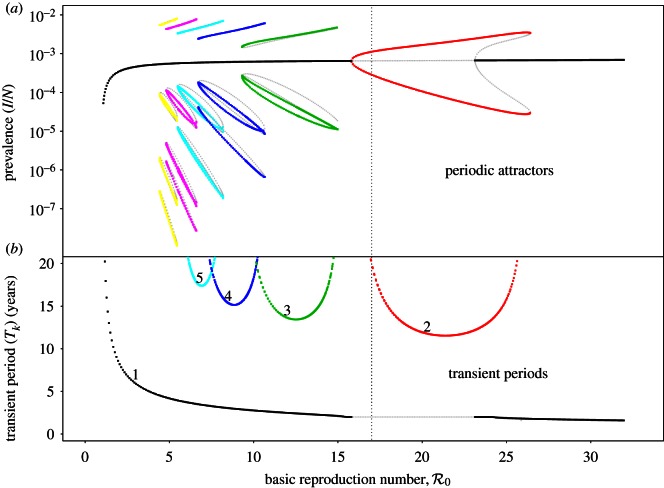
Consequently, we can use a bifurcation diagram with the transmission rate β, or equivalently the basic reproduction number (because 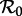is proportional to β), as the control parameter to predict transitions in dynamical behaviour induced by changes in susceptible recruitment rate. Figure 2 shows such a bifurcation diagram based on the sinusoidally forced SI¹R model (equation (1.2), n = 1) with parameters chosen to correspond to measles (and with an estimated value of 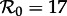at some given time, say t₀, marked with a dotted vertical line). If the susceptible recruitment rate was ν₀ at time t₀ and ν₁ at time t₁, then we would predict that at time t₁ the system would behave as if the basic reproduction number had changed by the factor ν₁/ν₀, i.e. the effective reproduction number at time t, is

2.4

Figure 2.

Asymptotic and perturbation analysis of the sinusoidally forced SI¹R model (equations (1.2), n = 1) parameterized for measles (γ⁻¹ = 13 days, ν = 0.02 yr⁻¹, α = 0.08). (a) Asymptotic analysis: the bifurcation diagram for the model with control parameter 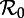. The ordinate shows the proportional prevalence of infection at the start of each year, so annual cycles are indicated by a single point at each 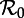, biennial cycles by two points, triennial cycles by three, and so on. Heavy curves correspond to stable cycles while light curves indicate unstable cycles. A dotted vertical line is drawn at 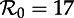, indicating the estimate of the basic reproduction number at the ‘anchor time’ t₀. Two types of bifurcations occur in this diagram: period doublings (also called pitchforks or flips) and tangent bifurcations (also called folds or saddle–node bifurcations). (b) Perturbation analysis: the natural period of damped oscillations (the transient period) onto each attractor, as described in step 2 of §2.2. The transient period curves are labelled according to the corresponding attractor in the (a): transient period of the annual attractor (1), biennial attractor (2), triennial (3) and so on. The light line indicates a region where the annual cycle is unstable and the period of repelled transients is phase-locked at exactly 2 years [37]. (Online version in colour.)

There is an important subtlety upon which our ability to predict transitions depends critically. In the equation for dS/dt (equations (1.2a)), the susceptible recruitment rate appears as a constant (ν does not depend explicitly on time t or population size N), and we use mass-action incidence (βSI) rather than standard incidence (βSI/N). If the susceptible recruitment term were taken to be νN rather than νN₀, and we were to use standard incidence then the variable change in equation (2.1) would have no effect (the differential equations are invariant to the scaling transformation given by equation (2.1)) and we would never predict dynamical transitions resulting from changes in the susceptible recruitment rate. One can debate on theoretical grounds whether one model formulation or another is most plausible biologically [38]; we favour our formulation because it leads to correct predictions concerning dynamical transitions [13,15]. We are interested in the effects of changes in ν over time, but the changes of interest occur slowly compared with the epidemic timescale, which is why we can treat ν as constant in the dS/dt equation.

2.2. The method of transition analysis

Given a time series of reported disease incidence or mortality (for a disease for which we have estimates of the mean latent and infectious periods), a full transition analysis proceeds as follows [13,15]. First, in order to clarify what needs to be explained, plot the disease time series together with its estimated frequency structure at each time point (e.g. Fourier power spectra for subsets of the full time series or, preferably, a wavelet spectrum for the full time series [39,40]). Second, for some ‘anchor time’ t₀ in the time series, obtain an estimate of the basic reproduction number 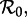preferably using data other than the focal time series (e.g. annual age-specific data [1]). Third, estimate the susceptible recruitment rate ν at each point of the disease time series and infer the effective reproductive number 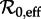at all times by inserting the estimated ν values into equation (2.4) (where ν₀ = ν(t₀) and ν₁ = ν(t) for an arbitrary time t). Fourth, identify time intervals during which ν is roughly constant (hence during which the dynamical features of the disease time series can be expected to be approximately stationary). Finally, based on the estimated value of 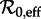in each of the ‘dynamically stationary time intervals’, predict transitions in qualitative dynamical behaviour (e.g. changes in the structure of the wavelet spectrum, especially the positions of peaks), as follows.

1. Asymptotic analysis (to identify the periods of attractors of the model, which are reached asymptotically) [10–15]: construct a bifurcation diagram with 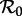as the control parameter, over a range of 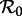that includes the value estimated for time t₀ and the full range of 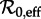determined via equation (2.4) (figure 2a). From this diagram, we can easily infer the periods of cyclical attractors of the system. We call these resonant periods because they are exact subharmonics (i.e. integer multiples) of the period of seasonal forcing (1 year). (See the electronic supplementary material ‘Bifurcation analysis of the seasonally forced SIR model using XPPAUT’ for a step-by-step guide to creating diagrams such as figure 2 using XPPAUT [41].)

2. Perturbation analysis (to estimate the periods of the transients associated with each attractor): over the same range of 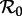as in the asymptotic analysis, plot the periods of the transients associated with—i.e. the periods of damped oscillations onto—each cyclical attractor (figure 2b). We call these non-resonant periods because they can take any real value and are not entrained by seasonal forcing. Non-resonant periods may be detected in observed epidemic time series, because transients can be sustained by demographic stochasticity [15,42]. Non-resonant periods can be calculated by linearizing about the fixed points and cycles of the model's 1-year-stroboscopic map [14,15]. If the period of a given attractor is k and the dominant eigenvalue of the associated k-cycle of the stroboscopic map is λk (which is complex for typical disease parameters), then the associated transient period is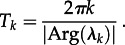

   2.5

3. Stochastic analysis (to estimate the relative importance of transient versus asymptotic dynamics): the wavelet spectrum has peaks at the most important periods in the time series (which we attempt to predict with steps 1 and 2) but also shows the magnitude of the peaks, which cannot be estimated by asymptotic and perturbation analysis of a deterministic model. The relative magnitudes of spectral peaks of observed time series can be estimated from spectra of simulations of stochastic realizations of the model, with the expectation that smaller population sizes (which are subject to greater demographic stochasticity) will stimulate more transient dynamics, leading to larger spectral peaks at non-resonant periods [3,15]. Because the stochastic analysis addresses the details rather than the main features of dynamical transitions, we do not conduct it in this paper (though we make occasional reference to stochastic effects). We note, however, that understanding these details is an area of very active research, and powerful analytical approaches for estimating power spectra for recurrent epidemic processes have been developed recently [11,43–45]. Ultimately, a complete transition theory would need to account for all the dynamical characteristics of stochastic epidemic models, which include alternation between asymptotic and transient behaviour [15], switching between different attractors [13,46], phase-locked cycles at one fixed period [37] and interactions with repellors [47].

In §3, we use the SIⁿR and SE^mIⁿR models to conduct transition analysis of the well-known New York City measles time series [34]. Our main question is: do we predict different transitions if we base our theoretical analysis on the SIⁿR rather than on the SI¹R model, or the SE^mIⁿR rather than SE¹I¹R model?

Another question that we will address is: can we approximate the dynamics of the SE^mIⁿR model using the SIⁿR model? This question is motivated by the fact that the dynamics of the SE¹I¹R model can be approximated using the SI¹R model. It is well-known that the equilibrium and stability properties (e.g. the period of damped oscillations onto the equilibrium) of the unforced SI¹R and SE¹I¹R models correspond if the mean infectious period in the SI¹R model is associated with the sum of the mean latent and mean infectious periods in the SE¹I¹R model [1, p. 668]. The measles bifurcation diagram shown in figure 2 for the sinusoidally forced SI¹R model is virtually identical to the term-time forced SE¹I¹R measles bifurcation diagram produced previously by Earn et al. [13]. Therefore, we analyse the SIⁿR model with mean infectious period 1/γ = 13 days (the sum of the real mean latent period of 8 days and the real mean infectious period of 5 days for measles).

3. Transition analysis using SIⁿR and SE^mIⁿR models

In this section, we use the well-known measles incidence time series for New York City (1928–1972) as an illustrative example with which to compare the results of transition analysis using SIⁿR and SE^mIⁿR models with stage duration distributions varying from exponential to fixed. The New York City measles data were originally digitized and studied by London & Yorke [25,34]. Previous transition analysis of these data [13,15] has been restricted to the pre-vaccine period (up to 1963). Here, we are able to extend our analysis to 1972 using vaccination data for 1963–1972 (see the electronic supplementary material, section ‘Vaccination level calculations’).

3.1. Description of the data

3.1.1. Reported incidence and inferred frequency structure

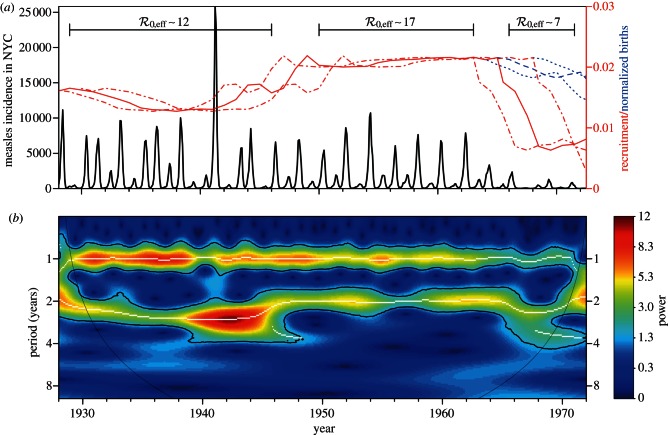
Figure 3a shows monthly reported cases of measles in New York City (together with estimated susceptible recruitment rate) and figure 3b shows the frequency structure of the data over time as a wavelet spectrum. Two spectral peaks are evident for the full duration of the time series, one at a period of 1 year and a second at a period that changes over time (2–3 years from 1928 to about 1946, exactly 2 years from about 1946 to 1965, and 2–4 years from about 1965 to the end of 1972).

Figure 3.

Measles in New York City, 1928–1972. (a) Monthly reported measles cases (heavy solid oscillating curve) and annual susceptible recruitment relative to the population size in 1960 (upper solid curve). Before the introduction of vaccination in 1963, annual susceptible recruitment coincided with annual births (dashed). The susceptible recruitment curve is shifted forward by 2 years to account for the delay between birth and entering the well-mixed population. Dotted-dashed curves show the susceptible recruitment rate without delay (2 years earlier than the solid curve) and with a delay of 5 years (3 years later than the solid curve). Similarly, the dotted curves after 1963 show the birth rate without delay and with a 5-year delay. The line segments at the top of panel (a) highlight time intervals with distinct effective 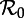, estimated with equation (2.4). (b) The wavelet power spectrum of the measles incidence time series (log-transformed and normalized to unit variance). The white curves show the local maxima of wavelet power (squared modulus of wavelet coefficients [48, p. 291]) at each time. The black curves indicate 95% confidence regions, estimated from 1000 bootstrapped time series [48, pp. 292–293]. Below the ‘cone of influence’ [48,49], the calculation of wavelet power is less accurate because it includes edges of the time series that have been zero-padded to make the length of the series a power of 2. The wavelet spectrum was computed using Matlab code kindly provided by Bernard Cazelles [48–50]. (Online version in colour.)

3.1.2. Estimated susceptible recruitment

Based on age-incidence and age-seroprevalence data for England and Wales (1950–1968), the basic reproduction number for measles has been estimated to be 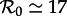in the pre-vaccination era [1, fig. 3.9 and 3.10, and table 4.1, p. 70]. Because, in New York City, the birth rate was approximately the same as in England and Wales (in the pre-vaccination era), we use this value as an estimate for 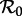in New York City in 1960, which we take to be our ‘anchor time’ t₀.

Measles vaccine was introduced in the United States in 1963 [51], so susceptible recruitment until 1963 can be taken to be associated entirely with births. However, newborns do not enter the well-mixed susceptible pool immediately, for two reasons: (i) maternally acquired immunity can take up to a year to wane [1, p. 50], (ii) before entering pre-school, children typically have much lower contact rates with other susceptibles. Hence, the impact of changes in birth rate on transmission dynamics is delayed, approximately by the time between birth and entering the well-mixed susceptible pool. We took this delay, τ_S, to be 2 years, but our conclusions are not sensitive to this parameter (e.g. taking it to be 0 or 5 years makes little difference (dotted-dashed and dotted curves in figure 3)). Note that τ_S should be less than 5 because the mean age at infection was about 5 years [1, fig. 8.1, p. 156]. Thus, we take the susceptible recruitment rate in 1960 to be the ratio of the number of births in 1958 (B(t₀ − τ_S) = 167 660) to the estimated population of New York City in 1960 (N₀ = 7 781 984), i.e. 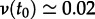[52]. At other times t,

3.1

where p(t) is the proportion of new recruits at time t who were vaccinated before entering the well-mixed susceptible pool. Note in equation (3.10) we use N₀, not N(t): recruitment is normalized relative to the population size at the ‘anchor time’ t₀ [13]. After 1963, the susceptible recruitment rate is substantially reduced by the introduction of vaccination (figure 3).

The birth and measles vaccination data that we insert in equation (3.1) are discussed in the electronic supplementary material, section ‘Vaccination level calculations’. The resulting annual susceptible recruitment rate is shown in figure 3a. There are three distinct periods during which the recruitment rate was roughly constant: 1929–1946 with ν ≈ 0.015, 1950–1963 with ν ≈ 0.02 and 1966–1971 with ν ≈ 0.008. Therefore, from equation (2.4), we estimate the effective reproduction number to be 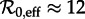for 1928–1946, 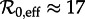for 1950–1963 and 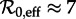for 1966–1971.

3.2. Asymptotic and perturbation analysis

Previous transition analyses of the New York City measles incidence time series were based on the SE¹I¹R model with mean latent and infectious periods τ_E = 8 days and τ_I = 5 days, respectively [13,15]. Given data from which the full latent and infectious period distributions can be estimated (rather than just their means), it would be sensible to fit Erlang distributions to the actual stage duration distributions and begin the transition analysis from the corresponding SE^mIⁿR model. For example, Wearing & Rohani [9] used measles case data from Gloucestershire, UK, for the period 1947–1951 [53] to estimate τ_E = 8 days with the shape parameter m ≈ 20 and τ_I = 5 days with the shape parameter n ≈ 20. Even in situations in which only the means of the stage duration distributions can be estimated, an SE^mIⁿR model (with m > 1 and n > 1) is likely to be a more accurate representation of reality than an SE¹I¹R model. So, for example, Keeling & Grenfell [8] considered an SE^mIⁿR model with m = 8 and n = 5, i.e. one day on average in each latent and infectious substage, as a reasonable improvement of the SE¹I¹R model.

Our primary question, however, is how the predictions of transition analysis vary as a function of stage duration distribution and whether the previous transition analyses based on the SE¹I¹R model have led us to correct or incorrect inferences. We therefore consider the full range of Erlang distributions for the latent and infectious periods and study the SE^mIⁿR model with 1 ≤ m ≤ ∞ and 1 ≤ n ≤ ∞. Note that we chose the mean latent and infectious periods to be fixed (1/σ = 8 days; 1/γ = 5 days). Because our general goal is to evaluate the robustness of dynamical inferences to model structure, we begin by analysing the simpler SIⁿR model with 1 ≤ n ≤ ∞.

3.2.1. Predictions of the SIⁿR model

3.2.1.1. Asymptotic analysis

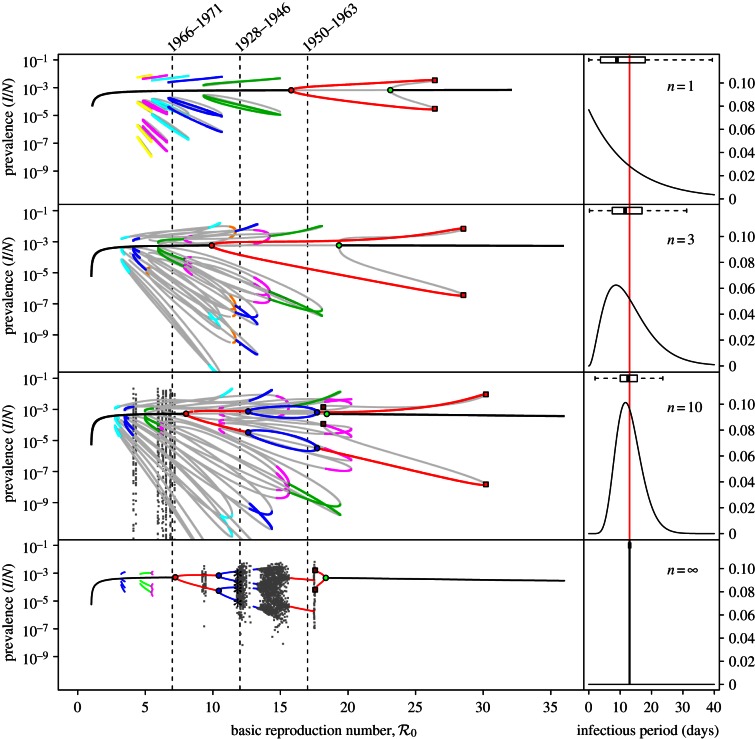
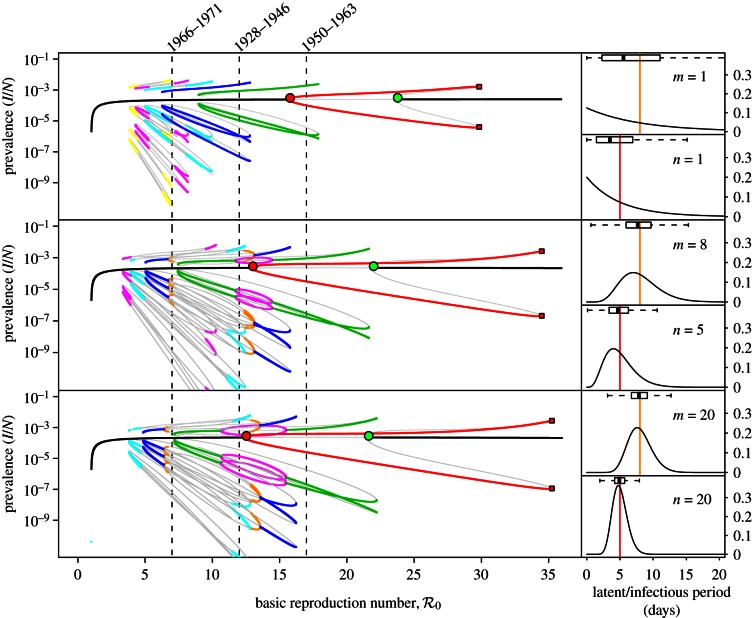
Figure 4 shows a sequence of SIⁿR bifurcation diagrams for various values of the shape parameter (n = 1, 3, 10, ∞) together with the corresponding distributions of the infectious period (each with a mean of 13 days). Stable branches are shown as heavy curves, whereas unstable branches are shown as light curves (in the online version, stable branches of different periods are shown in different colours). The case n = 1 is identical to figure 2a. As n increases from 1 to ∞, each of the branches undergoes further bifurcations. Chaotic attractors (superimposed in light grey) are evident for n = 10 and dominate for a substantial range of 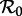for n = ∞.

Figure 4.

SIⁿR measles bifurcation diagrams as a function of 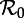for several values of the shape parameter of the infectious period distribution (n = 1, 3, 10, ∞), with other parameters fixed (mean infectious period 1/γ = 13 days, birth rate ν = 0.02 per year, seasonal forcing amplitude α = 0.08). Heavy curves show attractors. In the online version, attractors of different periods are drawn in different colours. Light grey curves show unstable branches. Circles represent period-doubling (flip) bifurcations while squares denote tangent (saddle–node) bifurcations of the main branch. Dashed vertical lines highlight 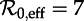, 12 and 17, which correspond to the estimated effective reproduction number for measles in New York City for the year ranges indicated, as in figure 3. Each right panel shows the corresponding probability distribution of the infectious period and a box plot showing the 5%, 25%, 50%, 75% and 95% quantiles of the distribution; a vertical line shows the mean infectious period (13 days). For finite n, the bifurcation diagrams were computed using standard continuation software (XPPAUT [41]), whereas the fixed-delay limit (n = ∞) was computed by ‘brute force’, i.e. by numerical integration of the delay differential equation (see the electronic supplementary material, equation S12) until convergence onto an attractor; hence, unstable branches are not shown in the limit n = ∞. Brute force bifurcation diagrams were also computed for finite n to reveal regions of chaotic behaviour which are shown in grey. (Online version in colour.)

The vertical dashed dark grey line at 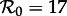in figure 4 corresponds to the estimated basic reproduction number for the year t₀ = 1960. The effective reproduction number is also estimated to be 17 throughout the 13 year period t = 1950–1963, because the birth rate did not change appreciably during this time and measles vaccine was not yet invented. The other two vertical dashed grey lines at 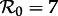and 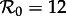correspond, respectively, to the estimated effective reproduction number during the periods t = 1928–1946 and t = 1966–1971, as computed from equations (2.4) and (3.1).

The bifurcation tree of the standard SI¹R model (n = 1) shows a biennial cycle for 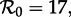coexistence of annual and triennial cycles for 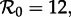and coexistence of annual and 4- and 5-year cycles for 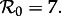Hence, the model correctly predicts the biennial pattern observed from 1950 to 1963 in New York City, but appears at first sight to predict incorrectly that there are multiple coexisting non-annual cycles at other times.

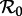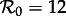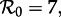However, in the ranges of for which multiple attractors coexist, and in particular for and stochastic simulations spend almost all of their time in the basin of the annual attractor [15]. Thus, the resonant period of 1 year observed in New York City from 1928 to 1946 and from 1966 to 1971 is also consistent with the SI¹R model.

Because of the series of bifurcations that occur rapidly as n is increased, the SIⁿR model for any n > 1 exhibits more complex dynamics than the SI¹R model and is harder to reconcile with the observed transitions in New York City measles. More often than the SI¹R model, the SIⁿR model with n > 1 has coexisting long-period stable cycles that are not observed in practice. As with the SI¹R model, stochastic simulations can be expected to remain primarily in the vicinity of the ‘primary’ attractor, but unlike the SI¹R model, the primary attractor of the SIⁿR with n > 1 often predicts the wrong resonant period for New York City measles. For example, for n = 10, the dominant attractor for 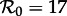has a period of 4 years (not 2 years), and the dominant attractor for 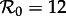has period two (not one). In the presence of noise, the 4-year cycle may be difficult to distinguish from a 2-year cycle, but the predicted 2-year cycle for 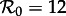is nothing like the measles data it ought to explain.

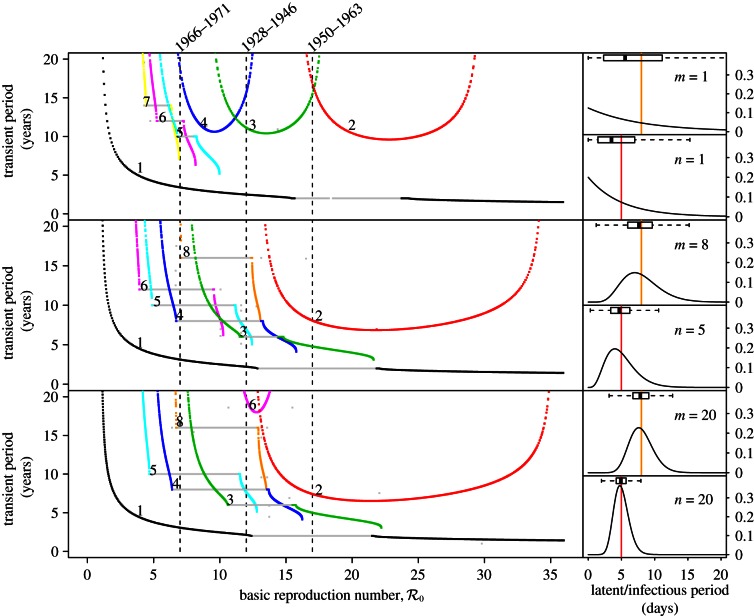
3.2.1.2. Perturbation analysis

Just as perturbing an orbit away from a stable equilibrium can induce transient, damped oscillations onto the equilibrium, perturbing an orbit away from a periodic attractor can induce transient, damped oscillations onto the stable cycle. Although more cumbersome to calculate for a non-equilibrium attractor [15], transient orbits in the vicinity of a periodic attractor have a well-defined characteristic period of oscillation.

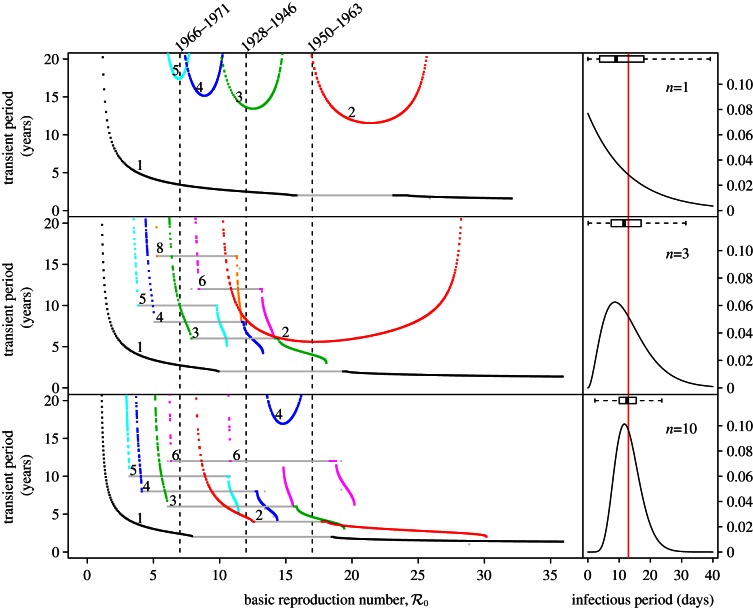
Figure 5 summarizes the transient dynamics of the SIⁿR models for n = 1, 3 and 10. For each periodic attractor, the non-resonant period, i.e. the period of damped oscillations onto the attractor, is plotted on the y-axis as a function of 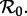The curves are labelled according to the period of the corresponding attractors in figure 4. Light grey lines are used in ranges of 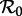where the corresponding periodic orbits are unstable; in these regions, the model displays phase-locked transient dynamics at the indicated period (i.e. the transient period is fixed and is the same as the period of the stable attractor), which is a prerequisite for a period-doubling bifurcation [37].

Figure 5.

Transient dynamics of the measles SIⁿR model for n = 1, 3 and 10 as a function of 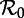. This figure complements figure 4. Each panel shows the transient periods associated with the periodic attractors. Transient period curves are labelled according to the period of the attractor that they reach asymptotically (and in the online version are coloured correspondingly); thus the curve labelled 1 shows the transient period associated with the annual attractor shown in figure 4. The light grey lines show ranges of 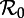where the associated periodic solutions exist but are unstable (i.e. are repellors rather than attractors). Dashed vertical lines correspond to values of 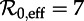, 12 and 17. As in figure 4, the right panels show the associated infectious period distribution. (Online version in colour.)

In the case of the SI¹R model, the non-resonant periods associated with all the non-annual attractors are too long to be observable in the New York City measles time series. The non-resonant period associated with the annual attractor does agree well with the wavelet spectrum shown in figure 3. For the SIⁿR models with n > 1, the non-resonant periods associated with multi-year attractors are shorter and often should be observable in principle. For example, for 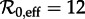the SI¹⁰R model (n = 10) predicts a transient period of 4.5 years. However, it is not observed in the incidence power spectra (figure 3). The lack of any indication of non-resonant periods associated with non-annual attractors in the wavelet spectrum for measles in New York City appears to cast further doubt on the usefulness of the SIⁿR model for measles.

3.2.1.3. Summary of SIⁿR transition analysis

Overall, from the point of view of measles transition analysis, the SI¹R model is just as successful as the SE¹I¹R model studied previously [13,15]. However, the SIⁿR model with n > 1 is far less successful; as n increases the dynamical structure of the model becomes more and more complex and the predicted resonant and non-resonant periods stray further and further from the observed spectral peaks in the New York City measles time series.

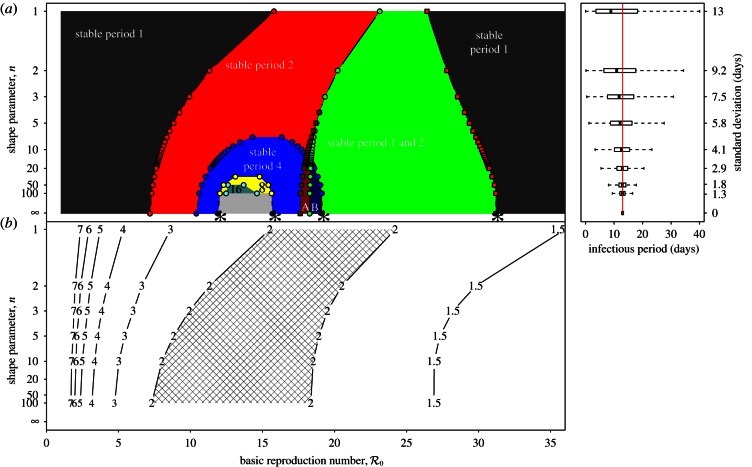
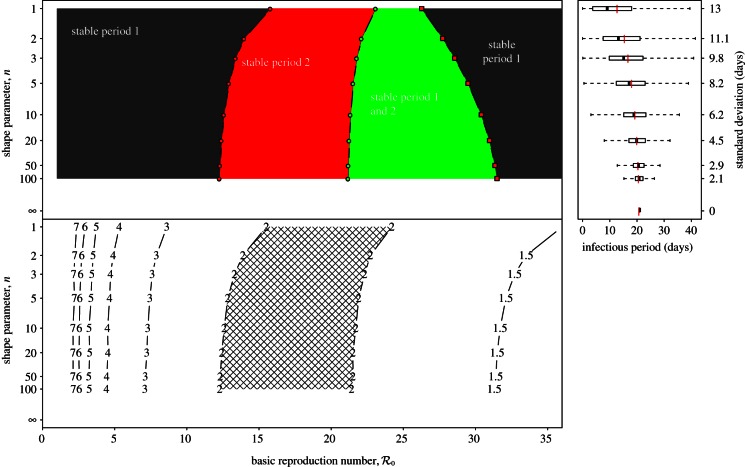
Figure 6a summarizes our asymptotic analyses of the full sequence of SIⁿR measles models (n = 1 to ∞) with a two-parameter 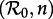bifurcation diagram for the main branch of the bifurcation tree in figure 4. The boundaries of the regions in figure 6 correspond to the major bifurcation points highlighted with circles (for flips) and squares (for saddle–nodes) in figure 4. As n → ∞ (i.e. as the infectious period distribution approaches a delta function), the main branch of the bifurcation tree undergoes a period-doubling cascade in the grey region (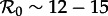). Figure 6b also describes the 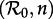plane, but shows contours of constant non-resonant periods associated with the annual cycle on the main branch (this is the most likely non-resonant period to be observable because it is the shortest; figure 5). The hatched region is characterized by phase-locked transient dynamics at a period of 2 years.

Figure 6.

Dynamical structure of the SIⁿR model with a mean infectious period 1/γ = 13 days. (a) Two-parameter (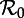 versus n) bifurcation diagram corresponding to the main branch of the one-parameter bifurcation diagrams shown in figure 4. Circles represent period-doubling (flip) bifurcations while squares denote tangent (fold) bifurcations as in figure 4. Regions are labelled according to the asymptotic dynamics on the main branch; the labels indicate which attractors are detected in each region of the 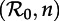plane: ‘stable period 1’ (a single annual attractor), ‘stable period 2’ (a single biennial attractor), ‘stable period 4’ (a single 4-year attractor), ‘8’ (a single 8-year attractor), ‘16’ (a single 16-year attractor), ‘stable period 1 and 2’ (coexistence of annual and biennial attractors), ‘A’ (coexistence of two distinct biennial attractors or coexistence of biennial and 4-year attractors) and ‘B’ (coexistence of annual and 4-year attractors). In the unlabelled light grey region below the region marked ‘16’, there are cascades of further period doublings that appear to end in chaos as n → ∞. The stars indicate bifurcation points that were estimated by extrapolation to n = ∞ rather than by direct calculations based on the fixed-delay model (see the electronic supplementary material, equation S12). (b) Contours of constant transient period (associated with the annual cycle) in the 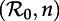plane (cf. black curves in figure 2b and in each panel of figure 5). In the hatched region, the transient period is phase-locked at precisely 2 years [37], whereas the transient period changes smoothly between the other contours. (Online version in colour.)

Note that because n is a discrete parameter it cannot be used as a continuation parameter in XPPAUT, hence we had to resort to separate continuation analyses for each n. The sequence of main-branch bifurcation diagrams that we constructed for the SIⁿR measles model (using 24 values of n from 1 to ∞) is shown in the electronic supplementary material, section ‘Main branch of the SIⁿR model’.

3.2.2. Predictions of the SE^mIⁿR model

We now apply precisely the same analyses to the more realistic SE^mIⁿR models. Figures 7–9 for the SE^mIⁿR models correspond to figures 4–6 for the SIⁿR models.

Figure 7.

SE^mIⁿR bifurcation diagrams as a function of 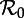for several values of the shape parameters of the latent and infectious period distributions. The mean stage durations are chosen to correspond to measles (mean latent period 1/σ = 8 days, mean infectious period 1/γ = 5 days). The other fixed parameters are the birth rate (ν = 0.02 per year) and the amplitude of (sinusoidal) seasonal forcing (α = 0.08). Heavy curves show attractors while light curves indicate unstable branches. In the online version, attractors of different periods are drawn in different colours. Circles represent period-doubling (flip) bifurcations while squares denote tangent (fold) bifurcations on the main branch. Dashed vertical lines highlight 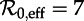, 12 and 17 associated with year ranges indicated in figure 3. The right-hand side panels show probability densities and box plots of the latent and infectious periods, with means highlighted by vertical lines and labelled according to the values of the shape parameters (m for the latent period distribution and n for the infectious period distribution). (Online version in colour.)

Figure 8.

Transient dynamics of the measles SE^mIⁿR model for (m,n) = (1,1), (8,5) and (20,20) as a function of 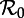. Each panel shows the transient periods associated with the periodic attractors shown in figure 7. Transient period curves are labelled according to the periods of the attractors they reach asymptotically (and in the online version are coloured according to the corresponding attractor in figure 7). Light grey lines indicate regions of 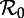where the corresponding periodic cycles exist but are unstable. Dashed vertical lines correspond to values of 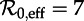, 12 and 17. As in figure 7, the right panels show the associated latent and infectious period distributions. (Online version in colour.)

Figure 9.

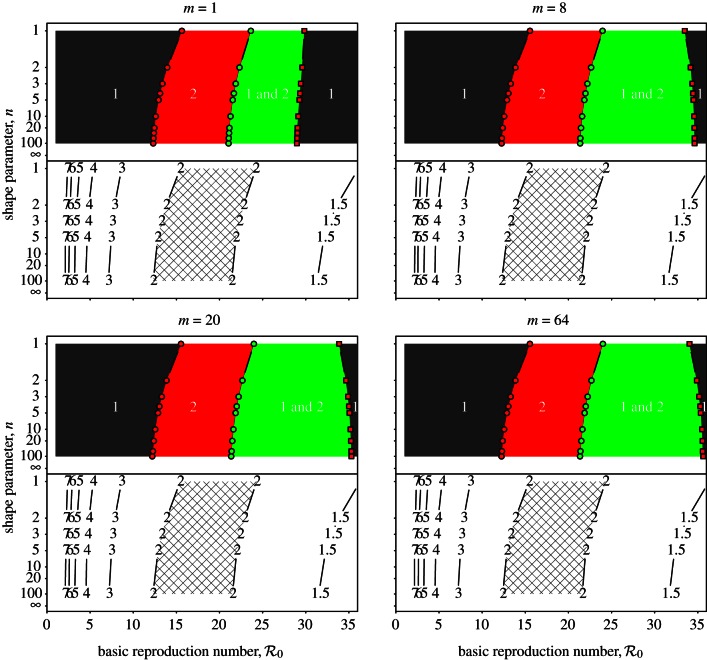
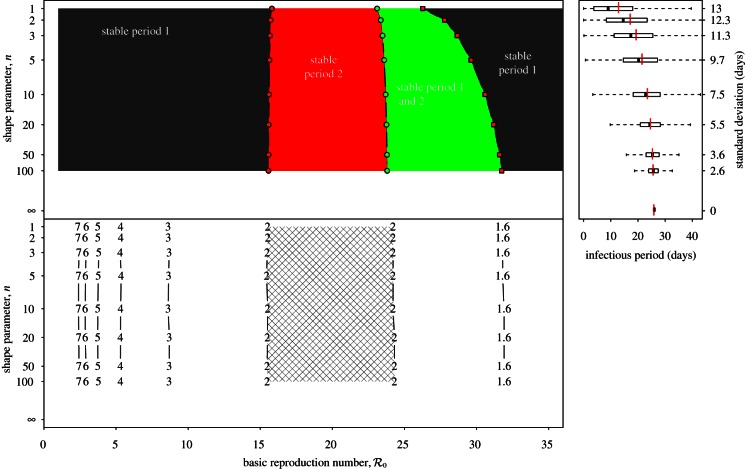
Two-parameter bifurcation diagrams and transient-period contour plots for the measles SE^mIⁿR model (mean latent period 1/σ = 8 days, mean infectious period 1/γ = 5 days). Each panel corresponds to different values of the shape parameter (m) of the latent period distribution. Regions are labelled according to the asymptotic dynamics on the main branch: ‘1’ (single annual attractor), ‘2’ (single biennial attractor), ‘1 and 2’ (coexistence of annual and biennial attractors). Other annotations are as in figure 6. (Online version in colour.)

Because we are now modelling both the latent and infectious stages directly, we can use accepted estimates for their mean durations (mean latent period 1/σ = 8 days, mean infectious period 1/γ = 5 days) [9]. In addition, we now have two shape parameters (m for the latent stage and n for the infectious stage). We examine several illustrative m,n values studied previously in the literature: m = 1, n = 1 [1,13], m = 8, n = 5 [8] and m = 20, n = 20 [9].

Figure 7 presents asymptotic analysis of the SE^mIⁿR model. The bifurcation structure of the model changes as m and n are increased, but the changes are less substantial than figure 4 shows as n is increased in the SIⁿR model. Figure 8 presents the results of perturbation analysis of the SE^mIⁿR model. Again, narrowing the stage duration distributions alters the transient periods, but less than figure 5 shows for the SIⁿR model.

The degree of dependence of SE^mIⁿR dynamics on stage duration distributions is clearest from the two-parameter bifurcation diagrams and transient-period contour plots shown in figure 9, which should be compared with figure 6 for the SIⁿR model. Regardless of the shapes of the stage duration distributions, the predicted resonant and non-resonant periods are very similar. Regardless of m and n, for 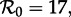we predict a resonant period of 2 years and an unobservably long non-resonant period (more than 7 years), for 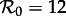we predict a 1-year resonant period and a 2–3 year non-resonant period, and for 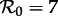we predict a 1-year resonant and 3–4 year non-resonant period. Consequently, transition analysis based on any of these SE^mIⁿR models is consistent with the New York City measles time series and wavelet spectrum (figure 3) as well as for the other measles time series considered previously [13–15].

We are led to conclude that transition analysis is robust to the shapes of the distributions of the latent and infectious periods (provided we include both).

4. The role of the generation time distribution in the dynamics of the SIⁿR and SE^mIⁿR models

It is surprising that narrowing the infectious period distribution in the SIⁿR model (apparently making it more realistic) makes the model worse as a predictor of dynamical transitions (figure 6). Because the effect of narrowing the shapes of the latent and infectious period distributions in the SE^mIⁿR is much smaller (figure 9), it is tempting to infer that the inclusion of a latent stage is essential for producing a robust model of the population dynamics of an infection that really does have a significant latent period. In fact, in this section, we identify the key factor that changes the structure of the SIⁿR bifurcation diagram as n gets larger, and we argue ultimately that any SIⁿR or SE^mIⁿR model is as good as any other from the point of view of transition analysis (including the SI¹R or SE¹I¹R models) provided they are parametrized appropriately.

When using an SIR rather than SEIR model, we chose the mean infectious period to be 13 days, the sum of the actual mean latent (8 days) and mean infectious (5 days) periods. Our motivation was that it is well known that the dynamics of the unforced SI¹R model is almost identical to that of the unforced SE¹I¹R model if this association is made. In particular, the period of damped oscillations about the equilibrium is then identical in the SI¹R and SE¹I¹R models [1, p. 668].

It is instructive to note that the mean disease generation time¹ in the SE¹I¹R model is equal to the sum of the mean latent and infectious periods. So, the association we have made between the mean infectious period in the SI¹R model and the sum of the mean latent and infectious periods in the SE¹I¹R model amounts to making sure both models have the same mean generation time. But for more general SE^mIⁿR models, the mean generation time is not equal to the sum of the mean latent and infectious periods. Indeed, the mean generation time in an SE^mIⁿR model is [55, eqn. 5.9]

4.1

From formula (4.1), we see that the mean generation time does not depend on the shape of the latent period distribution (only its mean 1/σ), but decreases as the infectious period distribution gets narrower (i.e. as n increases) if the mean infectious period is kept fixed. If the mean generation time is the key factor affecting the dynamics of the SE^mIⁿR model then we can now easily see why figure 6 shows so much more variation than figure 9: the mean generation time T_gen decreases from 13 to 6.5 days as n increases from 1 to ∞ in the SIⁿR model (1/σ = 0, 1/γ = 13 days), whereas T_gen decreases only from 13 days to 10.5 days as n increases from 1 to ∞ in the SE^mIⁿR model (1/σ = 8 days for any value of m, 1/γ = 5 days).

Figure 10 shows another version of the two-parameter (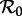 versus n) bifurcation diagram for the SIⁿR model. Rather than fixing the mean infectious period as in figure 6, for each n we set the mean generation time to be the same as that in the SE^mIⁿR model with the same value of n. The result in figure 10 is now negligibly different from each of the panels of figure 9 (some details are also discussed in the electronic supplementary material, section ‘Invariance of the period-doubling bifurcation point’).

Figure 10.

Two-parameter bifurcation diagram and transient-period contour plot for the measles SIⁿR model with the mean generation time chosen to be the same as in the SE^mIⁿR model for each value of the shape parameter of the infectious period distribution, n. Annotation is as in figure 6. Note the similarity between this figure and the SE^mIⁿR model diagrams in figure 9. (Online version in colour.)

Finally, in figure 11, we show yet another version of the 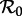versus n bifurcation diagram for the SIⁿR model, this time keeping the mean generation time fixed at 13 days for all values of n (in contrast to figure 10, where the mean generation time for each SIⁿR model was chosen to be the same as in the SE^mIⁿR model with the same value of n). Figure 11 makes clear that from the point of view of transition analysis—and to a large extent more generally for understanding the dynamics of SE^mIⁿR models—the key parameter that needs to be estimated is the mean generation time, not the mean latent or mean infectious period themselves and certainly not the shapes of these distributions. For a given mean generation time, it makes little difference which SIⁿR or SE^mIⁿR model we use, so we might as well work with the simplest, the SI¹R model.

Figure 11.

Two-parameter bifurcation diagram and transient-period contour plot for the measles SIⁿR model with fixed mean generation time, T_gen = 13 days. Annotation is as in figure 6. Note that the main period-doubling bifurcation point from annual to biennial cycle occurs for approximately the same value of 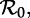regardless of the shape (n) of the infectious period distribution. The bottom panel shows that the transient period associated with the annual cycle is almost exactly the same for all values of n, i.e. this transient period is almost independent of the shape of the generation time distribution. (Online version in colour.)

5. Discussion

We set out to determine whether the results of previous ‘transition analyses’ of recurrent epidemic patterns of childhood diseases [3,13,15] were robust to the assumed shapes of the latent and infectious period distributions (which were taken to be exponential in previous work). We focused on measles and undertook a systematic analysis of the sequence of SIⁿR and SE^mIⁿR models for measles, and concluded that for a given mean generation time, transition analyses based on any SIⁿR or SE^mIⁿR model will lead to the same predictions for measles. Consequently, transition analyses of measles dynamics can be safely conducted using the very simplest SI¹R model. It is important to emphasize, however, that the mean generation time must be estimated correctly for this to work; in particular, it is not true that the real mean generation time is the sum of the mean latent and infectious periods.

The key graph that establishes that SIⁿR dynamics are nearly invariant for measles, if the mean generation time is fixed, is figure 11 (where the mean generation time is set to 13 days). In future work, we will construct the equivalent graph for a sequence of mean generation times that covers the range of typical recurrent infectious diseases, in order to determine whether transition analyses of other diseases can also be safely conducted with the simple SI¹R model. There is also considerable scope for analytical developments that complement our numerical analysis and build on previous analytical work associated with the role of the generation time distribution [56–59].

Consistent with previous work [6,7,10], we found that if we fix the mean infectious period (rather than the mean generation time) then narrowing the infectious period distribution (which reduces the mean generation time) leads to more complex dynamics. Previous work has also investigated the stochastic dynamics of SIⁿR and SE^mIⁿR models and examined characteristics such as the critical community size for disease persistence [6,12]. In future work, we will re-examine inferences concerning the stochastic dynamics of these models in light of the now-evident importance of the mean generation time for their deterministic dynamics.