Span efficiency in hawkmoths

Abstract

Flight in animals is the result of aerodynamic forces generated as flight muscles drive the wings through air. Aerial performance is therefore limited by the efficiency with which momentum is imparted to the air, a property that can be measured using modern techniques. We measured the induced flow fields around six hawkmoth species flying tethered in a wind tunnel to assess span efficiency, e_i, and from these measurements, determined the morphological and kinematic characters that predict efficient flight. The species were selected to represent a range in wingspan from 40 to 110 mm (2.75 times) and in mass from 0.2 to 1.5 g (7.5 times) but they were similar in their overall shape and their ecology. From high spatio-temporal resolution quantitative wake images, we extracted time-resolved downwash distributions behind the hawkmoths, calculating instantaneous values of e_i throughout the wingbeat cycle as well as multi-wingbeat averages. Span efficiency correlated positively with normalized lift and negatively with advance ratio. Average span efficiencies for the moths ranged from 0.31 to 0.60 showing that the standard generic value of 0.83 used in previous studies of animal flight is not a suitable approximation of aerodynamic performance in insects.

1. Introduction

The efficiency of lift production, span efficiency, significantly influences the limits of performance of all flying animals and has wide ranging implications for ecologically important variables such as maximum range of flights between feeding, maximum load lifting capacity and peak acceleration during manoeuvres.

An ideal wing generating lift in the optimal way, i.e. with the least amount of induced drag, does so by deflecting the oncoming airflow downwards uniformly across the span [1,2]. The reason this configuration is the most efficient is simplest to understand when examining the equation for kinetic energy, E_k = mv²/2, where m is mass and v is velocity. If the downwash behind the wing is non-uniform, but the same momentum is generated, p = mv, then any lower downwash velocities along the span need to be compensated for by higher velocities somewhere else. Owing to the squared velocity term in the kinetic energy equation, the cost of generating the higher velocities exceeds the gain of generating the lower velocities elsewhere. Thus, any deviation from a uniform downwash will be associated with an extra cost in the form of increased induced drag and thereby an increased power requirement from the flight muscle. By quantifying the deviation from uniformity of the downwash distribution for a given wing, the inviscid span efficiency, e_i, can be calculated [2,3]. This value is the ratio of the ideal power requirement to the actual power required for any given lift and ranges from 0 to 1, where 1 corresponds to the ideal case with uniform downwash. As an example, a wing with e_i = 0.5 would require twice the power of the ideal one to generate the same amount of lift. The span efficiency of a flapping wing is determined by a combination of its shape and kinematic pattern. From theory, we expect wing loading and aspect ratio (AR) to affect span efficiency as well as wingbeat frequency or perhaps more relevantly, advance ratio, which includes wingbeat frequency [4–6].

To date, the value of span efficiency, or its reciprocal, the induced drag coefficient, k, has been largely unknown and so has often been fitted rather than measured when modelling animal flight (typically k has been set to a value between 1.1 and 1.2, corresponding to e_i = 0.91 and 0.83 [3–7]). More recently, span efficiency has been calculated based on measurements of the flow generated by flying animals. It is a performance metric suitable for interspecific comparison but, to date, there are insufficient data for controlled tests, and the species selected are too taxonomically diverse to determine the mechanistic basis for the observed variations in their efficiency factors. In sum, only two species of insects [8–10], two species of birds [11,12] and two species of bats [13] have been measured. One method for calculating span efficiency from the wakes of flying animals was established and described in detail by Bomphrey et al. [8], and the method was further developed and adapted for time-resolved analysis by Henningsson & Bomphrey [9]. Henningsson & Bomphrey [9] measured both instantaneous values throughout the wingbeat cycle and multi-wingbeat averages of span efficiency in the desert locust (Schistocerca gregaria, Forskål) based on flow visualizations made using high-speed stereo particle image velocimetry (stereo-PIV).

Using the same method, here we test several factors that are predicted to determine an animal's span efficiency by studying the wakes of six species of hawkmoths (table 1) selected to provide a range of wingbeat frequencies, wing loading and preferred flight speeds. We make use of the fact that our test species are all hawkmoths and retain similar gross morphological characteristics, e.g. wing AR and second moment of area [14]. This allows us to test across the range of body sizes while controlling, in the main, for the effect of shape which is known to also have an effect on span efficiency. Our moths are all hovering nectarivores found in open woodland or woodland-edge habitats and all but one (Deilephila elpenor, L.) are migratory. The selected species are shown to scale in figure 1, ranging in wingspan from 40 to 112 mm, in mass from 0.2 to 1.97 g, in wing loading from 0.49 to 1.22 kg m⁻² and in wing beat frequency from 20 to 51 Hz.

Table 1.

Morphological details and flight speeds of the hawkmoths used in the experiments.

species	individual	mass (g)	wingspan (mm)	wing area (mm2)	wing loading (kg m−2)	aspect ratio	flight speeda (m s−1)	Reynolds numberb
Hemaris fuciformis	1	0.20	41	242	0.83	6.94	1.33	519
	2	0.20	39	238	0.84	6.41	1.43	577
Macroglossum stellatarum	1	0.33	45	379	0.88	5.42	1.5	834
	2	0.31	40	365	0.93	4.80	1.5	834
Hyles euphorbiae	1	0.91	67	905	1.01	4.93	2.1	1890
	2	0.80	58	708	1.12	4.68	2.2	1790
	3	0.95	66	781	1.22	5.51	2.1	1653
Deilephila elpenor	1	1.00	71	893	1.12	5.63	1.45	1209
	2	0.70	65	808	0.87	5.29	1.45	1189
Sphinx ligustri	1	1.48	89	1400	1.04	5.64	1.8	1894
Manduca sexta	1	1.97	112	1400	1.02	6.55	3.2	3621
	2	1.64	108	1900	0.88	6.28	3.1	3529
	3	0.89	98	1800	0.49	5.32	3.2	3918

^aThe flight speed used in the experiments, based on measured preferred flight speed.

^bReynolds number at the flight speed used in the experiments and using mean chord as characteristic length and standard kinematic viscosity at 20°C (ν = 15.11 × 10⁻⁶ m² s⁻¹).

Figure 1.

The six species of hawkmoth to scale showing the size range and the similarity in wing planform.

2. Material and methods

2.1. The hawkmoths

The selected species are broad-bordered bee hawkmoth (Hemaris fuciformis, L.), hummingbird hawkmoth (Macroglossum stellatarum, L.), spurge hawkmoth (Hyles euphorbiae, L.), elephant hawkmoth (D. elpenor, L.), privet hawkmoth (Sphinx ligustri, L.) and tobacco hawkmoth (Manduca sexta, L.). From here on, this is the order that will be referred to when results are given for the different species. Morphological details of the hawkmoths are presented in table 1.

Pupae were obtained from breeders (World Wide Butterflies, UK; Lepidoptera Breeders Association, UK and Department of Biology and Biochemistry, University of Bath, UK) and kept in an enclosure at 22°C and 50 per cent humidity until emergence. Following emergence, individuals were given at least 24 h to allow for expansion and drying of the wings and to develop motivation for foraging prior to flight in the wind tunnel. Individuals were chosen for experiments if they exhibited signs of general good health, such as undamaged wings and good free-flight abilities. Prior to flight, the moths were rigidly tethered on the ventral side of the thorax using cyanoacrylate glue to a brass shaft (2.5 mm diameter) which could be clamped into a mount in the test section of the tunnel. This tethering location allows uninhibited fluid flow over the dorsal surface of the body (where the wings attach to the thorax) and does not restrict the movement of the wings. The 2.5 mm diameter tether shaft is small in comparison with the wingspan and has little effect on vertical velocities measured in the moth wake since the wake from the shaft is largely two-dimensional with velocity fluctuations owing to vortex shedding appearing principally in the horizontal plane.

Before commencing wind tunnel experiments, three to five individuals of each moth species were flown in free flight in an indoor flight arena to measure their preferred flight speeds. The flight arena is a 2 × 3 × 1.5 m room painted white along three walls. Two synchronized and calibrated high-speed cameras (Photron SA3: 500 fps, 1024 × 1024 px, Photron Ltd, UK) film bouts of free flight, and from the stereo-sequences, three-dimensional flight trajectories of the moths were reconstructed. Trajectories were filtered beneath wingbeat frequency, and the average flight speed was calculated using numerical differencing of the positional data (cf. [15]). The mean of the modal flight speeds, of three to five sequences for each individual within the species, was taken as the preferred flight speed of that species and used for setting the wind tunnel speeds during the tethered PIV experiments. Preferred flight speeds for the different moths are presented in table 1.

Wind tunnel experiments for each individual were performed within a day and typically over the course of 4–5 h. The wing condition of the moths was monitored continuously throughout the experimental session, and the moths were fed periodically with a honey solution (honey and water, 1 : 10). The body angle (defined as the angle between the oncoming flow and the head to tip-of-abdomen line) was adjusted to approximately 15° based on estimates from the free-flight experiments.

2.2. Particle image velocimetry

The wind tunnel was seeded with a mist of olive oil droplets generated by a compressed air seeding generator (LaVision UK Ltd, UK). The seeding particles were illuminated using a 10 mJ dual cavity pulsed laser (Litron LDY-300PIV, Nd : YLF, 527 nm, Litron Lasers Ltd, UK). The laser beams were spread into a 2 mm thick sheet using −20 mm cylindrical lens and directed from above such that the sheet was normal to the freestream. Images of the illuminated seeding particles were captured over a sampling area of 100 × 100 mm behind the flying moths using two high-speed CMOS-sensor cameras (Photron SA3: 2000 fps, 1024 × 1024 px, Photron Ltd) fitted with macro lenses (Sigma 105 F2.8 EX DG) mounted on Scheimpflug adapters (LaVision UK, Ltd).

Cameras and laser were operated using DaVis v. 7.2.2 software and synchronized by a high-speed controller (LaVision UK, Ltd) at a rate of 1000 image pairs per second. The system was post-triggered by a single communal TTL signal and each recording capture 1361 image pairs (limited by camera buffer size). The two cameras were calibrated using the calibration procedure in DaVis v. 7.2.2 and a 105 × 105 mm calibration plate (type 11, LaVision UK, Ltd). The calibration was further refined after recording using the DaVis self-calibration routine, which applies a correction to the calibration data that account for small misalignment of the calibration plate and the laser sheet at the time of calibration.

Measurements were taken with the moths positioned 4.4 ± 0.8 (mean ± s.d.) mean chord lengths upstream of the light sheet. At this position, none of the insects appeared in the background of the PIV images, and therefore no masking was required prior to processing. This distance was chosen based on a study on wake development in the same wind tunnel (J. T. Horstmann, P. Henningsson, G. K. Taylor, A. L. R. Thomas, R. J. Bomphrey 2012, unpublished data) indicating this to be a distance far enough for the wake to contract and for vorticity to roll up into the tip vortices but not so far that the wake becomes twisted or deformed to any large degree. Pure contraction of the wake does not introduce error in the measurement of lift in the method we use because, owing to conservation of momentum, a contraction will also be associated with a corresponding increase in velocity. Span efficiency is also unaffected by contraction because it is a measure of the shape of the induced flow distribution irrespective of the length of span. Deformation (e.g. twisting of the wake), on the other hand, may introduce errors in both lift and span efficiency estimates because it can modify the orientation of the flow to the point where it ceases to be representative of its orientation at the time of creation. Despite our efforts to minimize the effect of wake deformation, it cannot be completely ignored as a potential source of error but it may be reasonable to assume that the effect is small in this dataset, because the measurement plane is close to the trailing edge of the wings. The effect of energy dissipation in the wake from the time of generation to the time of recording is assumed to be negligible since this duration was, on average, 27 ms in our experiments (average distance of 0.054 m divided by average speed of 2.0 ms⁻¹ across all moths), and it can be shown that the energy dissipation of a vortex is 1 per cent over a period of 54 ms at Re = 4500 [16].

The span of all moth species, apart from the largest, M. sexta, fitted within the measurement area so that the complete wake width was captured including both wingtip vortices. The wakes of the M. sexta were recorded from one half of the animals and later mirrored to create a representation of the full wake with an assumption of kinematic and aerodynamic symmetry.

Raw images were pre-processed by subtracting a sliding minimum over three frames to remove any stationary elements in the images (e.g. reflections or uneven lighting). After filtering, the images were used for calculating vector fields by multi-pass stereo cross-correlation with decreasing interrogation window size from 64 × 64 (two passes, 25% overlap) to 16 × 16 (two passes, 50% overlap). The PIV calculations were performed using the graphical processing unit module of DaVis v. 8.0.8. Post-processing of vector fields involved deletion of erroneous vectors (vectors having larger magnitude than twice the neighbourhood root mean square, r.m.s.), filling up of empty spaces by interpolation and a 3 × 3 smoothing.

Freestream velocities were recorded for every set of experiments, and the mean and r.m.s. of the velocities were calculated over 100 vector fields from each background sequence. Root mean square across the 100 vector fields was 0.20 ms⁻¹ and can be viewed as an estimate of the average error of the velocities in the dataset, grouping together the effect of spatial variation in velocities, wind tunnel turbulence and PIV vector calculation errors.

2.3. Data analysis

The method used here to extract downwash distributions from the wake of a flying insect has been described in detail previously by Henningsson & Bomphrey [9], and the reader is referred to this paper and to [2] for its theoretical foundation, so only the most salient features and modifications will be described here. The centre position of the wingtip vortices in every third vector field within a sequence was manually digitized using custom-written Matlab software (MathWorks Inc., Natick, MA, USA). After both left and right wingtip vortex trajectories were recorded for a full sequence, they were plotted and their common centre of rotation was recorded to represent a notional common wing hinge. The wingtip vortex positions for the remaining frames were estimated by using shape-preserving cubic interpolation of the recorded positions. Taking one sequence of 1361 measurements and comparing its interpolated results with those where every frame had been manually digitized resulted in a mean underestimate of lift and span efficiency of less than 5 per cent. Using the two locations of the wingtip vortices together with the location of the common centre of rotation, a V-shaped transect was drawn through the vector fields and the velocity vectors closest to this line were extracted. These vectors were considered representative of the induced flow distribution along the span. In order to sample the full width of the wake, tails were added to the transect to ensure that velocity vectors outboard of the wingtip vortex core centres were captured. The tails were sufficiently long that measured induced flow magnitudes at the most distal part had decreased to values comparable with the estimated noise level.

The resultant-induced flow velocity transects were used to calculate the instantaneous lift and span efficiency for each vector field according to the method described in the electronic supplementary materials.

Phase-averaged lift and span efficiency was calculated by standardizing the duration of each wingbeat period based on the inverse of the wingbeat frequency (dominant frequency in the vortex vertical coordinate). Finally, a generic wingbeat of lift and span efficiency was calculated for each species by averaging across the phase-averaged wingbeats calculated for each individual.

Mean span efficiency was calculated for each sequence as the ratio between the total ideal-induced power (the power an optimal wing would need to create the measured lift) and the real induced power (the power the real wing required) according to

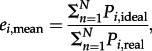2.1

where N is the total number time steps of one wingbeat, standardized to N = 100.

3. Results

3.1. Induced flow distribution

This study is based on six hawkmoth species, comprising 13 individuals. In two species, three individuals were sampled, in three species, two individuals and in one species one individual (table 1). For each individual across all species, an average of 103 ± 55 (mean ± s.d.) wingbeats were sampled. The total dataset contained 1307 wingbeats and 34 025 informative vector fields.

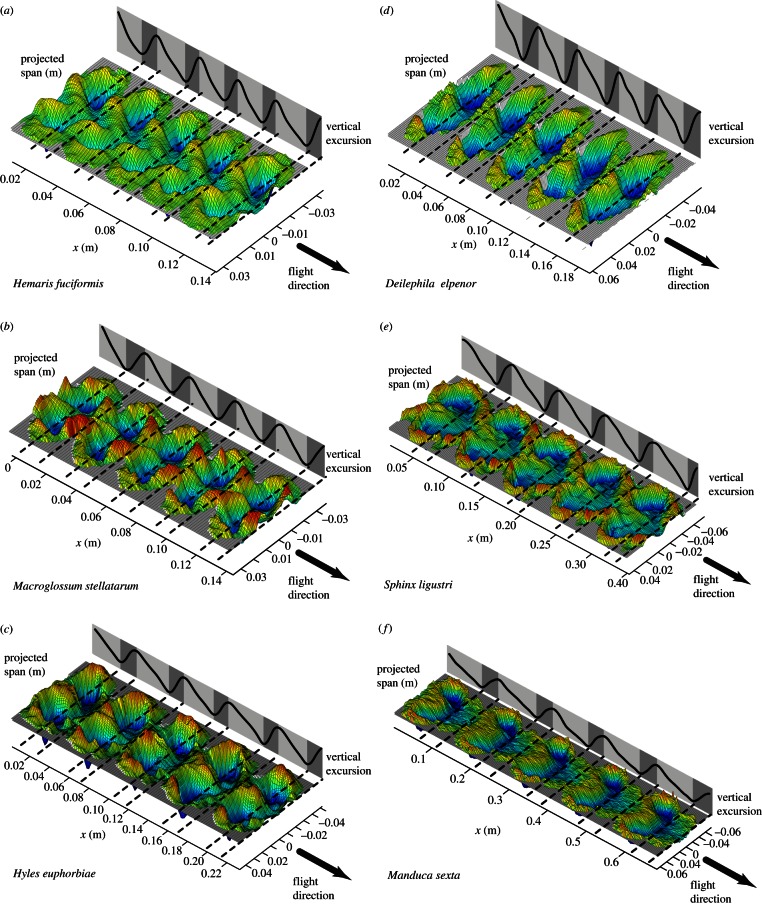
The induced flow measured for the six moth species can be visualized in an easily interpreted way by compiling each instantaneous transect measurement and plotting them stacked with spacing based on flight speed (according to the Taylor hypothesis [17], but see §4 for details). Figure 2 shows, as an example, five consecutive wingbeats taken from a single typical sequence of each species. The mean wingbeat frequency of the six different moth species was 46 ± 3.4 (N = 4), 48 ± 1.6 (N = 6), 44 ± 2.5 (N = 4), 41 ± 2.0 (N = 3), 27 ± 0 (N = 2) and 22 ± 3.0 (N = 6) Hz. N-values, means and standard deviations correspond to total number of sequences per species. With a repetition rate of 1000 Hz of the PIV system this resulted in, on average, 22, 21, 23, 24, 37 and 45 vector fields captured per wingbeat. The wingbeat frequencies as measured from the free-flight experiments on a different set of individuals were 65 ± 4.6 (N = 9), 55 ± 2.3 (N = 7), 42 ± 2.6 (N = 9), 41 ± 2.6 (N = 9), 25 ± 0.1 (N = 3) and 22 ± 0.7 (N = 6). N-values correspond to total number of sequences per species; on average, three individuals examined per species.

Figure 2.

(a–f) Examples of induced flow track from five consecutive wingbeats of each of the six species (x = V × dt, where V is the freestream velocity and dt is the time between measurements). Both the relief and the colour represent velocity magnitudes, with shades in blue/cyan representing downward velocities corresponding to positive lift and shades in red/yellow upward velocities corresponding to negative lift. These are scaled to the individual plots for clarity, so that colour shades range from min-to-max velocities. The solid line projected onto the far side of the plot shows the mean vertical excursion of the two wingtip vortices with light-grey-shaded sections showing downstroke and dark grey upstroke. Dashed lines mark the instances of stroke reversal.

A few general features are prominent across the size range. As expected, the induced flow spanwise distribution is not perfectly uniform at any instance over the wingstroke for any of the moths, and all plots show upwash outboard of the wingtip vortex core. Furthermore, it is also clear that all our moths induce upwash behind the body during the early downstroke, albeit to a varying degree. Most prominently, a universal feature is the generation of strong downwash during the latter stage of the downstroke through stroke reversal and into the beginning of the upstroke. For all moths, the remainder of the upstroke is a period of greatly reduced lift generating induced flow, if any, and at some points even some upwash in the wake indicates negative loading on the wing and negative lift (figure 2).

3.2. Span efficiency: instantaneous and average

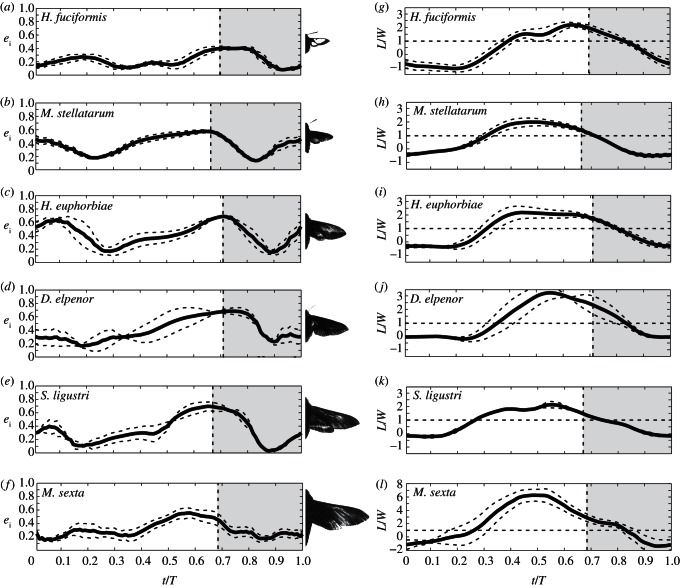
Span efficiency was found to vary considerably within the wingbeat cycle in all moth species. The phase-averaged time history of span efficiency for each species, beginning at pronation, is plotted in figure 3a–f. In all cases, span efficiency begins at a low level (typically less than 0.3), until about mid downstroke, when it starts to rise. The peak in span efficiency occurs, in all cases, around the end of the downstroke and is on average e_i = 0.60 ± 0.11 (mean of all species ± s.d., N = 6).

Figure 3.

Span efficiency (a–f) and normalized lift (g–l) over time through the phase- and species-averaged wingbeat of each species beginning at pronation. Solid curves represent the average and dashed curves represent standard error of the mean. Vertical dashed lines show the transition from downstroke to upstroke, and grey area denotes the upstroke. Horizontal dashed lines show L/W = 1, which is when the lift generated is equal to the weight of the animal.

Mean wingbeat-averaged span efficiency across individuals and sequences, as calculated according to equation (2.1), for the six moth species was e_i = 0.31 ± 0.038 (N = 4), 0.46 ± 0.067 (N = 6), 0.51 ± 0.036 (N = 4), 0.60 ± 0.019 (N = 3), 0.41 ± 0.049 (N = 2) and 0.46 ± 0.11 (N = 6), respectively (N-values, means and standard deviations correspond to total number of sequences per species). As one might expect, magnitude of peak and average span efficiency typically correlated with each other (p < 0.001, R² = 0.58), so that higher peak values are associated with higher average values, but it is not always the case. The most striking example of this is S. ligustri which has a peak of 0.70 (the second highest) but an average of only 0.41 (the second lowest; figure 3e).

3.3. Lift: instantaneous and average

The time history of normalized lift (lift divided by weight, L/W) over the generic phase-averaged wingbeat for each species is shown in figure 3g–l. The pattern is rather similar between species. All show very little or sometimes even slightly negative lift at the beginning of the downstroke. The upstroke/downstroke ratio is approximately 0.7/0.3 and for all six species, it takes until about t/T ≈ 0.25 before lift builds up. The peak in lift occurs approximately at t/T ≈ 0.5 in most cases. Lift is still generated in excess of the weight of the animal into the upstroke until t/T ≈ 0.8 by all species. The mean weight support across all moth species, individuals and sequences was L/W = 1.02 ± 0.49 (mean ± s.d., N = 25).

3.4. What morphological and kinematic features determine span efficiency in hawkmoths?

The average span efficiency (calculated according to equation (2.1)) is a measure of overall efficiency of lift production and was used as the characteristic value for each individual when testing for factors that influence span efficiency. As span efficiency is determined solely by the shape of the induced flow distribution normal to the incident flow, wake width (determined by wing span), velocity magnitudes (determined by body mass) and flight speed have no effect. The following parameters of interest were tested: normalized lift (L/W), wing AR, wing loading (Q = W/S, where S is wing planform area) and advance ratio (J = V/2αfR, where α is wingbeat amplitude in radians, f is wingbeat frequency and R is root-to-tip wing length, here approximated as semispan, b/2; [4]). The parameters were analysed separately as general linear models in PASW Statistics v. 18 (SPSS Inc., Chicago, IL, USA). Mean span efficiency was set as a dependent factor and the different parameters, in turn, as covariates. Significance level was set to p ≤ 0.05 and adjusted by Bonferroni correction to p ≤ 0.013 for the four individual tests. The results show that two factors have a significant effect on span efficiency: normalized lift (p = 0.007, R² = 0.28 of complete model, slope = 0.078) and advance ratio (p = 0.004, R² = 0.31 of complete model, slope = −0.202). Scatter plots are presented in figure 4.

Figure 4.

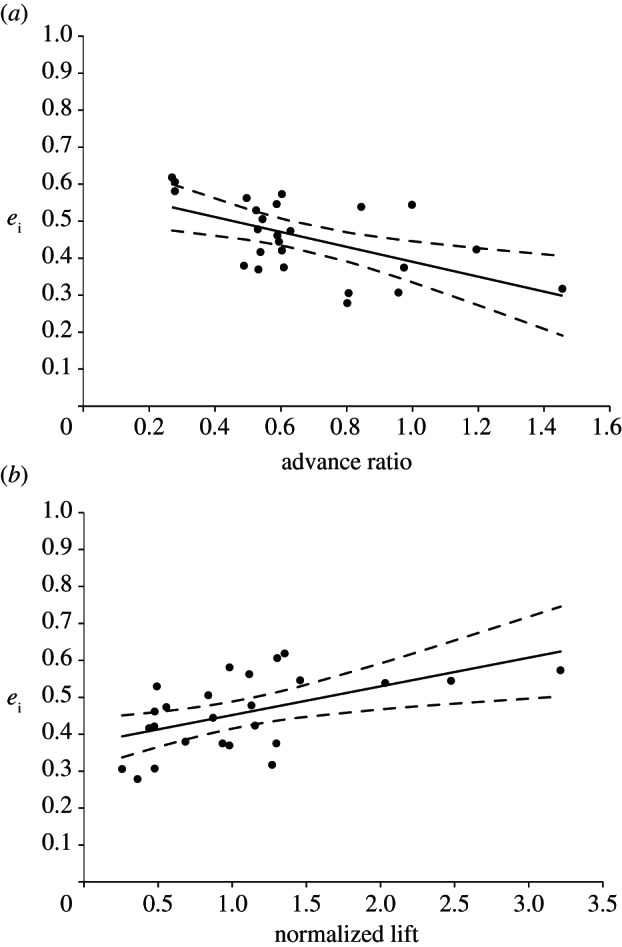
The two parameters that correlate with span efficiency (e_i). (a) Advance ratio, J, is negatively correlated with e_i (e_i = −0.202 J + 0.592, R² = 0.31). (b) Normalized lift, L/W, is positively correlated with e_i (e_i = 0.078 L/W + 0.374, R² = 0.28). Solid lines show the least-squares regression, and the dashed lines show the 95% CI.

To further investigate the effect of these two significant parameters, post hoc tests were carried out with the individual identity of each moth included in the model as a categorical fixed factor to account for the expected similarity within individuals and added before the parameter (type I sums of squares). The slopes remained similar for each, although the fit of the model increased for both parameters: for normalized lift, slope = 0.136, p < 0.001, R² = 0.93 of complete model and for advance ratio, slope = −0.0232, p = 0.022, R² = 0.86 of complete model.

4. Conclusion and discussion

4.1. Simplifying the complexity of animal wakes

Animal flight in general, and flapping flight in particular, is challenging to study because of its highly complex and time-variant nature. The forces that are created vary greatly, both in magnitude and direction, within the short duration of a wingbeat. In most cases, the wakes of animals incorporate several distinctly different vortex elements, such as wingtip and wing root vortices (e.g. craneflies [18]; bees [15]; bats [19]; flycatchers [11]; swifts [20] and blackcaps [21]). Using PIV, it is possible to capture these vortex elements as they are shed behind the flying insect. Over the past decade, this method has been adopted as a standard procedure for studying the aerodynamics of animal flight. However, owing to the limitations in laser power and repetition rate, coupled with the high wingbeat frequency of the study animals, time-resolved reconstructions of wakes have only been possible for the past few years [22]. Among flying animals, insects tend to have among the highest wingbeat frequencies and, to date, only one previous study has shown time-resolved wake measurements using a PIV system with a repetition rate of 1 kHz [9]. Figure 2 illustrates how the induced flow distribution varies over time and because the plots show both time and space on the x-axis, they are generated under the assumption of the Taylor hypothesis of frozen, homogeneous, turbulent wakes [17]. In reality, the wake will gradually deform as it travels downstream from its origin (cf. [23]), and therefore, the representation is to be viewed as a record of the time-dependent variation of induced flow and not as a representation of the time-dependent topography of the wake as it evolves.

The method used in the paper [9] is the foundation of the method used in this current one. One of the goals was to establish a method of reducing the complexity in the wake in order to quantify simply the aerodynamic performance of a range of animals, in this case using span efficiency as the metric of interest. Span efficiency only reflects induced drag and so other forms of drag are ignored (i.e. parasite and profile drag). However, it describes the efficiency of lift production and because lift is, in general, greater than thrust in flight, it is one of the most influential variables on the overall flight efficiency. Analytical estimates for the relative contribution to the uncertainty in calculation of total mechanical power rank span efficiency as the third most important factor behind wingspan and body mass which are both readily measured to a high degree of accuracy [24]. Moreover, because it focuses on lift production alone, it is also a more valuable measure of the performance of the wing per se and can therefore give design guidelines for the development of wings for flapping wing micro air vehicles.

4.2. Span efficiency in relation to lift

Examining the time history of instantaneous lift and span efficiency over the course of the wingbeat shows a phase lag between the magnitude of lift and span efficiency (figure 3). In most cases, the peak in span efficiency is phase-shifted behind the peak in lift with a lag of approximately 20 per cent of the wingstroke period, so that the peak in lift occurs during the second half of the downstroke, and the peak in span efficiency occurs close to supination. Unlike the desert locusts, where span efficiency plateaus for a large portion of the wing stroke [9], the moths instead show a more notable peak in span efficiency. Span efficiency in locusts starts to rise almost perfectly in synchronization with the rise in lift at the beginning of the downstroke, whereas for moths there appears to be a lag. A fundamental difference between locusts and hawkmoths is that, while they are all four-winged animals, the moths are functionally two-winged because the fore- and hindwings are overlapping and beating together as one single wing surface. The locusts beat the fore- and hindwing with a slight phase shift and might therefore potentially be able to control the generation of downwash to a greater extent. A study of other four-winged insects would allow us to examine if this holds true.

This difference may also be due to the strength of wing root vortices. In all the hawkmoths, clear wing root vortices were present at the beginning of the downstroke. This is not surprising, because hawkmoths typically have a relatively wide thorax in relation to their wingspan. Several studies of animal wakes have shown the presence of wing root vortices and they seem to form either as an effect of the body disrupting the downwash profile or by petiolation of the wing planform. Two striking examples are the bumble-bee [15] and the cranefly [17]: in both cases, the left and right wings generate almost completely independent wakes (cf. [25]). Wing root vortices have a detrimental effect on the uniformity of downwash distribution and consequently span efficiency. In the case of the moths, where the root vortices are prominent, it may imply that it takes longer (farther into the downstroke) before the circulation around the wings increases to a level high enough to bridge the gap over the body and to connect the wakes of the two wings. This might explain why span efficiency remains low for a large portion of the downstroke even when lift production is already relatively strong. Regardless of the mechanistic reason for this mismatch, it is a costly way to fly because, in effect, it means that by the time the downwash distribution has reached its most efficient configuration, the majority of the lift has already been generated. On the other hand, it may be that, similar to bumble-bees, it is beneficial for moths to retain aerodynamic independence between the two wing pairs for control authority and to facilitate manoeuvring [15].

The overall pattern of the time history of lift production is rather similar between the moths. They all have a period in the beginning of the downstroke where very little or sometime negative lift is generated. It takes about 25 per cent of the duration of the wingstroke cycle before lift starts to rise. This pattern is not dissimilar from that of the desert locust, but it is more pronounced, because the duration for the locusts is about 15 per cent of the wingstroke cycle [9].

4.3. Variation in span efficiency and factors that predict it

Span efficiency is well suited for both intra- and interspecific comparison because it allows an important aspect of aerodynamic performance to be quantified dynamically, or even reduced to a single number—wingbeat average span efficiency. In this study, we have applied the method to six different hawkmoth species—doubling the number of species measured to date—and among the parameters tested, normalized lift and advance ratio were the significant ones. Normalized lift can also be view as a measure of ‘effort’, because it shows how much of its own weight the animal is supporting. Although, as mentioned in this section, the instantaneous lift and e_i do not follow each other tightly, our results show that average normalized lift was positively correlated with average span efficiency. This implies that the more effort the animals put in the more efficient they were. This seems reasonable if considering that the more lift is required, the more important it will be to produce it efficiently. Advance ratio was negatively correlated with average span efficiency, so that at lower advance ratio, i.e. close to the hovering flight mode when energetic burden on flight is high, span efficiency was high. Because all the hawkmoths in this study hover to feed from flowers, it is interesting and potentially advantageous that their wing morphology and kinematics combine to reduce cost of flight during foraging.

Because wingbeat frequency of the smallest species was found to be rather different in the free flight compared with tethered (65 compared with 46 Hz), we tested that our results were robust to the exclusion of that species (L/W: p = 0.001, J: p = 0.03). AR was not significantly correlated with span efficiency, which was expected because all species of hawkmoths were deliberately chosen to be similar in AR. In addition, the second moment of area was tested and found not to be significant (p = 0.693).

The wingbeat average span efficiencies of all moths are lower than most other measurements of span efficiency of animals found in literature. Previous studies have shown that bats have wing beat average span efficiencies of around 0.8 [13], birds around 0.9 [11,12] and insects between 0.53 [9] and 0.62 [10]. There are methodological differences between these studies so direct comparison is not possible, but the results may still be indicative of a lower overall performance in insects. If we compare these results from the moths with those of the desert locust—which was analysed using the same method [9]—all but D. elpenor have lower values of e_i than the locusts. Furthermore, the value of e_i = 0.83 (k = 1.2), which has been used as rule of thumb before in various models of animal flight [5,26–30], is likely to be a large overestimate of the aerodynamic performance of insects.