Abstract
Transitions between steady states of a multi-stable stochastic system in the perfectly mixed chemical reactor are possible only because of stochastic switching. In realistic cellular conditions, where diffusion is limited, transitions between steady states can also follow from the propagation of travelling waves. Here, we study the interplay between the two modes of transition for a prototype bistable system of kinase–phosphatase interactions on the plasma membrane. Within microscopic kinetic Monte Carlo simulations on the hexagonal lattice, we observed that for finite diffusion the behaviour of the spatially extended system differs qualitatively from the behaviour of the same system in the well-mixed regime. Even when a small isolated subcompartment remains mostly inactive, the chemical travelling wave may propagate, leading to the activation of a larger compartment. The activating wave can be induced after a small subdomain is activated as a result of a stochastic fluctuation. Such a spontaneous onset of activity is radically more probable in subdomains characterized by slower diffusion. Our results show that a local immobilization of substrates can lead to the global activation of membrane proteins by the mechanism that involves stochastic fluctuations followed by the propagation of a semi-deterministic travelling wave.
Keywords: multi-stability, Markov process, spatially extended system, kinetic Monte Carlo on the lattice, kinase autophosphorylation, cell signalling
1. Introduction
Living cells receive stimuli and process information with a circuitry of interacting genes and proteins. From the mathematical perspective, cell fates can be identified with attractors of the dynamical system defined by the interaction network [1]. Accordingly, cellular decisions correspond to transitions between multiple steady states of this dynamical system [2], allowing for phenotypical differentiation of genetically uniform cells [3]. Remarkably, many key biological regulatory and signalling modules are controlled by bistable switches, often leading to binary cellular responses of crucial importance, such as death or survival, senescence or proliferation [4,5]. In this work, we consider state-to-state transitions leading to the activation of proteins diffusing on the plasma membrane.
1.1. State-to-state transitions in homogeneous and heterogeneous reactors
Transitions between steady states in the perfectly mixed chemical reactor are possible only because of stochastic switching. (The classic monographs on stochastic processes covering material used in this study are those by van Kampen [6], Gardiner [7] and Nicolis & Prigogine [8].) In well-mixed reactors, however, the expected time to switch τ depends exponentially on the system size, 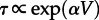 , α > 0, assuming a constant concentration of molecules N/V [9]. The number of reacting molecules in the plasma membrane is of order N = 103 to 105 [10,11], implying an infinitesimal rate of switching between macroscopic states of activity and inactivity in the well-mixed approximation. In spatially extended reactors, the characteristic size of the well-mixed subcompartment is effectively controlled by diffusion. Relatively small diffusion coefficients of membrane proteins, D ≈ 10−2 to 10−1 μm2 s−1 [12,13], coinciding with fast reaction rate constants of order c ≈ 1/s [14] imply a correlation length
, α > 0, assuming a constant concentration of molecules N/V [9]. The number of reacting molecules in the plasma membrane is of order N = 103 to 105 [10,11], implying an infinitesimal rate of switching between macroscopic states of activity and inactivity in the well-mixed approximation. In spatially extended reactors, the characteristic size of the well-mixed subcompartment is effectively controlled by diffusion. Relatively small diffusion coefficients of membrane proteins, D ≈ 10−2 to 10−1 μm2 s−1 [12,13], coinciding with fast reaction rate constants of order c ≈ 1/s [14] imply a correlation length 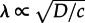 shorter than 1 μm. The membrane can be therefore heterogeneous without any molecular structure imposed by cytoskeletal corrals, protein scaffolds or lipid rafts. In stochastic spatially extended bistable systems, the diffusion-limited number of interacting molecules controls the transition rates between macroscopic states. Interestingly, even when in the deterministic approximation a system is monostable, the volume of the well-mixed stochastic reactor can serve as a ‘bifurcation parameter’ controlling the emergence of noise-induced bimodality [15].
shorter than 1 μm. The membrane can be therefore heterogeneous without any molecular structure imposed by cytoskeletal corrals, protein scaffolds or lipid rafts. In stochastic spatially extended bistable systems, the diffusion-limited number of interacting molecules controls the transition rates between macroscopic states. Interestingly, even when in the deterministic approximation a system is monostable, the volume of the well-mixed stochastic reactor can serve as a ‘bifurcation parameter’ controlling the emergence of noise-induced bimodality [15].
In deterministic spatially extended reactors, transitions between steady states of bistable systems can result from the propagation of heteroclinic travelling waves. (See the book by Murray [16] for an extensive introduction.) A local state-to-state transition can initiate the propagation of a travelling front driving the whole system towards the ‘more stable’ steady state, in which the system would eventually persist. Crucially, for a bistable birth–death process, the deterministically preferred steady state (global deterministic attractor) can be different from the steady state in which the stationary probability distribution (SPD) concentrates (global stochastic attractor) [17,18]. For gradient systems, the macroscopic (deterministic) state-coexistence line in the parameter space is obtained for the potential which exhibits minima of equal depth. In spatially extended systems, this coexistence line corresponds to standing heteroclinic wave solutions. The stochastic state-coexistence line results from the solution of the (stochastic) chemical master equation, and in particular cases can be found analytically in the limit of zero noise by the Maxwell-type construction [19]. This implies that the spatially extended reactor may remain in a stochastically preferred steady state until a local but sufficiently large fluctuation initiates a semi-deterministic transition of the whole reactor to the state preferred in the deterministic approximation [20].
Simulations of Newtonian hard sphere dynamics provided evidence [21] that in the bistable perfectly stirred system the global attractor is correctly defined by the (stochastic) master equation, while using the Fokker–Planck equation with either linear (additive) or nonlinear (multiplicative) noise may lead to incorrect predictions [9]. Baras et al. [21] used the Bird's direct simulation Monte Carlo method [22] to study the chemical kinetics in a homogeneous Boltzmann gas by associating the entire system volume with a single collisional cell. The method was proposed to perform simulations of rarified gas for which the Knudsen number is greater than 1, which is equivalent to the assumption of perfect homogeneity. By employing on-lattice kinetic Monte Carlo (KMC) simulations, we recapitulate here this result in the infinite diffusion limit (see [23]). We will demonstrate, however, that in reactors characterized by finite diffusion the global attractor can be prescribed either through the deterministic or through the stochastic approach, depending on the diffusion coefficient. Interestingly, the deterministic description in which the system is modelled by means of reaction–diffusion equations predicts the same global attractor as that obtained in the Langevin approach based on the macroscopic (deterministic) law of evolution into which an external additive noise term is incorporated. This places the discrepancy between the master equation and the diffusion approximation in the new context.
1.2. State-to-state transitions in biological membrane systems
The highly organized structure of cells, comprising zones of confinement [24,25] or altered motility [26–28], should allow signalling systems to employ intricately both transition modes, i.e. stochastic switching and semi-deterministic travelling wave propagation. Thus far, selected aspects of these phenomena have been investigated in the context of membrane-proximal signalling and spontaneous cell polarization. It has been shown that the self-recruitment of cytoplasmic proteins to the cell membrane leads to the generation of a single cluster of active molecules and thus may define a unique axis of cell polarity [29]. A local increase in the density of molecules in the presence of positive feedback is able to work as an activating switch [30]. In the context of Ras nanoswitches, it has been demonstrated that at uniform slow motility the sole positive feedback in the interaction network of membrane-anchored proteins generates expanding activity patches [31]. In excitable networks, transient clans of activated molecules emerge and vanish spontaneously, even without directional spatial cues [32,33]. Spatio-temporal oscillations of membrane-recruited Min proteins in Escherichia coli were demonstrated to be enabled by the inherent noise [34]; on the other hand, macroscopically stable homogeneous oscillations can be abolished by local fluctuations, depending critically on the size and dimensionality of the reactor [35]. In stimulated thin neuronal protrusions, it has been observed that slowly diffusing autocatalytic CaMKII kinases exhibit pulsatile compartmentalized activity [36]; a spatially extended bistable system can spontaneously generate subregions, where different steady states dominate [37]. Self-organized foci of activity can generate activating travelling waves [38]. Propagation of waves can give rise to long-lasting cell polarity when the fast-diffusing inhibitor accumulates proportionally to the amount of slow-diffusing activated molecules so that the wavefront can be stalled. This mechanism, known as wave pinning, has been investigated for bistable systems [39,40]. When the diffusion coefficient of the inhibitor is very large (in principle, infinite), the mechanism of polarization is known as the local excitation, global inhibition [41,42].
1.3. Overview of results
In order to provide a comprehensive view and to be able to recognize new mechanisms of macroscopic state-to-state transitions available in spatially extended systems, we study a generic bistable system of membrane-bound autophosphorylating kinases and phosphatases by means of KMC simulations on the hexagonal lattice. These simulations are compared with the simulations of the Markov process in the perfectly mixed reactor and with the deterministic approximation, i.e. reaction–diffusion partial differential equations (PDEs).
In the limit of infinite diffusion, unsurprisingly, the SPD in the spatial on-lattice KMC simulations converges to the SPD obtained from Gillespie algorithm simulations of the well-mixed system. For slower diffusion, however, we observe that the SPD is qualitatively different from the case of the perfectly mixed system; specifically, the bimodality can emerge or vanish. We demonstrate that the probability mass fraction concentrated in the stochastically and deterministically preferred steady states depends on the speed of diffusion and properties of the reactor, such as volume and shape. We show that the state-to-state transitions in large reactors can follow from the propagation of semi-deterministic travelling waves. These waves can be induced deterministically by the externally triggered state transition in a sub-volume of the spatially extended reactor; they can also arise spontaneously as a result of local stochastic fluctuations. We found that the expected time to transition on the membrane grows exponentially with diffusivity. For a given diffusion coefficient, the expected time to transition increases exponentially with the volume of the reactor V as long as the reactor is perfectly mixed, and then it decreases as 1/V. At slow diffusion, for some parameters, the reactor may exhibit a dynamical structure of perpetual local activations and inactivations, and refrain from assuming uniformly a single steady state. Finally, we identify a novel mechanism in which the coexistence of stochastic and deterministic effects can give rise to the global activation of membrane proteins in response to a localized cue.
2. Material and methods
2.1. Model
The analysed system of reactions involves two molecular species: kinases and phosphatases. Each kinase molecule contains two indistinguishable phosphorylation sites, hence it can assume three states: dephosphorylated, monophosphorylated or bisphosphorylated. The (auto)phosphorylation activity of a kinase increases with its phosphorylation level. Phosphatases are explicitly present in the system although they are not modified in any process.
The interaction network comprises the variant of the two-step phosphorylation–dephosphorylation motif, where kinases autophosphorylate one another and are dephosphorylated by phosphatases, which act non-specifically with respect to the level of phosphorylation of a substrate kinase [15,43]. The system encompasses the simplest case of the ubiquitous multi-site phosphorylation and exhibits bistability [44,45]. Since it consists of eight reactions, it may be viewed as far from minimal [46]; however, in contrast to other small bistable systems [47,48], all its reactions are bimolecular and elementary (i.e. only one of two reacting molecules changes its state), rendering the system appropriate for microscopic lattice-based simulations of diffusion-influenced reaction kinetics.
2.2. Reaction–diffusion system: kinetic Monte Carlo on the lattice
The spatial and stochastic simulations of the system are performed using the on-lattice KMC at the single molecule resolution. Molecules are allowed to hop between adjacent sites of a hexagonal lattice with propensity proportional to the diffusion coefficient. It is assumed that two molecules cannot occupy the same lattice site. Kinases  and phosphatases
and phosphatases 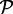 can react only when in adjacent sites according to the following rules:
can react only when in adjacent sites according to the following rules:
Phosphorylation by a dephosphorylated kinase:
| 2.1a |
| 2.1b |
Phosphorylation by a monophosphorylated kinase:
| 2.2a |
| 2.2b |
Phosphorylation by a bisphosphorylated kinase:
| 2.3a |
| 2.3b |
Dephosphorylation (by a phosphatase):
| 2.4a |
| 2.4b |
The relative activity of a kinase increases strongly with its phosphorylation level: c1 < c2 < c3 (parameter values are given in the electronic supplementary material, table S1). Two molecules can diffuse away without reacting; on the other hand, a series of reactions involving two molecules is allowed, and such consecutive events are more probable at small diffusion coefficients when contacts last longer. The total numbers of kinases 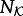 and phosphatases
and phosphatases 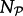 are constant in a simulation and their fractional surface concentrations (i.e. the fraction of lattice sites occupied by a species) are assumed to be
are constant in a simulation and their fractional surface concentrations (i.e. the fraction of lattice sites occupied by a species) are assumed to be 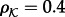 and
and 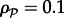 , respectively. For the sake of simplicity, we assume the same motility M of kinases and phosphatases; the propensity of hopping to a neighbouring empty site of a hexagonal lattice is M/6. We will consider both spatially uniform and non-uniform motility to account for subdomains of slower diffusion, e.g. large lipid rafts [27]. In a two-dimensional reactor, the macroscopic diffusion coefficient D depends on the total fractional concentration of membrane molecules
, respectively. For the sake of simplicity, we assume the same motility M of kinases and phosphatases; the propensity of hopping to a neighbouring empty site of a hexagonal lattice is M/6. We will consider both spatially uniform and non-uniform motility to account for subdomains of slower diffusion, e.g. large lipid rafts [27]. In a two-dimensional reactor, the macroscopic diffusion coefficient D depends on the total fractional concentration of membrane molecules 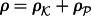 and the lattice constant ℓ,
and the lattice constant ℓ,
| 2.5 |
The lattice constant is equal to the characteristic mean centre-to-centre spacing between neighbouring membrane proteins, which is of order ℓ = 10 nm [49].
2.3. Spatially homogeneous Markov process: Gillespie algorithm
The Gillespie algorithm for KMC was employed for stochastic simulations in the limit of the perfectly mixed chemical reactor [50]. To provide a basis for the comparison of well-mixed Gillespie (superscript G) with on-lattice (superscript L) KMC simulations, kinetic rate constants 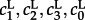 have to be rescaled according to the general rule
have to be rescaled according to the general rule
| 2.6 |
which reflects the fact that the propensity of each reaction in the perfectly mixed reactor is inversely proportional to the volume (or, here, surface) of the reactor V and is proportional to the number of possible contacts (nc = 6 for the hexagonal lattice). The scaling ensures that in the limit of M → ∞ the SPD obtained in on-lattice KMC simulations converges to that obtained with Gillespie KMC simulations (see the electronic supplementary material, figure S1c) [23].
2.4. Spatially extended deterministic approximation: partial differential equations
We will also consider the deterministic limit of the on-lattice KMC described by a system of PDEs. For this approximation, kinetic rate constants 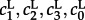 are scaled according to the following rules:
are scaled according to the following rules:
| 2.7a |
| 2.7b |
These coefficients are used to parametrize dimensionless reaction–diffusion PDEs. Since we assume that the diffusion coefficient of kinase molecules is independent of their phosphorylation level, we may introduce fractional concentrations of dephosphorylated, monophosphorylated and bisphosphorylated kinases denoted by k, kp and kpp (k + kp + kpp = 1). The fraction of phosphorylated kinases, kp + kpp, will be considered as a measure of activity of the system. The resulting PDEs read as follows:
| 2.8a |
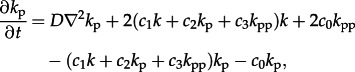 |
2.8b |
| 2.8c |
Evolution of the above system was simulated using the finite-element method implemented in Comsol Multiphysics (Comsol Inc., Sweden).
For a certain range of parameters, equations (2.8a–c) exhibit bistability (figure 1). The stable steady state corresponding to a high and a low value of kp + kpp will be referred to as the active and the inactive state, respectively. For default parameters: c0 = 1, c1 = 0.02, c3 = 4 (see the electronic supplementary material, table S1) and c2 = 0.2, in the active state kp + kpp = 0.86 and in the inactive state kp + kpp = 0.07 (see the electronic supplementary material, figure S1b).
Figure 1.
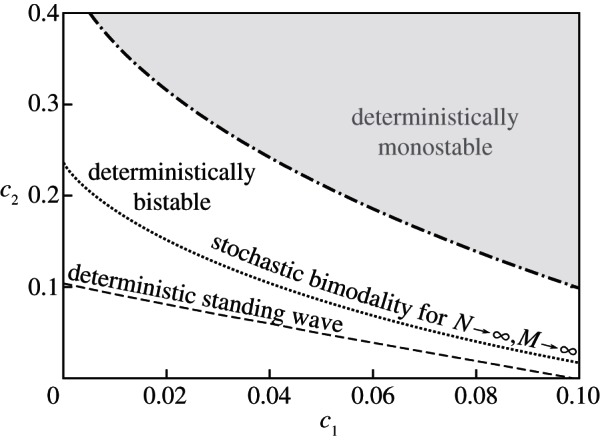
Bistability region of equations (2.8a–c) in the parameter space of (c1,c2); remaining parameters are fixed: c3 = 4 and c0 = 1. The region is divided into two lines: the deterministic coexistence line (dashed), obtained numerically in Comsol, and the stochastic coexistence line (dotted), obtained numerically as an approximate limit of curves determined for increasing numbers of molecules in the perfectly mixed regime. Above and below these lines global deterministic and stochastic attractors converge in the active and inactive steady state, respectively. Between these lines, the well-mixed stochastic system is preferentially inactive, while activating travelling waves may propagate.
2.5. Estimation of the stationary probability distribution for rarely switching systems
An important characteristic of (homogeneous or heterogeneous) stochastic bistable systems is the expected time to switch from one to the other steady state, or the mean first-passage time (MFPT). Numerical estimates of the MFPT for activation τon and deactivation τoff can be obtained from running multiple (parallel) simulations with initial conditions in both basins of attraction. When switches are too rare to provide a reliable estimation of the SPD from a single trajectory, MFPTs allow one to quantify relative probabilities of finding a system in the basin of attraction of the active steady state pon = τoff/(τon + τoff) and inactive steady state poff = 1 − pon.
If n independent simulations of the initially inactive system were running until finite times 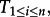 it could happen that spontaneous activations were observed only in a fraction of trajectories at times
it could happen that spontaneous activations were observed only in a fraction of trajectories at times 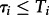 . Then one can use the maximum-likelihood estimate for τon,
. Then one can use the maximum-likelihood estimate for τon,
| 2.9 |
where non is the number of observed on switches [51]; τoff can be estimated analogously.
3. Results
3.1. General considerations
We are interested primarily in macroscopic state-to-state transitions of a bistable reaction–diffusion Markov process on the membrane. Depending on the chemical reaction rate parameters, diffusion coefficients of molecules and the size of the domain, the process can be approximated by means of the perfectly mixed stochastic system, perfectly mixed deterministic system or the spatially extended deterministic system:
— The reactor can be considered as perfectly mixed when its diameter L is smaller than the characteristic distance λ travelled by a molecule in the characteristic time τr between two subsequent reactions. In estimations of λ and τr, we employ the rate constant c0, because the dephosphorylation reaction is both relatively fast and density-independent (
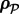 is constant, while densities of kinases at a particular phosphorylation level evolve in time). We assign τr = 1/c0 and obtain
is constant, while densities of kinases at a particular phosphorylation level evolve in time). We assign τr = 1/c0 and obtain 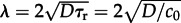 [6,52]. When λ > L, the positions of a molecule subjected to subsequent reaction events can be regarded as uncorrelated.
[6,52]. When λ > L, the positions of a molecule subjected to subsequent reaction events can be regarded as uncorrelated.- — The process in the well-mixed reactor can be considered in the deterministic approximation when MFPTs of macroscopic state-to-state transitions are longer than the duration of other processes modifying the system; for instance, the duration of the cell cycle T. The characteristic MFPT τ grows exponentially with the size of the well-mixed reactor [9],
When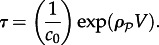
3.1 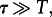 the process can be considered as deterministic, in the sense that the chance for a stochastic transition in the considered time interval T is negligible.
the process can be considered as deterministic, in the sense that the chance for a stochastic transition in the considered time interval T is negligible. - — In the non-mixed reactor, the volume of the mixed subcompartment in two dimensions can be defined as V0 = D/c0. The characteristic transition time for such a sub-volume is
As we will see, a stochastic transition in any subcompartment, depending on parameters, may trigger travelling waves leading to the macroscopic state-to-state transition of the whole reactor. In large reactors for which V0 < V, the MFPT for such locally induced transition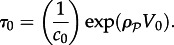
3.2 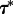 is given as the waiting time of V/V0 concurrent processes,
is given as the waiting time of V/V0 concurrent processes,
It is assumed here that the expected time to switch is much longer than the time of the wavefront propagation over the whole reactor, and that every local ignition can effectively give rise to a propagating front. When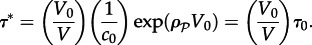
3.3 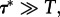 the process can be considered deterministic: the chance for a stochastic state-to-state transition is negligible at the considered time scale.
the process can be considered deterministic: the chance for a stochastic state-to-state transition is negligible at the considered time scale.
Although in the above considerations we used D, in the further analysis of the on-lattice system the speed of diffusion will be expressed in terms of the motility M. According to equation (2.5), for default parameters in non-dimensionalized units M = 8D.
3.2. Different preferred steady states of the stochastic system and its deterministic approximation
The bistability domain of equations (2.8a–c) in the (c1, c2) parameter space for fixed c3 = 4 and c0 = 1 is shown in figure 1. The domain is divided by the c2(c1) line (dashed) on which the standing wave solutions exist. These heteroclinic solutions connect the active and inactive stable steady states. For parameters from above the dashed line, travelling waves propagate from the active to the inactive state. This can be interpreted as the domination of the active steady state. For parameters below the line, the travelling waves propagate in the opposite direction, i.e. the inactive state is dominant. This deterministic separatrix (dashed line) can be compared with the separatrix for the stochastic perfectly mixed system (dotted line). For parameters from the latter line the SPD of the perfectly mixed process described by reactions (2.1a–2.4b) remains bimodal in the limit of the infinite reactor volume. In the same limit, for parameters above (below) the line, the SPD converges to the Dirac delta in the active (inactive) steady state [17]. Interestingly, these two separatrices do not overlap and they delineate a region where the system of PDEs prefers the active state, while the stochastic perfectly mixed system in the limit of the infinite reactor volume is inactive. The divergence of these separatrices suggests that for realistic reactors characterized by a finite diffusion the choice between the active and the inactive state depends on the speed of diffusion and the size or even shape of the reactor [20].
3.3. Diffusion and size of the reactor control system activity
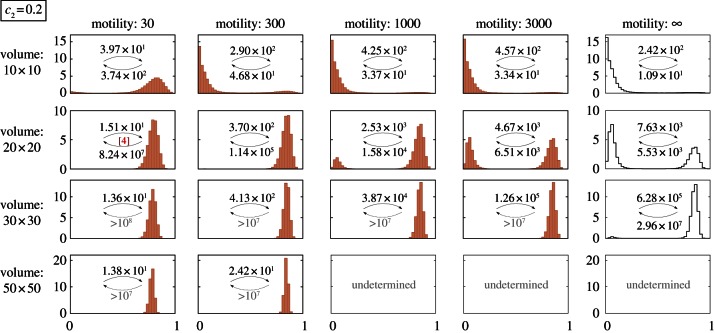
Here, we analyse the expected activity of the kinase–phosphatase system by means of the SPD obtained in on-lattice KMC simulations, as a function of the compartment volume (surface) V and reactants motility coefficient M. First, let us remember that when M → ∞ the SPD from on-lattice KMC simulations converges to that obtained from Gillespie KMC simulations (M = ∞). For M = 3000, the difference is still discernible (last two columns in figure 2) but the agreement becomes nearly perfect for M = 10 000 (see the electronic supplementary material, figure S1c). In figure 2, we consider the case of (c1 = 0.02, c2 = 0.2), for which the stochastic system and its deterministic approximation are preferentially in the active state. As shown, the probability of the active state increases with V for finite M as well as in the limit of the perfectly mixed reactor (M = ∞, last column in figure 2). For large motility (M ≥ 300), the active state probability increases from nearly 0 to almost 1 as the compartment volume increases from V = 10 × 10 to V = 30 × 30. It demonstrates that the relative stability of steady states is controlled by the volume of the reactor. For perfectly mixed systems, this effect has been reported previously by Zheng et al. [53].
Figure 2.
SPDs for different motility coefficients and square domains of different sizes. The lattice-based KMC simulations were performed on toroidal domains (i.e. square domains with periodic boundary conditions) for (c1 = 0.02, c2 = 0.2) and the remaining parameters with their default values: c3 = 4, c0 = 1. In the last column, SPDs were obtained using (spatially homogeneous) Gillespie algorithm simulations. The MFPTs τon and τoff are shown in each panel. A small number in square brackets reports the number of observed switches non or noff if smaller than 20. The SPD is marked as ‘undetermined’ when no switches were observed during simulations. (Online version in colour.)
In figure 3, we consider a more interesting case of (c1 = 0.02, c2 = 0.15), for which the stochastic perfectly mixed system is preferentially in the inactive state, but its deterministic approximation is preferentially active. In this case, in addition to the compartment volume, the activity of the system is controlled by the substrate motility M. For chosen parameters, the system is preferentially in the active state for small motility (M = 30) and in the inactive state for large motility (M ≥ 1000). For intermediate values (100 ≤ M ≤ 300), the choice of the dominant state is controlled by the volume of the reactor. The tendency of the system to inactivate as M → ∞ is visible also in figure 2, although it is pronounced only for small system volumes, for which the perfectly mixed system remains prevalently in the inactive state.
Figure 3.
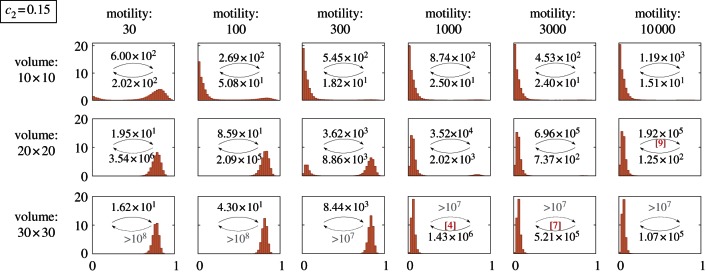
SPDs for different motility coefficients and square domains of different sizes. The simulations are in the same set-up as for figure 2 but with kinase activity coefficient c2 = 0.15 (instead of c2 = 0.2). (Online version in colour.)
In the subsequent analysis, we employ the mean first-passage time of the transition from the inactive to active steady state τon and the time for the reverse transition τoff. At large substrate motility (M ≥ 1000), MFPTs (given in each panel of figures 2 and 3) increase dramatically with the volume of the compartment. It is known that in a perfectly mixed reactor MFPTs increase exponentially with its volume [9]. In the case of finite motility, the situation is more complicated. Let us consider the case of a fixed motility for which one can determine a characteristic distance λ and the well-mixed sub-volume V0. When the reactor diameter exceeds λ, it should be considered as a composition of multiple (≈V/V0) well-mixed sub-reactors. In such a structured reactor, the transition to the active steady state can result from a stochastic switch occurring in any of these sub-reactors, followed by the propagation of the activating wave, as discussed in §3.4. In this regime, τon decreases with the number of well-mixed subcompartments (≈V/V0), and thus it is inversely proportional to the volume of the reactor, 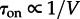 . These diverging limiting behaviours jointly result in the non-monotonic dependence of τon on the volume of the reactor (figure 4a): τon increases exponentially until the volume of the reactor V exceeds the volume of the well-mixed compartment V0, and then decreases with the reactor volume as
. These diverging limiting behaviours jointly result in the non-monotonic dependence of τon on the volume of the reactor (figure 4a): τon increases exponentially until the volume of the reactor V exceeds the volume of the well-mixed compartment V0, and then decreases with the reactor volume as 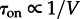 . Since larger motility implies larger perfectly mixed sub-volumes, the volume of the reactor for which the MFPT reaches its maximum increases with motility. The activation and inactivation processes are not symmetric, because for given parameters either activating or inactivating travelling waves may propagate. For the parameters considered in figure 4a, the activating travelling waves propagate. As a result, after a local inactivation, the activity is promptly recovered by waves from surrounding subcompartments, and thus the only possible mode of transition towards inactivity requires simultaneous inactivation of the whole reactor. Consequently, while τon decreases for small motility (V > V0 regime) and increases for large motility (V < V0 regime), τoff grows exponentially with V in both regimes (figures 2 and 3).
. Since larger motility implies larger perfectly mixed sub-volumes, the volume of the reactor for which the MFPT reaches its maximum increases with motility. The activation and inactivation processes are not symmetric, because for given parameters either activating or inactivating travelling waves may propagate. For the parameters considered in figure 4a, the activating travelling waves propagate. As a result, after a local inactivation, the activity is promptly recovered by waves from surrounding subcompartments, and thus the only possible mode of transition towards inactivity requires simultaneous inactivation of the whole reactor. Consequently, while τon decreases for small motility (V > V0 regime) and increases for large motility (V < V0 regime), τoff grows exponentially with V in both regimes (figures 2 and 3).
Figure 4.
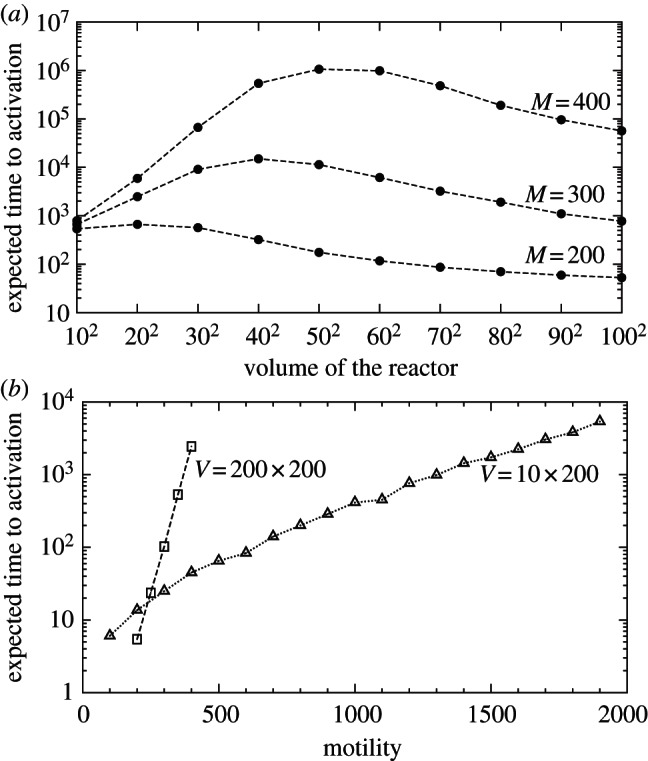
(a) Mean first-passage time for activation τon as a function of the volume V of the square-shaped reactor with periodic boundary conditions, obtained in on-lattice KMC simulations for three values of motility and (c1 = 0.02, c2 = 0.15), and other parameters with default values. For small V, τon grows exponentially with V (well-mixed regime), while for large V, τon decreases as 1/V. Every τon is a maximum-likelihood estimate from a time series with fixed censoring time, calculated based on thousands of trajectories and at least non = 10 observed switches. (b) Dependence of τon on the motility M for reactors of two different geometries, for the same parameters as in (a). For the square-shaped reactor, the expected τon grows exponentially with increasing motility M; for the long rectangular reactor with periodic boundary conditions, τon grows faster than 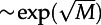 but slower than
but slower than 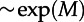 .
.
Irrespective of the volume of the reactor and for both considered values of c2, one can observe that for sufficiently low motility the active state is preferred. There are two properties of the system that give rise to such behaviour at decreased motility: (i) in addition to the less effective distributive mechanism, the more effective processive phosphorylation reactions are more likely to happen (when two kinase molecules stay in contact longer, it is more probable that the substrate kinase will be phosphorylated twice by the same catalytic kinase; also, once the substrate kinase is phosphorylated it becomes more amenable to ‘fire back’ and to activate the first kinase) and (ii) the catalytic capacity of less abundant phosphatase molecules becomes dampened after they saturate their neighbourhoods (a phosphatase molecule can dephosphorylate all kinases in its vicinity, rendering itself idle).
3.4. Propagation of waves of kinase activity on cylindrical domains
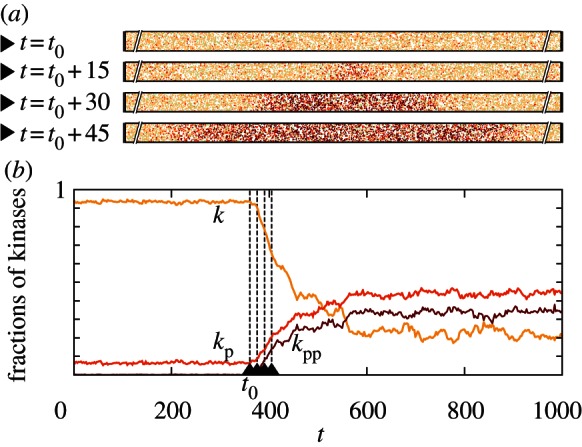
In this section, we consider travelling wave propagation on long cylindrical domains. Elongated thin membrane protrusions constitute, for example, pseudopodia of motile cells and dendritic spines of neurons. First, we focus on parameters (c1 = 0.02, c2 = 0.15) lying in the range in which the preferred steady states for well-mixed and spatially extended reactors diverge (figure 1). For these parameters and large motility, M = 3000, the 30 × 30 reactor is principally inactive (figure 3). However, in a semi-one-dimensional array of a large number of such reactors the activating travelling waves can propagate as predicted by the deterministic approximation, equations (2.8a–c). In figure 5a, we show snapshots from on-lattice KMC simulations of the stochastic travelling wave in the cylindrical domain 30 × 1100 (top–bottom boundary conditions are periodic, left–right reflecting). At t = 0, the left 30 × 100 area (‘seed’) is assigned to be in the active steady state and the rest of the cylinder, 30 × 1000, is set to the inactive state. At the very beginning of the simulation, the transition between the active and the inactive region becomes smooth and a wave profile is formed, which then propagates so that eventually the whole reactor adopts the active steady state (figure 5a,b). This surprising divergence of system behaviours in a small 30 × 30 and in a long 30 × 1100 reactor is due to the fact that motility M = 3000 renders the small reactor mixed, but it is by far too small to mix the longer reactor: 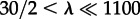 , where 30/2 is the effective diameter of the 30 × 30 reactor in periodic boundary conditions, and
, where 30/2 is the effective diameter of the 30 × 30 reactor in periodic boundary conditions, and 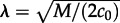 . Therefore, in the long reactor, the system converges to the attractor preferred by the deterministic approximation. Moreover, since the number of molecules on the wavefront (the width of which grows
. Therefore, in the long reactor, the system converges to the attractor preferred by the deterministic approximation. Moreover, since the number of molecules on the wavefront (the width of which grows 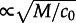 ) is quite large, the stochastic wave profile resembles the deterministic profile obtained from PDEs (figure 5c,d).
) is quite large, the stochastic wave profile resembles the deterministic profile obtained from PDEs (figure 5c,d).
Figure 5.
Kinase activity wave propagation on the cylindrical domain 30 × 1100 for parameters (c1 = 0.02, c2 = 0.15) and M = 3000. At t = 0, a fragment of the cylinder (30 × 100) is in the active state. (a) Three snapshots from an on-lattice KMC simulation. (b) Time profile of the kinase activity profile integrated over the whole domain. (c) Kinase activity profile across the domain at time t = 150, averaged using the sliding window of width w = 11. (d) Kinase activity profile obtained from corresponding PDEs in Comsol. (Online version in colour.)
For parameters (c1,c2) below the deterministic standing wave line (figure 1), the travelling wave can propagate in the opposite direction such that the whole system becomes inactive, provided that the diffusion is sufficiently fast, as discussed in §3.5 (see the electronic supplementary material, figure S6).
With increasing motility, the velocity of the wave in on-lattice KMC simulations approaches the velocity in PDEs, which is 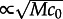 (see the electronic supplementary material, figure S3). The number of molecules on the length of the wavefront increases with motility and, as a consequence of the reduced noise, at higher motilities the activating front propagates more steadily. The size of the activating seed also increases with motility and at higher motilities seeds are more likely to be swept away (see the electronic supplementary material, figure S2). Consequently, as we will see in §3.5, at large motility the stochastic wave initiations are much less frequent: they need the creation of a larger seed, and thus the initiating stochastic fluctuation must involve a larger number of molecules.
(see the electronic supplementary material, figure S3). The number of molecules on the length of the wavefront increases with motility and, as a consequence of the reduced noise, at higher motilities the activating front propagates more steadily. The size of the activating seed also increases with motility and at higher motilities seeds are more likely to be swept away (see the electronic supplementary material, figure S2). Consequently, as we will see in §3.5, at large motility the stochastic wave initiations are much less frequent: they need the creation of a larger seed, and thus the initiating stochastic fluctuation must involve a larger number of molecules.
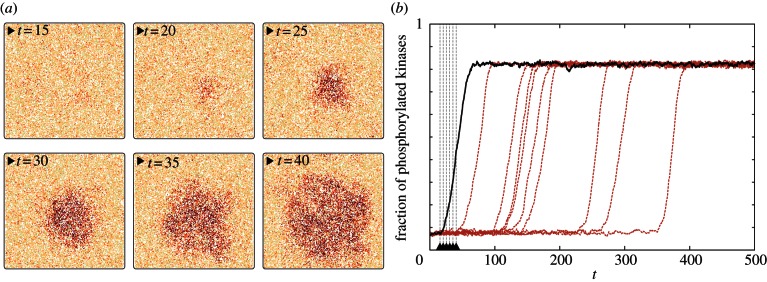
3.5. Spontaneous wave activation
The two already discussed transition modes, the stochastic switching in a well-mixed system and semi-deterministic travelling wave propagation in a spatially extended system, can work in conjunction. The initially inactive system can be excited owing to a local fluctuation, which could in turn initiate an activating travelling wave. We investigate this mechanism in the system with (c1 = 0.02, c2 = 0.15) and M = 1000 in the semi-one-dimensional reactor of V = 20 × 1000 (figure 6). A spontaneous local activation, occurring in a random place of the reactor, gives rise to two fronts, which propagate in opposite directions, driving the whole reactor to the active state. The average time to switch on was estimated as 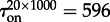 (from non = 16 switches). Based on the analysis in §§3.3 and 3.4, the activation mechanism can be understood as follows: the 20 × 1000 reactor can be considered as an array of 50 smaller 20 × 20 sub-reactors. These small sub-reactors switch on and off with switching times
(from non = 16 switches). Based on the analysis in §§3.3 and 3.4, the activation mechanism can be understood as follows: the 20 × 1000 reactor can be considered as an array of 50 smaller 20 × 20 sub-reactors. These small sub-reactors switch on and off with switching times 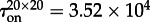 ,
, 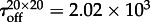 (figure 3). Thus, the expected time to switch on in the whole reactor can be estimated as
(figure 3). Thus, the expected time to switch on in the whole reactor can be estimated as 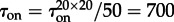 , which agrees (unexpectedly well) with the measured
, which agrees (unexpectedly well) with the measured 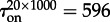 .
.
Figure 6.
Spontaneous initiation of the activity wave in a subdomain of the cylindrical domain 20 × 1000 for parameters (c1 = 0.02, c2 = 0.15) and M = 1000. The expected waiting time for the activation is τon = 596 s. (a) Four snapshots from an on-lattice KMC simulation (inessential parts of the reactor are truncated) and (b) time profile. (Online version in colour.)
The same reasoning fails for a two-dimensional reactor of V = 200 × 200. For the same parameters, a spontaneous activation was not observed in long simulations (with total simulation time ≈ 2 × 104). In the two-dimensional case, the spontaneously appearing seeds of activity are extinguished by the inactive neighbourhood more easily than in the reactor of cylindrical geometry. The spontaneous activation was observed only after reducing motility to M = 300 (figure 7).
Figure 7.
Spontaneous initiation of the activity wave on the square domain 200 × 200 for parameters (c1 = 0.02, c2 = 0.15) and M = 300. For larger motility M = 1000, activity waves were not self-initiated. Snapshots in (a) correspond to the trajectory represented by the solid black line in (b). (Online version in colour.)
Increasing motility increases the number of communicated molecules and thus reduces the switch rate: τon grows exponentially with the motility in the case of the two-dimensional reactor (figure 4b). One could expect that τon(M) for the one-dimensional reactor grows 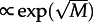 . However, such dependence does not fit well to obtained data points, although it yields a better fit than
. However, such dependence does not fit well to obtained data points, although it yields a better fit than 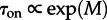 . The divergence from the ‘
. The divergence from the ‘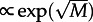 ’ prediction can be due to the fact that in the cylindrical reactor τon(M) spans the large range of motilities involving the change of the stochastically preferred steady state (figure 3).
’ prediction can be due to the fact that in the cylindrical reactor τon(M) spans the large range of motilities involving the change of the stochastically preferred steady state (figure 3).
The observation that the reduced motility increases the probability of system activation suggests that regions of reduced diffusivity can serve as ignition points for the activation of the whole reactor. We verified this hypothesis by performing simulations of the 200 × 200 domain with a spatially varying diffusion coefficient. The overall motility was set to M = 1000, while in a circular region of r = 14 motility was reduced 10 times to Mpatch = 100. In order to minimize possible peculiarities caused by the sharp jump on the brink of the patch, the motility in its vicinity was increasing linearly, concentrically until reaching the outer circle of radius 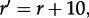 beyond which M = 1000. Within this set-up, we observed that the patch of lowered diffusivity acts as an ignition centre: stochastic activation switches are much more probable in this region, and the local activation, with some probability, again, can start the semi-deterministic travelling wave (figure 8). As one can expect, τon decreases sharply with the radius of the patch (see the electronic supplementary material, figure S7).
beyond which M = 1000. Within this set-up, we observed that the patch of lowered diffusivity acts as an ignition centre: stochastic activation switches are much more probable in this region, and the local activation, with some probability, again, can start the semi-deterministic travelling wave (figure 8). As one can expect, τon decreases sharply with the radius of the patch (see the electronic supplementary material, figure S7).
Figure 8.
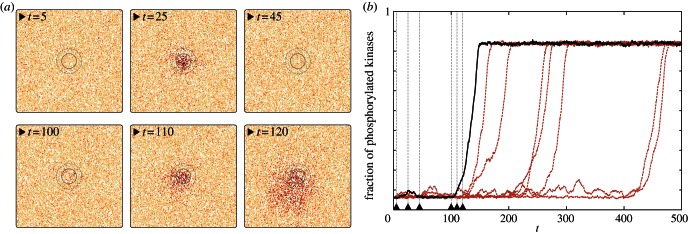
Activity wave initiation in the domain 200 × 200 owing to the locally reduced motility coefficient (M = 100 in the inner circle, M = 1000 outside the outer circle, and gradually increasing M in between circles) for parameters (c1 = 0.02, c2 = 0.15). Snapshots in (a) correspond to the trajectory represented by the solid black line in (b). (Online version in colour.)
For completeness, it should be noted that, when the stochastic and deterministic global attractors coincide in the active state (which happens for parameters c1 and c2 above the stochastic bimodality curve in figure 1), the initially inactive system is more likely to be activated by local stochastic fluctuations: for small diffusion, the activating seeds plausibly appear in several places simultaneously, giving rise to several travelling fronts (see the electronic supplementary material, figure S4).
In the already considered case of (c1 = 0.02, c2 = 0.06) depicted in the electronic supplementary material, figure S6, the stochastic and deterministic global attractors coincide in the inactive state. In this case, simultaneous local inactivations can occur probably in various places of the compartment. To avoid spontaneous switching and illustrate the possibility of the propagation of the inactivating wave, we considered M = 10 000 in the wider 50 × 1100 reactor, where stochastic switches are rare.
Interestingly, in the 30 × 1000 toroidal domain at M = 300, the reactor is able to maintain a fractional activity (see the electronic supplementary material, figure S5). Since in the parameter space the point (c1 = 0.02, c2 = 0.06) is closer to the curve of the deterministic standing wave than point (c1 = 0.02, c2 = 0.2), it can be expected that for (c1 = 0.02, c2 = 0.06) inactivating travelling waves are not formed as easily as activating waves for (c1 = 0.02, c2 = 0.2). Hence, scattered local on or off switches do not propagate; they render the reactor dynamically yet persistently spatially structured. As a consequence, most of the probability mass is contained between stable steady states of the deterministic system, in contrast to all previously analysed cases.
4. Discussion
In this study, in order to understand the principal mechanisms of biochemical information processing and cellular decision-making, we systematically investigated transition modes available to a generic bistable reaction system in the spatially extended reactor. We used primarily microscopic simulations on the two-dimensional lattice complemented by the analysis of approximations neglecting either stochasticity or spatial resolution. In the well-mixed compartment (the size of which is determined by the diffusion coefficient), the transition rates between macroscopic steady states of the system decrease exponentially with the number of reacting molecules or the size of the compartment. In larger, non-mixed compartments, transition rates are controlled by the number of diffusively communicated molecules, which is typically much smaller than the total number of molecules. We demonstrated that the local stochastic state-to-state transitions occasionally initiate travelling waves, which expand in the semi-deterministic manner leading to the (in)activation of the whole reactor: either a local activation or inactivation can be amplified spatially, depending on the reaction rate constants. At increasing diffusivity, more molecules become communicated and local transitions become less probable. On the other hand, travelling waves can propagate only when the diffusion is sufficiently fast. At large diffusion coefficients, the wavefronts are thicker, contain more molecules and thus are less affected by fluctuations. As a result, in the limit of large diffusion, the velocity of a wavefront in the discrete stochastic system converges to that of its deterministic approximation modelled by PDEs.
Importantly, there exists a range of parameters for which the macroscopic, stochastically preferred steady state (or global stochastic attractor, i.e. the state which is prevalently occupied in a perfectly mixed regime) is different from the steady state preferred deterministically (or global deterministic attractor, i.e. the state which expands as a result of the propagation of travelling waves) [17,20]. We demonstrated that in this range of parameters, even when a small compartment is predominantly inactive, a travelling wave may spread the active state over the larger reactor. If parameters are such that global stochastic and deterministic attractors converge (in either the active or inactive state), the system is effectively monostable, i.e. the escapes from the ‘less stable’ macroscopic steady state can arise spontaneously with a high probability. Consequently, the reactor settles in the more stable steady state or remains spatially heterogeneous with its regions flipping between steady states, giving rise to transient clans of activated molecules [37]. Our macroscopic analysis thus implies that the well-known mechanism of state-to-state transitions arising in bistable reaction–diffusion systems is restricted only to the subdomain of the bistability domain in the parameter space. Only these bistable systems which exploit in the parameter space the region of diverging stochastic and deterministic attractors are expected to be both resistant to spontaneous autoactivation (caused by stochastic switching) and sensitive to external stimuli (allowing for deterministic activation by means of the propagation of travelling waves). This physiologically relevant region in the parameter space (delineated by two separatrices in figure 1) grows with the increasing differences between reaction rate constants, 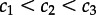 . We note that the catalytic activity of a kinase can grow with its phosphorylation level even stronger than is assumed in the analysed system, i.e. kinetic rate constants can span several orders of magnitude:
. We note that the catalytic activity of a kinase can grow with its phosphorylation level even stronger than is assumed in the analysed system, i.e. kinetic rate constants can span several orders of magnitude: 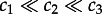 [54].
[54].
In living cells, travelling waves may be induced by an external stimulus; for example, upon binding of a specific extracellular ligand (antigen and chemoattractant) by membrane receptors. We demonstrated that partial immobilization of a tiny fraction of kinases on the membrane may lead to the global activation of the system. Since the locally constrained motility does not lead to a locally increased surface concentration of molecules, this activation mechanism is different from the recently proposed density-dependent switch [30]. In the mechanism introduced here, there is an inherent threshold number of activated clustered molecules required for triggering a travelling wave with a sufficiently high probability. It has been proposed theoretically and recently investigated numerically that a tiny fraction of membrane receptors clustered upon binding of antigens are capable of initiating immunogenic responses in B cells (see [55] and references therein). In other cases, proteins can become co-sequestered in lipid microdomains after the activation. Such confinement reduces their lateral diffusion and presumably facilitates subsequent signalling events [56].
We analysed exhaustively the SPD with respect to the diffusion coefficient and size of the reactor. In the context of the recruitment of cytoplasmic proteins to the membrane milieu, Abel et al. [57] showed that decreasing motility or altering the depth of a submembrane layer promotes or suppresses SPD bimodality, depending on the topology of the interaction network. In their case, the unimodal distribution arises from averaging over the reactor and peaks between two steady states. In the system analysed in this study, the unimodality results from the preference of one of two steady states of the deterministic approximation. We showed that the SPD is controlled by both the motility of molecules and the volume of the reaction chamber. In our case, a single reaction rate parameter dictates the state to which the system converges at the increasing diffusivity. We found that, despite the system being bistable, the SPDs may be bimodal only in small well-mixed compartments. Large compartments have, generically, unimodal SPDs analogously to the perfectly mixed systems of large numbers of molecules [20,58].
In a spatially extended system, which in the case of slow diffusion can be considered as a composition of multiple well-mixed reactors, the expected time to activation has been shown to shorten with increasing volume, which is in stark contrast to a perfectly mixed reactor, for which the time increases exponentially with the volume. Furthermore, spatially extended reactors of similar volumes but different geometries can have vastly different expected times to activation. In a two-dimensional reactor, the minimal size of the ‘nucleation centre’ required for the initiation of a wave is larger than in a semi-one-dimensional reactor, and thus the expected time to the stochastic activation is longer. Propagation of waves is also dependent on the reactor geometry. In a semi-one-dimensional reactor, the front curvature is negligible, while in a two-dimensional reactor the curvature reduces the velocity of the travelling front, and may prohibit spreading of the wave when the initial cluster is too small [55].
Our work provides further evidence that biochemical reactions on the membrane can be reproduced only with spatial stochastic simulations. In addition to the discussed phenomena, in which local stochastic fluctuations lead to global state-to-state transitions not captured by deterministic reaction–diffusion equations, we found that in the discrete system the effective reaction rates are controlled by the diffusion. It can be observed that, in the case of slow diffusion, the more effective processive phosphorylation mode prevails over the less efficient distributive mechanism, boosting the system's activity [59,60]. Additionally, molecular crowding (and self-crowding), which is reflected explicitly in our lattice-based simulations and is expected to be significant at assumed surface densities of reacting molecules, facilitates consecutive phosphorylation events [61,62]. In the well-mixed approximation, kinases are dephosphorylated at the rate proportional to the product of phosphatase activity and the number of phosphatases. Phosphatases, which are modelled explicitly in spatial simulations, can become unemployed after dephosphorylating all their neighbouring kinases, resulting in the reduction of their effective enzymatic activity [63].
The applied method of on-lattice KMC simulates the master equation in continuous time and discretized space at the single event and single molecule resolution. For large systems, such simulations are inevitably computationally demanding, but provide accurate estimations of MFPTs, which are crucial for the performed analysis. Spatially or temporally coarse-grained algorithms have lower computational cost but also lower, in fact unknown, accuracy. The results presented in this paper consumed years of aggregate CPU time of a computer cluster, but in the hope that they could be used to calibrate faster approximate algorithms.
In summary, transitions in a bistable system on the membrane employ both stochastic and deterministic effects. Transitions between macroscopic steady states of spatially extended systems are qualitatively different from transitions available in well-mixed compartments. These transitions employ travelling waves that can be initiated spontaneously as a result of stochastic fluctuations. We demonstrated that the SPD and MFPTs depend strongly on the diffusion coefficient, size and shape of the reactor. These factors (in addition to reaction rates) decide the activity (or inactivity) of a spatially extended bistable system.
Acknowledgements
This study was supported by the Foundation for Polish Science grant TEAM/2009-3/6 and Polish Ministry of Science and Higher Education grant no. N N501 13 29 36. Numerical simulations of on-lattice KMC were carried out at the Zeus computer cluster at the ACK Cyfronet AGH in Kraków and at the Grafen computer cluster of the Ochota Biocentre in Warsaw.
References
- 1.Huang S, Eichler G, Bar-Yam Y, Ingber DE. 2005. Cell fates as high-dimensional attractor states of a complex gene regulatory network. Phys. Rev. Lett. 94, 128701. 10.1103/PhysRevLett.94.128701 (doi:10.1103/PhysRevLett.94.128701) [DOI] [PubMed] [Google Scholar]
- 2.Ozbudak EM, Thattai M, Lim HN, Shraiman BI, Oudenaarden AV. 2004. Multistability in the lactose utilization network of Escherichia coli. Nature 427, 737–740 10.1038/nature02298 (doi:10.1038/nature02298) [DOI] [PubMed] [Google Scholar]
- 3.Smits WK, Kuipers OP, Veening J-W. 2006. Phenotypic variation in bacteria: the role of feedback regulation. Nat. Rev. Microbiol. 4, 259–271 10.1038/nrmicro1381 (doi:10.1038/nrmicro1381) [DOI] [PubMed] [Google Scholar]
- 4.Ferrell JE. 2002. Self-perpetuating states in signal transduction: positive feedback, double-negative feedback and bistability. Curr. Opin. Cell Biol. 14, 140–148 10.1016/S0955-0674(02)00314-9 (doi:10.1016/S0955-0674(02)00314-9) [DOI] [PubMed] [Google Scholar]
- 5.Das J, Ho M, Zikherman J, Govern C, Yang M, Weiss A, Chakraborty AK, Roose JP. 2009. Digital signaling and hysteresis characterize Ras activation in lymphoid cells. Cell 136, 337–351 10.1016/j.cell.2008.11.051 (doi:10.1016/j.cell.2008.11.051) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.van Kampen N. 2007. Stochastic processes in physics and chemistry. Amsterdam, The Netherlands: Elsevier [Google Scholar]
- 7.Gardiner CW. 1985. Handbook of stochastic methods for physics, chemistry and the natural sciences, 2nd edn Berlin, Germany: Springer [Google Scholar]
- 8.Nicolis G, Prigogine I. 1977. Self-organization in non-equilibrium systems. Hoboken, NJ: Wiley [Google Scholar]
- 9.Vellela M, Qian H. 2009. Stochastic dynamics and non-equilibrium thermodynamics of a bistable chemical system: the Schlögl model revisited. J. R. Soc. Interface 6, 925–940 10.1098/rsif.2008.0476 (doi:10.1098/rsif.2008.0476) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kasai RS, Suzuki KGN, Prossnitz ER, Koyama-Honda I, Nakada C, Fujiwara TK, Kusumi A. 2011. Full characterization of GPCR monomer–dimer dynamic equilibrium by single molecule imaging. J. Cell. Biol. 192, 463–480 10.1083/jcb.201009128 (doi:10.1083/jcb.201009128) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kalay Z, Fujiwara TK, Kusumi A. 2012. Confining domains lead to reaction bursts: reaction kinetics in the plasma membrane. PLoS ONE 7, e32948. 10.1371/journal.pone.0032948 (doi:10.1371/journal.pone.0032948) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Elowitz MB, Surette MG, Wolf PE, Stock JB, Leibler S. 1999. Protein mobility in the cytoplasm of Escherichia coli. J. Bacteriol. 181, 197–203 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ramadurai S, Holt A, Krasnikov V, van den Bogaart G, Killian JA, Poolman B. 2009. Lateral diffusion of membrane proteins. J. Am. Chem. Soc. 131, 12 650–12 656 10.1021/ja902853g (doi:10.1021/ja902853g) [DOI] [PubMed] [Google Scholar]
- 14.Faeder JR, Hlavacek WS, Reischl I, Blinov ML, Metzger H, Redondo A, Wofsy C, Goldstein B. 2003. Investigation of early events in FcɛRI-mediated signaling using a detailed mathematical model. J. Immunol. 170, 3769–3781 [DOI] [PubMed] [Google Scholar]
- 15.Bishop LM, Qian H. 2010. Stochastic bistability and bifurcation in a mesoscopic signaling system with autocatalytic kinase. Biophys. J. 98, 1–11 10.1016/j.bpj.2009.09.055 (doi:10.1016/j.bpj.2009.09.055) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Murray JD. 2007. Mathematical biology. New York, NY: Springer [Google Scholar]
- 17.Nicolis G, Lefever R. 1977. Comment on the kinetic potential and the Maxwell construction in non-equilibrium chemical phase transitions. Phys. Lett. A 62, 469–471 10.1016/0375-9601(77)90069-X (doi:10.1016/0375-9601(77)90069-X) [DOI] [Google Scholar]
- 18.Baras F, Malek Mansour M. 1997. Microscopic simulations of chemical instabilities. Adv. Chem. Phys. 100, 393–474 10.1002/9780470141595.ch5 (doi:10.1002/9780470141595.ch5) [DOI] [Google Scholar]
- 19.Ge H, Qian H. 2009. Thermodynamic limit of a nonequilibrium steady state: Maxwell-type construction for a bistable biochemical system. Phys. Rev. Lett. 103, 148103. 10.1103/PhysRevLett.103.148103 (doi:10.1103/PhysRevLett.103.148103) [DOI] [PubMed] [Google Scholar]
- 20.Zuk PJ, Kochańczyk M, Jaruszewicz J, Bednorz W, Lipniacki T. 2012. Dynamics of a stochastic spatially extended system predicted by comparing deterministic and stochastic attractors of the corresponding birth–death process. Phys. Biol. 9, 055002. 10.1088/1478-3975/9/5/055002 (doi:10.1088/1478-3975/9/5/055002) [DOI] [PubMed] [Google Scholar]
- 21.Baras F, Malek Mansour M, Pearson JE. 1996. Microscopic simulation of chemical bistability in homogeneous systems. J. Chem. Phys. 105, 8257–8261 10.1063/1.472679 (doi:10.1063/1.472679) [DOI] [Google Scholar]
- 22.Bird GA. 1994. Molecular gas dynamics and the direct simulation of gas flows. Oxford, UK: Clarendon [Google Scholar]
- 23.Stamatakis M, Vlachos DG. 2011. Equivalence of on-lattice stochastic chemical kinetics with the well-mixed chemical master equation in the limit of fast diffusion. Comput. Chem. Eng. 35, 2602–2610 10.1016/j.compchemeng.2011.05.008 (doi:10.1016/j.compchemeng.2011.05.008) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Potma EO, de Boeij WP, Bosgraaf L, Roelofs J, van Haastert PJ, Wiersma DA. 2001. Reduced protein diffusion rate by cytoskeleton in vegetative and polarized dictyostelium cells. Biophys. J. 81, 2010–2019 10.1016/S0006-3495(01)75851-1 (doi:10.1016/S0006-3495(01)75851-1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sbalzarini IF, Mezzacasa A, Helenius A, Koumoutsakos P. 2005. Effects of organelle shape on fluorescence recovery after photobleaching. Biophys. J. 89, 1482–1492 10.1529/biophysj.104.057885 (doi:10.1529/biophysj.104.057885) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Luby-Phelps K. 2000. Cytoarchitecture and physical properties of cytoplasm: volume, viscosity, diffusion, intracellular surface area. Int. Rev. Cytol. 192, 189–221 10.1016/S0074-7696(08)60527-6 (doi:10.1016/S0074-7696(08)60527-6) [DOI] [PubMed] [Google Scholar]
- 27.Lu S, Ouyang M, Seong J, Zhang J, Chien S, Wang Y. 2008. The spatiotemporal pattern of Src activation at lipid rafts revealed by diffusion-corrected FRET imaging. PLoS Comput. Biol. 4, e1000127. 10.1371/journal.pcbi.1000127 (doi:10.1371/journal.pcbi.1000127) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kalwarczyk T, et al. 2011. Comparative analysis of viscosity of complex liquids and cytoplasm of mammalian cells at the nanoscale. Nano Lett. 11, 2157–2163 10.1021/nl2008218 (doi:10.1021/nl2008218) [DOI] [PubMed] [Google Scholar]
- 29.Altschuler SJ, Angenent SB, Wang Y, Wu LF. 2008. On the spontaneous emergence of cell polarity. Nature 454, 886–889 10.1038/nature07119 (doi:10.1038/nature07119) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Jilkine A, Angenent SB, Wu LF, Altschuler SJ. 2011. A density-dependent switch drives stochastic clustering and polarization of signaling molecules. PLoS Comput. Biol. 7, e1002271. 10.1371/journal.pcbi.1002271 (doi:10.1371/journal.pcbi.1002271) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Das J, Kardar M, Chakraborty AK. 2009. Positive feedback regulation results in spatial clustering and fast spreading of active signaling molecules on a cell membrane. J. Chem. Phys. 130, 245102. 10.1063/1.3149861 (doi:10.1063/1.3149861) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Postma M, Roelofs J, Goedhart J, Gadella TWJ, Visser AJWG, Haastert PJMV. 2003. Uniform cAMP stimulation of Dictyostelium cells induces localized patches of signal transduction and pseudopodia. Mol. Biol. Cell. 14, 5019–5027 10.1091/mbc.E03-08-0566 (doi:10.1091/mbc.E03-08-0566) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hecht I, Kessler DA, Levine H. 2010. Transient localized patterns in noise-driven reaction–diffusion systems. Phys. Rev. Lett. 104, 158301. 10.1103/PhysRevLett.104.158301 (doi:10.1103/PhysRevLett.104.158301) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fange D, Elf J. 2006. Noise-induced Min phenotypes in E. coli. PLoS Comput. Biol. 2, e80. 10.1371/journal.pcbi.0020080 (doi:10.1371/journal.pcbi.0020080) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Malek Mansour M, Dethier J, Baras F. 2001. Onset of homogeneous oscillations in reactive systems. J. Chem. Phys. 114, 9265–9275 10.1063/1.1367389 (doi:10.1063/1.1367389) [DOI] [Google Scholar]
- 36.Lee S-JR, Escobedo-Lozoya Y, Szatmari EM, Yasuda R. 2009. Activation of CaMKII in single dendritic spines during long-term potentiation. Nature 458, 299–304 10.1038/nature07842 (doi:10.1038/nature07842) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Elf J, Ehrenberg M. 2004. Spontaneous separation of bi-stable biochemical systems into spatial domains of opposite phases. Syst. Biol. 1, 230–236 10.1049/sb:20045021 (doi:10.1049/sb:20045021) [DOI] [PubMed] [Google Scholar]
- 38.Arai Y, Shibata T, Matsuoka S, Sato JM, Yanagida T, Ueda M. 2010. Self-organization of the phosphatidylinositol lipids signaling system for random cell migration. Proc. Natl Acad. Sci. USA 107, 12 399–12 404 10.1073/pnas.0908278107 (doi:10.1073/pnas.0908278107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mori Y, Jilkine A, Edelstein-Keshet L. 2008. Wave-pinning and cell polarity from a bistable reaction–diffusion system. Biophys. J. 94, 3684–3697 10.1529/biophysj.107.120824 (doi:10.1529/biophysj.107.120824) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Walther GR, Marée AFM, Edelstein-Keshet L, Grieneisen VA. 2012. Deterministic versus stochastic cell polarisation through wave-pinning. Bull. Math. Biol. 74, 2570–2599 10.1007/s11538-012-9766-5 (doi:10.1007/s11538-012-9766-5) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Xiong Y, Huang C-H, Iglesias PA, Devreotes PN. 2010. Cells navigate with a local-excitation, global-inhibition-biased excitable network. Proc. Natl Acad. Sci. USA 107, 17 079–17 086 10.1073/pnas.1011271107 (doi:10.1073/pnas.1011271107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Jilkine A, Edelstein-Keshet L. 2011. A comparison of mathematical models for polarization of single eukaryotic cells in response to guided cues. PLoS Comput. Biol. 7, e1001121. 10.1371/journal.pcbi.1001121 (doi:10.1371/journal.pcbi.1001121) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Huang Q, Qian H. 2009. Ultrasensitive dual phosphorylation dephosphorylation cycle kinetics exhibits canonical competition behavior. Chaos 19, 033109. 10.1063/1.3187790 (doi:10.1063/1.3187790) [DOI] [PubMed] [Google Scholar]
- 44.Lisman JE. 1985. A mechanism for memory storage insensitive to molecular turnover: a bistable autophosphorylating kinase. Proc. Natl Acad. Sci. USA 82, 3055–3057 10.1073/pnas.82.9.3055 (doi:10.1073/pnas.82.9.3055) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Markevich NI, Hoek JB, Kholodenko BN. 2004. Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J. Cell. Biol. 164, 353–359 10.1083/jcb.200308060 (doi:10.1083/jcb.200308060) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wilhelm T. 2009. The smallest chemical reaction system with bistability. BMC Syst. Biol. 3, 90. 10.1186/1752-0509-3-90 (doi:10.1186/1752-0509-3-90) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Schlögl F. 1971. On thermodynamics near a steady state. Z. Physik. 248, 446–458 10.1007/BF01395694 (doi:10.1007/BF01395694) [DOI] [Google Scholar]
- 48.Ferrell JE, Xiong W. 2001. Bistability in cell signaling: how to make continuous processes discontinuous, and reversible processes irreversible. Chaos 11, 227–236 10.1063/1.1349894 (doi:10.1063/1.1349894) [DOI] [PubMed] [Google Scholar]
- 49.Phillips R, Ursell T, Wiggins P, Sens P. 2009. Emerging roles for lipids in shaping membrane-protein function. Nature 459, 379–385 10.1038/nature08147 (doi:10.1038/nature08147) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Gillespie DT. 1977. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81, 2340–2361 10.1021/j100540a008 (doi:10.1021/j100540a008) [DOI] [Google Scholar]
- 51.Lawless JF. 2003. Statistical models and methods for lifetime data. Hoboken, NJ: Wiley-Interscience [Google Scholar]
- 52.Kuramoto Y. 1974. Effects of diffusion on the fluctuations in open chemical systems. Prog. Theor. Phys. 52, 711–713 10.1143/PTP.52.711 (doi:10.1143/PTP.52.711) [DOI] [Google Scholar]
- 53.Zheng Q, Ross J, Hunt KLC, Hunt PM. 1992. Stationary solutions of the master equation for single and multi-intermediate autocatalytic chemical systems. J. Chem. Phys. 96, 630–640 10.1063/1.462446 (doi:10.1063/1.462446) [DOI] [Google Scholar]
- 54.Alessi DR, Saito Y, Campbell DG, Cohen P, Sithanandam G, Rapp U, Ashworth A, Marshall CJ, Cowley S. 1994. Identification of the sites in MAP kinase kinase-1 phosphorylated by p74raf-1. EMBO J. 13, 1610–1619 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hat B, Kazmierczak B, Lipniacki T. 2011. B cell activation triggered by the formation of the small receptor cluster: a computational study. PLoS Comput. Biol. 7, e1002197. 10.1371/journal.pcbi.1002197 (doi:10.1371/journal.pcbi.1002197) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Wang Q, Zhang X, Zhang L, He F, Zhang G, Jamrich M, Wensel TG. 2008. Activation-dependent hindrance of photoreceptor G protein diffusion by lipid microdomains. J. Biol. Chem. 283, 30 015–30 024 10.1074/jbc.M803953200 (doi:10.1074/jbc.M803953200) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Abel SM, Roose JP, Groves JT, Weiss A, Chakraborty AK. 2012. The membrane environment can promote or suppress bistability in cell signaling networks. J. Phys. Chem. B 116, 3630–3640 10.1021/jp2102385 (doi:10.1021/jp2102385) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Jaruszewicz J, Zuk PJ, Lipniacki T. 2013. Type of noise defines global attractors in bistable molecular regulatory systems. J. Theor. Biol. 317, 140–151 10.1016/j.jtbi.2012.10.004 (doi:10.1016/j.jtbi.2012.10.004) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Takahashi K, Tanase-Nicola S, ten Wolde PR. 2010. Spatio-temporal correlations can drastically change the response of a MAPK pathway. Proc. Natl Acad. Sci. USA 107, 2473–2478 10.1073/pnas.0906885107 (doi:10.1073/pnas.0906885107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Mugler A, Bailey AG, Takahashi K, ten Wolde PR. 2012. Membrane clustering and the role of rebinding in biochemical signaling. Biophys. J. 102, 1069–1078 10.1016/j.bpj.2012.02.005 (doi:10.1016/j.bpj.2012.02.005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Zhou H-X. 2009. Crowding effects of membrane proteins. J. Phys. Chem. B 113, 7995–8005 10.1021/jp8107446 (doi:10.1021/jp8107446) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Aoki K, Yamada M, Kunida K, Yasuda S, Matsuda M. 2011. Processive phosphorylation of ERK MAP kinase in mammalian cells. Proc. Natl Acad. Sci. USA 108, 12 675–12 680 10.1073/pnas.1104030108 (doi:10.1073/pnas.1104030108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Dushek O, van der Merwe PA, Shahrezaei V. 2011. Ultrasensitivity in multisite phosphorylation of membrane-anchored proteins. Biophys. J. 100, 1189–1197 10.1016/j.bpj.2011.01.060 (doi:10.1016/j.bpj.2011.01.060) [DOI] [PMC free article] [PubMed] [Google Scholar]