Computational fluid dynamic simulations of image-based stented coronary bifurcation models

Abstract

One of the relevant phenomenon associated with in-stent restenosis in coronary arteries is an altered haemodynamics in the stented region. Computational fluid dynamics (CFD) offers the possibility to investigate the haemodynamics at a level of detail not always accessible within experimental techniques. CFD can quantify and correlate the local haemodynamics structures which might lead to in-stent restenosis. The aim of this work is to study the fluid dynamics of realistic stented coronary artery models which replicate the complete clinical procedure of stent implantation. Two cases of pathologic left anterior descending coronary arteries with their bifurcations are reconstructed from computed tomography angiography and conventional coronary angiography images. Results of wall shear stress and relative residence time show that the wall regions more prone to the risk of restenosis are located next to stent struts, to the bifurcations and to the stent overlapping zone for both investigated cases. Considering a bulk flow analysis, helical flow structures are generated by the curvature of the zone upstream from the stent and by the bifurcation regions. Helical recirculating microstructures are also visible downstream from the stent struts. This study demonstrates the feasibility to virtually investigate the haemodynamics of patient-specific coronary bifurcation geometries.

1. Introduction

Computational fluid dynamics (CFD) offers the possibility to investigate local haemodynamics of stented coronary artery bifurcations at a level of detail not always accessible with experimental techniques [1]. The increasing impact of CFD in studying the haemodynamics in stented arteries with great resolution is based on the widely accepted evidence that the biological processes leading to stent failure (e.g. in-stent restenosis) have been found to be partially flow-dependent [2]. For this reason, in recent years, sophisticated numerical models have been proposed in the literature, considering coronary bifurcations and introducing increasingly refined haemodynamic indicators for the risk of restenosis. Williams et al. [3] quantified altered fluid dynamics due to main branch (MB) stenting with and without subsequent side branch (SB) angioplasty that removed struts from the ostium of a representative coronary bifurcation. The geometry of their bifurcation model was ideal, and the stent was simply drawn inside the MB. Consequently, the fluid domain was based purely on geometrical assumptions. To take into account vessel deformation during stent implantation, Morlacchi et al. [4] proposed a sequential structural and fluid dynamic approach. First, the provisional side branch (PSB) technique, which nowadays is the preferred coronary bifurcation stenting technique [5], was simulated in an ideal coronary bifurcation through structural simulations. Second, the final geometrical configurations obtained through structural simulations were used as fluid domains to perform transient fluid dynamic analyses. A further study based on the same sequential approach was proposed by Chiastra et al. [6]. The authors examined the different haemodynamic scenarios provoked by the final kissing balloon (FKB) inflation performed with a proximal or a distal access to the SB. This procedure consists of the simultaneous expansion of two balloons in both the branches and usually concludes the PSB [7]. The haemodynamic influence of the FKB was also studied by Foin et al. [8] comparing this technique with a simpler two-step sequential post-dilatation of the SB and MB. In vitro models where stents were deployed replicating clinical implanting procedures were used as a starting point to create the numerical models.

Although the models proposed in the above-mentioned works are sophisticated, patient-specific geometries are not considered, limiting the discussion to a comparison between different techniques. Only two recent works have reconstructed the fluid domains from patient-specific data. Gundert et al. [9] developed a method to virtually draw a stent in a left anterior descending (LAD) coronary artery model created from computed tomography (CT) scans. Two different stent designs (an open-cell ring-and-link design and a close-cell slotted tube prototype design) were compared from the fluid dynamic point of view. In a further study by the same research group [10], the fluid dynamics of a stented left circumflex coronary artery with a thrombus was investigated. The geometry of the vessel was reconstructed combining optical coherence tomography (OCT) and CT images, whereas the stent was drawn inside the artery applying their previously developed method [9]. Those two works are affected by the same limitation: the deformation provoked by stent implantation is not considered, probably leading to an altered quantification of the local haemodynamics.

In this context, the aim of this work is to study the fluid dynamics in image-based stented coronary artery models which replicate the complete clinical procedure of stent implantation, with particular emphasis on how local haemodynamic structures might influence flow-related processes leading to restenosis. In particular, two cases of pathologic LAD with their bifurcations treated at University Hospital Doctor Peset (Valencia, Spain) are studied. The vessels are reconstructed using the pre-operative computed tomography angiography (CTA) and conventional coronary angiography (CCA) images [11]. Then, the fluid domains are obtained from the structural simulations which replicate the stenting procedures followed by the clinicians who performed the interventions [12].

Both near-wall and bulk-flow quantities are investigated, thus providing a complete study of the haemodynamics of the two analysed cases. Specific ranges of the wall shear stresses (WSS) and the other near-wall quantities such as the oscillatory shear index (OSI) or the relative residence time (RRT) have shown to be stimuli for the processes which can cause restenosis [13]. As for the impact that the stenting procedure has on bulk flow, here we focus on the analysis of helical flow, which is a peculiar feature of the natural blood flow present in arteries [14,15], and which has been recently found to be instrumental in suppressing flow disturbances, both in healthy vessels [16] and in stented arteries and bypass grafts [2,17–19].

2. Material and methods

2.1. Fluid dynamic models

The haemodynamics of two clinical cases of adult females treated with a provisional T-stenting technique without FKB inflation was studied. Case A involves the proximal section of the LAD, whereas case B both the proximal and mid-part of the LAD. Two different cobalt–chromium alloy drug-eluting stents were used in the interventions. In case A, the Xience Prime (Abbott Laboratories, Abbott Park, IL) was implanted. This device is characterized by an external diameter of 1.76 mm (uncrimped configuration), a length of 28 mm and a strut thickness of 81 µm. In case B, two Endeavor Resolute (Medtronic, Minneapolis, MN) were deployed. These devices have an external diameter of 1.6 mm (uncrimped configuration), a length of 15 mm and strut thickness of 91 µm.

Pre-treatment CTA and CCA were used to create the internal surfaces of the pre-stenting geometries following the methodology proposed by Cárdenes et al. [11]. The combination of these two modalities provides a more realistic reconstruction than just using one of them alone. CTA gives the three-dimensional trajectories followed by the arteries while CCA gives accurate lumen radius estimations. The internal surfaces were used to construct three-dimensional solid models of the two investigated coronary bifurcations (figure 1a) [12]. The external wall surfaces were created by smoothly connecting circumferential cross sections perpendicular to the centre lines of the models using the CAD software Rhinoceros v. 4.0 Evaluation (McNeel & Associates, Indianapolis, IN) [12]. The diameters of the external walls were chosen in order to comply with the internal diameter and wall thickness of arterial branches investigated in a physiological healthy state [20].

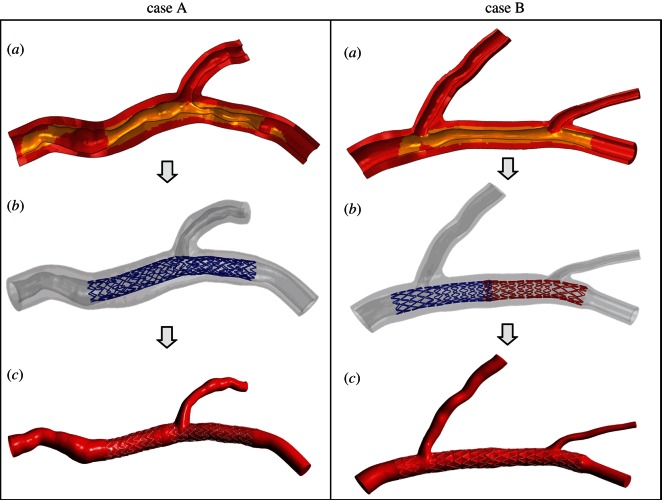
Figure 1.

(a) Sectional view of the three-dimensional solid models of case A (left panel) and case B (right panel). The arterial wall is coloured red (dark grey in the printed version of the article) and the plaques are coloured yellow (light grey in the printed version). (b) Final geometrical configurations obtained through structural simulations that replicate all the stent implantation steps performed by the clinicians. (c) Fluid domains extracted from structural simulations in (b). (Online version in colour.)

Subsequently, structural simulations which replicate all the stent implantation steps performed by the clinicians were carried out by means of the finite-element commercial software Abaqus (Dassault Systemes Simulia Corp., RI) (figure 1b) [4,12,21]. Two CAD models were created resembling the stents implanted during the interventions and including the real cross-section geometry, namely squared for Xience Prime and circular for the Endeavor Resolute. The atherosclerotic plaques were considered and they were appropriately defined with an identification process based on the calculation of the distance between each structural mesh node and the centre line of the external wall. A comprehensive description on these patient-specific structural models may be found in Morlacchi et al. [12].

Lastly, the final geometrical configurations obtained through the structural simulations were used as fluid domain to perform the fluid dynamic analyses (figure 1c) [4]. The fluid domains are characterized by the following dimensions: regarding case A, the inlet diameter is 3.36 mm, whereas the diameter of the outlet of MB is 2.33 mm and of SB is 1.52 mm; for case B, the inlet diameter is 3.45 mm, the diameter of the outlet of the MB is 1.97 mm and the diameters of the SB are 2.13 and 0.90 mm, respectively, for the first bifurcation and the second bifurcation.

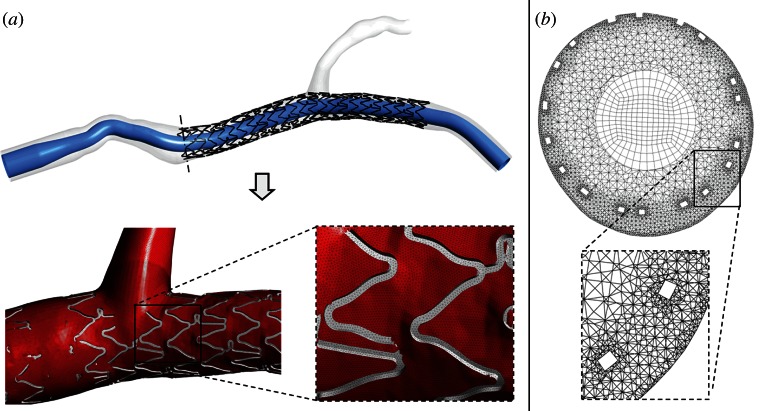
In order to reduce the computational time a hybrid discretization method [6] which uses both tetrahedral and hexahedral elements was applied using ANSYS ICEM CFD v. 14.0 (ANSYS Inc., Canonsburg, PA) (figure 2). A curved internal cylinder was created inside the geometrical models following the tortuous centre line of the MB of each analysed case (figure 2a). This cylinder was meshed with only hexahedral elements, whereas the region between the cylinder and the arterial wall was discretized with tetrahedral elements which can easily adapt to highly complex geometries such as the stent struts (figure 2b). A layer of pyramidal elements was created at the common interface of the hexahedral and tetrahedral meshes to make them conformal. The final meshes used in the work have 8 869 716 and 7 527 350 elements (1 633 883 and 1 387 985 nodes), respectively, for case A and B. The squared stent struts of case A are discretized by five to eight elements on each side of the strut, whereas the circular struts of case B by about 25 elements, radially.

Figure 2.

(a) Generation process of the hybrid mesh: first, an internal cylinder is created inside the geometrical model and discretized using hexahedral elements (top); second, the region between the cylinder and the arterial wall is meshed with tetrahedral mesh obtaining the final grid (bottom). (b) Example of a cross section of the proximal region of case A characterized by the hybrid mesh. Hexahedral elements are clearly visible in the core region of the section. Tetrahedral elements are present in the external regions and they are smaller near the wall and the stent struts. It is possible to notice that the top stent struts are in contact with the arterial wall while the bottom struts are malapposed. A magnification of the tetrahedral mesh around two malapposed struts is shown in the box. (Online version in colour.)

Transient fluid dynamic simulations were carried out by means of ANSYS Fluent v. 14.0 (ANSYS Inc.). At the inlet cross section, a pulsatile flow tracing which is representative of a human LAD (figure 3) [22] was applied as a paraboloid-shaped velocity profile. The flow curve amplitude was tuned on the inlet diameters of the two analysed cases in order to obtain the average flow rate calculated through the equation proposed by van der Giessen et al. [23]:

2.1

where q is the flow and d is the diameter of the coronary artery. The coefficients of this equation were obtained by van der Giessen and co-workers fitting the data of blood flow of 18 human coronary bifurcations [24] by means of a nonlinear regression analysis. From these data, the blood flow and diameter for each coronary branch were calculated assuming a parabolic flow profile and circular vessel area [23]. Applying equation (2.1), an average flow rate of 42.2 ml min⁻¹ was calculated for case A and 45.1 ml min⁻¹ for case B.

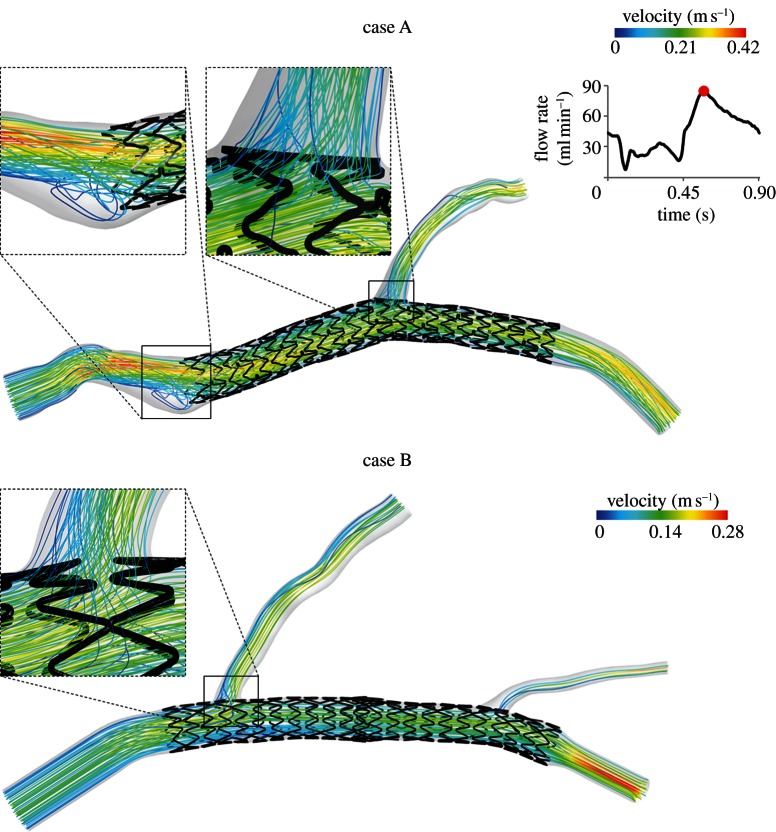
Figure 3.

Velocity streamlines for case A (top) and B (bottom) at the peak of flow rate. In the magnification boxes of case A, an evident recirculation and stagnation zone near the external side (left) and the disturbed flow through the stent struts near the bifurcation region (right) are clearly detectable. In the magnification box of case B, the flow passing through the struts of the first bifurcation is evident. On the top right, the shape of the flow waveform which was applied at the inlet section of the models is shown. The flow curve amplitude was scaled on inlet diameters of each case to obtain the average flow rate calculated through the relations by van der Giessen et al. [23]. (Online version in colour.)

The same measurements [24] were used by van der Giessen et al. [23] to derive the relation between the diameter ratio of two daughter branches and the flow ratio through the branches:

2.2

where q_D1 and q_D2 are respectively the flow through the daughter branches D₁ and D₂. Starting from equation (2.2), the following flow splits were imposed to the models: case A, 72.8 per cent for the MB and 27.2 per cent for the SB; case B, 57.6 per cent for the MB, 32.9 per cent for the proximal SB and 9.5 per cent for the distal SB.

The no-slip boundary condition was applied to all the surfaces representing the arterial wall and the stent struts. The arterial wall and the stents were assumed to be rigid. The blood density was considered constant with a value of 1060 kg m⁻³. The non-Newtonian nature of the flow was taken into account using the Carreau model written as:

2.3

where μ is the dynamic viscosity, μ₀ and μ_∞ are the viscosity values as the shear rate goes to infinity and zero, 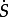is the shear rate, λ is the time constant and n is the power-law index. The following Carreau model values were used in this work [25]: μ_∞ = 0.0035 Pa s, μ₀ = 0.25 Pa s, λ = 25 s and n = 0.25.

The flow was assumed to be laminar because the maximum Reynolds number was 195 for case A and 260 case B at the peak of flow rate (79.1 ml min⁻¹, and 84.7 ml min⁻¹, respectively). These values are an order of magnitude smaller than the Reynolds number for transition to turbulence (2300–4000) and hence justify consideration of flow to be laminar. The Womersley number was approximately 1.9 for case A and 1.4 for case B.

A coupled solver was used with a second-order upwind scheme for the momentum spatial discretization and second-order implicit scheme for the time. The flow Courant number was set to 50. The under-relaxation factors were set to 0.15 for the pressure and the momentum and to 1 for density. Convergence criterion was set to 10⁻⁵ for continuity and 10⁻⁶ for velocity residuals. A time step of 0.009 s was chosen for running the simulations (100 time steps were necessary for one cardiac cycle). This time step is sufficient to ensure temporal convergence [6]. One cardiac cycle was simulated. As verified in previous studies [4,6], stand-alone fluid dynamic analyses without coupling with lumped parameter models that represent the downstream districts do not require multiple cardiac cycles to guarantee correct results. Computations were performed in parallel on one node of a cluster (two quad-core Intel Xeon CPU E5620 at 2.40 GHz, 24 GB RAM for each node, InfiniBand Mellanox for the main cluster interconnections).

In order to ascertain from simulation results what effects on haemodynamics are due to the stent presence per se and what effects are attributable to the complex vascular geometry, two additional transient simulations in the same geometries of case A and B with the stents removed were also performed. All the simulation settings were kept equal to those applied to case A and B.

As for the quality of the simulated flow fields, a sensitivity analysis was performed on case B in order to ensure the independence of the results on the mesh size. The same procedure as in Chiastra et al. [6] was followed. Briefly, three meshes were considered, from a coarser to a finer one: 4 034 069, 7 527 350 and 11 375 228 elements. Steady-state simulations were performed applying the average flow rate (45.1 ml min⁻¹) at the inflow section. All the other simulation settings were kept equal to those previously described. The different meshes were compared considering the area-weighted average WSS (awa-WSS) in the stented region. As the maximum difference between the intermediate and the finest mesh was lower than 0.5 per cent for the awa-WSS the intermediate mesh (7 527 350 elements) was considered sufficiently accurate for the transient simulation. The same meshing strategy was applied to case A.

2.2. Quantities of interest

The primary process leading to in-stent restenosis is the excessive growth of tissue inside the stented region. This process, known as neointimal hyperplasia, is triggered by chemical signals from sources that include endothelial cell damage and dysfunction, platelet adhesion, white blood cell infiltration and smooth muscle cell signalling [13]. Abnormal haemodynamics is a stimulus to neointimal hyperplasia through the production of abnormal stresses on the endothelial cells and also through the increased advection of platelets and white blood cells to the arterial wall [13]. Therefore, different haemodynamic quantities were investigated in this study.

As near-wall quantities, WSS and RRT were calculated. The WSS vector is defined by the following relation:

2.4

where is the normal vector to a surface and is the fluid viscous stress tensor. The WSS is a vector whose magnitude is equal to the viscous stress on the surface, and whose direction is the direction of the viscous stress acting on the surface.

For time-dependent flows, the time-averaged WSS (TAWSS) is introduced. It is defined as

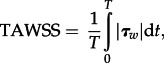2.5

where T is the duration of cardiac cycle. Endothelial cells subjected to WSS greater than 1 Pa tend to elongate and align in the direction of flow, whereas those experiencing WSS lower than 0.4 Pa or oscillatory WSS are circular in shape and do not show any preferred alignment pattern [26]. Those circular cells, coupled with the blood stagnation usually observed in areas of low WSS, lead to increased uptake of blood-borne particles to the arterial wall, which is prevalent in atherosclerosis, as a result of increased residence time and increased permeability of the endothelial layer. It has been demonstrated that tissue growth in a stented coronary artery was prominent at the sites of low WSS [27].

RRT is defined as

2.6

where OSI is calculated as

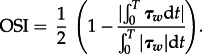2.7

OSI values range between 0, when there is no oscillatory WSS, to 0.5 when there is the maximum oscillatory WSS. Regions of high OSI (greater than 0.1) [3] are associated with an increased risk of neointimal hyperplasia in the stented artery. In particular, sites characterized by high oscillatory WSS have shown a greater risk of arterial narrowing from atherosclerosis [28]. Endothelial permeability to blood-borne particles has also been shown to be increased with high OSI [29]. Oscillatory WSS has led to increased production of the gene endothelin-1 mRNA which increases cell proliferation [30]. In addition, it has been shown that low and oscillatory WSS increases the expression of inflammatory markers including intercellular adhesion molecular (ICAM)-1 and vascular cell adhesion molecule (VCAM)-1 [31,32], thus indicating cell activation. In an experimental work, Yin et al. [33] found that when coronary endothelial cells are exposed to low pulsatile shear stresses, cell surface ICAM-1 expression is significantly enhanced, indicating endothelial cell activation. These results suggested that this haemodynamic condition is an atherogenic one, in agreement also with the findings from other studies [34,35].

RRT was recently introduced to combine the information provided by WSS and OSI [29]. RRT is also associated with the residence time of the particles near the wall [29]. High RRT is recognized as critical for the problem of atherogenesis and in-stent restenosis [36].

The impact of coronary stenting on local haemodynamics was contextualized with respect to the helicity, a quantity successfully applied to quantify the interplay between rotational and translational blood motion in stenosed [37] and healthy arteries [15,16]. Note that helicity-based descriptors have also been recently applied to characterize the onset/interplay of primary and secondary velocities in stented vessels [6,18].

By definition, the helicity H of a fluid flow confined to a domain D of the Euclidean space R³ is given by the integral value of the kinetic helicity density H_k, defined as [38]

2.8

where is the velocity vector and (∇×v) is the vorticity. To achieve a more effective quantity for the visual inspection of topological features of the flow field [16], the kinetic helicity density can be normalized with the velocity and vorticity magnitude resulting in a local normalized helicity (LNH):

2.9

where θ is the angle between and 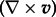. Physically, the non-dimensional quantity LNH describes the arrangement of blood streams into spiral patterns as they evolve within arteries [17]. In fact, by definition, it is a measure of the alignment/misalignment of the local velocity and vorticity vectors and its sign is a useful indicator of the direction of rotation of helical structures: positive (negative) LNH values indicate left (right)-handed rotating fluid structures, when viewed in the direction of forward movement.

2.3. Quantitative analysis of time-averaged wall shear stresses results

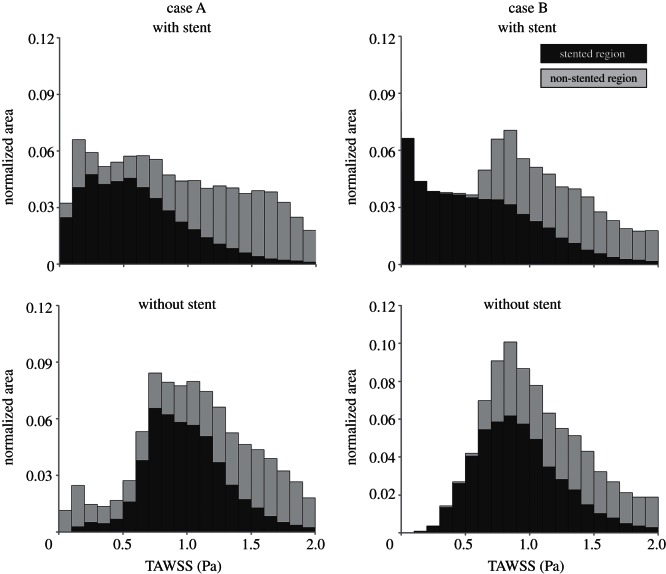
The TAWSS was investigated not only by means of a contour map but also in a quantitative way. In particular, the percentage area exposed to low TAWSS was calculated in the arterial wall which contains the stent (in the following, we refer to it as the ‘stented region’) as the ratio between the area exposed to WSS lower than 0.4 Pa and the total area of the stented region. Moreover, the area distribution of TAWSS was visualized using histograms by displaying the amount of area of the stented region contained between specific intervals of the variable value [6,39]. The area-averaged mean, skewness and kurtosis of the distributions were calculated.

The area-averaged mean of TAWSS is defined as

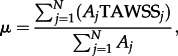2.10

where TAWSS_j is the face-averaged TAWSS value at the face j, A_j is the surface area of the face j and the summation is over N faces.

The area-averaged skewness of the TAWSS distributions is calculated as

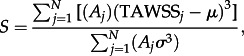2.11

where σ is area-averaged standard deviation calculated as:

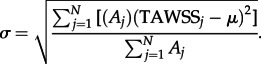2.12

The skewness is a measure of the lack of symmetry of a distribution. The skewness for a normal distribution is zero, and any symmetric data have a skewness near zero. Negative values for the skewness indicate data that are skewed left and positive values for the skewness indicate data that are skewed right.

The area-averaged kurtosis is defined as

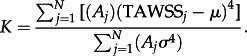2.13

where the terms are as above. Kurtosis characterizes the relative peakedness or flatness of a distribution compared with the normal distribution. Positive kurtosis indicates a relatively peaked distribution. Negative kurtosis indicates a relatively flat distribution.

3. Results

Figure 3 shows the streamlines of the two computational models at the peak of flow rate, coloured by velocity magnitude. The proximal part of case A, immediately before the device, is characterized by a jet with the highest velocity directed towards the stent and an evident recirculation and stagnation zone near the external side (figure 3a). This flow pattern is caused by the particular tortuosity of the vessel. It is also possible to note that the first stent struts are not well apposed to the wall. This aspect is captured by the fluid dynamic model, because the streamlines pass throughout these malapposed struts. Lastly, the flow patterns in the bifurcation regions of the two cases are highlighted. The flow division is clearly visible at the bifurcations; it is possible to observe that the direction of the fluid elements inside these regions is locally modified by the presence of the stent. The stent struts behave as an obstacle to the blood flow inducing a ripple effect on the streamlines (especially in case A).

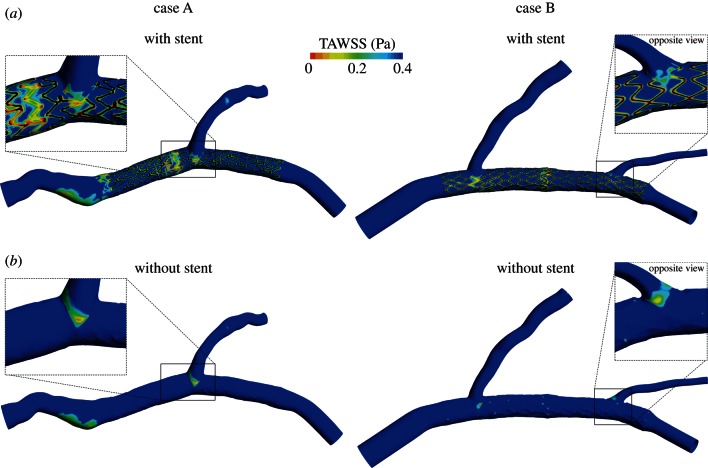
Figure 4 shows the contour maps of TAWSS along the arterial wall for case A and B, with and without stent. Considering the stented cases (figure 4a), low WSS are located next to all the struts in both the models. Moreover, larger areas of low WSS are present near the bifurcations and, for case B, in the overlapping zone between the two stents. The regions outside the stents have WSS higher than 0.4 Pa except the proximal part of case A. In this region, the stagnation zone which results in low WSS is clearly visible. The percentage area exposed to low TAWSS in the stented region is 35.0 per cent and 38.4 per cent, respectively, for case A and B. Considering the cases without stent (figure 4b), low WSS are only located in the regions near the branches and, for case A, in the proximal part of the model. The low WSS spot which appears in the stented region of case B are probably provoked by the surface of the arterial wall which remained lightly pleated after the removal of the stents. The percentage area exposed to low TAWSS in the ‘stented region’ is 2.6 per cent and 3.5 per cent, respectively for case A and B without stent.

Figure 4.

Contour maps of TAWSS along arterial wall for case A (left) and case B (right), with (a) and without (b) the presence of the stents. Low WSS regions are indicated in red (light grey in the printed version of the article). Regions where the stent struts are in contact with the arterial wall are coloured black. (Online version in colour.)

The distribution of TAWSS is presented in figure 5 where dark grey bars refer to the stented region, whereas the light grey bars to the remaining part of the arterial wall (‘non-stented region’). The mean TAWSS value, the skewness and the kurtosis of the distributions are reported in table 1.

Figure 5.

TAWSS distribution in case A (left) and case B (right), with and without the presence of the stents. Each bar of the histograms represents the amount of normalized area with a defined range of TAWSS. Dark grey bars refer to the stented region, whereas the light grey bars to the remaining part of the arterial wall. Bar widths are 0.1 Pa.

Table 1.

Statistical quantities associated with the TAWSS distribution of case A and B, with and without stent: mean, skewness and kurtosis.

		mean (Pa)	skewness	kurtosis
case A (with stent)	stented region	0.599	2.086	13.338
	whole model	1.046	2.010	12.679
(without stent)	stented region	1.020	1.628	10.882
	whole model	1.207	2.205	14.273
case B (with stent)	stented region	0.633	2.901	21.802
	whole model	1.189	1.770	9.732
(without stent)	stented region	0.976	3.834	33.288
	whole model	1.298	2.267	12.548

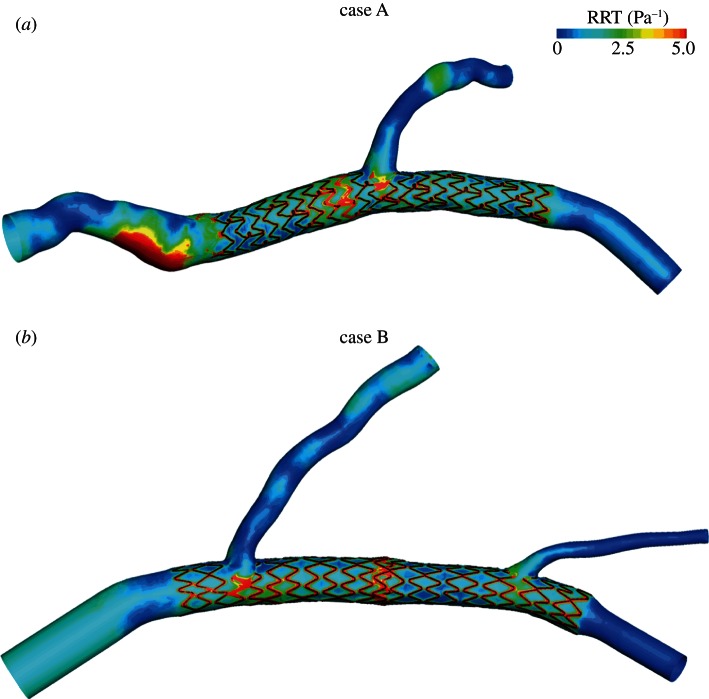
In figure 6, the contour maps of RRT lower than 5 Pa⁻¹ are presented. High values of RRT are located next to all the stent struts, to the bifurcations and to the stent overlapping zone. Also, the stagnation zone of the proximal part of case A is characterized by high RRT.

Figure 6.

Contour maps of RRT for (a) case A and (b) case B. (Online version in colour.)

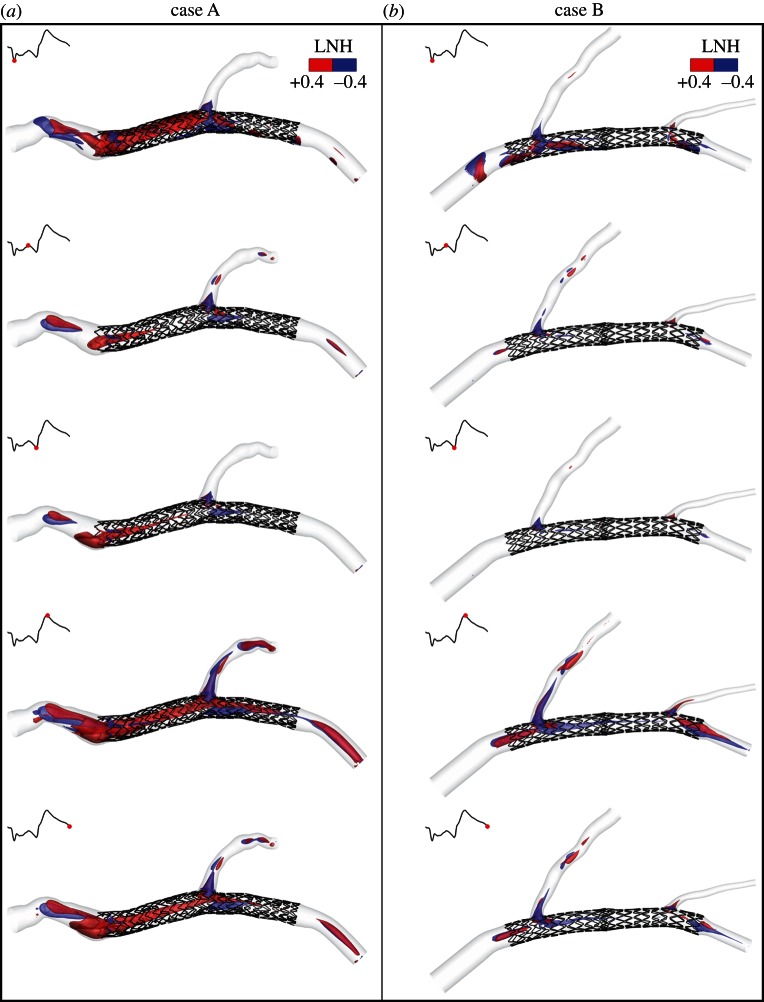
To visualize peculiar topological features in the bulk flow, the mutual orientation of velocity and vorticity vectors, given by LNH, is used. Adopting a threshold value of LNH (±0.4) for the visualization of fluid structures, different topological blood flow features can be observed in figures 7 and 8. As a general observation, in both the two investigated cases helical flow structures originate in the region of the vessel upstream from the stent, with a helicity-generation process which appears to be mainly driven by the curvature, tortuosity and torsion of the non-stented segment upstream from the stented one. This statement is enforced by the observation that: (i) for case A, large LNH isosurface regions appear immediately upstream from the stent, where the flow arrangement consists in counter-rotating helical structures that persist throughout the cardiac cycle due to the tortuous path of the blood flow (figure 7a: left-handed, negative LNH values; right-handed, positive LNH values). Notably, LNH isosurfaces emphasize the flow separation region that has been pointed out previously in figure 3; (ii) for case B, the arrangement of the streaming blood in helical patterns is less marked, most likely because the upstream region in case B is less tortuous than case A (figure 7b).

Figure 7.

Isosurfaces of LNH at five different phases of the cardiac cycle for (a) case A and (b) B. Threshold values of LNH (±0.4) are used for the visualization of the mutual alignment of velocity and vorticity vector fields (i.e. the necessary condition revealing the presence of helical flow structures). Positive and negative LNH values indicate counter-rotating flow structures. (Online version in colour.)

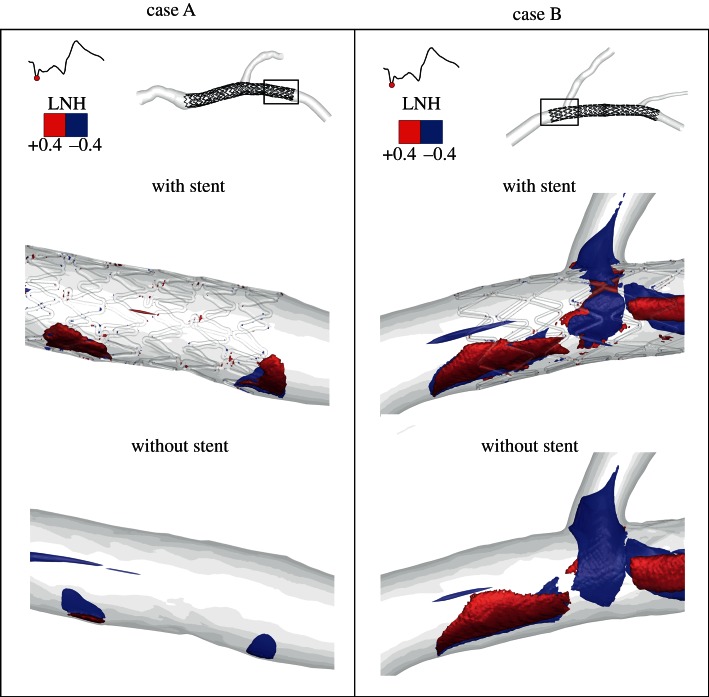
Figure 8.

Example of LNH isosurfaces visualization (LNH = ± 0.4) used to highlight the presence of helical structures at different length scales close to the wall. LNH isosurfaces are relative to the systolic phase. Left panels: case A, with and without stent; right panels: case B, with and without stents. (Online version in colour.)

From figure 7, it emerges also that the straightening of the vessel as induced by the stent implantation determines the gradual disappearance of large helical fluid structures and that the presence of branching vessels is involved in the generation of helical fluid structures, their strength being related to organ perfusion from branch vessels (due to the centripetal spin, i.e. imparted tangential velocities, induced in blood), as previously observed by Frazin et al. [40].

Using LNH for the visualization of the topological features of the flow field, it is possible to observe the impact that the presence of stent struts has on near-wall flow patterns. Figure 8 (top) shows that helical fluid structures at different length scales are present close to the wall, going from the order of magnitude of strut dimensions to larger structures. These larger helical structures are also present in the correspondent cases without stent (figure 8 bottom), whereas the small structures are absent.

4. Discussion

The mechanisms and the causes of in-stent restenosis in coronary arteries are not fully understood. One of the most relevant phenomena which seems to be associated with the formation of neointimal hyperplasia is an altered haemodynamics in the stented wall region which leads to persistent low WSS [41]. Local measurements of the velocities and velocity gradients in human coronary arteries in vivo are very difficult and can therefore not be applied to map the shear stress distribution at the wall [41]. Alternatively, virtual models of patient-specific coronary arteries enable local fluid dynamics to be studied and calculation of the WSS and other quantities, which can be related to the risk of restenosis. As a consequence, these models also give some indications to the clinicians.

In this work, a comprehensive study of the fluid dynamics of two image-based stented coronary models was carried out. Looking at the near-wall quantities, both the stented cases are characterized by low WSS next to the struts (figure 4), in agreement with the findings by Gundert et al. [9] and Ellwein et al. [10]. In particular, for each repeating stent cell, the values of TAWSS increase from the zones near the stent struts towards the centre of each cell, as previously found in other studies [42,43].

A wider area with low TAWSS is present in the region close to the branches. This is due to vessel geometry and not to the presence of stents. In fact, the wider area with low TAWSS is evident both in the cases with stent and in the correspondent cases without stent (figure 4). As experimentally observed in left and right human coronary arteries by Asakura & Karino [44], the flow in the proximity of the outer wall of the branches is slow with the formation of slow recirculation and secondary flows which lead to low WSS in those zones.

A wider area characterized by low TAWSS is also visible in the stent overlapping zone of case B. In this zone, stent struts protrude inside the lumen in a more marked way compared with the other stented regions. The protrusion locally generates a more disturbed flow, with the consequence that a wider area is subjected to low TAWSS.

Considering the stented region, the percentage area exposed to values of TAWSS lower than 0.4 Pa, which are strongly correlated with endothelial permeability and can promote neointimal hyperplasia [26,45], is significant: 35 per cent for case A and 38.4 per cent for case B. This result is also evident in the TAWSS distributions (figure 5 top, dark grey bars). As reported in table 1, these distributions are characterized by a similar value of area-averaged mean TAWSS (about 0.6 Pa), but the distribution of case B is more peaked (higher kurtosis value) and more skewed to the right (higher skewness value). This means that the entire stented wall region of case B is characterized by a larger area with low WSS and, from a merely fluid dynamic point of view, might be more prone to the risk of restenosis.

In case A, the region immediately before the stent shows values of TAWSS lower than 0.4 Pa. This is due to the marked tortuosity of the vessel which causes the formation of an evident recirculation and stagnation zone (figure 3a). The contribution of this region to low TAWSS distribution can be appreciated looking at the light grey bars in figure 5 (top). This contribution is lower if compared with the one caused by the stent presence. In case B, the contribution of the non-stented vessel segments to TAWSS lower than 0.4 Pa is almost zero. These results confirm that the regions of the arterial wall with low TAWSS are mainly induced by the presence of the stents.

Comparing the TAWSS distributions of cases with and without the stent presence, it can be appreciated that the stent induces lower TAWSS values at the arterial wall of the stented regions. In more detail: (i) TAWSS distributions of models without stent are more shifted to the right than the cases with stents; (ii) in the stented region (figure 5, dark grey bars), the percentage area exposed to TAWSS lower than 0.4 Pa is significantly higher for the cases with stent.

The RRT contour maps (figure 6) confirm the results obtained on the two computational models for TAWSS: high values of RRT are located next to the stent struts, to the bifurcations and to the stent overlapping zone. RRT is a more complete quantity than TAWSS because it considers not only the magnitude of WSS but also the oscillatory WSS. High values of RRT also indicate that the residence time of the particles near the wall is prolonged [29] with the possibility of inducing the in-stent restenosis phenomenon.

As natural blood flow in arteries has been found to be helical [14–16], in this work, an helicity-based description was used to characterize the bulk-flow structures in stented coronary arteries. More in depth, the analysis was focused on the helical flow because it has been demonstrated that it is the consequence of the natural optimization of fluid transport processes in the cardiovascular system [14,15], that it is strictly related to transport phenomena of oxygen and lipoproteins [46,47] and that it is instrumental in suppressing flow disturbances [16,17].

By visualization of LNH isosurfaces as an indicator of the alignment/misalignment of velocity and vorticity vectors, it was observed that: (i) large helical structures differently characterize the bulk flow in the stented regions, in the two investigated cases (figure 7); (ii) small helical structures are generated as a consequence of the presence of the stent struts protruding into the lumen of the vessel (figure 8); in fact, these small structures can be only observed in the stented vessels and not in the same geometries where the stent is removed.

While it is still not fully clarified which role (i.e. beneficial or detrimental) the small-scale helical flow structures play in the in-stent restenosis, here, the arrangement of fluid structures in large helical patterns seems to be mainly driven by the shape of the vessel upstream from the stented segment of the vessel and partially by the presence of branched vessels. On the contrary, the straightening induced by the device implantation promotes mitigation of large helical fluid structures along the stented segment.

Interestingly, it was also found that, at the same time, the percentage area of the stented region exposed to low WSS is mildly lower for case A than for case B and it is accompanied by the presence of a more marked arrangement of the flow field in helical structures for case A (figure 7). These findings, even if preliminary, confirm previous observations in healthy vascular districts [16], in surgical connections [17] and in stented vessels [18,48], that there is a link between the surface area exposed to disturbed shear and helical fluid structures in the bulk flow.

The regions of the coronary arteries where the risk of in-stent restenosis is higher from the fluid dynamic point view have been identified for the two analysed cases. However, other aspects should be contemporarily studied to make the virtual model more predictive. In particular, the study of the drug release from the stents would be extremely important. A virtual model that takes into account the haemodynamics, and the drug release would be useful in order to better predict the in-stent restenosis regions. In the literature, some works on the study of the fluid dynamics coupled with drug transport have been already proposed but they consider simplified vessel geometries [49] or they approximate the stent as a line and not as a complex three-dimensional structure [50,51]. Clinical follow-ups of the studied cases will help in a better understanding of the link between haemodynamics and in-stent restenosis.

4.1. Limitations

The reconstruction of the vessel models was made under the assumption of a circular cross section of the vessel, which is true in 70–80% of the cases [52], but not necessarily in the presence of stenosis. This could result in a suboptimal representation of the stent and wall interaction during stent expansion.

The arterial wall and the stents were assumed to be rigid. This assumption could result in slightly different local haemodynamics. Because of the complexity of the problem, fluid–structure interaction (FSI) simulations of stented coronary bifurcations have not been proposed in the literature yet. FSI simulations were performed only on patient-specific coronary arteries without the presence of stents [53].

Also the movements and the vessel deformations caused by the presence of a beating heart were not taken into account. However, myocardial motion has only a minor effect on the flow distribution within the coronary tree [54]. It influences the instantaneous WSS field but does not significantly affect the TAWSS field [55].

Concerning the choice of the boundary conditions, it was not possible to perform the recording of blood flow velocity nor velocity profile on the patients and locations selected for this study. As a consequence, an assumption was made imposing a flow waveform of a human LAD taken from the literature [22] and using the relations by van der Giessen et al. [23] to calculate the mean flow rate and the flow splits. An additional assumption was needed on the shape of the velocity profile at the inlet section (as requested by the imposition of a Dirichlet condition as inflow boundary), because any information about the velocity profile entering the LAD models was available. The choice of imposing a paraboloid-shaped velocity profile at the inlet section, which is a reasonable assumption that has been previously used by other authors for fluid dynamics studies in coronary arteries [23,49], was made.

5. Conclusion

A comprehensive study of the fluid dynamics of two realistic stented coronary bifurcation models that replicate the complete clinical procedure of stent implantation was proposed. The attention was focused on how local haemodynamic structures might influence flow-related processes leading to in-stent restenosis. Thus, both near-wall quantities and the bulk flow were investigated.

Results of WSS and RRT showed that the regions more prone to the risk of restenosis are located next to stent struts, to the bifurcations and to the stent overlapping zone. Looking at the bulk flow, helical flow structures were generated by the shape of the vessel upstream from the stented segment and by the bifurcation regions. Helical recirculating microstructures were also visible downstream of the stent struts.

This work proves how a realistic virtual model can be useful to better understand the effect on the local haemodynamics of stent implantation in coronary bifurcations, identifying, from a merely fluid dynamic point of view, the regions that are more prone to the risk of restenosis. In the future, a patient-specific virtual model that combines the accurate study of the local haemodynamics proposed in this work with the drug release analysis would be useful to better predict the risk of in-stent restenosis.