Joint kinematics and kinetics of overground accelerated running versus running on an accelerated treadmill

Abstract

Literature shows that running on an accelerated motorized treadmill is mechanically different from accelerated running overground. Overground, the subject has to enlarge the net anterior–posterior force impulse proportional to acceleration in order to overcome linear whole body inertia, whereas on a treadmill, this force impulse remains zero, regardless of belt acceleration. Therefore, it can be expected that changes in kinematics and joint kinetics of the human body also are proportional to acceleration overground, whereas no changes according to belt acceleration are expected on a treadmill. This study documents kinematics and joint kinetics of accelerated running overground and running on an accelerated motorized treadmill belt for 10 young healthy subjects. When accelerating overground, ground reaction forces are characterized by less braking and more propulsion, generating a more forward-oriented ground reaction force vector and a more forwardly inclined body compared with steady-state running. This change in body orientation as such is partly responsible for the changed force direction. Besides this, more pronounced hip and knee flexion at initial contact, a larger hip extension velocity, smaller knee flexion velocity and smaller initial plantarflexion velocity are associated with less braking. A larger knee extension and plantarflexion velocity result in larger propulsion. Altogether, during stance, joint moments are not significantly influenced by acceleration overground. Therefore, we suggest that the overall behaviour of the musculoskeletal system (in terms of kinematics and joint moments) during acceleration at a certain speed remains essentially identical to steady-state running at the same speed, yet acting in a different orientation. However, because acceleration implies extra mechanical work to increase the running speed, muscular effort done (in terms of power output) must be larger. This is confirmed by larger joint power generation at the level of the hip and lower power absorption at the knee as the result of subtle differences in joint velocity. On a treadmill, ground reaction forces are not influenced by acceleration and, compared with overground, virtually no kinesiological adaptations to an accelerating belt are observed. Consequently, adaptations to acceleration during running differ from treadmill to overground and should be studied in the condition of interest.

1. Introduction

1.1. General introduction

Although rare in daily life, most studies on animal and human locomotion published so far deal with steady-state conditions. Only relatively recently, focus shifted towards unsteady-state locomotion, but many aspects, such as, for instance, manoeuvring or velocity transients, remain poorly understood. Accelerations are now more frequently studied, aiming at further completion of the knowledge on the neuromechanical interactions during locomotion [1–10]. Maximal sprint accelerations are already well understood, but surprisingly, detailed biomechanical analyses on submaximal overground accelerated running are unavailable in the literature.

Because of practical and methodological advantages, several of the studies referred to opted for the use of a motorized treadmill [11,12]. For steady-state conditions, treadmill locomotion is, despite small kinesiological differences [13], a valuable, validated alternative for overground performance. However, a recent study documented that ground reaction forces of overground accelerated running and running on an accelerating treadmill belt differ significantly. In line with mechanical principles [14], they found that with increasing acceleration, treadmill performance becomes less and less representative for the overground condition [15].

How this difference translates to the joint and actuator level, or in other words how representative treadmill acceleration actually is for overground conditions at the level of the segmental and joint kinematics and kinetics, is unknown. To fill this void, acceleration effects on segmental and joint kinematics and kinetics should be compared for overground and treadmill accelerations. Therefore, this study collects kinetic and kinematic data of submaximally accelerated overground running and of running on an accelerating belt in the same test population in order to be able to compare both conditions. Because of the proportionally differing ground reaction forces according to acceleration overground [15], we hypothesize that segmental and joint kinematics and kinetics at the level of ankle, knee and hip will also change according to acceleration overground. Ground reaction forces on a treadmill are not influenced by acceleration [15]; therefore, also no changes to segmental and joint kinematics and kinetics are expected on a treadmill. Summarizing: a different acceleration effect overground than on a treadmill on the level of segmental and joint kinematics and kinetics is hypothesized.

1.2. Accelerating overground

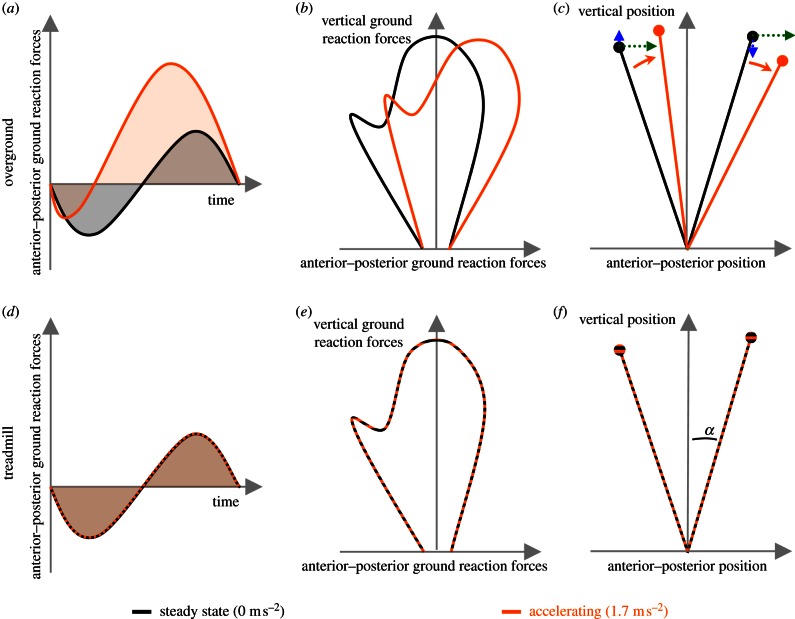
Ground reaction forces differ between steady-state and accelerated running overground [15,16] (figure 1a,d). When submaximally accelerating during running, anterior–posterior ground reaction forces are adjusted to form a net propulsive force impulse (i.e. the time integral of the anterior–posterior forces) by decreasing the braking impulse (related to a shorter duration and smaller magnitude of the braking forces) and increasing the propulsive impulse (related to a longer duration and larger magnitude of the propulsive forces). The same strategies are also found during sprinting in humans [8], and accelerated running [17] and hopping [18] in animals. Effects of horizontal acceleration on vertical ground reaction forces are, however, more variable (although the vertical impulse should remain more or less identical). Sprinting humans are likely to decrease the peak vertical ground reaction force [8], whereas animals are likely to enlarge this peak force [17,18] as acceleration rises. Nevertheless, looking at both forces combined, and thus at the angle of the ground reaction force relative to the vertical, acceleration is logically always related to a more forward-oriented ground reaction force vector. For sprint running performance, the ability to generate this forward orientation is identified as more important than the magnitude of the force itself [10].

Figure 1.

(a,d) Anterior–posterior ground reaction forces, (b,e) butterfly drawing of vertical and anterior–posterior ground reaction forces and (c,f) body lean α at initial contact and toe-off when running at steady state (black) and accelerating (grey; orange in online version), overground (a–c) and on a treadmill (d–f). Circles indicate the BCOM. (Online version in colour.)

Theoretically, in order to keep balance during accelerated running, over the course of a stance phase (or a series of stances), the impulse of the resultant moment about the body centre of mass (BCOM) should be zero (i.e. no angular momentum about the BCOM should be gained). This implies that the direction of the ground reaction force vector (figure 1b,e) should remain more or less aligned with the BCOM (figure 1c,f). As such, the body lean (vector connecting the centre of pressure (COP) and the BCOM) is related to the direction of the ground reaction force vector [16]. The orientation of the body lean vector can be affected by changing the relative position of the BCOM with respect to the COP (or vice versa), in both the horizontal (green arrows in figure 1c,f) and vertical direction (blue arrows in figure 1c,f). As a result of these adaptations, the body lean vector is oriented more vertically at touchdown and more forwardly at toe-off. This implies that the BCOM passes over the COP earlier in the stance phase. As such the switch from braking to propulsion occurs earlier as well [15], which has also been demonstrated for accelerated walking [19].

Even though body lean has been demonstrated to be related to acceleration in running, it has not yet been studied how it is established kinematically. Although rotations of all body segments may theoretically contribute to the shifts in the relative position of the BCOM with respect to the COP, optimization of the neuromusculoskeletal interaction can be expected. Indeed, next to keeping balance, the neuromusculoskeletal system has to maintain an optimal running pattern while mainly changing anterior–posterior ground reaction forces. Moreover, it was demonstrated that moments about the hip, knee and ankle joint should be redistributed to obtain a different orientation of the ground reaction forces in an optimal manner. This is done by, among others, a different function of biarticular muscles [20]. In addition, the forward kinetic energy of the body should be enlarged during stance, which necessitates that positive work should be delivered by the neuromusculoskeletal system [18]. Evidence for this adapted neuromechanical interaction (interaction between the neuromusculoskeletal system and external mechanics, in this case ground reaction forces) has not yet been provided for submaximal running accelerations in humans.

1.3. Running on an accelerating treadmill

Running on an accelerating treadmill is mechanically different from accelerating overground. In contrast to the overground condition, where anterior–posterior ground reaction forces are tuned to create a net accelerating impulse, on a treadmill, anterior–posterior ground reaction forces remain balanced during a stance phase [15,21]. This is logical, because linear whole body inertia, related to the net acceleration of the BCOM in the laboratory reference frame, is absent on a treadmill. As such, there is no need to account for it by the neuromuscular system. In other words, the treadmill accelerates underneath the subject, whereas the subject stays in place in the laboratory reference frame. Because the braking and propulsive forces are not adapted to the magnitude of acceleration of the treadmill [15], we hypothesize that the direction of the ground reaction forces will not change with the imposed acceleration, thus not necessitating a change in the body angle, segmental configuration and movement or joint kinetics when acceleration of the treadmill changes.

1.4. Aims of this research

From a mechanical point of view, at the whole body level, running on an accelerating treadmill is different from accelerating overground [15]. How these differences translate to the segmental level, and how these differences change according to the degree of acceleration are important in different situations.

For example, accelerations are frequently used in fundamental research on gait transitions, in which studies are conducted both overground [1] as well as on a treadmill [12,22]. It was already shown that the realization of this transition differs between treadmill and overground [4], yet the mechanism behind this difference is still unknown. Understanding the effect of acceleration on different aspects of locomotion might provide further insights into this question and give indications about when to use or not to use a treadmill in experiments. This is also valuable in a more applied research context in which treadmills are also used to study non-steady-state gait such as during sprinting [23] or in virtual reality environments [24]. Furthermore, in the rehabilitation of functional gait, an important aspect is to relearn the ability to change speed, where treadmills have obvious practical advantages. More specifically, treadmills on demand, which automatically change belt speed in response to the subjects' actions, are being developed [25]. However, if changing locomotor speed on a treadmill would be a different task for the human body from changing speed overground, then the transfer from the acquired acceleration on a treadmill to the daily-life overground situation might be impossible. A similar question could arise in a sports training setting, where a treadmill is considered a valuable asset. Because many sports are characterized by bursts of accelerated running [26], it can be questioned whether a treadmill can also be used to train the players for the sport-specific accelerations.

Therefore, segmental and joint kinematics and joint kinetics over a range of accelerations (and speeds) should be compared between treadmill and overground. Surprisingly, little or no experimental data are available to date on submaximal overground or treadmill acceleration, and it is presently unknown how acceleration is modulated by the neuromusculoskeletal system over an ecologically relevant range. Therefore, experiments overground and on a treadmill must be carried out and analysed in parallel in order to formulate an integrated answer to the questions posed above. Based on the mechanical inequality of both situations, it is hypothesized that also the biomechanics differ, and that these differences enlarge as the acceleration enlarges. Overground, a correlation between acceleration and forward body lean (related to a more anterior position of the BCOM relative to the COP) is expected due to the proportionally more forward orientation of the ground reaction force vector. As ground reaction forces and segment kinematics combine in inverse dynamics, possible adaptations to joint moments and powers are less predictable. On a treadmill, none of these adaptations to acceleration are expected to occur when running on an accelerating belt.

2. Methods

2.1. Population

Ten healthy subjects (men and women, age: 26 ± 3 years, height: 1.61 ± 0.32 m, weight: 71 ± 10 kg) participated in the study. The ethical committee of the Ghent University Hospital approved the experimental protocol, and all subjects signed an informed consent form.

2.2. Protocol

All subjects ran overground on an instrumented runway and on a motor-driven treadmill, using a range of accelerations varying from 0 to 3 m s⁻², and speeds from 2 to 7 m s⁻¹. Overground and on a treadmill separately, acceleration and speed conditions were offered in a randomized order. In both experiments, a habituation period to all conditions was given and sufficient rest was allowed between trials. Experiments overground were conducted first, then followed by experiments on the treadmill on a separate day. The body mass m was measured prior to each test.

2.2.1. Overground tests

Overground tests were performed on a 30 m long instrumented indoor runway, including four built-in force platforms (0.5 m AMTI, 1 m AMTI, 0.6 m Kistler, 2 m AMTI). The three components of the ground reaction forces were sampled at a data frequency of 1000 Hz. Three-dimensional full-body kinematics, enabling determination of the position of the BCOM (Visual 3D, C-motion), were recorded using a 12 camera Qualisys Pro Reflex system (200 Hz). Subjects were asked to run at different starting velocities and then to accelerate gently, intermediately and explosively in the measuring zone. In addition, steady-state running trials were captured (acceleration of the BCOM during the stance phase between −0.045 and 0.045 m s⁻²). Per subject 126 (±30) stances were collected.

2.2.2. Treadmill tests

A motor-driven treadmill (h/p/Cosmos stellar; power: 2.2 kW; running surface: 1.7 m long and 0.65 m wide) instrumented with four force transducers (Arsalis, Belgium) was used to perform the treadmill tests. Technical details of the instrumentation of the treadmill are published elsewhere [27]. Instantaneous belt speed was measured using an optical sensor (V_tm). The three components of the ground reaction forces (F_grf) were recorded, and the speed of the belt was digitized at 1000 Hz. Three-dimensional kinematics were recorded using six Qualisys Oqus cameras (200 Hz). Subjects ran at different velocities on the continuously accelerating treadmill. Belt accelerations (programmed by the manufacturer of the treadmill) of 0.07, 0.15, 0.30, 0.60, 1.10 and 1.70 m s⁻² were executed, yet actual acceleration realized by the treadmill was slightly lower. For comparative purposes also running at steady state at speeds between 2 and 7 m s⁻¹ was captured. Per subject 1374 (± 242) stances were collected.

2.3. Data analysis

2.3.1. Dynamic multi-body model

A 15-segment dynamic model (consisting of feet, shanks, thighs, pelvis, trunk, head, upper arms, forearms and hands) was developed using Visual 3D (C-motion) using standard available inertial parameters (segment masses [28] and moments of inertia [29]). The respective body masses of overground and treadmill tests were used to scale the models for both testing conditions. Anthropometrics were collected following the overground test. Anatomical markers were bilaterally placed on the shoe at the location of first and fifth metatarsal heads, medial and lateral calcanei and the navicular bone, on medial and lateral malleoli, medial and lateral epicondyles of the femur, greater trochanter, anterior superior iliac spine, posterior superior iliac spine, iliac crest acromion, medial and lateral epicondyles of the humerus, ulnar and radial styloid processes and centrally on C7 and solar process of the sternum. Clustered tracking markers on rigid plates, firmly but comfortably attached to the segments, were placed on shanks (4), thighs (4), lower arms (2), upper arms (3), and a single marker was placed on the dorsal aspect of the trunk at the level of T8. Sagittal segment angles were calculated relative to the laboratory reference frame and were normalized to standing position. Sagittal joint angles were calculated as the deviation from the anatomical position, normalized to standing posture. Kinetic and kinematic data were filtered using a second-order Butterworth lowpass filter at a cut-off of 20 Hz [30].

2.3.2. Inverse dynamics

Standard Visual 3D (C-Motion) calculation procedures using Newton–Euler formalisms were used to calculate joint moments and powers. COP trajectories obtained on the treadmill were not adequate for inverse dynamics calculations. Therefore, for each subject (with consequent heel strike running pattern on the treadmill) and for each individual treadmill stance phase, the best-matching (in terms of acceleration, speed, step length and body side) COP trajectory from a stance phase overground was selected and fitted to the foot on the treadmill.

Overground, speed was measured as the mean horizontal speed of the BCOM during stance. Assuming that air resistance can be neglected, the mean anterior–posterior acceleration of the BCOM is calculated as

where n is the number of samples collected between initial contact and toe-off. On the treadmill, speed was calculated as the mean treadmill speed during stance, acceleration as the mean treadmill acceleration during stance.

2.3.3. Body lean and angle of the ground reaction force vector

Body lean was determined as the angle between the vertical and the line connecting the COP and the BCOM, for which a positive angle indicates a more anterior position of the BCOM relative to the centre of force application. The angle of the ground reaction force vector is calculated as the tangent of the vertical divided by the anterior–posterior ground reaction force. A positive angle indicates a forward-oriented force. When referring to the mean angle, the mean angle during the stance phase is intended.

2.4. Data selection

Overground, two groups of trials could be distinguished for each subject in the data: sprint-like (presenting a dorsiflexion velocity after initial contact) and running-like (presenting the typical plantarflexion velocity after initial contact). The former has been documented in the literature [7,31,32]. The stances overground (28 ± 8%) were considered sprinting stances based on this definition. In our data for the treadmill, only running-like stances occur spontaneously. Therefore, overground only the running-like stances were included in the comparison.

2.5. Statistics

Multiple linear regressions of dependent variables versus acceleration and speed were fitted per subject. By taking speed into account, the acceleration effects are corrected for the speed effect (i.e. speed can be considered a covariate). Slopes indicate as such the net acceleration effect. Statistics were computed using Matlab (R2007B, The Mathworks Inc.). Slopes were considered significant if the median p-value of the subjects was less than 0.05 (for a trend 0.1). Treadmill–overground differences were considered significant if a paired samples t-test (between significant slopes) indicated a p-value less than 0.05.

2.6. Presentation

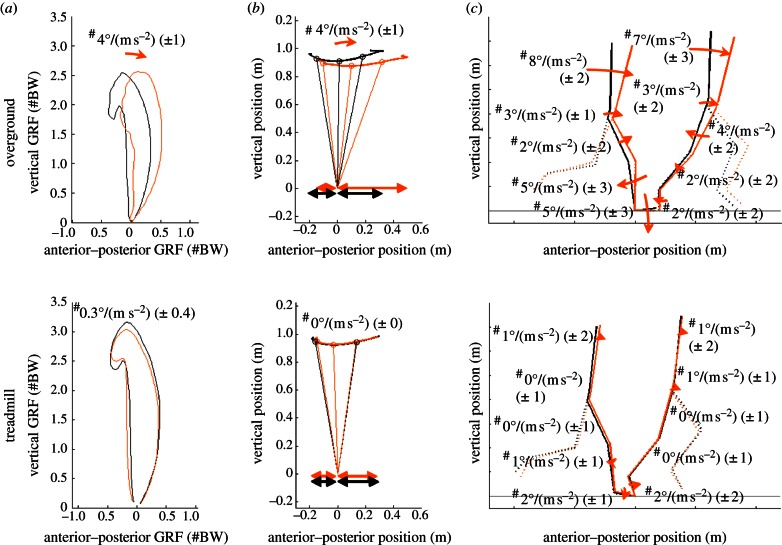
This study aims at presenting the effects of accelerating. These consist of the coefficient of acceleration in the multiple linear regression. Although accelerations studied were spread randomly between 0 and 4 m s⁻², this coefficient can functionally be translated into the change in the variable per 1 m s⁻². Acceleration effects in the range from 0 to 4 m s⁻² are expressed for all 10 subjects through the multiple regression acceleration coefficient per 1 m s⁻². To enable its functional interpretation, the latter is inserted by arrows in curves and stick figures (figures 2–4) that are both based on data of four subjects of which data at steady state and accelerating at 1.7 m s⁻² (both at 3.7 m s⁻¹) were available overground and on the treadmill.

Figure 2.

(a) Ground reaction force butterfly representations, (b) Body lean (1–25–50–75–100% stance) and distance between BCOM and COP application at initial contact and toe-off (arrows) and (c) segment orientations when running at steady state (black) and accelerating (1.7 m s⁻², grey; orange in online version) overground (top panels) and on accelerating treadmill (bottom panels), both at 3.7 m s⁻¹. Arrows indicate the changes in the variable per rise in acceleration of 1 m s⁻². Hash symbol indicates a significant difference between the acceleration effect overground and on the treadmill. Figures are the mean of four representative subjects; arrows and numbers indicate the acceleration effects (corrected for speed) for all 10 subjects. (Online version in colour.)

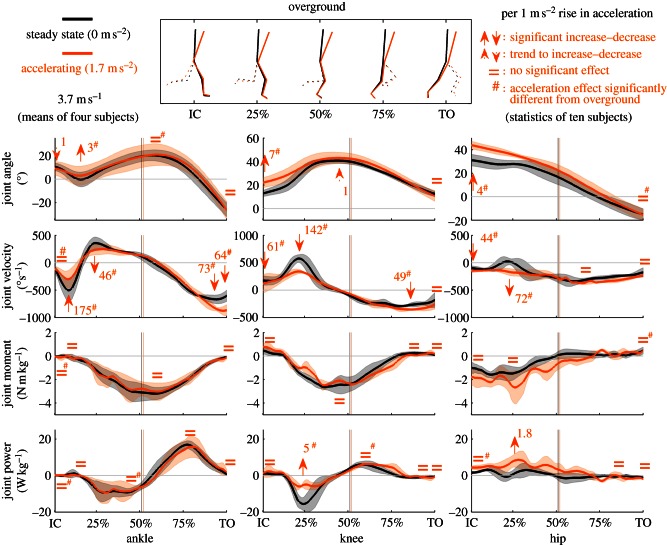
Figure 3.

Joint kinematics and kinetics of the stance leg when accelerating overground. Mean of four subjects running at 3.7 m s⁻¹ steady state (black) and accelerating at 1.7 m s⁻² (grey; orange in online version). Flexion is positive, extension is negative. Power generation is positive, power absorption is negative. Bands around the means represent 1 s.d. Full arrows indicate significant acceleration effects (p < 0.05), dotted arrows indicate trends (p < 0.1) and = indicates no significant acceleration effect (all corrected for the covariate speed) for all 10 subjects. Numbers next to the arrows indicate the magnitude of the effect per rise in acceleration of 1 m s⁻². Vertical lines indicate instants of zero-crossing, i.e. the transition from braking to accelerating. Hash symbol indicates the acceleration effect retrieved is significantly different from the acceleration effect on the treadmill (p < 0.05). (Online version in colour.)

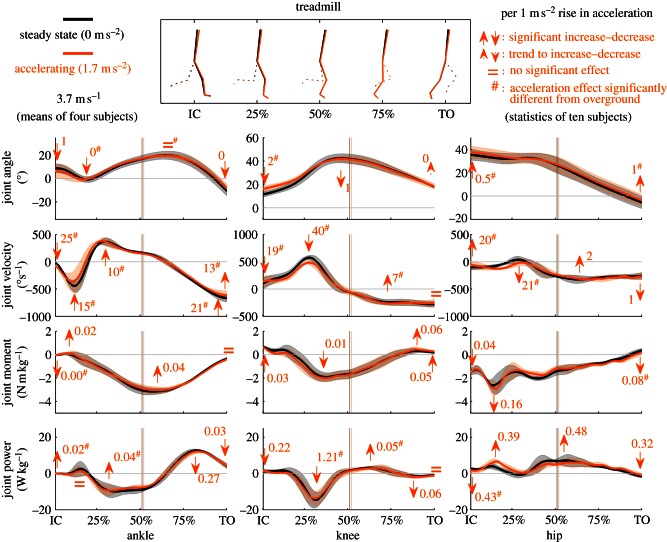
Figure 4.

Joint kinematics and kinetics of the stance leg when accelerating on a treadmill. Mean of four subjects running at 3.7 m s⁻¹ steady state (black) and accelerating at 1.7 m s⁻² (grey; orange in online version). Flexion is positive, extension is negative. Power generation is positive, power absorption is negative. Bands around the means represent 1 s.d. Full arrows indicate significant acceleration effects (p < 0.05), dotted arrows indicate trends (p < 0.1) and = indicates no significant acceleration effect (all corrected for the covariate speed) for all 10 subjects. Numbers next to the arrows indicate the magnitude of the effect per rise in acceleration of 1 m s⁻². Vertical lines indicate instants of zero-crossing, i.e. the transition from braking to accelerating. Hash symbol indicates the acceleration effect retrieved is significantly different from the acceleration effect on the treadmill (p < 0.05), to indicates a trend (p < 0.1). (Online version in colour.)

3. Results

3.1. Spatio-temporal characteristics

Per 1 m s⁻² rise in acceleration, step duration shortened in a similar way overground (12 ± 11 ms) and on the treadmill (10 ± 9 ms), but only appeared significantly on the treadmill. Acceleration did not influence stance duration overground. This differs significantly from the significant decrease by 9 ± 6 ms/(m s⁻²) on the treadmill. Flight duration overground decreases by 14 ± 12 ms/(m s⁻²) and on the treadmill by 2 ± 9 ms/(m s⁻²). There is a trend towards a different acceleration effect on flight duration overground and on the treadmill.

3.2. Kinetics and body lean

Per 1 m s⁻² extra acceleration, mean angle of the ground reaction force vector and body lean vector are both oriented 4 ± 1° more anteriorly overground. Both adaptations are significantly different (p < 0.001) from those on the treadmill: ground reaction force angle becomes slightly (0.3 ± 0.4°), but statistically significantly, more backwardly oriented, whereas the body angle does not change. The mean magnitude of the ground reaction force normalized to body mass during stance is not influenced by acceleration overground, whereas a trend (p = 0.091) towards a marginal decrease (−0.012 m s⁻²/(m s⁻²)) is observed on the treadmill. At peak braking force and at peak propulsive force, the body angle is 4 ± 1°/(m s⁻²) less backwardly and more forwardly oriented, respectively. Both are significantly (p < 0.001) different from the treadmill situation, during which body lean is not altered by acceleration at these instants. In both environments, angular momentum of the body around the BCOM is thus kept close to zero by aligning the mean body lean with the mean ground reaction force vector during stance.

At 15 per cent of overground stance, the BCOM moves 0.08 ± 0.11 m/(m s⁻²) anterior and lowers 0.02 ± 0.01 m/(m s⁻²) relative to the point of support. On the treadmill, the BCOM moves 0.01 ± 0.01 m/(m s⁻²) anterior relative to the point of support and remains vertically in the same position. All these effects are significant. The effect on the horizontal distance shows a trend (p = 0.075) towards a significant difference between treadmill and overground; the effect on the vertical distance is significantly different (p < 0.001). At 85 per cent of stance, the BCOM moves 0.08 ± 0.17 m/(m s⁻²) anterior and lowers 0.02 ± 0.01 m/(m s⁻²) relative to the point of support overground. On the treadmill, no effects are observed. The effect on the vertical distance is significantly different between overground and treadmill (p < 0.001).

3.3. Kinematics during stance

3.3.1. Segment angles

At initial contact and toe-off, overground and on an accelerating treadmill, segment angles of the stance leg change significantly according to acceleration as represented in figure 2. All adaptations to acceleration in segment angles differ significantly between overground and treadmill.

3.3.2. Joint angles

Figures 3 and 4, respectively, show results for overground and treadmill conditions of joint kinematics and kinetics. For every rise in the acceleration of 1 m s⁻² overground (compared with steady-state running), maximal initial ankle plantarflexion of the stance ankle significantly diminishes by 3 ± 2°. Knee angle at initial contact decreases significantly by 7 ± 4°/(m s⁻²). The hip is 4 ± 3°/(m s⁻²) significantly more in flexion at initial contact. On the treadmill, besides small (less than or equal to 1°/(m s⁻²)), but significant, adaptations in joint angles, ankle plantarflexion at toe-off diminishes (2 ± 1°/(m s⁻²)), whereas knee flexion at initial contact enlarges (2 ± 1°/(m s⁻²)). The acceleration effect on maximal initial plantarflexion and knee and hip angle at initial contact differs significantly between treadmill and overground.

3.3.3. Joint velocities

Overground, peak initial ankle plantarflexion velocity during stance diminishes by 175 ± 118° s⁻¹/(m s⁻²), maximal dorsiflexion velocity diminishes by 46 ± 40° s⁻¹/(m s⁻²). Maximal plantarflexion velocity approaching toe-off and velocity at toe-off enlarge (73 ± 30 and 64 ± 59° s⁻¹/(m s⁻²)). Knee flexion velocity at initial contact decreases by 61 ± 57° s⁻¹/(m s⁻²), maximal knee flexion velocity decreases by 142 ± 40° s⁻¹/(m s⁻²) and maximal knee extension velocity enlarges by 49 ± 24° s⁻¹/(m s⁻²). Hip extension velocity at initial contact enlarges (54 ± 36° s⁻¹/(m s⁻²)), maximal flexion velocity decreases (72 ± 52° s⁻¹/(m s⁻²)) and mean hip extension velocity enlarges by 21 ± 12° s⁻¹/(m s⁻²). On the treadmill, the ankle plantarflexes more rapidly (25 ± 18° s⁻¹/(m s⁻²)) at initial contact, peak initial ankle plantarflexion velocity during stance diminishes by 15 ± 21° s⁻¹/(m s⁻²) and maximal dorsiflexion velocity enlarges by 10 ± 15° s⁻¹/(m s⁻²). Maximal plantarflexion velocity approaching toe-off and velocity at toe-off decrease (21 ± 19 and 13 ± 19° s⁻¹/(m s⁻²)). Knee flexion velocity at initial contact decreases by 19 ± 33° s⁻¹/(m s⁻²), maximal knee flexion velocity decreases by 40 ± 22° s⁻¹/(m s⁻²) and maximal knee extension velocity decreases by 7 ± 12° s⁻¹/(m s⁻²). Hip extension velocity at initial contact decreases (20 ± 12° s⁻¹/(m s⁻²)) and maximal flexion velocity decreases (21 ± 19° s⁻¹/(m s⁻²)). All acceleration effects discussed earlier differ significantly between treadmill and overground, except for the knee velocity at toe-off.

3.3.4. Joint moments

Overground, joint moments of the stance leg are not significantly altered by acceleration. On the treadmill, joint moments are significantly influenced, but only to a very small degree. Peak hip extension moment enlarges by 0.16 ± 0.24 N m kg⁻¹/(m s⁻²), the hip flexion moment at toe-off decreases by 0.08 ± 0.07 N m kg⁻¹/(m s⁻²). The latter significantly differs from overground.

3.3.5. Joint powers

Overground, peak power absorption of the knee of the stance leg decreases by 4.9 ± 1.6 W kg⁻¹/(m s⁻²). At the hip, peak power generation enlarges by 1.8 ± 1.5 W kg⁻¹/(m s⁻²). On the treadmill, in the ankle, power generation enlarges at initial contact (0.02 ± 0.01 W kg⁻¹/(m s⁻²)), and peak power absorption decreases (0.04 ± 0.77 W kg⁻¹/(m s⁻²)). Both significantly differ from overground. Peak ankle power generation decreases (0.27 ± 0.58 W kg⁻¹/(m s⁻²)). Knee power generation at initial contact decreases (0.22 ± 0.29 W kg⁻¹/(m s⁻²)), peak absorption increases (1.21 ± 1.40 W kg⁻¹/(m s⁻²)) and peak generation enlarges (0.05 ± 0.68 W kg⁻¹/(m s⁻²)). The two latter significantly differ from overground. Peak absorption during the second half of stance enlarges (0.06 ± 0.24 W kg⁻¹/(m s⁻²)). Hip power generation at initial contact decreases (0.43 ± 0.45 W kg⁻¹/(m s⁻²)), this significantly differs from overground. Peak power generation during the first and second half of stance, respectively, enlarges by 0.39 ± 0.63 W kg⁻¹/(m s⁻²) and 0.48 ± 0.37 W kg⁻¹/(m s⁻²). Absorption at toe-off enlarges (0.32 ± 0.27 W kg⁻¹/(m s⁻²)).

4. Discussion

The first part of the discussion will elaborate on the kinesiology of accelerated running overground, the second part on the kinesiology of running on an accelerating treadmill belt. The third part will focus on the different acceleration effects between both and the possible consequences of these differences for past and future research of unsteady-state gait on a treadmill.

4.1. How to accelerate overground?

The mechanical goal of accelerated running overground consists of a more anteriorly oriented ground reaction force vector proportional to the intended acceleration (figure 2). Our results confirm results of Kugler & Janshen [16] which indicate that consequently body lean at toe-off becomes indeed oriented more forwardly (+4°/(m s⁻²)) as acceleration rises. Furthermore, our results extend this towards the braking and the propulsion phases, during which at peak braking and propulsive force, body lean is as the ground reaction forces also 4°/(m s⁻²) more forward-oriented. Body configuration determines this forward body lean.

4.1.1. Configuration

4.1.1.1. Braking

During the braking phase, this forward body lean is realized by placing the foot less anterior relative to the BCOM, which is in accordance with observations of lower braking forces during sprinting [8] and accelerations in running turkeys [17]. A key element is that at initial contact trunk and pelvis segments head–arms–trunk (HAT) are already oriented more forwardly. Comprising 68 per cent of the body mass, they position the BCOM more anterior relative to the COP. The thigh segment is more anteflexed (i.e. the knee is positioned more anterior relative to the hip), which also aids in a more forward position of the BCOM, but which at the same time brings the COP more forward. The latter would counteract the forward lean. Nevertheless, a larger backward orientation of the shank (i.e. knee more anterior than the ankle) brings the force application point more backward, whereas to a lesser extent (mass of the shank constitutes only 5% of the total body mass) moving the BCOM slightly backwards. The foot evolves from landing with the heel lower than the toes more towards landing with a flatter foot. This tends to bring the force application point more forward, but coincides with an active touchdown [8], which has been described as typical and beneficial for (accelerated) sprinting.

4.1.1.2. Propulsion

During the propulsive phase, mainly a more anterior, and second, a lower vertical position of the BCOM relative to the point of support contribute to a forward body lean. At toe-off, all segment orientations (trunk, pelvis, thigh, shank, foot) contribute to both factors. This is also the case for the thigh, which thus turns from an increased anteversion at the start of braking towards an increased retroversion, necessitating a pronounced extension action at the hip, which has also been described during sprinting [8,32] and is discussed further on.

4.1.2. Movement

4.1.2.1. Braking

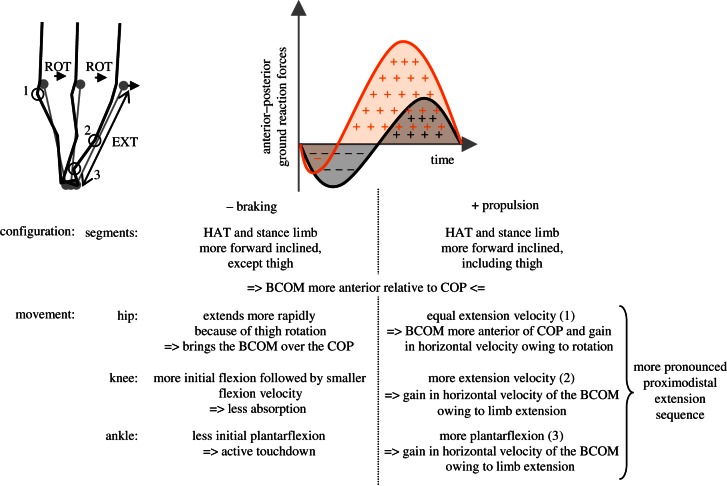
The hip is according to acceleration more flexed at initial contact owing to the increased forward flexion of the pelvis and anteversion of the thigh. During the braking phase, an increased hip extension velocity is observed, which is during maximal sprinting also related to a larger acceleration [8]. This can probably be related to the shorter duration of the braking phase: by extending the hip the BCOM is brought earlier over the COP. The latter is referred to as rotation (‘ROT’ in figure 5) of the body over the support foot.

Figure 5.

How to accelerate overground? Summary of the main results. (Online version in colour.)

The knee is, as a function of acceleration, more flexed at initial contact and evolves owing to a decreased peak (excentric) flexion velocity towards the same maximal flexion at midstance. Owing to this decreased flexion velocity, less power is absorbed (figure 3), which can be related to a smaller decrease in forward momentum, thus less braking.

In the ankle, initial plantarflexion after initial contact is less pronounced. Thus, the ankle is more dorsiflexed during the first 25 per cent of stance. This is caused by a smaller peak plantarflexion and dorsiflexion velocity. This coincides with the flatter foot placement and active touchdown. Human sprinting, indeed, realizes decreased braking by an active touchdown [7,8], which is next to the less anterior position of the COP relative to the BCOM and flatter foot placement already mentioned also characterized by other kinematic adaptations [8]: (i) an increased (concentric) hip extension velocity at touchdown (which is also to a lesser extent also observed in our data), (ii) a larger knee flexion velocity (at touchdown) and (iii) a larger posterior-oriented foot velocity relative to the ground. However, the two latter observations are imperative in maximal sprinting, and are not necessary for submaximally accelerated running.

4.1.2.2. Propulsion

Starting with a more pronounced hip extension velocity in the braking phase, and followed by a larger peak knee extension velocity during propulsion, the larger ankle plantarflexion velocity points at a more pronounced proximodistal extension sequence in the stance limb when accelerating overground [31]. The proximodistal sequence fulfils the geometrical constraint to optimize horizontal velocity of making optimal use of rotation of the body over the support foot, evoked by hip extension (early in stance), and then extending the limb only when this contributes to the forward velocity [33]. The more explicit use of the kinematic rotation–extension sequence, as depicted in the scheme in figure 5, is reinforced by one of the few correlations between joint kinetics and acceleration: a trend (p = 0.066) towards increased hip extension work during the braking phase.

4.1.3. Conclusion: overground accelerations

Thus, in order to accelerate overground, the body is tilted more anteriorly, while maintaining a constant speed running pattern (presenting some adaptations to accelerating). More surprisingly, joint moments are not influenced by acceleration. This can be understood, because the magnitude of the ground reaction force vector during stance is not significantly influenced by acceleration. A qualitative observation of the butterfly representation in figure 2a, indeed, suggests that the form of this butterfly figure mainly is maintained in a more forward orientation when accelerating. Only the passive impact peak becomes less obvious which can be related to the active touchdown discussed earlier. As such, this may indicate an identical motor control of steady-state and accelerated running: acceleration could be realized by actuating the joints in a similar manner as during steady-state running, but with the whole body in a different orientation and configuration.

Nevertheless, an energy input is needed to increase overall kinetic energy of the body when accelerating. Therefore, the acceleration independent joint moments are in combination with acceleration-dependent joint angular velocities still related to differences in net joint power. In the knee and hip, the decreased flexion velocity during the first half of stance, respectively, leads to less power absorption and more power generation. The latter is responsible for a trend towards increased hip extension work during both the braking and whole stance phase. The acceleration-dependent angular velocities and joint angles cause the muscles to perform at different conditions in their force–length–velocity relationship. The current data do not allow one to demonstrate acceleration effects on a muscular level. However, the current observations lead to the hypothesis that given an identical motor control, muscle activation levels will be different. On the level of a muscular fibre, a larger contraction velocity results in a lower force output. Therefore, in order to obtain the same joint moment two adaptations can occur (simultaneously): more fibres should be activated and/or fibres should be activated at a higher intensity. Both these adaptations result in a larger cost.

As such, most significant adaptations to accelerations overground are found in body lean and kinematics. Nevertheless, our test population consisted of non-skilled accelerators, thus exhibiting a rather large variability in performing the acceleration task which counteracts obtaining statistical significances. This is reflected in the large standard deviations (see §3), which might impede obtaining statistical significances.

Comparisons with steady-state running indicate that the mechanisms associated with the increase in steady-state running speed differ from those of actual accelerations. In the zone of speeds we investigated, during stance peak power absorption and generation at the ankle increase as steady-state running speed increases, whereas no changes in both are found when accelerating. Peak power absorption at the knee increases when steady-state running speed increases, whereas it decreases as acceleration rises [34].

4.2. How to accelerate on a treadmill?

On a treadmill, the mean orientation of the ground reaction force is only very slightly altered by acceleration (0.3 ± 0.4°/(m s⁻²) more backward). Previous research demonstrated that, because of the absence of overall linear whole body inertia while running on an accelerating treadmill belt, horizontal ground reaction forces are not influenced by belt acceleration [15]. Also, the slightly backward-oriented ground reaction force is in concordance with a small backwards displacement of the subject's BCOM during the stance phase, which is known to be related to treadmill acceleration [15]. Nevertheless, average body lean is not significantly altered by acceleration. All segmental and joint adaptations to acceleration on a treadmill are in magnitude only a fraction of those overground (except for the more forward-oriented trunk and flatter foot placement) and possibly cancel out in terms of total body lean. This combination of non-altered ground reaction forces and kinematics also does not lead to large changes in joint kinetics.

4.3. What can we learn from the differences between both?

It was already known from previous research that accelerated running overground mechanically differs from running on an accelerating treadmill belt [15]. Therefore, inequalities in the kinesiology leading to the generation of these ground reaction forces were expected.

Acceleration clearly has a different effect on the kinesiology of running overground and on a treadmill. Overground, ground reaction forces, body orientation and body movement are associated with less braking and more propulsion when accelerating, whereas on a treadmill, no such adaptations take place. As such, unsteady-state locomotion should be studied/rehabilitated/trained in the condition of interest, as both are not representative of each other. Therefore, when the acceleration is of interest (as for example during gait transition studies for which the treadmill–overground difference was already demonstrated [4]), researchers/physiotherapists/sports coaches should be aware of these differences when choosing the treadmill or overground environment. However, if a treadmill is needed for methodological reasons, refuge can be taken in torque treadmills, which provide just enough power to overcome belt friction, but the subjects have to accelerate the belt themselves [23,35], or by implementing inertial feedback on the treadmill [24].

All the same, we agree with Riley et al. [13] that, although as for steady state, also for unsteady state, treadmill locomotion cannot be generalized to overground locomotion, both the treadmill and the overground condition are valuable methods to study and gain insights for locomotion in their own setting.

5. Conclusion

Overground, the pattern of less braking forces and more propulsive forces when accelerating during running can mainly be attributed to a forward body lean. Less braking is, in addition, realized by a larger hip extension velocity, a smaller peak knee flexion velocity and smaller peak plantarflexion velocity. The larger propulsion is in addition to the forward body lean related to a larger knee peak extension velocity and a larger ankle peak plantarflexion velocity. In the absence of clear correlations between acceleration and joint moments, acceleration might be realized by actuating the joints the same way as during steady-state running, but with the whole body in a different orientation. However, in order to increase the kinetic energy of the body, an energy input is needed, which is reflected in a smaller power absorption at the knee, and a larger power generation at the hip. On a treadmill, mechanics, kinematics and joint kinetics do not change remarkably in response to belt acceleration. Therefore, accelerated running overground is not equal to running on an accelerating treadmill belt.