Built for rowing: frog muscle is tuned to limb morphology to power swimming

Abstract

Rowing is demanding, in part, because drag on the oars increases as the square of their speed. Hence, as muscles shorten faster, their force capacity falls, whereas drag rises. How do frogs resolve this dilemma to swim rapidly? We predicted that shortening velocity cannot exceed a terminal velocity where muscle and fluid torques balance. This terminal velocity, which is below V_max, depends on gear ratio (GR = outlever/inlever) and webbed foot area. Perhaps such properties of swimmers are ‘tuned’, enabling shortening speeds of approximately 0.3V_max for maximal power. Predictions were tested using a ‘musculo-robotic’ Xenopus laevis foot driven either by a living in vitro or computational in silico plantaris longus muscle. Experiments verified predictions. Our principle finding is that GR ranges from 11.5 to 20 near the predicted optimum for rowing (GR ≈ 11). However, gearing influences muscle power more strongly than foot area. No single morphology is optimal for producing muscle power. Rather, the ‘optimal’ GR decreases with foot size, implying that rowing ability need not compromise jumping (and vice versa). Thus, despite our neglect of additional forces (e.g. added mass), our model predicts pairings of physiological and morphological properties to confer effective rowing. Beyond frogs, the model may apply across a range of size and complexity from aquatic insects to human-powered rowing.

1. Introduction

The study of spectacular frog jumps [1,2] has enriched our understanding of muscles [3] as well as muscle–tendon joint mechanics [4]. Less celebrated is their impressive swimming ability [5–7] which has revealed important mechanisms of fluid propulsion [8–10], making frogs ideal models to probe the limits of muscle-powered swimming.

From frog muscle studies, the principles of muscle contraction are well understood. As active muscle shortens, the available force rises then falls depending on overlap between thick and thin filaments as the muscle's operating length changes [11]. In addition, muscle force capacity decays to zero as contraction speed approaches maximum shortening velocity, V_max [12]. Along with time-dependent properties (such as rates of force rise and decay), these force–length and force–velocity (F–V) properties define the ceiling of force and power which muscle cannot exceed. Yet, independent from the familiar F–V property, fluid dynamics dictate that drag force is approximately proportional to approximately velocity². Hence, Daniel et al. [13] observed a dilemma: as muscle shortening velocity increases, force capacity falls owing to the F–V limitation while drag force rises steeply. Given this conflict between muscle versus fluid properties, how can a muscle move a limb rapidly for swimming?

We illustrate Daniel's dilemma with a hypothetical muscle moving a flat plate in water (figure 1). In this simple case where we neglect both added mass effects [13] and changes in fluid force orientation, drag is proportional to muscle shortening velocity (V_m)². Thus, F–V and drag curves can be superimposed. As the muscle contracts, the plate accelerates until drag balances the limiting force of the F–V curve where the curves intersect (point ‘X’). V_m cannot exceed X because drag force at faster speeds would exceed available muscle force, constraining the muscle to operate leftward of X. Furthermore, both muscle properties (physiological cross-sectional area ‘PCSA’ and V_max) as well as plate morphology influence the location of point X. For example, decreasing the plate area lowers the drag force at any given velocity, thus shifting X rightward (dashed line, figure 1). Reciprocally, decreasing PCSA lowers maximum muscle force, shifting X leftward (dashed-dotted line, figure 1). Hence, we name X the ‘morphological V_max 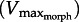’ because both the morphology of the muscle and of the plate determine the maximum V_m, regardless of the physiological V_max.

Figure 1.

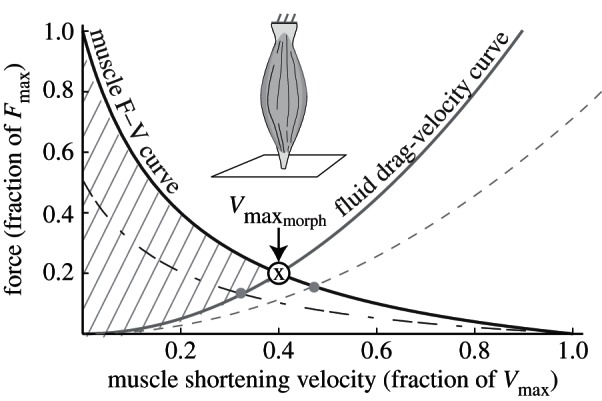
Daniel's dilemma [13]: the muscle force–velocity (F–V) curve (black) opposes the rising drag force (grey). A muscle moving a flat plate through water predicts that the intersection point (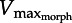) limits shortening velocity because faster speeds incur drag forces above the F–V curve. Theoretically, muscle must operate both below the F–V curve and above the drag curve (hatched region) since the muscle must generate at least enough force to overcome drag. The current study predicts that decreasing plate area decreases drag, shifting 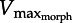rightward (dashed). Decreasing muscle cross-sectional area (lowering maximum force) shifts 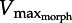leftward (dashed-dotted).

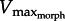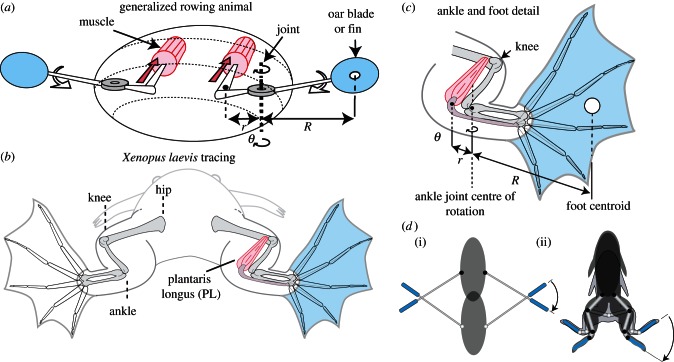
In light of , we attempt to resolve Daniel's dilemma. Because muscle power (force × velocity) peaks at approximately 1/3V_max we expect 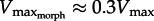for rapid swimming. We consider Xenopus laevis, an obligatorily aquatic frog which catches prey and avoids predators [14] using webbed foot rowing. The plantaris longus (PL) in X. laevis attaches to a lever rotating a joint at a distance r (inlever; figure 2) to generate propulsive drag at an outlever distance, R. The resulting joint rotation causes tangential velocity (velocity tangent to the foot's arc rotating about the ankle joint) creating propulsive fluid reaction force which is a function of gear ratio (‘GR’ = R/r). Since drag is proportional tangential velocity² (=R² · joint angular velocity²), drag owing to muscle shortening rises with GR. Knowing that drag is a major component of the fluid force acting on X. laevis feet [15], we can analytically demonstrate that 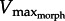decreases with GR because increasing GR raises the muscle force required to move a given load [16,17]. Moreover, foot area increases drag, therefore, will decrease 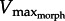. Therefore, since muscle power peaks at approximately 1/3V_max [3], increases in foot area (or GR) will either increase or decrease muscle power, depending on whether 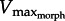lies above or below 1/3V_max, respectively. Thus, we predict that X. laevis hindlimb morphology (GR and area) is ‘tuned’ to the muscle intrinsic properties to maximize muscle power output. Using the PL from X. laevis, we derived analytical predictions that were then verified using a ‘musculo-robotic’ frog foot [18].

Figure 2.

Anatomy of a hypothetical animal rower (a) showing a pair of rowing appendages that rotate about an angle (θ) driven by muscles contracting against an inlever (r). Propulsive drag arises at the end of the outlever (R). A tracing of Xenopus laevis (b) shows the PL muscle as the main motor for swimming. A sketch of the lower limb (c) shows how r and R are defined with respect to the ankle joint. Schematic diagrams (d) of a notonectid insect (i) and a frog (ii) illustrate how the oars rotate with respect to the water as the body moves forward.

2. Material and methods

2.1. The analytical model

Based upon recent models [19,20], we assumed that muscle F–V properties dominate muscle function in frog swimming. For a rigid, flat, fin rotating at 90° angle-of-incidence, we expressed hydrodynamic thrust in terms of inertia, muscle contractile properties, gearing and fin size. Equations were modified from earlier work [20]. Inertial torque on the foot is the difference of muscle torque and drag torque,

2.1

where I is the system moment of inertia (see below), and θ is the anterior–posterior foot angle with respect to the body midline (i.e. 0° points to the forward direction of swimming). The inlever is r and the outlever is R (figure 2). Note that because the orientation of the F_drag vector can change through time, R can also be time-varying (see §4). Drag torque is

2.2

where C_D is the foot drag coefficient (=2 for this study; [15]), A_fin is the fin surface area, ρ is water density. R · dθ/dt is the tangential rotational velocity vector normal to the foot surface. Translational velocity terms represent the backward push of the legs relative to the body (v_backward) and the forward motion of the centre of mass (v_COM) [8]. Note, the fluid force vector is normal to the foot with pure rotational motion, however when translational motion is substantial, the vector deviates from normal (see §4). For an initial kick of X. laveis from rest, translational terms nearly cancel [15], leaving drag only a function of tangential rotational velocity². Thus, in our simple analytical model, we neglect translational velocity (see §4). For our rotational model, the inertial torque is the sum of the foot's moment of inertia (I_foot) and the added mass torque, each calculated about the centre of foot rotation,

2.3

where M_ij is the 6 × 6 added mass coefficient matrix describing j force components caused by i velocity components which vary depending on orientation and shape of the foot. M₆₆ is the purely rotational added mass coefficient. Translational terms introduce substantially more complex equations which have been previously described [15]. For our simple analytical model, we exclude added mass (see below).

For the PL muscle, we considered a simplified Hill-type muscle model,

2.4

where Act(t) is the time-varying activation of the muscle (representing both the active state as well as the maximum isometric force) and FV(t) and FL(t) (see equation (2.10)) are time-varying gain functions signifying the contributions of F–V and F–L effects. As we aim to model peak muscle performance, we assume FL = 1 and Act = maximum, assuming that a muscle should reach maximum activation at L_o, the plateau of the F–L curve. This is a valid assumption for frogs given their ability to begin muscle contractions at long lengths (starting length > L_o) such that they reach L_o at peak activation ([21,22]; i.e. FL = 1 at maximum activation). If starting length were to vary significantly, our exclusion of F–L properties would be invalid (see §4). Thus, we estimate the muscle force limit

2.5

with peak isometric stress = 20 N cm^–2 and PCSA = 0.3 cm² [23], giving a maximum force of 6 N at peak activation. The F–V curve was fitted from the following equation [18]:

2.6

where average V_max ≈ 8 [22]. Since drag forces dominate in X. laevis swimming [15], we assumed peak fluid force occurs when drag is maximum (i.e. at peak rotational velocity and rotational acceleration = 0). Thus, at peak fluid force, we ignore added mass effects (although they are included in the physical model experiments below). Finally, for small angular changes

2.7

Substituting GR = R/r into equation (2.2) given the torque balance at 0 acceleration equation (2.1), we obtain

2.8

and

2.9

where PCSA is in cm² and V_m is in terms of muscle lengths s⁻¹ (ML s⁻¹) and l_rest is the resting muscle length. 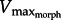is found either by setting equation (2.8) = equation (2.9) or by plotting the curves and finding the intersection point. Note that our simplified model assumes that maximum activation occurs nearly simultaneous with the peak of the FL curve (see §4).

2.2. Musculo-robotic experiments

Predictions from the analytical model were tested with a bio-robotic setup (see the electronic supplementary material, figure S1) that was recently described [18]. Briefly, circular rigid plexiglass feet were mounted to a rotating servo motor resting above an aquarium. Three foot areas were chosen (areas = 2, 5 and 10 cm²) corresponding to 0.4 ×, 1 × and 2 × natural X. laevis foot area. The motor was controlled either by a living muscle isolated in vitro (in vitro-robotic method) or by a computational model simulating the behaviour of a Hill-type muscle (in silico-robotic method). For in vitro-robotic experiments, PL muscle was removed from the animal and mounted to a 305C-LR servo ergometer (Aurora Scientific, Inc., Aurora, Ontario, Canada) as described previously [23]. The muscle was stimulated supramaximally with a 80 ms train of 1 ms pulses at 250 Hz using parallel stainless steel plate electrodes. Using a ‘real-time’ platform (cRio9074 FPGA controller, National Instruments, Austin, TX, USA), force recoded from the muscle was multiplied by a virtual inlever, r, and applied as a torque command signal to the robotic foot. Following a 0.1 ms feedback delay, displacement of the robotic foot was then relayed back to the ergometer enabling the muscle to shorten as if actuating the robotic fin directly. For in silico-robotic experiments, the computational model was fed an activation waveform output (see below) from a USB-6289 A/D module (National Instruments). In the real-time controller, position data from the motor were monitored and input into F–V and F–L equations to compute force at the next 0.1 ms time step. Force was converted to torque via r in software. For both in vitro or in silico experiments, R was assumed to be the constant distance between the motor centre of rotation and the foot centroid, and GR could be controlled by changing r in software. Although F–L properties were excluded from the simple analytical model, experimental trials included both F–L and F–V curves. Consequently, the robotic foot behaves as an ankle joint actuated by a simplified Hill-type model (equation (2.4)) with F–V properties (described above) and the following F–L equation [22,24]:

2.10

where L/L_o = instantaneous length/optimal length, b = −2.53, s = −0.59 and a = 1.41. Activation dynamics were simulated by inputting a train of spikes (identical to the stimulation used for in vitro-robotic experiments) into a three-stage activation equation [25]

2.11

where i is the activation stage (i from 1 to 3), a_i−1 is the activation waveform from the previous stage, a₀ is the input waveform of spikes and a₃ is the output muscle active state, Act, used to simulate muscle force (equation (2.4)). Values of τ and β were obtained using a genetic algorithm [26] in Labview 2011 (National Instruments) to match both twitch and tetanic force profiles from isometric contractions of the X. laevis PL. To minimize confounding FL effects, for each in silico-robotic trial, muscle starting length was adjusted between 1.0 and 1.26 to enable peak activation to coincide with peak force [22]. Given the simplifying assumptions of our above analytical model (table 1), in silico-robotic and in vitro-robotic experiments were used for verification.

Table 1.

Summary of simplifying assumptions made in the analytical versus experimental approaches used.

property included	analytical model	musculo-robotic experiments (in silico-robotic and in vitro-robotic)
muscle activation dynamics	absent	present
muscle force–length effects	absent	present
muscle force–velocity effects	present	present
fluid added mass effects	absent	present
fluid drag effects	present	present

Hydrodynamic force was measured from strain gauges mounted to a custom-built sensor attached at the base of the robotic foot (see [18] for details). The force signal was amplified using a model 2120 amplifier (Vishay Intertechnology, Inc., Malvern, PA, USA). All signals were recorded using a National Instruments A/D board (USB-6289).

2.3. Estimating in vivo gear ratios

Estimates for GRs were from small adult male X. laevis frogs (28.59 ± 4.34 g mean ± s.d. body mass; N = 5). The PL inlever, r, value of 0.14 cm was obtained from the tendon travel technique [27]. To calculate R, the foot centroid was located from digital tracings of photographs of the feet (ImageJ, U.S. National Institutes of Health, Bethesda, MD, USA). R was estimated at ‘mid-stroke’ (foot angle = 90° to flow). Using joint kinematics data [15], a line was drawn normal to the foot originating at the centroid. R was calculated as the perpendicular distance between the drawn line and the ankle joint at mid-stroke.

3. Results

3.1. Morphological V_maxmorph predictions from the model compared with in vivo data

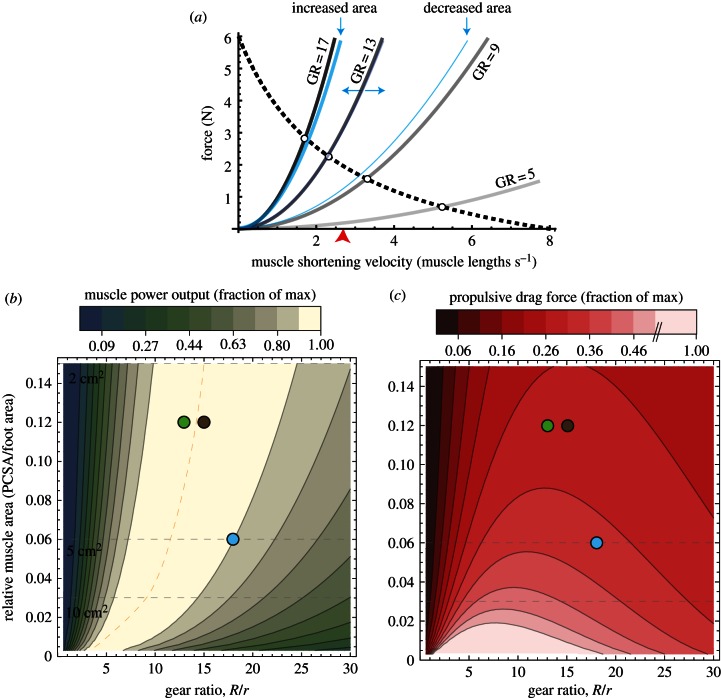
For a 5 cm² foot (similar to the size of a X. laevis foot), the model predicted drag force curves of increasing steepness as GR varied from 5 to 17 (figure 3a). 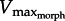decreased from 5.2–3.3 to 2.3–1.7 muscle lengths s⁻¹ (ML s⁻¹). Similarly, increasing foot area from 2 to 10 cm² (at GR = 13) caused 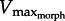to decrease from 3.1 to 1.8 ML s⁻¹. Increasing either GR or area also caused power to increase then decrease as 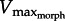shifted towards then away from 1/3V_max. For any given relative muscle area (muscle PCSA/foot area), both muscle power and hydrodynamic force rise and fall about an ‘optimal’ GR value. This optimal GR was predicted to shift rightward as relative muscle area increases (figure 3b,c). From this theoretical performance map, the GR of the X. laevis PL (relative area = 0.3 cm²/5 cm² = 0.06) was predicted to be approximately 11. Near this predicted maximum muscle power and fluid force, estimates of in vivo GR ranged from 11.5 to 20, measured at different points of the foot stroke and GR ≈ 18 at mid-stroke.

Figure 3.

(a) The force–velocity curve for Xenopus laevis (black, dashed) is plotted against fluid drag (grey, solid) predicted for a foot area of 5 cm² (typical for X. laevis) at gear ratios (GR) of 5, 9, 13 and 17. Blue lines indicate the leftward or rightward shifts due to a foot area increase (10 cm²) or decrease (2 cm²) at GR = 13, respectively. Note how increases in either GR or foot area are predicted to compress the muscle's operating range. The red arrow indicates maximum power at 1/3V_max. (b) A theoretical map of muscle power output and (c) propulsive drag force show how ‘optimal’ GR depends on relative muscle area (and vice versa). Dotted grey lines predict values for foot areas of 2, 5 and 10 cm² tested with in silico-robotic experiments. Dots represent GR versus relative area values for example aquatic (X. laevis, blue) and semi-aquatic species (Rana pipiens, brown; Rana catesbeiana, green) at mid-stroke. Semi-aquatic species values were estimated from previous literature (see §2).

3.2. Musculo-robotic measurements of morphological V_max

Following electrical stimulation, in vitro muscle force developed in response to hydrodynamic force (figure 4). Since experiments to determine the F–V curve could not be performed on the same muscle preparations as in vitro-robotic trials, 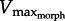could not be found precisely. However, the data clearly show muscle force and velocity increasing until reaching a maximum velocity near the predicted range of 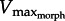(figure 5a). As GR increased from 5 to 11 to 17, the operating range of the muscle also shifted leftward, as predicted by the superimposed drag curves from the model. To more precisely test predictions of 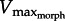, in silico-robotic experiments were performed. Similar to in vitro-robotic trials, both force and velocity increased rapidly until near the point of maximum activation, at which time muscle force reached the limit imposed by the F–V curve (figure 5b). Plots of force versus velocity intercepted with the F–V curve near the predicted values of 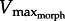. Reflecting in vitro-robotic experiments, increasing GR compressed the muscle velocity range (i.e. approx. 0–5 MLs versus approx. 0–1.8 for GR = 5 versus 17). Although the analytical model predicted muscle force and velocity values to only occur above the drag force curve, both in vitro and in silico data fell below the drag curves during the relaxation phase of the muscle. This underestimate could be due to (i) slight deviations of the fluid reaction force vector causing lower outlever values than estimated by our model (see §4) or (ii) backward-directed force caused by added mass effects which counteract fluid drag late in the swimming stroke [15]. Consequently, slightly underestimated actual peak V_m values.

Figure 4.

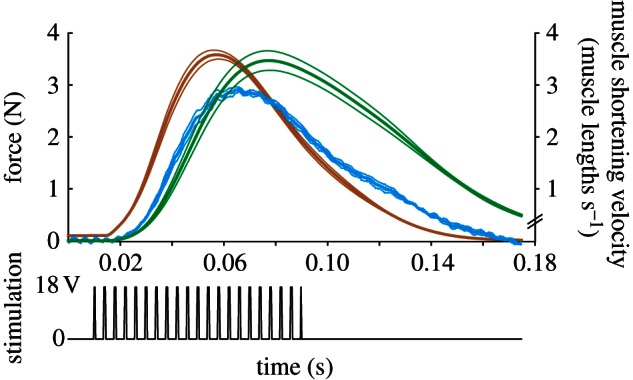
Traces of living in vitro-robotic muscle force (brown), shortening velocity (green), hydrodynamic force × 10 (blue) and muscle stimulation pulses (black) for GR = 11 (the predicted optimal value), foot area = 5 cm². Thick lines are mean and thin are standard deviation for N = 3 frogs.

Figure 5.

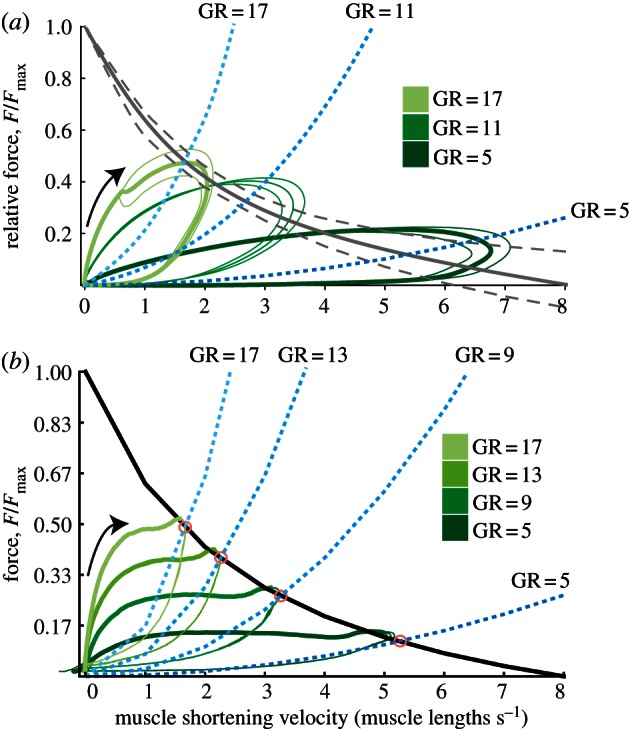
Force versus velocity plots for (a) in vitro-robotic and (b) in silico-robotic experiments. Grey curves are F–V curves. Dotted grey lines are 95% confidence bands representing uncertainty of matching in vitro-robotic data with F–V curves from separate experiments. Drag curves (blue, dotted) predict the diminishing operating range of the muscle as GR increases. Bold lines are mean and thin are standard deviation (N = 3 frogs or N = 3 replicates for in vitro-robotic or in silico-robotic trials, respectively). For in silico trials, thick lines represent data prior to peak muscle activation.

3.3. Bio-robotic measurements of muscle power and hydrodynamic force

Relative peak muscle power (peak trial power relative to the maximum value observed) and hydrodynamic force were tested over a range of GR and foot sizes. For foot sizes of 2, 5 and 10 cm², the analytical model predicted maximum power and hydrodynamic force to occur at GR = 9, 11.4 and 15, respectively (figure 3b,c). In close agreement with theoretical predictions, in silico-robotic tests revealed that GR = 9, 11 and 13 for maximum peak muscle power (figure 6a) and GR = 9, 11 and approximately 11–15 for maximum peak hydrodynamic force (figure 6b).

Figure 6.

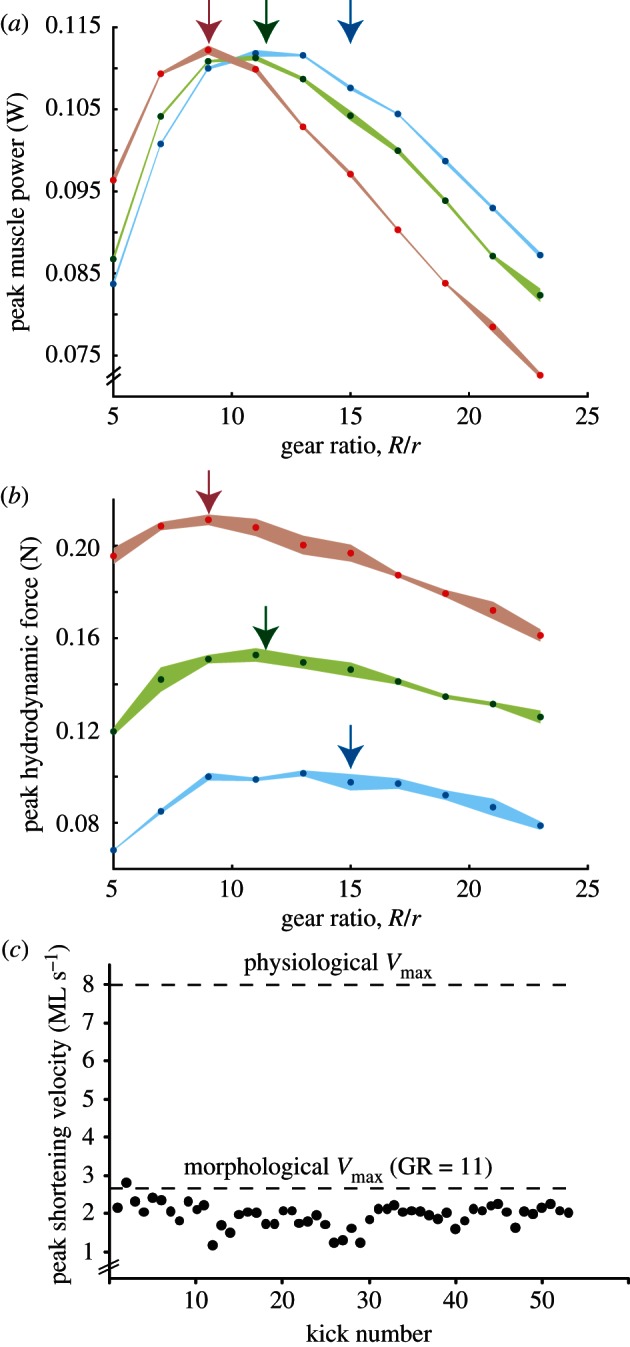
(a) Peak muscle power and (b) peak hydrodynamic force for GR = 5, 7, 9, 11, 13, 15, 17, 21 and 23 tested using circular foot sizes of 2 (blue), 5 (green) and 10 cm² (red). Arrows show analytically predicted locations of maxima (along dotted grey lines of contour plots; figure 3b,c). Dots are mean values and shaded areas are ± standard deviation for N = 3 replicates. Muscle starting length was adjusted so that peak force coincided with peak activation (see §2). (c) Peak in vivo PL muscle shortening velocity during X. laevis swimming [28].

4. Discussion

4.1. Optimal gear ratio for muscle power output can be predicted from limb morphology

During locomotion, muscle power output may be limited by its coupling to the load, rather than by intrinsic muscle properties. Because muscle power output correlates with swimming speed and acceleration [28] power likely limits performance. Aiming to explore conditions under which power is ‘optimized’ (i.e. shortening velocity ≈ 1/3V_max), we developed a predictive model that was tested using recent musculo-robotic tools. As predicted, results from both the analytical model and experimental trials suggest that aquatic frog physiological and limb morphological properties may be tuned for swimming. Findings also suggest that there need not be a trade-off between swimming and jumping ability.

Our analytical model, despite its simplicity, accurately predicted how changes in external morphology (e.g. foot area) and in internal morphology (e.g. joint gear ratio, ‘GR’) limit muscle power. Simple analysis reveals that drag force experienced by the muscle is proportional to A_fin × GR³ (equation (2.9)). Thus, we expected slower contraction speeds (lower 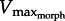) owing to increases in either GR or foot area, as demonstrated by our experimental data (figure 5). In addition, as expected, increases in GR caused peak muscle power to rise and fall as 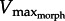approached then regressed from 1/3V_max. More broadly, current findings suggest that for high Reynolds number rowing, the limits to muscle power and hydrodynamic force can be predicted as a simple function of muscle area relative to foot area (relative area = PCSA/foot area) and GR. Consequently, our analytical model reveals two general strategies for maximizing muscle power against a fluid load: (i) high gear with large relative muscle area (e.g. large muscle, small fin) or (ii) low gear with small relative muscle area (e.g. small muscle, large fin). Specifically, larger feet (smaller relative muscle area) require lower GR to maintain a given power output against a fluid load, whereas small feet (large relative muscle area) would not be sufficiently loaded if the GR were too low. Xenopus laevis frogs, for example, have larger fin areas and smaller PL PCSA than Rana pipiens or Rana catesbeiana of similar body mass (relative area = 0.06 versus 0.12; (this study, [4,21,29–31]). From these interspecific morphological differences, our model predicts X. laevis to operate at slightly lower gears (GR = 11) than ranid frogs (GR = 14). Consistent with model predictions, GR measurements of X. laevis ranged from 11 to 20 (depending on limb kinematics) and estimated GR values from previous literature [4,21,29–31] for R. pipiens and R. catesbeiana were GR ≈ 15 and 13, respectively (figure 3b). However, because GR varies in vivo (see below), these species are all likely to operate over a similar gearing range.

4.2. Estimated morphological V_max predicts maximum in vivo shortening velocity in Xenopus laevis

In addition to exploring how limb morphology might be tuned for rowing, our current findings have important implications on our understanding of in vivo muscle data. In traditional approaches to dynamic muscle function, one might use in vitro work loops [32,33] to address whether in vivo muscle operates at or near its intrinsic power limits. For example, some muscles may produce less power in vivo compared with their intrinsic potential measured in vitro [34]. However, muscle physiological approaches do not explain why muscle power output may be submaximal in vivo. Our current model predicts that if muscle contractile properties are not matched to the surrounding fluid via appropriate limb morphology, a muscle will operate below its power limits. Knowing that X. laevis operates at a minimum GR of approximately 11, shortening velocity should not exceed the 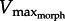of approximately 2.7 ML s⁻¹. Data from experiments performed previously [28] show that in vivo PL shortening velocity remains below the predicted limit of approximately 2.7 ML s⁻¹ (figure 6c). The match between 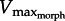predictions and in vivo data suggests three points: (i) the PL is velocity-limited during swimming, (ii) the maximum contractile velocities observed in vivo approach 0.3V_max which is optimal for power generation, and (iii) in vitro work loop experiments performed above the 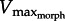would produce results that are not physiologically possible for the muscle in vivo.

4.3. Jumping frogs may also possess morphological tuning for rowing at no expense to jumping performance

Armed with an understanding of how fluid loading may limit in vivo muscle function, we describe how the current model can be applied to address questions of comparative functional morphology. We illustrate the applications of the model by an analogy to human-powered rowing. Hypothetically, the rower represents a muscle which must operate within intrinsic speed and strength limits. The oar blade and oar lock represent the webbed foot and limb joint, respectively, whose gearing is determined by the inboard and outboard oar lengths (i.e. ‘rigging’). Finally, the rules and regulations of the rowing sport represent functional constraints which may, for example, constrain the size of the oar blade. Knowing the strength and speed capacities of the rower, one should be able to predict the appropriate rigging to match the capabilities of a particular rower to optimize muscular power output.

Given the relationship between rowing ability, limb morphology and muscle properties, our model could be used to address morphological trade-offs between swimming and other locomotor tasks. Frog jumping ability [1,2] correlates to modifications of the skeleton [35], potentially in conflict with swimming. However, morphology of ranids (jumper–swimmers; [36]) and swimming performance of ranids versus pipids (swimmers; [37]) reveal no evidence that jumping diminishes swimming capacity. How can the musculoskeletal system excel both at swimming and jumping? The map of muscle power versus GR and relative area (figure 3b) suggests that there exist multiple combinations of foot size and GR which maximize muscle power. This broad ‘solution space’ perhaps could accommodate specializations for jumping while maintaining swimming ability (or vice versa). For instance, the recoil of elastic tendons to amplify muscle–tendon power output for jumping [4] requires appropriate tuning of GR to body mass [38], suggesting that jumping requirements may constrain GR. In such cases, changes in foot area could compensate (i.e. moving vertically along the power map). Alternatively, foot area may be constrained due to shorter feet. Large forces during jumping [4,10] may limit foot length in order to minimize joint torques. Indeed, the feet of hylid frogs, the champion jumpers, are short despite their elongated total hindlimb length relative to fully aquatic species [35]. In this case, adjustments of GR can move the limb horizontally along the power map to optimize power when faced with a foot area constraint. Thus, we speculate that due to the many pairings of GR and foot area that confer power output during swimming, there need not be a swimming–jumping trade-off—a ‘specialized’ jumper may still be morphologically tuned to optimize power during rowing. Further modelling would be necessary to address the consequences of morphological constraints on swimming versus jumping.

4.4. Variation in V_max probably influences the ‘optimal’ limb morphology for rowing

In addition to the morphological predictors of muscle performance, physiological properties such as V_max influence the relationship between limb morphology and power output. Specifically, increasing or decreasing V_max causes a leftward or rightward shift of the entire power map, respectively. For ectothermic animals such as anurans, large fluctuations in environmental temperature (either seasonally or with climate change [39]) would influence V_max, affecting where muscles operate on the FV curve. V_max in X. laevis increases with temperature (V_max ≈ 0.004 × temperature² + 0.11 × temperature + 2.5 ML s⁻¹; [40]). Given that X. laevis swim to catch active prey and escape predators [14], climate fluctuations might influence their ecological success. Yet, the invasive population of X. laevis of the Santa Clara River (CA, USA) thrive year-round [14], despite average daily temperature fluctuations from approximately 7 to 24°C [41]. At the higher temperature extreme, the PL muscle functions slightly rightward of the predicted optimum (figure 3b). However during winter, V_max may drop to approximately 3.7 ML s⁻¹, causing a rightward shift in peak GR from 11.4 to 18. Consequently, the PL produces approximately 90 per cent of its maximum power during warm months and approximately 100 per cent of its potential power (given the depressed V_max) during colder months. Thus, although colder temperatures depress absolute muscle power, the rightward shift of the power map might enable muscles to use their full power potential at that given temperature by maintaining the muscle's ability to operate at approximately 1/3V_max. Alternatively, if X. laevis limbs were to operate leftward the predicted peak power (GR < 11), falling temperatures would further reduce performance. For example, if X. laevis operated at GR = 9, it would produce approximately 98 per cent of its maximum power at 22°C, but only approximately 70 per cent at 7°C. In addition to low temperature effects, power would likely also be depressed at higher temperatures (despite greater V_max) owing to a rightward shift away from the optimum GR measured at laboratory temperature (22°C). Perhaps the right-shift of the power map could explain the depressed swimming performance of Xenopus at high temperatures [39]. One should note however, that beyond our simple model, animals might also respond to temperature changes by modifying stroke kinematics or the dynamic shape of their feet. Regardless, such influences of temperature imply that limb morphology of birds and mammals might be more tightly tuned, given that their V_max would remain constant at their physiologically regulated temperature.

Using published V_max data, one also can make broad taxonomic comparisons among high Reynold's number rowers. For example, notonectid insects swim using a slow muscle (V_max approx. 1 ML s⁻¹; [20]) compared with frogs (V_max ∼ 9). Consequently for notonectids, we see a very high GR (approx. 40) given both the rightward-shifted 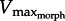and their small rowing appendage. By contrast, aquatic bird and mammal muscles operate at higher physiological temperatures, causing V_max to be higher [42], perhaps requiring relatively lower GR values. This requires further investigation.

4.5. Simplifying assumptions of the current model are appropriate for certain cases of aquatic locomotion, but not for others

Our model is simple, thus has physiological and morphological limitations which must be addressed. The most evident morphological simplification is the neglect of leg joints proximal to the ankle. We justify this simplification for X. laevis where ankle rotation produces most of the thrust. However, ranids rely considerably less on their ankle joint (producing approx. 50% of total thrust; [37]). Nevertheless, even in ranids, both ankle rotation and ankle stabilization (to maintain the foot's position as the proximal joints push backward) require great amounts of power produced at the ankle, justifying our model's focus on distal rather than proximal joints. Regardless of the model's simplicity, identical principles of 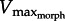tuning would apply to more complex future models. In terms of the physiological simplifications, the interactions among F–V and F–L effects are potentially confounding given that large length changes reduce the optimal V/V_max for producing power [43]. However, recent work demonstrates that muscle contractions beginning at longer starting lengths (stretched slightly beyond optimal length) enable the muscle to reach the plateau of the F–L curve at the time of maximum muscle activation [22]. Thus, at the time point of peak activation and muscle power, F–L effects would not influence maximum muscle power for the current model. Indeed, our in silico-robotic experiments, which do include F–L effects, match well with our simple model predictions (figure 6).

Secondly, experiments were performed in still water without translational motion of the foot. In a simple rower (figure 2d), oar blades would have an aft-directed rotational and translational component as they rotate about their base. Therefore, in a tethered animal, the oar would ‘slip’ backward. However if untethered, the body moves forward with respect to the water, whereas the blade moves backward with respect to the body. As a result, an oar's backwards translation is cancelled by forward swimming such that the motion of the oar base is nearly fixed in the global reference frame, as evident in swimming insects [20], aquatic frogs [8,15] and in human-powered rowing [44]. In these cases, we capture important aspects of muscle–fluid dynamics in the absence of modelling forward body motion. In cases where rowing appendages are thrust backwards (e.g. ranid frogs [10]), our model is less accurate. In either forward or backward translation cases, our simple model would overestimate outlever (R) length as the fluid reaction force vector deviates from normal to the foot surface [8]. Consequently for large foot sizes which cause large fluid forces and faster swimming speeds, our simple model would overestimate GR. For our current results, such an overestimation would shift our estimates of in vivo GR rightward (away from the predicted optimum for ranids and towards the optimum for X. laevis; figure 3b). Thus, in cases of fast forward swimming (e.g. the second or third kick when the foot rotates as the body is already in motion) or in rapid backward translation (common in ranids), one must quantify translational and rotational velocity components to account for the deflection of the fluid reaction force vector [8]. In addition, the current simple analytical model is not appropriate for acceleration-based swimming. In cases when limb accelerations are extreme and fluid dynamic loads are dominated by the acceleration reaction (e.g. very small frogs [8] or suction feeding fish [45]), our model does not apply because the coupling between shortening velocity and fluid drag would be relatively unimportant. Finally, we address time-varying gearing. Although inlever (r) does not vary over the in vivo range of frog ankle joint motion [27,30,31], the outlever (R) may vary due to (i) the angle of the fluid reaction force vector changing with respect to the foot orientation [8] or (ii) as the foot's position relative to the ankle changes throughout a stroke. To address this, R can be estimated at various points in the foot stroke (see §2).

4.6. Summary

We present an approach which may be used to predict muscle performance during swimming using morphological (GR, foot area) and physiological (V_max, F_max) constants. We found that X. laevis hindlimbs possess morphology that is appropriate given muscle intrinsic properties and PCSA. Such ‘tuning’ of morphological and physiological properties probably enable the muscle to shorten near 1/3V_max to approach maximal power during swimming.

More generally, the current study addresses dilemmas that arise when limb morphology is considered without regard to underlying muscle properties (and vice versa). Based on fin area alone, one might falsely conclude that ranid frogs produce lower power outputs in fluid than aquatic frogs which possess larger feet. However, based on the larger PCSA of ranids compared with X. laevis, one might reach the opposite conclusion. We resolve such dilemmas with a model that predicts functional relationships among morphological and physiological properties. Perhaps our simple approach can be used to suggest pathways by which natural selection influences performance through the modification of either muscle or limb properties.