How does tooth cusp radius of curvature affect brittle food item processing?

Abstract

Tooth cusp sharpness, measured by radius of curvature (RoC), has been predicted to play a significant role in brittle/hard food item fracture. Here, we set out to test three existing hypotheses about this relationship: namely, the Blunt and Strong Cusp hypotheses, which predict that dull cusps will be most efficient at brittle food item fracture, and the Pointed Cusp hypothesis, which predicts that sharp cusps will be most efficient at brittle food item fracture using a four cusp bunodont molar. We also put forth and test the newly constructed Complex Cusp hypothesis, which predicts that a mixture of dull and sharp cusps will be most efficient at brittle food item fracture. We tested the four hypotheses using finite-element models of four cusped, bunodont molars. When testing the three existing hypotheses, we assumed all cusps had the same level of sharpness (RoC), and gained partial support for the Blunt Cusp hypotheses. We found no support for the Pointed Cusp or Strong Cusp hypotheses. We used the Taguchi sampling method to test the Complex Cusps hypothesis with a morphospace created by independently varying the radii of curvature of the four cusps in the buccolingual and mesiodistal directions. The optimal occlusal morphology for fracturing brittle food items consists of a combination of sharp and dull cusps, which creates high stress concentrations in the food item while stabilizing the food item and keeping the stress concentrations in the enamel low. This model performed better than the Blunt Cusp hypothesis, suggesting a role for optimality in the evolution of cusp form.

1. Introduction

There are two different approaches to reconstructing the diets of extinct animals based on their tooth morphology. The first is comparative and uses extant animals as a model for inferring diet from dental morphology and tooth wear [1–3]. In mammals, this has led to the development of many useful metrics for quantifying the occlusal surface of teeth, including: the shearing quotient [4–6], the relief index [7,8], orientation patch counts [9,10], relative enamel thickness and enamel decussation [11–14] and Dirichlet normal energy [15,16].

The second approach is to use engineering principles to quantify complex sets of interactions surrounding the tooth–food interaction. Given its complexity, this approach requires both assumptions and simplifications. One common simplification is to model a single tooth cusp in contact with a food item prior to and during the process of fracturing the food item [17–19]. For example, Evans & Sanson [18] proved that punches with sharper cusps and tips require less force and energy to fracture beetles than punches with duller cusps and tips. This is because sharper cusps and tips reduce the contact area between the punch and the food item, reducing the force needed to obtain the principal stresses needed to fracture the exoskeleton. This is one of the reasons why tooth cusp sharpness, measured by radius of curvature (RoC) (teeth with higher RoCs are duller and teeth with lower RoCs are sharper), has become a metric of interest in recent years [18,20–24]. The assumption that cusps act independently to fracture food items has been a necessary and useful simplification. In this study, we propose to investigate how the multiple cusps of mammalian molars contribute to the process of fracturing food items.

Modelling the material properties of food items is a critical first step in investigating how they fracture. Many of the metrics mentioned earlier focus on how tooth morphologies reflect the extent to which the foods that an animal eats are mechanically challenging. Mechanically challenging foods are generally broken into two categories: tough or displacement limited, and hard or stress limited [22]. Traditionally, hard food items have also been classified as brittle [25–31]. However, this classification system may not always be useful, as some tough food items are brittle and some hard food items are not. Moreover, it does not describe how food items fail. Here, we suggest two categories for mechanically challenging food items taken from materials science: brittle and ductile. Brittle items exhibit little to no plastic deformation prior to failure, while ductile items absorb a large level of strain energy and exhibit significant plastic deformation prior to fracture (figure 1). These two categories are used extensively in material science [32,33] and have been applied to other biological materials [34,35].

Figure 1.

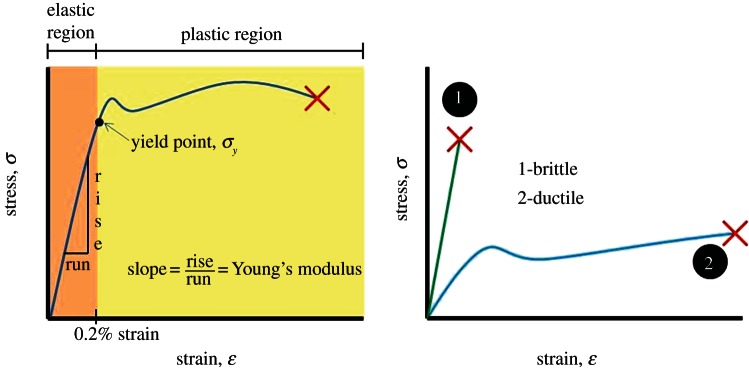
Tension tests allow the user to calculate both the stress and strain of the material at any given point in time up to fracture (denoted by X). A stress–strain plot can be obtained by plotting stress on the y-axis and strain on the x-axis and can used to calculate several material properties of the specimen being tested. For example, the slope of the stress–strain curve in the linear, elastic region is Young's modulus. The elastic region of the stress–strain curve ends at the yielding point, which usually occurs after 0.2% strain. Brittle materials tend to fracture soon after the yielding point while ductile materials continue to deform in the plastic region until fracture occurs. (Online version in colour.)

This study focuses on the interaction between multi-cusped teeth and brittle food items. Brittle materials can have either high (i.e. cast iron) or low (i.e. porcelain, leaves and rock salt) moduli of elasticity (Young's modulus), but they exhibit little to no yielding on a stress–strain curve prior to fracture (figure 1). Brittle materials tend to deform strictly in the elastic region of the stress–strain curve and fracture at or soon after the yield stress is reached, while ductile materials continue to experience high levels of strain and deformation (with little increase in stress) prior to fracture. In contrast to brittle materials, ductile materials leave the elastic region and have a large plastic region on their stress–strain curves prior to fracture. They also tend to absorb high levels of strain energy per unit volume (defined as the area under the stress–strain curve) and have high toughness values (as defined by Callister [32]). The concept of toughness in feeding biomechanics differs from the concept of toughness in materials science. Toughness in feeding biomechanics has units of Joules per square metre, while toughness in materials science has units of Joules per cubic metre. The concept of toughness used in feeding mechanics is identical to the engineering concept of work of crack propagation per area of crack (G).

Studies of enamel fracture have drawn from concepts in fracture mechanics. Fracture mechanics is based on the idea that all materials have inherent flaws and microcracks, and, once a certain amount of energy has been absorbed by the material through the application of tensile stresses, these cracks will propagate through the materials [36]. One metric for a materials resistance to crack propagation that has been used in recent studies of enamel chipping is fracture toughness [37,38]. Fracture toughness is not the same as toughness (mentioned earlier) and has units of Pascals Here, we test three existing, sometimes contradictory, hypotheses, and one novel hypothesis concerning the relationship between brittle food items and optimal occlusal morphology of mammalian upper molars [20]. The first is the Blunt Cusp hypothesis, which encompasses two predictions. First, it predicts that teeth comprised entirely of dull cusps can fracture brittle food items with lower force or energy than teeth comprised entirely of sharp cusps. Second, it predicts that teeth comprised entirely of dull cusps can fracture brittle food items with lower force or energy than teeth comprised of a mixture of sharp and dull cusps [20,39]. This hypothesis is based on the observation that mammals that consume hard (brittle) food items tend to have teeth with dull cusps [5,40]. This hypothesis would be supported if strain energy absorbed by a brittle food item is negatively correlated with RoC (figure 2).

Figure 2.

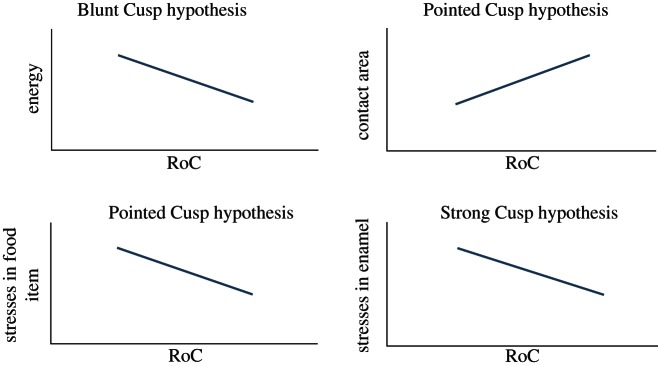
Correlations between RoC and energy, contact area, stresses in the food item and stresses in the enamel expected under the Blunt, Pointed and Strong Cusp hypotheses. (Online version in colour.)

The second hypothesis is the Pointed Cusp hypothesis, which contradicts the Blunt Cusp hypothesis and states that teeth with sharp cusps are the most efficient at fracturing brittle food items. The rationale behind this hypothesis is that sharper cusps can apply a given force over a smaller contact area, creating high stress concentrations in a food item [20,21]. Indeed, sharp, man-made tools (with low RoCs) such as knives and blades require less force to fracture/deform thin surfaces than do blunt tools [18,41,42]. (Note, however, that these are ‘single cusped’ tools, meaning that the total contact area between the tool and the surface is a function of RoC. This relationship may or may not hold true for ‘multiple cusped’ tools, such as mammalian molars.) The Pointed Cusp hypothesis predicts that the contact area between a food item and a tooth is positively correlated with RoC and that stresses in the food item are negatively correlated with RoC (figure 2).

The third hypothesis is the Strong Cusp hypothesis, which, similar to the Blunt Cusp hypothesis, states that dull cusps are most efficient at fracturing brittle food items. However, the Strong Cusp hypothesis states that dull cusps are more efficient because they prevent high stresses from forming in the enamel. This prevents microcracks, which can ultimately lead to enamel fracture, from forming in the enamel [11,20,43,44]. This hypothesis predicts that tensile stresses in the enamel should be negatively correlated with RoC (figure 2).

There is a significant body of evidence demonstrating that a considerable number of microcracks form at the enamel dentine junction (EDJ) over the useful life of human molars [45], any of which could cause enamel chipping to occur. Here, we assume that microcracks are randomly distributed along the EDJ. Because crack propagation requires tensile stresses, we assume that higher tensile stresses increase the likelihood of a crack of random size and orientation resulting in an energy release rate greater than the critical energy release rate, thus increasing the probability of crack propagation.

We also test the novel Complex Cusp hypothesis. This hypothesis embraces both the Strong and Pointed Cusp hypotheses, and incorporates the idea that it may be advantageous to simultaneously preserve enamel integrity and maximize the efficiency of processing brittle food items. The Complex Cusp hypothesis predicts that the optimal tooth morphology for fracturing brittle food items exhibits a mixture of both dull and sharp cusps; the dull cusps act to minimize stress in the enamel while the sharp cusps serve to maximize stress in the food item. We define the optimality criterion by the function

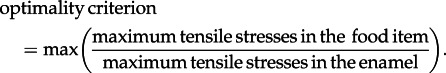1.1

Unlike the other hypotheses, this hypothesis does not predict a relationship between RoC and any single measure of performance in either the tooth or food item. Rather it predicts that the optimal tooth morphology will exhibit a combination of sharp and dull cusps (i.e. low and high RoCs).

Both the Blunt and Pointed Cusps hypotheses deal strictly with the function of breaking down food items (minimizing strain energy or maximizing stresses in the food item), making them applicable to all mammals. Conversely, the Strong Cusp hypothesis and the Complex Cusp hypothesis place high value on conserving enamel. Therefore, the latter two hypotheses may not apply to all mammalian teeth as some animals are affected less by enamel fracture than others.

2. Material and methods

2.1. Finite-element analysis and model construction

We used ANSYS APDL v. 13.0 finite-element program (Canonsburg, PA, USA) to test our hypotheses, because it supports nonlinear elastic contact simulations and parametric modelling through the ANSYS Parametric Design Language (APDL). We wrote an APDL code to automatically construct a parametric model of a tooth, a brittle food item and to execute simulated interactions between them. We assigned 19 parameters to the model, including the heights of the cusps (four parameters), the distances between the cusps in the mesiodistal and the buccolingual directions (two parameters), the heights of the valleys in between the cusps (four parameters), the RoCs of the cusps in the mesiodistal direction (four parameters), the RoCs of the cusps in the buccolingual direction (four parameters) and enamel thickness (one parameter; figure 3). We held enamel thickness constant over the entire occlusal surface of the tooth at 1 mm. We set the heights of the cusps and valleys at 5 and 3 mm, respectively. The distance between the cusps in the buccolingual direction was held at 15.4 mm, and the distance between the cusps in the mesiodistal direction was held at 15.7 mm. Distances between cusps are based on the average width and length of a male gorilla tooth [46]. The eight RoCs were the only variables allowed to vary from model to model.

Figure 3.

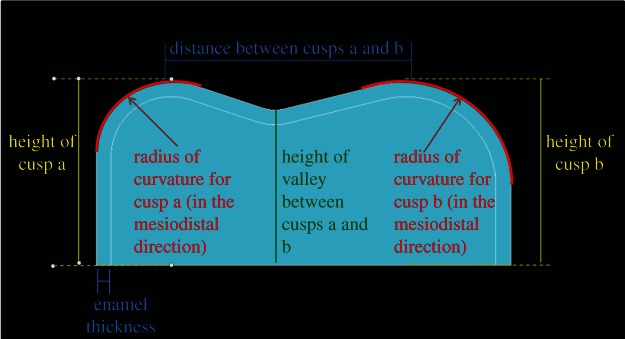
Cross section in the mesiodistal direction between two cusps, a and b, showing a number of the parameters that can be assigned to this parametric model. (Online version in colour.)

To begin constructing the tooth model, we created four cross sections of the tooth, each of which traversed two cusp tips and modelled enamel and dentine separately. This defined the tooth in two mesiodistal and two buccolingual planes. We then used splines to create an outline of the bottom of the tooth, again keeping enamel distinct from dentine. We used Coons patches (patches that are fitted between four arbitrary curves) to create the occlusal surface of the tooth, the EDJ and the bottom of the tooth crown. The Coons patches were used to construct the dentine and the enamel cap volumes. These volumes were meshed separately with 10-noded brick elements, which are quadratic elements with nodes at the four vertices and on the mid-side of the six edges of the element. The use of the mid-side nodes allows the elements to properly mimic the curved geometry of the tooth (figure 4), as well as enable the stress and strain fields to vary linearly within the element. We assigned isotropic material properties to the enamel cap (Young's modulus = 84 100 MPa, Poisson's ratio = 0.3) and the dentine (Young's modulus = 8600 MPa Poisson's ratio = 0.31) [47]. Following Berthaume et al. [20], we constructed a hemispherical model of a brittle food item (diameter = 28.2 mm) with a Young's modulus of 2000 MPa and a Poisson's ratio of 0.4.

Figure 4.

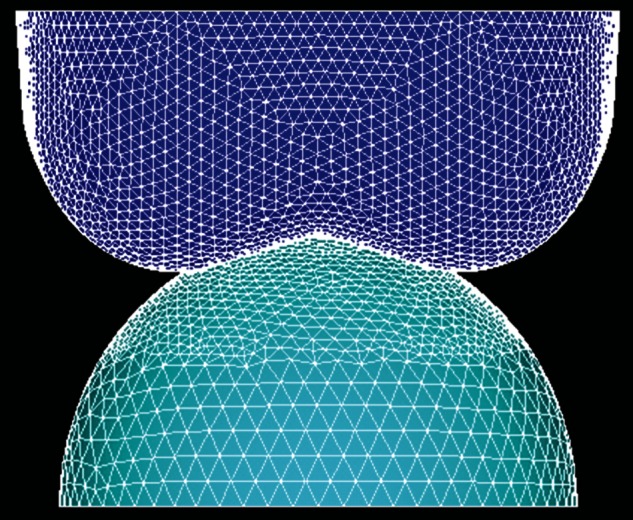
One of the completed models, where all RoCs of the tooth are being held constant at 5 mm. (Online version in colour.)

The food item was centred over the occlusal surface of the tooth, and constraints were applied to the bottom of the tooth and the food item. The tooth had constraints applied to bottom of the crown, preventing translation in the buccolingual and mesiodistal directions. It also had a 3 mm displacement applied to the bottom of the crown in the vertical direction, which moved the tooth towards the food item to simulate biting. Constraints were applied to the bottom of the food item preventing translation in the vertical direction and rotation around an imaginary axis running through the centre of the food item in the vertical direction. The rotational constraints stabilized the food item while allowing it to translate in the buccolingual and mesiodistal directions, thus allowing it the food item to settle into the position of lowest potential energy during the simulations [20].

The simulations were solved in 10 substeps, and results (displacement, reaction force, contact area and tensile stresses for the enamel and food item) were extracted at each substep. Quadratic equations of the displacement of the food item in the vertical direction versus reaction force and were used to interpolate the displacement that resulted in a 2 kN reaction force. Quadratic equations were also used to relate displacement to reaction force, strain energy and contact area, while cubic equations were used to relate displacement to tensile stresses. The equation relating displacement to reaction force was used to determine displacement corresponding to a 2 kN force (the maximum bite force of an orangutan [48]), and the subsequent equations were used to calculate the strain energy, contact area and tensile stresses at the calculated displacement. Linear regression analyses testing the Blunt, Pointed and Strong Cusp hypotheses were carried out using R (www.r-project.org, [49]).

2.2. Failure criterion

Although a compressive force was applied to the tooth and the food item during mastication, it is tensile stresses (i.e. maximum principal stresses) and not compressive stresses that cause failure in these structures [50,51]. Tensile stresses along the EDJ are of concern for the enamel because failure tends to initiate at microcracks along the EDJ, which is where tensile stresses are the highest in both experimental studies [11,50,52] and our models. For the food items, fracture was initiated on the inner surface of the hemisphere where tensile stresses are the highest, and then propagated to the outer surface.

We tested the Blunt, Pointed and Strong Cusp hypotheses by assuming that the RoC for all the cusps was equal, and then varied the RoCs from 2.5 to 7.6 mm (the dullest model that could be made using this model) in 0.25 mm increments (figure 5). Based on the correlations predicted in figure 2, both the Blunt and Strong Cusp hypotheses would be supported if a tooth comprised entirely of dull cusps performed best. Similarly, the Pointed Cusp hypothesis would be supported if a tooth comprised entirely of sharp cusps performed best.

Figure 5.

Six of the 23 models used to test the three existing hypotheses, ranging in RoC from 3 mm (left) to 7.6 mm (right). (Online version in colour.)

To test the Complex Cusps hypothesis, that the optimal tooth morphology for fracturing brittle food items exhibits some combination of both dull and sharp cusps, we created a morphospace by altering the mesiodistal and buccolingual RoCs of the tooth cusps and mapped the optimality function (equation (1.1)) onto that space. If each of the eight RoCs were allowed to have three discrete values (dull, 7 mm; medium, 5 mm or sharp, 3 mm), a full factorial set of simulations would require 6561 simulations to construct the morphospace. Instead, we used the more efficient Taguchi method to run a partial factorial set of simulations to define the morphospace and capture the main effects [53–56]. The Taguchi method uses orthogonal arrays (in this case, an L18 orthogonal array (table 1)) to examine the morphospace. After generating the basic morphospace, we ran additional simulations to define the most optimal area of the morphospace in more detail.

Table 1.

RoC of each of the cusps (sharp, medium or dull). T1–T18 represent the 18 teeth produced using the Taguchi method (i.e. T1 = first tooth produced using Taguchi method), optimum is the optimal tooth morphology, and SubOpt1–3 are the three suboptimal tooth morphologies. The subscripts next to RoC tell which cusp is being described (cusps a, b, c and d) and the direction in which the RoC is being described (1, mesiodistal plane; 2, buccolingual plane).

tooth	RoC(a1)	RoC(b1)	RoC(c1)	RoC(d1)	RoC(a2)	RoC(b2)	RoC(c2)	RoC(d2)
T1	sharp	sharp	sharp	sharp	sharp	sharp	sharp	sharp
T2	sharp	sharp	medium	medium	medium	medium	medium	medium
T3	sharp	sharp	dull	dull	dull	dull	dull	dull
T4	sharp	medium	sharp	sharp	medium	medium	dull	dull
T5	sharp	medium	medium	medium	dull	dull	sharp	sharp
T6	sharp	medium	dull	dull	sharp	sharp	medium	medium
T7	sharp	dull	sharp	medium	sharp	dull	medium	dull
T8	sharp	dull	medium	dull	medium	sharp	dull	sharp
T9	sharp	dull	dull	sharp	dull	medium	sharp	medium
T10	medium	sharp	sharp	dull	dull	medium	medium	sharp
T11	medium	sharp	medium	sharp	sharp	dull	dull	medium
T12	medium	sharp	dull	medium	medium	sharp	sharp	dull
T13	medium	medium	sharp	medium	dull	sharp	dull	medium
T14	medium	medium	medium	dull	sharp	medium	sharp	dull
T15	medium	medium	dull	sharp	medium	dull	medium	sharp
T16	medium	dull	sharp	dull	medium	dull	sharp	medium
T17	medium	dull	medium	sharp	dull	sharp	medium	dull
T18	medium	dull	dull	medium	sharp	medium	dull	sharp
optimum	sharp	dull	sharp	sharp	dull	dull	sharp	sharp
SubOpt1	sharp	dull	medium	medium	dull	dull	sharp	sharp
SubOpt2	medium	dull	dull	dull	dull	dull	sharp	sharp
SubOpt3	medium	dull	medium	medium	dull	dull	sharp	sharp

3. Results

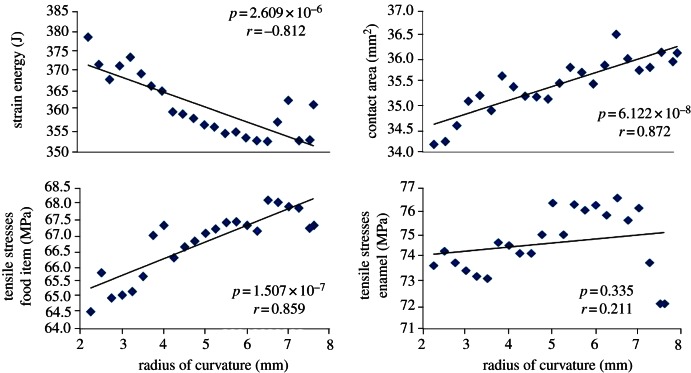
As predicted by the Blunt Cusp hypothesis, there was a significant, negative relationship between RoC and strain energy when all RoCs are assumed to be equal (p < 0.01, y = −3.74 × x + 380.12, r = 0.812; figure 6). However, there was no evidence that teeth composed entirely of dull cusps performed any worse (exhibited higher strain energy) than teeth with both sharp and dull cusps (table 2). In addition, the magnitude of the strain energy varied over a relatively small range (353–379 J) relative to the range of values seen in the Taguchi simulations (362–554 J; table 2).

Figure 6.

Results depicting the changes in strain energy in the food item, contact area between the occlusal surface and the food item, tensile stress in the food item and tensile stress in the enamel as RoC increases. Numerical results can be found in the electronic supplementary material. (Online version in colour.)

Table 2.

Results of the Taguchi simulations. Teeth are arranged from most optimal (top) to least optimal (bottom). SubOpt1–3 are three suboptimal teeth that had optimality ratios extremely close to the optimal tooth's optimality ratio.

			food item		enamel
tooth	reaction force (kN)	contact area (mm2)	maximum tensile stress (MPa)	strain energy (J)	maximum tensile stress (MPa)	optimality ratio
optimum	2	30.61	150	495	91	1.640
SubOpt1	2	30.33	149	489	94	1.594
SubOpt2	2	31.38	136	490	87	1.570
SubOpt3	2	31.80	140	492	89	1.570
T5	2	32.01	140	554	96	1.469
T18	2	32.23	128	414	96	1.336
T8	2	33.27	99	399	75	1.320
T10	2	34.29	122	394	93	1.315
T11	2	34.48	119	382	92	1.296
T6	2	32.75	113	415	90	1.259
T12	2	32.03	110	399	89	1.227
T4	2	34.98	106	393	88	1.202
T9	2	34.84	111	399	92	1.202
T16	2	33.03	105	423	87	1.197
T14	2	33.98	108	381	91	1.188
T15	2	33.47	114	412	97	1.177
T13	2	33.02	107	390	93	1.158
T7	2	32.70	93	400	84	1.106
T17	2	34.64	90	364	86	1.047
T3	2	35.95	72	368	78	0.929
T2	2	34.13	69	362	77	0.892
T1	2	35.10	65	372	73	0.886
range	—	5.62	85	192	24	0.754

The Pointed Cusp hypothesis predicted a positive correlation between contact area and RoC and, as a consequence, a negative correlation between RoC and tensile stresses in the food item (figure 2). We did find a significant positive correlation between contact area and RoC (p < 0.01, y = 0.31 × x + 33.91, r = 0.872). (Note that this correlation is not higher because contact area calculations are dependent on element sizes, which are finite.) However, we found a positive relationship between tensile stresses in the food item and RoC (p < 0.01, y = 0.53 × x + 64.10, r = 0.859) (figure 6). This is probably because of the complex interactions occurring between the tooth and the food item, where forces are being transferred from the tooth to the food item at a variety of angles.

Under the Strong Cusp hypothesis, we predicted a negative correlation between tensile stresses in the enamel and RoC. We did not find a correlation between these two variables (figure 6), but the lowest tensile stresses in the enamel did occur when the cusps were as dull as possible.

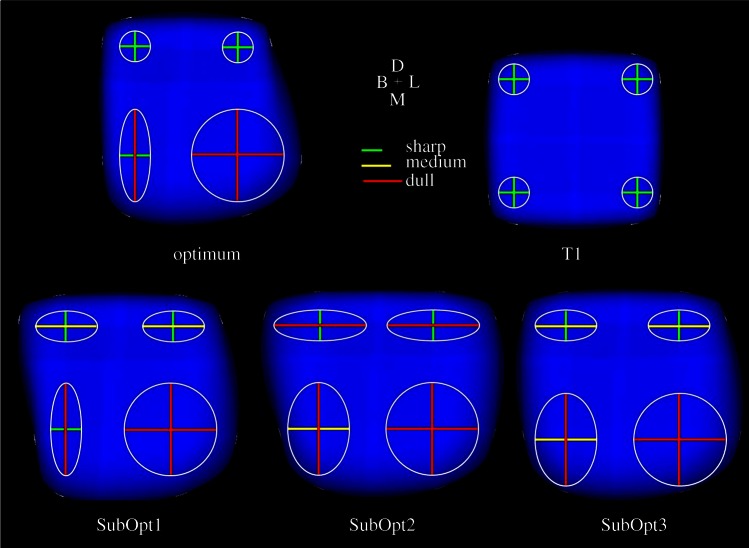
As predicted under the Complex Cusps hypothesis, the optimal tooth exhibits a combination of sharp and dull cusps (figure 7). The four most optimal teeth (optimum, SubOpt1, SubOpt2 and SubOpt3) have very high optimality ratios compared with the least optimal tooth (T1; table 2). In general, for the four most optimal teeth, there is one dull cusp which acts to create high stresses in the food item while decreasing the stresses in the enamel, while the other cusps are acting to stabilize the food item.

Figure 7.

Occlusal view of the most optimal tooth (optimum, upper left), the least optimal tooth (T1, upper right), and three suboptimal teeth (SubOpt1–3, bottom) using the optimality criterion set forth in this paper. Short, green lines on the occlusal surface of the tooth depict sharp cusps, medium length, yellow line depicts a cusp with a medium level of sharpness, and long, red lines depict dull cusps. Cusp a is the lower, left hand cusp, cusp b is the lower right, cusp c is the upper left and cusp d is the upper right.

4. Discussion

Our results support the Complex Cusp hypothesis and portions of the Blunt and Pointed Cusp hypotheses, but fail to support the Strong Cusp hypothesis. There was a significant negative correlation between RoC and strain energy as predicted by the Blunt Cusp hypothesis, although strain energy differed by only 26 J between the sharpest and dullest tooth models we tested (which raises the question whether the difference in performance between a tooth comprised of all dull and a tooth comprised of all-sharp cusps is biologically significant). However, when we inspected the optimality morphospace, in which RoCs among cusps were varied independently, we found that several teeth comprised primarily of sharp cusps caused less strain energy in the food item than teeth comprised entirely of dull cusps (SubOpt2 and SubOpt3 models in table 2). This fails to support the second part of the Blunt Cusp hypothesis, which predicts that given equal bite forces, a tooth comprised of a combination of dull and sharp cusps will cause a food item to absorb lower strain energy than a tooth containing primarily sharp cusps. We also found that the optimality score of a tooth comprised entirely of dull cusps was lower (model all dull, table 2) that the optimality ratio in teeth that contained both sharp and dull cusps (i.e. models T17, 1.047 and SubOpt2, 1.570; table 2). Within the confines of this study, teeth comprised of both sharp and dull cusps have an advantage over teeth comprised entirely of dull cusps.

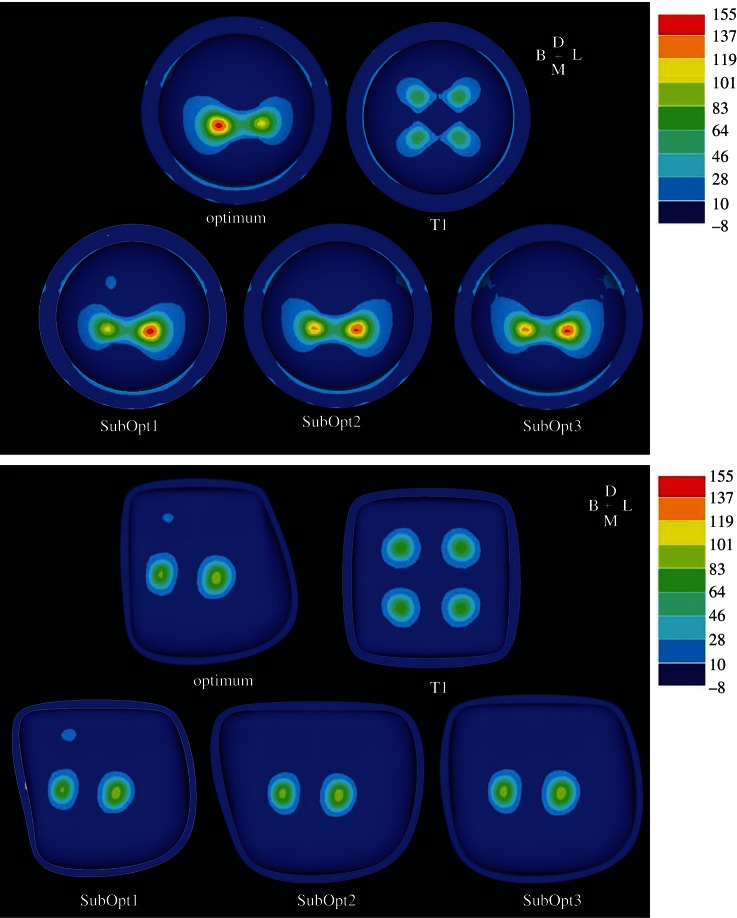
In terms of optimality of the tooth shapes spanned by the model morphospace, the tooth comprised entirely of sharp cusps has the worst optimality ratio; stresses were higher in the enamel than in the food item (T1, table 2). In contrast, the optimal tooth was comprised of a mixture of dull, medium and sharp cusps (model optimum, table 2); here, the food item experienced much higher tensile stresses than the enamel. To visualize the difference between the most and least optimal teeth, it is useful to examine the distributions of tensile stress in the food item and along the EDJ of optimum, SubOpt1, SubOpt2, SubOpt3 and T1 (figure 8). The least optimal tooth morphology (T1) was comprised of four equally sharp cusps and produced four, low stress concentrations in the food item and four areas of higher tensile stress in the enamel at the EDJ. This is the stress distribution predicted for crushing via uniform compression.

Figure 8.

Tensile stress distributions for the most optimal (upper left), least optimal (upper right), and suboptimal (bottom) teeth. The top contour plots are the tensile stress distributions on the underside of the food item, and the bottom are the tensile stress distributions along the EDJ. These are the stress distributions at a 2 kN bite force.

The optimal tooth morphology (figure 7; tables 1 and 2) produced a single, extremely high stress concentration in the food item, which should promote crack initiation and propagation, and only two areas of high tensile stress along the EDJ, both of which are lower than the stress concentrations in the food item (figure 8). This is because the morphologies of the two cusps on the mesial side of the tooth act to deform the food item in the distal direction. At the same time, the combined morphology of the cusps on the distal side prevents the food item from deforming too far in the distal direction and effectively stabilizes the food item. This forces the food item to remain in contact with the cusps on the mesial side of the tooth. The area of high stress in the food item, surprisingly, does not come from the food item interacting with any of the sharp cusps, but from the food item interacting with the cusp comprised entirely of dull RoCs.

The stress concentrations in the enamel along the EDJ in the most optimal tooth morphologies are restricted to the valleys between the cusps, while the stress concentrations in the least optimal tooth are closer to the tips of the cusps. It is interesting that the stress concentrations in the optimal tooth models correspond to where enamel tends to be thicker, harder and stronger in some mammals (i.e. the great apes and modern humans), while the stress concentrations in the least optimal tooth correspond to where enamel tends to be thinner, more compliant and weaker in primates [12,52,57,58].

There are a number of factors researchers have used to measure effective brittle food item fracture (strain energy, stresses in the food item and stresses in the enamel). From the perspective of inducing high stresses in a food item, the food item experienced the highest stresses when the RoCs were varied independently. However, the level of strain energy in the food item and the tensile stresses in the enamel tend to be lowest in teeth in which the RoCs were modelled as equal, and higher in teeth in which the RoCs were allowed to vary independently. If minimizing strain energy in the food item or minimizing the maximum tensile stresses in the enamel were more important than producing high stresses in the food item, then having a tooth where all the RoCs are equal would be beneficial. However, if producing high stresses in the food item were more important, having a tooth comprised of both sharp and dull cusps would be beneficial.

5. Conclusions

We were unable to support the Strong Cusp hypothesis. The results did support the first part of the Blunt and Pointed Cusp hypotheses, but not the second part. Our exploration of optimal designs supports the Complex Cusps hypothesis: a combination of sharp and dull cusps is the most efficient morphology for fracturing a brittle, hemispherical food item because it produces high stress concentrations in the food item while minimizing stresses in the enamel. However, if the function of a tooth is to minimize strain energy absorbed by the food item or to preserve the integrity of the enamel (and not fracture a brittle food item), having a tooth that is comprised of cusps with equal RoCs in all directions is optimal.

Our results show that optimally shaped teeth have a combination of sharp and dull cusps, where some cusps are acting to initiate fracture while others are acting to stabilize the food item. This indicates that the mechanics of biting a food item sufficiently large enough to be contacted by multiple cusps cannot be addressed by considering only single cusp/food item interaction. For large food items, the morphology of the entire occlusal surface becomes important, and the mechanical relationship between the occlusal surface and the food item becomes complex. This may explain, in part, while the molars of most mammals have cusps with different radii of curvature.

It is not uncommon to use FEA to understand how aspects of tooth morphology affect function [20,47,59–63]. However, these models tend to be simplistic, dealing with small, calculable aspects of tooth morphology or represent a small sample of possible tooth morphology, making it difficult, if not impossible to fully understand the complexity of tooth/food item interactions. As demonstrated in this study, the combination of FEA and parametric modelling allows for multiple parameters to be analysed at once and for a large sample size to be generated. Results of such a study can lead to a better understanding of the complex role of tooth–food item interactions.