Skip to main content
PMC home page
Journal of the Royal Society Interface logoLink to Journal of the Royal Society Interface
. 2013 Jul 6;10(84):20130246. doi: 10.1098/rsif.2013.0246

Unravelling daily human mobility motifs

Christian M Schneider 1,✉, Vitaly Belik 1,2, Thomas Couronné 3, Zbigniew Smoreda 3, Marta C González 1,4
PMCID: PMC3673164  PMID: 23658117

Abstract

Human mobility is differentiated by time scales. While the mechanism for long time scales has been studied, the underlying mechanism on the daily scale is still unrevealed. Here, we uncover the mechanism responsible for the daily mobility patterns by analysing the temporal and spatial trajectories of thousands of persons as individual networks. Using the concept of motifs from network theory, we find only 17 unique networks are present in daily mobility and they follow simple rules. These networks, called here motifs, are sufficient to capture up to 90 per cent of the population in surveys and mobile phone datasets for different countries. Each individual exhibits a characteristic motif, which seems to be stable over several months. Consequently, daily human mobility can be reproduced by an analytically tractable framework for Markov chains by modelling periods of high-frequency trips followed by periods of lower activity as the key ingredient.

Keywords: networks, mobile phone, human dynamics, motifs

1. Introduction

Our modern society and the environment are shaped by people's mobility patterns at different scales. Long-time and long-distance trips consist generally of rare and infrequent events such as international flights or movements between cities. By contrast, short-time trips mostly consist of intracity travels such as commuting to work or grocery shopping. These trips exhibit high regularity, typically following the daily circadian rhythm. Studies of human mobility at large scales, motivated by understanding the global spreading of epidemics [1–6], have unravelled interesting properties of the underlying mobility patterns.

Nowadays, large-scale human mobility patterns are described by three widely accepted indicators: the trip distance distribution p(r), the radius of gyration rg(t) and the number of visited locations S(t) over time [7–9]. The trip distance distribution of the entire population follows a power law 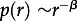Inline graphic with β ≈ 1.59 [7].

Individual trajectories can be extracted from mobile phone data [10–13]. This enables the study of the area an individual visits which is characterized by the radius of gyration rg(t) [8]. This individual rg can be understood as the characteristic distance an individual travels during a given time-period t. The distribution of the radius of gyration reveals heterogeneity in the population; most individuals travel within a short radius, but others cover long distances on a regular basis. Thus, each individual follows p(r) within his or her characteristic distance rg(t). The distribution p(rg) within the population yields the power law observed in the aggregated trip distance distribution p(r).

The frequent return to previously visited locations is captured by the number of visited places over time S(t). This value grows sublinearly as S(t) ∼ tµ with μ = 0.6 capturing individuals' tendency for revisiting locations [9]. These three measures contain the basic ingredients to describe the individual trajectories, in which frequent travels occur between a limited number of places, with less frequent trips to new places outside an individual radius. Such behaviour for large time scales can be reproduced by an exploration and preferential return model with the displacement distribution as an input [9] which can be used to model epidemic spreading on the airline network [14].

However, the current model is designed to capture the long-term mobility behaviour. For example, the number of visited locations S(t) does not show a robust scaling exponent μ, for t < 24 h [9]. Additionally, the radius of gyration stabilizes only after a few months of observation [8]. These indications suggest different underlying mechanisms for modelling mobility at the intercity and the intracity scale.

Current studies at the daily, intracity scale focus on forecasting traffic demand and on predicting human decisions based on optimizing a score function or a utility function. Such modelling approaches assume that each individual human tries to minimize his/her effort depending on socioeconomic characteristics [15]. Therefore, agent-based models have been deployed, usually based on detailed data from travel surveys [16–23].

In this study, we investigate the common underlying mechanisms for daily human mobility patterns by combining the advantages of different large-scale data sources. In each dataset, we observe ubiquitous daily mobility patterns, which we statistically reproduce with an analytical model. Because the generated patterns of our model are only sensitive to the presence or absence of periods of activity followed by periods of inactivity, it implies that humans’ daily trips follow a universal law.

2. Human mobility patterns

Human mobility is characterized by a sequence of visited locations and the trips among them. As an example, we show in figure 1 the aggregated mobility profile of two users and their corresponding daily profiles for a 10 day observational period. The time-dependent trajectories for different days are coloured from brown (first day) to red (10th day) from bottom to top. The black circles and grey lines in the xy-plane are the projection of the daily trajectories. Both the daily and the aggregated profiles can be described as directed networks, in which nodes represent the visited locations and directed edges stand for trips between them. To classify these networks on a daily basis, we further discard any additional information about the purpose of the activity, the travel time and the activity duration as well as the distances and the number of trips between the visited locations, consequently neither the nodes nor the edges are weighted. Only the trip direction is incorporated by the direction of the edge as highlighted for the last day in figure 1.

Figure 1.

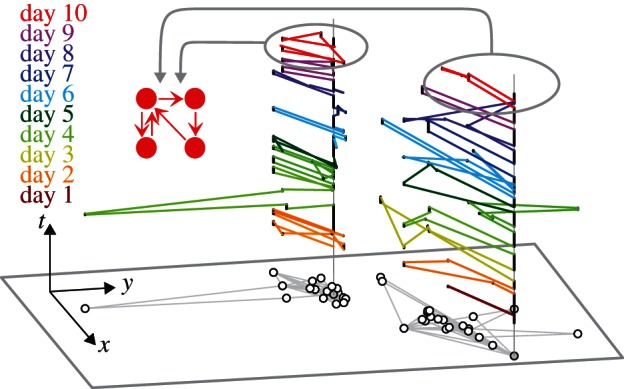
Figure 1.

Open in a new tab

Decomposition of the mobility profile over 10 days into daily mobility patterns for two anonymous mobile phone users. The home location of each user is highlighted and connected over the entire observation period with a grey line. While the entire mobility profiles (black circles and grey lines in the xy-plane) are rather diverse, the individual daily profiles (brown to red from bottom to top for different days) share common features. The aggregated networks consist of N = 16 (22) nodes and M = 37 (43) edges with an average degree of 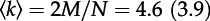Inline graphic. By contrast, the daily average number of nodes is 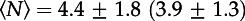Inline graphic, and the average number of edges is 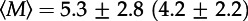Inline graphic. The left user prefers commuting to one place and visits the other locations during a single tour, whereas the right user prefers to visit the daily locations during a single tour. On the last day, both users visit not only four locations, but also share the same daily profile consisting of two tours with one and two destinations, respectively.

We first investigate the distribution of the number of different visited locations, which is the size distribution of the daily networks. As shown in figure 2, the size distributions f(N) of the networks are similar for all datasets (see §3 for more detail). The shape of the observed distributions f(N) can be approximated by a log-normal distribution

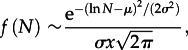2. 2.1

with the parameters μ = 1 ± 0.1 and σ = 0.5 ± 0.1. The average number of locations 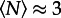Inline graphic is small; hence, most people visit only a few locations. In fact, 90 per cent of the population visit less than seven locations on a daily basis. All three datasets follow the same distribution despite the difference between the cities and if the dataset is a travel survey or phone data.

Figure 2.

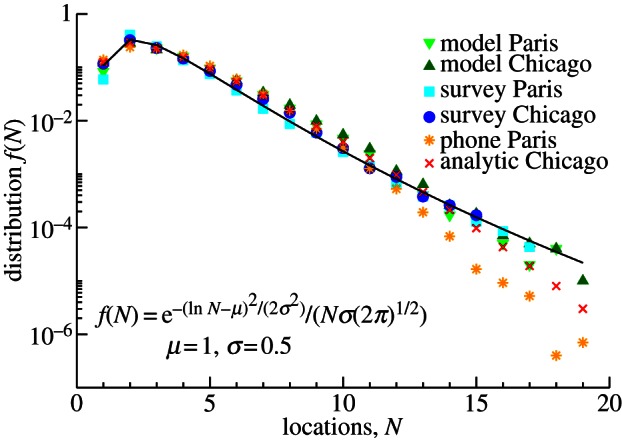
Figure 2.

Open in a new tab

Daily human mobility patterns seem to follow a universal law. The daily number of visited locations can be approximated with a log-normal distribution 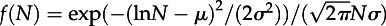Inline graphic with μ = 1 and σ = 0.5. The distributions extracted from activity and travel surveys as well as from mobile phone billing data show similar behaviour. Moreover, the distributions of our perturbation model (see §3 and figure 6 for details) generated both analytically and numerically have the same shape. The broad distribution shows that although most of the people visit less than five locations, a small fraction behave significantly differently because people report visits up to 17 different places within a day in our surveys. Note that due to the mobile phone data limitations, the tail of the corresponding distribution is below the other datasets.

To further study the observed daily mobility patterns, the number of different daily networks is investigated. These networks reveal whether people prefer to visit different locations in a single round tour before returning to the starting location, or if they prefer to return to their starting location before visiting another location. In fact, for a given network size N, Np edge combinations exist:

2. 2.2

Because we are interested in networks that picture human daily trips, the number of reasonable networks can be significantly reduced mainly due to two constraints: the need for sleep, and the consistency of trips. The need for sleep imposes that the trips start and finish at the same location, most likely at home. The consistency ensures that each of the N locations is visited at least once. These two conditions imply that for N > 1 all nodes have at least one ingoing and one outgoing edge. By counting the number of feasible daily networks that fulfil these two constraints, we obtain a large number Nf increasing rapidly with the number of locations (Nf(1) = 1, Nf(2) = 1, Nf(3) = 5, Nf(4) = 83, Nf(5) = 5048, Nf(6) = 1 047 008). Nevertheless, up to 90 per cent of the measured trips can be described with only 17 different daily networks for the surveys and the mobile phone data.

We call these 17 daily networks motifs in analogy to motifs in complex networks [24]. Many systems represented as networks consist of various subnetworks, either topological or temporal [25]. If these subnetworks occur more often than in randomized versions of the entire network, these subnetworks are called motifs. Because randomized versions of the mobility networks are not feasible, we call motifs the daily networks which are found on average more often than 0.5 per cent in the datasets (see the electronic supplementary material for further networks). Consequently, nearly the entire aggregated mobility network of a population can be constructed with these motifs.

In figure 3, the motifs obtained from Chicago and Paris surveys, mobile phone data from Paris, and our proposed model are compared. They are ordered by their size and their frequency of occurrence. Although the data sources cover different cities from different countries, the frequencies to observe a specific motif behave similarly. We can suppose that the extracted motifs are general daily mobility characteristics that can be further used to model and simulate urban activity. The most common motif (ID 2) consists of two visited locations and two trips among them, followed by a motif with only a single location (ID 1). The next likely motifs are three locations with four trips, all starting and ending at the same location (ID 3), or with one round trip (ID 4). Interestingly, in none of the datasets is a motif with size N and more than N + 2 trips observed.

Figure 3.

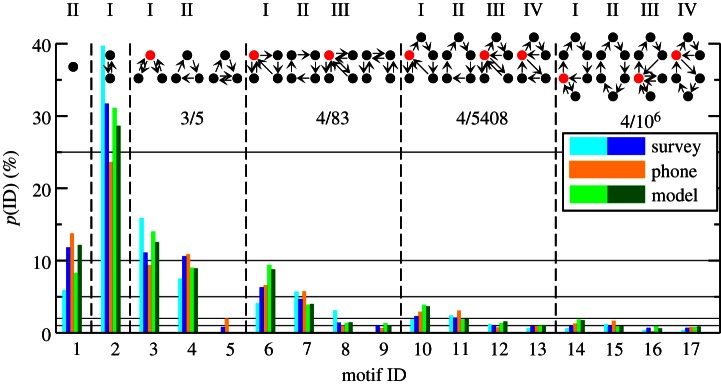
Figure 3.

Open in a new tab

Possible daily mobility patterns are limited, because up to 90% of the identified daily mobility networks can be described with only 17 different motifs. The probability p(ID) to find one of these 17 motifs in the surveys (cyan, Paris; blue, Chicago), the phone data (orange, Paris), and the model (light green, Paris; dark green, Chicago) is presented. The motifs are grouped according to their size separated by dashed lines. For each group, the fraction of observed over feasible motifs No/Nf is shown and the central nodes are highlighted. Most motifs can be classified by four rules: (I) motifs of size N consist of a tour with only one stop and another tour with N – 2 stops. (II) Motifs of size N consist of only a single tour with N stops. (III) Motifs of size N consist of two tours with one stop and another tour with N – 3 stops. (IV) Motifs of size N consist of a tour with two stops and another tour with N – 3 stops. Despite the fact that the number of workers is significantly different in both cities, the rank and the probability to find a specific motif exhibit similar behaviour.

All motifs have at most one ‘central’ location, defined as a node with more than two directed edges, except the motifs with ID 5 and ID 9. This central node is the origin for a tour T(x), a trip visiting x other locations before returning to the origin with x < N. The presence of a unique central node ensures that the edges of the motifs belong to exactly one tour. Hence, multiple trips along the same directed edge are suppressed, and the entire motifs are composed of a single Eulerian cycle: it is possible to visit all edges exactly once and this path ends at the starting node.

The motifs can be classified by four rules:

  • (I) T(1) and T(N − 2)

  • (II) T(N − 1)

  • (III) T(1), T(1) and T(N − 3)

  • (IV) T(2) and T(N − 3)

The rule that describes each motif is written on the top of figure 3. If a rule leads to a motif with a tour T(x) visiting a negative number of nodes x < 0, then the motif is forbidden. By contrast, if a rule leads to a tour visiting no nodes, then only this tour T(0) is ignored. For a given number of locations N, the likelihood of observing a motif is related to the rule number; thus the most likely motif can be described with the first rule. For N ≤ 6, the upper limit of daily tours is three; thus the larger the size of the motif the more trips within a tour. Furthermore, we have found that the most common daily networks with more than six locations also follow these rules (see the electronic supplementary material).

Previous results on human predictability [13], as shown in the trajectories in figure 1, suggest that each individual has a typical daily motif; thus, the observed motifs are similar over several days. To verify this stability, the correlations between motifs of individual users are studied based on phone data, because our surveys provide only information for up to 2 days. The observed sequence is compared with the sequence of an average user based on the distribution from figure 3. In figure 4, the correlations are shown:

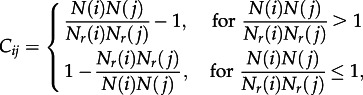2. 2.3

with the observed N(i) and average Nr(i) number of motifs with ID i. First, the highest correlation of each motif is the self-correlation Cii which is usually 10–30 times more likely than expected by selecting individual motifs according to the observed distribution. Second, the likelihood to find a motif with similar number of visited places with small variations (±2 locations) behaves like the average, but for higher differences, the probability is significantly suppressed. Additionally, active users N > 4 seem to be active during the entire observational period, because they have significantly higher probability to visit any motif with N > 4. Interestingly, within the blocks of motifs with size four, five and six some correlations are suppressed or enhanced. We observe that the correlations are enhanced if both motifs follow the same rule with different number of visited locations N, for example visiting all locations within one tour. By contrast, the correlations are suppressed if the motifs are less similar, i.e. if the number of tours differs by more than one. In fact, this is observed for motifs created according to rules (II) and (III).

Figure 4.

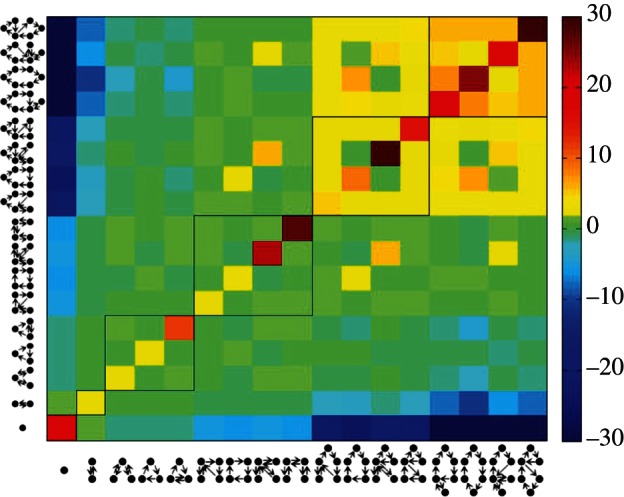
Figure 4.

Open in a new tab

Daily human mobility patterns are stable over several months. The values, calculated by equation (2.3), show how more or less likely a motif is found during the observation period of six months under the condition that the individual has a given motif on another day. Positive values (yellow to red colours) indicate that these motifs are more likely than expected and negative values (cyan to blue colours) that these motifs are suppressed. The probability to find the same daily motif during another day is significantly larger compared with the randomized dataset. Additionally, active users, which visit more than four locations per day, seem to be active over time, whereas inactive users remain inactive. The emerging patterns of transitions between active motifs could be explained by the similarity of motifs. While transitions between motifs of group II are preferred, transitions between groups II and III are suppressed, because the number of tours is most different. As a guide to the eye, motifs with the same number of locations are marked with boxes.

In general, motifs may not be unique, because a person may repeat a tour several times within a day. However, the repetition of tours is uncommon; thus, an edge corresponds to exactly one trip. In the survey data, the observed motifs without multiple trips are sufficient to reproduce over 95 per cent of the travel behaviour correctly and we observe that tours T(x) with x > 1 are performed only once during a day (for details see the electronic supplementary material).

These observations imply that each person has a characteristic daily motif although the visited locations can change. Thus, a user has a personal number of preferred places on a daily basis, which are most likely visited in a specific sequence given by its characteristic motif.

3. Perturbation-based model

It is surprising that nearly the entire population can be described with a few unique daily motifs. To understand this observation, we study the time spent at certain locations as well as the time between the starting time of an activity and the next activity of the same kind.

From both surveys, the frequency of staying at a place for a particular time period is extracted for three groups of activities, home, work and other, as shown in figure 5a. The time spent for working and staying at home is relatively flat distributed with some characteristic durations of 3.5 and 8.6 at work and 14 h at home. By contrast, the probability of an activity at another place decreases with its duration. This staying-time distribution has no characteristic duration, suggesting that the location changes are not distributed evenly over time, but in groups interspersed with periods of inactivity. To support this observation, we study the time between two similar activities, shown in figure 5b. While the time based on home and work is governed by the daily routines, the time between other locations follows a broad distribution. Such short inter-event time dynamics has been reported in specific human activities such as Web browsing, printing patterns, e-mail and phone communication [26–37], but it has not been incorporated in models of human mobility. Inspired by these observations, we developed a perturbation-based model, to reproduce not only the observed daily motifs, but also their frequency of occurrence.

Figure 5.

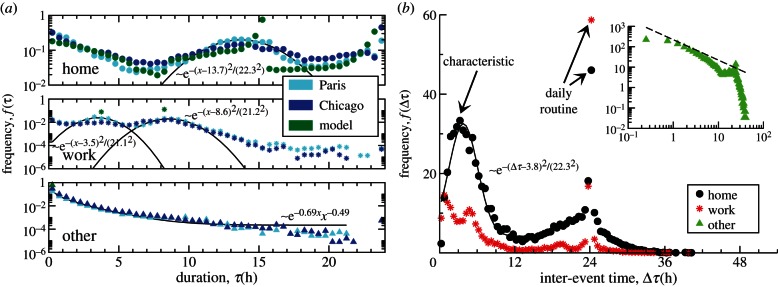
Figure 5.

Open in a new tab

Fundamental differences between home/work and other locations. (a) The duration spent at either home or work is relatively flat distributed with peaks around characteristic time spans of 14 h at home as well as 3.5 and 8.6 h at work. By contrast, the time spent at other activities is broadly distributed. For a guide to the eye, Gaussian distributions are fitted around the characteristic durations for home/work locations and a power law with an exponential cut-off is fitted for other locations. Our model captures these main characteristics. (b) The frequency of observing an inter-event time τ between the beginning of two similar activities, if another location has been visited in between. For the home and work location, daily routines dominate the distribution with additional characteristic times. By contrast, the distribution for other locations exhibits a broad distribution dominated by short inter-event times with a suppressed daily routine. For a guide to the eye, the characteristic inter-event time between home location is approximated by a Gaussian distribution and in the inset a power law with exponent −1 is included.

In the following, the model for a non-working (NW) agent is explained and additional, minor features for working (W) agents are described in the electronic supplementary material. Accounting for the difference of home and other locations, the model assumes a fixed activity at home and any number of flexible activities elsewhere (shopping, recreation, etc.). Agents prefer staying at home and perform other activities as a kind of perturbation only; thus they return home after finishing a flexible activity, if they have no other flexible activity scheduled. On the other hand, when people are already perturbed, it is more likely that they perform another flexible activity afterwards (e.g. after having dinner in the city, visiting a nearby bar).

In the model, the day is divided into K = 48 30-min intervals. The actual number of discrete time slots is insignificant as long as it is larger than the maximal number of visited locations K > 20. For each of these time slots, the agent receives a task with the corresponding time-dependent probability pNW(t), and assigns it to the next free time slot. Initially, all time slots are free, besides a 9 h sleeping period during night. Because most tasks occur and are executed during daytime, we use the simple assumption that the probability to receive a task is related to the circadian daily rhythm. This rhythm is approximated by the normalized phone activity p(t) of the entire population as shown in figure 6b: 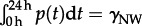Inline graphic with the parameter γNW (see the electronic supplementary material). The most important ingredient for modelling the observed motifs from surveys and phone data is the assumption that after receiving a task pNW(t) = p(t), the probability to get another task pNW(t + 1) = αp(t + 1) for the next time slot is significantly higher, α > 1, as shown in figure 6c. For the sake of simplicity, we increase the probability by one order of magnitude α = 10. This ensures that the inter-event time distribution of flexible activities is dominated by short times as observed in figure 5b and generates the daily tours. In figure 6a–d, an example of modelling a NW agent is shown. The peaks in pNW(t) in figure 6c correspond to activities outside home.

Figure 6.

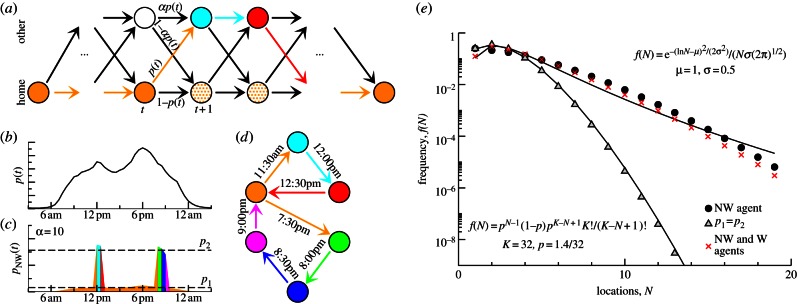
Figure 6.

Open in a new tab

The introduced model is illustrated for a non-working agent. (a) The possible trajectories of an agent are shown. The agent starts the day at home and finishes it at home. At a given time t, depending on the actual location of the agent, the probability to be at home at time t + 1 is either 1 − p(t) or 1 − αp(t) with a parameter α and with probability p(t) and αp(t) the agent travels to another location. The filled circles and the coloured path is an exemplary trajectory. The time-dependent probabilities can be related to the circadian rhythm of activity, shown in (b). (c) The location-dependent probabilities for the exemplary agent with α = 10 are shown. The time-dependent probabilities can be approximated by only two values, p1 and p2 for being at home and being at another location. With this approximation, the model can be solved analytically. (d) The exemplary trajectory is converted into the corresponding motif with six locations and seven trips among them. (e) The daily number of visited locations obtained from the analytical model under three different conditions is shown. While the removal of workers does not change the tail of the log-normal distribution, α = 1 leads to a binomial distribution; thus periods of activities are key for the observed behaviour. Note that the absolute difference between analytical and numerical model is less than 0.01.

Note that the model has no assumptions about the locations of the individual tasks, their number or the number of trips. Only the average number of different visited locations is controlled by the parameter γNW, and the fraction of working and NW agents is preset. However, this is sufficient to reproduce the overall behaviour of the data as shown in figures 2, 3 and 5. Additionally, the model also reproduces the fraction of trips between home, work and other locations with an absolute error of at most 2 per cent (see the electronic supplementary material).

The model can be treated analytically by mapping it on a coin flipping or independent non-identical Bernoulli trials problem, with the reasonable assumption of only two different probabilities 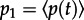Inline graphic and p2 = 10p1 instead of a time-dependent variable (figure 6c). A person, having K free time slots, flips a coin to change the location in the next slot. A success H leads to stay at home or return home, whereas failures T lead to the exploration of new locations. The coin flipping occurs with different probabilities dependent on the current state:

3.
3.
3.
3.

By applying the modified finite Markov chain embedding technique [38] for independent non-identical Bernoulli trials, the probability for the number N of locations visited during a day or equivalently the number of successes P(N) after K Bernoulli trials can be written as

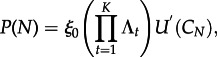3. 3.1

with ξ0 being an initial condition vector in the state space of the corresponding Markov chain, Λt the transition probability matrix, and 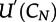Inline graphic a transposed vector corresponding to the subspace with N successes (for details see the electronic supplementary material). As one can see in figure 2, this simple coin flipping model can reproduce the empirical findings very well.

To confirm that the assumption 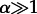Inline graphic is the key to get the broad distribution of the number of daily visited locations, we show in figure 6e the analytical results for three different models: one with two kinds of agents, one with only non-workers and one with only one probability α = 1. While the presence of two kinds of agents has a minor impact on the overall motifs and their size distribution, the removal of the perturbation (p2 = p1) changes the results from an approximately log-normal size distribution, to a binomial size distribution. Moreover, not only the motif distribution changes, but different motifs which are not present in the surveys, mostly star-like ones, emerge. Therefore, the ‘perturbed’ behaviour p2 = 10p1 is the crucial ingredient to reproduce daily mobility.

4. Final remarks

Advances in transforming large data into meaningful information are essential to improve our understanding of socio-technical systems. In our study, we contribute to this end by analysing networks of daily trips obtained from individuals' surveys and anonymized mobile phone data. We found that both travel surveys and phone traces from two different cities reveal the same set of ubiquitous networks that we called motifs. We can suppose that these motifs are general human mobility characteristics that can be further used to model and simulate urban activity. Besides, we found that perturbed states with periods of high activity followed by periods of low activity is the indispensable ingredient to correctly reproduce those motifs. We remark that owing to the limited observation period of at most 2 days in our survey, the question whether a heavy tail occurs in the inter-event time distribution in figure 5b remains open.

Our model successfully reproduces the frequency of visiting different locations and the occurrence rate of the motifs, but it is designed for a single day and therefore it does not incorporate the correlations of motifs between different days. The model captures main characteristics of the duration spent at home by assuming fixed duration for the other activities. The model's inter-event time distributions share some common features with the data, but owing to the duration differences as well as the restriction to a single day it cannot accurately reproduce the observed distributions (see the electronic supplementary material).

The future avenues for related research are diverse. Understanding daily routines promises a better assessment of planning and control, which is the core interest of urban and epidemiological applications. Our findings reduce the dimensionality of choices in agent-based modelling helping to enhance current urban simulators (http://www.matsim.org/, http://code.google.com/p/transims/). In epidemic spreading, usually only up to three locations, daily visited by a host, are considered in modelling contagious dynamics [39–42]. Thus, our presented insights can straightforwardly extend mobility in current epidemiological models.

5. Material and methods

To identify motifs, we use three different datasets: a survey and mobile phone billing data from Paris and a survey from Chicago (http://www.cmap.illinois.gov/travel-tracker-survey). In the surveys, 23 764 and 23 429 weekdays of people were selected in such a way that the data are representative for the entire population of Chicago and Paris, respectively. In the Chicago survey, each participant answered a questionnaire with his/her activity information for one or two entire days, containing the following information: weekday, duration, location, reason for and mode of trip. With this information, it is possible to reproduce the entire daily activity patterns of the anonymous individuals. The Paris survey has the same information, but instead of geographical locations only the trip lengths are provided. Because weekday and weekend behaviour can be rather different, we focus in this study only on weekdays.

From phone billing data of millions of mobile phone users, the extraction of relevant information needs preprocessing. The phone company provides information about the incoming and outgoing calls and short-message services. Thus, we have locations of the operating towers, time of the events and user identification numbers. With this information, we reconstruct daily mobility networks of the users during a six month period. The main challenge is converting call information into the corresponding mobility profile of a user. Therefore, only the 39 820 most active users are investigated according the following scheme (the rules are visualized in the electronic supplementary material, figures S1 and S2):

  • — the day, starting at 03.00, is divided into 48, 30-min slots for each of the 154 days;

  • — to remove towers which are only used during travel, all towers which are less frequently visited than a certain threshold are ignored; in this study, less than 0.5 per cent during the entire observational period;

  • — to eliminate signal transitions between neighbouring towers, these towers are merged for one day, if more than three back and forward transitions between them are recorded during a single day;

  • — to remove towers used during travel on daily basis, records are taken into account only if the next records have the same tower location;

  • — to identify an activity location, only the most frequently observed location during each time slot is assigned as an activity location for this time slot;

  • — a day is discarded, if less than a certain number (in this case eight) of time slots exhibit location information. Too small a number would favour smaller motifs, whereas too large a threshold would exclude too many individuals. The results are stable for different threshold values;

  • — to overcome the small number of night calls, the location which is visited most frequently during all nights between 24.00 and 06.00 of a single user is assigned as the user's home location; in our survey this assumption correctly identifies over 98 per cent of the home locations for a single day. User starts and finishes its day at home, if the user has no other information in the corresponding night-time slots at 03.00 and 03.30; and

  • — based on the activity locations for each time slot, the motifs shown in figure 3 are constructed for weekdays only.

We have published C++ code of our proposed model, the algorithms how to identify motifs and simulated data to test all algorithms on our website at http://humnetlab.mit.edu/downloads.

Acknowledgements

V.B. gratefully acknowledges the financial support by the Volkswagen Foundation. This work was funded by New England UTC Year 23 grant, awards from NEC Corporation Fund, the Solomon Buchsbaum Research Fund.

References

Articles from Journal of the Royal Society Interface are provided here courtesy of The Royal Society

RESOURCES