An HMM-based algorithm for evaluating rates of receptor–ligand binding kinetics from thermal fluctuation data

Abstract

Motivation: Abrupt reduction/resumption of thermal fluctuations of a force probe has been used to identify association/dissociation events of protein–ligand bonds. We show that off-rate of molecular dissociation can be estimated by the analysis of the bond lifetime, while the on-rate of molecular association can be estimated by the analysis of the waiting time between two neighboring bond events. However, the analysis relies heavily on subjective judgments and is time-consuming. To automate the process of mapping out bond events from thermal fluctuation data, we develop a hidden Markov model (HMM)-based method.

Results: The HMM method represents the bond state by a hidden variable with two values: bound and unbound. The bond association/dissociation is visualized and pinpointed. We apply the method to analyze a key receptor–ligand interaction in the early stage of hemostasis and thrombosis: the von Willebrand factor (VWF) binding to platelet glycoprotein Ibα (GPIbα). The numbers of bond lifetime and waiting time events estimated by the HMM are much more than those estimated by a descriptive statistical method from the same set of raw data. The kinetic parameters estimated by the HMM are in excellent agreement with those by a descriptive statistical analysis, but have much smaller errors for both wild-type and two mutant VWF-A1 domains. Thus, the computerized analysis allows us to speed up the analysis and improve the quality of estimates of receptor–ligand binding kinetics.

Contact: jeffwu@isye.gatech.edu or cheng.zhu@bme.gatech.edu

1 INTRODUCTION

During the early stage of hemostatic and thrombotic processes, platelets tether to and roll on the immobilized von Willebrand factor (VWF), which is mediated through binding between the 45 kDa N-terminal domain of the alpha subunit of the GPIb-IX-V complex (GPIbα) and the A1 domain of the VWF (Ruggeri and Mendolicchio, 2007). Disease-related mutations in the VWF have been found to change the mechanical regulation of platelet adhesion, resulting in the bleeding disorder von Willebrand disease (VWD) (Ruggeri, 2007). From a biophysical perspective, these mutations alter VWF–GPIbα binding kinetics. It has been shown that single-residue mutation R1450E that exhibits the type 2B VWD phenotype increases VWF–GPIbα binding affinity and supports the rolling of more platelets at slower velocities without a minimum shear requirement (Auton et al., 2010; Coburn et al., 2011). Another single-residue mutation G1324S that exhibits the type 2M VWD phenotype decreases the binding affinity between these two molecules (Coburn et al., 2011; Morales et al., 2006).

The binding affinity is the ratio of the on- to off-rates, which quantifies the net effects of receptor–ligand association and dissociation. To measure the on- and off-rates separately, mechanical methods, such as the thermal fluctuation assay, that use ultrasensitive force probes, e.g. the biomembrane force probe (BFP; Chen et al., 2008) and optical tweezers (Lister et al., 2004; Molloy et al., 1995; Sun et al., 2009; Veigel et al., 1999), have been developed to measure the interactions of proteins immobilized on surfaces. The idea stems from the observation that force probes used for single-molecule experiments are usually susceptible to thermal fluctuations. The formation of a molecular bond spanning across the gap between the force probe and the target physically connects the two surfaces and reduces the thermal fluctuation of the force probe. In other words, the newly formed bond is equivalent to adding a constraint to the force probe (Chen et al., 2008). In the analysis of experimental data, bond formation is detected from the reduction in the thermal fluctuation of the probe position, and bond dissociation is detected from the resumption of thermal fluctuation, as judged by the sliding standard deviation moving below or above certain thresholds. Although this descriptive statistical method is simple, it has several disadvantages: it is time-consuming, not robust, susceptible to noise and subjective. To overcome these drawbacks, we developed a Hidden Markov model (HMM)-based algorithm that provides an automatic and systematic procedure for analyzing thermal fluctuation data efficiently. We first assume a hidden state, bound or unbound, for each observed probe position. Given the hidden states, the probe positions are assumed to be independent and normally distributed with unknown parameters. The forward–backward algorithm (Baum et al., 1970; Dempster et al., 1977; Welch, 2003) was used to estimate the underlying states and unknown parameters.

Because of its versatility in modeling and robustness in prediction performance, HMM has wide applications in computational biology. For example, HMMs can detect tumor subtypes with microarray data (Zhang et al., 2011) and identify protein-binding sites in DNA (Cardon and Stormo, 1992). However, to the best of our knowledge, no HMM-based computer algorithm has been developed for analyzing thermal fluctuation data. In the thermal fluctuation assay, if the probe is in either the bound or unbound state at one moment, it is more likely to be in the same state at the next moment. This memory effect can be successfully captured by assuming a Markovian structure at the transition of the underlying states (Y.Hung et al., submitted for publication). Furthermore, HMM enables us to provide statistical inference such as the confidence interval and the prediction interval. In particular, by using the likelihood ratio test based on the fitted HMM, we can verify the memory effect objectively and rigorously in repeated adhesions (Y. Hung et al., submitted for publication).

This article is organized as follows. Sections 2.1 and 2.2 describe the experiment setup and the existing method. Section 2.3 illustrates the procedures to analyze thermal fluctuation data. Sections 2.4–2.7 discuss the modeling and computation of HMM. In Section 3, we use the HMM to derive kinetic rates by analyzing thermal fluctuation data obtained for the interaction of VWF-A1 and glycocalicin (GC), the extracellular portion of GPIbα. We also show the performance of the HMM method in comparison to the manual method based on descriptive statistics. In addition to running a performance test of the HMM method with the dataset of wild-type (WT) A1, we ran more performance tests with datasets of two single-residue A1 VWD mutants, R1450E (type 2B) and G1324S (type 2M). All above show that the HMM method is far easier to use. Section 4 presents the discussion and concluding remarks.

2 METHODS

2.1 Experimental setup

The recombinant WT VWF-A1 domain (residues 1238–1471) and two single-residue mutants, R1450E that exhibits the gain-of-function (GOF) phenotype of type 2B VWD and G1324S that exhibits the loss-of-function (LOF) phenotype of type 2M VWD, were gifts from Dr Miguel Cruz (Baylor College of Medicine, TX). The GPIbα extracellular domain GC was a gift from Dr Jing-fei Dong (Puget Sound Blood Research Institute, WA).

The BFP system (Chen et al., 2008) and the interacting molecules are respectively illustrated in Figure 1A and B. The VWF-A1 and GC were covalently coupled to the probe bead (Fig. 1B, left) and the target bead (Fig. 1B, right), respectively. Human red blood cells (RBCs) were purified from peripheral blood of healthy donors by finger prick and biotinylated using a protocol approved by the Institutional Review Board of the Georgia Institute of Technology. To enable attachment to the apex of the biotinylated RBC, streptavidins were coated to probe beads. The pressurized RBC by micropipette aspiration serves as an ultrasensitive force transducer with a soft spring constant of 0.15 pN/nm by tuning the water pressure through a custom-made manometer system. A homemade Labview^TM program was used for data acquisition by tracking the probe bead displacement with 0.7 ms temporal and ±3 nm spatial resolution.

Fig. 1.

Thermal fluctuation assay. (A) BFP photomicrograph. A micropipette-aspirated RBC with a bead (left, termed ‘probe’) attached to the apex was aligned with a bead (right, termed ‘target’) aspirated by another micropipette. (B) BFP functionalization. VWF-A1 and streptavidin were covalently coupled to the probe bead. GC was covalently coupled to the target bead. The schematic is no to scale as the sizes of the molecules have been enlarged relative to the sizes of the beads. (C) Thermal fluctuation data. Data plot of the instantaneous horizontal position x of the probe versus time t collected from one test cycle of the thermal fluctuation assay. During the experiment, the target bead was driven to approach the probe bead (black), contact for 0.1 s (green), retract (purple) and be held (blue and red) stationary with at a preset position. Blue and red traces annotate, respectively, bound and unbound states detected by the descriptive statistical method. Five minutes on average were taken to finish the manual annotation on one trace. (D) Plot of σ₉₀ (the sliding standard deviation of 90 consecutive x positions from data in C around t) versus t. The same color coding is used as C

The experiment used a high-speed camera at 1500 frames per second to track the axial (horizontal) position of the probe in discrete time points. The raw data of probe position x versus time t consist four phases (Fig. 1C). The target bead was driven by a computer-controlled piezoelectric translator to approach the probe bead at a speed of 2 μm/s (Fig. 1C, black). After a short contact of ∼0.1 s (green), the target was retracted (purple) and held from the probe by a separation distance of ∼10 nm for 10–15 s (blue and red). The Brownian motion of the probe bead was monitored with the same BFP spring constant for all experiments. Experiments were performed at room temperature (25°C).

2.2 Descriptive statistical method

The underlying idea is that anchoring the probe bead to the target bead via a VWF-A1–GC bond reduces the thermal fluctuations. This is because the stiffness of the system (k_sys) is the BFP stiffness (k_BFP) without a bond but is changed to the sum of the BFP stiffness and the molecular bond stiffness (k_mol), i.e. k_sys = k_BFP + k_mol, with a bond. The reduction in thermal fluctuation follows from the equipartition theorem, k_sysσ² = k_BT, where k_B is the Boltzmann constant, T is absolute temperature and σ² is the ensemble variance of the displacements that represents a metric of thermal fluctuations. At constant temperature, an increase in k_sys would cause a decrease in σ². Thus, the decrease in σ² indicates bond association, while the increase in σ² indicates bond dissociation. The variance of bound portion should be smaller than that of unbound portion.

In the descriptive statistical method, we approximated the ensemble standard deviation σ by a sliding standard deviation of 90 consecutive data points, σ₉₀, from the x-t sequence and plotted it versus t (Fig. 1D). We chose 90 points by balancing the competing needs for an approximate σ value and temporal resolution. Note that the number of points chosen to plot the standard deviation can affect analysis results. We then draw two horizontal lines to represent the thresholds to identify bond association (solid line in Fig. 1D) and dissociation (dashed line). The choice of thresholds also requires the experimenter’s judgment and can cause variation in annotation of bound versus unbound states. The descriptive statistical-based method selects data points with a σ₉₀ lower than the association threshold to be in the bound state and those higher than the dissociation threshold to be in the unbound state. This method is time-/labor-consuming, which may take several days to finish the analysis of data generated from a 1-day experiment. To obtain statistically meaningful results, a large number of distance curves need to be collected, making data analysis the bottleneck of the output. Moreover, this analysis uses personal judgment to select the window width of sliding standard deviation and the thresholds for state annotation. This will inevitably bring in subjectivity and errors.

2.3 Data preparation: removing erroneous data and correcting drift

To overcome drawbacks of the descriptive statistical-based algorithm, we developed an HMM-based algorithm. Before applying either method, a careful automated prescreening of x versus t raw data is required. This is because some of the curves exhibit large magnitude of rapid shifting, probably due to environmental perturbations and human errors during experiments (× in Fig. 2). The poor quality of such data prevents reliable analysis by either algorithm. In particular, it may affect HMM learning by causing false-positive bond annotation. As a first step of data preparation, erroneous data are removed (Fig. 2, Step 1). For the acceptable data (✓ in Fig. 2), there may still be slow drift in the holding phase, which might be caused by misaligned contact between the probe and the target during the assembly of the BFP. As the second step of data preparation, a high-order polynomial is used to fit the position data and corrects the drift (Step 2). After prescreening, the clean data are ready for both descriptive statistical-based algorithm to use and HMM training and annotation. In the learning process, we train HMM to get the tuning parameter using cross validation as described in Section 2.6 (Step 3). Then HMM is ready for batch data annotation (Step 4) and kinetic analysis (Step 5).

Fig. 2.

Data preparation flowchart. Step 1, prescreening; Step 2, drift removal; the first two steps were applied to both descriptive and HMM methods; Step 3, HMM parameter estimation; Step 4, identification of states by HMM; Step 5, evaluation of on- and off-rates by analysis of waiting time and bond lifetime distributions, respectively

2.4 An HMM-based algorithm for analyzing thermal fluctuation data

We developed an HMM method to analyze x-t curves from the thermal fluctuation assay (Fig. 3). The objective is to computerize the bond state annotation similar to the descriptive method but with a higher efficiency (Fig. 3A). The statistical methodology can be found in Y.Hung et al. (submitted for publication). Here we model the molecular interaction on a BFP as a process with the hidden bound state following Markovian structure (Fig. 3B). Let x_t denote the horizontal position of the probe at time t. For each observation x_t, there is an unobservable variable z_t representing the binding state at time t. The indicator variable z_t takes value 0 (Fig. 3B, blue) when there is no bond between the probe and the target at time t, and 1 (Fig. 3B, red) otherwise. The change of state z_t can be described by a stationary Markov chain with two states, transition probability P_ij = P(z_{t + 1} = j| z_t = i) and stationary probability P_i, where i, j take values of 0 or 1. Stationary probability P₁/P₀ can be interpreted as the probability of observing bound/unbound event in the experiment. When the corresponding binding state z_t is given to be k, the corresponding probe position xt is assumed to be mutually independent and normally distributed with mean μ_HMM and variance . From Section 2.2, we have 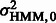> . As a result, the HMM method divides an x-t curve into a series of segments. Each segment is characterized by a constant μ_HMM and . This will distinguish the bound and unbound portions, thus making the threshold much easier to be seen (Fig. 3C).

Fig. 3.

Developing an HMM method for thermal fluctuation data. (A) Bound and unbound status annotation by the HMM analysis from the same data in Figure 1C. The average time spent for the algorithm to finish the annotation of one trace is 30 s. (B) Illustration of the HMM. At time t, let x_t be the observed horizontal position of probe and z_t be the unobserved binding state. Observation x_t can be classified into two states: z_t = 0 (blue) or z_t = 1 (red). Also, z_t follows a Markov chain and x_ts are independent normally distributed given z_t. (C) Plot of σ_HMM (the predicted standard deviation from the HMM analysis of A) versus t. Each segment of C corresponds to the estimated standard deviation of bound or unbound period of A in red or blue by the HMM analysis

2.5 HMM computation

A forward–backward algorithm is used to compute the parameters and unknown states. Stationary probability of the unbound state P₀ is the only tuning parameter in the algorithm. The reason for using P₀ is to incorporate biological knowledge of the binding frequency into HMM. This tuning parameter can be chosen through cross validation. In fact, we can show that the analysis result is insensitive to the initial choice of P₀ as long as it lies in a proper range (Section 3.2). The forward–backward algorithm is a two-step procedure that computes the estimate as follows: in the forward step, it computes P(z_m|x₁ , … , x_m) for all m≤ n, where n is the length of the sequence; then in the backward step, the algorithm computes P(x_{m + 1} , … , x_n|z_m). It is known that the algorithm converges to the maximum-likelihood estimate (Baum et al., 1970).

2.6 On- and off-rate estimates

This subsection describes how to statistically estimate kinetic on- and off-rates (k_on and k_off) of receptor–ligand interaction through the previously annotated bound and unbound states versus time segments. Because association and dissociation of single biomolecular bonds are stochastic events, the moments when they occur and their durations are random. The on- and off-rates represent statistical characteristics underlying these probabilistic kinetic processes. Therefore, they are determined by the totality of the data rather than individual points in the collection. As such, k_on and k_off are insensitive to small disturbance and error, such as missing or false alarm in a small number of events. This property can be used to train the tuning parameter in HMM (Section 2.7) and explain the performance comparison of the HMM- and descriptive statistical-based algorithms (Section 3).

Let waiting time t_w be the period from the dissociation moment of the existing bond to the association moment of the next bond, and bond lifetime t_b be the period from the moment of bond association to dissociation. A pooled collection of waiting times should follow the distribution of the first-order kinetics of irreversible association of single bonds:

(1)

where the cellular on-rate = A_cm_rm_lk_on is a product of four parameters: A_c is the contact area (considered as a constant for all experiments), m_r and m_l are the respective receptor (GC) and ligand (A1) densities measured by flow cytometry (Yago et al., 2004) and k_on is the molecular on-rate. P_w is the probability for a bond to form after waiting time t_w. P_w can be estimated by survival frequency as the fraction of events with waiting time ≥t_w. Thus, the cellular on-rate can be estimated from the negative slope of the ln(1 − P_w) versus t_w plot (Fig. 4A).

Fig. 4.

Comparison of effective on-rates derived from analysis of waiting times collected by the descriptive statistical and HMM methods. (A). Exponential waiting time distributions for the interaction of WT A1 and GC. An ensemble of ∼40 waiting times, defined as the intervals from the moment of a bond dissociation to the moment of the next bond association, was measured by the descriptive statistical method and pooled (blue squares). Another ensemble of ∼200 waiting times was measured by HMM from the same raw data and pooled (red squares). For each method, the natural log of the survival frequency with waiting times >t_w was plotted against t_w and fitted by a straight line (solid line). The negative slopes of the best-fits represent the cellular on-rate = m_rm_lA_ck_on estimated by the two methods. The variations in these values are shown by the 95% confidence interval of the best-fit (dotted lines). The red dotted lines are obscured because they overlap with the red solid line. (B). Comparison of effective on-rate A_ck_on estimated by descriptive statistical and HMM methods for WT, G1324S (Type 2M) and R1450E (Type 2B) A1s versus GC. A_ck_on was calculated by dividing by the product of the protein densities on the probe (m_l for A1) and target (m_r for GC) beads, i.e. m_rm_l = 1.96, 2.8 and 0.19 × 10⁵ µm⁻⁴ determined by flow cytometry for respective conditions. The error bars indicate the 95% confidence interval for each method

Similarly, a pooled collection of bond lifetimes should follow the distribution of the first-order kinetics of irreversible dissociation of single bonds:

(2)

where P_b is the probability for a bond formed at t = 0 to survive at t_b and can be estimated by survival frequency with bond lifetime ≥t_b. The negative slope of the ln(P_b) versus t_b plot provides an estimate for the off-rate k_off (Fig. 5A). Our recent work (Ju,L. et al., submitted for publication) suggested that the VWF-A1–GC bond has two states at low force: one major state that features events with short lifetime (0.01 s < t_b < 0.5 s) and one minor state with long lifetime (t_b 0.5 s). Usually long lifetime events mingle with multiple bond events and become susceptible to drifting-induced noise, while events with very short lifetime (t_b ≤ 0.01s) are highly suspected as non-specific events. For illustrative purposes, we only demonstrate the accuracy and reliability of HMM with events in short lifetime regime (0.01 s < t_b < 0.5 s).

Fig. 5.

Comparison of off-rates derived from analysis of bond lifetimes collected by the descriptive statistical and HMM methods. (A). Exponential bond lifetime distributions for the interaction of WT A1 and GC. An ensemble of ∼50 bond lifetimes, defined as the time span from association to dissociation of one bond, was pooled by the descriptive statistical method (blue squares). Another ensemble of ∼200 bond lifetimes was measured by the HMM method from the same raw data and pooled (red squares). For data obtained by each method, the natural log of the survival frequency with bond lifetimes >t_b was plotted against t_b and fitted by a straight line. The negative slopes of the best-fits represent the off-rate k_off. (B). Comparison of off-rates estimated by the descriptive statistical and HMM for WT, G1324S (Type 2M) and R1450E (Type 2B) A1s versus GC. The error bars show the 95% confidence interval for each method

2.7 Training of HMM

To choose the tuning parameter and test the robustness of the algorithm, we implement a half-sampling cross validation method (Celeux and Durand, 2008), which preserves the underlying Markov chain structure. We segregate the complete sequence of probe position observations X = (x₁,x₂, … ,x_n) into the odd, i.e. X1 = (x₁,x₃ , …), and even, i.e. X2 = (x₂,x₄ , …), subsequences. Denote the off-rate of the HMM result from the odd subsequence as 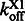and the even subsequence as . The relative error ε_c between the two subsequences is defined as follows:

We can similarly define the relative error of off-rate between HMM and descriptive statistical methods. Let be the off-rate of X using descriptive statistical method and be the result of HMM. The relative error ε_r is defined as follows:

We choose tuning parameter P₀ such that the relative error ε_c is small. Later, we shall illustrate the robustness of HMM by showing that the range of P₀ with small ε_c overlaps with that with small ε_r (Section 3.2).

3 RESULTS

3.1 Justification of HMM with the VWF-A1–GC interaction

We compare kinetic rate estimates from descriptive statistical analysis with those from HMM on the same set of thermal fluctuation data. For the interaction of GC with VWF-A1 (Fig. 1A), the HMM method (Fig. 3A) performs as well as the descriptive method in bond annotation (Fig. 1C). The linearized distributions of respective waiting times and bond lifetimes determined by the two methods overlapped and showed similar slopes, suggesting similar cellular on-rate (Fig. 4A) and off-rate (Fig. 5A) estimates from two methods. Indeed, the means and 95% confidence intervals of the cellular on-rate by the descriptive statistical algorithm and HMM are 1.302 ± 0.079 s⁻¹ and 1.395 ± 0.046 s⁻¹, respectively (Fig. 4B). The two confidence intervals overlap, indicating that the parameter estimates are statistically close to each other. For the off-rate, the means and 95% confidence intervals by the descriptive statistical algorithm and HMM are 26.58 ± 0.92 s⁻¹ and 26.46 ± 0.18 s⁻¹, respectively (Fig. 5B), which also overlap with each other.

In addition to the above analysis of the WT VWF-A1 data, we compared performance of the HMM and descriptive statistical methods using data from two single-residue mutations in VWF-A1 that alter their interactions with GPIb in biologically important ways: (i) G1324S that exhibits type 2M VWD phenotype and (ii) R1450E that exhibits type 2B VWD phenotype. To compare molecular on-rates requires removal of the site density effect. We measured the site densities of VWF-A1 and GC respectively and divided the cellular on-rate by m_rm_l. corresponding to each A1 construct (WT or mutant). The result is the effective on-rate, A_ck_on. Because the contact area A_c was kept as close to constant as possible between experiments, the A_ck_on is a good measure for on-rate comparison (Chen et al., 2008).

Both the descriptive and HMM methods show that mutation G1324S decreased effective on-rate, from 6.64 ± 0.20 to 2.07 ± 0.05 × 10⁻⁶μm⁴s⁻¹ (descriptive) and 7.12 ± 0.12 to 2.24 ± 0.03 × 10⁻⁶μm⁴s⁻¹ (HMM) (Fig. 4B), but had little effect on off-rate (Fig. 5B). This correlates with the LOF phenotype of G1324S as it induces less platelet agglutination compared with WT A1 (Rabinowitz et al., 1992). Both the descriptive and HMM analyses indicate that the R1450E mutation resulted in an ∼8-fold increase in the effective on-rate: 6.64 ± 0.20 to 76.59 ± 1.51 × 10⁻⁶μm⁴s⁻¹ (descriptive) and 7.12 ± 0.12 to 82.64 ± 2.79 × 10⁻⁶μm⁴s⁻¹ (HMM) (Fig. 4B), which are in good agreement. Similar to G1324S, R1450E had little effect on stress-free off-rates of the short state (Fig. 5B). The result correlates with the GOF phenotype of R1450E. Type 2B VWD mutations in the A1 domain have been shown to result in abnormal interactions between platelet GPIbα and soluble VWF, such that R1450E A1 requires less ristocetin or lower shear to induce platelet agglutination (Matsushita and Sadler, 1995). Such abnormal interactions have been suggested to lead to prolonged bleeding time due to either the lack of unbound GPIbα on platelet surface to interact with immobilized VWF at sites of vascular injury, reduced platelet counts due to early clearance of platelet aggregates or both (Ruggeri and Mendolicchio, 2007).

Note that HMM has much narrower width of 95% confidence intervals compared with that of descriptive statistical method for both cellular on-rate (Fig. 6A) and off-rate (Fig. 6B) for all three molecular interactions tested here. Thus, the HMM method is more accurate (less error) than the descriptive method presumably because it reduces the errors brought by subjective judgment of the experimenter. Moreover, the HMM method can measure far more events than the descriptive statistical method from the same set of raw data, e.g. 112–40 for waiting times (first group in Fig. 6C) and 169–46 for bond lifetimes (first group in Fig. 6D) for the WT A1 case. In the mutant cases, the HMM measurements also outnumbered the descriptive statistical measurements (Fig. 6C and D), indicating that many of the waiting times and bond lifetimes gone undetected by the descriptive method can be resolved by HMM.

Fig. 6.

Performance comparison of the descriptive statistical and HMM methods. (A and B) Errors (measured as 95% confidence interval, CI) of the estimated cellular on-rates (A) and off-rates k_off (B) for 2D binding kinetics of GPIbα–VWF-A1 interaction under the following biological conditions: the WT VWF-A1 (circles), the LOF VWF-A1 mutant G1324S (squares) and the GOF VWF-A1 mutant R1450E (triangles). The errors were plotted for both the descriptive statistical method (blue) and the HMM method (red). (C and D) The numbers of waiting times (C) and bond lifetimes (D) that the descriptive statistical method (blue) and the HMM method (red) are respectively capable of measuring from the same set of raw data

Although the kinetics parameters differ for different molecular interactions, the estimates from HMM are consistent with the anticipated biological effects and match the results from the descriptive statistical method. These results validate HMM as a reliable and accurate method for evaluating the on- and off-rate change of each mutation relative to WT.

3.2 Tuning parameter reliability of HMM

In HMM, the probability of observing a data point in the unbound state P₀ is the only tuning parameter in the algorithm. Based on the half-sampling cross validation in Section 2.7, we plot the relative error ε_c (Fig. 7A) and ε_r (Fig. 7B) against different P₀. The P₀ that gives the lowest ε_c ranges from 0.85 to 0.96 from which we choose the value in our prediction algorithm. It can be seen from Figure 7B that different choices of P₀ do not render much inconsistency between the results from descriptive statistical method and HMM, as the relative error is smaller than 0.025. This shows the robustness in the prediction performance and the reliability of the HMM-tuning parameter.

Fig. 7.

Tuning parameter selection by half-sampling cross validation. (A) Half-sampling cross validation. The relative error of off-rate from odd sequence versus off-rate from even sequence was plotted against P₀. (B) The relative error of off-rate versus P₀ by comparing the HMM with descriptive statistical method with the same data as the whole sequence

3.3 HMM learning curve

To further verify that HMM reduces the time required for data analysis by the descriptive method, we did the following performance tests:

1. Compare the time required for a new student to learn the HMM and the descriptive method

2. Compare the time required for an experienced student to analyze the same set of raw data using the two methods.

For the first test, we surveyed two new students in our lab who just started learning the thermal fluctuation assay. We plot their learning curves by tracking their performance from week 0 to week 8 (Fig. 8A). For each week, we recorded the time required for them to finish analyzing similar amount of thermal fluctuation data by using both manual method (blue) HMM method (red). We found that it took much less time for both to finish the analysis by HMM than by the descriptive method every week: 20 versus 4 h at week 0, and 8 versus 1 h at week 8. The HMM is much less time-consuming than the descriptive statistical method.

Fig. 8.

Learning curve comparison between the descriptive statistical method and the HMM. (A) Comparison of the times spent by a new student to learn the descriptive statistical method (blue) and the HMM (red). Two students who were new to both methods were surveyed. The times for them to finish analysis of one dataset were plotted versus different time checkpoints. Each curve represents a surveyed student. (B) Comparison of the times spent by the experienced students to analyze the same set of raw data using the descriptive statistical method (blue) and the HMM (red). Two students were surveyed

For the second test, we collected information from two students who had experience in analyzing BFP thermal fluctuation data. We assigned the same dataset used in Figures 4 and 5 to them and recorded the times it took for them to finish the analysis using the two methods (Fig. 8B). Consistently, using the HMM (red) took much less time than using the descriptive method (blue), 1 versus 5–6 h.

4 DISCUSSION

It has long been recognized that changes in thermal fluctuation can be used to identify single-molecule events. This idea was implemented in early work to probe the duration and contact stiffness of myosin motors interacting with actin filament (Lister et al., 2004; Mehta et al., 1997; Molloy et al., 1995; Veigel et al., 1999). More recently, it was used to analyze 2D kinetics of adhesion molecules interacting with their ligands (Chen et al., 2008, 2010; Huang et al., 2010; Sun et al., 2009), to measure molecular elasticity (Chen et al., 2012; Marshall et al., 2006; Sarangapani et al., 2011), and to determine protein conformational changes (Chen et al., 2012). Some studies used BFP that was custom-designed and home-made in a handful of laboratories (Chen et al., 2008, 2010, 2012; Huang et al., 2010). Others used optical tweezers (Mehta et al., 1997; Molloy et al., 1995; Sun et al., 2009; Veigel et al., 1999) and atomic force microscope (Marshall et al., 2006; Sarangapani et al., 2011) that are commercially available in many laboratories. Therefore, these methods have high potential for a broad range of applications by many investigators. Unfortunately, previous analyses were done using merely eyeballing (Lister et al., 2004; Mehta et al., 1997; Molloy et al., 1995; Veigel et al., 1999) or descriptive statistical analysis (Chen et al., 2008, 2010, 2012; Huang et al., 2010; Marshall et al., 2006; Sarangapani et al., 2011; Sun et al., 2009). The drawbacks of these primitive analyses may limit the applications of the thermal fluctuation methods because the descriptive statistical-based algorithm is time-consuming, subjective and prone to noise and error. In this study, we developed a computational algorithm based on analytical statistics rather than descriptive statistics. The HMM-based algorithm automates and high-throughputs the processing of data and has the advantage of being rigorous and objective. We used the VWF-A1–GC system to test the HMM method. The estimates from HMM are comparable with those from the descriptive statistical method (manual analysis) (Figs 1C and 3A) with the same tuning parameters (Figs 4 and 5).

This article compares the on- (Fig. 4) and off- (Fig. 5) rates of GC interactions with WT and two mutant A1 domains. At static conditions, platelet GPIbα does not bind WT VWF unless a modulator ristocetin is added to induce the conformational activation of the A1 domain (Berndt et al., 1988). By comparison, the type 2B VWD mutant R1450E binds GPIbα spontaneously without ristocetin (Auton et al., 2010; Matsushita and Sadler, 1995), whereas the type 2M VWD mutation G1324S abolishes the ristocetin-induced binding to GPIbα (Morales et al., 2006; Rabinowitz et al., 1992). Our kinetics measurements correlate well with these biochemical characterizations in that the R1450E mutant gains the function with an increased on-rate, whereas the G1324S mutant loses the function with a decreased on-rate (Fig. 4B). The data indicate that the association kinetics reflect the conformational states of VWF-A1. There has recently been significant progress in correlating protein structure and binding kinetics. A web server has been developed for prediction of association rate constant by incorporating the protein conformational changes based on the archived protein–ligand complex structures (Qin et al., 2011). Complementing such efforts, the HMM method combined with the thermal fluctuation assay provides experimentally measured binding kinetics and their correlation to protein structure and function.

The HMM method consistently shows higher accuracy than the manual method regardless of the biological variation embedded inside the datasets (Fig. 6A and B). Furthermore, it also detects far more waiting time and bond lifetime events than the descriptive method (Fig. 6C and D). Possible reasons for the descriptive method to capture less events include the following: first, the calculation of sliding standard deviation σ₉₀ may not resolve short bonds if their lifetimes are shorter than the chosen length of the sliding window. Thus, the calculation mixes both bound and unbound observations, which may miss many waiting times and short bond lifetime events; second, the decision rule (bound versus unbound) of the descriptive statistical method heavily relies on an empirical threshold. In most cases, this threshold will be manually drawn in a conservative way to avoid false positive annotation caused by noise. Because the reduction of variance by bond formation is relatively small and may not be detected sometimes, the manual method tends to miss bonds when experimental noise is not well controlled.

Aside from its advantage of robustness in prediction (Fig. 7), the HMM method is more convenient and requires less learning times than the descriptive method (Fig. 8). The comparison was made after an automated prescreening process to eliminate erroneous data resulted from the experimental errors, drifting and noises (Fig. 2). It should be noted that the HMM method shares the same biophysical rationales as the descriptive method, but provides the statistical basis to computerize the manual analysis. Yet, it requires on average 30 s for the HMM to finish annotation of one data trace but it takes 5 min for the manual method to do so (Figs 1C and 3A).

Although the proposed HMM is motivated by the study of thermal fluctuation experiments, it can be directly applied to different types of studies in bioinformatics (Koshi and Goldstein, 2001). Based on the proposed HMM method, extensions to higher orders models with unknown number of states (Y. Hung et al., submitted for publication) can be made. Therefore, such a framework is particularly attractive in the study of computational biology such as the analysis of gene expression (Seifert et al., 2011), protein and DNA sequences (Marioni et al., 2006), where the conventional first-order HMM is not sufficient (Seifert, 2013). The HMM method developed in this article is also applicable to other areas, including signal processing (Chambaz et al., 2009; Kaleh and Vallet, 1994) and environmental science (Hughes and Guttorp, 1994).

For future work, we will include the receptors of two or multiple species on a cell and study the cooperative binding of multiple receptors. Unlike a bead target, a cell target is characterized by its soft membrane and instant mobility. Thus, more noise is expected in a cell system than in a purified protein system. The next-generation algorithm should be more powerful in correcting thermal fluctuation drifting and noise caused by a restless cell surface. Moreover, multiple receptors will bring in more complex binding kinetics or multiple states such as unbound, receptor-1 bound, receptor-2 bound and cooperative bound states. To discriminate these states, this method requires higher sensitivity. We hope that continuous improvement of the HMM-based algorithm will allow us to shed new light on examining protein interactions on the single-molecule level.