Adaptive Distributed Video Coding with Correlation Estimation using Expectation Propagation

Abstract

Distributed video coding (DVC) is rapidly increasing in popularity by the way of shifting the complexity from encoder to decoder, whereas no compression performance degrades, at least in theory. In contrast with conventional video codecs, the inter-frame correlation in DVC is explored at decoder based on the received syndromes of Wyner-Ziv (WZ) frame and side information (SI) frame generated from other frames available only at decoder. However, the ultimate decoding performances of DVC are based on the assumption that the perfect knowledge of correlation statistic between WZ and SI frames should be available at decoder. Therefore, the ability of obtaining a good statistical correlation estimate is becoming increasingly important in practical DVC implementations. Generally, the existing correlation estimation methods in DVC can be classified into two main types: pre-estimation where estimation starts before decoding and on-the-fly (OTF) estimation where estimation can be refined iteratively during decoding. As potential changes between frames might be unpredictable or dynamical, OTF estimation methods usually outperforms pre-estimation techniques with the cost of increased decoding complexity (e.g., sampling methods). In this paper, we propose a low complexity adaptive DVC scheme using expectation propagation (EP), where correlation estimation is performed OTF as it is carried out jointly with decoding of the factor graph-based DVC code. Among different approximate inference methods, EP generally offers better tradeoff between accuracy and complexity. Experimental results show that our proposed scheme outperforms the benchmark state-of-the-art DISCOVER codec and other cases without correlation tracking, and achieves comparable decoding performance but with significantly low complexity comparing with sampling method.

1. INTRODUCTION

Nowadays, many-to-one digital video applications are becoming more and more popular, such as video surveillance with multiple tiny cameras, where each tiny camera has only limited communication bandwidth, computational power and battery life. Therefore, it is extremely crucial to restrict the encoding complexity to reduce the power consumption, as well as guarantee the encoding performance to save the communication bandwidth. Driven by these emerging applications, the industry is anxious for an entirely new coding paradigm, which could significantly reduce the encoding complexity, even though the expense is to increase decoding complexity at the server side. Although the traditional video coding standard (e.g., H.264) is very promising in a centralized setup, it could not be easily tailored to fit such a new coding paradigm, as the encoder of H.264 standard has large computational complexity due to the existence of motion estimation. Fortunately, distributed video coding (DVC)^{1, 2} provides a workaround for these difficulties, where the complexity could be efficiently shifted from the encoder side to the decoder side. The DVC technique is based on the distributed source coding (DSC) principle brought a paradigm shift from the conventional centralized video coding architecture to a totally distributed manner, where the computationally-expensive motion compensation and correlation extraction procedures will be taken at the decoder side.

From the information-theoretic perspective, DSC refers to separate compression and joint decompression of multiple correlated sources. DSC started as an information-theoretic problem in the renowned 1973 paper of Slepian and Wolf.³ Slepian and Wolf considered the lossless compression of two physically separated sources, and demonstrated that, roughly speaking, there is no performance loss compared to joint compression as long as joint decompression is performed. In 1976, Wyner and Ziv⁴ considered a lossy version (i.e., with a distortion constraint) of the asymmetric Slepian-Wolf (SW) problem known as Wyner-Ziv (WZ) coding, where one source is available at the decoder as side information (SI) (e.g, through entropy coding). Wyner and Ziv showed that for some particular correlation models (e.g. Gaussian, Laplace, etc.), there is no performance loss due to the absence of SI at the encoder.

DVC exploits WZ coding principles by performing computationally-expensive motion compensation at the decoder instead of at the encoder. The beauty of WZ coding (DSC in general) is that there is no need for the encoder to be aware of the SI, which makes it possible to accomplish predictive coding without encoder motion compensation. In a nutshell, a block of pixels/coefficients in a certain video frame (a.k.a., WZ frame) could be efficiently WZ encoded into a stream (i.e., syndromes) without any reference to any other video frames. To recover a WZ frame at the decoder side, a SI frame will be first generated based on the received key frames through motion compensation, where key frames can be decoded independent of other frames. Then the WZ decoder could decompress the WZ frame based on the received syndromes and the generated SI through DSC principle. The state-of-the-art WZ coding designs based on turbo, LDPC, and other graph-based codes have been widely used in DVC studies (see^5–7 and references therein).

Note that a key difference between conventional WZ coding and DVC is that the correlation statistics among sources in the former case is usually assumed to be known as a constant at both the encoder and decoder. In DVC, however, such assumption is normally far-fetched, as correlation statistics between WZ and SI frames would be unknown and dynamically change over time and the location of pixels/coefficients, no matter how well SI frame is generated. Indeed, due to the non-stationarity of real scenes, WZ coding in DVC has to deal with varying correlation noise statistics. Therefore, estimating correlation statistics has been identified as one of key challenges in DVC.

Most DVC designs so far (with few exceptions) usually tackle the problem by modeling correlation noise, i.e., the difference between the WZ and SI frames, as a Laplace distribution parametrized by the correlation parameter λ. The non-stationarity of between scenes can be dealt mainly by estimating correlation parameter λ (e.g., on the block or frame level) based on previously decoded frames,^8–12 which usually refers to the pre-estimation mode as the estimation starts before decoding. However, in reality, pre-estimation mode itself could not guarantee the precise estimate of correlation parameter, as potential changes between frames (especially for high motion sequences) might be unpredictable. Therefore, a more practical approach (i.e., on-the-fly (OTF) correlation estimation mode) is to refine the pre-estimated correlation iteratively with decoding, where the currently decoded information can be used to improve the estimate and vice versa.

In this paper, we propose an efficient way for handling OTF correlation estimation between frames by augmenting the factor graph model of belief propagation (BP) based decoder to include correlation variable nodes and incorporating deterministic approximation (i.e., expectation propagation (EP)) algorithm to tackle the intractability in calculating the exact posterior probability (i.e., belief) of each correlation variable node. The proposed adaptive DVC framework with EP based OTF correlation estimator is carried out in pixel-domain with a feedback channel for rate-adaptive decoding using joint bit-plane LDPCA code.¹³

This paper’s contributions can thus be summarized as:

1. We carefully constructed a single factor graph that connects BP based joint bit-plane SW decoder and EP based correlation estimators together for enabling the OTF correlation estimation between SI and WZ frame.

2. We modeled the correlation parameter λ in the context of Gamma distribution and tackled the intractability in calculating the exact posterior distribution of λ through EP based deterministic approximation method.

3. As one of deterministic approximation method, the proposed EP based OTF correlation estimation significantly reduced the computational complexity compared with sampling based methods.^{14, 15}

The paper is organized as follows. In Sections 2, we outline the previous work of correlation estimation and discusses the correlation model used in DVC. The proposed adaptive DVC framework including factor graph construction and message passing rules is explained in Section 3. Moreover, in Section 4, we derived the EP based correlation estimation scheme. In Section 5, we verified the proposed framework through experimental results built on a pixel-based DVC setup. The paper concludes with Section 6.

2. RELATED WORK OF CORRELATION ESTIMATION

Since the capability of correlation parameter estimation has strong impact on the WZ video coding efficiency, many research work has been done for improving correlation estimation in the literature. At the beginning, most WZ video coding schemes assume that the correlation noise statistics are stationary along both in time and space,^{5, 16, 17} where the correlation noise statistics could be obtained through training video sequences. However, the aforementioned assumption and estimation methods have many limitations, as the correlation statistics strongly depends on the video contents and may vary with both time and space. To bridge this gap, non-stationary correlation models (e.g., on the block or frame level) are studied in papers.^{9–12, 18, 19}

In paper,⁹ the correlation is modeled as Laplace distribution, but to capture the non-stationary nature of the scene, the correlation parameter was varied from pixel to pixel. The noise power increases if the pixel difference between motion compensated blocks in the two key frames used to generate side information is high; otherwise, it decreases. The reason behind this method is that if the difference between the two key frames is high then we have less confidence in their average and the noise variance is higher. Thus, incorporating this model within SW decoding ensures that the channel code (employed for SW decoding) assigns higher reliability to pixels that have been predicted with higher accuracy, that is, the difference between the key frames is smaller. Similarly, in paper,¹⁰ the Laplace distribution is also used with the parameter pre-estimated at the sequence, frame, block, and pixel level from decoded frames at the decoder. Improved pre-estimated channel estimators^{11, 12} are proposed that attempt to address the difficulty in adaptive correlation in smaller spatial regions due to the difficulty in acquiring sufficient statistics. The above correlation models determine their parameters based on the noise realization in a given temporal or spatio-temporal neighborhood. In paper,¹⁹ a side information dependent correlation noise model is proposed where the standard deviation of the Laplacian model is a function of a particular realization of the side information at each pixel position.

Note that, non-stationarity of a scene^{8–12, 19} is addressed by changing correlation model in advance of decoding and supplying the SW decoder with different initial reliability estimates. However, once SW decoding starts (e.g., via BP), the correlation is fixed.

Since the SW decoding process refines starting beliefs, our prior works^{14, 15} demonstrated that unifying the process of correlation estimation using sampling method and joint bit-plane decoding into a single joint process (i.e., OTF estimation mode) can provide better statistics estimate and consequently improved performance for both pixel- and transform-domain DVCs. Additionally, this unification of correlation estimation and SW decoding will also enable the correlation estimator to take into account side information statistics and any of the methods of^8–12 can be used as an initial point that will be refined during SW decoding. While OTF estimation is also discussed in our prior works,^{14, 15} our prior schemes were based on the sampling method for dynamically tracking the correlation statistics, which result a large computational complexity at the decoder side. Instead of incorporating particle filtering method into BP algorithm for correlation tracking,^{14, 15} an ultra-low complexity alternative (i.e. EP algorithm) is studied and proposed in this paper. Before introducing the proposed EP based framework, the Laplacian correlation model will be first described in the next subsection.

2.1 Laplacian Correlation Model

The correlation between the source and side information (SI) frames is modeled as a virtual communication channel which can be expressed in the form X = Y +N, where X is the source frame to be recovered, Y is the SI frame and N is the virtual channel noise. Based on experimental observations, most DVC designs so far^{10, 20, 21} (with few exceptions) model the correlation noise as Laplace distribution as follows:

$$p[WZ(x,y)-SI(x,y)]=\frac{\lambda }{2}\text{exp}[-\lambda |WZ(x,y)-SI(x,y)|],$$ (1)

where WZ(x, y) and SI(x, y) are the pixel values at the location (x, y) in WZ and SI frames, respectively, p(·) denotes the probability density function. Here, λ is the Laplace distribution parameter defined as

$$\lambda =\sqrt{\frac{2}{{\sigma }^2}}$$ (2)

where, σ² is the variance of residuals between WZ and SI frames. Moreover, the correlation parameter λ can vary along both time and space, since the residual errors are usually large, when there are high motions between frames or illumination changes within a frame.

3. SYSTEM ARCHITECTURE

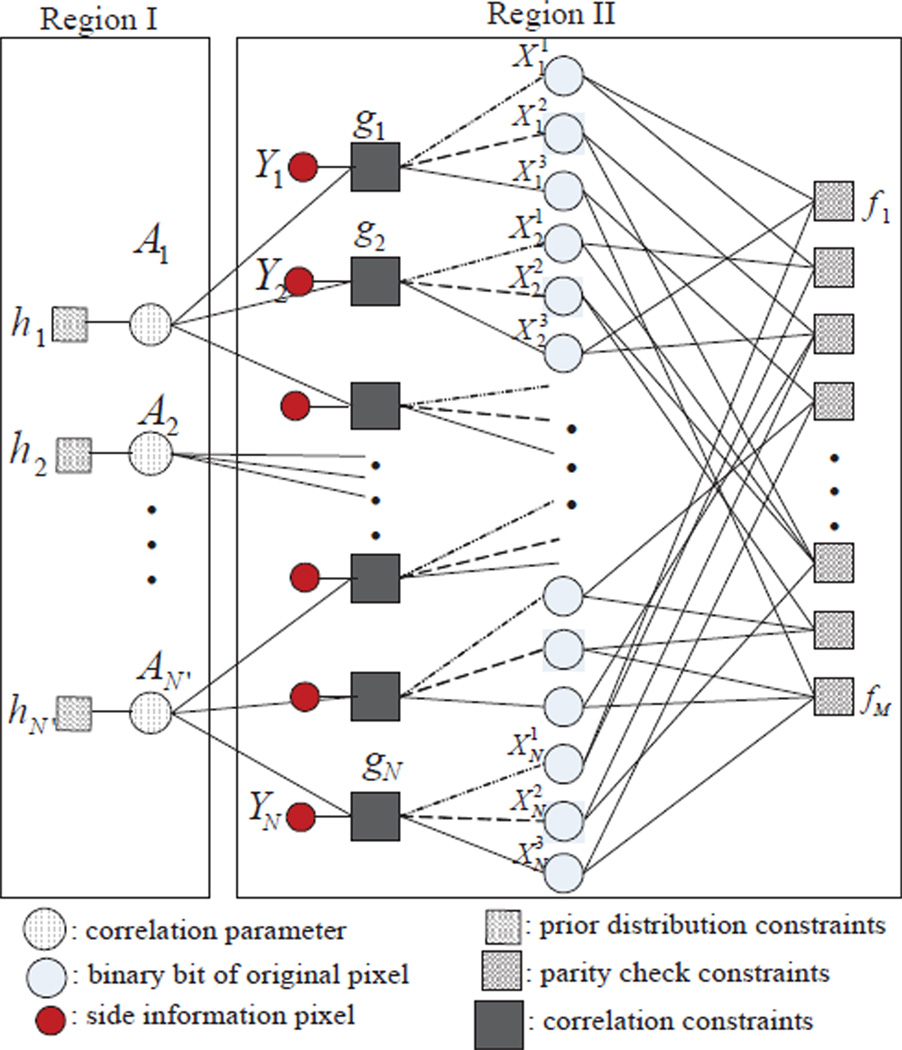
To precisely catch the correlation between frames while recovering source frames, we proposed an adaptive DVC framework. In Bayesian perspective, capturing correlation corresponds to estimating the posterior distribution of correlation parameter. Since a factor graph, as a particular type of graphical model, enables efficient computation of marginal distributions through message passing algorithm, our proposed framework is carried out on the factor graph as shown in Fig. 1. The key steps of the proposed adaptive DVC framework can be outlined as follows: 1) factor graph construction: design a factor graph with appropriately defined factor functions to capture and connect SW coding and correlation tracking (see Section 3.1); 2) message passing algorithm implementation: perform message passing algorithm on the constructed factor graph to calculate the posterior distribution of interested variables (see Section 3.2).

Figure 1.

Factor graph of joint bit-plane SW decoding with correlation estimation.

3.1 Factor graph construction

DVC, a video compression technology based on DSC principle, is usually implemented on a factor graph utilizing WZ coding scheme. Compared with standard DVC, the factor graph (see Fig. 1) of the proposed adaptive DVC with correlation tracking consists of two regions, where Region I refers to the correlation parameter tracking and Region II corresponds the traditional WZ coding. In Fig. 1, variable nodes (usually depicted by a circle) denote unknown variables such as coded bits, correlation parameter, and factor nodes (depicted by small squares) represent the relationship among the connected variable nodes.

3.1.1 Joint bit-plane SW coding (Region II)

WZ coding, a.k.a. the lossy version of SW coding, is usually realized by quantization followed by SW coding of the quantized indices based on channel coding.²² Here, for WZ coding, we carry out LDPC based joint bit-plane SW coding after performing quantization, the factor graph of which is described as Region II in Fig. 1.

Note that we suppose a N-length source sample x_i, i = 1, ⋯ , N is quantized into Q[x_i] using 2^q levels quantization, where q = 3 is taken as an example in Region II of Fig.1. We denote $x_i^1{x}_i^2,\cdots ,x_i^q$ as the binary format of the quantization index Q[x_i], and denote $\mathbf{B}=x_1^1,x_1^2,\cdots ,x_1^q,x_2^1,x_2^2,\cdots ,x_N^q$ as the block which combines all the bit variables together. The block B is then encoded using LDPC-based SW codes and generates an M-length syndrome bits S = s₁, s₂, ⋯ , s_M, which results in a qN : M SW compression ratio.

Similar to the standard LDPC decoding, the factor nodes f₁, f₂, ⋯ , f_M in Region II take into account the constraints imposed by the received syndrome bits. Thus, the factor function of factor node f_a, a = 1,…, M is defined as

$$f_a({\mathbf{x̃}}_{\mathbf{a}},s_a)=\{\begin{array}{cc}1,\hfill & \hfill \text{if}{s}_a\oplus ⨁{\mathbf{x̃}}_{\mathbf{a}}=0,\hfill \\ 0,\hfill & \hfill \text{otherwise}.\hfill \end{array}$$ (3)

where x̃_a denotes the set of neighbors of factor node f_a, and ⨁ x̃_a denotes the binary sum of all elements of the set x̃_a.

Let a N-length sample y_i, i = 1, ⋯ , N, the realizations of variable nodes Y_i, be the side information available at the decoder. The factor nodes g_i are introduced in the factor graph to capture the correlation constraints as shown in (1) between source x_i and side information y_i for SW decoding. Since source samples are first passed through a quantization process, the correlation constraints (i.e., the factor function of g_i) between the quantized indices Q[x_i] and the side information y_i can be expressed as:

$$g_i(Q[x_i],y_i,\lambda )={\int }_{P(Q[x_i])}^{P(Q[x_i]+1)}\frac{\lambda }{2}{e}^{\lambda |x-y_i|}dx,$$ (4)

where λ is the correlation parameter of the Laplace distribution, P(•) denotes the lower boundary of quantization partition at index “•”, e.g. if a coefficient x_i satisfies P(•) ≤ x_i < P(• + 1), the quantization index Q[x_i] of coefficient x_i is equal to “•”. Actually, given a parameter λ, the factor node g_i plays a role of providing a predetermined likelihood p(y_i|Q[x_i], λ) to variable node $X_i^j$, j = 1, ⋯ , q for LDPC based SW decoding.

3.1.2 Correlation parameter tracking (Region I)

As described in Section 2.1, the correlation parameter, denoted by ${\lambda }_l^t$, can vary along both time and space, where the superscript t indicates the time dependence (i.e., frame) and the subscript l corresponds to the location of a single pixel or a group of pixels (i.e., block). In this paper, for the simplicity of notation, we drop the superscript t and denote λ_l as the correlation of the l-th pixel block in a given frame, where each pixel block possesses C number of pixels. Then, the correlation parameter λ in (4) can be replaced by λ_l for different pixel block.

Let us denote by N′ the number of pixel blocks within a frame. Then, we introduce additional variable nodes A_l, l = 1, 2,…, N′ to represent the correlation parameters λ_l in factor graph (see, Region I of Fig. 1). Since a block of C source samples (i.e., pixels) share the same correlation parameter, every C number of factor nodes g_i in Region II will be connected to the same variable node A_l, where we call C ^* as the connection ratio. Moreover, to initialize a prior distribution for correlation parameter λ_l, additional factor nodes h_l, l = 1, ⋯ ,N′ are introduced, where Gamma distribution is assigned to each factor function h_l(λ_l) for the mathematical convenience. Then, by implementing message passing rules introduced in the next subsection on the proposed factor graph, each factor node g_i will periodically update the likelihood p(y_i|Q[x_i], λ_l) for the corresponding bit variable nodes $X_i^1{X}_i^2,\cdots ,X_i^q$ when a new estimate of correlation parameter λ_l is available, instead of using a predetermined likelihood p(y_i|Q[x_i], λ).

Consequently, by introducing correlation parameter estimation in Region I, likelihood factor function in (4) will be updated as

$$g_i(Q[x_i],y_i,{\lambda }_l)={\int }_{P(Q[x_i])}^{P(Q[x_i]+1)}\frac{{\lambda }_l}{2}{e}^{{\lambda }_l|x-y_i|}dx.$$ (5)

3.2 Message passing on the constructed factor graph

In Bayesian inference, message passing algorithm (e.g., BP) on a factor graph offers an very efficient way to calculate the marginal distributions (i.e. beliefs) of the unknown variables represented by their corresponding variable nodes. In the proposed adaptive DVC factor graph (see Fig. 1), we are interested in two unknown variables, which are represented by source variable nodes $X_i^j$ in Region II and correlation parameter variable nodes A_l in Region I, respectively.

In Region II, without considering the connection to the Region I, the factor graph is identical to that of standard LDPC codes with discrete variables $x_i^j$. Hence, the posterior distribution of $x_i^j$ can be calculated through standard BP algorithm. However, in region I, BP algorithm cannot be applied directly, as the correlation parameter λ_l represented by the variable node A_l is generally non-Gaussian continuous variable and BP algorithm only handles discrete variable with small alphabets size or continuous variable with linear Gaussian distribution.

To seek a workaround for this difficulty, let us start with the derivation of posterior distribution of the correlation parameter λ_l. According to Bayes’ rule and the message passing rule, the posterior distribution of correlation parameter λ_l can be expressed as:

$$p({\lambda }_l|{\mathbf{y}}_l)=\frac{1}{Z_l}\prod _{i\in {𝒩}^{\backslash h_l}(A_l)}p({\lambda }_l)p(y_i|{\lambda }_l)=\frac{1}{Z_l}\prod _{i\in {𝒩}^{\backslash h_l}(A_l)}{\int }_{Q[x_i]}p({\lambda }_l)p(Q[x_i])p(y_i|Q[x_i];{\lambda }_l)=\frac{1}{Z_l}h({\lambda }_l)\prod _{i\in {𝒩}^{\backslash h_l}(A_l)}\sum _{{\mathbf{x}}_i^q}g(y_i;Q[x_i],{\lambda }_l)\prod _{j\in 1,2,\cdots ,q}{m}_{X_i^j\to g_i}(x_i^j)=\frac{1}{Z_l}{m}_{h_l\to A_l}({\lambda }_l)\prod _{i\in {𝒩}^{\backslash h_l}(A_l)}{m}_{g_i\to A_l}({\lambda }_l),$$ (6)

where Z_l is a normalization constant, ${\sum }_{{\mathbf{x}}_i^q}$ denotes a sum over all the bit variables in ${\mathbf{x}}_i^q$, the value of message $m_{x_i^j\to g_i}(x_i^j)$ is updated iteratively by variable node $X_i^j$ in Region II according to BP update rule, message m_hl→Al (λ_l) = h(λ_l) comes from prior factor node in Region I, and message $m_{g_i\to A_l}({\lambda }_l)={\sum }_{{\mathbf{x}}_i^q}g(y_i;Q[x_i],{\lambda }_l){\prod }_{j\in 1,2,\cdots ,q}{m}_{X_i^j\to g_i}(x_i^j)$ comes from likelihood factor node in Region II according to the BP update rule.

So far, we have shown that the posterior distribution of correlation variable λ_l can be expressed as the product of all the incoming messages. In the rest of this subsections, we investigate how to efficiently compute the posterior distribution using BP and EP based approximation algorithms.

3.2.1 Belief propagation

The BP algorithm²³ is an efficient and exact inference algorithm for computing local marginals over variables on tree-structured graphs. For graphs with loops, a lot of applications (e.g. LDPC deocoding²⁴) show that BP algorithm (or loopy BP algorithm) still provides a good performance. While this technique is extremely powerful in handling variables of small alphabet sizes, they cannot handle a continuous variable with arbitrary distribution or even a variable of a medium alphabet size as the computational complexities of these algorithms increase exponentially with the alphabet size.

For our problem in (6), since all the bit variables $x_i^j$, j = 1, ⋯ , q, in ${\mathbf{x}}_i^q$ are discrete and taking values 0 or 1, the message $m_{g_i\to A_l}({\lambda }_l)={\sum }_{{\mathbf{x}}_i^q}g(y_i;Q[x_i],{\lambda }_l){\prod }_{j\in 1,2,\cdots ,q}{m}_{X_i^j\to g_i}(x_i^j)$ has 2^q terms and the product of all the messages ∏_{i∈𝒩^\hl (Al)} m_gi→Al (λ_l) is a mixture of 2^qC number of Laplace distributions, where C = |𝒩^\h_l (A_l)| is the connection ratio, q is the number of bit-planes, and qC can be a large number. Thus, the direct evaluation of the posterior distribution using BP would be infeasible.

3.2.2 Expectation propagation

An approximate inference for solving the problem in (6) is to parametrize the variables through variational inference. Deterministic approximation schemes (e.g. EP²⁵) provide some low complexity alternatives based on the analytical approximations to the posterior distribution. For example, suppose that posterior distribution p(θ) of parameter θ is infeasible to be calculated directly. If the posterior can be factorized as p(θ) = ∏_{k gk}(θ), where each factor function g_k(θ) only depends a small subset of observations, EP solves this difficulty by replacing the true posterior distribution p(θ) with an approximate distribution q(θ) = ∏_{k g̃k}(θ) by sequentially computing each approximate term g̃_k(θ) for g_k(θ). The general workflow of the EP algorithm has been listed in Table 1. In particular, for our problem in (6), EP is used to sequentially compute approximate messages m̃_hl→Al (λ_l) and m̃_gi→Al (λ_l) in replace of true messages m_hl→Al (λ_l) and m_gi→Al (λ_l) in (6), then get an approximate posterior on λ_l by combining these approximations together. The details of correlation parameter estimation through EP for our problem will be discussed in the next section.

Table 1.

Expectation Propagation

Initialize the term approximation g̃k(θ) and $q(\theta )=\frac{1}{Z}{\prod }_{k=1}^C{\mathrm{g̃}}_k(\theta )$, where $Z={\int }_{\theta }{\prod }_{k=1}^C{\mathrm{g̃}}_k(\theta )$

repeat

for k = 1, …, C do

Compute q\k(θ) ∝ q(θ)/g̃k(θ)

Minimize Kullback Leibler (KL) divergence between q(θ) and gi(θ)q\k(θ) by performing moment matching

Set approximate term g̃k(θ) ∝ q(θ)/q\k(θ)

end for

until parameters converged

4. POSTERIOR APPROXIMATION OF CORRELATION PARAMETER USING EXPECTATION PROPAGATION

In this section, we will derive the proposed EP based correlation estimator, which can provide a fast and accurate way to approximate the posterior distribution on the factor graph as shown in Fig. 1. The procedures of the proposed EP algorithm has been detailed as follows:

1. Initialize the prior term

   $$h_l({\lambda }_l)=\text{Gamma}({\lambda }_l,{\alpha }_l^0,{\beta }_l^0)=z_l^0{\lambda }_l^{{\alpha }_l^0-1}\text{exp}(-{\beta }_l^0{\lambda }_l)$$ (7)

   with ${\alpha }_l^0=2,{\beta }_l^0=\frac{{\alpha }_l^0-1}{{\lambda }^0},z_l^0=\frac{{\beta }_l^{0{\alpha }_l^0}}{\mathrm{\Gamma }({\alpha }_l^0)}$, where λ⁰ is the initial correlation parameter, and ${\beta }_l^0$ and ${\alpha }_l^0$ are scale and shape parameters for Gamma distribution, respectively. The selection of the initial values for the above parameters guarantees the mode of prior distribution equals to the initial correlation λ⁰.
2. Initialize the approximation term (uniform distribution)

   $${\mathrm{m̃}}_{g_i\to A_l}({\lambda }_l)=\text{Gamma}({\lambda }_l,{\alpha }_{il},{\beta }_{il})=z_{il}{\lambda }_l^{{\alpha }_{il}-1}\text{exp}(-{\beta }_{il}{\lambda }_l)$$ (8)

   with β_il = 0, α_il = 1, z_il = 1.

3. Initialize ${\alpha }_l^{\text{new}}$ and ${\beta }_l^{\text{new}}$ for approximate posterior $q({\lambda }_l)=\text{Gamma}({\lambda }_l,{\alpha }_l^{\text{new}},{\beta }_l^{\text{new}})$, where ${\alpha }_l^{\text{new}}={\alpha }_l^0=2$, and ${\beta }_l^{\text{new}}={\beta }_l^0$.

4. For each variable node λ_l

For each factor node g_i, where g_i ∈ 𝒩(λ_l)

1. Remove m̃_gi→Al (λ_l) from the posterior q(λ_l), we get $q^{\backslash g_i}({\lambda }_l)=\text{Gamma}({\alpha }_l^{\text{tmp}},{\beta }_l^{\text{tmp}})$

   $${\alpha }_l^{\text{tmp}}={\alpha }_l^{\text{new}}-({\alpha }_{il}-1){\beta }_l^{\text{tmp}}={\beta }_l^{\text{new}}-{\beta }_{il}$$ (9)
2. Update q^new(λ_l) by minimizing the Kullback Leibler (KL) divergence D(q^\g_i (λ_l)m_gi→Al (λ_l)‖q^new(λ_l)) (i.e., performing moment matching (Proj)) (see Section 4.1 for detail).

   $$q^{\text{new}}({\lambda }_l)=\frac{1}{Z_l}\mathbf{\text{Proj}}[q^{\backslash g_i}({\lambda }_l)m_{g_i\to A_l}({\lambda }_l)]$$ (10)

   where Z_l = ∫_λl q^\g_i (λ_l)m_gi→Al (λ_l).
3. Set approximated message

   $${\alpha }_{il}={\alpha }_l^{\text{new}}-({\alpha }_l^{\text{tmp}}-1){\beta }_{il}={\beta }_l^{\text{new}}-{\beta }_l^{\text{tmp}}{z}_{il}=Z_l\frac{{\beta }_l^{{\text{new}}^{{\alpha }_l^{\text{new}}}}}{\mathrm{\Gamma }({\alpha }_l^{\text{new}})}{\left(\frac{{\beta }_l^{{\text{tmp}}^{{\alpha }_l^{\text{tmp}}}}}{\mathrm{\Gamma }({\alpha }_l^{\text{tmp}})}\right)}^{-1}{\left(\frac{{{\beta }_{il}}^{{\alpha }_{il}}}{\mathrm{\Gamma }({\alpha }_{il})}\right)}^{-1}$$ (11)

4.1 Moment matching

Through moment matching, q(λ_l) is obtained by matching the mean and variance of q(λ_l) to those of q^\g_i (λ_l)m_gi→Al (λ_l). Then, we get the updated ${\alpha }_l^{\text{new}}$ and ${\beta }_l^{\text{new}}$, the parameters of q(λ_l) as follows,

$${\alpha }_l^{\text{new}}=m_1{\beta }_l^{\text{new}}{\beta }_l^{\text{new}}=m_1/(m_2-m_1^2),$$ (12)

where m₁ and m₂ are the first and second moments of the approximate distribution as shown below.

$$m_1=\frac{1}{Z}\sum _{Q[x_i]}({ℱ}_1(z_1)-{ℱ}_1(z_2))\prod _{j=1}^{j=q}{m}_{X_i^j\to g_i}(x_i^j)m_2=\frac{1}{Z}\sum _{Q[x_i]}({ℱ}_2(z_1)-{ℱ}_2(z_2))\prod _{j=1}^{j=q}{m}_{X_i^j\to g_i}(x_i^j)Z=\sum _{Q[x_i]}({ℱ}_0(z_1)-{ℱ}_0(z_2))\prod _{j=1}^{j=q}{m}_{X_i^j\to g_i}(x_i^j)$$ (13)

Here, Z is the normalization term and these unknown functions in (13) can be evaluated according to (14).

$$z_1=P(Q[x_i]+1)z_2=P(Q[x_i]){ℱ}_0(z)=A(z)+B(z){ℱ}_1(z)=\frac{{\alpha }^{\text{tmp}}}{{\beta }^{\text{tmp}}}A(z)+\frac{{\alpha }^{\text{tmp}}}{{\beta }^{\text{tmp}}+|z-y_i|}B(z){ℱ}_2(z)=\frac{{\alpha }^{\text{tmp}}({\alpha }^{\text{tmp}}+1)}{{({\beta }^{\text{tmp}})}^2}A(z)+\frac{{\alpha }^{\text{tmp}}({\alpha }^{\text{tmp}}+1)}{{({\beta }^{\text{tmp}}+|z-y_i|)}^2}B(z)A(z)=\frac{1}{2}(1+\text{sgn}(z-y_i))B(z)=-\text{sgn}(z-y_i)\frac{1}{2}{\left(\frac{{\beta }^{\text{tmp}}}{{\beta }^{\text{tmp}}+|z-y_i|}\right)}^{{\alpha }^{\text{tmp}}}$$ (14)

5. RESULTS

In this section, we employ a pixel-based DVC setup to demonstrate the benefit of the proposed OTF correlation tracking. As in references,^{1, 10, 21} group of pictures (GOP) is equal to 2 in our study, where all even frames are treated as WZ frames and all odd frames are considered as key frames. The key frames are conventionally intra-coded, for example, using H.264 Advanced Video Coding (AVC)²⁶ intra coding mode. WZ frames are first quantized pixel-by-pixel and then all bit-plane of the resulting quantization indices are combined together and compressed using an LDPCA codes. At the decoder, side information frame Y is generated using motion-compensated interpolation of the forward and backward key frames.^{1, 21} Spatial smoothing,²¹ via vector-median filtering, is used to improve the result together with half-pixel motion search. Each WZ frame is decoded by the proposed EP based OTF WZ decoder described in Section 3. Moreover, we incorporate LDPCA codes with a feedback channel for rate adaptive decoding.

To verify the effectiveness of correlation tracking across WZ-encoded frames in a video sequence, we tested the above set-up with three standard QCIF (i.e., 176 × 144) video sequences, carphone, foreman and soccer, with different scene dynamics of low, medium and high motions, respectively. All the results are based on the average of 50 WZ frames. The quantization parameters Q of H.264/AVC encoder for different video sequences with different WZ quantization bits q have been listed in Table 2. The selections of quantization parameters Q for different WZ quantization bits q make sure that both the decoded key and WZ frames have similar visual qualities in terms of PSNR. Moreover, we split each 176 × 144 WZ frame into 16 sub-frames with size 44 × 36 (i.e. N = 1584) for efficient coding purpose. Within each sub-frame, the block size for correlation estimation is equal to 4 × 6 (i.e., C = 24) for total N′ = 66 number of blocks.

Table 2.

H.264/AVC quantization parameter Q for different video sequences

Quantization bits	Carphone	Foreman	Soccer
	Q	Q	Q
2	46	46	44
3	36	36	34
4	28	28	26
5	22	21	19

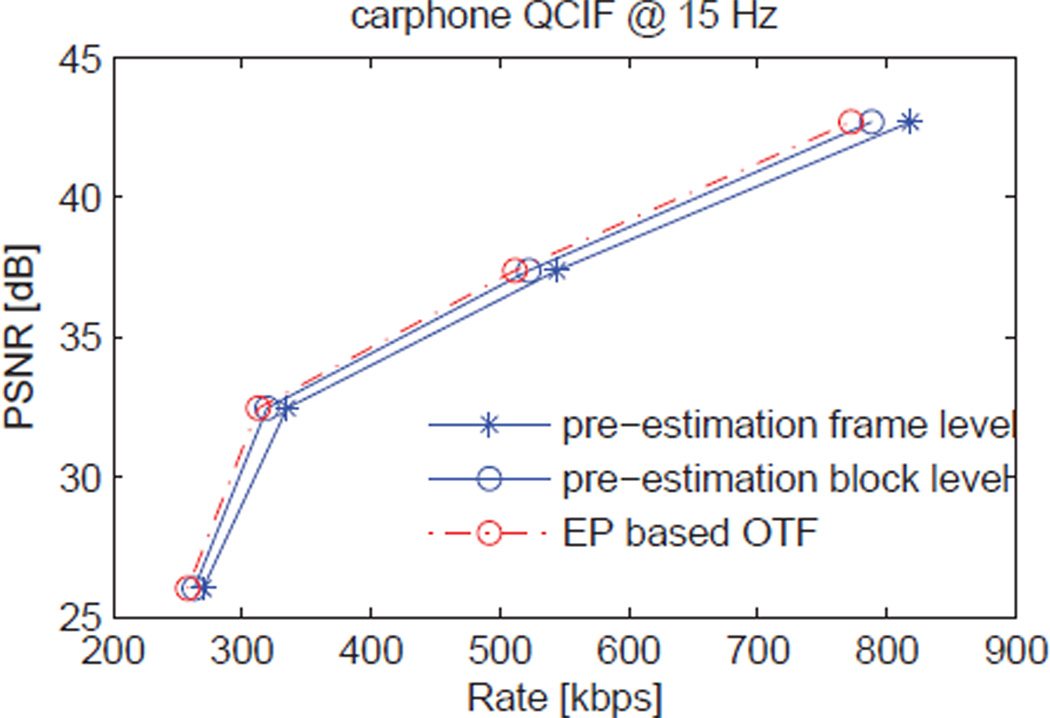
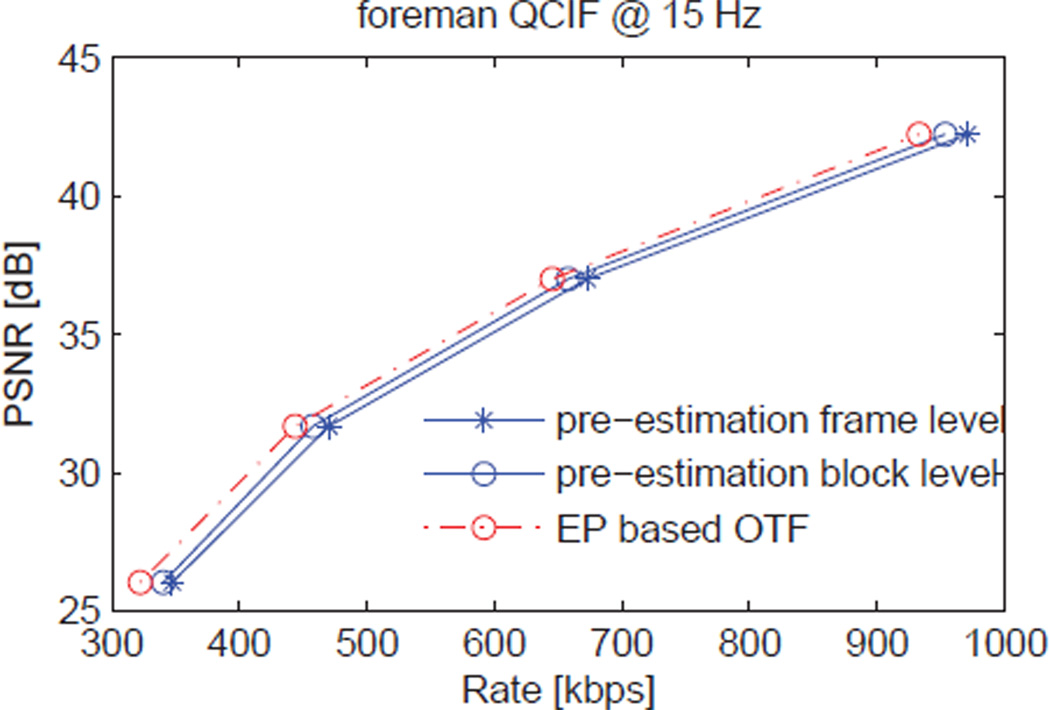
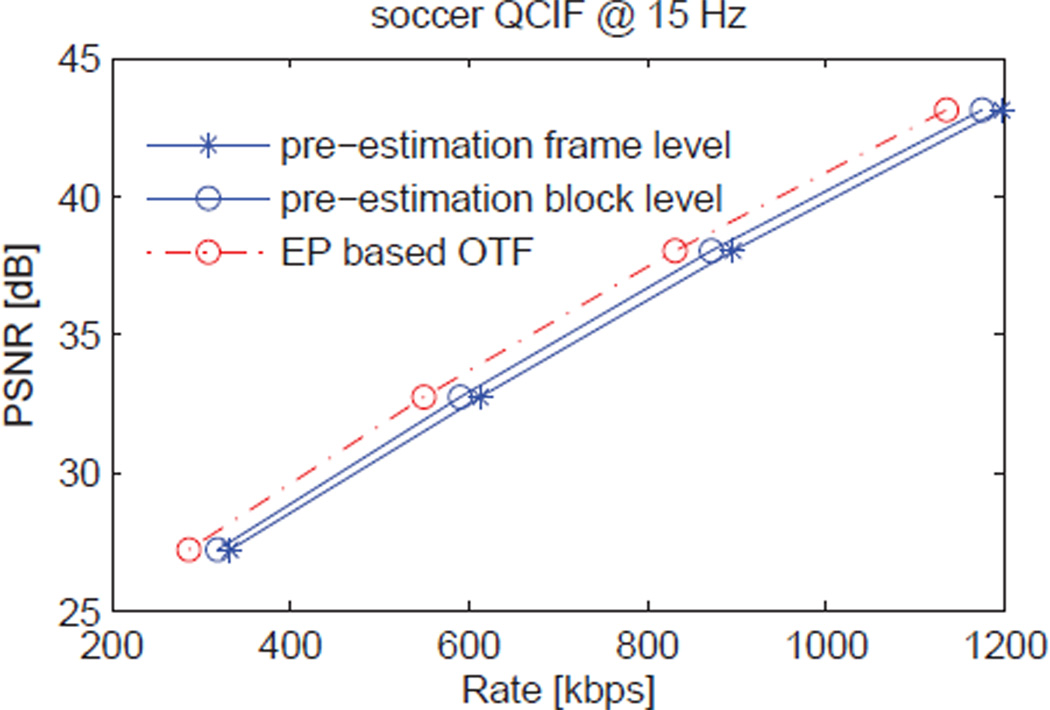
Results comparing the relative performance of pre-estimation in frame level DVC,¹⁰ pre-estimation in block level DVC,¹⁰ and the proposed EP based OTF DVC for the carphone, foreman, and soccer video sequences, respectively, are shown in Figs. 2, 3, 4, where the implementation of standard DVC codec is based on the DISCOVER framework¹⁰ with joint bit-plane setup.

Figure 2.

PSNR comparison of the proposed EP based OTF and pre-estimation DVC for the QCIF carphone sequence, compressed at 15 fps.

Figure 3.

PSNR comparison of the proposed EP based OTF and pre-estimation DVC for the QCIF foreman sequence, compressed at 15 fps.

Figure 4.

PSNR comparison of the proposed EP based OTF and pre-estimation DVC for the QCIF soccer sequence, compressed at 15 fps.

The pre-estimation methods,¹⁰ either in frame or block levels, model the correlation as Laplace distribution, whose correlation parameter is estimated using the difference between backward and forward motion compensated frames/blocks at the decoder. Our proposed OTF estimator unifies the process of correlation estimation using EP and joint bit-plane decoding into a single joint process, where the updated decoding information can be used to improve the correlation estimation and vice versa. As expected, pre-estimation in block level has better performance than that of frame level in terms of bit rate saving, since block level correlation offers a finer granularity than the frame level correlation. More importantly, our proposed EP based OTF codec always achieves the best performance for all sequences (slow, medium and fast motions), since the proposed EP based OTF estimator can iteratively refine the correlation statistics in each block.

In particular, for the carphone sequence (slow motion), to obtain the same visual qualities (i.e., PNSRs), our proposed EP based OTF codec achieves about 10 kbps and 30 kbps saving compared to pre-estimation in block and frame levels, respectively. For foreman sequence (medium motion), the average rate decrease of EP based OTF codec is 20 kbps for pre-estimation in block level and 30 kbps for pre-estimation in frame level. Moreover, for soccer sequence with fast motion, we again observe the superiority of our proposed EP based OTF codec over the pre-estimation codecs, where the proposed EP based OTF codec offers about 38.25 kbps and 56.5 kbps saving compared to pre-estimation in block and frame levels, respectively. These results demonstrated that our proposed EP based OTF codec are more powerful for video sequences with fast motions.

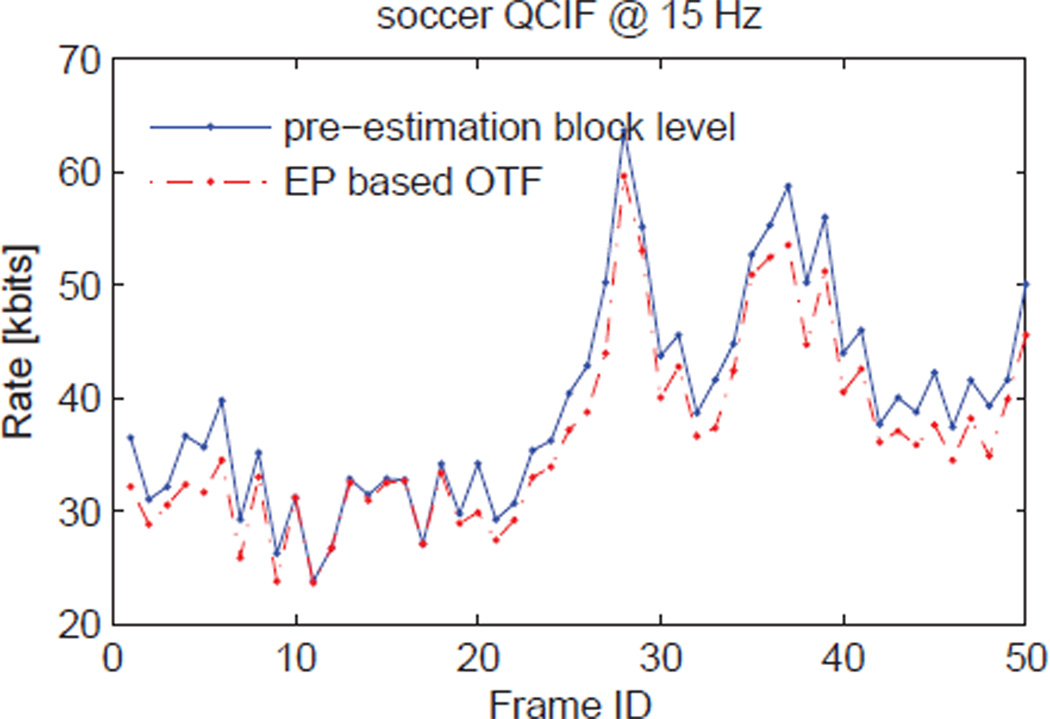
A sub-frame-by-sub-frame (i.e., the first sub-frame of each WZ frame) rate variation for the soccer sequence with quantization bits equal to 3 is shown in Fig. 5. We found that the rate variation across frames is about 36.01 kbits for the proposed EP based OTF DVC codec and 40.01 kbits for DVC codec with pre-estimation in block level. Moreover, the result shows that the rate fluctuations of EP based OTF and pre-estimation in block level DVC codecs have similar trend and the proposed EP based OTF codec always has equal or lower code rate than that of the pre-estimation in block level DVC codec. The maximum difference of code rate between EP based OTF and pre-estimation block level codecs is about −5.32 kbits. Similar results are obtained for other sub-frames in all three testing sequences.

Figure 5.

Subframe-by-subframe rate variance for soccer sequence with quantization bits equal to 3.

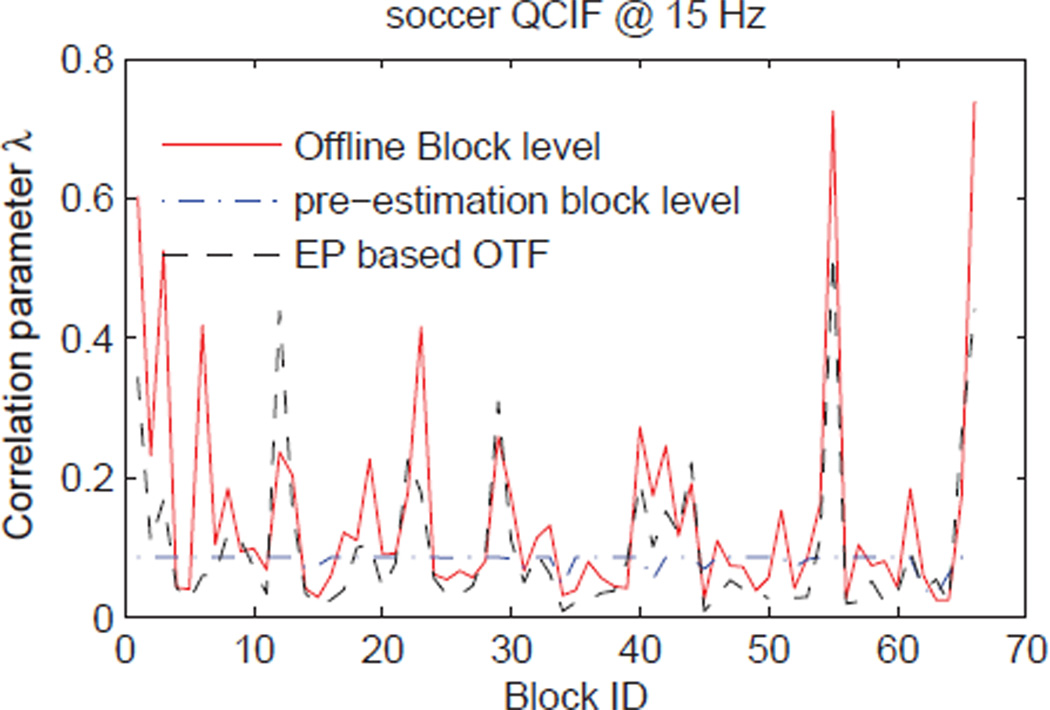
The estimation accuracy of correlation parameter is studied in Fig. 6 for the soccer sequence. Here, we use the offline estimated correlation parameter as benchmark, where the benchmark Laplacian parameter is calculated offline at the block level for each frame using the residual between the WZ frame and the side information frame. We can see that the proposed OTF correlation estimation scheme improves the estimates obtained through pre-estimation method,¹⁰ which also explains why the proposed EP based OTF DVC outperforms the pre-estimation based DVC codec.

Figure 6.

Estimation accuracy of the proposed EP based OTF DVC for the correlation parameter of the soccer sequence

Finally, the proposed EP based OTF estimator offers a very low complexity overhead compared with the standard BP algorithm. The complexity of the proposed estimator lies in the evaluation of equations (12), (13) and (14) as shown in Section 4.1. Roughly speaking, the EP based OTF estimator introduces less than 10% computational overhead compared with the standard BP algorithm.

6. CONCLUSION

This paper proposes an on-the-fly (OTF) correlation estimation scheme for distributed video coding using expectation propagation (EP). Unlike previous work performing pre-estimation where estimation starts before decoding, our proposed correlation estimation technique is embedded within the WZ decoder itself, thus ensuring dynamic estimation of correlation changes in block level. This is achieved by augmenting the SW code factor graph to connect correlation parameter variable nodes together with additional factor nodes. Inference on the factor graph for continuous correlation parameter variable is achieved through EP based deterministic approximation methods, which offers better tradeoff between accuracy and complexity compared with other methods. The proposed scheme boosts coding performance together with the ease of integration with existing DVC codecs. We demonstrate the benefits of using the proposed scheme via a pixel-based DVC setup. Simulation results show significant performance improvement due to correlation tracking for multiple video sequences with the Laplacian correlation model.