Important Considerations in Conducting Statistical Mediation Analyses

Abstract

An investigator wishes to examine mediation in a randomized control trial of the effectiveness of an intervention, which consists of a computerized decision aid for promoting colorectal cancer screening. Mediation is a naturally occurring process, and in any given instance, research investigators seek to ascertain whether it has occurred. In the case of a prevention intervention for a specific chain of events, mediation occurs (1) when the prevention intervention effects a change on a targeted intermediate condition: a mediator, for example, a person’s intentions to get a colorectal screening examination; and (2) when, at a later point in time, this condition effects a change on a targeted outcome, for example, the actual behavior of getting a colorectal screening exam. Full mediation is said to occur when the effectiveness of the intervention on the targeted outcome only takes place through the intermediate condition and does not directly affect the targeted outcome. Partial mediation is said to occur when the intervention causes changes in both the intermediate condition and the targeted outcome. The assessment of mediation is important because conclusions about the efficacy of a public health intervention may depend on how these indirect influences are assessed.

The proposed study regarding the effectiveness of this aforementioned decision aid would include 200 individuals who will be randomized to a decision aid (intervention) condition or to a usual care (control) condition. Thus, the group variable that contains these 2 conditions serves as the independent variable. The researcher hypothesizes that the independent variable will cause changes in a mediator variable (e.g., increased intentions to get screened for colorectal cancer). The mediator variable is then hypothesized to cause changes in the outcome (the dependent variable), which is the actual screening behavior that would occur at a later time point.

STATISTICAL MEDIATION

A popular way to test the described relationship is derived from the work of Baron and Kenny,¹ and is known as the causal steps approach to statistical mediation. The causal steps approach involves estimating the following regression equations:

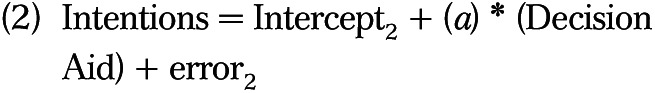An overlooked assumption² underlying mediation analysis is that it is a causal process in which the independent variable transmits an effect onto the mediator variable, which in turn transmits an effect onto the outcome variable. This modeling approach is preferred to an analysis that simply controls for the effect of each variable on all others, as a hypothesized causal mechanism is being tested. Moreover, such approaches result in increased type I errors.³

Under the causal steps approach, mediation is said to occur under the following conditions: (1) there must be a statistically significant slope, c, in equation 1; (2) there must be a statistically significant slope, a, in equation 2; (3) there must be a statistically significant slope, b, and the size of c′ in equation 3 must be smaller in magnitude than is c in equation 1. If the c′ slope in equation 3 is no longer statistically significant, then full mediation is said to have occurred. If the c′ slope in equation 3 is smaller in magnitude than the original c but is still statistically significant, then partial mediation is said to have occurred. From the equations above, it is also known that

There are several problems associated with the causal steps approach for assessing mediation. First, this approach requires that the total effect of the decision aid intervention on screening, c, be statistically significant. If equation 1 does not result in a statistically significant slope, the assessment of mediation terminates. Thus, a researcher who hypothesizes that the decision aid intervention will only have an indirect effect on screening cannot test this hypothesis with the causal steps approach.

Second, this approach¹ never directly tests the indirect effect formed by the cross product of ab and infers it from a series of tests. Given the increasing attention to report effect sizes in mediation analyses,⁴ strategies are needed that directly test and quantify this ab effect. Moreover, the statistical significance of ab does not depend on the statistical significance of c.⁵

Third, the causal steps procedure involves a series of multiple tests in which each test has its own type I and type II error rate and, at present, is the least powerful approach in assessing mediation.⁶

Fourth, the presence (or absence) of the requisite slopes in equations 2 and 3 does not mean that the ab cross product is (or is not) statistically significant.

Last, the distinction between full and partial mediation using the causal steps approach is problematic. For example, as sample size increases, the SE of the c′ will become smaller, which increases the likelihood that the c′ effect will be statistically significant. Conversely, the likelihood of demonstrating full mediation decreases as sample size increases. Moreover, the presence of full mediation does not rule out the possibility that other mediator variables could have fully mediated the effect or that the inclusion of other mediator variables in the presence of full mediation could be detected.⁷

To assess mediation, approaches must be used that test the ab cross product directly. In approaches in which the outcome variable is continuous, the Sobel⁸ test has been used to test the ab cross product, but this test assumes that the sampling distribution of the ab cross product is normally distributed. This assumption is not reasonable in smaller samples. Alternative approaches include the distribution of products approach,⁹ Monte Carlo simulations,¹⁰ and bootstrapping approaches. The distribution of products approach involves taking the estimates of a and b in equations 2 and 3, converting them into z scores, and then calculating their product.

The resulting cross product is compared with a statistical table of cross products,¹¹ which accounts for nonnormality of standardized cross products. The values from this table would replace the customary ±1.96 from the standard normal distribution, and 95% confidence limits around the point estimate of the cross product can be created.¹² These confidence intervals (CIs) are readily available in the statistical program, RMediation.⁹ If the CI does not contain 0, we conclude mediation is present.

Monte Carlo simulations require the assumption that estimates of a and b in equations 2 and 3 are normally distributed. Given the estimates of the a and b parameters and their SEs, a researcher would randomly select values from a normal distribution of a and b and create the ab cross product. This procedure would be repeated 9999 times to create a distribution of 10 000 ab cross products. The middle 95% of this distribution would constitute a CI. The absence of 0 from this interval would indicate that the ab cross product is statistically significant. This procedure works well when raw data are not available and software is readily available to perform such simulations.¹³

Bootstrapping is a distribution-free resampling method that allows the estimation of a sampling distribution of a statistic. In our example of the randomized control trial involving a total sample of 200 individuals, a researcher samples (with replacement) from the original sample to create a sample of 200 individuals. It should be noted that some individuals from the original sample could appear more than once in this second sample, and other individuals from the original sample may not appear at all. The investigator would then estimate equations 2 and 3 in this new sample to derive estimates of a and b and form an ab cross product.

Thus in bootstrapping, this procedure of sampling with replacement from the original sample to form samples of 200 individuals would be repeated 9999 more times to create a sampling distribution of 10 000 ab cross products. From this distribution of 10 000 cross products, the researcher can create a 95% CI by taking the cross product values that fall at the 97.5th and 2.5th percentiles. No distributional assumptions have been imposed to construct this CI. If 0 does not fall in this interval, then we can declare that the ab cross product is statistically significant.

Bias associated with the bootstrapping procedure can also be addressed by adjusting the upper and lower bounds of this interval. Hayes¹⁴ has developed SAS and SPSS macros that perform bootstrapping for his forthcoming text. Unlike the distribution of products and Monte Carlo simulations, bootstrapping can be used for outcome variables that are either continuous or binary.¹⁴

CONCLUSIONS AND RECOMMENDATIONS

Given the availability of easy-to-use software, there is no reason to continue using the causal steps approach to assess mediation. Adopting more powerful approaches like those derived from bootstrapping, Monte Carlo simulations, or the distribution of products approach provides a more robust assessment of indirect intervention effects. Finally, researchers are encouraged to abandon the nomenclature of full and partial mediation. Instead, researchers should report effect size measures of the indirect effect, such as the proportion of the maximum indirect effect.⁴