Abstract
Knowledge of nanopore size and shape is critical for many implementations of these single-molecule sensing elements. Geometry determination by fitting the electrolyte-concentration-dependence of the conductance of surface-charged, solid-state nanopores has been proposed to replace demanding electron microscope-based methods. The functional form of the conductance poses challenges for this method by restricting the number of free parameters used to characterize the nanopore. We calculated the electrolyte-dependent conductance of nanopores with an exponential-cylindrical radial profile using three free geometric parameters; this profile, itself, could not be uniquely geometry-optimized by the conductance. Several different structurally simplified models, however, generated quantitative agreement with the conductance, but with errors exceeding 40% for estimates of key geometrical parameters. A tractable conical-cylindrical model afforded a good characterization of the nanopore size and shape, with errors of less than 1% for the limiting radius. Understanding these performance limits provides a basis for using and extending analytical nanopore conductance models.
Keywords: Electric double layer, nanopore surface charge, nanopore conductance, nanopore shape, silicon nitride nanopore, silicon oxide nanopore
Introduction
Nanopores are the foundation of myriad powerful new devices and methods for single-molecule biosensing applications and fundamental biophysical investigations1-4. In usual practice, the nanopore membrane is used to divide an electrolyte-containing fluid chamber so that when a voltage is applied across the membrane, ions flow through the nanopore to produce a measurable current. Single molecules can be sensed when their passage through the nanopore perturbs the electrolyte-only current. The nanopore size, shape and surface chemistry are key factors that determine the open-pore conductance and the performance of nanopore devices and methods. Knowledge of the full radial profile of the nanopore is thus critical to the design and interpretation of nanopore experiments. An inner cylinder, for instance, may require the extension of probe oligonucleotides in nanopore hybridization experiments5-6. The increasing popularity of nanopores fabricated in silicon dioxide and silicon nitride by ion- and electron-beam milling7-12 and, more recently, by ion-track-etching13, has brought unique advantages and challenges. These solid-state nanopores are composed of nanofabrication-compatible materials and offer mechanical and chemical stability, and nanopore-size tuneability. Full characterization of the size and shape of solid-state nanopores using transmission electron microscope (TEM)-based methods such as electron tomography and electron energy loss spectroscopy (EELS) is time-, facility- and expertise-intensive. Typically, therefore, only two parameters are used to characterize solid-state nanopore sizes: the membrane thickness that is well-defined during preliminary fabrication steps, and the minimum nanopore radius, r0, that can be observed post-fabrication by TEM imaging. Even such ostensibly straightforward imaging, though, must be done with caution to prevent unwanted electron-beam-induced alteration of the nanopore dimensions, such as transition from a double-conical shape to a double-conical-cylindrical profile14. A small number of groups have performed detailed nanopore geometry characterizations8,15-18 and have established that for TEM-fabricated pores, the nanopore size and shape show strong sensitivity to the fabrication conditions14,16 and for solution-based fabrication of ion-tracked nanopores, the radial profile from one membrane surface to the other depends strongly on the details of the etching configuration13.
Liebes et al.18 recently proposed to replace the TEM-based determination of nanopore profiles with a dramatically simpler approach that leverages the dependence of the nanopore conductance on the pore size, shape and surface chemistry. They proposed to determine nanopore dimensions by geometry-optimizing a radial profile to obtain exact agreement with the measured conductance of the nanopore as a function of electrolyte concentration. Depending on fabrication conditions, nanopore size can unfortunately change during use14 and so aside from convenience, such a simple characterization approach would offer a real-time measurement of the nanopore size during the course of an experiment. Nanopore fabrication methods that rely on solution-phase deposition and etching would also benefit from such a real-time characterization13,19-20. Liebes et al.18 performed a careful EELS-based characterization of a TEM-fabricated nanopore that revealed an exponential-cylindrical radial profile and yielded values for its three geometrical dimensions. Combination of this independently-determined geometry with a theoretical treatment of the effect of the charged nanopore surface on the conductance allowed them to accurately model the experimental conductance as a function of electrolyte concentration. While the authors extracted geometrical parameters for their exponential-cylindrical model from a fit to the measured electrolyte-dependent conductance, we show that the nature of the electrolyte-dependent conductance does not generate a discrete set of optimized exponential-cylindrical geometries. More fundamentally, we show that accurate calculation of the nanopore conductance does not guarantee, nor should it take precedence over, the accurate determination of the nanopore size and shape. The substantial benefits of conductance-based nanopore sizing nevertheless warrant further examination of the approach, using profiles that can be geometry-optimized using the conductance to a discrete number of solutions. We consider models invoking common simplifying approximations, models representative of experimentally observed profiles, and models designed for special applications8,15-18, and we determine limits of performance. We focus on small, r0 ≤ 10nm, nanopores for which the nanopore access resistance is a negligible contribution to the measured conductance 17, and which is moreover the length scale of greatest interest for a large number of applications1. This length scale faces the most significant challenges in terms of pore-to-pore fabrication reproducibility19 and thus a straightforward, complete sizing method would have tremendous benefit. We focus, in addition, on nanopores that are symmetric about the membrane midpoint, so that an experimental measurement of their conductance, with identical electrolyte composition on either side of the membrane, will yield a conductance independent of the applied voltage polarity. We finally show that the conductance-based optimization of a judiciously chosen approximate nanopore model is capable of extracting largely reasonable nanopore radii for small nanopores, albeit with a penalty in the accuracy of the remaining dimensions.
Theory
The bulk conductance of an electrolyte-filled tube of varying cross-section in an insulating membrane is described by21
| (1) |
where K is the electrolyte conductivity and r(z) is the nanopore radius as a function of distance along the nanopore length, using cylindrical coordinates. For a cylindrical nanopore, for example, where the length is equal to the membrane thickness, L, r(z) is constant at r0 and the bulk nanopore conductance is , ignoring corrections due to end effects21. In the bulk limit, the nanopore conductance decreases linearly as the electrolyte conductivity decreases with reduced electrolyte concentration19,22. Experimental results and theoretical studies of nanoscale channels, including nanopores, however, have shown that when the surface is charged, the conductance falls less rapidly as the electrolyte concentration is reduced18-19,22-28. Solution counterions attracted to the surface charge respond to the applied electric field and give rise to a conductance denoted here as the surface conductance, Gsurface
| (2) |
where σ is the surface charge density and μ is the mobility of the counterions, assuming a single species. For a surface with a single type of surface-chargeable species and an electrolyte composed of only monovalent ions, the effect of the surface charge is captured by the following coupled equations describing the surface charge density, σ, and the diffuse layer potential, ψD29
| (3) |
and
| (4) |
where ∊∊0 is the solution permittivity, β is the inverse of the product of the Boltzmann constant with absolute temperature (298K for all calculations), e is the elementary charge, Γ is the surface concentration of the chargeable species, pH is the bulk solution pH, pKa is the acid dissociation constant for the surface chargeable species and C is the Stern layer’s phenomenological capacity. The Debye screening length, κ−1, is itself determined from κ2 = βe2n/∊∊0 where n is the bulk concentration of ions. Effects of activity and curvature of the nanopore are ignored in this treatment29, which has been shown experimentally to apply to nanopores in the size range considered18,26.
The total conductance, G, is the sum of the bulk and surface terms and can be written in the general form
| (5) |
where i denotes a particular nanopore shape, and and are purely geometric parameters dependent on that shape, arising from the integrals in equations 1 and 2, and wholly independent of the electrolyte concentration. This form of the total nanopore conductance, Gi(K,σ), fundamentally limits the number of free parameters that can be included in a nanopore model in order for the geometry optimization to return a discrete number of solutions.
Methods
The nanopore shape was taken to be described by the three free parameter, exponential-cylindrical profile determined experimentally by Liebes et al.18 This nanopore profile was used to calculate the electrolyte-dependent conductance using equation 5, and served as the reference for geometry-optimizing the nanopore models. Model schematics are shown in Figure 1 and the corresponding and parameters are given in Table 1. The parameters and were calculated for reference nanopores with radii, r0,ref, varying from 2 to 10nm, and with fixed lref=11nm, and bref=0.19nm−1. All two-parameter models were geometry-optimized by exploiting that Gi = Gref is satisfied for all electrolyte concentrations when the model i-specific geometrical parameter values simultaneously satisfy and . To restrict the geometry-optimization of the conical-cylindrical model to a discrete set of results, the number of free parameters was reduced from three to two by constraining the outer radius to be a function of the inner radius, R = r0 + 10nm an assignment consistent with typical nanopore dimensions17. Membrane thicknesses were fixed at L = 30nm, except for one cylindrical model optimization in which it was used as a free parameter without strict physical meaning.
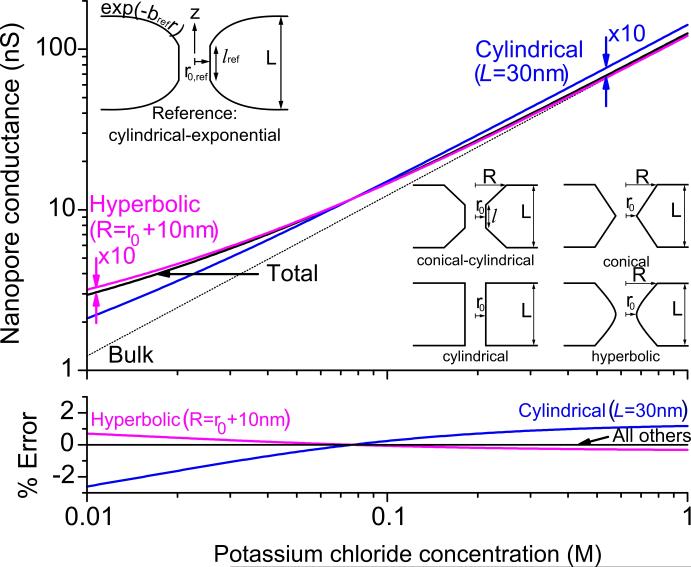
Figure 1.
a) Calculated conductance of an r0,ref = 4.9nm, l=11nm, bref=0.19nm−1 reference (exponential-cylindrical) nanopore18 versus molar electrolyte concentration in the surrounding medium. The inclusion of surface charge in all models caused a dramatic departure from the bulk conductance at low electrolyte concentration, in agreement with experiment18. The error between the best-fit and reference conductance was multiplied by 10, in (a) only, for all profiles for greater clarity. Schematics show the radial profiles of nanopore models listed in Table 1. b) The unaltered percent error between the best-fit and reference conductance curves showed that all but the R-constrained and fixed-L cylindrical models were able to accurately fit the conductance over the entire range of electrolyte concentration.
Table 1.
Model-specific nanopore geometrical parameters used to calculate bulk and surface-chargedependent nanopore conductances, Gbulk, and Gsurface
| model | A bulk | B surface |
|---|---|---|
| Reference: exponential cylindricala |
||
| where | ||
| conical cylindricalb |
||
| conical | ||
| cylindricalc | ||
| hyperbolicd | ||
r0,ref ∈ [2nm, 10nm],lref=11nm, bref=0.19nm−1, Ref. 18
restricted to two free parameters by setting R = r0 + 10nm
optimized as a one free parameter profile with L=30nm or as a two free parameter profile with L free
optimized as a two or one free parameter model via R free or R = r0 + 10nm, Ref. 17
Insufficient parameter flexibility required that one-parameter models be optimized by evaluating equation 5 over a range of electrolyte conductivities, K, and varying the single geometrical parameter to minimize the sum of the squared relative deviations between the model-i conductance and the reference conductance, . The bulk electrolyte conductivity was calculated from K = ecKCl(μK + μCl), where e is the electron charge, cKCl is the formal electrolyte concentration, and the potassium and chloride ion mobilities were μK = 7.6 × 10−8m2/(V·s) and μCl = 7.9 × 10−8m2/(V·s)26. The nanopore surface chemistry was treated as being governed by the single surface equilibrium . To calculate the surface charge, the Stern layer phenomenological capacitance was taken as , independent of electrolyte concentration29. The aqueous solution pH was 7.5 and the potassium chloride concentration was varied from 10−2 to 1M. The lowest electrolyte concentration considered, 10mM, was shown by Liebes et al.18 to permit agreement between the experimentally measured conductances and those calculated using equation 5. The mobility of the potassium counterions next to the negative surface was approximated by the bulk solution mobility, μ = 7.61 × 10−8m2/V·s18,26,31-32. The recursive iterative solution of equations 3 and 4 was unstable, particularly at higher electrolyte concentrations. To circumvent this difficulty, a repeated one-sided search with decreasing step-size was used until the seed value, σseed, agreed to with the output of σ(ψD(σseed)).
In summary, all two-parameter pore profiles were geometry-optimized by adjusting the free geometry parameters listed for each profile in Table 1 to simultaneously satisfy and . The conical-cylindrical model was constrained to two free parameters by setting R = r0 + 10nm, and the free-L cylindrical profile allowed the membrane thickness to take on nonphysical values to yield two free geometry parameters for optimization. All one free parameter profiles were optimized by minimizing : this included the cylindrical and R = r0 + 10nm-constrained hyperbolic profiles. The best-fit parameters were compared to the known reference geometry parameters to determine the performance limits of using the nanopore conductance to extract meaningful nanopore dimensions.
Results
Figure 1a shows the conductance curves calculated for a reference nanopore with radius r0,ref = 4.8nm, along with the corresponding best-fit model conductances. The significant departure of the total from the bulk-only conductance at low electrolyte concentrations underscores the need to correctly treat surface charges for nanoconfined surfaces18,22-28. The functional dependence of the conductance (equation 5) prevented the three parameter exponential-cylindrical model from being uniquely geometry-optimized to the known values. Supplemental figure S1 shows the continuous distribution of best-fit r0, l and b giving exact agreement with the conductances of several single reference nanopores with fixed r0,ref, lref, = 11nm, and bref = 0.19nm−1. All best-fit two-parameter models also produced conductances in exact agreement with the reference conductances because simultaneous solutions to and existed. Lack of parameter flexibility meant that none of the single-parameter models could match the reference conductance curve over the entire electrolyte concentration range. The error in best-fit versus reference conductance is shown in Figure 1b for the r0,ref = 4.9nm reference nanopore. Whether the single-parameter model conductance curves agreed better with the reference conductance at low, intermediate or high electrolyte concentration—that is, the importance accorded to the effect of the surface charge—could be adjusted by changing the weighting of the deviation during the geometry optimization (results not shown). When minimizing , the best-fit cylindrical model underestimated the conductance at low electrolyte concentrations and overestimated it at high electrolyte concentrations. The R-constrained hyperbolic model showed the reverse trend, but with a lower overall disagreement. Of all the models considered, the commonly used one-parameter cylindrical model was clearly the worst at fitting the conductance curve. While the full range of electrolyte concentrations shown was not required to optimize the one-parameter conductance equation (equation 5), it was plotted to illustrate the performance of the fit across a range of experimentally reasonable electrolyte concentrations.
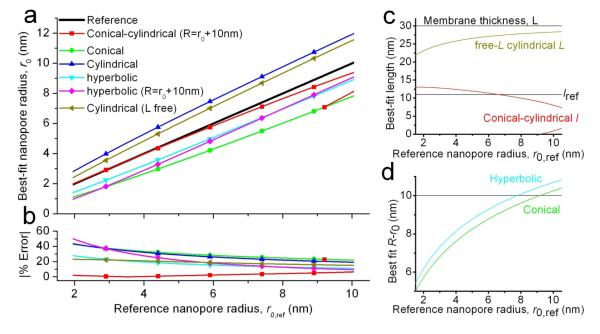
Figure 2 summarizes the values of all the geometric parameters, for each model, that assured the best agreement with the electrolyte-dependent conductances calculated for reference nanopores with radii, r0,ref, between 2 and 10nm. Figure 2a is a plot of the best-fit radii, r0, by nanopore model, as a function of the known reference nanopore radii, r0,ref. The one-parameter cylindrical and the R-constrained hyperbolic best-fit results could not accurately reproduce the conductance curve and, reassuringly, the best-fit radii were also a poor estimate of the reference radii. The remaining models exactly reproduced the conductance versus electrolyte concentration curve of the reference nanopore, but the best-fit model radii still differed from the known reference nanopore radii. Figure 2b shows the absolute value of the percent error of the best fit r0 versus the reference r0,ref, which reached, depending on model and reference radius, values exceeding 40%. The R-constrained conical-cylindrical model produced excellent agreement with the reference nanopore radius, although the deviation increased somewhat for reference pores of larger radius. Figure 2c shows, however, that the best-fit length, l, of the cylindrical component of this model had to vary by up to 3 nm from the cylinder length in the reference pores in order to achieve this level of agreement. The free-L cylindrical model had a best-fit radius closer to the reference value than the cylindrical model (Figure 2a), but only by yielding a nonphysical membrane thickness departing as much as ~25% from the 30nm reference value (Figure 2c). The unconstrained hyperbolic model underestimated the nanopore radius, r0,ref, for all nanopore sizes considered and the absolute error increased as the nanopore radius increased. For the reference nanopores with larger radii, the R-constrained conical-cylindrical model generated a second solution which Figure 2c shows had rather strong conical character and thus in Figure 2a, its best-fit r0 closely matched the conical results. Supplemental Figure S2 shows how changes in r0.ref, lref and bref from the values used here affect whether optimization of the R-constrained conical-cylindrical model gives one or two distinct solutions.
Figure 2.
Nanopore models (see Table 1, and schematics in Figure 1a) were geometry optimized by fitting to the conductance versus electrolyte concentration dependence for reference nanopores of various sizes (r0,ref, lref=11nm, bref=0.19nm−1). The resulting best fit parameters—a) radius and b) % error in radius; c) cylinder height and membrane thickness and d) difference in nanopore radius between the membrane surface and interior—are plotted as a function of reference nanopore radius. Markers in (a) and (b) are for clarity: the spacing does not representing sampling frequency.
For the two-parameter models with no formal cylindrical section, the reference conductance is matched by variation of the limiting radius, r0, and the larger radius at the membrane surface, R. Figure 2d shows the difference R – r0 plotted as a function of the reference nanopore radius. For small nanopores, this difference was substantially less than the fixed 10nm difference used for the conical-cylindrical pore, but eventually grew to exceed this 10nm as the nanopore radius increased. The conical model R – r0 showed the same trend as the hyperbolic model, but the conical r0 showed worse agreement with r0,ref—over 40% error for the smallest nanopores. The conical model R – r0 unsurprisingly took on values close to the fixed 10nm for reference nanopores that produced a second, conical-like optimization of the R = r0 + 10nm-constrained conical-cylindrical model.
Overall, the nanopore models lacking an explicit internal cylindrical section optimized so that r0 < r0.ref. The purely cylindrical models both produced r0 < r0,ref with better radial agreement resulting from diminishment of the nanopore length. Supplemental Figure S3 summarizes all fitting trends by model by superimposing the best-fit nanopore profiles on the profiles of the corresponding reference nanopores. Exact knowledge of the reference nanopore sizes and shapes allowed geometry optimization of the two-parameter models via simultaneous solution of the equations and , without the need to explicitly consider the electrolyte- and nanopore surface-dependent terms K and σ. The results of these optimizations are therefore independent of the particular values of K and σ. In practice, when the experimental nanopore profile is unknown, conductance-based optimization of two-parameter models would require the same minimization of that was performed for the one-parameter models. To illustrate the effect of imperfect knowledge of the nanopore surface charge density, σ, for example, Supplemental Figure S4 presents the optimized r0 and l for repeated geometry optimizations of identical reference pores using inaccurate values for the fit σ.
Discussion
Liebes et al.18 used EELS to characterize the full radial profile of a TEM-fabricated nanopore and introduced an elegant physical model described by only three geometrical parameters: a minimum radius, r0,ref, a cylinder length, lref, and a parameter describing its exponential widening, bref. Combining this profile with the conductance terms in equation 5 allowed accurate calculation of the measured electrolyte-dependent conductance of their pore. We showed, however, through the functional form of equation 5 and Supplemental Figure S1, that measurement of the electrolyte-dependent conductance alone could not uniquely recover the three known geometrical parameters of the exponential-cylindrical nanopore. Variation of the three free exponential-cylindrical geometrical parameters to satisfy the reference conductance returned exponential-cylindrical models with profiles varying continuously from conical-like (l~0) to cylindrical-like (l~L, the membrane thickness) with quite different best fit radii, r0 (Supplemental Figure S1). Despite having generated the reference conductance using an exponential-cylindrical profile, this same profile could not be unambiguously optimized by the conductance data. All two-parameter models quantitatively reproduced, at all electrolyte concentrations, the conductance of the reference, three-parameter exponential-cylindrical nanopore. Each model produced different values for the nanopore size descriptors. The method could therefore determine the nanopore size within the context of the assumed shape, but the method could not determine the true nanopore shape. The ability to accurately calculate the nanopore conductance as a function of electrolyte concentration does not, therefore, guarantee that the correct nanopore shape has been selected or that the size has been determined.
In spite of the deficiencies of common conductance-based nanopore size- and shape-characterizations, the ease with which the measurements can be made in real-time and without alteration to the nanopore experimental setup or operation means that such size determinations are commonly performed, albeit always carefully circumscribed by a statement of the assumed nanopore geometry. It is important, therefore, to explore the effect of the assumption of a nanopore geometry on the accuracy of the best-fit nanopore size and shape. Such a study additionally provides a basis for the necessary eventual inclusion of surface charge in the analytical calculation of molecule-induced current blockages17.
We examined a number of simple, tractable and commonly used models that capture the essential features of experimentally-determined nanopore geometries8,15-18. Constraint of either lref or bref in the reference model inconveniently involves the nanopore radius in an integral that complicates routine optimizations so it was not considered further. We did consider deficient single-parameter models: errors of at most a few percent in the conductance were accompanied by substantially larger errors in r0.
The reference nanopore shape used to calculate the conductance can be broadly described as consisting of a central cylinder with a limiting radius, r0,ref, opening to a larger radius at the membrane surfaces. For the cylindrical extreme of this shape, the correct balance between bulk and surface conductances could only be achieved by a widening of the nanopore and nonphysical thinning of the membrane (Figure 2a,c). For the conical model, the inner radius, r0, was substantially smaller than r0,ref (Figure 2a). For the smallest of the conical fits, the geometry optimization kept the outer radius, R, closer in size to the inner radius, r0, than for the larger nanopores (Figure 2d), thereby imparting greater cylindrical character. Despite exactly describing the conductance at all electrolyte concentrations, neither the conical nor the free-L cylindrical profile adequately captured the global shape or size of the nanopore: either the constriction was too long and too wide, or it was too narrow and too short. For all nanopore sizes considered, though, the r0 optimized using cylindrical and conical models bounded the r0,ref for the exponential-cylindrical model, and the cylindrical model provided an upper bound for all model radii.
The conical-cylindrical model provides a balance between a well-defined, constrained cylindrical section and larger openings at the membrane surfaces. It is moreover consistent with prior shape determinations using electron tomography16 and the general shape of the Liebes et al.18 profile. Guided by typical measured nanopore profiles, we constrained R = r0 + 10nm17 to ensure a finite number of optimized geometries for this model. This left the full amount of parameter flexibility in the constricted cylinder where surface effects are most significant. An optimal description of the constricted cylindrical zone is also critical for quantifying molecule-induced blockages, evaluating the likelihood of molecule-surface interactions and designing molecular constructs used in nanopore force spectroscopy-based studies5-6, for example. The inclusion of an explicit cylindrical section, a prominent feature in the reference nanopore profile, allows the conical-cylindrical model to reproduce the crucial reference nanopore radius, r0,ref, better than any other model. The reference cylinder length, however, is somewhat less ably matched by the conical-cylindrical model. The favorable agreement between r0 and r0,ref instead of between l and lref was a natural outcome of the interplay between surface and bulk terms and the particular form of the experimentally-reasonable constraint R = r0 + 10nm, and was not otherwise artificially selected during the optimization. The conical-cylindrical fitting can, however, be deliberately biased towards a particular result by changing the constraint. Setting r0 = r0,ref and l = lref and solving for the values of R/r0 that satisfy and separately, sets upper and lower bounds (Supplemental Figure S5) on the relation
| (6) |
that can be expanded to first-order to yield the constraint . For bref = 0.19nm−1, this yields R ≃ r0 + 10.5nm, similar to the constraint used throughout this work. Supplemental Figure S6 shows the outcome of this constraint when used to guide the geometry-optimization of the conical-cylindrical model. The agreement between r0 and r0,ref is improved, and the variation in l with nanopore radius is reduced compared to the optimization performed under the constraint R = r0 + 10nm. The slightly more restrictive constraint on R has the added benefit of yielding only a single unique optimized conical-cylindrical geometry for the nanopore sizes considered, rather than the two unique optimized conical-cylindrical geometries shown for the larger nanopores in Figure 2.
The hyperbolic nanopore model is an interesting alternative to the models considered so far. It lacks a well-defined inner cylindrical section, but smoothly varies from an internal constriction to a larger outer radius in a two-parameter model that requires no additional constraints. This model was recently proposed as an improvement on the usual cylindrical model and was used to describe molecule-induced nanopore current blockages and nanopore access resistance in the bulk conductance limit17. The restriction R = r0 +10nm provided greater tractability in Kowalczyk et al.’s implementation17, but in the present report in which the effect of the surface charge was included, the restriction on the outer radius prevents the geometry-optimized model from describing the reference conductance across the entire range of electrolyte concentrations. Given the broad structural similarity between the conical and hyperbolic models and the analogous free parameters, it is not surprising that the difference R – r0 calculated for both models followed a similar trend versus nanopore radius, r0,ref. While the one-parameter R-constrained hyperbolic model could not accurately fit the conductance over the entire electrolyte concentration range, it better-reproduced the radius of larger nanopores than the free-R hyperbolic model that could exactly fit the conductance. This underscores the fundamental challenge of conductance-based determinations of nanopore geometries: the geometric parameters are derived from a fit to the conductance, and the conductance, alone, cannot distinguish between a number of shapes which produce seemingly reasonable but nevertheless inaccurate dimensions. In the absence of knowledge of the true structural parameters or an additional independent measurement characterizing the nanopore, the physical significance and accuracy of these conductance-optimized geometries cannot be evaluated. Nevertheless, in the context of an at least approximately known pore shape, a judiciously chosen model can provide an extremely good estimate of the nanopore dimensions and comparison between a variety of models can provide reasonable limits on those dimensions. While the principal and compelling appeal of conductance-based determinations of nanopore geometries is to leverage the conductance measurement already being performed and to thereby avoid the challenges associated with TEM-based characterization methods, the results in Figure 2a show that an approach combining conductance measurements with traditional TEM imaging could yield considerable insights into the nanopore geometry. For the particular nanopore geometries considered, an accurate TEM measurement of only the limiting nanopore radius would readily allow exclusion of conical, cylindrical and hyperbolic nanopore profiles based on the value of their conductance-based best-fit radii. Reasonable approximations to the remaining nanopore dimensions could then be derived from the limiting radius-restricted conductance-based fit.
Conclusions
The exact determination of nanopore size and shape solely from its electrolyte-dependent conductance is a compelling goal faced with challenges. The foremost challenge is that the form of the electrolyte-dependent conductance places strict limits on the number of geometric parameters that can be optimized. Thus, even an elegant, experimentally derived exponential-cylindrical nanopore profile with only three free parameters18 could not be geometry-optimized by its own electrolyte-dependent conductance without additional constraints. We showed, though, that a host of two-parameter radial profiles could exactly reproduce the nanopore’s conductance, but with the geometry optimization then generating quite different geometries and dimensions. Thus emerges an additional challenge: the ability to accurately reproduce the conductance does not guarantee the accuracy of the nanopore size and shape. Nevertheless, our results show that a judicious choice of an approximate radial profile guided, for example, by knowledge of the initial fabrication conditions, can yield quite good dimensions. For applications where the exact nanopore size and shape must be known to high accuracy, however, more elaborate determinations must be undertaken. Careful TEM-based measurement of only the limiting radius, for example, combined with conductance-modelling can dramatically restrict uncertainty regarding the three-dimensional nanopore size and shape. We have quantified the performance limits of a number of different nanopore models within the greater framework of the constraints of a nanopore measurement coupling nanopore geometry and surface chemistry. More fundamentally, this work has established a number of key principles that will aid in the development of more sophisticated analytical models of nanopore conductance, including those that address molecule-induced nanopore current perturbation.
Supplementary Material
Acknowledgements
This research has been supported by a subcontract of NIH grant R01 HG003248 to URI, and by the University of Rhode Island and the URI Council for Research. We thank the URI Undergraduate Research Initiative: Awards for Scholarly, Creative and Artistic Projects (Spring 2011) for awarding CMF a research fellowship. We thank Yael Liebes for providing clarification of a number of technical details in reference 18, and Elaine Foun for assistance with figure preparation and for helpful discussions. JRD acknowledges the support of NSF CAREER award CBET-1150085.
Footnotes
Supporting Information Available: Plots and figures showing (S1) best-fit parameter ranges arising from the nonunique conductance-based optimization of several exponential-cylindrical nanopores; (S2) regions of parameter values where the conical-cylindrical model geometry optimization returns two different geometries; (S3) the reference and best-fit radial profiles of all nanopores considered in Figure 2; (S4) geometry optimization with inaccurate σ; (S5) analytical expression for constraint on conical-cylindrical R; and (S6) conical-cylindrical optimizations using various constraints. This material is available free of charge via the Internet at http://pubs.acs.org.
REFERENCES
- (1).Branton D, Deamer DW, Marziali A, Bayley H, Benner SA, Butler T, Di Ventra M, Garaj S, Hibbs A, Huang XH, Jovanovich SB, Krstic PS, Lindsay S, Ling XSS, Mastrangelo CH, Meller A, Oliver JS, Pershin YV, Ramsey JM, Riehn R, Soni GV, Tabard-Cossa V, Wanunu M, Wiggin M, Schloss JA. Nat. Biotechnol. 2008;26:1146–1153. doi: 10.1038/nbt.1495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Howorka S, Siwy Z. Chem. Soc. Rev. 2009;38:2360–2384. doi: 10.1039/b813796j. [DOI] [PubMed] [Google Scholar]
- (3).Ma L, Cockroft SL. ChemBioChem. 2010;11:25–34. doi: 10.1002/cbic.200900526. [DOI] [PubMed] [Google Scholar]
- (4).Bayley H, Martin CR. Chem. Rev. 2000;100:2575–2594. doi: 10.1021/cr980099g. [DOI] [PubMed] [Google Scholar]
- (5).Tabard-Cossa V, Wiggin M, Trivedi D, Jetha NN, Dwyer JR, Marziali A. ACS Nano. 2009;3:3009–3014. doi: 10.1021/nn900713a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Tropini C, Marziali A. Biophys. J. 2007;92:1632–1637. doi: 10.1529/biophysj.106.094060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Li J, Stein D, McMullan C, Branton D, Aziz MJ, Golovchenko JA. Nature. 2001;412:166–169. doi: 10.1038/35084037. [DOI] [PubMed] [Google Scholar]
- (8).Wu M-Y, Smeets RMM, Zandbergen M, Ziese U, Krapf D, Batson PE, Dekker NH, Dekker C, Zandbergen HW. Nano Lett. 2009;9:479–484. doi: 10.1021/nl803613s. [DOI] [PubMed] [Google Scholar]
- (9).Storm AJ, Chen JH, Ling XS, Zandbergen HW, Dekker C. Nature Materials. 2003;2:537–540. doi: 10.1038/nmat941. [DOI] [PubMed] [Google Scholar]
- (10).Kim MJ, Wanunu M, Bell DC, Meller A. Adv. Mater. 2006;18:3149. + [Google Scholar]
- (11).Nam S-W, Rooks MJ, Kim K-B, Rossnagel SM. Nano Lett. 2009;9:2044–2048. doi: 10.1021/nl900309s. [DOI] [PubMed] [Google Scholar]
- (12).Yang J, Ferranti DC, Stern LA, Sanford CA, Huang J, Ren Z, Qin L-C, Hall AR. Nanotechnology. 2011;22:285310. doi: 10.1088/0957-4484/22/28/285310. [DOI] [PubMed] [Google Scholar]
- (13).Vlassiouk I, Apel PY, Dmitriev SN, Healy K, Siwy ZS. Proc. Natl. Acad. Sci. U. S. A. 2009;106:21039–21044. doi: 10.1073/pnas.0911450106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).van den Hout M, Hall AR, Wu MY, Zandbergen HW, Dekker C, Dekker NH. Nanotechnology. 2010;21:115304. doi: 10.1088/0957-4484/21/11/115304. [DOI] [PubMed] [Google Scholar]
- (15).Venkatesan BM, Dorvel B, Yemenicioglu S, Watkins N, Petrov I, Bashir R. Adv. Mater. 2009;21:2771–2776. doi: 10.1002/adma.200803786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Kim MJ, McNally B, Murata K, Meller A. Nanotechnology. 2007;18 [Google Scholar]
- (17).Kowalczyk SW, Grosberg AY, Rabin Y, Dekker C. Nanotechnology. 2011;22:315101. doi: 10.1088/0957-4484/22/31/315101. [DOI] [PubMed] [Google Scholar]
- (18).Liebes Y, Drozdov M, Avital YY, Kauffmann Y, Rapaport H, Kaplan WD, Ashkenasy N. Appl. Phys. Lett. 2010;97:223105. [Google Scholar]
- (19).Ayub M, Ivanov A, Instuli E, Cecchini M, Chansin G, McGilvery C, Hong J, Baldwin G, McComb D, Edel JB, Albrecht T. Electrochim. Acta. 2010;55:8237–8243. [Google Scholar]
- (20).Wharton JE, Jin P, Sexton LT, Horne LP, Sherrill SA, Mino WK, Martin CR. Small. 2007;3:1424–1430. doi: 10.1002/smll.200700106. [DOI] [PubMed] [Google Scholar]
- (21).DeBlois RW, Bean CP. Rev. Sci. Instrum. 1970;41:909–916. [Google Scholar]
- (22).Stein D, Kruithof M, Dekker C. Phys. Rev. Lett. 2004;93:035901. doi: 10.1103/PhysRevLett.93.035901. [DOI] [PubMed] [Google Scholar]
- (23).Daiguji H, Yang P, Majumdar A. Nano Lett. 2004;4:137–142. [Google Scholar]
- (24).Karnik R, Fan R, Yue M, Li D, Yang P, Majumdar A. Nano Lett. 2005;5:943–948. doi: 10.1021/nl050493b. [DOI] [PubMed] [Google Scholar]
- (25).Karnik R, Castelino K, Fan R, Yang P, Majumdar A. Nano Lett. 2005;5:1638–1642. doi: 10.1021/nl050966e. [DOI] [PubMed] [Google Scholar]
- (26).Smeets RMM, Keyser UF, Krapf D, Wu M-Y, Dekker NH, Dekker C. Nano Lett. 2006;6:89–95. doi: 10.1021/nl052107w. [DOI] [PubMed] [Google Scholar]
- (27).Ho C, Qiao R, Heng JB, Chatterjee A, Timp RJ, Aluru NR, Timp G. Proc. Natl. Acad. Sci. U. S. A. 2005;102:10445–10450. doi: 10.1073/pnas.0500796102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Schoch RB. Appl. Phys. Lett. 2005;86:253111. [Google Scholar]
- (29).Behrens SH, Grier DG. J. Chem. Phys. 2001;115:6716–6721. [Google Scholar]
- (30).van der Heyden FHJ, Stein D, Dekker C. Phys. Rev. Lett. 2005;95:116104. doi: 10.1103/PhysRevLett.95.116104. [DOI] [PubMed] [Google Scholar]
- (31).Chang H, Kosari F, Andreadakis G, Alam MA, Vasmatzis G, Bashir R. Nano Lett. 2004;4:1551–1556. [Google Scholar]
- (32).Siwy Z, Kosińska ID, Fuliński A, Martin CR. Phys. Rev. Lett. 2005;94:048102. doi: 10.1103/PhysRevLett.94.048102. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.