Random effects coefficient of determination for mixed and meta-analysis models

Abstract

The key feature of a mixed model is the presence of random effects. We have developed a coefficient, called the random effects coefficient of determination, $R_r^2$, that estimates the proportion of the conditional variance of the dependent variable explained by random effects. This coefficient takes values from 0 to 1 and indicates how strong the random effects are. The difference from the earlier suggested fixed effects coefficient of determination is emphasized. If $R_r^2$ is close to 0, there is weak support for random effects in the model because the reduction of the variance of the dependent variable due to random effects is small; consequently, random effects may be ignored and the model simplifies to standard linear regression. The value of $R_r^2$ apart from 0 indicates the evidence of the variance reduction in support of the mixed model. If random effects coefficient of determination is close to 1 the variance of random effects is very large and random effects turn into free fixed effects—the model can be estimated using the dummy variable approach. We derive explicit formulas for $R_r^2$ in three special cases: the random intercept model, the growth curve model, and meta-analysis model. Theoretical results are illustrated with three mixed model examples: (1) travel time to the nearest cancer center for women with breast cancer in the U.S., (2) cumulative time watching alcohol related scenes in movies among young U.S. teens, as a risk factor for early drinking onset, and (3) the classic example of the meta-analysis model for combination of 13 studies on tuberculosis vaccine.

1 Introduction and motivation

The linear mixed effects model has become a major tool for the analysis of clustered/correlated data. Several books have been published recently on the topic including Vonesh and Chin-chilli (1997), Brown and Prescott (1999), Demidenko (2004), Jiang (2007), and McCulloch et al. (2008), among others. In many applications, the mixed model is applied to the analysis of longitudinal data, e.g. Verbeke and Molenberghs (2000) and Diggle et al. (2002). Several books focus exclusively on software for mixed models, e.g. Pinheiro and Bates (2000) and Littell et al. (2006).

Despite a plethora of publications on this topic, a fundamental question remains difficult to answer, Why fit a mixed model, or equivalently, why random effects? Although employing random effects models has become trendy, these models have disadvantages and may add unneccesary complexity to the analysis. It would be very desirable to have a measure/coefficient by which one could judge whether fitting a mixed model was appropriate versus a traditional linear regression model. If that coefficient was close to zero, one might say that the data may be analyzed by standard linear regression because there are no random effects, and when that coefficient departs from 0, the presence of random effects is strong and mixed model would be valid. The goal of the present paper is to introduce such a coefficient, which will be called the random effects coefficient of determination. This coefficient reflects the reduction of the variance of the dependent variable due to the presence of random effects.

Several other measures of explained variance in the framework of linear mixed model have been developed previously in the literature including Snijders and Bosker (1994), Vonesh and Chinchilli (1997), Xu (2003), Gelman and Pardoe (2006). Those measures resemble the coefficient of determination as they reflect the goodness-of-fit with fixed effects, as emphasized in a recent paper by Edwards et al. (2008). Specifically, the fixed effects coefficient of determination in the framework of linear mixed effects model y_i = X_iβ + Z_ib_i + ε_i is a straightforward generalization of the classical coefficient of determination,

$$R_f^2=1-\frac{{\sum }_{i=1}^N({\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\widehat{\mathit{\beta }})\prime {\widehat{\mathbf{\text{V}}}}_i^{-1}({\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\widehat{\mathit{\beta }})}{{\sum }_{i=1}^N({\mathbf{\text{y}}}_i-{\overline{y}}_i{\mathbf{1}}_i)\prime {\widehat{\mathbf{\text{V}}}}_i^{-1}({\mathbf{\text{y}}}_i-{\overline{y}}_i{\mathbf{1}}_i)},$$ (1)

where N is the number of clusters, β̂ is the maximum likelihood estimator of fixed effects, and V̂_i is an estimate of the intra cluster covariance matrix (it is assumed that fixed effects contain an intercept term), ȳ_i is the average value of the dependent variable in cluster i, and 1_i is the vector-column of ones. Similarly to the classical coefficient of determination, we interpret $R_f^2$ as the proportion of the variance of the dependent variable, y explained by predictors X.

The goal of this paper is to develop a similar figure of merit for random effects, the random effects coefficient of determination, $R_r^2$. Such coefficient should take larger values for larger values of the variance of the random effect but on a fixed scale, so that comparisons can be made across mixed models. While (1) shows the strength of fixed effects, $R_r^2$ characterizes the strength of random effects in a linear mixed model. The measures $R_f^2$ and $R_r^2$ reflect the strength of a linear mixed effects from different perspective and we believe they should be a part of the software output every time a linear mixed effects model is estimated.

The organization of the paper is as follows. In the next section we introduce the notation and lay out basic facts about linear mixed model. In Section 3, we introduce the F-test for the presence of random effects, which will be used in the next section to define the random effects coefficient of determination. We derive explicit formulae for three special cases of mixed model: random intercept, growth curve, and meta-analysis models. Finally, in Section 5, we illustrate the computation of $R_r^2$ with three examples: In the first example, we use mixed model with random intercepts that represent the state-specific travel time of breast cancer patients to cancer centers in the U.S. In the second example, we demonstrate the validity of the growth curve model applied to the longitudinal data on alcohol movie watching among young adolescents and its association with drinking initiation. In the third example, we show the application of $R_r^2$ to the meta-analysis model using the classic data set on 13 studies with the overall effect of a tuberculosis vaccine.

2 Preliminaries

In this paper, we use the linear mixed effects (LME) model

$${\mathbf{\text{y}}}_i={\mathbf{\text{X}}}_i\mathit{\beta }+{\mathbf{\text{Z}}}_i{\mathbf{\text{b}}}_i+{\mathit{\varepsilon }}_i,$$ (2)

where i indicates the cluster (subject or unit); y_i is the n_i × 1 vector of observations of the dependent variable; X_i is the n_i × m matrix of fixed effects variables/covariates; β is the m × 1 vector of unknown fixed effects coefficients; Z_i is the n_i × k design matrix of random effects; b_i is the k × 1 vector of random effects with zero mean and unknown covariance matrix σ²D; ε_i is the error term with zero mean and covariance matrix σ²I, i = 1,2,…, N (number of clusters). We assume that the observations between clusters do not correlate, but do correlate within clusters due to the presence of random effects. Also, it is assumed that random vectors are normally distributed, b_i ∼ N(0,σ²D) and ε_i ∼ N(0,σ²I). To avoid degeneration, we shall assume that matrix ${\sum }_{i=1}^N{\mathbf{\text{X}}}_i^{\prime }{\mathbf{\text{X}}}_i$ is nonsingular (boldface is used for vectors and matrices).

If matrix D is known, the generalized linear least squares (GLS) estimator of β takes the form

$${\widehat{\mathit{\beta }}}_{\mathit{\text{GLS}}}={\left[\sum _{i=1}^N{\mathbf{\text{X}}}_i^{\prime }{(\mathbf{\text{I}}+{\mathbf{\text{Z}}}_i{\mathbf{\text{DZ}}}_i^{\prime })}^{-1}{\mathbf{\text{X}}}_i\right]}^{-1}\left[\sum _{i=1}^N{\mathbf{\text{X}}}_i^{\prime }{(\mathbf{\text{I}}+{\mathbf{\text{Z}}}_i{\mathbf{\text{DZ}}}_i^{\prime })}^{-1}{\mathbf{\text{y}}}_i\right],$$ (3)

where ${\mathbf{\text{V}}}_i=\mathbf{\text{I}}+{\mathbf{\text{Z}}}_i{\mathbf{\text{DZ}}}_i^{\prime }$ is the intra cluster covariance matrix. If random effects are not present (the variances of random effects are zero), the LME model (2) reduces to a linear regression

$${\mathbf{\text{y}}}_i={\mathbf{\text{X}}}_i\mathit{\beta }+{\mathit{\varepsilon }}_i.$$ (4)

Then, since errors do not correlate, we can combine data over i and apply ordinary least squares, which produces an efficient estimator of the fixed effects coefficients. Alternatively, we can derive this estimator by letting D = 0 in (3), β̂_LS, which may be called the zero random effects estimator. The least squares (LS) estimator yields the residual sum of squares

$$S_{LS}={\sum _{i=1}^N\Vert {\mathbf{\text{y}}}_i={\mathbf{\text{X}}}_i{\widehat{\mathit{\beta }}}_{LS}\Vert }^2.$$ (5)

A more interesting extreme situation is when the variances of random effects become large. Specifically, we are interested in the limit of β̂_GLS when matrix D goes to infinity. That is, we set D = dI, where I is the k × k identity matrix, and let d→∞. Omitting some algebra, we arrive at the estimator

$${\widehat{\mathit{\beta }}}_{\infty }={\left[\sum _{i=1}^N{\mathbf{\text{X}}}_i^{\prime }(\mathbf{\text{I}}-{\mathbf{\text{Z}}}_i{\mathbf{\text{Z}}}_i^{+}){\mathbf{\text{X}}}_i\right]}^{+}\left[\sum _{i=1}^N{\mathbf{\text{X}}}_i^{\prime }(\mathbf{\text{I}}-{\mathbf{\text{Z}}}_i{\mathbf{\text{Z}}}_i^{+}){\mathbf{\text{y}}}_i\right],$$ (6)

where ⁺ means the Moore-Penrose generalized matrix inverse. Note that it is necessary to use the generalized matrix inverse operation because matrix Z_i may be not of full rank. We call this estimator the fixed effects estimator because (6) can be viewed as the least squares estimate from the linear regression

$${\mathbf{\text{y}}}_i={\mathbf{\text{X}}}_i\mathit{\beta }+{\mathbf{\text{Z}}}_i{\mathbf{\text{b}}}_i+{\mathit{\varepsilon }}_i,$$ (7)

treating {b_i} as fixed and unknown, similarly to β, with the minimal sum of squares

$$S_{min}=\underset{\mathit{\beta },{\mathbf{\text{b}}}_1,\dots ,{\mathbf{\text{b}}}_N}{min}\sum _{i=1}^N{\Vert {\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\mathit{\beta }-{\mathbf{\text{Z}}}_i{\mathbf{\text{b}}}_i\Vert }^2.$$ (8)

Clearly, S_min ≤ S_LS. Practically, we obtain this residual sum of squares by running linear regression

$$\text{y}=\mathbf{\text{W}}\mathrm{\gamma }+\mathit{\varepsilon }$$

with combined data

$$\mathbf{\text{y}}=\left[\begin{array}{c}{\mathbf{\text{y}}}_1\\ {\mathbf{\text{y}}}_2\\ {\mathbf{\text{y}}}_N\end{array}\right],\mathbf{\text{W}}=\left[\begin{array}{ccccc}{\mathbf{\text{X}}}_1& {\mathbf{\text{Z}}}_1& \mathbf{0}& \cdots & \mathbf{0}\\ {\mathbf{\text{X}}}_2& \mathbf{0}& {\mathbf{\text{Z}}}_2& \mathbf{0}& \mathbf{0}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ {\mathbf{\text{X}}}_N& \cdots & \mathbf{0}& \mathbf{0}& {\mathbf{\text{Z}}}_N\end{array}\right],\mathrm{\gamma }=\left[\begin{array}{c}\mathit{\beta }\\ {\mathbf{\text{b}}}_1\\ ⋮\\ {\mathbf{\text{b}}}_N\end{array}\right],$$ (9)

assuming that

$$\mathit{\text{rank}}(\mathbf{\text{W}})>m.$$ (10)

This is the reason we call (6) the fixed effects estimator. Alternatively, one can compute S_min as the residual sum of squares in the OLS regression after regressing the residuals from regression of y_i and X_i on Z_i in each cluster on X.

For finite matrix D, the GLS for β and random effects, {b_i,i = 1,2,…,N} are found from the penalized least squares

$$\underset{\mathit{\beta },{\mathbf{\text{b}}}_1,\dots ,{\mathbf{\text{b}}}_N}{min}\sum _{i=1}^N\left[{\Vert {\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\mathit{\beta }-{\mathbf{\text{Z}}}_i{\mathbf{\text{b}}}_i\Vert }^2+{\mathbf{\text{b}}}_i^{\prime }{\mathbf{\text{D}}}^{-1}{\mathbf{\text{b}}}_i\right].$$

Some algebra shows that the solution to this optimization problem is (6) and the estimate of the ith random effect is

$${\widehat{\mathbf{b}}}_i={({\mathbf{\text{Z}}}_i^{\prime }{\mathbf{\text{Z}}}_i+{\mathbf{\text{D}}}^{-1})}^{-1}{\mathbf{\text{Z}}}_i^{\prime }{\mathbf{\text{r}}}_i,$$ (11)

where r_i = y_i − X_iβ̂_GLS is the residual vector for the ith cluster.

It is easy to see that we come to the same limit sum of squares (8) assuming that D =dD₀, where D₀ is any positive definite fixed matrix. Indeed, we can express D₀ = TT′, and letting U_i = Z_iT, reduce the problem to the previous case with D =dI. Since U_ib_i = Z_i(Tb_i) and b_i is unrestricted, the minimal sum of squares remains the same (8) as in the case D₀ = I.

Now we are ready to introduce the F-test which is the basis of our random effects coefficient of determination. While the fixed effects coefficient of determination (1) is a straightforward generalization of the classical regression model, the random effects coefficient of determination requires more insight into the nature of the mixed model.

3 The F-test for the presence of random effects

In order to prove that the LME model does not reduce to standard linear regression, we need to test the hypothesis

$$H_0:\mathbf{\text{D}}=\mathbf{0}.$$ (12)

The justification of our test below is as follow: The two sums of squares (5) and (8) represent two extreme case with D = 0 and D = ∞. If D ≠ 0, it is plausible to expect that the latter sum of squares is much smaller than the former one. In order to construct the test for (12), we recall the F-test for linear regression when testing the hypothesis on a linear combination of parameters H₀ : Cβ = 0,

$$F=\frac{(S_0-S_{min})/q}{S_{min}/(n-m)},$$ (13)

where S₀ and S_min are residual sums of squares under restrictions and with no restriction, q is the number of restrictions, n is the number of observations, and m is the dimension of vector β. In effect, we apply the same F-test to regression (7) to test whether the coefficients {b_i, i = 1, 2,…, N} are zero. Specifically, the following fact holds (Demidenko, 2004, p. 137).

Theorem 1

For linear mixed model (2) under the null hypothesis (12), we have

$$\frac{(S_{LS}-S_{min})/(r-m)}{S_{min}/(N_T-r)}\sim F(r-m,N_T-r),$$ (14)

where r = rank(W) and $N_T={\sum }_{i=1}^N{n}_i$.

This test, applied to single random effect variance, has deep roots in ANOVA and the variance components literature: Seely and El-Bassiouni (1983), Searle et al. (1992), Mathew and Sinha (1992), Khuri et al. (1998), starting from a pioneering work of Wald (1947). A comprehensive comparison study is found in a recent paper Scheipl et al. (2008). Note that (a) test (14) is exact, it yields the exact significance level, and (b) it applies to multivariate random effects. To the best of our knowledge, this test is not a part of existing software on mixed models, including SAS and S-Plus. This test is the basis for our random effects coefficient of determination.

4 Random effects coefficient of determination

As follows from the previous section, S_LS and S_min are the two extreme values of the residual sum of squares (8); the former corresponds to when random effects, are zero (b_i = 0), and the latter corresponds to when there is no restriction on random effects, or in other words, random effects are fixed effects, S_min ≤ S_LS. When the mixed model is estimated we obtain estimates of random effects, b̂_i with the sum of squares

$$S_{MM}=\sum _{i=1}^N{\Vert {\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i{\widehat{\mathit{\beta }}}_{\mathit{\text{GLS}}}-{\mathbf{\text{Z}}}_i{\widehat{\mathbf{\text{b}}}}_i\Vert }^2.$$

We use subscript MM to indicate that the sum of squares is computed from the mixed model. Apparently, S_min and S_LS are the lower and upper bounds of sum of squares in the estimated mixed model, S_min ≤ S_MM ≤ S_LS.

We associate these three residual sum of squares with conditional variance similarly to regression analysis. Apparently, S_MM/N_T can be viewed as the variance of y conditional on the estimated random effects. Then S_LS/N_T is the highest and S_LS/N_T is the lowest variance of y with (S_MM – S_min)/N_T as the reduction of the conditional variance due to the presence of the random effects. Finally, the random effects coefficient of determination for mixed model is defined as the reduction of the conditional variance of y with respect to the maximum reduction, (S_LS – S_min)/N_T, namely,

$$R_r^2=1-\frac{S_{MM}-S_{min}}{S_{LS}-S_{min}},$$ (15)

or alternatively,

$$R_r^2=\frac{S_{LS}-S_{MM}}{S_{LS}-S_{min}}.$$ (16)

This coefficient lies in the interval from 0 to 1 under assumption (10), see Appendix for a rigorous proof. If $R_r^2=1$ then S_MM = S_min so that random and fixed effects coincide (D = ∞). If $R_r^2=0$ then S_LS = S_MM and random effects are not present (matrix D = 0). We interpret $R_r^2$ as the proportion of the reduction of the conditional variance of the dependent variable on the scale of maximum reduction due to random effects.

Below, we illustrate the computation of the random effects coefficient of determination with three popular special cases of the LME model and provide closed-form solutions.

4.1 Random intercept model

This model is a special case of the linear mixed model with one random effect: It is assumed that the intercepts are random and deviations of the cluster-specific intercepts from the common intercept are independent and identically distributed with zero mean and variance σ²d, where d is the relative variance of the random intercept. Mathematically, the random intercept model is expressed as a system of linear regression with a cluster-specific intercept,

$${\mathbf{\text{y}}}_i={\mathbf{\text{X}}}_i\mathit{\beta }+b_i{\mathbf{1}}_i+{\mathit{\varepsilon }}_i,$$

where b_i ∼ N(0,σ²d), assuming that all elements in the first column of matrix X_i are 1 (the common intercept is the first element of vector β), and 1_i is the n_i × 1 vector of ones, i = 1, 2,…, N. Omitting some algebra, we derive

$$S_{min}={\sum _{i=1}^N\Vert {\stackrel{\sim }{\mathbf{\text{y}}}}_i-{\stackrel{\sim }{\mathbf{\text{X}}}}_i\stackrel{\sim }{\mathit{\beta }}\Vert }^2,$$ (17)

where ‘tilde’ means deviation from the mean (centerized data), ỹ_i = y_i − 1_iȳ_i and ${\stackrel{\sim }{\mathbf{\text{X}}}}_i={\mathbf{\text{X}}}_i-{\mathbf{1}}_i{\overline{\mathbf{x}}}_i^{\prime }$ and

$$\stackrel{\sim }{\mathit{\beta }}={\left(\sum _{i=1}^N{\stackrel{\sim }{\mathbf{\text{X}}}}_i^{\prime }{\stackrel{\sim }{\mathbf{\text{X}}}}_i\right)}^{-1}\left(\sum _{i=1}^N{\stackrel{\sim }{\mathbf{\text{X}}}}_i^{\prime }{\stackrel{\sim }{\mathbf{\text{y}}}}_i\right).$$ (18)

Note that X̃_i is a n_i × (m − 1) matrix, so only slope coefficients are computed in (18) because intercepts are eliminated. Alternatively, S_min could be computed using standard linear regression with dummy intercepts. Finally, for the random intercept model,

$$R_r^2=\frac{{\sum }_{i=1}^N{\Vert {\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\widehat{\mathit{\beta }}\Vert }^2-S_{MM}}{{\sum }_{i=1}^N{\Vert {\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\widehat{\mathit{\beta }}\Vert }^2-{\sum }_{i=1}^N{\Vert {\stackrel{\sim }{\mathbf{\text{y}}}}_i-{\stackrel{\sim }{\mathbf{\text{X}}}}_i\stackrel{\sim }{\mathit{\beta }}\Vert }^2},$$

where S_MM is computed after the mixed model is estimated by restricted or standard maximum likelihood (procedure mixed or lme in S-Plus/R). It is easy to see that the rank of matrix W for the random intercept model is r = N + m.

4.2 Growth curve model

The growth curve model is another popular mixed model, which can be reduced to (2) letting X_i = Z_iA_i, where A_i is a k × m fixed matrix. We assume here that matrices {Z_i, i = 1, 2,…, N} have full rank. In this case, β_i = A_iβ − b_i and b_i are not restricted and therefore

$$S_{min}={\sum _{i=1}^N\Vert {\mathbf{\text{y}}}_i-{\mathbf{\text{Z}}}_i{\widehat{\mathit{\beta }}}_i\Vert }^2,$$

where

$${\widehat{\mathit{\beta }}}_i={({\mathbf{\text{Z}}}_i^{\prime }{\mathbf{\text{Z}}}_i)}^{+}{\mathbf{\text{Z}}}_i^{\prime }{\mathbf{\text{y}}}_i$$

is the cluster-specific LS estimator. Thus, finally,

$$R_r^2=\frac{{\sum }_{i=1}^N{\Vert {\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\widehat{\mathit{\beta }}\Vert }^2-S_{MM}}{{\sum }_{i=1}^N{\Vert {\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\widehat{\mathit{\beta }}\Vert }^2-{\sum }_{i=1}^N{\Vert {\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i{\stackrel{\sim }{\mathit{\beta }}}_i\Vert }^2},$$

where β̂_i is the LS estimate from cluster i. For this model r = Nm.

4.3 Meta-analysis model

The meta-analysis model became a very popular statistical model for combination of studies to improve statistical power for detection of the overall treatment effect. Usually the metaanalysis model is formulated as a simple random-effect model

$$\begin{array}{cc}{y}_i=\mu +b_i+{\mathit{\varepsilon }}_i,& i=1,2,\dots ,n,\end{array}$$ (19)

where y_i the variable of interest, say, log odds ratio of the treatment effect from the ith study (we shall use this interpretation hereafter), μ is the overall treatment effect, b_i is the random effect that reflects the studies' heterogeneity, and ε_i is the error term due to uncertainty of y_i estimation from study i (Demidenko, 2004, chapter 5; Borenstein et al., 2009). The estimates y_i and their variances $\mathit{\text{var}}({\mathit{\varepsilon }}_i)={\sigma }_i^2$ are known but the variance of the random effect, var(b_i) = τ² are not and is subject of estimation along with μ. We associate τ² with heterogeneity of the studies: if τ² = 0 the only variation factor is due to imprecision within the study; if τ² is significantly apart from 0 studies are heterogeneous. The difference with the general mixed model described in Section 2 is that the variances of ε_i are not equal and given so we have to consider the weighted least squares instead of ordinary least squares. If the heterogeneity variance τ² is fixed the estimates of the common treatment and random effects are found from minimization of the penalized weighted least squares

$$S({\tau }^2)=\sum _{i=1}^n\frac{{(y_i-\mu -b_i)}^2}{{\sigma }_i^2}+\frac{1}{{\tau }^2}\sum _{i=1}^n{b}_i^2,$$

that yields

$$\begin{array}{cc}\widehat{\mu }({\tau }^2)=\frac{{\sum }_{i=1}^n{y}_i/({\tau }^2+{\sigma }_i^2)}{{\sum }_{i=1}^{n}1/({\tau }^2+{\sigma }_i^2)},& {\widehat{b}}_i({\tau }^2)=\frac{{\tau }^2}{{\tau }^2+{\sigma }_i^2}(y_i-\widehat{\mu })\end{array}$$ (20)

with

$$S_{min}({\tau }^2)=\sum _{i=1}^n\frac{{(y_i-\widehat{\mu }-({\tau }^2))}^2}{{\tau }^2+{\sigma }_i^2}.$$

When τ² = 0 we have μ̂(0) = ỹ, b̂_i (0) = 0 and the weighted least squares gives

$$S_{W\mathit{\text{LS}}}=\sum _{i=1}^n\frac{{(y_i-\stackrel{\sim }{y})}^2}{{\sigma }_i^2},$$

where $\stackrel{\sim }{y}=(\sum y_i/{\sigma }_i^2){(\sum 1/{\sigma }_i^2)}^{-1}$ is the weighted average. When τ²→ ∞ we have μ̂(∞) = ȳ, b̂_i(∞) = y_i − y and S_min = 0. Following formula (15) we obtain

$$R_r^2=1-\frac{S_{MM}}{S_{W\mathit{\text{LS}}}},$$ (21)

where S_MM = S_min(τ̂²) and τ̂² is an estimate of τ². This estimate is usually obtained using method of moments or maximum likelihood (DerSimonian and Laird, 1986; DerSimonian and Kacker, 2007). We prove in the Appendix that $0\le R_r^2\le 1$. We interpret $R_r^2$ for the metaanalysis model as the proportion of conditional variance of y explained by the heterogeneity of studies reflected in the random effect. When studies are homogeneous (the heterogeneity variance is zero) $R_r^2=0$. When studies are highly heterogeneous $R_r^2$ is close to 1. Note that the fixed effects coefficient of determination for the meta-analysis model does not make sense.

5 Examples

We illustrate the application of the random effects coefficient of determination with three examples. The random intercept model is used in the first example to account for variation in breast cancer patients travel time to the nearest National Cancer Institute (NCI) Cancer Center. In this example, we have a relatively small number of clusters (states) and a large number of individuals in each cluster. In the second example, we model the cumulative time of watching alcohol movie scenes as a predictor of drinking initiation among young adolescents. This is an example of longitudinal data analysis where there are a few observations in each cluster (4 surveys), but many clusters/individuals (about five thousand). In both examples, the validity of the mixed model is under question and we address it through computation of $R_r^2$. The third example illustrates the random effects coefficient of determination with a meta-analysis of 13 studies on tuberculosis vaccine previously used in several publications.

5.1 Travel time to the nearest NCI Cancer Center

Access to specialized cancer care is an important issue of national concern given that cancer is the leading cause of death in people under age 85, Twombly (2005). Of particular importance is the analysis of patients' geographic access to cancer centers expressed in terms of travel time, Onega et al. (2008). Understanding the differences in travel time may help in efficient allocation of existing resources and in the development of new cancer centers. In this example, we analyze travel time (TT) in minutes for Medicare breast cancer patients (a comprehensive description of the data is found in the above reference); the total number of observations/patients N_T = 47,383 from 46 states. Special attention is paid to racial differences when it comes to cancer treatment accessibility. To identify the differences, five races were modeled via a dummy variable approach: Caucasian, African American, Asian, Hispanic, Native American, other/unknown (Caucasian is the reference). It is suspected that TT varies significantly across states, so the random (state-specific) intercept model seems appropriate here. Travel time is heavily skewed to the right, so log transformation is used to reduce the bias towards long travel. For these data there are N = 46 clusters and the number of variables in the model is m = 8 (without intercept). Besides racial factors, three other variables were chosen to explain variation in TT: age of woman, breast cancer stage expressed on the nominal scale from 0 to 4, and whether breast surgery occurred (1) or not (0).

Three methods of estimation are used: (a) ordinary least squares, (b) fixed effects least squares, (c) a linear mixed (random intercept) model; the results are presented in Table 1. The sum of squares for the linear mixed model was computed by

Table 1. Estimation of TT model by three methods.

Variable	(a) OLS, β̂		(b) Fixed Effects, β̃		(c) LME, β̂ML
	Coefficient	SE	Coefficient	SE	Coefficient	SE
Intercept	4.3291	0.0624			4.8851	0.1334
Age	-0.0058	0.0007	-0.00418	0.0005	-0.00418	0.0005
African American	-0.2657	0.0194	-0.36309	0.0146	-0.36307	0.0146
Asian	-0.4990	0.0518	-0.34313	0.0379	-0.34321	0.0379
Hispanic	-0.8740	0.0445	-0.61353	0.0327	-0.61376	0.0327
Native American	-0.2863	0.0448	-0.09938	0.0329	-0.09947	0.0329
Race unknown	0.6248	0.1364	0.56905	0.0099	0.56898	0.0099
BC stage	0.0098	0.0023	0.00886	0.0017	0.00883	0.0017
Surgery	0.0564	0.0221	0.03700	0.0162	0.03695	0.0161
Sum of Squares	SOLS = 56278		Smin = 29864		SMM = 29867

$$S_{MM}={\sum \Vert {\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i{\widehat{\mathit{\beta }}}_{ML}-{\widehat{b}}_i\Vert }^2,$$

where b̂_i is the estimated random effect, or deviation of the random intercept from its common value (function lme was used in S-Plus). As follows from Table 1, the estimates in methods (b) and (c) are very close; the estimates of the standard deviations of the error term and random intercept are σ̂_ε = 0.79 and σ̂_a = 0.82 which imply $\widehat{d}={\sigma }_{\mathit{\varepsilon }}^2/{\widehat{\sigma }}_{\alpha }$ and ρ = 0.52 indicating that the variation across states in comparable with the variation around the model.

We see considerable differences of TT across races. For example, using the LME model, Asian women spend (1 − e^−0.61376) × 100% = 46% less time on travel than White women. On the other hand, Native American women spend considerably more time. We attribute these differences to where the majority of women live: Asian women live in urban areas while Native Americans live in remote parts of the country. Neither breast cancer stage nor surgery contribute much to TT. We compute the national average of the travel time in hours for a White woman of age 80 as e^{4.9035–0.00418×80}/60 = 1.6 (1 hour 40 min) based on the estimate from LME model.

Now we turn our attention to testing of the validity of the LME model. The F-test (14) gives

$$F=\frac{(55278-29864)/(54-8)}{29864/(47383-54)}=876,$$

with the critical value 1.36—the random effect is highly significant. The random effects coefficient of determination is

$$R_r^2=\frac{56278-29867}{56278-29864}=\mathrm{0.999.}$$

We conclude that this model can be estimated by the dummy variable approach where each state has its own intercept term. Indeed, as follows from Table 1, the difference of estimates between fixed effects and random effects approaches are practically equivalent.

We present the differences in TT across the U.S. states graphically in Figure 1. As we see, there are substantial differences across states. For example, a white woman of 80 years spends only 30 minutes on travel to an NCI Cancer Center in New York state. On the other hand, this woman would spend more than 9 hours living in Montana.

Figure 1.

State-specific averages estimated from the random intercept model. There are substantial differences in TT across states, $R_r^2=0.999$. The mixed model reduces to the dummy variable approach.

5.2 Alcohol drinking initiation in young adolescents

Early onset of alcohol use, when drinking begins in early adolescence, is a cause of many behavioral and life problems, including reckless driving, school dropout, and accidental death (DeWit, 2000; Hingson et al., 2000). Several studies have confirmed that early drinkers also have a higher risk of developing alcoholism in adulthood, Kraus et al. (2000). Recently researchers have drawn a parallel between early drinking and alcohol depiction in movies, Sargent et al. (2006). In this section, we apply a linear mixed model to analyze timed exposure to movie alcohol depiction using data described in the above paper. More than five thousand U.S. teens were surveyed through telephone interviews approximately every 8 months over two years (four waves of interviews, kids of age from 10 to 14 at the baseline). Covariates include parents' education, family income, whether the teen owned branded merchandise and whether he/she had ever drunk alcohol. The teen were interviewed at home: to ensure privacy and honesty of answers to sensitive questions, teens were able to key in their answers using the telephone pad rather than answering by voice. Special attention was given to measuring exposure to alcohol depiction in movies. Children were asked what popular movies they have seen from a list of the most popular recent movies. A team of researchers at Dartmouth quantified the length of the alcohol scenes in those movies and the time of exposure to movie alcohol has been reconstructed for each adolescent over four waves.

We hypothesize that the cumulative exposure to alcohol scenes in movies is one of the factors contributing to early drinking. As in the previous example, the dependent variable is heavily skewed, so the log transformation is used. The log cumulative movie alcohol time was modeled as a function of age adjusting for the following binary variables: drinking status (Drinker=1, otherwise=0), sex (Boy=1, Girl=0), race (White=1, otherwise=0), having any alcohol branded merchandise (Alcohol item=1, otherwise=0), parents' education (High school or higher education=1, otherwise=0), family income (income < $20K =1, otherwise 0), and performance in school (below average=1, otherwise 0). The intercept and slope at age were assumed to be random and teen specific. The total number of observations is N_T = 18,482 with the number of clusters/subjects N = 5,124. The results of estimation by two methods are presented in Table 2 and graphically illustrated in Figure 2. As follows from this figure and Table 2, drinkers saw many hours of alcohol scenes in movies, and the cumulative exposure increased exponentially with age. White adolescents are more exposed to alcohol in movies, while other factors, such as parents' education or income had only a small effect. Since all independent variables/predictors, other than age, did not change with time, we obtained S_min simply by regressing each y_i on Age and taking the sum of squares of residuals, which yields S_min = 61. The MLE of the linear mixed model gives σ̂_ε = 0.089 with SD intercept =1.92 and SD slope=0.134.

Table 2.

Estimation results of cumulative exposure to alcohol scenes in movies among teens.

Variable	OLS, β̂		LME, β̂ML
	Coefficient	SE	Coefficient	SE
Intercept	-0.5272	0.0396	-2.3264	0.0390
Drinker	0.3223	0.0102	0.1783	0.0199
Age	0.1779	0.0030	0.3250	0.0022
Boy	0.0129	0.0089	0.0100	0.0181
White	0.2396	0.0156	0.2463	0.0307
Alcohol item	0.2202	0.0146	0.1787	0.0294
Parents' education	-0.0289	0.0100	-0.0334	0.0196
Family income	0.0630	0.0131	0.0429	0.0262
School performance	-0.0784	0.0096	-0.0525	0.0196
Sum of Squares	SOLS = 6582		SMM = 76

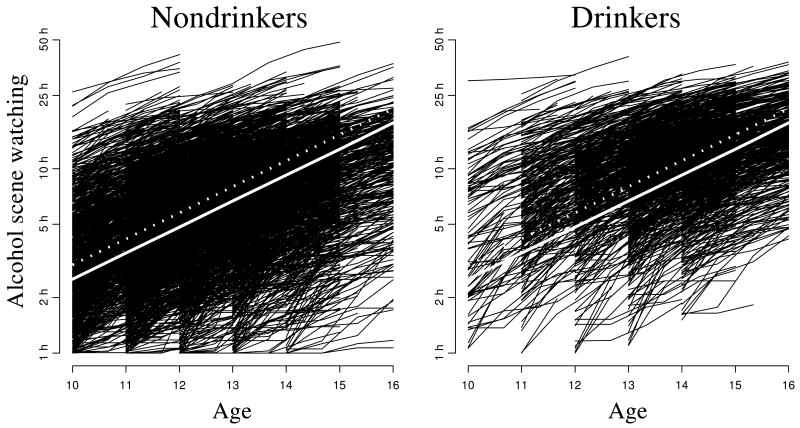
Figure 2.

Cumulative length of alcohol scene watched in movies for the two groups of adolescents as a function of age. The solid and dotted lines represent the cumulative growth in nondrinker and drinker groups, respectively.

In Figure 2, we show the cumulative time of alcohol scene watching as function of age for two groups of adolescents, nondrinkers and drinkers. The two parallel lines represent nondrinkers (drinker=0, solid) and drinkers (drinker=1, dotted); the distance between these lines is 0.3223. The rank of matrix W in this example is r = 2 × 5124, and we obtain

$$F=\frac{(6582-61)/(2\times 5124-9)}{61/(18482-2\times 5124)}=86,$$

yielding the p-value < 0.001. The random effect coefficient of determination,

$$R_r^2=\frac{6582-76}{6582-61}=0.997,$$

which indicates a very strong support of random effects in this model. This means that variation between adolescents is much higher than change in habit of movie watching as they get older.

As in the previous example, the variation of the baseline alcohol movie watching (at age 10) is so large that the random effects model can replaced with the fixed effects model estimated by the dummy variable approach.

5.3 Meta-analysis model for vaccine studies

To illustrate the random effects coefficient of determination for the meta-analysis model we use an example from Berkey et al. (1995). The log odds-ratio of the efficacy of the BCG vaccine for prevention of tuberculosis along with its variance was estimated in 13 studies with different sample sizes. The treatment effect with the 95% confidence intervals (horizontal segments) is shown in Figure 3. We start with resting the homogeneity of the studies using the Q-statistic, DerSimonian and Laird (1986), which in our notation is S_LS. Apparently, under the null, H₀ : τ² = 0, this statistic has a chi-square distribution with n – 1 = 12 degrees of freedom. In our case Q = S_WLS = 152 but the critical value is 22, so the p-value = 0; there is a strong indication of the presence of random effects.

Figure 3.

Log odds ratios from 13 studies of the tuberculosis vaccine effect with estimation of the overall effect using the meta-analysis model. The studies are highly heterogeneous because $R_r^2=0.91$.

Now we turn our attention to computation of the random effect coefficient of determination. The original data (log OR) for each study is depicted by a circle, the data adjusted by the random effect, depicted by a cross, is computed as y_i − b̂_i (τ̂²), an “estimate” of ε_i using formula from (20). The meta-analysis model (19) is estimated by maximum likelihood which yielded an overall vaccine effect μ̂_ML = −0.71 (OR = e^−0.71 = 0.49) and the heterogeneity variance ${\widehat{\tau }}_{ML}^2=0.28$ (SE = 0.53). The 95% confidence band (shaded rectangular) for the overall vaccine effect is shown in Figure 3. The weighted least squares estimate, ỹ = −0.43 with S_WLS = 152 yielding $R_r^2=0.91$. We conclude that studies are quite heterogeneous because 91% of the conditional variance of log OR can be explained by the random effect. The strong presence of the random effect is seen from the figure—the LOG OR adjusted for the random effect substantially “move” toward 0.

6 Conclusion

In this paper, we aimed at answering two fundamental questions in the framework of linear mixed model: “Why fit a linear mixed model and how to measure the strength of the presence of random effects?” We have developed such a measure, called the random effects determination coefficient by appealing to the proportion of the residual sum of squares on the scale from its minimum to maximum values. $R_r^2$ is originated from the F-test based on the fixed effects estimation. It estimates the proportion of the conditional variance of the dependent variable, with respect to the maximum reduction, explained by random effects. $R_r^2$ close to zero indicates that the data can be modeled using the standard linear model—the presence of random effects is weak. On the other hand, if $R_r^2$ is apart from 0, the random effects lead to a significant reduction in the variance due to the presence of random effect. If $R_r^2$ is close to 1 random effects lead to the maximum reduction so that the mixed model can be replaced with a linear model with fixed effects estimated by the dummy variable approach.

In the examples presented, $R_r^2$ was close to 1 indicating that random effects can be replaced with fixed effects using the dummy variable approach estimated by the standard linear regression which simplifies the analysis and the theory considerably (for example, using standard linear hypothesis vehicle one may test whether dummy coefficients/intercepts are equal in some specific clusters). This finding could be easily overlooked without computation of the random effects determination coefficient.

Fixed and random effects coefficients of determination represent the quality of a mixed linear model from two perspectives and are equally important. While the former reflects the strength of the fixed effects, the latter characterizes the presence of the random effects. It would be beneficial if these figures of merits were computed as a standard output software every time a mixed model or a meta-analysis models are estimated.

8 Appendix: Proofs

1. Proof that $0\le R_r^2\le 1$ for the general linear mixed effects model defined in equation (16). The denominator is positive if rank(W) > m and S_LS > 0. This follows from the following fact of linear regression analysis [24]: if X^n×m and H^n×k such that the space spanned by vector-columns of matrix X is a subspace of space spanned by vector-columns of matrix H, and rank(X) <rank(H) <n and min_β ‖y − Xβ‖² > 0 then min_γ ‖y − H_γ‖² < min_β ‖y − Xβ‖². Now we prove that for any fixed D we have S_min ≤ S_MM ≤ S_LS. Expressing b_i through β as in (11) and denoting ${\mathbf{\text{P}}}_i={\mathbf{\text{Z}}}_i{({\mathbf{\text{Z}}}_i^{\prime }{\mathbf{\text{Z}}}_i+{\mathbf{\text{D}}}^{-1})}^{-1}{\mathbf{\text{Z}}}_i^{\prime }$ we can rewrite

$$S_{MM}=\underset{\mathit{\beta }}{min}\sum _{i=1}^N({\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\mathit{\beta })\prime {(\mathbf{\text{I}}-{\mathbf{\text{P}}}_i)}^2({\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\mathit{\beta })\le \underset{\mathit{\beta }}{min}\sum _{i=1}^N({\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\mathit{\beta })\prime ({\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\mathit{\beta })\le S_{LS}$$

because 0 ≤ I − P_i ≤ I, the right inequality is established. To prove the left inequality we notice that

$$S_{min}=\underset{\mathit{\beta },b_1,\dots ,b_N}{min}\sum _{i=1}^N{\Vert y_i-X_i\mathit{\beta }-Z_i{b}_i\Vert }^2\le \underset{\mathit{\beta }}{min}\sum _{i=1}^N{\Vert y_i-X_i\mathit{\beta }-Z_i{\widehat{b}}_i(\mathit{\beta })\Vert }^2$$

for any function b̂_i(β) because S_min is the unconstrained minimum. Particularly, this is true for (11), which proves S_min ≤ S_MM.

2. Proof that $0\le R_r^2\le 1$ for the meta-analysis model defined in equation (21). The inequality $R_r^2\le 1$ follows from the fact that S_WLS and S_min are nonnegative. Now we prove that S_min(τ²) is a decreasing function of τ². Indeed, applying the chain rule the derivative is

$$\frac{d{S}_{min}({\tau }^2)}{d{\tau }^2}=-\sum _{i=1}^n\frac{{(y_i-\widehat{\mu }({\tau }^2))}^2}{{({\tau }^2+{\sigma }_i^2)}^2}-\sum _{i=1}^n\frac{y_i-\widehat{\mu }({\tau }^2)}{{\tau }^2+{\sigma }_i^2}\times \frac{d\widehat{\mu }({\tau }^2)}{d{\tau }^2}.$$

But the second term vanishes due to (20). This implies that the derivative is nonnegative and S_min(τ²) ≤ S_min(0) = S_WLS which proofs $R_r^2\ge 0$.