Quantifying accumulation or exclusion of H⁺, HO⁻, and Hofmeister salt ions near interfaces

Abstract

Recently, surface spectroscopies and simulations have begun to characterize the non-uniform distributions of salt ions near macroscopic and molecular surfaces. The thermodynamic consequences of these non-uniform distributions determine the often-large ion-specific effects of Hofmeister salts on a very wide range of processes in water. For uncharged surfaces, where these nonuniform ion distributions are confined to the first few layers of water at the surface, a two-state approximation to the distributions of water and ions, called the salt ion partitioning model (SPM) has both molecular and thermodynamic signiicance. Here, we summarize SPM results quantifying the local accumulation of H⁺, exclusion of HO⁻, and range of partitioning behavior of Hofmeister anions and cations near macroscopic and molecular interfaces. These results provide a database to interpret or predict Hofmeister salt effects on aqueous processes in terms of structural information regarding amount and composition of the surface exposed or buried in these processes.

1. Introduction

The Hofmeister series is a qualitative ranking of salt anions and cations, originally based on their effectiveness (typically at molar concentrations) as protein precipitants and subsequently found to be applicable to many other protein processes where water-accessible surface area (ASA) changes significantly (e.g. folding, assembly) as well as model processes like creating air-water surface or dissolving model compounds[1, 2, 3, 4]. Considering these processes in the direction in which protein (or model compound) ASA is reduced (e.g. folding, subunit assembly, crystallization, precipitation) the general ranking of ions [5, 2], in descending order of effectiveness in driving these processes, is:

$$\begin{array}{c}{\text{SO}}_4^{2-}>{\mathrm{F}}^{-}>{\text{Ac}}^{-}>{\text{Cl}}^{-}>{\text{Br}}^{-}>{\text{NO}}_3^{-}>{\mathrm{I}}^{-}>{\text{ClO}}_4^{-}>{\text{SCN}}^{-}\\ {\mathrm{K}}^{+}={\text{Na}}^{+}>{\text{Li}}^{+}>{\text{NH}}_4^{+}>>{\text{GuH}}^{+}\end{array}$$

For protein processes, a corresponding series of nonelectrolytes is often observed, extending from stabilizing osmolytes like glycine betaine and trimethylamine oxide to destabilizing denaturants like urea [6, 7, 8].

Salts of ions from the extremes of the Hofmeister series are widely used at high concentrations in biochemistry (e.g. ammonium sulfate for precipitation and crystallization; guanidinium chloride or thiocyanate for denaturation), but the molecular basis of their ion-specific effects remains controversial. Hofmeister ions have often been discussed as either water structure breakers (“chaotropes”) or structure makers (“kosmotropes”) [9], and Hofmeister effects have been attributed to the “ordering” or “disordering” of bulk water structure effected by a particular ion; however, proposals of long-range ordering (or disordering) of water in concentrated salt solutions are not supported by water activity data [10] nor by recent spectroscopic results [11, 12]. The various effects of different ions on water structure (bulk and/or local), while potentially of interest, are not the direct origins of the thermodynamic effects. Instead, non-uniform ion distributions (accumulation, exclusion) near surfaces are responsible for the thermodynamic effects of concentration of Hofmeister salts on a very wide range of aqueous processes. The thermodynamic description of Hofmeister effects (as well as Coulombic and osmotic effects of salts, and the spectrum of effects of nonelectrolytes) on biopolymer processes is most fundamentally based on preferential interaction coefficients, which quantify the thermodynamic consequence of the local accumulation or exclusion of the salt ion or solute from the vicinity of the hydrated biopolymer surface as a function of salt or solute concentration [4, 6].

An example of the effect of non-uniform ion distributions on thermodynamics is provided by the varying effect of different Hofmeister salts on the surface tension of water. Surface-sensitive spectroscopic experiments [13, 14, 15, 16], molecular dynamics (MD) simulations that utilize polarizable potentials for water and ions[17, 18, 19], and various theoretical/experimental collaborations [20, 21, 22] have provided evidence, recently reviewed [23], that, although “hard” and multiply-charged ions are highly excluded from the air-water surface, large polarizable anions (e.g. SCN⁻, I⁻) and the proton are present there, accumulating to concentrations greater than in the bulk solution. Based on surface potential data, it has long been recognized that some ions must be present at higher concentration at the air-water surface than others [24, 25, 26]; simulations and spectroscopic investigations are now refining various features of ion distributions at the surface. The classical proposal of a salt-free surface layer [27] appears applicable only when both ions of a salt are “hard” and/or multiply-charged (e.g. NaF and Na₂SO₄). For other salts, MD simulations using polarizable potentials show exclusion of halide cations and different degrees of anion accumulation at the air-water surface [20]; for these cases, a correspondingly wide range of positive surface tension increments have been reported [28]. In simulations where nonpolarizable potentials are used, almost identical distributions (exclusion) of cation and anion are observed, and the charge separation described above is not observed [29, 30].

2. The Solute Partitioning Model (SPM) of the distribution of ions or uncharged solutes in the vicinity of macroscopic or molecular surfaces

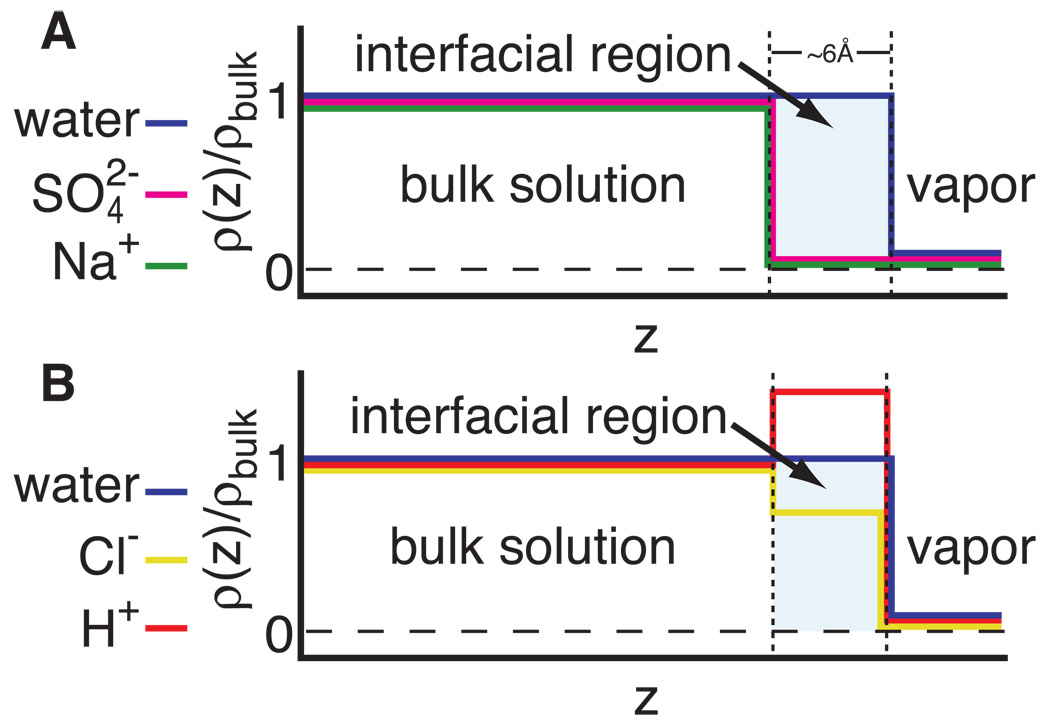
Nonuniform distributions of ions and of uncharged solutes near uncharged surfaces (and also near charged surfaces at high salt concentration) are expected to be significant only in the first few layers of water [17]. In this case, a two-state approximation to the distributions of water and ions (the SPM) appears to have molecular as well as thermodynamic significance. This model is shown schematically for a salt where both ions are highly excluded from the air-water surface in (Na₂SO₄; Fig. 1A), and for a salt where the anion is modestly accumulated (i.e. local concentration higher than bulk) and the cation is strongly excluded (NaI; Fig. 1B). For comparison, distributions of Na⁺ and ${\text{SO}}_4^{2-}$ ions, derived from molecular dynamics simulations [31], are shown in Fig. 2. In Fig. 1, the two key SPM quantities are the amount of water in the local region per Ų of surface and the concentration of the salt ion or solute in that local water, relative to its bulk concentration. Key questions, addressed below, are 1) whether the amount of local water is characteristic only of the surface being hydrated or whether the definition of “local domain” differs for different solutes, and 2) how the concentration of solute in the local water is related to its bulk concentration.

Figure 1.

A) SPM two-state representation of the ion distribution for the completely excluded salt Na₂SO₄.B) Representation of the distribution of an acid, HC1, where the chloride ion is moderately excluded (K_p=0.7, i.e. the average concentration of Cl⁻ near the surface is ~2/3 as large as the bulk concentration) and the H⁺ ion is moderately accumulated (K_p=l.5, i.e. the average concentration of H⁺ near the surface is 1.5 times as large as the bulk concentration).

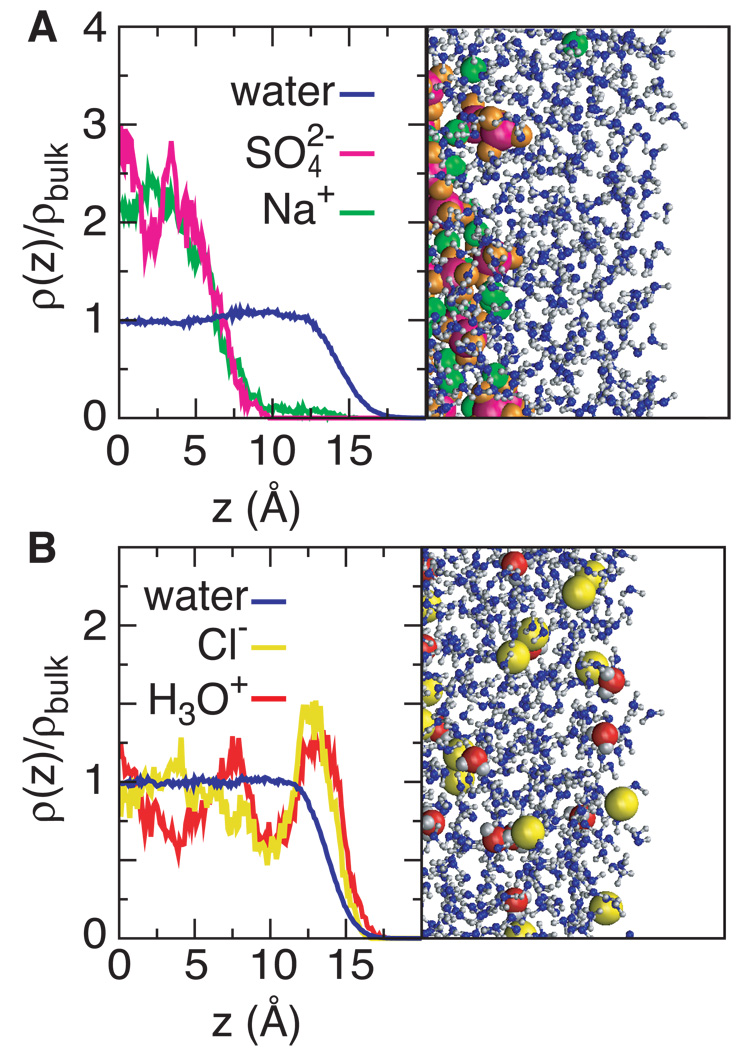
Figure 2.

Ion distributions and snapshots at the air-water interface from molecular dynamics simulations of Jungwirth, Tobias, and coworkers [20, 31]. The complete exclusion of Na⁺ and ${\text{SO}}_4^{2-}$ from the surface water in panel A agrees well with the treatment of Na₂S0₄ in the SPM as a completely excluded reference salt. In panel B, both hydronium and chloride ions are predicted by the simulation to be modestly accumulated at the surface; compare with the SPM prediction in Fig. 1B.

To apply the SPM to model compounds and biopolymers, the water accessible surface area (ASA) is calculated using a spherical model for water and the vanderWaals (unified atom) surface of the model compound or biopolymer [32]. This ASA is decomposed at a coarse-grained level into contributions from nonpolar (C), polar amide (N, O), other polar (N, O), cationic (N) and anionic (O) functional groups. To apply the SPM to processes involving model compounds or biopolymers in solution (e.g. micelle formation by amphiphilic monomers, folding of a randomly-coiling polypeptide chain into an extended alpha helix or a compact globular protein), ASA values of both the initial and final conformation are calculated, and the difference ΔASA is considered the surface of interest to analyze the effects of an uncharged solute or the non-Coulombic effects of a Hofmeister salt on a process [7, 33].

How does a locally nonuniform distribution of salt ions or of an uncharged solute near a macroscopic or molecular surface affect the thermodynamics of forming a macroscopic surface or exposing molecular surface of a model compound or biopolymer to water? Solutes that are completely excluded from the surface water increase the work of transferring water from bulk to surface, and thus increase the surface tension. This is a bulk osmotic effect analogous to freezing point depression; an increase in salt concentration increases the thermodynamic (entropic) cost of “unmixing” bulk water from a salt solution to form pure water at the air-water interface, just as bulk water must be “unmixed” from the solution to form pure ice in the case of freezing point depression). Conversely, surface-active solutes that partition into surface water (i.e. accumulate at local concentrations that exceed their bulk concentration) lower surface tension by reducing the work of transferring water to the surface.

3. Analysis of surface tension increments and other free energy increments for effects of salts and solutes on aqueous processes using the SPM

3.1. Uncharged solutes

The free energy change ΔG per unit surface area (A) for the process of creating a macroscopic air-water interface (i.e. the surface tension γ) is observed to vary linearly with the concentration of solute (see Fig. 3A); this is analogous to the linear dependence on solute concentration of observed free energy changes for a very wide range of aqueous processes, including dissolving model compounds and unfolding proteins. Surface tension increments STI=dγ/dm₃=(1/A)(dΔG/dm₃) are analyzed via the SPM¹:

$$\mathit{\text{STI}}=\frac{1}{\mathit{\text{RT}}}\frac{d\mathrm{\Delta }G/A}{d{m}_3}=-\frac{(m_3^{\mathit{\text{local}}}/m_3^{\mathit{\text{bulk}}}-1)b_1(1+{\epsilon }_3)}{55.5}.$$ (1)

In Eq. 1, $m_3^{\mathit{\text{local}}}$ and $m_3^{\mathit{\text{bulk}}}$ represent the molal concentrations of solute in the surface and bulk regions, respectively, b₁ is the number of water molecules in the surface region per unit area, and the quantity ε₃ is a nonideality correction which typically is small in magnitude compared to unity. For the STI to be independent of $m_3^{\mathit{\text{bulk}}}$ (see Fig. 3A), the ratio $m_3^{\mathit{\text{local}}}/m_3^{\mathit{\text{bulk}}}$ must also be independent of $m_3^{\mathit{\text{bulk}}}$. This constant local-bulk concentration ratio $m_3^{\mathit{\text{local}}}/m_3^{\mathit{\text{bulk}}}$ is the microscopic analog of an equilibrium constant for partitioning a solute between two macroscopic phases and is designated K_p,3. Equation 1 for a nonelectrolyte solute becomes:

$$\frac{1}{\mathit{\text{RT}}}(\frac{d\mathrm{\Delta }G/A}{d{m}_3})=-\frac{(K_{p,3}-1)b_1(1+{\epsilon }_3)}{55.5}.$$ (2)

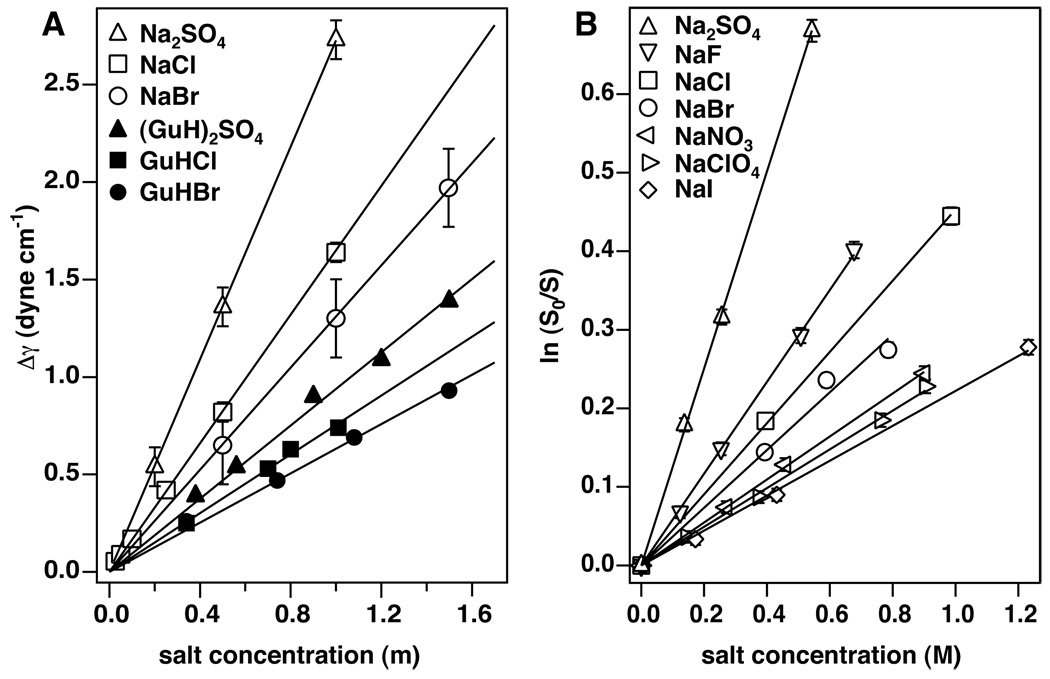
Figure 3.

A) Representative surface tension (panel A) and solubility data (panel B) for selected Hofmeister salts. In panel A, open symbols represent sodium salts [67], while the corresponding filled symbol denotes the guanidinium salt of the same anion [68]. The symbols for the various anions are as follows: sulfate (triangle), chloride (square), and bromide (circle). Error bars for the sodium salts are taken from the source; precision estimates provided for the guanidinium salts seem abnormally high (± ~ 0.35) and are not shown. B) Reduced standard free energies of dissolving benzene as a function of sodium salt concentration are shown in panel B; Na₂SO₄ is the most effective ”salting-out” agent, and NaI has the least effect on solubility. Data are from McDevit and Long [69] with error bars determined from reported accuracy of solubility measurements.

Equation 2 is also applicable to model compound solubility increments $(\mathit{\text{dlnS}}/d{m}_3=-(1/\mathit{\text{RT}})d\mathrm{\Delta }{G}_{\mathit{\text{obs}}}^{\mathrm{o}}/d{m}_3)$ and to the corresponding quantity for dissociation of micelles into monomers $\mathit{\text{dlnCMC}}/d{m}_3=-(1/\mathit{\text{RT}})d\mathrm{\Delta }{G}_{\mathit{\text{obs}}}^{\mathrm{o}}/d{m}_3$ as well as to so-called m-values (slopes) characterizing the linear dependence of $\mathrm{\Delta }{G}_{\mathit{\text{obs}}}^{\mathrm{o}}$ of protein unfolding (and other biopolymer processes) on m₃. For dissolving a model compound, the relevant area is the solvent accessible surface area (ASA) of the compound, and for analysis of CMC (critical monomer concentration) increments and biopolymer m-values, the area of interest is the surface exposed or buried in the process (ΔASA). Although the derivation of Eq. 2 differs for the different processes the final form is the same for all processes [34, 35, 7].

3.2. Electrolyte solutes

Surface tension increments for electrolyte solutes are also interpreted via the SPM, in terms of single-ion partition coefficients:

$$\frac{1}{\mathit{\text{RT}}}\left(\frac{d\mathrm{\Delta }G/A}{d{m}_3}\right)=-\frac{[{\nu }_{+}(K_{p,+}-1)+{\nu }_{-}(K_{p,-}-1)]b_1(1+{\epsilon }_{\pm })}{55.5}.$$ (3)

The ion partition coefficients (K_p,+, K_p−) are related to that which would be obtained if the electrolyte were treated as an electroneutral component (K_p,3):

$$\nu K_{p,3}\equiv {\nu }_{+}{K}_{p,+}+{\nu }_{-}{K}_{p,-}.$$ (4)

Application of Eq. 3 to surface tension increments allowed us to utilize extant literature surface tension data and compare our results to the observations from recent molecular dynamics simulations and surface-sensitive spectroscopies. Analysis of air-water surface tension increments (Fig. 3A) and hydrocarbon solubility increments (Fig. 3B) provides biochemically-relevant information about the accumulation or exclusion of solutes and Hofmeister salts near a homogenous nonpolar macroscopic or molecular surface in water. Analysis of Hofmeister salt (and solute) effects on biopolymer processes requires additional assumptions to separate Coulombic and non-Coulombic effects of salts and to decompose contributions from different surface types.

If a solute or salt ion is completely excluded from surface water or water of hydration of the model compound or biopolymer (K_p=0), then changing its concentration makes a purely osmotic contribution to the SFEI; if both cation and anion of a salt are completely excluded, then ν(K_p,3−1)=−ν. Such a salt (e.g. Na₂SO₄ in the case of hydrocarbon model compounds, see below) is the best “salting out” salt because addition of this salt only changes the water activity, thereby disfavoring hydration of the dissolved solute. For situations where (K_p,3−1)= 0, addition of the salt has no effect on the process. For a salt, this can result from a situation in which K_p,+=1 and K_p,−; =1, where no local concentration gradient exists for either cation or anion; more generally (K_p,3−1)= 0 whenever (ν₊K_p,₊+ν₊K_p,₊)/ν =1, which can occur if one ion is accumulated and the other is excluded (e.g. K_p,− > 1, K_p+ <1). In either case, if the local concentration of salt ions is equal to its bulk, complete compensation is achieved between Hofmeister (K_p,i) and osmotic effects of that salt. For solute-salt combinations where K_p,3 >1, the model compound is “salted in”, even if one ion is locally excluded as long as the other ion is sufficiently accumulated in the local hydration water of the solute.

4. Conclusions from the SPM-based molecular thermodynamic analysis of acid, base, and Hofmeister salt effects on the formation of nonpolar macroscopic (air-water) and molecular (dissolved hydrocarbon-water) interfaces

4.1. The local domain at the surface of bulk water or of dissolved hydrocarbons has ~0.2 H₂O Å⁻²

Of the investigated electrolytes (Hofmeister salts, acids, and bases; see [34] for the full data set), Na₂SO₄ has the largest STI and hydrocarbon SFEI (benzene and toluene) and thus is the most excluded from both the macroscopic air-water and molecular hydrocarbon-water interfaces (see Fig. 1–Fig. 3). Analysis of effects of Na₂SO₄, which is assumed to be completely excluded, yields the same number of water molecules per unit area of both surface regions (~0.2 H₂O Å⁻², or a surface layer approximately two water molecules thick at bulk density). We previously deduced that glycine betaine is excluded from approximately two layers of hydration water surrounding anionic oxygen (protein carboxylate, nucleic acid phosphate) surface of biopolymers [36] and that sucrose is excluded from a similar amount of water at the air-water surface [37]. The similarity of the amount of water in the surface region per unit surface area for these very different surfaces and solutes leads us to propose that ~0.2 H₂O Å⁻² is a universal hydration; this is logical because while the first layer of water is unique in some way by being at the surface/interface, the second layer of water is interacting only with water, so that any unique aspects of the surface would be expected to have little effect on subsequent layers. Indeed, a recent simulation study concludes that while the effects of a protein on the surrounding water extend beyond the first hydration layer, the thickness is invariant for different regions of the protein surface [38].

4.2. Partition coefficients of ions are independent and additive

A surface region with a thickness of two water molecules is a nanophase which need not be electroneutral [39]. Hence the cation and anion of a salt can be accumulated or excluded to very different extents, and the accumulation/exclusion of the cation is independent of that of the anion, and vice versa. For both air-water and hydrocarbon-water surfaces, where data are the most extensive, salt ion partition coefficients are found to be additive and independent of salt concentration and of the identity of the other salt ion up to at least 1 M bulk salt concentration. For the air-water interface, partition coefficients defined relative to ${\mathrm{K}}_{p,N{a}^{+}}={\mathrm{K}}_{p,S{O}_4^{2-}}=0$ are shown in Table 1. For example, anion partition coefficients deduced from STI data for sodium salts (in which case the cation is completely excluded: K_{p, Na+}=0) and for acids (in which case the cation is strongly accumulated: K_{p,H +}=1.5) are the same within experimental uncertainty.

Table 1.

Partition coefficients for cations ^a and anions ^b at the air-water surface calculated from SPM-based analysis of surface tension increments

Anion	Average±s.d.	Kp,Na+=0.00±0.05	Kp,K+=0.12±0.08	Kp,Li+=0.08±0.21	$K_{p,N{H}_4^{+}}=0.25\pm 0.07$	KP,GuH+=0.67±0.21	KP,H+=1.50±0.04
${\text{SO}}_4^{2-}$		0.00 ± 0.05	-	-	-	-	-
${\text{CO}}_3^{2-}$	0.22 ± 0.15	0.37 ± 0.13	0.07 ± 0.18	-	-	-	-
F−	0.53 ± 0.02	0.55 ± 0.05	0.51 ± 0.13	-	-	-	-
HO−	0.58 ± 0.04	0.64 ± 0.09	0.53 ± 0.11	0.58 ± 0.23	-	-	-
Cl−	0.69 ± 0.04	0.70 ± 0.14	0.63 ± 0.13	0.76 ± 0.24	0.66 ± 0.14	-	-
Br−	0.86 ± 0.08	0.92 ± 0.16	0.83 ± 0.06	1.01 ± 0.22	0.76 ± 0.09	0.80 ± 0.26	0.82 ± 0.09
${\text{NO}}_3^{-}$	0.98 ± 0.09	1.01 ± 0.05	0.91 ± 0.09	1.04 ± 0.22	0.84 ± 0.10	-	1.07 ± 0.05
I−	1.18 ± 0.12	1.18 ± 0.07	1.00 ± 0.14	1.34 ± 0.22	1.18 ± 0.11	-	-
Ac−	1.30 ± 0.05	1.34 ± 0.05	1.34 ± 0.10	1.30 ± 0.21	-	-	-
${\text{ClO}}_3^{-}$	1.44 ± 0.03	1.41 ± 0.12	1.47 ± 0.33	-	-	-	-
SCN−	1.64	1.64 ± 0.09	-	-	-	-	-
${\text{ClO}}_4^{-}$	1.77 ± 0.04	1.83 ± 0.06	-	1.74 ± 0.21	-	-	1.75 ± 0.23

^aValues for cations relative to K_p,_Na⁺=0 are column headings.

^bValues for anions of each electrolyte are compared in body of table.

4.3. Local concentrations of H⁺ (accumulated) and HO⁻ (excluded) are consistent with the bulk ion product of water

Analysis of STI (Table 1) reveals that the proton is the most accumulated cation in the vicinity of the macroscopic air-water surface, with a surface concentration that is predicted to exceed its bulk concentration by 50%. The hydroxide ion is predicted to be excluded, with a surface concentration that is predicted to be only 60% of its bulk concentration (Table 1). Anions of many inorganic acids ${\text{SO}}_4^{2-},{\text{CO}}_3^{2-},{\mathrm{F}}^{-},{\text{Cl}}^{-},{\text{Br}}^{-}$ are also excluded (to different extents) from the vicinity of the air-water surface. At a qualitative level, the decrease in surface tension caused by the addition of most inorganic acids to water indicates a net surface accumulation of the acid component, as has long been recognized [26, 28]. At the level of individual ions, our finding that the proton has an enhanced surface concentration relative to the bulk is consistent with the predictions of molecular dynamics simulations and indirect experimental observations [40, 20, 41, 14, 42]. Since many atmospheric reactions are pH-dependent and/or acid-catalyzed [43], knowledge of the extent of proton accumulation at (and hydroxide exclusion from) the surface is important in understanding atmospheric processes. Our finding that hydroxide is moderately excluded is somewhat more controversial [44] although consistent with predictions from simulations and experimental results [20, 44, 42]. Significantly, the ion product of water [H⁺][HO⁻] in the vicinity of the air-water surface calculated from K_p,H+ and K_p,HO− (Table 1) is found to be the same within uncertainty (0.9 ± 0.1 ×10⁻¹⁴ M²) as in the bulk (1×10⁻¹⁴ M²). The equivalence of surface and bulk ion products for water, which is not imposed by the analysis, provides additional support for the conclusion that the SPM has both molecular and thermodynamic significance.

4.4. Rank orders of cation and anion partition coefficients near nonpolar surfaces correlate well with protein-based Hofmeister series

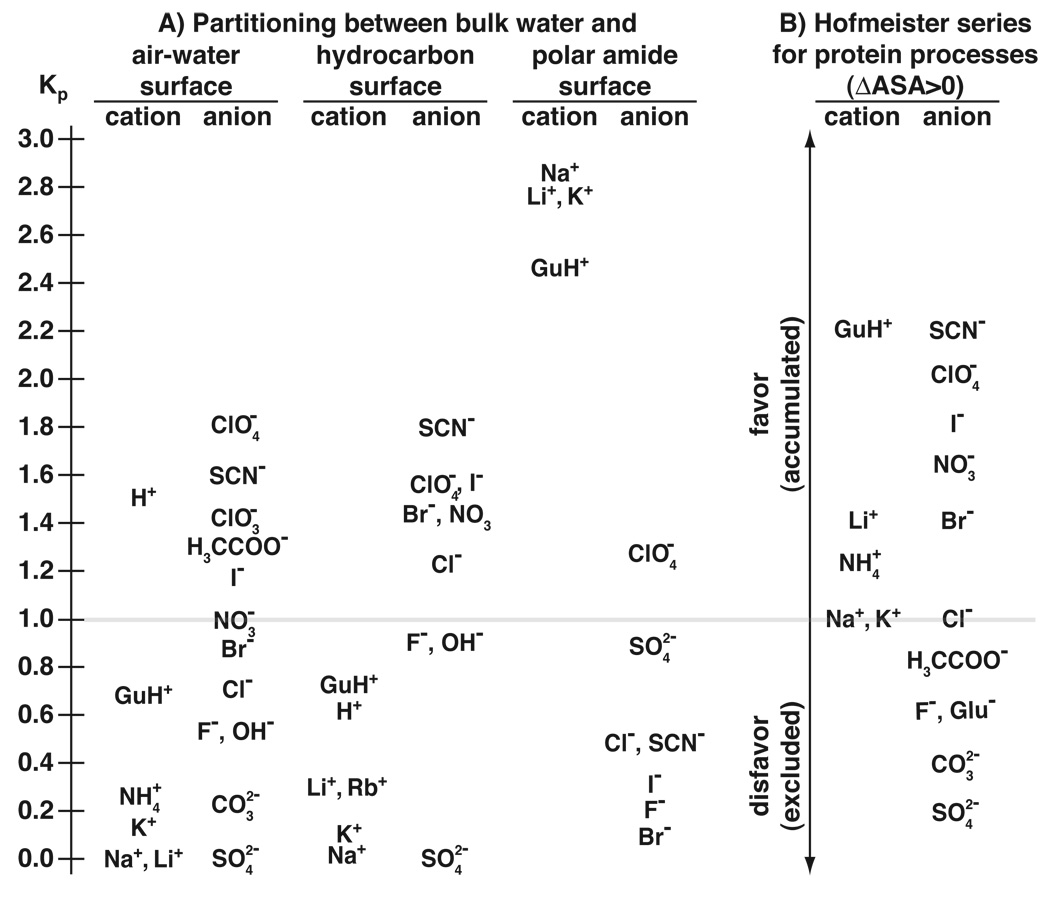
For air-water and molecular hydrocarbon-water interfaces, rank orders of cation and anion K_p values (except acetate at air-water) are quite “normal” Hofmeister, as shown by comparison of K_p series with that inferred from published studies of salt effects on transition temperatures of protein unfolding (Fig. 4). As this figure illustrates, Na⁺ (defined as K_p=0) and the other alkali metal cations are the most excluded cations from air-water and molecular hydrocarbon-water interfaces. The modest exclusion of GuH⁺ (K_p=0.7), as compared with the almost complete exclusion of Na⁺ and K⁺ is consistent with the separation observed in the effects of these cations on protein unfolding (Fig. 4). The cation series is highly offset in the direction of exclusion from the position of cations for protein unfolding, implying compensatory cation accumulation at other protein surface. For both nonpolar surfaces, sulfate is the most excluded anion (K_p defined as 0); perchlorate and thiocyanate are the most accumulated, with local concentrations approaching twice that of bulk.

Figure 4.

A) Comparison of single-ion partition coefficients K_p,i for partitioning of ions between bulk water and the air-water, hydrocarbon, and amide surfaces. B) Relative Hofmeister rankings of anions and cations for processes which expose protein surface to water (e.g. unfolding). NaCl and KC1 occupy neutral positions in the middle of the Hofmeister series for unfolding of globular proteins [5, 3], and so K⁺, Na⁺, and Cl⁻ (with K_p,i ~1) divide the cations and anions into those that are accumulated (and thus drive unfolding) and the excluded protein stabilizers.

Among the cations, only ${\text{NH}}_4^{+}$ and GuH⁺, with partition coefficients of 0.3 and 0.7, respectively, exhibit significantly less than complete exclusion from air-water and molecular hydrocarbon-water interfaces. In addition to being of biochemical significance themselves, these two cations are models for the end groups of the amino acid side chains of lysine and arginine. A topic of current interest in the ion channel community is the feasibility of burial of arginine-rich helical segments in the lipid environment [45, 46, 47], as in the proposed movement of the S4 helix of the voltage-gated potassium channel, KvAP, through the bilayer [48]. Our partition coefficients for GuH⁺ and ${\text{NH}}_4^{+}$ are not necessarily relevant to this question, since they describe transfer of these cations from bulk water to the local water at a nonpolar surface. But if water accompanies the cation into the membrane [49], they may be relevant; if so they indicate that arginine should be easier to put into that environment than lysine, and that the free energy cost of doing so is relatively small, consistent with experimental results [45].

4.5. Predicting/Interpreting Hofmeister salt effects on micelle formation

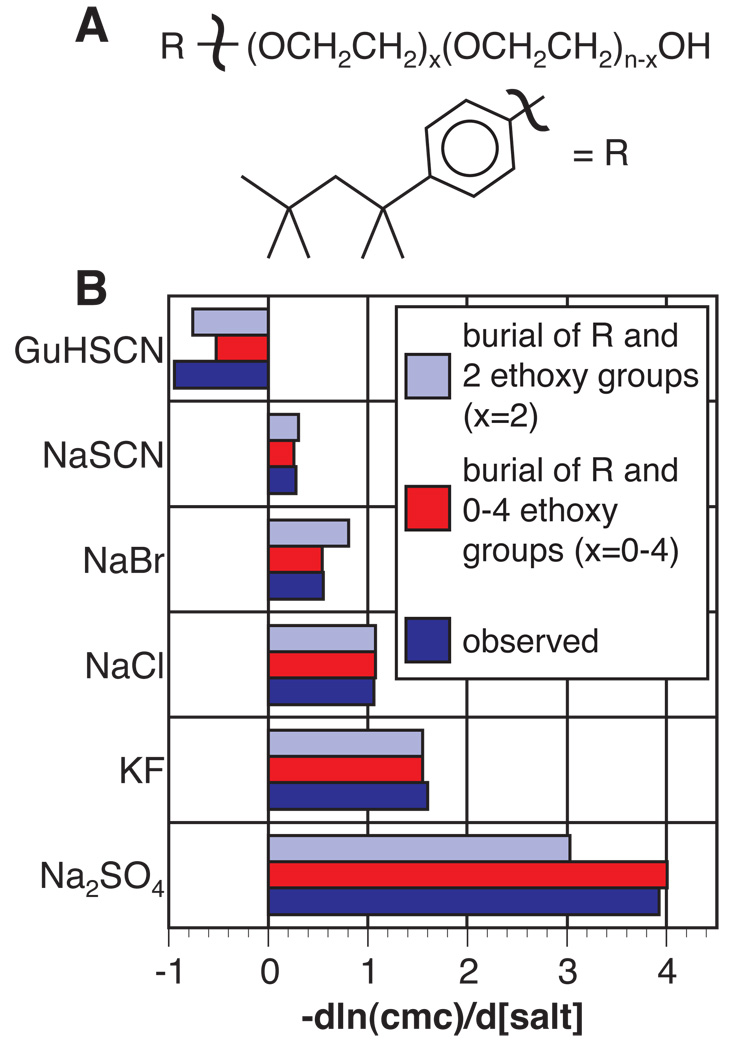
The analysis presented here predicts that for a process involving only changes in ASA of (aliphatic) nonpolar surface, all salts investigated would drive the process in the direction of burial of nonpolar surface; salt-specific differences would be determined by the extent of anion accumulation at the nonpolar surface. For example, consider the formation of a model micelle, where nonpolar surface is buried and the polar headgroup remains equally exposed in both the solution and micellar states. Alkali fluorides would drive micelle formation because of strong exclusion of the alkali metal cation and slight exclusion of F⁻from nonpolar surface. On the other end of the Hofmeister series, alkali iodides and thiocyanates would only minimally affect micelle formation because of largely compensating effects of anion accumulation and cation exclusion at nonpolar surface. The dark blue bars in Fig. 5 summarize experimentally-determined Hofmeister salt effects on the critical micelle concentration for a p-tert-octylphenoxy(polyethoxy)ethanol micelle [50, 51]. The light blue bars are predictions based on the hydrocarbon solubility data for a micelle structure in which the p-tert-octylphenoxy group and two ethoxy groups (with the ether oxygen treated as equivalent to hydrocarbon surface) are buried. The agreement between the experimental data and the model predictions is remarkably good given the simplicity of the model and the possibility that the choice and/or concentration of salt perturbs micellar structure [52]. Indeed, agreement is significantly improved if one assumes that fewer ethoxy groups (0–1) are buried in the presence of micelle-destabilizing salts and that additional ethoxy groups (3–4) are buried in micelle-stabilizing salts (red) [51].

Figure 5.

Predicted vs. observed Hofmeister salt effects on micelle formation by a nonionic surfactant (OPE) A) Chemical formula for an OPE_n monomer, where n=9–10 or 30 ethoxy groups. Salt effects on micelle formation were observed to be indistinguishable for the two polymer sizes [50]. B) Prediction of salt effects on micelle formation. Experimental data of Hofmeister salt effects on the formation of an OPE_n micelle [50] are represented by the dark blue bars. The best fit of the experimental to the calculated data for all salts is obtained if it is assumed that two ethoxy groups are buried along with the R group (light blue). Even better agreement is attained if the number of ethoxy groups buried is varied from 0–4 (red).

5. Conclusions from analysis of salt effects on aqueous solubility of amide model compounds and implications for prediction of salt effects on protein unfolding

To interpret or predict Hofmeister salt effects on the thermodynamics of biopolymer processes, individual thermodynamic contributions of interactions of anions and cations with amide and other types of polar biopolymer molecular surface as a function of salt concentration are needed. SPM-based analysis of salt effects on solubility of peptides and amides reveals that cations and anions partition very differently in the vicinity of amide surface than near nonpolar surface (Fig. 4). Separation of salt-amide partition coefficients into single-ion contributions was accomplished by making an assumption based on the classical observations that NaCl and KCl typically exhibit little if any Hofmeister-osmotic (i.e. non-Coulombic) effect on unfolding transitions of globular proteins and that Cl⁻, Na⁺, and K⁺ ions are centrally positioned in individual anion and cation series derived from unfolding data [5, 3]. We conclude that the NaCl and KCl component partition coefficients for the surface exposed in unfolding the typical globular protein must be near unity and that the single-ion partition coefficients of these ions must be similar to one another and close to unity as well. These semiquantitative observations and an assumption that the hydration b₁ of the surface is uniform (assumed to be 0.2 H2O/Ų, as discussed above) allow determination of single-ion partition coefficients for amide surface (Fig. 4).

From these ion partition coefficients for nonpolar and polar amide surfaces, one can now interpret or predict, for the first time, most of the non-Coulombic effect of Hofmeister salts on amide or peptide solubility, protein unfolding, and other protein processes in terms of structural information (the amount and composition of the ΔASA in the process) [51, 53]. For example, protein unfolding exposes surface (ΔASA) which is ~1/3 polar (divided equally between amide groups and other polar or charged surface) and 2/3 nonpolar; therefore, quantitative analysis of the thermodynamic consequences of accumulation (or exclusion) of salt cations and anions near both nonpolar and polar surface is of key importance for the interpretation of Hofmeister salt effects on protein unfolding. Because most anions are excluded to a similar extent from amide surface (Fig. 4, [51]), the effect of a particular anion on unfolding is determined by whether it is accumulated (like iodide, perchlorate) or excluded (like fluoride, sulfate) near nonpolar surface. Most cations are excluded from nonpolar surface but strongly accumulated at polar amide surface and as a result are nearly neutral at driving unfolding [34, 51]. Guanidinium cation is much less excluded from nonpolar surface than other cations, but equally accumulated at amide surface [34, 51]; this behavior provides a novel quantitative explanation of its effect as a protein unfolding agent. The Hofmeister order of anions and cations arises from the extent of accumulation or exclusion of these ions near nonpolar surface [3, 51]. Although interactions of cations and anions with polar amide surface do not exhibit the Hofmeister order, favorable cation-amide interactions are crucial for determining whether a given Hofmeister salt will favor or disfavor a biopolymer or model process in which both nonpolar and amide surface are exposed.

6. Other recent progress towards an understanding of non-Coulombic interactions of ions with biopolymer surfaces

Vibrational Sum Frequency Spectroscopy (VSFS) has been used to probe the effects of various sodium salts on the local aqueous environment of an adsorbed surface layer of poly-(N-isopropylacrylamide) [54]. Anions from the surface-accumulated (biopolymer structure-destabilizing) end of the Hofmeister series (e.g. SCN⁻, I⁻) generate stronger water orientation than those on the locally excluded (structure-stabilizing) end ${\text{SO}}_4^{2-},{\mathrm{F}}^{-}$ [54]. This effect on local water structure is interpreted as anion accumulation in the region surrounding the adsorbed monolayer. By varying salt concentration and fitting the data to a modified Langmuir isotherm, the authors calculated apparent dissociation equilibrium constants K_D for the various anions. Although the heterogeneous nature of the adsorbed monolayer as well as uncertainty about its structure make it difficult to interpret these K_D values in terms of interactions with hydrocarbon or amide surface, VSFS is a powerful tool that will provide molecular and thermodynamic information regarding the interactions of ions with biopolymer surfaces.

In principle, simulations are capable of providing all of the information necessary to predict the interactions of Hofmeister ions with biopolymer surfaces and hence the Hofmeister contribution to salt effects on biopolymer processes [55]. Molecular dynamics simulations have been used to obtain ion distributions surrounding hydrophobic solutes (e.g. microscopic particles and macroscopic plates) [56, 57, 58]. Most studies to date have utilized nonpolarizable potentials. Perhaps consequently, results for common inorganic salts (e.g. NaCl) are generally qualitatively similar to simulations of the air-water interface in which nonpolarizable potentials are utilized [29, 59]; anions are sometimes observed closer to the surface than cations, but both are effectively excluded from the local region at the surface of the hydrophobic solutes. This is at odds with the current view of the air-water interface (see above), and a recent simulation study that utilized polarizable potentials for water and ions resulted in accumulation of I⁻ and Br⁻ in (and exclusion of Na⁺ from) the local region at a hydrophobic self-assembled monolayer [60]. In these simulations, ion size and charge density are also observed to influence surface propensity [57, 59, 61, 62, 63], but the relative importance of each contribution remains to be untangled. Simulations have also been performed for salt solutions containing compounds with heterogeneous surfaces (a tripeptide [64] and several proteins [65, 66]; for the protein simulations, it was concluded that polarizable potentials were not necessary. However, significant Coulombic interactions of the ions with the charged groups on these compounds, as well as the heterogeneous nature of peptide and protein surfaces, may complicate the interpretation of these results.

7. New frontiers: Experimental determination and interpretation of Hofmeister salt effects on protein crystallization, DNA helix formation, and protein-DNA binding

Crystallization of globular proteins and protein-protein interactions in formation of quaternary structures of globular proteins bury large amounts of protein surface. The composition of the surface buried in assembly (ΔASA) is typically more polar than that buried in protein folding. Surfaces buried in forming alpha helices, nucleic acid helices, and protein-nucleic acid complexes are even more polar than those in quaternary structures of globular proteins. For example, the ASA buried in protein folding is approximately 30% polar, while that buried in alpha helix formation by an alanine-rich oligopeptide is approximately 50% polar, and that buried in forming protein-DNA complexes and assembling DNA helices is 60–75% polar. If interactions of Hofmeister salt ions with these various polar surfaces are analogous to their interactions with polar amide surface, one can predict that salts like sodium sulfate or potassium fluoride will be less effective at driving these processes, per unit of total surface area buried, than they are at driving protein folding, and that salts like sodium or potassium chloride which have little net effect at high concentration on protein stability will exert modestly-destabilizing effects on these assemblies which bury more polar surfaces. Since many of these processes also exhibit strong (nonspecific) Coulombic effects of salt concentration, which are dominant at low salt concentration, it is necessary to quantify this common Coulombic contribution and separate it from the salt-specific Hofmeister contribution which becomes dominant at high salt concentration. Current research in our laboratory is directed at obtaining data on a variety of these systems, separating Coulombic and non-Coulombic effects of salt concentration, and testing the extent to which single-ion partition coefficients for polar amide surface can model the polar surface buried in these assemblies [53].