Determination of the interfacial rheological properties of a PLA encapsulated contrast agent using in vitro attenuation and scattering

Abstract

The stabilizing encapsulation of a microbubble based ultrasound contrast agent (UCA) critically affects its acoustic properties. Polymers, which behave differently from commonly used materials—e.g. lipids or proteins—for the monolayer encapsulation, hold potential for better stability and control over encapsulation properties. Air-filled microbubbles coated with Poly (D, L-lactide) (PLA) are characterized here using in vitro acoustic experiments and several models of encapsulation. The interfacial rheological properties of the encapsulation are determined according to each of these models using attenuation of ultrasound through a suspension of these microbubbles. Then the model predictions are compared with scattered nonlinear—sub- and second harmonic—responses. For this microbubble population (average diameter 1.9 μm), the peak in attenuation measurement indicates a weighted average resonance frequency of 2.5–3 MHz, which, in contrast to other encapsulated microbubbles, is lower than the resonance frequency of a free bubble of similar size (diameter 1.9 μm). This apparently contradictory result stems from the extremely low surface dilatational elasticity (around 0.01–0.07 N/m) and the reduced surface tension of the PLA encapsulation as well as the polydispersity of the bubble population. All models considered here are shown to behave similarly even in the nonlinear regime because of the low value of the surface dilatational elasticity. Pressure dependent scattering measurements at two different excitation frequencies (2.25 and 3 MHz) show strongly non-linear behavior with 25–30 dB and 5–20 dB enhancements in fundamental and second-harmonic responses respectively for a concentration of 1.33 μg/mL of suspension. Subharmonic responses are registered above a relatively low generation threshold of 100–150 kPa with up to 20 dB enhancement beyond that pressure. Numerical predictions from all models show good agreement with the experimentally measured fundamental response, but not with the second harmonic response. The characteristic features of subharmonic response and the steady response beyond the threshold are matched well by model predictions. However, prediction of the threshold value depends on property values and the size distribution. The variation in size distribution from sample to sample leads to variation in estimated encapsulation property values—the lowest estimated value of surface dilatational viscosity better predicts the subharmonic threshold.

Introduction

Encapsulated microbubbles with diameter 1–10μm are used as contrast enhancing agents for diagnostic ultrasound imaging. Encapsulating shells for ultrasound contrast agents (UCA) are typically made of proteins [e.g. Optison^™, GE Healthcare], lipids [e.g. Definity^®, Lantheus Imaging ; BR 14, SonoVue^®, Bracco Diagnostics; Sonazoid, GE Healthcare] and other common surfactants (Postema and Schmitz 2006). The shell stabilizes a microbubble against diffusion driven dissolution which otherwise would cause the microbubble to dissolve in a few milliseconds to seconds (Katiyar et al. 2009; Sarkar et al. 2009; Katiyar and Sarkar 2010). Recently, contrast agents with various polymeric shells have been developed that hold promises of enhanced stability (El-Sherif and Wheatley 2003b; Pisani et al. 2006; Eisenbrey et al. 2008) and improved control of the encapsulation properties (Yang et al. 2009). Here we characterize and model linear and nonlinear acoustic behaviors of Polylactic acid (PLA) encapsulated microbubbles.

Various polymeric microbubbles have been investigated for ultrasonic imaging (Forsberg et al. 2004; Lavisse et al. 2005; Ketterling et al. 2007; Grishenkov et al. 2009a; Grishenkov et al. 2009b; Lu et al. 2009; Yang et al. 2009; Sciallero et al. 2012) and targeted drug delivery/therapeutics (Wheatley et al. 2007; Jie et al. 2008; Lu et al. 2009; Sirsi et al. 2009) (see the review by Xiong et al (Xiong et al. 2011)). Specifically, PLA as well as PLGA—a block copolymer with varying lactic to co-glycolic acid ratios—has been investigated as an encapsulating material for contrast microbubbles. Preliminary acoustic experiments with PLGA (50:50 ratio of lactic to co-glycolic acid) contrast agents have shown around 20dB enhancement both in vitro (El-Sherif and Wheatley 2003b; Wheatley et al. 2006) and in vivo (Forsberg et al. 2004; Wheatley et al. 2006) dose response studies. The Forsberg study also investigated the role of varying ratios of glycolide to lactide in the PLGA in vivo. As lactide content was increased the shell became more hydrophobic and increased in circulation time. These agents were conjugated with breast cancer targeting ligands (Wheatley et al. 2007) making them a potential vehicle for cancer-drug delivery. PLA shelled contrast agents have also been loaded with the chemotherapeutic drug doxorubicin (Dox) for ultrasound mediated delivery (Eisenbrey et al. 2009; Eisenbrey et al. 2010a; Eisenbrey et al. 2010b). The maximum acoustic response achieved using drug loaded contrast agents showed around 19 dB enhancement in vitro (at 5 MHz excitation and 690 kPa peak pressure) and around 14 dB enhancement in vivo (with 5 MHz pulsed Doppler ultrasound) (Eisenbrey et al. 2010a). Size measurements on insonated Dox loaded contrast agents showed a decrease in average size above the peak acoustic excitation pressure of 690 kPa, possibly due to bubble destruction through fragmentation or diffusive loss of gas (Eisenbrey et al. 2010b). Lavisse and co-workers have also independently studied PLA microparticles both in vitro and in vivo (Lavisse et al. 2005) to report 18 dB enhancement in their in vitro dose response studies conducted at 10 MHz, 275 kPa excitation.

A complete understanding of the key parameters contributing to the stability, echogenicity and drug release requires reliable mathematical models. A number of models have been proposed to describe the dynamics of encapsulated microbubbles over the years (deJong et al. 1994; Church 1995; Hoff et al. 2000; Chatterjee and Sarkar 2003; Marmottant et al. 2005; Sarkar et al. 2005; Doinikov and Dayton 2007; Tsiglifis and Pelekasis 2008; Paul et al. 2010). Here we apply four different interfacial rheological models——1) Newtonian, 2) constant elasticity model, 3) strain-softening exponential elasticity model (Chatterjee and Sarkar 2003; Sarkar et al. 2005; Paul et al. 2010), all three developed in our lab, and 4) Marmottant model (Marmottant et al. 2005)—to analyze and characterize the PLA microbubbles. These models have mostly been applied to predict behaviors of lipid coated UCAs. Polymer coated UCAs have been reported to behave differently, e.g. lower elasticity than lipid or protein based contrast agents (Vos et al. 2007; Grishenkov et al. 2009a; Sciallero et al. 2012), or resonance frequency lower than that of a similar sized free bubble—typically shell elasticity increases resonance frequency (Wheatley et al. 2006). Such distinct behaviors of polymeric microbubbles warrant further investigation. We have developed a hierarchical two-pronged approach of modeling, where a model is applied to one set of experimental data to obtain model parameters, and then the model is validated against a second independent experiment (Chatterjee and Sarkar 2003; Sarkar et al. 2005; Paul et al. 2010). Model improvement/modification is initiated as warranted by the process of validation.

Here the same process of mechanical characterization using interfacial rheological models of encapsulation is applied to PLA microbubbles. Model parameters are determined using attenuation and then the model predictions are compared against scattering, specifically nonlinear second- and sub-harmonic scattering. Nonlinear scattering from these PLA microbubbles has not been measured before. The resonance frequency and the threshold for subharmonic generation and the latter’s critical dependence on bubbles size is investigated. The second section provides a description of materials and methods followed by a brief overview of the mathematical modeling and simulations. The third section presents and discusses the experimental and modeling results. The final section summarizes the outcome.

Materials and Methods

Microbubble preparation

Poly (lactic acid) ultrasound contrast agents were fabricated using a double emulsion technique (El-Sherif and Wheatley 2003b). Five hundred milligrams of PLA (100 DL MW=83 kDa, Lakeshore Biomaterials, Birmingham, AL) were dissolved in 10 ml of methylene chloride (Fisher Scientific, Waltham, MA) along with 50 mg of camphor (Sigma-Aldrich, St. Louis, MO). When the polymer was completely dissolved, 1 ml of ammonium carbonate solution (4% w/v, J.T. Baker, Phillipsburg, NJ) was added to the polymer solution, and then immediately sonicated on ice for 30 seconds (10 pulses of 3 seconds each separated by 1 second) with 110 W applied power (Misonix Inc. CL4 tapped horn probe with 0.5 inch tip, Farmingdale, NY). The resulting water in oil emulsion was immediately added to 50 ml of a cold 5% w/v poly(vinyl) alcohol solution (Polysciences, Warrington, PA) and homogenized for 5 minutes at 9500 rpm with a saw tooth homogenizer probe (Brinkmann Instruments, Westbury, NY). Immediately following homogenization, 100 ml of 2% v/v isopropyl alcohol (Fisher Scientific, Waltham, MA) was added to the emulsion, and then stirred for 1 hour to allow the methylene chloride to evaporate. The particles were then collected by centrifugation at 2500 g for 5 minutes and washed three times with hexane (Fisher Scientific, Waltham, MA). After allowing any residual hexane to evaporate the particles were washed in water then flash frozen and lyophilized for 48 hours with a Vitris Benchtop freeze dryer (Gardiner, NY). The water and ammonium carbonate from the core of the particles and the camphor from the polymer shell were allowed to sublimate during lyopholization to create a porous polymer shell encapsulating a void which is filled with air when the microbubbles are returned to atmospheric pressure. Contrast agent in the form of a dry powder was refrigerated and stored until ready for use.

Size distribution measurement

The size distribution was measured by dynamic light scattering using a Zetasizer Nano ZS (Malvern Instruments, Worcestershire, UK). One milligram of dry contrast agent was suspended in 1 ml PBS by vortexing for 10 seconds then transferred into a disposable cuvette and allowed to equilibrate for 3 minutes before taking measurements.

Experimental setup to measure attenuation

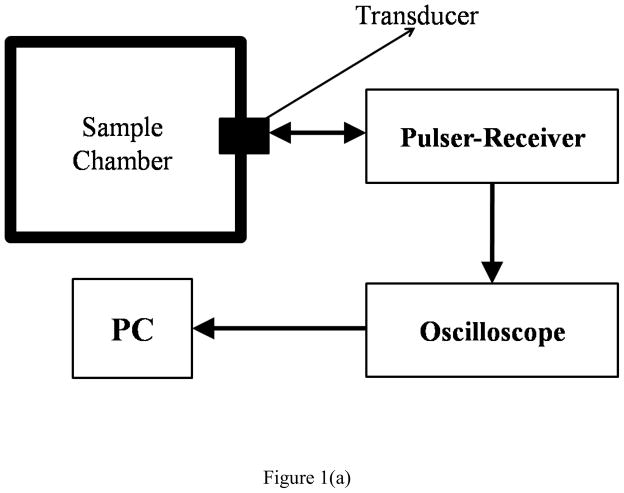
The experimental setup for attenuation measurement utilized a pulse-echo system at room temperature [Figure 1(a)] (Chatterjee et al. 2005a; Chatterjee et al. 2005b; Paul et al. 2012). Attenuation from a suspension of contrast agent (constantly stirred) was measured using three different unfocused broadband transducers (Olympus NDT, Waltham, MA, USA) with central frequencies 2.25 (V306-SU), 3.5 MHz (V382-SU) and 5 MHz (V309-SU) operated in transmit/receive mode. The -6dB bandwidth of the transducers were 1.178 to 3.32 MHz, 2.5 to 4.99 MHz and 3.13 to 6.19 MHz respectively. A pulser/receiver (Model 5800; Panametrics-NDT, Waltham, MA, USA) was used to excite the transducers at a PRF of 100 Hz; it generated a broadband pulse of duration of 440ns. The pulse generated at the face of the transducer traveled a total distance of 12 cm through the contrast agent suspension (from the transducer face to the container wall and back; container is made of polycarbonate sheet of thickness 1.17 cm) before being received and fed to the digital oscilloscope (Model TDS 2012; Tektronix, Beaverton, OR, USA) to observe the signal in real time. Signals were acquired from the oscilloscope via a GPIB IEEE 488 cable and a GPIB card, and saved on a desktop computer using LabView (Version 6.0.3; National Instruments, Austin, TX, USA). 20 voltage-time RF traces were acquired in an averaging mode (64 sequences are used for averaging) and saved. The data were then analyzed using Matlab® (Mathworks Inc., Natick, MA, USA) to calculate the attenuation coefficient for the contrast agent suspension. The excitation amplitude—200 kPa peak negative pressure—is low enough so that the frequency dependent broadband attenuation does not depend on the acoustic pressure (Chatterjee et al. 2005b). i.e., lowering the excitation did not affect it.

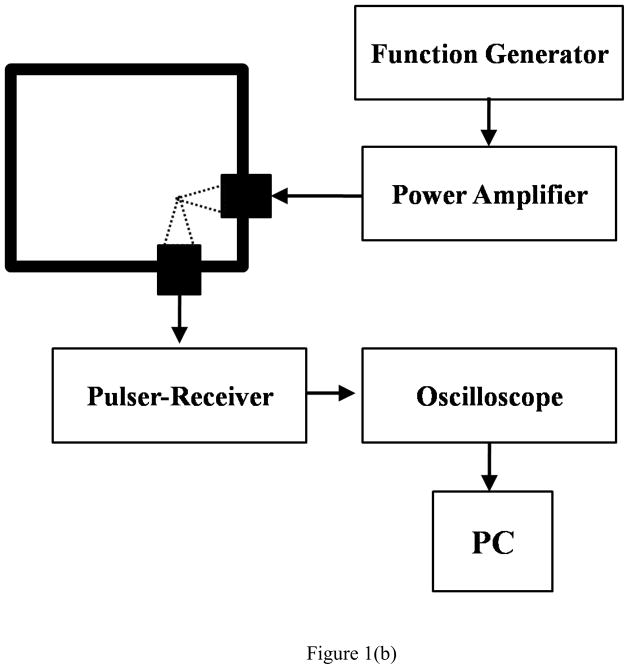
Figure 1.

Schematic of the experimental setup for in vitro measurement of (a) attenuation (b) scattering.

Experimental setup to measure scattering

Scattering setup [Figure 1(b)] used was similar to the one used by previous researchers (Shi and Forsberg 2000; Sarkar et al. 2005; Nahire et al. 2012; Paul et al. 2012). It employed two spherically focused transducers, each having an individual diameter of 1.6 cm and a focal length of 3.05 cm. The transmitting and receiving transducers were confocally positioned at right angles by placing them through circular holes drilled through the adjacent walls of a rectangular chamber. This configuration ensures similarity of scattered signals to backscattered echoes (Shi and Forsberg 2000) along with high spatial resolution (Sarkar et al. 2005). 150ml of contrast agent suspension was required for complete immersion of both the transducers. Two different transmitting transducers (Olympus NDT, Waltham, MA, USA) were employed with center frequencies of 3.62 MHz (V382 1.2 inch PTF) and 2.35 MHz (V306 1.2 inch PTF) and respective −6dB bandwidths of 83.84% and 80.68%. Another focused transducer of center frequency of 5.54 MHz (V309 1.2 inch PTF) and −6dB bandwidth of 85.06% was used to receive the scattered signal. An arbitrary/function generator (Model AFG 3251; Tektronix, Beaverton, OR, USA) was utilized to generate a 32 cycle sinusoidal pulse of desired frequency (2.25 and 3.5 MHz for this study) at a PRF of 100Hz. This signal was then amplified using a 55dB power amplifier (Model A-300, ENI, Rochester, NY, USA) and fed to the transmitting transducer. A 0.4 mm needle hydrophone (PZT-Z44-0400, Onda Corporation, CA, USA) was used to calibrate transducers. The contrast agent at the focal volume of the transducer scattered this signal back which was received by the receiving transducer utilizing a pulser/receiver (Model 5800; Panametrics-NDT, Waltham, MA, USA) in receiving mode with a 20dB gain. The amplified signals were then fed to the oscilloscope to view them in real time. Voltage time RF signals were saved onto the desktop using the same method used for attenuation experiments. For data analysis of the scattered signals, 50 acquisitions in averaging mode were saved on the computer.

Experimental procedure and data reduction

Contrast agent in the form of a dry powder was refrigerated and stored until ready for use. The dry powder was reconstituted in phosphate buffered saline to make a stock solution with a concentration of 1 mg powder/mL PBS (equivalent to a bubble concentration of 30×10⁶ bubbles/mL). This stock solution was subsequently used to achieve desired dilutions during acoustic experiments. Attenuation measurements were acquired for a range of contrast agent concentrations between 0.5–3.5 μg/mL. All scattering measurements were conducted at a concentration of 1.33 μg/mL. The stock solution was pipetted into the container with PBS (previously left to equilibrate for 5–10 mins to equilibrate with atmospheric oxygen concentration and for getting rid of any air bubbles created). An aliquot of 200 μl of stock sample was carefully added by automatic pipette and then allowed to mix for around 10 seconds using a magnetic stirrer to ensure a homogeneous suspension before application of ultrasound. The stirring was continued through the entire course of the experiment to maintain homogeneity. Reading taken of the sample without contrast agents showed no interference from entrained bubbles. The total volume of gas added with the agent was less than 100μl in a total volume of 150mL. Each attenuation and scattering experiment was repeated five times, i.e. five data sets were collected from five new suspensions prepared from the stock solution freshly taken into the experimental setups.

For attenuation, signals were obtained with and without UCAs. A Matlab® code was used to convert each of the voltage time response acquired to frequency domain using FFT (Fast Fourier Transform) followed by averaging the 20 acquisitions. The attenuation coefficient was calculated using the following expression

$$\alpha (\omega )=20{log}_{10}\left(\frac{{\overline{V}}_{\mathit{ref}}(\omega )}{{\overline{V}}_{\mathit{sig}}(\omega )}\right)/d,$$ (1)

where V̄_ref (ω) is the averaged response in frequency domain without any contrast agent in the medium, V̄_sig(ω is the averaged response in the frequency domain microbubbles suspended in the medium, and d is the total path traveled by the pulse before it is being received by the transducer.

For the time dependent attenuation study, a total of 200 voltage time acquisitions were obtained for study over a period of 20 minutes. Acoustic excitation was started as soon as the PLA shelled contrast agents were pipetted into the PBS solution and stirred for 10 seconds to attain homogeneity. Attenuation was averaged over each successive 30 second intervals. We compute the time dependent total attenuation normalized by its initial value using

$$NA(t)=\frac{A(t)}{A(0)};A=10{log}_{10}\left(\frac{{\sum }_{\omega }{V}_{\text{ref}}^2(\omega )}{{\sum }_{\omega }{V}_{\text{sig}}^2(\omega )}\right)/d.$$ (2)

Note that such a (summed-over-frequency) measure can be used even at higher excitation amplitudes unlike the frequency dependent attenuation (1) which would then be corrupted by nonlinear energy transfer across frequency spectrum (Chatterjee et al. 2005a).

For scattering a similar technique was used to get the average response in frequency domain (50 voltage time acquisitions were used). The scattered response is converted into a dB scale by taking the reference voltage to be unity. Responses at frequencies of interest were then appropriately extracted from the resultant data set to find the fundamental, second and sub-harmonic scattered responses.

Mathematical modeling

The dynamics of an encapsulated microbubble are governed by a Rayleigh-Plesset (RP) type equation. Many models have been proposed to describe the effects of the encapsulating shell of contrast microbubbles. Recently, we have shown that all models, including those that represent the shell as having a finite thickness and consisting of materials with bulk material properties, can be expressed in a single interfacial framework. It contributes two additional interfacial stress terms in the RP equation characterized by an effective surface tension γ(R) and an encapsulation dilatational viscosityκ^s(R) (Katiyar and Sarkar 2011)

$$\rho \left(R\ddot{R}+\frac{3}{2}{\stackrel{.}{R}}^2\right)=P_{G_0}{\left(\frac{R_0}{R}\right)}^{3k}\left(1-\frac{3k\stackrel{.}{R}}{c}\right)-\frac{2}{R}\gamma (R)-\frac{4\stackrel{.}{R}}{R^2}{\kappa }^s(R)-4\mu \frac{\stackrel{.}{R}}{R}-p_0+p_A(t).$$ (3)

R is the time dependent bubble radius, Ṙ and R̈ are the first and the second order time derivatives of the bubble radius, c is the velocity of sound in the surrounding liquid, ρ is the liquid density, μ is the liquid viscosity, R₀ is the initial bubble radius, P_G0 is the initial inside gas pressure, p₀ is the ambient pressure and p_A(t) is the excitation pressure. Gas diffusion is neglected. The inside gas pressure obeys a polytropic law with index k. We use four different models for the encapsulation:

Newtonian model (NM)(Chatterjee and Sarkar 2003):

$$\gamma (R)=\gamma (\text{constant})\text{and}{\kappa }^s(R)={\kappa }^s(\text{constant}).$$ (4)

The resonance frequency (f₀) of a bubble due to Newtonian model can be obtained from the linearized dynamics and is given by

$$f_0=\frac{1}{2\pi R_0}\sqrt{\frac{1}{\rho }\left(3{kp}_0+\frac{2\gamma }{R_0}(3k-1)\right)}.$$ (5)

Constant elasticity viscoelastic model (CEM) (Chatterjee et al. 2005a):

$$\gamma (R)=\{\begin{array}{ll}{\gamma }_0+E^s\beta \hfill & \text{for}{\gamma }_0+E^s\beta >0\hfill \\ 0\hfill & \text{for}{\gamma }_0+E^s\beta \le 0\hfill \end{array}\text{and}{\kappa }^s(R)={\kappa }^s(\text{constant}),$$ (6)

where γ₀ is constant interfacial tension and E^s is the constant dilatational elasticity and $\beta =\left(\frac{\mathrm{\Delta }\text{Area}}{{\text{Area}}_{\text{equilibrium}}}\right)=\left(\frac{R^2}{R_E^2}-1\right)$. The equilibrium radius R_E is given by $R_E=R_0{\left(1-\frac{{\gamma }_0}{E^s}\right)}^{-\frac{1}{2}}$. This ensures a balance of inside and outside pressure at initial radius. At the equilibrium radius the bubble encapsulation has no elastic stresses. The resonance frequency (f₀) due to CEM is given by

$$f_0=\frac{1}{2\pi R_0}\sqrt{\frac{1}{\rho }\left(3{kp}_0-\frac{4{\gamma }_0}{R_0}+\frac{4E^s}{R_0}\right)}.$$ (7)

Viscoelastic model with exponentially varying elasticity (EEM) (Paul et al. 2010):

$$\gamma (R)=\{\begin{array}{ll}{\gamma }_0+E^s\beta \hfill & \text{for}{\gamma }_0+E^s\beta >0\hfill \\ 0\hfill & \text{for}{\gamma }_0+E^s\beta \le 0\hfill \end{array}\text{and}{\kappa }^s(R)={\kappa }^s(\text{constant}),$$ (8)

where γ₀ is the constant interfacial tension, $E^s=E_0^s\beta exp(-{\alpha }^s\beta ),\beta =\left(\frac{R^2}{R_E^2}-1\right)$. Enforcing the balance of pressure at initial radius we have an expression of equilibrium radius given by $R_E=R_0{\left[1+\left(\frac{1-\sqrt{1+4{\gamma }_0{\alpha }^s/E_0^s}}{2\alpha }\right)\right]}^{-1/2}$. The expression for the resonance frequency (f₀) due to EEM is given as

$$f_0=\frac{1}{2\pi R_0}\sqrt{\frac{1}{\rho }\left(3{kp}_0+\frac{2E_0^s}{R_0}\left(\frac{\sqrt{1+4{\gamma }_0{\alpha }^s/E_0^s}}{{\alpha }^s}\right)\left(1+2{\alpha }^s-\sqrt{1+4{\gamma }_0{\alpha }^s/E_0^s}\right)\right)}.$$ (9)

Marmottant model (MM) (Marmottant et al. 2005):

$$\gamma (R)=\{\begin{array}{ll}0\hfill & \text{for}R\le R_{\mathit{buckling}}\hfill \\ \chi \left(\frac{R^2}{R_{\mathit{buckling}}^2}-1\right)\hfill & \text{for}{R}_{\mathit{bucking}}\le R\le R_{\mathit{rupture}}\hfill \\ {\gamma }_w\hfill & \text{for}R\ge R_{\mathit{rupture}}\hfill \end{array}\text{and}{\kappa }^s(R)={\kappa }^s(\text{constant}),$$ (10)

where χ (same as E^s in (6)) is the elastic modulus of the shell, R_buckling = R₀[1+γ(R₀)/χ]and ^−1/2 and R_rupture = R_buckling [1+γ_ω/χ]^1/2. Above R _rupture, the bubble is assumed to have a pure air-water interface and below R_buckling, it is in a buckled state where the effective interfacial tension is zero. The expression for the resonance frequency (f₀) due to MM is given as

$$f_0=\frac{1}{2\pi R_0}\sqrt{\frac{1}{\rho }\left(3{kp}_0-\frac{2\gamma (R_0)}{R_0}(3k-1)+\frac{4\chi }{R_0}\right)}.$$ (11)

Estimation of model parameters

We have developed a method to use the attenuation data measured to determine the parameters of the encapsulation models (Chatterjee and Sarkar 2003; Sarkar et al. 2005; Paul et al. 2010). The low amplitude excitation used to measure attenuation ensures that the attenuation data were collected at the linear regime of the bubble dynamics. The linearized form of the modified RP equation was used to determine the resonance frequency [according to one of the relations (5), (7), (9) or (11)] and the damping for each model. For our simulations we used ρ=1000 kg/m³, μ=0.001 kg/m s, c =1485 m/s, p₀ = 101325 Pa. We assumed an isothermal behavior for the air inside k = 1.0 which is appropriate for the size of microbubbles studied here (Prosperetti 1977b; Hilgenfeldt et al. 1998; Brenner et al. 2002). Knowing the damping and the size distribution we derived an expression for the attenuation through a suspension of contrast microbubbles. An error function between the measured α^meas (ω_i) and the modeled attenuation α(ω_i) was formulated:

$$Er(\gamma ,{\kappa }^s,\cdots )=\sum _i{\left[\alpha ({\omega }_i)-{\alpha }^{\mathit{meas}}({\omega }_i)\right]}^2$$ (12)

Model parameters were obtained through minimization of this error function using Matlab®. [Refer to previous publications by Sarkar and co-workers (Sarkar et al. 2005; Paul et al. 2010) for a detailed discussion of the parameter estimation technique].

Prediction of scattering

With the estimated expressions for the surface tension γ(R) and the dilatational surface viscosity κ^s(R) corresponding to a particular encapsulation model, the modified RP equation was solved for varying acoustic pressure amplitudes (P_A) using Matlab® with initial conditions of R(t=0)=R₀ and Ṙ(t=0)= 0. The scattered pressure P_s (t) and the scattering cross-section were calculated from the radial dynamics using the expressions (Brennen 1995; Paul et al. 2010)

$$P_s(r,t)=\rho \frac{R}{r}(2{\stackrel{.}{R}}^2+R\ddot{R})\text{and}{\sigma }_s(r,t)=\frac{4\pi \langle r^2{P}_s{(r,t)}^2\rangle }{{P_A}^2}.$$ (13)

Using Fast Fourier Transform (FFT) the computed scattered power was converted into the frequency domain and the total scattered power spectrum from the bubble suspension was calculated integrating the contribution from bubbles of all radii from R_min to R_max

$$S_s(\omega )=\underset{R_{min}}{\overset{R_{max}}{\int }}{\sigma }_s(R;\omega )n(R)dR.$$ (14)

Here n(R) is the number of microbubbles per unit volume per unit radius. The peak values corresponding to different frequencies (i.e. fundamental second- and sub-harmonic) were then extracted from the power spectrum to match with experimental results. The predicted fundamental response for both the excitation frequencies was matched with the experimentally measured response for the lowest acoustic pressure to account for the scattering volume and plotted and compared with experimental results. This same matching constant was also used to rescale the predicted second-harmonic and subharmonic responses and plotted for comparison with experiments.

Results and Discussion

Size distribution

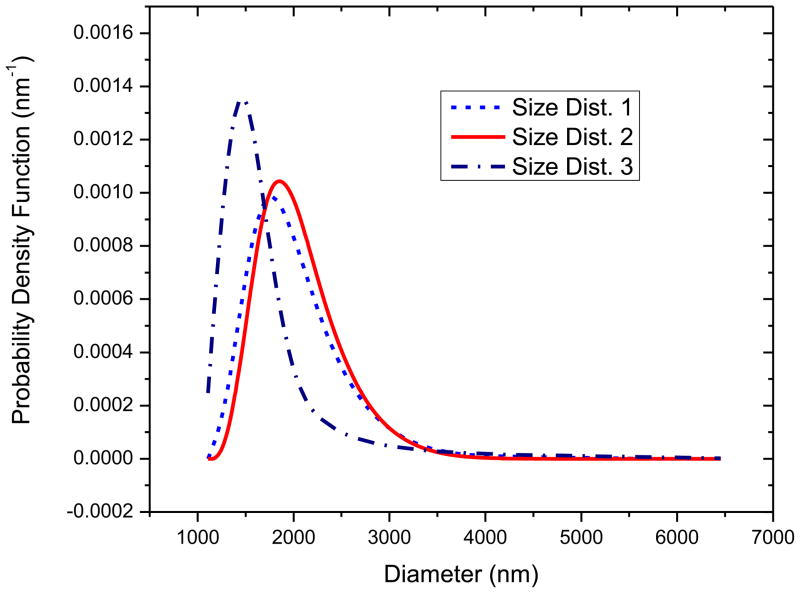
Figure 2 and Table 1 show the size distribution measurements for three different samples acquired from the same stock solution using dynamic light scattering equipment as described previously. The number averaged diameters (See Table 1) are similar for all three measurements except for slightly lower value for sample 3. However, note that the distribution for the sample 3 is markedly different from the other two with a tighter size distribution, lower peak diameter, and smaller number of bubbles above 1500 nm. Instead of using an average distribution, we use all three size distributions in our analysis and investigate the effects of size distribution variation on property estimation and scattering prediction. We will see below that the difference in size distribution leads to different predictions of subharmonic response.

Figure 2.

Size distribution of PLA shelled contrast microbubbles measured using DLS for three independent measurements.

Table 1.

Experimentally measured size distributions, z-averaged^* diameters and number averaged diameters for three separate measurements with PLA shelled microbubbles using Dynamic Light Scattering.

Diameter (nm)	Size Dist. 1 (%)	Size Dist. 2 (%)	Size Dist. 3 (%)
1106	0.0	0	4
1281	3.0	0	21.1
1484	14.9	9.8	33.2
1718	27.4	27.6	21.3
1990	25.1	30.5	7.7
2305	16.1	19.4	4.3
2689	8.3	9.2	2.7
3091	3.4	3	1.8
3580	0.9	0.5	1.3
4145	0.5	0	1.0
4801	0.4	0	0.8
5560	0	0	0.6
6439	0	0	0.2
Average Diameter
Number Averaged	1999 nm	2030 nm	1726 nm
z-Averaged	3486 nm	3377 nm	3151 nm

^*defined by Malvern as “the intensity weighted mean of the hydrodynamic size of the ensemble collection of particles”.

Attenuation and estimation of interfacial rheological properties

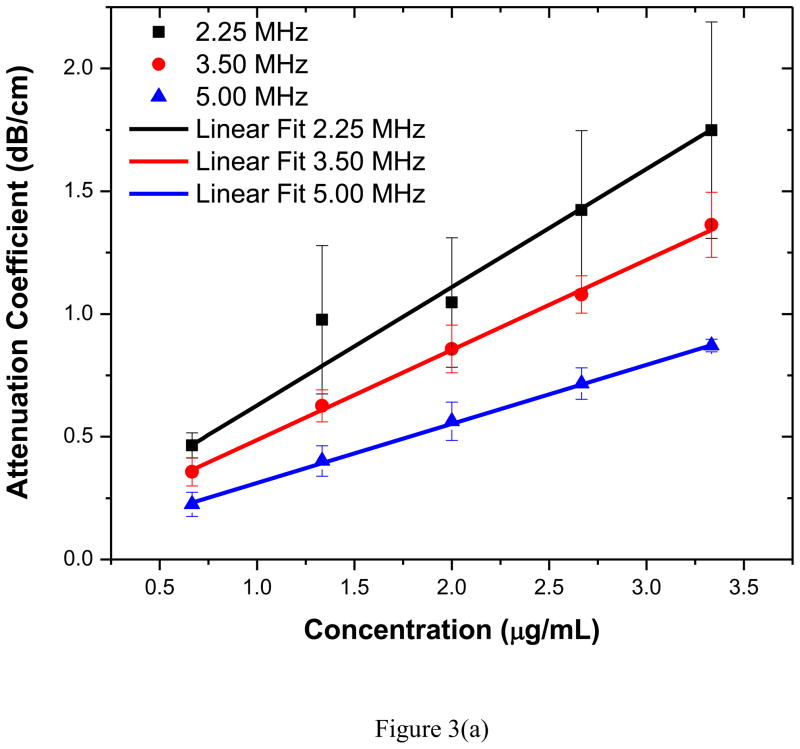
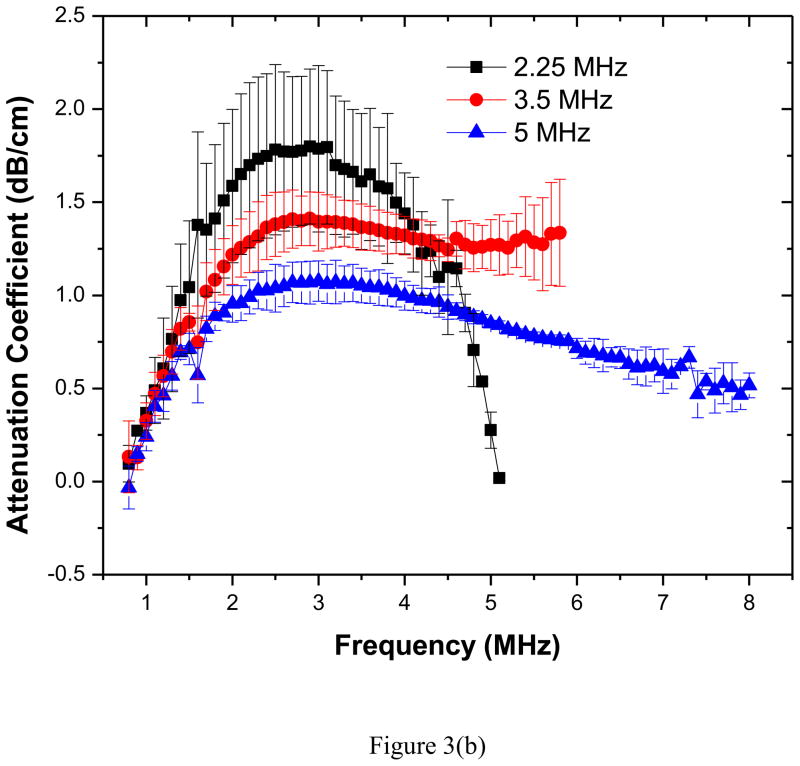
Attenuation measurements were obtained for five different concentrations of contrast agent using all three transducers. Frequency dependent attenuation coefficients plotted for each measurement were generated using the data reduction technique explained earlier. The value of the attenuation coefficient corresponding to the center frequency of each transducer was then extracted. The average value for each set of five experiments along with the corresponding standard deviation was then plotted in Figure 3(a). Note that for the range of concentrations studied here, the attenuation increases linearly for all three transducers used indicating minimal effects of multiple scattering for the dilute concentrations considered. Figure 3(b) shows the frequency dependent attenuation coefficient obtained for the highest concentration for three different transducers. Attenuation coefficients obtained with different transducers are similar in the region of their overlapping bandwidth frequencies. The peak of the attenuation curve occurs around 2.5–3 MHz indicating a weighted-average resonance frequency of the polydispersed sample within this range.

Figure 3.

(a) Attenuation coefficient at the central frequencies of the three transducers (2.25, 3.5, 5 MHz) as a function of bubble concentration (averaged over five different acquisitions). (b) Frequency dependent attenuation coefficient measured with three different transducers (with central frequencies 2.25, 3.5, 5 MHz) averaged over five different acquisitions.

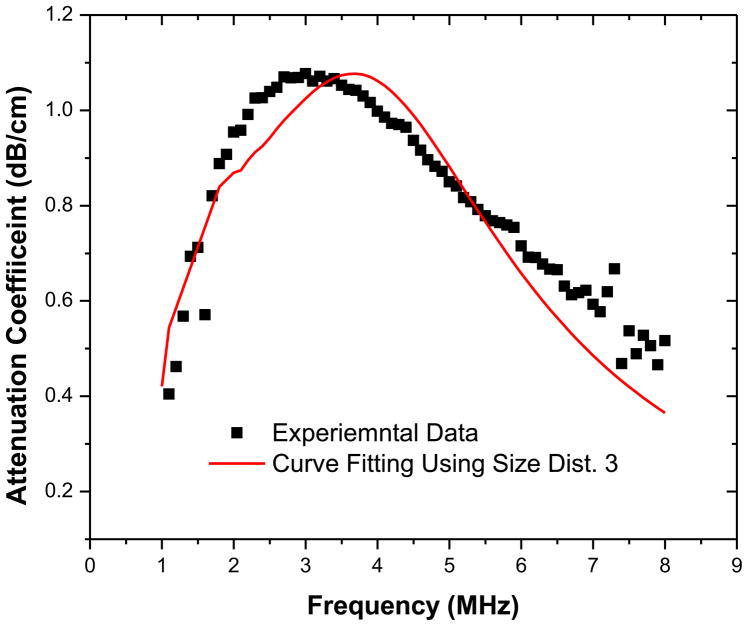
Using the method described earlier the unknown parameters pertaining to each model are calculated and given in Table 2 using the three different size distributions noted above. Note that for the Marmottant model, we assumed that the contrast agent is initially in a buckled state with a zero surface tension; this would render them initially stable in the absence of acoustic excitation. The frequency dependent attenuation curves obtained through modeling (using each bubble size distribution) match very well with experiment. We show the match only for the Newtonian model (Figure 4); others are very similar and not shown for brevity. However, note that unlike in our previous experience (Paul et al. 2010), using average size and total number did not work very well in estimating the parameters; depending on the initial guesses for the parameters at the start of the minimization, often the error minimization procedure did not converge, and when it converged, it gave rise to unphysical values for the material parameters. The inability of using an average diameter for parameter estimation indicates the importance of the polydispersity of the bubble size distribution and the limitation of the estimation process adopted here. One has to be careful in adopting such a process and interpreting the results.

Table 2.

Estimated property values characterizing the PLA shelled UCAs corresponding to three different models for encapsulated microbubbles and three different bubble distributions.

Encapsulation Model	Estimated Parameters
	Size distribution 1	Size distribution 2	Size distribution 3
Newtonian model (NM)	γ= 0.08 N/m	γ= 0.06 N/m	γ= 0.03 N/m
	κs= 7.5×10−9 N.s/m	κs= 8.5×10−9 N.s/m	κs = 2.0×10−9 N.s/m
Viscoelastic constant elasticity model (CEM)	γ0= 0.02 N/m	γ0=0.01 N/m	γ0=0.01 N/m
	Es = 0.07 N/m	Es= 0.05 N/m 0	Es= 0.02 N/m
	κs= 7.5×10−9 N.s/m	κs= 8.5×10−9 N.s/m	κs= 2.1×10−9 N.s/m
Viscoelastic exponential elasticity model (EEM)	γ0= 0.02 N/m	γ0= 0.01 N/m	γ0=0.01 N/m
	$E_0^s=0.07\text{N}/\text{m}$	$E_0^s=0.05\text{N}/\text{m}$	$E_0^s=0.02\text{N}/\text{m}$
	α= 1.5	α= 1.5	α= 1.5
	κs= 7.5×10−9 N.s/m	κs=8.5×10−9 N.s/m	κs=2.1×10−9 N.s/m
Marmottant Model (MM)	γ0= 0.00 N/m	γ0=0.00 N/m	γ0=0.00 N/m
	χ=0.08 N/m	χ=0.06 N/m	χ=0.04 N/m
	κs= 7.5×10−9 N.s/m	κs=8.5×10−9 N.s/m	κs=2.0×10−9 N.s/m

Figure 4.

Experimentally measured attenuation and prediction by the Newtonian model obtained during parameter estimation using sample 3 size distribution.

The estimated parameters for three different size distributions are similar except for slightly smaller dilatational viscosity for the size distribution 3 (Note also slightly smaller surface tension value for this distribution but only for the Newtonian model). The smaller dilatational viscosity for distribution 3 can be explained by noting that damping of a bubble increases as the radius decreases (Katiyar and Sarkar 2011; Katiyar and Sarkar 2012). Size distribution 3 has the largest fraction of smaller bubbles. Therefore, the same attenuation data gives rise to the smallest damping for this distribution. Note that the interfacial elasticity values predicted for PLA coated microbubbles (0.02–0.07 N/m) are an order of magnitude smaller than the values reported previously for phospholipid coated bubbles (~0.5 N/m) (Sarkar et al. 2005; van der Meer et al. 2007; Paul et al. 2010). However, the interfacial viscosity values (2×10⁻⁹–8.5×10⁻⁹ kg/s) are similar to those reported in the literature for other bubbles. Using size distribution 3 predicts the lowest values of surface dilatational viscosity and therefore correspondingly the lowest damping which critically affects the subharmonic response from microbubbles as discussed in a later section. Note that unlike Sonazoid, here we obtain a reasonable value of surface tension γ even for the Newtonian model. For the other models, it (γ₀) achieves a value lower than the air-water interface value (γ_w =0.07 N/m). The low surface tension along with an extremely low value of elasticity contributes to the low average resonance frequency seen for these microbubbles.

Resonance frequency

Figure 3(b) indicates that the measured attenuation increases with increasing frequency reaching a peak in the range of 2.5–3 MHz—indicating the incidence of the average resonance frequency there—and decreases thereafter. Because the response of a bubble is considerably higher at its resonance frequency, the peak in attenuation occurs there. However, note that the reasoning strictly holds for a monodisperse bubble population. The frequency for the peak response agrees well with the previously reported value of 2.28 MHz (El-Sherif and Wheatley 2003a). As noted before, resonance frequency of the PLA bubble was reported to be lower than that of a same sized free bubble, in contrast to other contrast microbubbles where the elasticity of the encapsulation increases the stiffness giving rise to a higher resonance frequency (van der Meer et al. 2007). The resonance frequency of a free bubble is often estimated using the well known Minneart formula

$$f_{\mathit{Minneart}}(\mathit{MHz})\approx \frac{3.26}{R_0(\mu m)}$$ (15)

However, note that this formula is more appropriate for bubbles of size mm and above; it includes only the term due to the gas compressibility—the first term inside the bracket in equation (5)—and neglects the contribution due to surface tension. The surface tension term becomes high for bubbles of micrometer size and is of the same order as the compressibility term. For a free air bubble in water with an average diameter of 1.9 μm, the resonance frequency computed with Minneart formula (3.43 MHz) becomes significantly larger (5.01 MHz) when corrected for the surface tension effects. Therefore, the decrease in resonance frequency with encapsulation is even higher (Wheatley et al. 2006), when one would expect the encapsulation to contribute to the stiffness of the damped mass-spring system and increase its resonance frequency. As we mentioned above, this paradox was noted before (Wheatley et al. 2006), and several hypotheses were proposed for explaining it, e.g. presence of gas-filled cells with an average diameter less than that of the entire capsule, or a highly porous capsule where tiny chambers have a greater contribution to the actual dynamics, or a disproportionate contribution from bubbles of different sizes to the overall dynamics. Note however that a smaller effective radius would lead to an even higher resonance frequency.

We argue that the result stems from several effects—the reduced surface tension, γ₀ extremely small dilatational surface elasticity and the polydispersity of the size distribution, which makes the average diameter irrelevant for determining average properties. It explains the difficulty in the property estimation using average diameter described above. The attenuation curve with its maximum peak position results from attenuation due to bubbles of different sizes from the entire size distribution that includes small number of larger bubbles with size different from the average of the size distribution. These bubbles have their peak attenuation at a frequency lower than the one corresponding to the average size. Using only average radius therefor inevitably leads to a larger resonance frequency, as it neglects the effects of these larger bubbles. Note also that nonlinearity can decrease the resonance frequency (Doinikov et al. 2009; Overvelde et al. 2010); for lipid shelled microbubbles it tends to decrease with increasing acoustic excitation pressure. We will see in the subsequent sections that the non-linearity of PLA bubbles sets in at much lower excitation pressures (around 100–150 kPa).

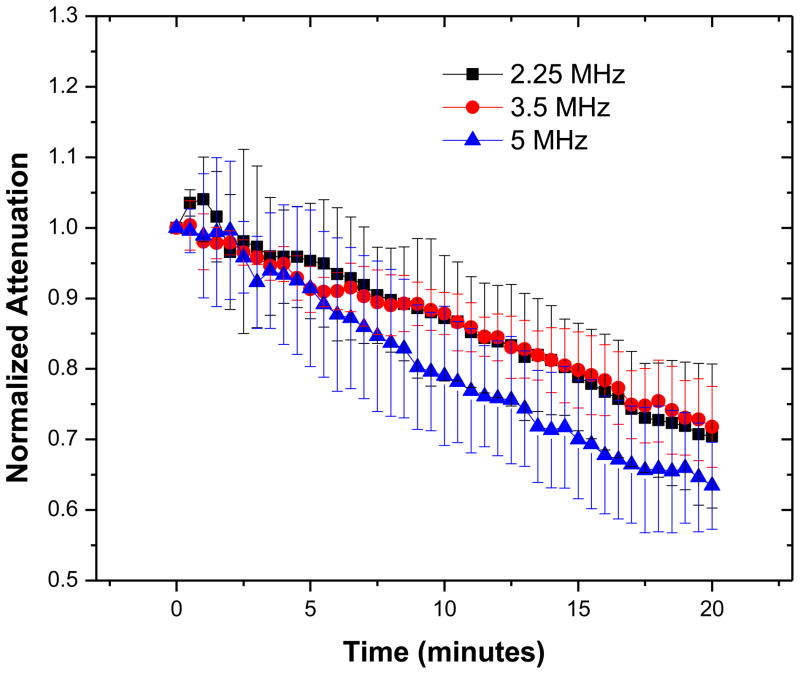
Time-dependent attenuation

Sustained acoustic excitation changes the state of the encapsulation which in turn affects bubble stability and lifetime (Eisenbrey et al. 2008). To investigate the bubble lifetime under acoustic excitation, attenuation was measured as a function of time and plotted in Figure 5. It shows a steady decrease with time, as was also observed previously (Krasovitski et al. 2004; Chatterjee et al. 2005a; Casciaro et al. 2007). Contrast agents containing gases other than air show a transient increase in attenuation initially before its eventual decrease. The increase in attenuation is caused by transient growth of bubble volume due to air diffusing much faster initially into them compared to the outward diffusion of low-solubility gases (Shi and Forsberg 2000). Air-filled PLA agents do not show any such transient increase. We notice that over the 20 min period the attenuation drops by 30–40%. Note that previous time response backscatter study with PLA (El-Sherif and Wheatley 2003b) and PLGA (50:50) (Wheatley et al. 2006) contrast microbubbles also noted a 15% loss in enhancement over the same time period.

Figure 5.

Normalized total attenuation coefficient with time. The data were averaged over five different acquisitions each collected continuously and averaged over consecutive 30 second intervals.

Scattering and comparison with model prediction

Fundamental and second harmonic responses

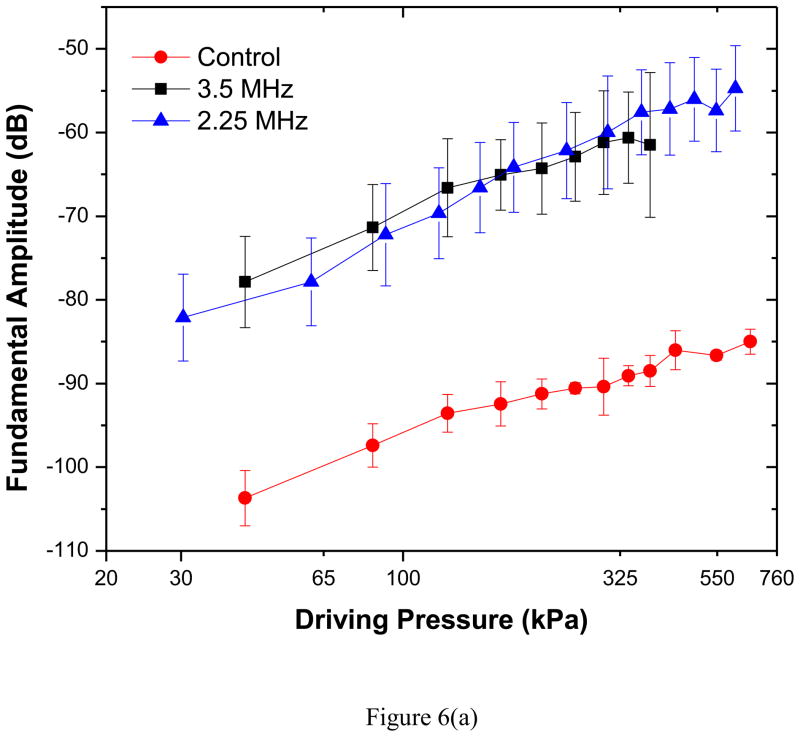
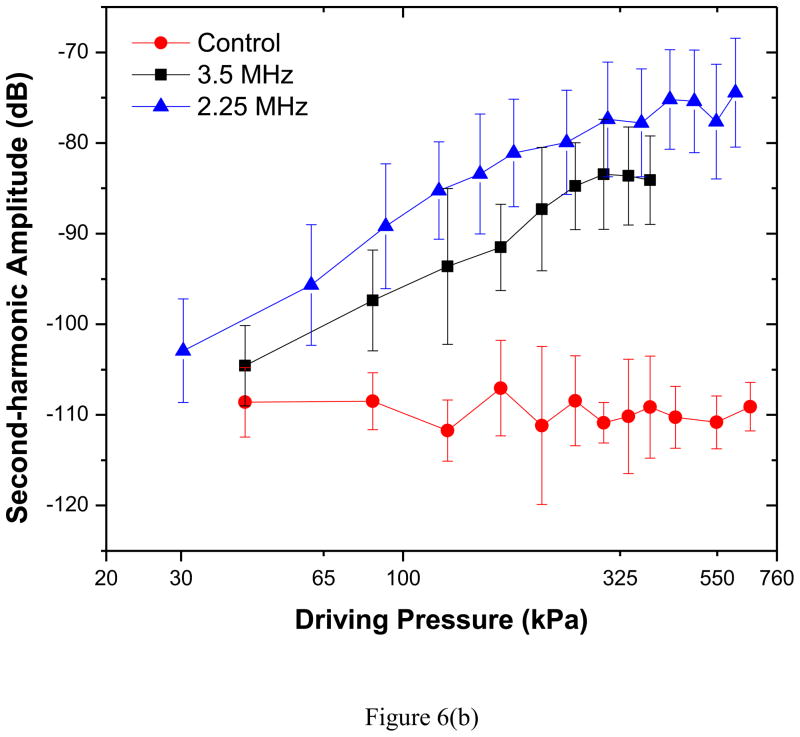
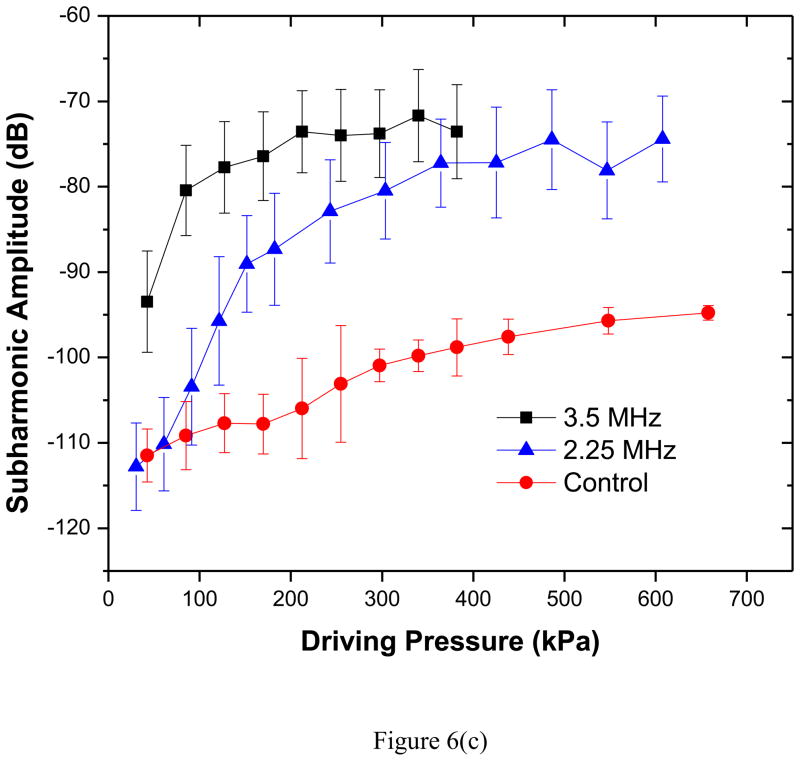
Scattered response from PLA shelled contrast agents was acquired varying acoustic pressure amplitudes at two different excitation frequencies of 3.5 and 2.25 MHz. Averages and standard deviations of five independent acquisitions at each pressure amplitude were then obtained through above mentioned data analysis technique. Fundamental (at excitation frequency), second-harmonic (at twice the excitation frequency) and subharmonic (at half the excitation frequency) responses for both the transducers are shown in Figures 6(a)–(c).

Figure 6.

Experimentally measured scattered response from PLA microbubbles for two different excitation frequencies (2.25 MHz, 3.5 MHz): (a) Fundamental (b) Second harmonic and (c) Subharmonic. Control indicates data without any bubbles introduced.

The fundamental response shows a 25–30 dB enhancement in the entire range of excitations for both frequencies. Previous in vitro scattering experiments with PLA microbubbles reported similar enhancement—around 17 dB at 5 MHz and 690 kPa excitation pressure (estimated from the dose response curve for the concentration of 1.33μg/ml) (Eisenbrey, Burstein 2010). For a PLGA (50:50) microbubble, the enhancements were 10 dB at 2.25 MHz and 20 dB at 5 MHz (Wheatley et al. 2006). The second harmonic shows an enhancement of 10–35 dB (2.25 MHz) and 5–25 dB (3.5 MHz). The results demonstrate the echogenicity of PLA agents, specifically their efficacy for harmonic contrast imaging, where the second harmonic response is imaged.

Both fundamental (Figure 6a) and second harmonic (Figure 6b) responses (plotted in a log-log scale) for each excitation frequency show an approximately linear increase with increasing acoustic pressures; They deviate from linearity at higher pressure; especially the second harmonic response curve flattens beyond 320 kPa, possibly due to bubble destruction. The slopes for the curves are found to be 0.92 at 3.5 MHz and 1.15 at 2.25 MHz for fundamental response and about 1.5 at both frequencies for second harmonic. Small amplitude perturbation analysis predicts them to be 1 (fundamental) and 2 (second harmonic). However, experimentally measured slope of second harmonic has been shown to deviate from its theoretical value of 2 (Shi and Forsberg 2000).

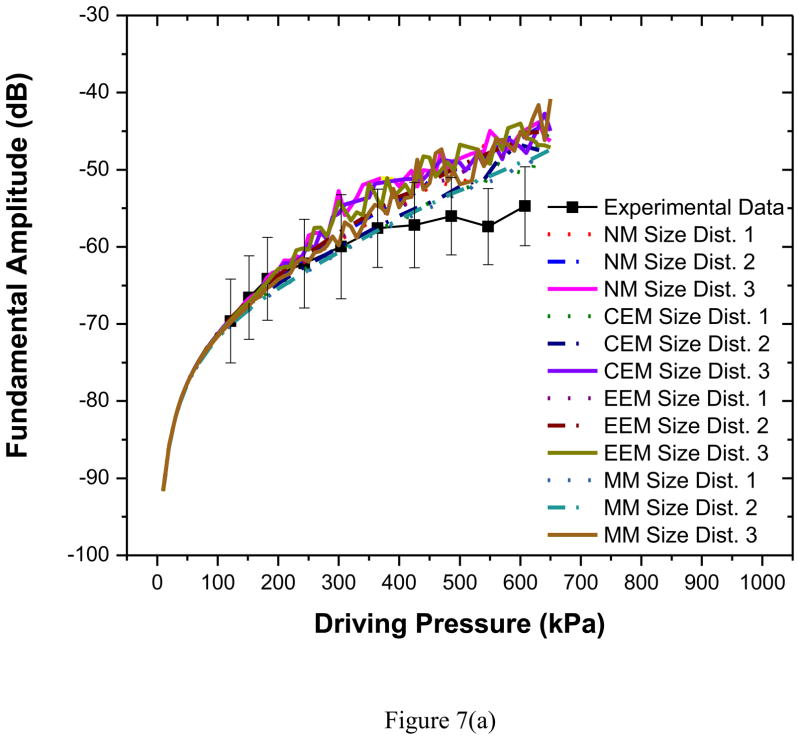
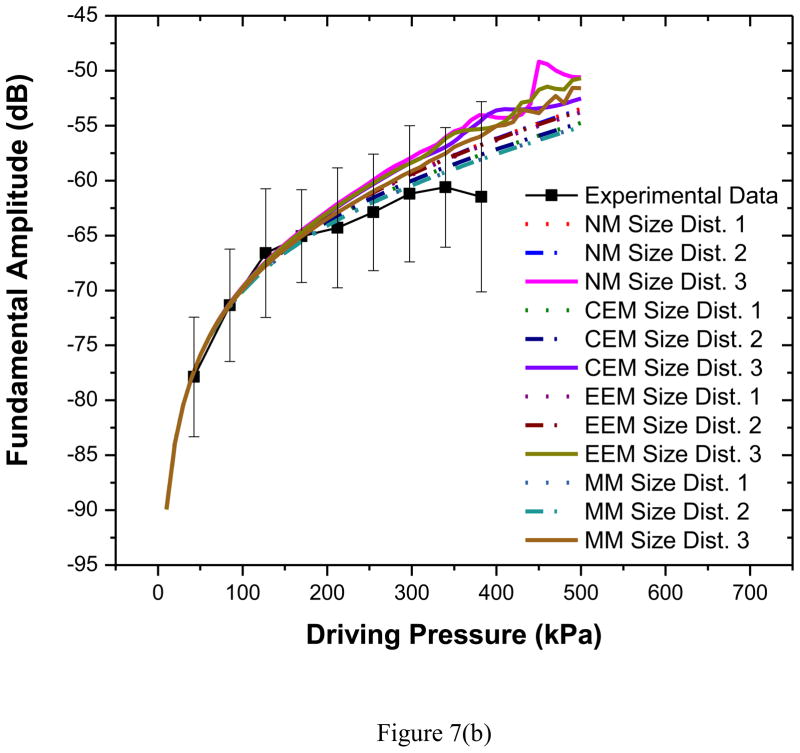
We also simulated the scattered response from the microbubbles using several models. Note that for each model, we obtained three different predictions, using three different set of parameter values obtained using the three different size distributions given in Table 1 and Figure 2. The scattered responses were computed using the corresponding size distributions. For both excitation frequencies, predicted fundamental response from all three models [Figures 7(a)–(b)] shows good agreement with experimental data for all three bubble distributions (size dist. 1–3). The experimental curve deviates at higher pressures from model predictions. The deviation occurs approximately around the same pressure value (320 kPa) where the linearity of the experimental result breaks down due to possible bubble destruction (Chatterjee et al. 2005a). Destruction is not accounted in any of the models which might explain the difference between the model prediction and the experimental observation.

Figure 7.

Comparison of experimentally measured and predicted scattered fundamental response from different models for PLA bubbles using three different size distributions at (a) 2.25 MHz excitation (b) 3.5 MHz excitation. NM: Newtonian Model, CEM: Constant Elasticity Model, EEM: Exponential Elasticity Model and MM: Marmottant Model.

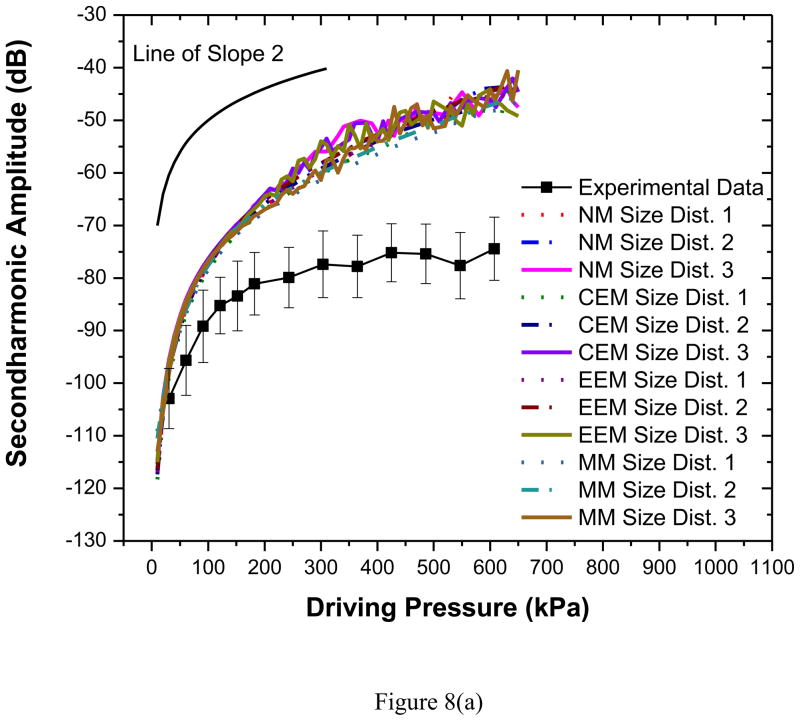
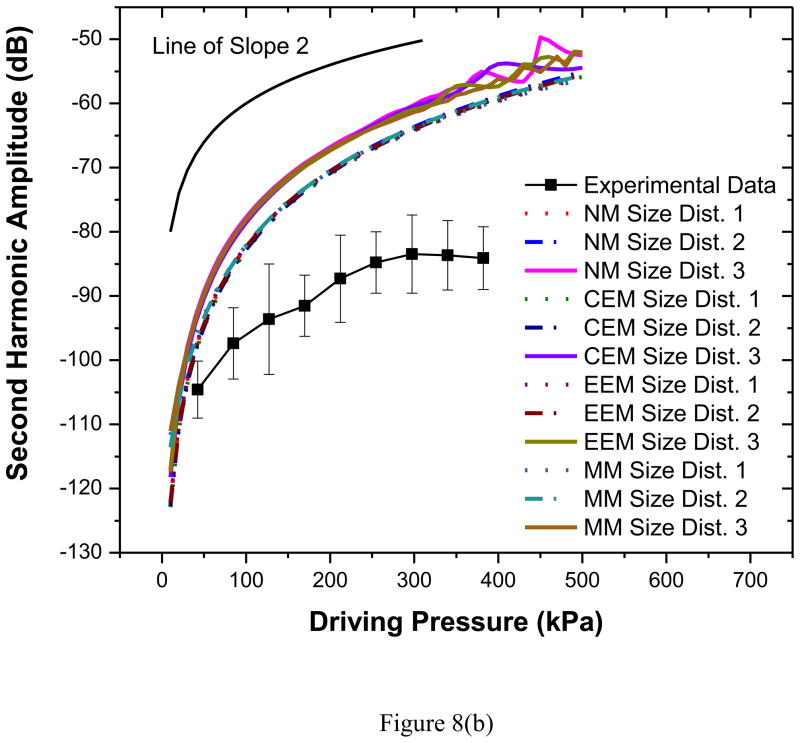
Second harmonic responses predicted by different models show a slope of 2, as they should, in contrast to the experiments as noted before [Figures 8(a) and (b)]. They do not match very well even for the lower acoustic pressures. However, the predictions from all three models and three size distributions are similar. Note that the second harmonic frequencies studied here are within the receiving bandwidth of the transducer used. The discrepancy in the model prediction points towards the inadequacies of the modeling effort. Also as mentioned before the bubble destruction that might affect the nonlinear response was not accounted for in the models.

Figure 8.

Comparison of experimentally measured and predicted scattered second harmonic response from different models for PLA bubbles at (a) 2.25 MHz excitation (b) 3.5 MHz excitation. NM: Newtonian Model, CEM: Constant Elasticity Model, EEM: Exponential Elasticity Model and MM: Marmottant Model. A line with a slope of 2 is also shown for comparison.

Subharmonic Response

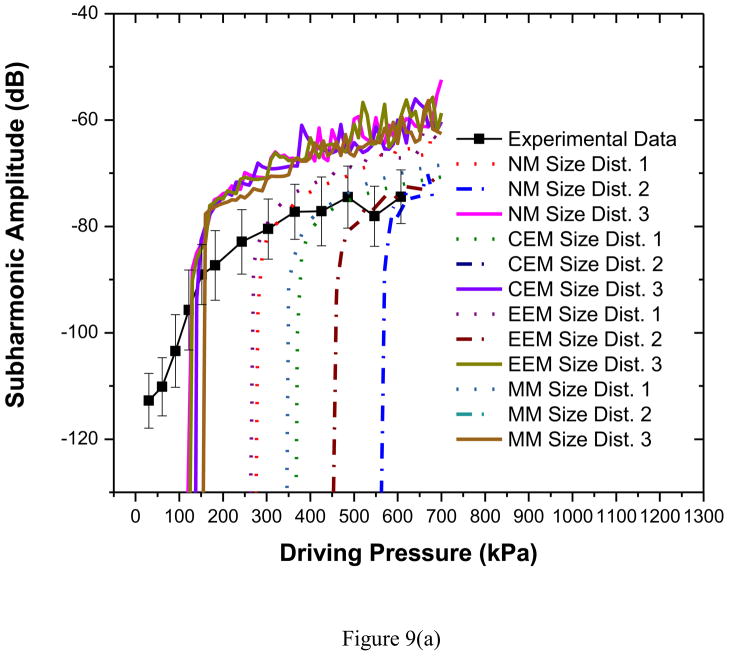
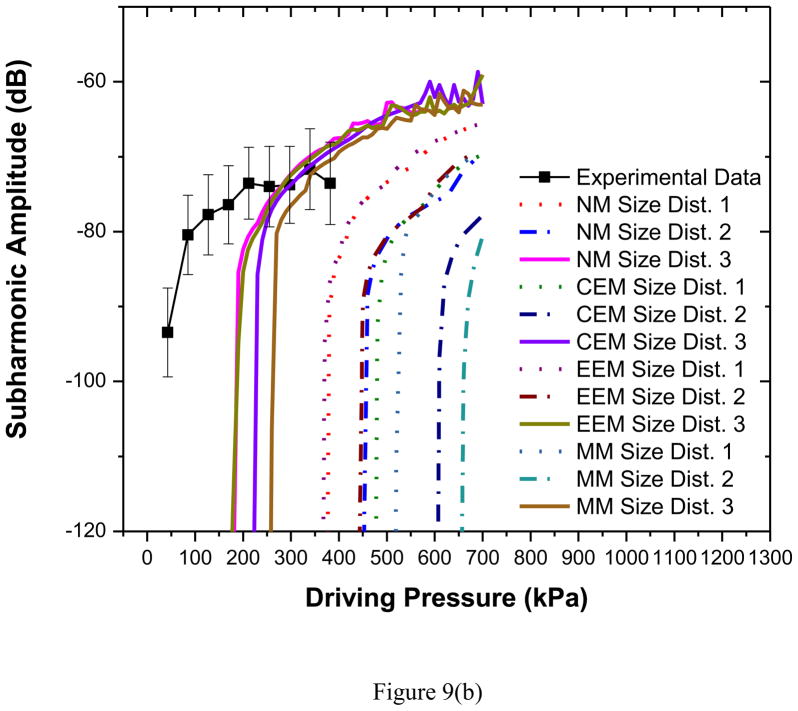
The scattered subharmonic response from PLA microbubbles [Figure 6(c)] shows the typical characteristics—initially no subharmonic before a threshold pressure value, at threshold a rapid rise followed by a saturation—at both frequencies (Shi and Forsberg 2000; Sarkar et al. 2005). The excitation threshold at excitation frequency of 2.25 MHz is 125 kPa, slightly higher than 100 kPa at 3.5 MHz. The classical bubble dynamics theory predicts minimum threshold for subharmonic generation to be at twice the resonance frequency (Eller and Flynn 1968; Neppiras 1968; Prosperetti 1977a). Observations for two different encapsulated microbubbles—Optison (Shankar et al. 1999) Definity (Kimmel et al. 2007) were reported to follow this theory. The frequency for minimum subharmonic threshold for PLA agents is therefore expected to be between 5 and 6 MHz. Note however that we have recently shown that the minimum threshold shifts towards resonance away from twice its value for encapsulated microbubbles due to large damping (Katiyar and Sarkar 2012). We also showed that the threshold is rather flat in the region between resonance and twice its value. We note that the threshold at 3.5 MHz is only slightly lower than that at 2.25 MHz.

All models considered here predict very low acoustic response until the threshold is reached (Figures 9a–b). Hence, model predictions are shown only when it is above −120 dB (above the noise level, −115 dB, of the experimental measurement). Unlike the fundamental response the simulated subharmonic response does not show an unqualified match for all bubble distributions. Note that the post-threshold response level is matched well for both frequencies. However, predicted threshold value varies. For both frequencies, the size distributions 1 and 2 exhibit much higher threshold values in comparison to experimental data [See Table 3]. The size distribution 3—which has larger fraction of smaller bubbles (Figure 2)—matches very well (solid curves) the threshold for 2.25 MHz excitation, and is closer to the experimental measurements for 3.5 MHz.

Figure 9.

Comparison of experimentally measured and predicted scattered subharmonic response from different models for PLA bubbles at (a) 2.25 MHz excitation (b) 3.5 MHz excitation. NM: Newtonian Model, CEM: Constant Elasticity Model, EEM: Exponential Elasticity Model and MM: Marmottant Model. The curves for CEM and MM, size distribution 2, 2.25 MHz have thresholds too high to be seen here.

Table 3.

Threshold pressure for subharmonic generation obtained experimentally and from different models for all three size distributions studied.

Frequency	2.25 MHz	3.5 MHz
Experiments	125kPa	100kPa
NM	Size Distribution 1: 280 kPa	Size Distribution 1: 380 kPa
	Size Distribution 2: 570 kPa	Size Distribution 2: 460 kPa
	Size Distribution 3: 130 kPa	Size Distribution 3: 190 kPa
CEM	Size Distribution 1: 370 kPa	Size Distribution 1: 480 kPa
	Size Distribution 2: 1500kPa	Size Distribution 2: 610 kPa
	Size Distribution 3: 140 kPa	Size Distribution 3: 230 kPa
EEM	Size Distribution 1: 270 kPa	Size Distribution 1: 370 kPa
	Size Distribution 2: 460 kPa	Size Distribution 2: 450 kPa
	Size Distribution 3: 130 kPa	Size Distribution 3: 190 kPa
MM	Size Distribution 1: 350 kPa	Size Distribution 1: 520 kPa
	Size Distribution 2: 830 kPa	Size Distribution 2: 660 kPa
	Size Distribution 3: 160 kPa	Size Distribution 3: 250 kPa

Model validation and their Predictive capability

In our previous modeling exercise, we have emphasized the need for independent model validation (Chatterjee and Sarkar 2003; Sarkar et al. 2005; Paul et al. 2010). We determined the model parameters through linear attenuation data, as is done here, and then validated the model by investigating its ability to predict subharmonic response obtained at higher excitations. In fact, our modeling exercise led to results that dictated model improvements from Newtonian to constant elasticity model to exponential elasticity model. For Albunex, Optison and Sonazoid (Chatterjee and Sarkar 2003) the Newtonian model resulted in an unrealistically large value of surface tension and hence deemed unsuitable for modeling encapsulated microbubbles. As a result, we introduced surface dilatational elasticity (Sarkar et al. 2005). However, here, we find a very low value of surface elasticity for the PLA encapsulation, and even the Newtonian model predicts low surface tension values; for the size distribution 3 it is lower than that of the air-water interface. As mentioned above, only for the size distribution 3, we get prediction match with experimentally measured thresholds. For this distribution all models predict similar value—constant elasticity and Marmottant models, predicting slightly higher than the Newtonian and exponentially elasticity, the latter two being the same. The Newtonian model therefore remains an effective model to describe PLA bubbles. We use it below to further examine certain features of PLA microbubbles.

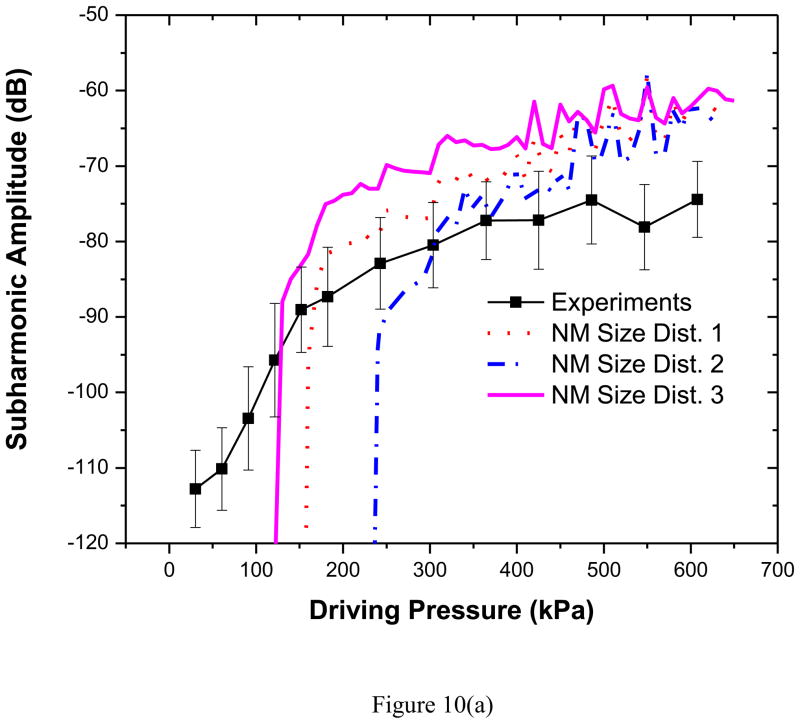
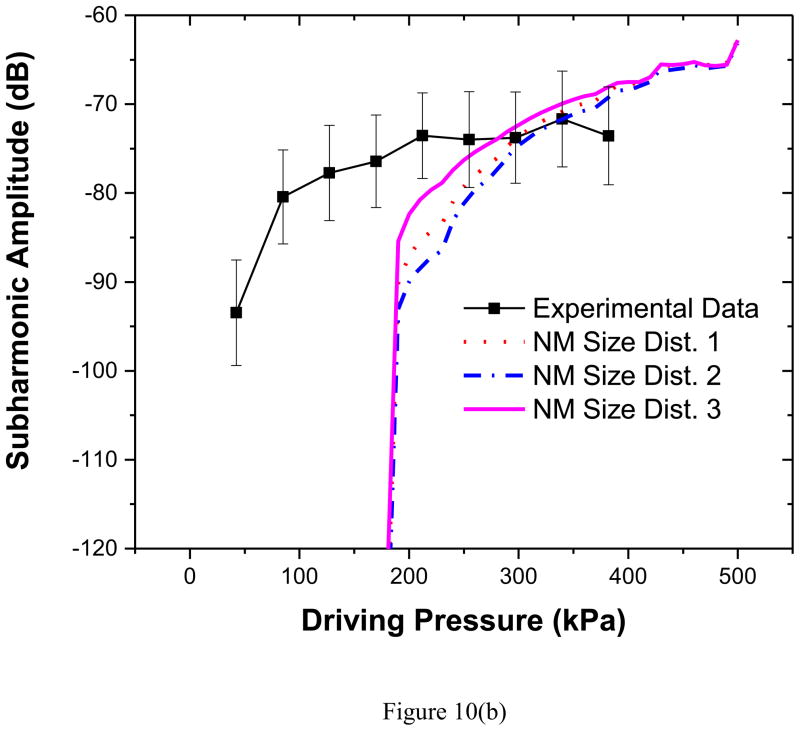
We note that all models perform poorly in predicting second harmonic response, and clearly more research is needed in resolving this discrepancy. However, for predicting subharmonic response, size distribution 3 fares the best (see Table 3 for subharmonic threshold), indicating that the behavior of any model describing dynamics of encapsulated microbubbles is critically dependent on the bubble size distribution (As mentioned above, such extreme sensitivity on size distribution, where in fact the different size distributions were obtained from the same batch, also insinuates the limitation of the parameter estimation technique used). Specifically, the subharmonic threshold depends on the ratio of the excitation frequency to the natural frequency and the natural frequency is determined by the bubble size (Katiyar and Sarkar 2011). More bubbles with lower threshold value for subharmonic threshold would lower overall threshold value as well. Also, as we noted already, variation in size distribution from sample to sample affected corresponding property values for the three samples; the sample 3 has the lowest value of surface dilatational viscosity—1/3–1/4 of the other two samples. Decreased damping lowers the subharmonic generation threshold (Katiyar and Sarkar 2011; Katiyar and Sarkar 2012). To further investigate the effects of the material parameters and the size distribution on the predicted subharmonic response, we use the material properties (low value of the dilatational viscosity κs = 2.0×10⁻⁹ N.s/m) determined using the size distribution 3 but compute subharmonic response with all distributions including 1 and 2. The results in Figure 10(a) and (b) show that the lower dilatational viscosity predicts subharmonic response closer to the experimentally measured value even with the other two size distributions. We therefore conclude that the lower dilatational viscosity (albeit determined with the size distribution corresponding to the sample 3) is the critical factor. This underscores the fact that accurate estimation of the average material parameters of the encapsulation critically depends on the ability to measure the size distribution, and inter-sample variation has to be taken into account (Commander and Prosperetti 1989).

Figure 10.

Comparison of experimentally measured and predicted scattered subharmonic response from PLA bubbles with Newtonian Model with different size distributions and Sample 3 parameter values at (a) 2.25 MHz excitation (b) 3.5 MHz excitation. NM: Newtonian Model.

Summary and Conclusion

In this article, we characterized PLA coated air containing microbubbles through in vitro scattering and attenuation experiments. Four different models—Newtonian, constant elasticity, exponential elasticity and Marmottant—of microbubble encapsulation were used to determine the interfacial rheological properties of the micobubble. Unlike our previous investigation of Sonazoid and Optison, we found low values for interfacial tension and surface dilatational elasticity, which explains similar results (and similar property values) from all models. However, sample to sample size distribution variation for the same batch of contrast agent gives rise to variation in properties determined using them.

The peak in the attenuation spectrum indicates a weighted average resonance at around 2.5–3 MHz in conformity with previous measurements. As noted before, this value of average resonance frequency is smaller than that of a free bubble of the same size (1.9 μm diameter). We offer a detailed discussion indicating the limitation of Minneart formula for the microbubbles showing that the reduced resonance frequency stems from the reduced surface tension, extremely low surface elasticity, and the polydispersity; normally the surface elasticity of an encapsulation results in an enhanced stiffness of the system thereby increasing the resonance frequency. The low value of the interfacial elasticity distinguishes PLA bubbles from other lipid and protein coated bubbles.

PLA microbubbles show both second and subharmonic scattered response due to nonlinear oscillations. All models predict similar dynamics and they match the fundamental scattered response very well, but fail in predicting the second harmonic response clearly indicating a need for further research. Experimentally measured second harmonic response shows a slope of 1.5 in contrast to the theoretical value of 2. The subharmonic response shows its characteristic features—its appearance only above a threshold excitation level (100–150 kPa) and then a sharp rise with increasing excitation strength. The models predict the characteristic features of subharmonic response and the post-threshold response amplitude. The size variation from sample to sample gives rise to variation in properties, in particular for surface dilatational viscosity. The lower value of the surface dilatational viscosity obtained using one of the measured size distribution results in better prediction of the experimentally measured subharmonic threshold value.

This experimental and modeling study of PLA coated contrast microbubbles using two independent acoustic experiments—linear attenuation for model determination and nonlinear scattering for validation—indicates several unique features of PLA coated microbubbles such as extremely low value of encapsulation elasticity, relatively low value of subharmonic threshold, and explains the low resonance frequency experimentally observed here as well as before. It also shows that contrast microbubbles are polydisperse complex systems and underscores the importance of careful analysis needed for analyzing experiments performed on them.