Aberration Compensation of an Ultrasound Imaging Instrument With a Reduced Number of Channels

Abstract

Focusing and imaging qualities of an ultrasound imaging system that uses aberration correction were experimentally investigated as functions of the number of parallel channels. Front-end electronics that consolidate signals from multiple physical elements can be used to lower hardware and computational costs by reducing the number of parallel channels. However, the signals from sparse arrays of synthetic elements yield poorer aberration estimates. In this study, aberration estimates derived from synthetic arrays of varying element sizes are evaluated by comparing compensated receive focuses, compensated transmit focuses, and compensated b-scan images of a point target and a cyst phantom. An array of 80 × 80 physical elements with a pitch of 0.6 × 0.6 mm was used for all of the experiments and the aberration was produced by a phantom selected to mimic propagation through abdominal wall. The results show that aberration correction derived from synthetic arrays with pitches that have a diagonal length smaller than 70% of the correlation length of the aberration yield focuses and images of approximately the same quality. This connection between correlation length of the aberration and synthetic element size provides a guideline for determining the number of parallel channels that are required when designing imaging systems that employ aberration correction.

I. Introduction

Ultrasonic b-scan imaging is widely used for detection and diagnosis of disease. However, current typical b-scan imaging instruments are limited by the lack of adjustable focusing in the elevation dimensions of typical apertures. In addition, focusing and imaging qualities can be greatly degraded by aberration induced by heterogeneity in the acoustic properties of tissue along the propagation path between the transducer and the region being imaged. Improved images can be formed by estimating and compensating for this aberration, but this requires acquisition of more received signals than are generally required for imaging. These observations motivate an examination of the qualities of focusing and imaging in an ultrasound imaging system as a function of the number of parallel channels when aberration corrections are applied.

Most current clinical ultrasound imaging devices treat the waveform propagation path as a homogeneous medium. However, arrival time, amplitude, and pulse-shape can be appreciably distorted by aberration in the propagation path when imaging the breast or when imaging through the abdominal wall [1]–[3]. Recognition of the degrading influence of aberration has led to various methods intended to correct wavefront distortions. Methods based on temporal cross-correlation are widely used in aberration estimation and correction [4]–[8], especially when waveforms originate from point reflectors. However, point reflectors are not usually available to provide waveforms for cross-correlation. Spatial coherence of waveforms is substantially degraded when an imaged target is surrounded by randomly distributed scatterers [9], [10], resulting in poor estimations of aberration. Nevertheless, even in a random scattering medium, near point-reflector responses can still be obtained by applying statistical methods to a filter-bank model [11] and improved compensation is realized when the filter bank is offset from the transducer array [12]. These statistical methods are based on the cross-spectral measurements of random media over a set of regions that are in one isoplanatic patch but far enough apart so that the scattering is uncorrelated.

Measurements show that aberration in the elevation direction is comparable to that in the array direction [1], [13]. The need for aberration correction in both directions motivates the wide use of multirow arrays and two-dimensional arrays in ultrasound research. Evaluations of the performance of multirow arrays indicate that focusing in the elevation direction provides better point resolution and contrast resolution than conventional one-dimensional arrays [14], [15]. Multirow arrays with relatively large element height in the elevation dimension are replacing conventional one-dimensional linear arrays in ultrasound research [16]–[19]. However, large element height can reduce the effectiveness of time-shift compensation, thereby degrading the focusing quality [20]–[25]. Thus, the study of the degree to which element elevation height affects aberration estimation and correction is of practical interest. Two-dimensional arrays with the same element pitch in the elevation and array dimensions have been used in current ultrasound research [26], [27] because these arrays provide identical focusing ability in the elevation dimension and the array dimension. For geometric focusing, the element pitch is usually about a wavelength at the center frequency. However, the effect of large square element sizes on focusing and imaging qualities in the presence of aberration correction for two-dimensional arrays has not been studied. Using signals from coarse arrays of large synthetic elements to estimate aberration may help reduce the associated computational cost of the data processing and the complexity of hardware. This reduction is a practical requirement for integration of aberration correction into current ultrasound imaging instruments.

Earlier studies and measurements mainly concentrated on the effect of element height on the one-way focusing quality for multirow arrays used for aberration correction [21]–[25]. Thus, more measurements and analysis of the effect of element size on focusing and imaging qualities that use other aperture geometries, element pitches, and improved aberration correction methods are needed. This study examines experimentally how aberration estimates derived from coarse arrays of synthetic elements affect the focusing and imaging qualities of an ultrasound imaging system. The aberration used in these experiments is produced by an aberration phantom that mimics strong aberration from the abdominal wall. The aberration was estimated using received signals from arrays of synthetic elements with a variety of different pitches in the elevation and array directions. A least-mean-square-error method [6] of time-shift estimation was used to estimate the aberration in echoes from a point reflector and a statistical method based on a filter-bank model [12] was used to estimate the aberration for imaging a scatterer-free (cyst-mimicking) region surrounded by random tissue-mimicking scatterers. The quality of receiver sensitivity patterns with compensations derived from synthetic arrays with different pitches were quantified in elevation and array directions by effective widths and radii as well as peripheral energy ratios. Transmit focuses with compensations derived from synthetic arrays with different element pitches were also measured, and were compared using the same metrics as the receive focuses. B-scan images of a point target and a cyst phantom (i.e., a scatterer-free region) were also generated using compensations derived from synthetic arrays with different pitches, and widths of the imaged point reflector and contrast ratios of the imaged cyst were used to evaluate the quality of the different compensations. The results of this study provide comprehensive comparisons of the effectiveness of aberration correction with different array partitions within a fixed two-dimensional aperture.

II. Method

A. Overview of the Measurements

The transducer array used for measurements in this study is a two-dimensional array of 80 × 80 elements spanning an area of 48 × 48 mm with a pitch of 0.6 × 0.6 mm [26]. This array was used to generate incident transmissions and was also used to collect the reflected echoes. Incident transmissions were formed by exciting each element of the array with a modulated Gaussian pulse. A pulse with the same center frequency (3 MHz) and the same Gaussian bandwidth (σ = 1.8 MHz) was transmitted from every physical element, but the times of the excitations were varied from element to element by time delays that focused the composed transmissions at a fixed distance along the array axis. Additional time delays were also introduced to compensate for aberration. The receive signals at each array element were sampled at 20 MHz with 12-bit resolution.

Coarse arrays of synthetic elements were formed by partitioning the physical array into rectangular subarrays. A receive signal from each synthetic element was generated by summing together the signals from all the physical elements belonging to the aperture of the synthetic element. In this summation, the signals from the physical elements were shifted by time delays that were chosen to synchronize the responses from the focal point and were also adjusted by amplitude factors that apodized the elements across the physical aperture. These time delays are the same as the time delays used to geometrically focus the entire array. Thus, the sum of the signals from the synthetic elements in each coarse array yields the same response as a geometric focus of the entire array of physical elements.

Responses from different coarse arrays of synthetic elements were simulated to assess the effect of using front-end electronics to consolidate the signals from local groups of physical elements. As previously noted, the degree of coarseness of the synthetic array does not alter the uncompensated focus because the time delays assigned to the physical element are not altered by the way that the physical array is partitioned. This is consistent with the intended purpose of the partitions because time delays used for geometric focusing are determined by the scanning protocol and can be supplied to the front-end electronics at the time that the signals are acquired. However, time delays needed to compensate for aberration must be derived from the received signals of the synthetic elements and are, therefore, not available when the signals are acquired. Aberration estimates derived from the received signals of the synthetic elements yield a coarse set of time delays that can only be used to compensate the physical elements on a block-by-block basis. Fig. 1 illustrates the difference between the way that the time delays for geometric focusing are applied and the way that the time delays for aberration compensation are applied when forming transmit and receive focuses.

Fig. 1.

Configuration of (a) receive focus and (b) transmit focus.

The physical array was partitioned into two different types of synthetic elements. Synthetic elements of the first type are comprised of one-dimensional subarrays of physical elements, and the enlarged dimension of these elements is referred to as the elevation direction. The dimension of the physical array that is orthogonal to the elevation direction is referred to as the array direction. Synthetic elements of the second type are comprised of square subarrays of physical elements that have the same pitch in both dimensions. Partitions of synthetic elements with four different elevation pitches and partitions of synthetic elements with four different square pitches were simulated. The dimensions and configuration of the synthetic elements in these partitions are listed in Table I. The partitions are all centered at the center of the physical array, and each partition spans approximately the same set of physical elements. However, some physical elements along the boundary of the array are omitted from each partition, and these elements do not contribute to either the transmit or receive focuses for that partition.

TABLE I.

Aperture Geometries and Channel Numbers of Different Array Partitions.

Pitch (mm)	Elements per channel	Rows	Columns	Physical elements
Elevation pitch
1.8 × 0.6	3	25	79	75 × 79
3.0 × 0.6	5	15	79	75 × 79
4.2 × 0.6	7	11	79	77 × 79
5.4 × 0.6	9	9	79	79 × 79
Square pitch
1.8 × 1.8	9	25	25	75 × 75
3.0 × 3.0	25	15	15	75 × 75
4.2 × 4.2	49	11	11	77 × 77
5.4 × 5.5	81	9	9	79 × 79

The objective of the measurements is to characterize the effect of channel consolidation on aberration compensation. The aberration for the measurements is provided by an aberration phantom that is an elongated slab with parallel top and bottom surfaces. The aberration strength of phantoms of this type can be quantified by the rms value of the arrival-time fluctuations (ATFs) that result when a plane wave is propagated through the phantom from the top surface to the bottom surface, and further characterization of the aberration is provided by the correlation length of the arrival times. The rms value of the ATFs for this phantom is 72.5 ns and the correlation length is 6.1 mm. These values are consistent with the first- and second-order statistics of the typical strong ATFs that result from transmission of ultrasound through abdominal wall [3]. The phantom is composed of a random distribution of spherical beads with diameters of 6 and 12 mm that are embedded in a fat-mimicking background. The beads are made of material similar to that of the background, but with a sound velocity that is 2% faster. The ATFs induced by the phantom reflects the accumulated effects of the small differences in acoustic path length that are introduced by the beads. A detailed description of the abdominal-wall phantoms is found in [28].

The experimental methods described later measure the quality of aberration compensation realized from different partitions of synthetic elements based on the width of the receive focus, the width of the transmit focus, the point resolution realized in a b-scan image, and the contrast resolution realized in a b-scan image. The results are used to evaluate the time-shift compensation determined from the consolidated signals associated with each of the eight partitions listed in Table I.

B. Receive Focus Measurements

The term receive focus refers to the sensitivity pattern of the partitioned transducer array to echoes that emanate from different locations in the focal plane when the array is focused at the center of the focal plane (i.e., at the point where the axis of the transducer array intercepts the focal plane). The receive focus that results when the echoes propagate through water is an ideal focus that is the same for all partitions. However, when aberration is introduced, the ideal focus is corrupted. In that case, the quality of the receive focus depends on the effectiveness of the time delays used to compensate for the aberration. Because each partition of the physical array yields different estimates for the time delays used for aberration compensation, each partition has a different receive focus.

Receive focuses were computed from measurements of the echoes from a point reflector positioned at the focal point. A stainless-steel rod with a hemispherical tip was used for the point reflector. The diameter of the hemispherical tip of this rod is 0.8 mm, which is small enough to ensure that the hemisphere responds like a point reflector, but is also large enough to produce appreciable echoes. The tip of the rod was positioned at a depth of 55 mm below the center of the transducer array. The transducer array and stainless-steel rod were both immersed in a water tank that was maintained at 30°C by a water heating and circulation system. A 35-mm-thick aberration phantom was placed immediately below the transducer array, leaving approximately 20 mm of water between the bottom surface of the phantom and the tip of the stainless-steel rod.

Echoes from the point reflector were collected at all of the physical elements in the transducer array. These echoes were induced by a pulse-transmission that was geometrically focused on the reflector. A peak arrival time was estimated for the received signal at each physical element and the arrival times were interpreted as measures of the lengths of the transmission paths from the reflector to the physical elements. Arrival times of echoes that travel through water from the reflector to the array are proportional to the distances between the reflector and the physical elements. However, insertion of the aberration phantom perturbs these arrival times in two ways. The spherical inclusions in the phantom introduce rapid short-range fluctuations, and refraction at the top and bottom surfaces of the phantom introduce gradual long-range variations. The refraction effects are experimental artifacts that would not occur in clinical measurements. To eliminate the refraction effects, a fourth-order polynomial (in two variables) was fitted to the two-dimensional array of arrival times. The difference between the fitted polynomial of arrival times and the time delays determined from the distances between the focal point and the physical elements was attributed to refraction.

The received signals were time-shifted by delays from the fitted polynomial that compensate for refraction and geometry, and were then summed over subarrays of physical elements to form received signals for the synthetic elements of each partition. ATF maps were then estimated for each partition of synthetic elements using the least-mean-square-error method described in [6]. In this method, ATFs from aberration are determined by fitting differences in the arrival times at adjacent elements to the time-shift peak in cross-correlations of received signals at corresponding elements.

The receive focus for each partition was generated by homogeneous back-propagation of the time-reversed echoes from the point reflector with time delays derived from the fitted polynomial to compensate for refraction (i.e., the difference between the fitted delays and the geometric delays) and also with additional time delays from the ATF map that compensate for aberration. The ATF time delay for each synthetic element was used to compensate all of the physical elements that belong to the synthetic element. Two-dimensional spatial Fourier transforms were used to back-propagate the monochromatic components of these signals from the surface of the transducer array to the focal plane.

This procedure cannot be used to image receive focuses when the aberration is distributed arbitrarily in the region between the transducer array and the focal plane. The procedure is only applicable when the aberration is concentrated near the plane of the aperture, which is often the case in ultrasonic measurements [12]. The effective depth of the aberration, i.e., the offset of the equivalent aberration phase screen from the aperture plane, in the phantom used in this study was estimated to be about 9 mm. This depth is consistent with the assumption that the aberration is concentrated near the plane of the aperture. For typical 35-mm-thick aberration phantoms, the effective depth is essentially constant in the temporal frequency range of interest [12].

To estimate focus quality, the peak value of the temporal envelope of the back-propagated pressure was computed at each point of the focal plane. One-dimensional cross sections of these peak values that were centered at the focal point were extracted along the elevation direction and the array direction, and these cross-sections are referred to as the elevation beam and the array beam, respectively. Effective widths for these beams were estimated by the offsets from the focal point at which the peak pressures drop to values that are a specified amount (in decibels) below the value at the focal point. Effective radii are defined as the geometric mean of the effective widths in elevation and array directions. A reference circle on the focal plane was specified using the −20-db effective radius of the receive beampattern obtained through a water path. A peripheral energy ratio (PER), defined as the ratio of total energy outside the reference circle to total energy inside the reference circle, was used to quantify the quality of the aberration compensations derived from different array partitions.

C. Transmit Focus Measurements

As illustrated in Fig. 1(b), transmit focuses for each partition are formed by emitting pulses from the physical elements of the transducer array with time delays to compensate for geometry that vary from element to element, and with time delays to compensate for aberration that are the same for all the physical elements that belong to the same synthetic element. Additional delays that vary from element to element were also included to compensate for refraction from the top and bottom surfaces of the aberration phantom. The transmit focus for each partition was measured with a hydrophone.

The experimental setup used for transmit focus measurements was similar to the experimental setup described in the previous section for receive focus measurements. However, the point reflector used in the receive focus measurements was replaced by a hydrophone with a 0.2-mm-diameter polyvinylidene fluoride (PVDF) tip. The hydrophone serves two purposes. Initially, the hydrophone was used as a point reflector to generate pulse-echo measurements. These measurements were used to compute the ATF maps for each of the array partitions, and also to estimate time delays to compensate for refraction from the top and bottom surfaces of the phantom. The methods used to estimate the ATF maps and the refraction time-delays are described in the previous section. Compensations derived from the ATF maps resulted in different transmit focuses for each partition.

The hydrophone was then used to measure the time-varying pressure of each focus at different locations in the focal plane. High-precision stepper motors translated the hydrophone in 0.2-mm increments along 10-mm intervals centered at the focal point in both the elevation and array directions at a depth of 55 mm. Each time the hydrophone was moved, the transmit focus was recreated by refiring the physical elements of the transducer array.

To estimate focus quality, the peak value of the signal envelope was computed at each hydrophone location. The peak values along the elevation direction are referred to as the elevation beam and the peak values along the array direction are referred to as the array beam. Effective widths for each transmit focus are estimated by the offsets from the focal point at which the peak signals drop to values that are a specified amount (in decibels) below the value at the focal point. Effective radii are defined as the geometric mean of the effective widths in elevation and array directions. The transmit focus was simulated in the focal plane as the product of the one-dimensional focuses in the elevation and array directions. Peripheral energy ratios are calculated for each simulated transmit focus using the reference circle determined by the −20-dB effective radius of the transmit focus obtained through a water path.

Reciprocity implies that the transmit focus and the receive focus should be the same for each partition, but the transmit focus is measured directly, whereas the receive focus is reconstructed by back-propagating the received signals. The transmit focus measurements are, therefore, more reliable. However, these measurements are also more time-consuming than the single-transmission measurements needed to compute the receive focus. Agreement between the transmit focus and the receive focus along the elevation and array directions validates the assumptions used to reconstruct the receive focus, which provides a more complete two-dimensional portrait of the focus.

D. Imaging a Point Target

B-scan images of a point reflector were generated to show the effects of different compensations on the point spread function of the b-scan imaging procedure. The imaging geometry is illustrated in Fig. 2(a). Each scan line was acquired along the axis of the transducer array, and scan lines at lateral offsets were formed by laterally translating the point reflector while keeping the array in a fixed position. Thus, the propagation path through the phantom was the same for every scan line. The scan lines were sampled along a 9-mm interval that was centered at 55 mm, which was the depth of the focus. A total of 46 scan lines were acquired at 0.2-mm increments, resulting in an image with a lateral span of 9 mm. Final images were interpolated to a resolution of 0.04 mm.

Fig. 2.

Configuration of b-scan image formation for (a) point reflector and for (b) scatterer-free area (cyst phantom).

For each partition, b-scan images were generated with: no compensation (Uncomp), transmit compensation (Tx), receive compensation (Rx), and full (i.e., transmit and receive) compensation. An ideal b-scan was also generated by scanning the point reflector without the aberration phantom (i.e., through a water path) as a benchmark for measuring the quality of the compensations. Time delays for geometric focusing and time delays to compensate for refraction from the top and bottom surfaces of the phantom were applied to the physical elements to form transmit and receive focuses at a depth of 55 mm, as described in the previous sections. Additional geometric delays were also applied to the received signals from the synthetic elements of each partition to move the receive focus up and down along the 9-mm scan line. Finally, time delays derived from the ATF maps for each partition were applied to the synthetic elements in the partition to compensate for aberration.

A lateral profile of each image was generated by extracting the maximum values along the axial direction. The 40-dB width of this lateral profile was used to evaluate the point resolution of the image.

E. Imaging a Cyst Phantom

B-scan images of a cyst phantom were generated to show the effects of different compensations on the contrast resolution of the b-scan imaging procedure. The cyst is simulated by a scatterer-free region within a cloud of tissue-mimicking randomly distributed subwavelength scatterers [speed: 1540 ± 6 m/s, attenuation: 0.50 ± 0.05 dB/(cm·MHz)] embedded in a soft-tissue-mimicking background [speed: 1554 m/s, attenuation: 0.46 dB/(cm·MHz)]. The scatterer-free region is spherical, with a diameter of 4 mm. An imaging procedure similar to the procedure described in the previous section was used to image this phantom. However, these scans were generated by laterally translating the transducer array rather than translating the imaged object, as illustrated in Fig. 2(b). The cyst phantom was placed just beyond, but in contact with, the aberration phantom, and the aberration phantom was offset from the transducer by about 3 mm to avoid contact with the upper surface of the phantom when moving the transducer. A total of 21 scan lines were acquired at 0.2-mm increments, resulting in a lateral span of 4 mm. The scan lines were sampled at 0.2-mm intervals over a distance of 12 mm and were centered around an axial offset of 55 mm. The dimensions of the scanned region were chosen to be small enough to ensure that the image would be contained within an isoplanatic patch for the aberration phantom [29] so that the same compensation time delays could be used for the entire image.

The image formation procedure was the same as the procedure described in the previous section for imaging the point target, except that the time delays used for geometric focusing were not supplemented with additional delays to correct for refraction from the top and bottom surfaces of the aberration phantom. Final images of the cyst phantom were produced by interpolating the coarse images derived from the sampled scan lines.

Because there are no isolated point reflectors in the cyst phantom, the aberration was estimated by a statistical method that employs cross-spectral estimates of scattering from delta-correlated scattering volumes [12]. In this method, scattering measurements are acquired from 11 transmit focuses that are a subset of the 75 focuses used in earlier studies [11]. The revised set of focuses was selected to maximize the statistical independence of the 11 scattering measurements. The method also estimates ATF maps in a plane that is axially offset from the transducer array. The offset is used to adjust the compensating delays for focuses at different lateral positions, which significantly improves the accuracy of these compensations. The ATF maps were estimated iteratively for each array partition. The estimated ATF map for each iteration was used to correct the transmit beam in the next iteration. Iteration was terminated when the changes in the ATF map from one iteration to the next were no longer appreciable.

For each partition, b-scan images were generated with: no compensation, transmit compensation, receive compensation, and full (i.e., transmit and receive) compensation. An ideal b-scan was also generated by scanning the cyst phantom without the aberration phantom (i.e., through a water path) as a benchmark for measuring the quality of the compensations.

The quality of each b-scan image was evaluated using a contrast ratio (CR) defined by

$$\mathrm{CR}=10{\log }_{10}\frac{{\mu }_{\mathrm{S}}}{{\mu }_{\mathrm{B}}},$$ (1)

where μ_S is the mean intensity in the cyst target region and μ_B is the mean intensity in the background region. The mean intensity of the background was found by averaging the intensities of four circular background regions. Averaging together the image intensities in four regions that surround the cyst provides a reliable estimate for the background intensity that reduces variability caused by imperfect time-gain compensation. The mean intensity inside the cyst was found by searching for a minimum of the mean intensities of disks with 1.7 mm diameters that have centers within a 4.0 × 4.0 mm rectangle that is centered in the image. The purpose of this minimization is to exclude responses from outside the cyst that might inadvertently be included in the central rectangle because of imperfect alignment of the cyst phantom and the transducer aperture. The distance in the depth dimension between the center of the disk used to estimate the mean cyst intensity and the centers of the disks used to estimate the background intensity was 3.4 mm, which is far enough to avoid inclusion of the bright spots at the top and bottom of the cyst caused by normal incidence.

III. Results

A. Receive Focus Computations

Receive focuses were computed using aberration compensations derived from each partition of the physical array. The first step in these computations was to estimate ATF maps for each partition from point-reflector echoes that were propagated through the aberration phantom. Fig. 3 presents representative ATF maps and an ATF map obtained from point-reflector echoes that were propagated through a water path. The ATF map for the water path is essentially uniform, as expected, but has very small fluctuations that result from nonidealities in the experimental apparatus. Aberration in the receive focus computations is characterized by the ATF map derived from the array of physical elements. Projections of the spherical inclusions in the scattering phantom are very clear in this ATF map, but are blurred in the ATF maps of coarser partitions. Furthermore, artificial discontinuities at the boundaries of the elements are more noticeable in the ATF maps of the coarser partitions. Degradation on the ATF maps derived from coarser partitions may be attributed to several causes: the samples of the ATF maps from coarse partitions are sparse, the estimates of the arrival-time differences between adjacent elements are less accurate because the centers of the synthetic elements are farther apart, and the arrival-time differences are also obscured by signal consolidation across the enlarged synthetic elements.

Fig. 3.

Arrival-time fluctuation (ATF; in nanoseconds) maps across the apertures of different pitches (in millimeters) with and without aberration along the propagation path. The maps are displayed on a linear scale with a maximum time delay of 150 ns represented by white and a minimum time delay of −150 ns represented by black. In each panel, horizontal and vertical axes correspond to the elevation and array direction, respectively, of each emulated aperture. The effective size of the element is below the panel in millimeters. std = standard deviation.

Compensated and uncompensated signals at the physical elements along three different cross sections of the two-dimensional aperture are compared in Fig. 4. Ideal waveforms obtained from water path propagation are also included in the figure. The compensated wavefronts are appreciably flatter than the uncompensated wavefronts, but retain some residual variations. The small residual fluctuations in the compensated waveforms obtained from the ATF map for the physical array are caused by aberration effects that are not represented in the time-shift model. Larger residual fluctuations in the compensated waveforms from the ATF maps for coarser partitions are attributed to incomplete time-shift compensation. Uniformity of the compensated waveforms degrades as the synthetic element size increases and is most appreciable in the waveforms that are compensated using time-shifts derived from the partition with the pitch of 5.4 × 5.4 mm.

Fig. 4.

Uncompensated, ideal, and compensated waveforms with different element pitches (in millimeters). Each column from left to right corresponds to waveforms in the 10th aperture array row, waveforms in the central (40th) aperture array row, and waveforms in the 70th aperture array row, respectively. The temporal bipolar waveforms are shown on a 50-dB log scale for each polarity. In each panel, the vertical axis spans 79 elements in the aperture array row, and the horizontal axis spans 4 μs of time.

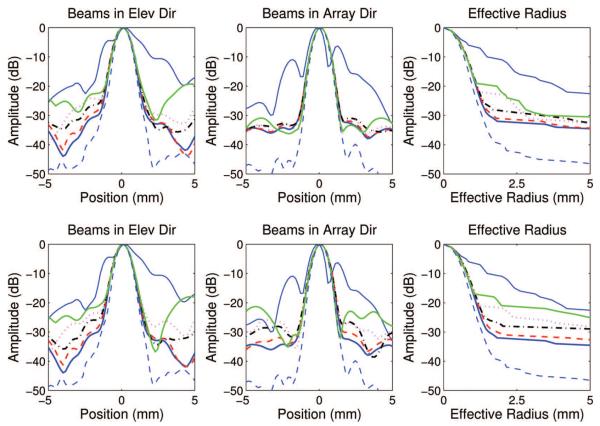
Receiver sensitivity patterns were obtained by homogeneous back-propagation of compensated echoes from the point reflector. The beam and radius profiles in the top panels of Fig. 5 are of focuses with compensations derived from partitions with enlarged elevation pitches and the beam and radius profiles in bottom panels of Fig. 5 are of focuses with compensations derived from partitions with square pitches. The asymmetry of the uncompensated beam profiles and the consequent large effective radius of the profiles reflects asymmetry in the aberration phantom. In all cases, these profiles show that time-shift compensation significantly improves the quality of receive focusing. The compensated focuses are more concentrated and have lower side-lobe levels, but are not as good as the focus derived through a water path.

Fig. 5.

Receive focuses and corresponding effective radii for (top row) elevation pitches and (bottom row) square pitches. For panels in the top row, thin blue solid line: uncompensated focus; blue solid line: compensated focus of 0.6 × 0.6 mm; red dashed line: compensated focus of 1.8 × 0.6 mm; black dash-dot line: compensated focus of 3.0 × 0.6 mm; pink dotted line: compensated focus of 4.2 × 0.6 mm; green solid line: compensated focus of 5.4 × 0.6 mm; thin blue dashed line: ideal focus. For panels in the bottom row, thin blue solid line: uncompensated focus; blue solid line: compensated focus of 0.6 × 0.6 mm; red dashed line: compensated focus of 1.8 × 1.8 mm; black dash-dot line: compensated focus of 3.0 × 3.0 mm; pink dotted line: compensated focus of 4.2 × 4.2 mm; green solid line: compensated focus of 5.4 × 5.4 mm; thin blue dashed line: ideal focus.

The −20-dB effective widths, corresponding effective radii, and PERs are listed in Table II. Almost all of the widths of the compensated profiles are essentially the same as the width of the ideal profiles. However, the beam profiles for the partition with the 5.4 × 0.6 mm pitch and the beam profiles for the partition with the 5.4 × 5.4 mm pitch have exaggerated −20-dB effective widths and effective radii because the amplitudes of the side lobes in these profiles are larger than −20-dB of the peak value. As a result, the effective widths and radii for these partitions do not measure the width of the central lobe.

TABLE II.

−20-dB Effective Width W, Radius R, and Peripheral Energy Ratio (PER) of Receive Focuses for Apertures Partitioned With Different Element Pitches.

Pitch (mm)	WElev (mm)	WArray (mm)	Reff (mm)	PER
Elevation pitch
Unc (0.6 × 0.6)	9.6	6.3	3.9	2.99
Ideal (0.6 × 0.6)	2.0	1.9	1.0	0.02
Comp (0.6 × 0.6)	2.3	2.2	1.1	0.12
Comp (1.8 × 0.6)	2.4	2.2	1.1	0.14
Comp (3.0 × 0.6)	2.4	2.2	1.1	0.19
Comp (4.2 × 0.6)	2.4	2.1	1.1	0.26
Comp (5.4 × 0.6)	6.4	2.1	1.8	0.36
Square pitch
Unc (0.6 × 0.6)	9.6	6.3	3.9	2.99
Ideal (0.6 × 0.6)	2.0	1.9	1.0	0.02
Comp (0.6 × 0.6)	2.3	2.2	1.1	0.12
Comp (1.8 × 1.8)	2.4	2.3	1.2	0.16
Comp (3.0 × 3.0)	2.4	2.3	1.2	0.25
Comp (4.2 × 4.2)	2.5	2.2	1.2	0.36
Comp (5.4 × 5.4)	6.9	2.1	1.9	0.55

Unc = uncompensated; Comp = compensated.

The main difference between the profiles of the receive focuses from different compensations is the degree of side lobe suppression. This difference is clearly quantified by the PERs listed in Table II. In general, compensations derived from coarse partitions result in focuses with higher side lobes and larger PER values. Furthermore, as shown in Fig. 5, compensations derived from partitions that are coarser in only the elevation direction result in focuses with side lobes that are only higher in the elevation direction.

B. Transmit Focus Measurements

Transmit focuses were measured for transmissions through the aberration phantom that were compensated by time shifts from the ATF maps of every partition of the physical array. The beam and radius profiles in the top panels of Fig. 6 are of focuses with compensations derived from partitions with enlarged elevation pitches, and the beam and radius profiles in the bottom panels of Fig. 6 are of focuses with compensations derived from partitions with square pitches. The compensated focuses are all much better than the uncompensated focuses.

Fig. 6.

Transmit focuses and corresponding effective radii for (top row) elevation pitches and (bottom row) square pitches. The line formats are the same as in Fig. 5.

The −20-dB effective widths of the transmit beam profiles, the corresponding effective radii, and the PERs are listed in Table III. These widths and radii measure the span of the central lobe of the focus in the array and elevation directions. The widths of the profiles of the compensated focuses are all essentially the same as the widths of the ideal profiles for partitions with small elevation pitches and square pitches.

TABLE III.

−20-dB Effective Width W, Radius R, and Peripheral Energy Ratio (PER) of Transmit Focuses for Apertures Partitioned With Different Element Pitches.

Pitch (mm)	WElev (mm)	WArray (mm)	Reff (mm)	PER
Elevation pitch
Unc (0.6 × 0.6)	6.3	6.3	3.2	1.98
Ideal (0.6 × 0.6)	1.7	1.6	0.8	0.11
Comp (0.6 × 0.6)	1.7	1.6	0.8	0.13
Comp (1.8 × 0.6)	1.7	1.6	0.8	0.14
Comp (3.0 × 0.6)	1.7	1.6	0.8	0.17
Comp (4.2 × 0.6)	1.7	1.6	0.8	0.19
Comp (5.4 × 0.6)	1.6	1.6	0.8	0.38
Square pitch
Unc (0.6 × 0.6)	6.3	6.3	3.2	1.98
Ideal (0.6 × 0.6)	1.7	1.6	0.8	0.11
Comp (0.6 × 0.6)	1.7	1.6	0.8	0.13
Comp (1.8 × 1.8)	1.7	1.7	0.9	0.15
Comp (3.0 × 3.0)	2.2	1.7	1.0	0.23
Comp (4.2 × 4.2)	2 2	1.7	1.0	0.24
Comp (5.4 × 5.4)	2.1	2.8	1.2	0.58

Unc = uncompensated; Comp = compensated.

The profiles of the transmit focuses exhibit the same type of variations as the profiles of the receive focuses. Transmit focuses with compensations derived from coarse partitions have larger side lobes, and transmit focuses with compensations derived from partitions that are coarser in only the elevation direction have side lobes that are only larger in the elevation direction. Increased side-lobe levels are more pronounced for the partitions with the 5.4 × 0.6 mm and 5.4 × 5.4 mm, and are clearly quantified by the PER values in Table III.

However, the widths of the beam profiles of the ideal transmit focuses reported in Table III are slightly smaller than the widths of the beam profiles of the ideal receive focuses reported in Table II. Comparison of the plots of the profiles of the ideal transmit and receive focuses also confirm that the transmit focuses are more concentrated than the receive focuses. Because reciprocity implies that transmit and receive focuses through a water path should be the same, the discrepancy in focal width must result from approximations in the mathematical model used to represent the receive focus. For example, frequency responses and directivity patterns of the physical elements may have an influence on the estimated beam profiles that is not completely accounted for. Nevertheless, because the same approximations apply to all of the receive focus computations, comparison of the receive focuses for different compensations should be largely unaffected by the approximations. This conclusion is also supported by the similarity of the variations in the transmit and receive focuses.

C. Imaging a Point Target to Estimate Point Resolution

B-scan images of a point reflector were generated to estimate the improvement in point resolution realized by compensations from different synthetic element sizes. Figs. 7 and 8 present representative b-scan images of the point target. The vertical axis in these images is the axial direction. The horizontal axes in Figs. 7 and 8 are the lateral directions that are aligned with elevation direction and array direction, respectively. Fig. 9 shows profiles of the maximum b-scan intensities along vertical (i.e., axial) scan lines and corresponding image width plots of the point target. The abscissa in the maximum-value scan and image width plots is the lateral offset of the axial scan lines.

Fig. 7.

B-scan images of a point target along the elevation direction using apertures with different element pitches (in millimeters) given below each panel. Uncomp = no compensation on either transmission or receiving. Tx+Rx = compensation on both transmission (Tx) and receiving (Rx). Ideal = water path. Each b-scan image panel shows the distribution of signal amplitude as a shade of gray on a 50-dB log scale; vertical and horizontal coordinate correspond to depth dimension and elevation direction, respectively, and both span 9 mm.

Fig. 8.

B-scan images of a point target along the array direction using apertures with different element pitches (in millimeters) given below each panel. Uncomp = no compensation on either transmission or receiving. Tx+Rx = compensation on both transmission (Tx) and receiving (Rx). Ideal = water path. Each b-scan image panel shows the distribution of signal amplitude as a shade of gray on a 50-dB log scale; vertical and horizontal coordinates correspond to depth dimension and array direction, respectively, and both span 9 mm.

Fig. 9.

Maximum-value lateral scans and image widths of point target. The top two panels are maximum-value lateral scans derived with physical pitch. Thin blue solid line: uncompensated image; red dashed line: transmit compensated image; black dash-dot line: receive compensated image; pink dotted line: full compensated image; thin blue dashed line: water-path image. The second-row and third-row panels are, respectively, maximum-value lateral scans and image widths of point target derived with different elevation pitches. The line formats in these panels are the same as in the top panels of Fig. 5. The fourth-row and fifth-row panels are, respectively, maximum-value lateral scans and image widths of point target derived with different square pitches. The line formats in these panels are the same as in the bottom panels of Fig. 5.

The compensated images in Figs. 7 and 8 are much better than the uncompensated images and are almost as good as the ideal images formed through a water path. However, the side lobes increase when the compensation is derived from coarser partitions and is distinctly higher in the images formed with compensation from the partitions with the pitches of 5.4 × 0.6 mm and 5.4 × 5.4 mm.

The maximum-value scans in the top two panels in Fig. 9 support the expectation that fully compensated (i.e., compensated on both transmit and receive) images are better than the receive-only and transmit-only compensated images. The presented maximum-value scans and point widths in Fig. 9 also indicate that the main difference between images formed with full compensations from different partitions is the size of the side lobes. Compensations obtained from partitions with enlarged elevation pitches result in larger side lobes in the elevation direction and compensations obtained from partitions with enlarged square pitches result in larger side lobes in both directions.

The −40-dB widths of b-scans in both the elevation and array directions are listed in Table IV. These widths generally measure the span of the central peak in the array and elevation directions. The size of the central peak is essentially the same in all of the fully compensated images. However, the images formed with compensations derived from the coarser partitions, such as the pitches of 5.4 × 0.6 mm and 5.4 × 5.4 mm, have side lobes that are greater than −40 dB below the peak value, and in those cases, the widths listed in Table IV do not measure the span of the central peak.

TABLE IV.

The −40-dB Image Width (mm) of B-Scan Images of the Point Target in Elevation/Array Directions Using Apertures of Different Element Pitches.

Pitch (mm)	Uncomp	Rx	Tx	Tx + Rx	Ideal
Elevation pitch
0.6 × 0.6	7.9/6.8	4.7/5.2	4.2/2.6	2.6/2.6	2.4/2.4
1.8 × 0.6	7.9/6.8	4.7/5.1	4.4/2.7	2.7/2.6	2.4/2.4
3.0 × 0.6	7.9/6.8	5.4/5.4	4.5/2.7	2.6/2.6	2.4/2.4
4.2 × 0.6	7.9/6.8	5.6/5.5	4.5/2.8	2.7/2.6	2.4/2.4
5.4 × 0.6	7.9/6.8	6.6/5.9	5.0/4.8	4.2/2.8	2.4/2.4
Square pitch
0.6 × 0.6	7.9/6.8	4.7/5.2	4.2/2.6	2.6/2.6	2.4/2.4
1.8 × 1.8	7.9/6.8	4.7/5.1	4.4/4.1	2.7/2.6	2.4/2.4
3.0 × 3.0	7.9/6.8	5.8/5.6	4.5/4.3	2.6/2.6	2.4/2.4
4.2 × 4.2	7.9/6.8	5.9/6.0	4.5/4.7	2.7/2.8	2.4/2.4
5.4 × 5.4	7.9/6.8	9.0/6.1	5.2/4.9	4.4/3.9	2.4/2.4

Uncomp = uncompensated; Rx = receive compensation; Tx = transmit compensation; Tx + Rx = full compensation.

D. Imaging a Cyst Phantom to Estimate Contrast Resolution

B-scan images of a cyst phantom were generated to show the effects of compensations with different synthetic element sizes on the contrast resolution of the b-scan imaging procedure. B-scan images of the cyst phantom derived from the physical array are shown in Fig. 10. The vertical axis in these images is the axial direction and the horizontal axis is the lateral direction that is aligned with the array direction. Representative b-scan images of the cyst phantom derived from different array partitions are shown in Fig. 11. Contrast ratios resulting from transmit compensation, receive compensation, and full (transmit and receive) compensation are summarized in Table V.

Fig. 10.

B-scan images of a cyst phantom along the array direction using physical pitch. Uncomp = no compensation on either transmission or receiving. Rx = compensation on receiving. Tx = compensation on transmission. Tx + Rx = compensation on transmission and receiving. Ideal = water path. Each b-scan image panel, spanning 12 × 4 mm², shows the distribution of signal amplitude as a shade of gray on a 40-dB log scale. Vertical coordinates correspond to the depth dimension. Horizontal coordinates correspond to the array direction. Outer red dashed circles: background regions, 1.7 mm diameter. Central yellow dashed circle: cyst target region, 1.7 mm diameter.

Fig. 11.

Representative fully compensated (compensated on both transmit and receive) b-scan images of a cyst phantom along array direction using apertures with a pitch (in millimeters) denoted below each panel. The formats in these panels are the same as in panels of Fig. 10.

TABLE V.

Contrast Ratio (dB) of B-Scan Images Along Elevation/Array Directions Using Apertures With Different Element Pitches.

Pitch (mm)	Uncomp	Rx	Tx	Tx + Rx	Ideal
Elevation pitch
0.6 × 0.6	−7.4/−5.4	−16.7/−13.9	−15.7/−14.1	−22.0/−20.3	−23.4/−21.8
1.8 × 0.6	−7.4/−5.4	−15.6/−13.2	−15.3/−13.1	−21.6/−18.3	−23.4/−21.8
3.0 × 0.6	−7.4/−5.4	−14.6/−11.6	−14.5/−12.2	−21.5/−16.8	−23.4/−21.8
4.2 × 0.6	−7.4/−5.4	−15.5/−13.1	−15.0/−12.3	−21.7/−16.5	−23.4/−21.8
5.4 × 0.6	−7.4/−5.4	−12.2/−10.6	−12.8/−11.1	−18.9/−15.4	−23.4/−21.8
Square pitch
0.6 × 0.6	−7.4/−5.4	−16.7/−13.9	−15.7/−14.1	−22.0/−20.3	−23.4/−21.8
1.8 × 1.8	−7.4/−5.4	−15.0/−12.6	−14.2/−12.3	−21.4/−18.0	−23.4/−21.8
3.0 × 3.0	−7.4/−5.4	−16.3/−13.3	−14.1/−13.1	−22.6/−17.0	−23.4/−21.8
4.2 × 4.2	−7.4/−5.4	−13.0/−13.5	−13.4/−11.1	−20.2/−16.1	−23.4/−21.8
5.4 × 5.4	−7.4/−5.4	−13.4/−13.3	−13.1/−9.8	−16.0/−12.7	−23.4/−21.8

Uncomp = uncompensated; Rx = receive compensation; Tx = transmit compensation; Tx + Rx = full compensation.

The fully compensated image in Fig. 10 is appreciably better than the uncompensated image, the transmit compensated image, and the receive compensated image. Furthermore, this fully compensated image resulting from compensation derived from the physical array (i.e., the image for the partition with pitch of 0.6 × 0.6 mm) is almost the same quality as the ideal water-path image. This indicates that the statistical method is providing accurate estimates of the aberration.

The compensated b-scan images in Fig. 11 are all similar, but the images with compensations derived from the larger partitions (i.e., elevation pitches larger than 4.2 × 0.6 mm and square pitches larger than 4.2 × 4.2 mm) have bright artifacts in the cyst target region. These artifacts result in smaller contrast ratios for these images.

IV. Discussion

Aberration correction of signals that are transmitted and received from an array of transducer elements is usually provided by an ATF map that is generated from differences in arrival time at adjacent elements. These differences can be estimated from the peak locations of cross-correlations of received signals at adjacent elements by assuming that the signals only differ by a time shift. If the ATF map is generated from the received signals of a partition of synthetic elements, then each received signal is a sum of signals from several physical elements. Consequently, the centers of adjacent synthetic elements are farther apart than the centers of adjacent physical elements. Furthermore, the received signals from the synthetic elements are spatial averages of the signals in subarrays of physical elements. These effects degrade the quality of the compensations that are derived from partitions of synthetic elements. The reported results quantify this degradation by measuring: 1) the quality of compensated receive focuses, 2) the quality of compensated transmit focuses, 3) the point resolutions of compensated b-scan images, and 4) the contrast resolution of compensated b-scan images. These measures of performance are also related to the strength and correlation length of the aberration. In these measurements, the aberration is provided by a phantom that mimics the aberration that results from propagation through the abdominal wall. The strength of the aberration is estimated to be 72.5 ns and the correlation length is estimated to be 6.1 mm.

The quality of receive and transmit focuses formed with compensations from synthetic arrays with different pitches is quantified by the effective widths, effective radii, and PERs reported in Tables II and III. The effective widths and radii for the receive focuses are not as good as the corresponding widths and radii for the transmit focuses, but PERs of the receive focuses are better than corresponding PERs of the transmit focuses. These differences are attributed to the mathematical model used to simulate the receive focuses, which assumes all of the aberration to be concentrated in the face of the transducer array. However, the variation from partition to partition of the effective widths, effective radii, and PERs of transmit focuses is very similar to the variations in the corresponding measures of the receive focuses. Furthermore, the cross-sections of the receive focuses in Fig. 5 and the cross-sections of the transmit focuses in Fig. 6 show similar degradation for compensations derived from partitions with larger pitches. The center lobes of all of the compensated receive focuses are essentially the same down to a level of about 20 dB below the peak and, similarly, the center lobes of all of the compensated transmit focuses are also essentially the same down to a level of about 20 dB below the peak. This results in effective −20-dB widths for the transmit focuses that are almost all the same, and effective −20-dB widths for the receive focuses that are also almost all the same. The anomalous widths reported for partitions of larger synthetic elements are caused by side lobes that exceed the −20 dB threshold. The level of the side lobes is the principal difference between focuses obtained from different partitions. If a −20 dB side-lobe level in transmit and receive focusing is used as a criterion for acceptable compensation, then partitions with elevation pitches that are less than or equal to 4.2 mm are satisfactory, whereas partitions with larger pitches are not. This is consistent with the criteria given in [23] of 75% of the aberration correlation length (0.75 × 6.1 mm = 4.6 mm) for the elevation pitch threshold of a multirow array that is intended to be used with aberration correction. The PERs of the transmit and receive focuses provide a more graduated measure of the side-lobe levels that appears to be a better measure of the effectiveness of compensation than the effective widths and radii.

The b-scan images of the point reflector shown in Figs. 7 and 8 illustrate how point resolution is affected by compensations that are derived from partitions with different pitches. All of the compensations result in images that are much better than the uncompensated image, but the main lobes and first side lobes of the compensated images are all very similar. The main difference between the b-scan images is the appearance of additional side lobes in the scans that use compensations derived from partitions with larger pitches. The −40-dB effective widths of the point responses listed in Table IV are consistent with this observation. For example, the effective widths in the Tx + Rx columns of the elevation pitch table and square pitch table are all essentially the same except for the entries in the rows for partitions with an elevation pitch or a square pitch of 5.4 mm. The anomalous effective widths for these partitions are caused by side-lobe amplitudes that exceed the −40 dB threshold rather than a broadening of the central lobe.

The b-scan images of the cyst phantom shown in Figs. 10 and 11 illustrate how contrast resolution of b-scan images is affected by compensations that are derived from partitions with different pitches. These images all have similar details, but the dark interior of the cyst becomes increasingly cloudy in images formed with compensations that are derived from partitions with larger pitch. The contrast ratios listed in Table V also increase as the pitch of the partitions increases. This change is gradual for smaller pitches but changes abruptly for compensations derived from partitions with elevation and square pitches of 5.4 mm. This is consistent with the threshold of 75% of the aberration correlation length for the pitch of the partition cited earlier. For most partitions, the contrast ratios of images oriented in the elevation direction are better than the corresponding contrast ratios of images oriented in the elevation direction. This is due to asymmetric aberration from the cyst phantom that is caused by pouring line interfaces. In our experiments, the pouring lines were parallel to the elevation direction of the transducer array, and this resulted in additional aberration in the scans that were oriented in the array direction.

The measurements all consistently indicate that aberration caused by the abdominal wall is effectively compensated using ATF maps for partitions with element pitches whose diagonal lengths do not exceed 4.2 mm (elevation pitches smaller than or equal to 4.2 × 0.6 mm and square pitches smaller than or equal to 3.0 × 3.0 mm) that is approximately 70% of the FWHM correlation length for the aberrator. For partitions that are only enlarged in the elevation direction, this threshold is slightly larger than the recommended elevation pitch of 3.0 mm cited in [24]. There are several possible reasons for this difference. Our study used different array geometries and a different aberration phantom to simulate the abdominal wall. There were also errors in the prior study in assigning time shifts to emulate the focus of a mechanical lens with one-dimensional curvature in the elevation direction. Furthermore, the least-mean-square-error estimation method used in the prior study to estimate ATF maps is not as effective as the statistical method described later.

The ATF maps used for compensating the receive focuses, the transmit focuses, and the b-scan images of the point reflector were derived from the echoes produced by a point reflector. However, echoes from a point reflector are generally not available when forming clinical images. The statistical method described in [11] and [12] provides a more practical technique for estimating ATF maps, and this method was used to determine the compensations used for imaging the cyst phantom. The efficacy of the method is demonstrated by comparison of the panels in Fig. 10 for the water-path and fully compensated images. The revised statistical method that includes deblurring [12] was used instead of the original formulation [11] because deblurring appreciably enlarges the isoplanatic region by using an offset phase screen, and also because the revised method only requires measurements from 11 focal points rather than 75 focus points. However, both methods are iterative and they both failed to converge in some instances because of refraction effects from the interface between the cyst phantom and aberration phantom. These convergence difficulties were usually eliminated by leveling the cyst phantom and making sure that the surfaces of the aberration phantom and the cyst phantom were in contact.

The aberration phantom used in this study was chosen to mimic measured characteristics of the strong aberration produced by the abdominal wall. The characteristics of four different aberration phantoms were considered. The aberration strengths and correlation lengths of these four phantoms cover the typical range of aberration that results from propagation through actual abdominal wall (rms of ATF: 56 ± 16.4 ns, correlation length of ATF: 6.42 ± 1.98 mm [3], [23]). The selected phantom produced aberration with the maximum magnitudes of residual phase error (RPE) [25] for partitions with large pitches. Receive focuses for each phantom and each partition were estimated by back-propagating compensated echoes from a point reflector, as described in Section II-B. The compensated receive focuses for the selected phantom were more sensitive to the pitch of the partition used to derive the compensation than the compensated receive focuses for the other phantoms. These studies also indicated that limitations on partition pitch can be relaxed for weaker aberration. Because aberration from the selected phantom was found, in every respect, to be more severe than the aberration from the other phantoms, the results derived using the selected phantom are considered to be conservative and generally applicable to imaging through the abdominal wall. Nevertheless, more experiments are desirable for aberration phantoms with both shorter and longer correlation lengths to obtain further quantification of the effect of element size on the focusing and imaging qualities of an ultrasound imaging system that includes aberration correction.

Ideal aberration estimates are obtained from ATF maps for arrays of small physical elements with small pitches. Estimates from arrays of larger synthetic elements with larger pitches require less hardware and computation, but only provide time-shifts that account for the average variation across each synthetic element. The results of this study indicate that synthetic elements as large as 3.0 × 3.0 mm are sufficient for estimating and correcting the aberration caused by propagation through the abdominal wall. If the pitch of the physical array is 0.6 mm, which is an appropriate dimension for geometric focusing at 3.0 MHz, then a synthetic array with a pitch of 3.0 × 3.0 mm will only contain 1/25 as many elements as the physical array. This substantially reduces the number of receive channels, and also substantially reduces the computations needed to estimate the ATF map. These reductions are a significant step toward practical integration of aberration correction in ultrasound imaging instruments.

V. Conclusion

Focusing and imaging qualities of an ultrasound imaging system that uses aberration compensation were studied as functions of the number of parallel channels that the system employs to estimate the aberration. The number of parallel channels is inversely related to the size of synthetic elements that are simulated by aggregating signals from the physical elements. In all cases, compensation produced substantially better focuses through an aberrator path than the focuses obtained without compensation, though not as good as the focuses obtained through a water path. The main effect on the transmit and receive focuses resulting from using larger synthetic elements to estimate aberration is an increase in the side-lobe levels of the focuses. The width of the center lobe of the focuses is essentially not affected by using aberration estimates from sparser synthetic arrays. B-scan images of a point target and a cyst target (i.e., a scatterer-free region surrounded by randomly distributed scatterers) also confirm that fully (transmit and receive) compensated images are appreciably better than images formed with only transmit compensation, only receive compensation, or no compensation at all. However, aberration estimates derived from sparse arrays of synthetic elements are less effective, and this results in b-scan images with poorer contrast resolution. The studies show that pitches of 4.2 × 0.6 mm and 3.0 × 3.0 mm are, respectively, the maximum elevation pitch and square pitch that can be used to effectively correct the strong aberration produced by the selected phantom. Both of these pitch thresholds have the same diagonal length, which is approximately 70% of the correlation length for typical strong abdominal-wall aberration. This implies that for the conditions of this study, which simulate imaging through strong abdominal-wall aberration, the aberration may be effectively estimated and corrected with a coarse array synthesized in the front-end electronics by using 1/25 the number of parallel channels suitable for geometric focusing at 3 MHz.

Biographies

Wei Jiang received a B.S. degree in electronic information engineering and an M.S. degree in underwater acoustic engineering, both from the Northwestern Polytechnical University, Xi'an, China, in 2004 and 2007, respectively. He received a Ph.D. degree in electrical engineering in 2011 from the University of Rochester. From September 2007 to April 2012, he was with the Diagnostic Ultrasound Research Laboratory of the University of Rochester, where he was a research assistant and later a postdoctoral research associate in the Department of Electrical and Computer Engineering. In May 2012, he joined Philips Healthcare, where he is now a senior systems design engineer. His research interests include aberration correction, ultrasonic propagation, global estimation of scattering object characteristics, and image reconstruction based on inverse scattering.

Jeffrey P. Astheimer received the B.A., M.A., and Ph.D. degrees, all in mathematics, from the University of Rochester in 1975, 1977, and 1982, respectively. After completing his Ph.D., he joined the faculty of Colgate University in 1984, but left in 1985 to co-found the Adaptable Laboratory Software company, which developed the Asyst software system. Dr. Astheimer spent 19 years in commercial scientific software development, but has also retained a long-term interest in the mathematics of wave propagation, especially as it relates to applications in medical ultrasound.

Robert C. Waag received his B.E.E., M.S., and Ph.D. degrees from Cornell University in 1961, 1963, and 1965, respectively. After completing his Ph.D. studies, he became a member of the technical staff at Sandia Laboratories, Albuquerque, NM, and then served as an officer in the United States Air Force from 1966 to 1969 at the Rome Air Development Center, Griffiss Air Force Base, NY. In 1969, he joined the faculty of the University of Rochester, where he is now Arthur Gold Yates Professor in the Department of Electrical and Computer Engineering, School of Engineering and Applied Science, and also holds an appointment in the Department of Radiology, School of Medicine and Dentistry. Prof. Waag's recent research has treated ultrasonic scattering, propagation, and imaging in medical applications. In 1992, he received the Joseph H. Holmes Pioneer Award from the American Institute of Ultrasound in Medicine. He is a life fellow of the Institute of Electrical and Electronics Engineers and a fellow of the Acoustical Society of America and the American Institute of Ultrasound in Medicine.