Abstract
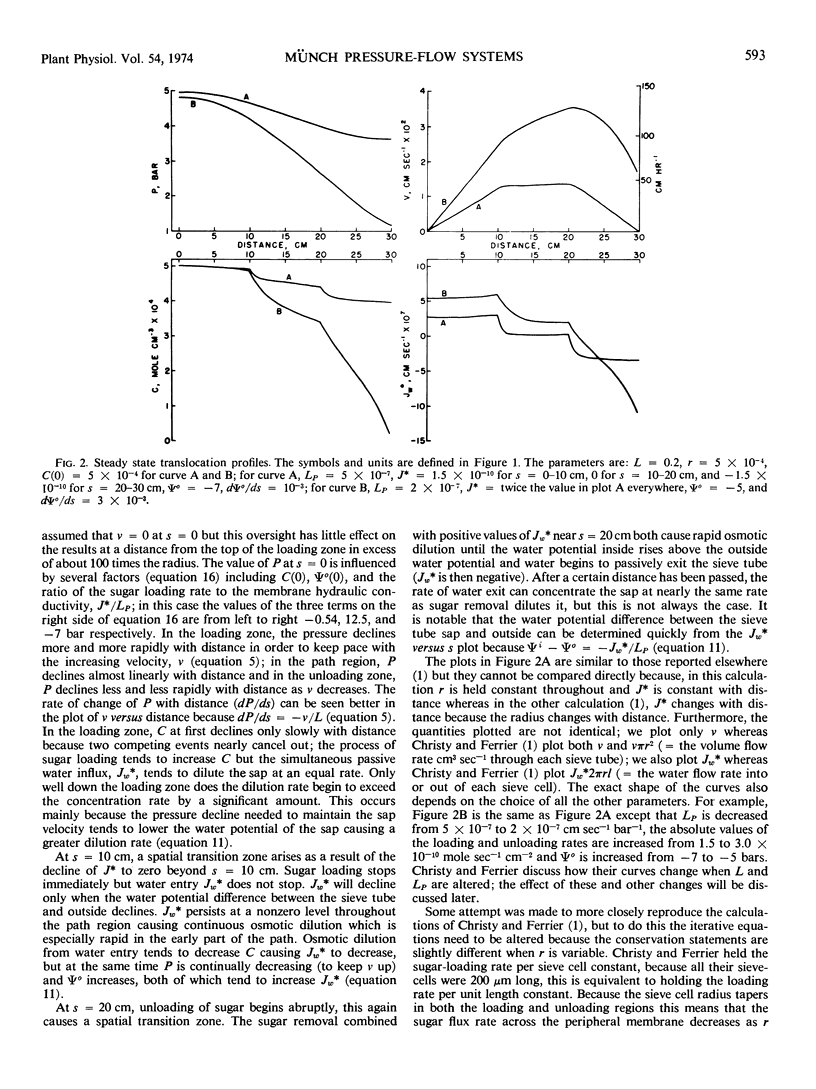
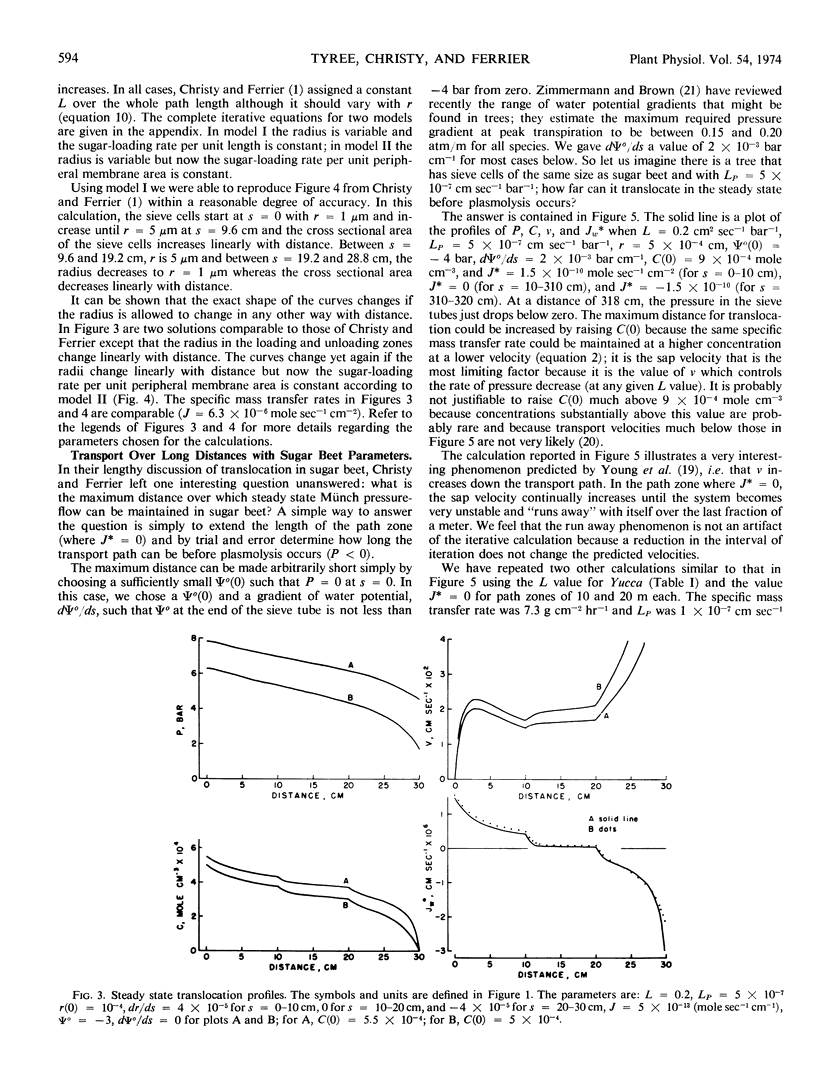
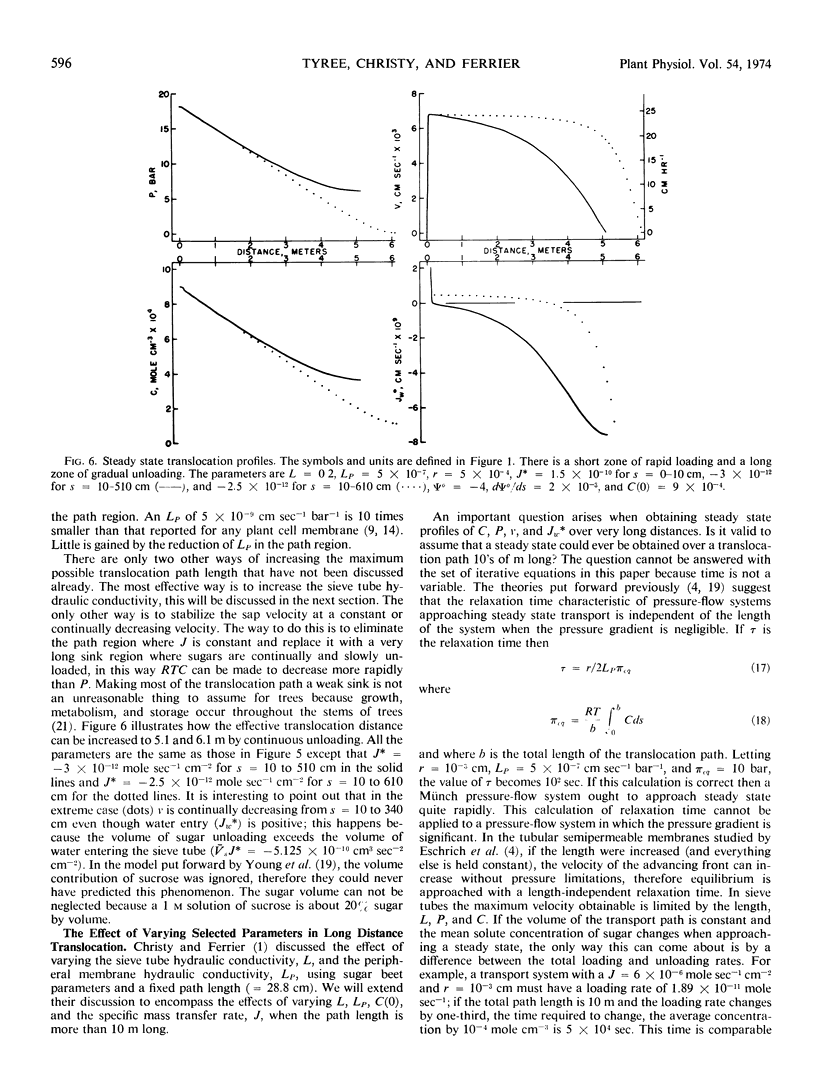
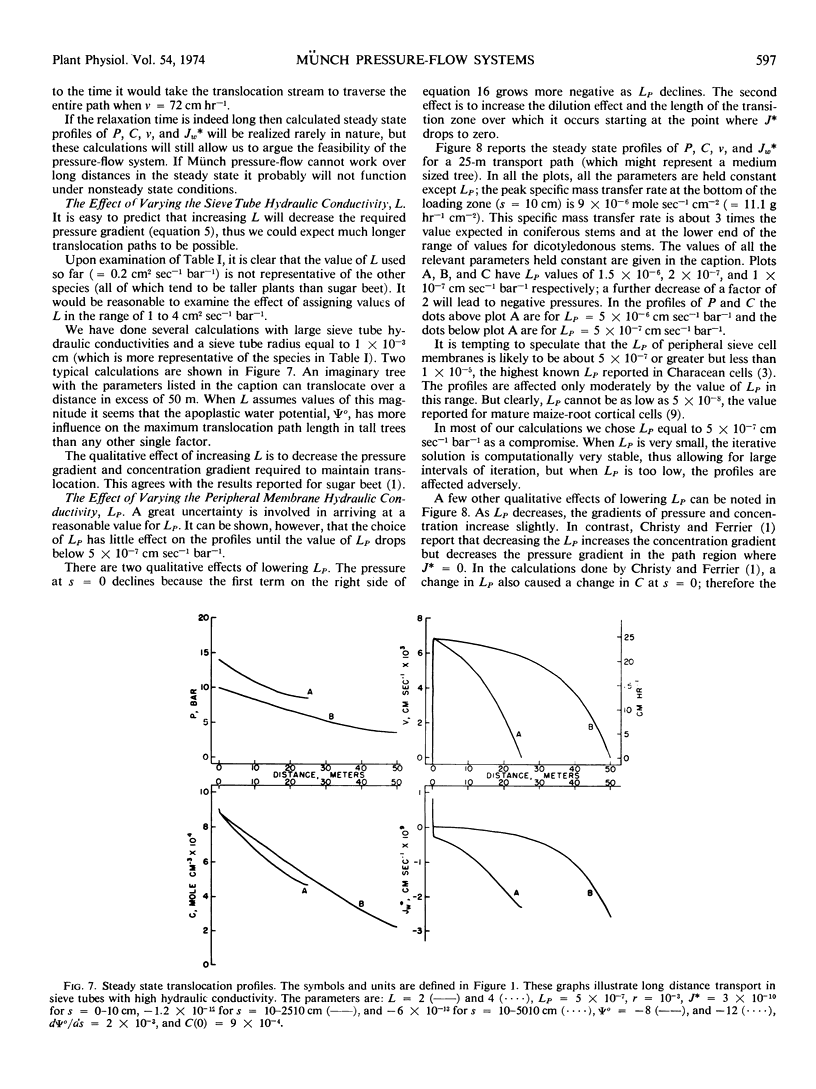
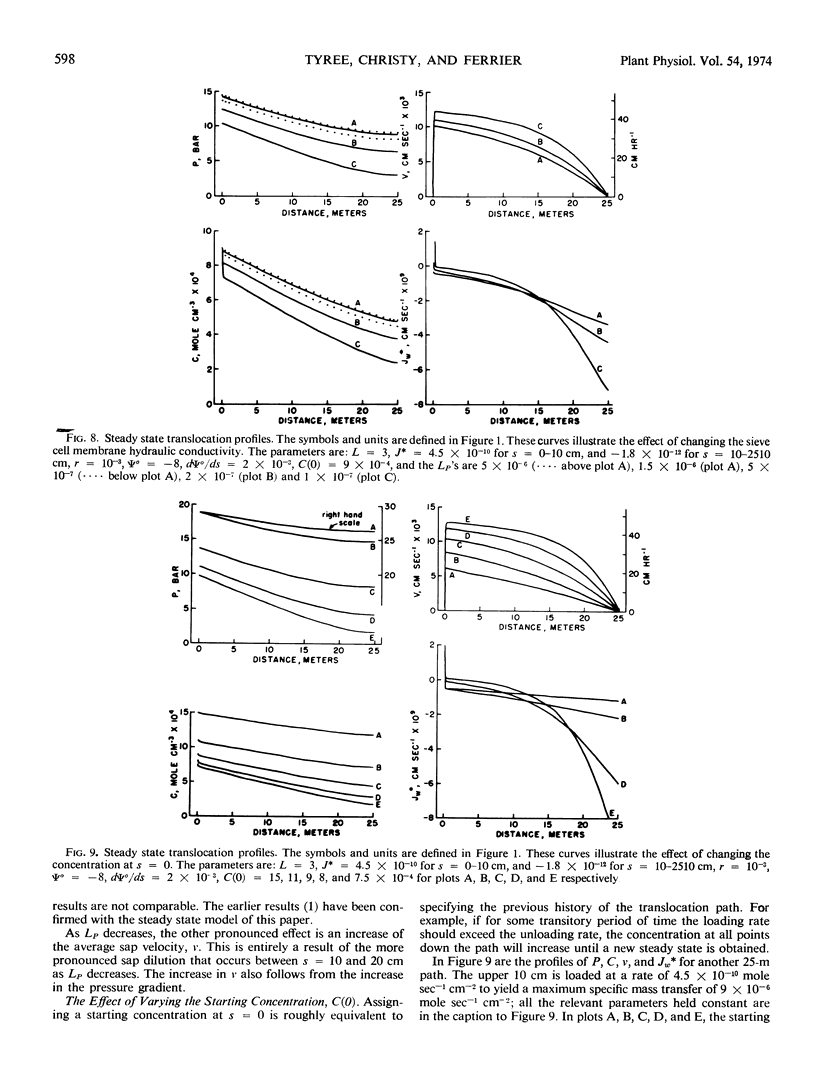
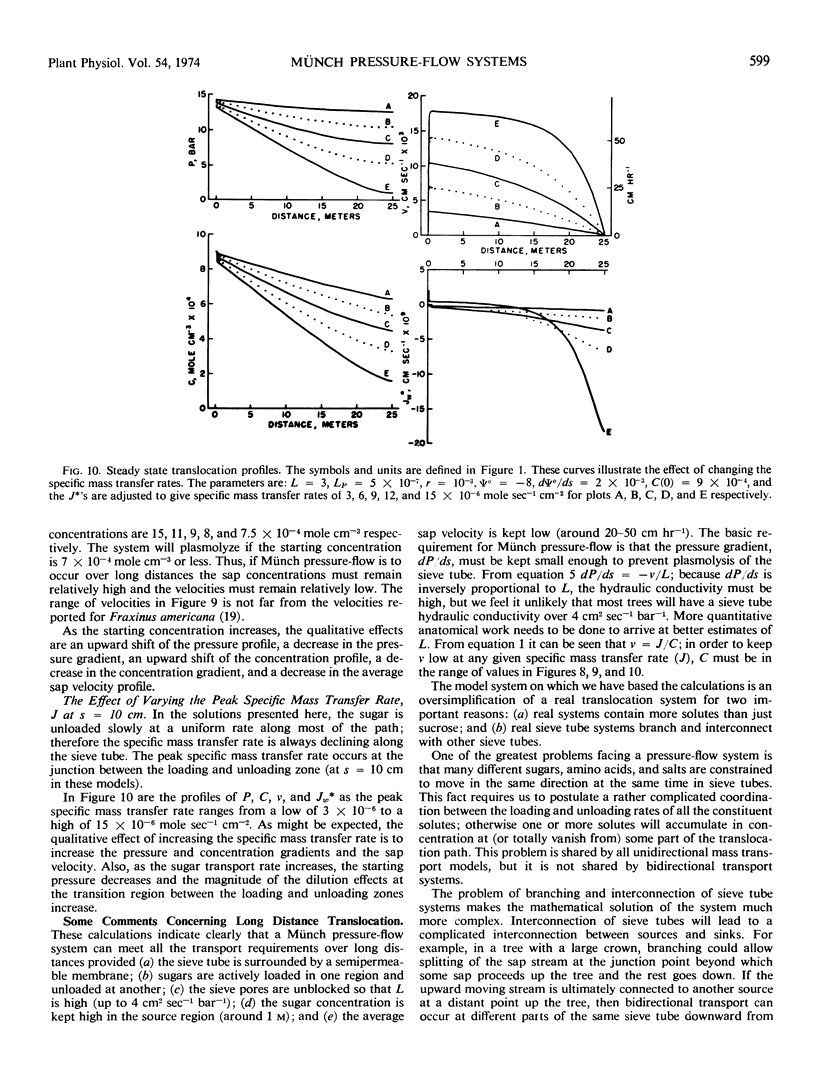
A simple steady state iterative solution of Münch pressure-flow in unbranched sieve tubes containing only water and sucrose is derived. The iterative equations can be solved on a programmable desk calculator. Solutions are presented for steady state transport with specific mass transfer rates up to 1.5 × 10−5 mole second−1 centimeters−2 (= 18.5 grams hour−1 centimeters−2) over distances in excess of 50 meters. The calculations clearly indicate that a Münch pressure-flow system can operate over long distances provided (a) the sieve tube is surrounded by a semipermeable membrane; (b) sugars are actively loaded in one region and unloaded at another; (c) the sieve pores are unblocked so that the sieve tube hydraulic conductivity is high (around 4 centimeters2 second−1 bar−1); (d) the sugar concentration is kept high (around one molar in the source region); and (e) the average sap velocity is kept low (around 20-50 centimeters hour−1). The dimensions of sieve cells in several species of plants are reviewed and sieve tube hydraulic conductivities are calculated; the values range from 0.2 to 20 centimeters2 second−1 bar−1. For long distance pressure-flow to occur, the hydraulic conductivity of the sieve cell membranes must be about 5 × 10−7 centimeters second−1 bar−1 or greater.
Full text
PDF





Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Christy A. L., Ferrier J. M. A Mathematical Treatment of Munch's Pressure-Flow Hypothesis of Phloem Translocation. Plant Physiol. 1973 Dec;52(6):531–538. doi: 10.1104/pp.52.6.531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DAINTY J., GINZBURG B. Z. THE MEASUREMENT OF HYDRAULIC CONDUCTIVITY (OSMOTIC PERMEABILITY TO WATER) OF INTERNODAL CHARACEAN CELLS BY MEANS OF TRANSCELLULAR OSMOSIS. Biochim Biophys Acta. 1964 Jan 27;79:102–111. doi: 10.1016/0926-6577(64)90043-9. [DOI] [PubMed] [Google Scholar]
- Geiger D. R., Cataldo D. A. Leaf structure and translocation in sugar beet. Plant Physiol. 1969 Jan;44(1):45–54. doi: 10.1104/pp.44.1.45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammel H. T. Measurement of turgor pressure and its gradient in the Phloem of oak. Plant Physiol. 1968 Jul;43(7):1042–1048. doi: 10.1104/pp.43.7.1042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horwitz L. Some Simplified Mathematical Treatments of Translocation in Plants. Plant Physiol. 1958 Mar;33(2):81–93. doi: 10.1104/pp.33.2.81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyree M. T. The symplast concept. A general theory of symplastic transport according to the thermodynamics of irreversible processes. J Theor Biol. 1970 Feb;26(2):181–214. doi: 10.1016/s0022-5193(70)80012-1. [DOI] [PubMed] [Google Scholar]
- Weatherley P. E., Johnson R. P. The form and function of the sieve tube: a problem in reconciliation. Int Rev Cytol. 1968;24:149–192. doi: 10.1016/s0074-7696(08)61399-6. [DOI] [PubMed] [Google Scholar]


