Magnesium Fluctuations Modulate RNA Dynamics in the SAM-I Riboswitch

Abstract

Experiments demonstrate that Mg²⁺ is crucial for structure and function of RNA systems, yet the detailed molecular mechanism of Mg²⁺ action on RNA is not well understood. We investigate the interplay between RNA and Mg²⁺ at atomic resolution through ten 2 microsecond explicit solvent molecular dynamics simulations of the SAM-I riboswitch with varying ion concentrations. The structure, including three stemloops, is very stable on this timescale. Simulations reveal that outer sphere coordinated Mg²⁺ ions fluctuate on the same time scale as the RNA, and that their dynamics couple. Locally, Mg²⁺ association affects RNA conformation through tertiary bridging interactions; globally, increasing Mg²⁺ concentration slows RNA fluctuations. Outer sphere Mg²⁺ ions responsible for these effects account for 80% of Mg²⁺ in our simulations. These ions are transiently bound to the RNA, maintaining interactions, but shuttled from site to site. Outer sphere Mg²⁺ are separated from the RNA by a single hydration shell, occupying a thin layer 3-5Å from the RNA. Distribution functions reveal outer sphere Mg²⁺ are positioned by electronegative atoms, hydration layers, and have a preference for the major groove. Diffusion analysis suggests transient outer sphere Mg²⁺ dynamics are glassy. Since outer sphere Mg²⁺ ions account for most of the Mg²⁺ in our simulations, these ions may change the paradigm of Mg²⁺-RNA interactions. Rather than a few inner sphere ions anchoring the RNA structure surrounded by a continuum of diffuse ions, we observe a layer of outer sphere coordinated Mg²⁺ that is transiently bound but strongly coupled to the RNA.

1 Introduction

Magnesium (Mg²⁺) has a profound effect on RNA structure and function.^1,2 This is not surprising in light of the high negative charge density along the RNA backbone. Although the importance of Mg²⁺ is experimentally undeniable, the molecular mechanism by which Mg²⁺ acts on RNA is not well understood in atomistic detail. Some Mg²⁺ effects can be explained by site-specific interactions^3–5 (e.g., Mg²⁺ mediated tertiary contacts), yet there is also evidence that Mg²⁺ acts collectively on the RNA.^6–8 Mg²⁺-RNA interactions have been previously categorized in terms of hydration layers in the pioneering works of Draper and co-workers.^9,10 Chelated ions make two or more direct site-specific contacts with the RNA, while diffuse ions further from the RNA are thought to be responsible for the collective action on RNA. Important molecular dynamics simulations of monovalent ion interactions with RNA have recently been performed.¹¹ Molecular dynamics simulations are also useful for further elucidating the mechanism of Mg²⁺-RNA interactions in atomic detail.

Riboswitches constitute a suitable class of RNAs for studying the effect of Mg²⁺ by simulation. These RNAs are sufficiently large to possess the intricate tertiary structures required for complex interactions with Mg²⁺, yet sufficiently small to be tractable for systematic studies (typically 50-100 nucleotides). Since many RNA systems, including ribozymes, the spliceosome, and the ribosome, contain tertiary interactions and Mg²⁺ dependent effects, the molecular mechanisms of Mg²⁺ interaction we discuss here should be widely relevant to other RNA systems.

Riboswitch RNAs control gene expression with high precision in response to the presence of specific metabolites.^12,13 Riboswitches occupy the 5’ untranslated region of mRNA and contain two partially overlapping domains: the aptamer, which binds to the metabolite; and the expression platform, which controls gene expression. The S-adenosylmethionine riboswitch I (SAM-I) controls SAM synthetase, a key player in sulfur metabolism (Figure 1). In the absence of SAM, a long terminator helix is formed, which causes transcriptional termination. In the presence of SAM, a compact aptamer is formed at the expense of the terminator helix, allowing gene expression to proceed.¹⁴ As one of the first riboswitches discovered, the SAM-I riboswitch is well studied and is an excellent model system.¹⁵ In this work, we use SAM-I to examine the effect of the ionic environment, and specifically Mg²⁺, on RNA.

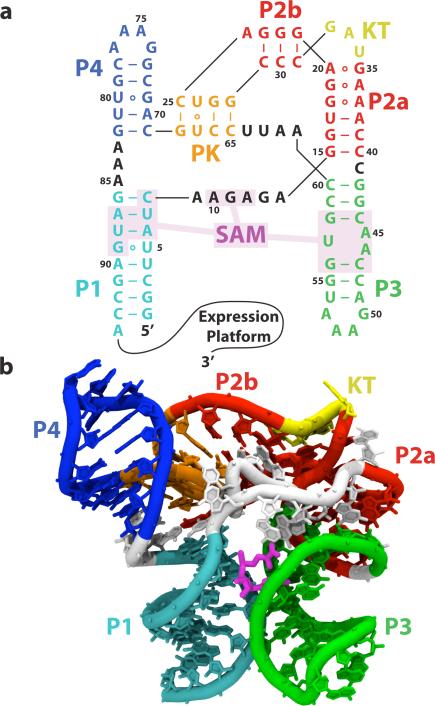
Figure 1.

The SAM-I riboswitch aptamer domain. (a) The secondary structure with the SAM binding pocket (nucleotides within 5 Å of SAM) shaded. Nucleotides are color-coded according to secondary structure element. Helices P1, P2a, P2b, P3, P4 are labeled, along with the kink-turn (KT) and pseudo-knot (PK). (b) The crystallographic structure of the SAM-I riboswitch aptamer domain solved by Batey and co-workers, colored using the same color scheme as (a). Magenta, SAM ligand.

RNA is strongly charged, so the ionic environment is of crucial importance in attenuating electrostatic repulsion as the tertiary structure of RNA packs it into a small volume.^9,10 In order to balance its strong negative charge and maintain electroneutrality, RNA attracts positive ions out of bulk solution and repel negative ions. The number of excess ions an RNA molecule attracts into its local environment is called the preferential interaction coefficient (Γ_i) for a species i, and depends strongly on available ionic concentrations.¹⁶ Local enrichment of Mg²⁺ and K⁺, along with a local depletion of anions, are responsible for balancing most of the RNA charge.

Mg²⁺ is especially important because RNA rarely forms tertiary structure in the absence of Mg²⁺.¹⁰ First, it is entropically cheaper to balance the charge with divalent Mg²⁺ because it requires only half as many condensed ions as monovalent ions to balance the charge. Furthermore, since Mg²⁺ is divalent, it can attract multiple phosphates at once, which results in attractive bridging interactions between what would otherwise be repulsive phosphates.^17,18 Lastly, due to its small size, Mg²⁺ is able to get closer to RNA, which enables it to outcompete other divalent ions.^19,20

The treatment of ions in theoretical models of RNA is an active area of research. Continuum approximations range from Debye-Hückel²¹ to more sophisticated non-linear Poisson-Boltzmann (NLPB) approaches.^22–24 These reduced description treatments are necessary in implicit solvent simulations or when atomistic calculations are impractical. Since these models treat the ionic environment as a continuum, molecular details of the ionic environment are necessarily lost, including ion-ion correlations and discrete ion effects.⁶ The importance of these discrete ion effects on the molecules with which they interact is an open question. In Manning counterion condensation theory, when the linear charge density of a polyelectrolyte chain is high enough, as it normally is in RNA, ions condense from aqueous solution to shield the phosphate backbone, effectively renormalizing its charge.²⁵ If the distance between these Manning condensed counterions is less than or equal to the Debye screening length (both are approximately 6.5 Å in our simulations), these counterions strongly interact with each other and behave as a strongly correlated ionic liquid or glass.²⁶

Here we carefully examine the interaction between RNA and its ionic environment through molecular dynamics simulations. We observe a previously underappreciated class of transient, outer-sphere coordinated Mg²⁺ with glassy dynamics, which couples to and modulates RNA kinetics. Outer-sphere ions are by far the largest group observed in our simulations (80%), and the focus of this paper. This class of Mg²⁺ is poorly represented by the continuum approaches we have outlined. While the thermodynamics of this class are captured with varying degrees of accuracy, these models are incapable of capturing the rich internal dynamics or the control over RNA kinetics by outer-sphere Mg²⁺.

Outer-sphere Mg²⁺ ions comprise one of four regimes of Mg²⁺ behavior we observe in our simulations. These regimes are largely delineated by the distance from the RNA, and are divided into the following classes: inner-sphere, outer-sphere, diffuse, and free. Inner-sphere ions, which include chelated ions as a subset, shed part of their hydration shell and bind directly to the RNA via inner-sphere contacts. Outer-sphere ions are coordinated with the RNA via outer-sphere contacts, and interact through a single hydration shell. Diffuse ions have multiple hydration shells and are poorly ordered, but are enriched above bulk concentration. Beyond the diffuse ions are the free ions, where the enrichment of ions ceases and the RNA charge has been screened out.

Our results show that outer-sphere Mg²⁺ local density fluctuations, residence times, and RNA fluctuations occupy similar timescales and kinetically couple. We observe that Mg²⁺ alters RNA kinetics in two ways. First, increased Mg²⁺ concentration tends to slow the kinetics of RNA fluctuations, and second, local Mg²⁺ density changes due to individual ion association events are correlated with RNA conformation. In order to better understand Mg²⁺ interactions, we characterize the behavior of Mg²⁺ in the presence of RNA. The Mg²⁺ distribution is controlled by electronegative RNA atoms, hydration shells, and a preference for the major groove. The differing distance classes of Mg²⁺ have different diffusive behavior, and careful analysis of the diffusion data suggests that the outer-sphere Mg²⁺ near RNA behaves like a supercooled strong ionic liquid. Because outer-sphere Mg²⁺ ions account for 80% of excess Mg²⁺ in our simulations, and because of their rich dynamics, they may change the paradigm of Mg²⁺-RNA interactions. Rather than a few inner sphere ions anchoring the RNA structure surrounded by a continuum of diffuse ions, our results reveal a layer of outer-sphere coordinated Mg²⁺ strongly coupled to the RNA.

2 Model and Methods

2.1 Simulation Details

Molecular dynamics simulations of the SAM-I riboswitch were performed with and without SAM in the presence of five varying Mg²⁺ concentrations. Individual simulations were 2 μs, for a total of 20 μs of sampling. Simulations were carried out using the Gromacs v4.5.1 molecular dynamics package.²⁷ The Amber 99 forcefield²⁸ was used, with modified K⁺ ion parameters and SPC/E water to prevent crystal formation.^29,30 Because of its importance for stability, we parameterized the SAM metabolite for AMBER. In order to parameterize the SAM, we used GAMESS quantum mechanics software³¹ and the RED software package³² to compute the charges on each atom using the Restrained ElectroStatic Potential method.^33,34 The remaining forcefield parameters were taken from GAFF (the Generalized Amber ForceField).³⁵ Simulations were run with a time step of 2 fs and bond lengths for hydrogen atoms were fixed using LINCS.³⁶ Particle mesh Ewald electrostatics³⁷ were used with an Ewald radius of 15 Å, and a Van der Waals cutoff of 15 Å.

Since the maximum linear dimension of the SAM-I aptamer is 70.7 Å, a water box of 100 Å was used to allow a careful examination of the ionic environment. Simulations contained approximately 98,000 atoms. The simulations had target concentrations of 100 mM KCl, and 0, 0^†, 1, 6, and 10 mM MgCl₂ in bulk. The 0 mM Mg²⁺ simulation contained no Mg²⁺ ions, while the 0^† simulation contained a single poorly resolved Mg²⁺ ion taken from the crystal structure (near A10 and U64) which we predict to be chelated (see below for details). The presence of a Mg²⁺ near this predicted chelation site has been suggested to be important for stability.^4,38 This ion was included in all remaining simulations. Since the RNA is strongly charged, it balances this charge by attracting Mg²⁺ and K⁺ ions into and repelling Cl^– ions from its local environment. These excess ions do not count towards the bulk concentration. Therefore, the ions in a simulation are a combination of excess ions which balance the RNA charge and bulk ions. The number of excess ions is equal to the preferential interaction coefficient. Each bulk ion contributes 1.7 mM for our box size. Since preferential interaction coefficients vary with concentration, several preliminary equilibrations were run to determine the correct number of ions to include so that the desired concentrations would remain in bulk. For example, in the 10 mM simulation, the predicted chelated ion and 32 hydrated Mg²⁺ ions were included, but 27 of these were excess ions and only 6 contributed to the bulk concentration. See Table 1 for more details.

Table 1.

Contains (from top to bottom) number of ions in each simulation, raw concentrations determined 20 Å beyond RNA (asterisk), concentrations corrected with a small potential perturbation approximation, and preferential interaction coefficients (Γ) obtained from the corrected concentrations.

	0 mM	0† mM	1 mM	6 mM	10 mM
N Mg2+	0	1	11	22	33
N K+	137	133	116	100	84
N Cl–	45	43	46	52	58
[Mg2+]*a	0.0 ± 0.0 mM	0.0 ± 0.0 mM	1.1 ± 0.9 mM	6.7 ± 2.6 mM	11.2 ± 1.6 mM
[K+]*	115.3 ± 2.6 mM	114.2 ± 1.6 mM	113.8 ± 1.9 mM	110.0 ± 4.9 mM	105.5 ± 2.7 mM
[Cl–]*	93.1 ± 1.8 mM	90.0 ± 1.1 mM	94.8 ± 1.2 mM	106.5 ± 1.4 mM	115.3 ± 0.7 mM
[Mg2+]b	0.0 ± 0.0 mM	0.0 ± 0.0 mM	0.9 ± 0.7 mM	5.8 ± 2.2 mM	10.2 ± 1.4 mM
[K+]	103.0 ± 2.0 mM	100.6 ± 1.2 mM	102.5 ± 1.7 mM	102.3 ± 4.6 mM	100.5 ± 2.5 mM
[Cl–]	103.0 ± 2.0 mM	100.6 ± 1.2 mM	104.2 ± 1.1 mM	113.9 ± 1.9 mM	120.8 ± 0.8 mM
Γ Mg2+	0.0 ± 0.0	1.0 ± 0.0	10.5 ± 0.4	18.7 ± 1.3	27.2 ± 0.8
Γ K+	78.0 ± 1.1	75.4 ± 0.7	57.3 ± 1.0	41.4 ± 2.6	26.5 ± 1.5
Γ Cl–	-14.0 ± 1.1	-14.6 ± 0.7	-13.7 ± 0.6	-13.2 ± 1.1	-11.2 ± 0.5

^aRaw concentration

^bCorrected concentration ∝ N – Γ

2.2 Equilibration

Equilibration began from the crystal structure (Protein Data Bank accession code 2GIS¹⁴), using our well established protocol.^39,40 The RNA was frozen and placed in a waterless box. Ions were placed randomly with larger Van der Waals radii to prevent them from condensing onto the RNA without an appropriate hydration shell. For the sole purpose of establishing the starting configuration of ions for explicit solvent simulations, the ions were equilibrated using stochastic dynamics and a dielectric constant of 80 to mimic water for 10 ns until the electrostatic energy converged. Then water was added to the box, and annealed to 300 K over 200 ps with the RNA and ions frozen. The ions were released and allowed to equilibrate at constant volume for 2 ns. Then the RNA was gradually released over 10 ns, spending 2 ns each with position restraints of 1000, 100, 10, 1, and 0 kcal/mol/nm², at constant pressure. This amounted to 10 ns of waterless equilibration followed by 12.2 ns of explicit solvent equilibration. From this point on, unrestrained explicit solvent simulations were performed including explicit solvent and explicit ions with full particle mesh Ewald electrostatics.

Upon the addition of water, the bulk concentration and the radial distribution functions of the K⁺ and Cl^– ions converged quickly, on a time scale of approximately 0.5 ns. The K⁺ distribution function changed due to a few K⁺ ions partially shedding their hydration shells, which was not allowed before the addition of water. Since the equilibration was much longer than 0.5 ns, K⁺ and Cl^– were well equilibrated. Post simulation analysis of relevant time scales, (see Section 3.1.2), validated that equilibration was reasonable for Mg²⁺ as well. While some Mg²⁺ sites had association times in excess of the simulation time, the largest density fluctuation times for Mg²⁺ of these sites were approximately 20 ns, and bulk Mg²⁺ concentration fluctuated with a time scale between 5 and 8 ns depending on the Mg²⁺ abundance. These time scales are all less than or comparable to the 12.2 ns of explicit solvent equilibration. Thus, this equilibration procedure allowed the RNA to equilibrate with the ionic environment while keeping it close to the crystal structure.

3 Results and Discussion

In Section 3.1, the simulations of the SAM-I riboswitch show that outer-sphere Mg²⁺ and RNA fluctuate on the same time scales and couple. Both collective effects (the bulk concentration of Mg²⁺) and local effects (individual Mg²⁺ association events) affect RNA dynamics. In Section 3.2, characterization of the Mg²⁺ diffusion and distribution reveals molecular mechanisms by which Mg²⁺ influences RNA: a layer of Mg²⁺ ions separated from the RNA by a single hydration layer constitutes the majority of the excess ions (Γ_Mg²⁺). Ions in this layer are positioned by electronegative RNA atoms, hydrations shells, and a preference for the major groove.

3.1 Mg²⁺-RNA Interactions and Time Scales

3.1.1 Global RNA Dynamics

In our simulations, the Mg²⁺ concentration has a measurable effect on global fluctuations (Figure 2a). To characterize the global dynamics of the RNA, global coordinates are needed. The explicit solvent molecular dynamics simulation trajectories were projected onto normal modes.^41–43 In this context, normal mode analysis is advantageous relative to principal component analysis⁴⁴ because normal mode analysis produces a consistent measure between all simulations (see SI for more details). A structure-based potential^45,46 was used to compute normal modes, rather than the typical Tirion potential.⁴⁷ This is the first time this potential has been used for normal modes to our knowledge.

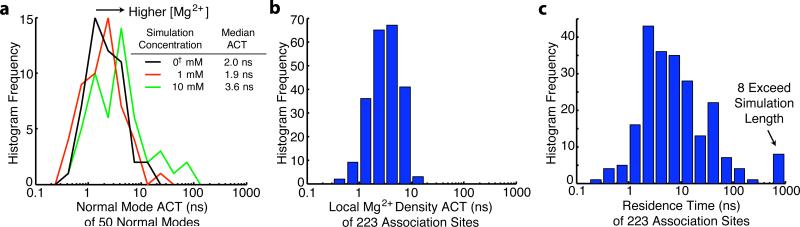
Figure 2.

Mg²⁺ affects RNA kinetics. (a) The distribution of autocorrelation times (ACT) for the MD trajectories projected onto the lowest 50 normal modes. The time scales of RNA fluctuations increase with Mg²⁺ concentration in accordance with experiment. This occurs because Mg²⁺ tightens RNA tertiary contacts and stabilizes compact conformations. (b) The distribution of autocorrelation times for the local Mg²⁺ density around several association sites. The time scales of RNA fluctuations are comparable to the time scale of the RNA fluctuations, which allows them to kinetically couple. (c) The residence time for the association sites.

In order to determine time scales of RNA motion, trajectories were projected onto the first 50 normal modes. After subtracting a linear fit to remove drift along unstable normal modes, autocorrelations were computed as a function of time (Eq. (S2)). The autocorrelations generally had long non-exponential tails, suggesting the presence of multiple time scales. This is to be expected because processes in RNA range over many orders of magnitude, up to the ligand dissociation time scale, which is too slow to observe in the simulations. To obtain the dominant time scale for each normal mode, the time when the autocorrelation fell below 1/e was taken. This dominant time scale represents the duration of the largest structural changes that occur within the 2 μs simulation. The peak of the distribution of times changes with Mg²⁺ concentration. The median time scale of the autocorrelations increased from 2.03 ns for 0^† mM Mg²⁺ to 3.55 ns for 10 mM Mg²⁺, showing that increasing Mg²⁺ concentration slows structural fluctuations.

It has been shown that while Mg²⁺ is much more effective than K⁺ at stabilizing RNA, Mg²⁺ also tends to slow transition rates by reducing the entropy of transition state ensembles.^17,48 The observed lengthening of autocorrelation time scales for RNA fluctuations in the presence of Mg²⁺ provides a mechanism for such a slowing in the presence of Mg²⁺. The Mg²⁺ stabilizes the compact structure, so the RNA must wait longer before a sufficiently large fluctuation occurs to induce a transition.

3.1.2 Local Mg²⁺ Dynamics

Before it is possible to quantify the effects of individual Mg²⁺ association events on RNA, it is necessary to identify sites where Mg²⁺ associates with RNA. Association sites were identified by finding the average position of a Mg²⁺ ion with respect to the RNA between times when its diffusion fell below 10 μm²/s and rose back above 100 μm²/s. (The experimental diffusion of aqueous MgCl₂ is 1100 μm²/s.) Diffusion as a function of time was computed by fitting 〈x²〉 = 6Dt to the mean squared deviation of Mg²⁺ positions (fitted to the RNA structure). We identified 223 sites where Mg²⁺ associates with RNA. Mg²⁺ dwell times in these sites ranged from a few ns to several hundred ns.

To quantify Mg²⁺ association with RNA, Mg²⁺ density near these association sites was computed as a function of time by counting the number of Mg²⁺ within a cutoff distance of the site. The cutoff used was typically 10 Å, which is large enough to accommodate two or three Mg²⁺, but values of 8 Å, 6 Å, and 4 Å were also tried with similar results. This density measure showed whether an association site was effectively occupied or unoccupied at any given time.

In order to determine the time scales of local Mg²⁺ density fluctuations, autocorrelations of the local Mg²⁺ density time traces were computed (Eq. (S2)). Most (approximately 85%) of the local density autocorrelations were generally exponential. Characteristic times were taken from when the autocorrelation crossed 1/e, and binned (Figure 2b). Nearly all sites have fluctuation times between 1 and 10 ns. A site may tend to be occupied for much longer, but in that case the fluctuation times correspond to transient periods when the site is empty, and these unoccupied times are generally less than 10 ns. Shell sizes other than 10 Å give comparable timescales (Figure S2), even though a 4 Å shell just captures if a Mg²⁺ is in that site, and 10 Å captures a broader picture of the local density.

Since residence times need not correspond with local Mg²⁺ density fluctuation times, it is informative to examine residence times as well. To determine residence times for each site, a modified autocorrelation approach was used. For each site and each Mg²⁺ a time-dependent boolean variable was assigned to one if the Mg²⁺ ion was within 4 Å of the association site, and zero otherwise. 4 Å was chosen to ensure only ions in that association site were considered associated, rather than ions in neighboring sites or more transient ions which might come within 10 Å. This boolean variable was then autocorrelated without subtracting the mean. These autocorrelations represent how long the same ion remains associated rather than how long a density fluctuation from the mean lasts. For each association site, the averages in (Eq. (S2)) were taken over time and over all Mg²⁺ ions. Due to the noisy tails of the autocorrelation functions, residence times were taken from when autocorrelations fell below 1/e.

Residence times occupy a much broader range, including 8 that are longer than the simulation time (Figure 2c). Residence times correlate well with the 4 Å shell density fluctuation times (Figure S2). Sites with longer residence times tend to have longer fluctuations, though the fluctuations are generally fast compared with the residence time. 10 Å density fluctuation times correlate poorly with the residence times due to the presence of faster ions further out in the shell. It is likely that long term outer-sphere association sites such as the 8 identified here contribute substantially to the enhanced stability of RNA in the presence of Mg²⁺, and modulate kinetics by anchoring their local RNA environments against fluctuations for long times while associated.

3.1.3 Local Mg²⁺ Events Affect Global Dynamics

Since RNA fluctuations occupy the same time scales as Mg²⁺ density fluctuations and Mg²⁺ residence times, they can couple. We now show that Mg²⁺ association in particular sites affects SAM-I conformation and dynamics. Mg²⁺ bridging interactions, in which a single Mg²⁺ mutually attracts phosphates, have been suggested as a mechanism for Mg²⁺ stabilization of tertiary structure.¹⁷ Temporal correlations (Eq. (S4)) between individual Mg²⁺ association events and phosphate-phosphate (P-P) distances in the simulations provide evidence for this mechanism (Figure 3). Mg²⁺ association events were modeled by the local ion density about association sites using 10 Å shells as described above.

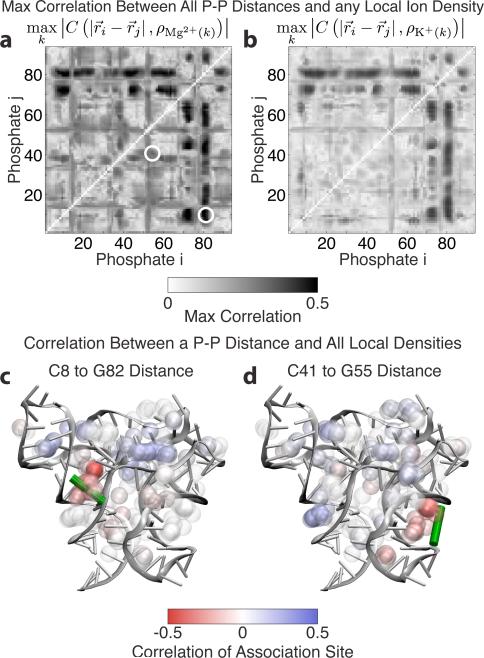
Figure 3.

Locally, individual Mg²⁺ association events pull phosphates together by bridging interactions. (a) The correlations between phosphate-phosphate (P-P) distance and the local Mg²⁺ density at the most strongly correlated association site (10 mM simulation). The pairs in panels (c) and (d) are circled. (b) The same plot for K⁺ shows lower correlations (0^† mM simulation). These correlations represent the passive changes in ionic concentration due to changing RNA structure. (c-d) Two representative P-P distances across a major groove (illustrated by the green bar). The Mg²⁺ density in the groove is negatively correlated (red) because when density in these regions increases, the P-P distance decreases. Balls represent association sites. The density about an association site is computed within a 10 Å shell, but the sites are plotted with a radius of 2.5 Å for clarity, and colored according to their correlation with the P-P distance.

Correlating time traces of P-P distances with time-dependent local Mg²⁺ densities shows several regions are especially susceptible to Mg²⁺ binding. Mg²⁺ binding within the P4 major groove (C8 to G82 phosphates) shows substantial correlation. When Mg²⁺ enters the P4 major groove, the groove partially closes (Figure 3c), resulting in negative (red) correlations between Mg²⁺ density within the groove and P-P distance. Several other regions also show strong correlations (Figure 3a), including the P3 groove (C41 to G55 phosphates) (Figure 3d), demonstrating that individual Mg²⁺ association events affect local RNA conformation.

The K⁺ correlations in Figure 3b provide a control for the conclusions drawn from the Mg²⁺ correlations in Figure 3a. K⁺ fluctuates more than an order of magnitude more quickly than Mg²⁺, so K⁺ cannot couple effectively with RNA motion. The observed correlations between local K⁺ density (at the Mg²⁺ sites) and P-P distances are indeed weaker than for Mg²⁺. They represent K⁺ passively responding to the RNA conformation rather than actively modulating it through bridging interactions as Mg²⁺ does.

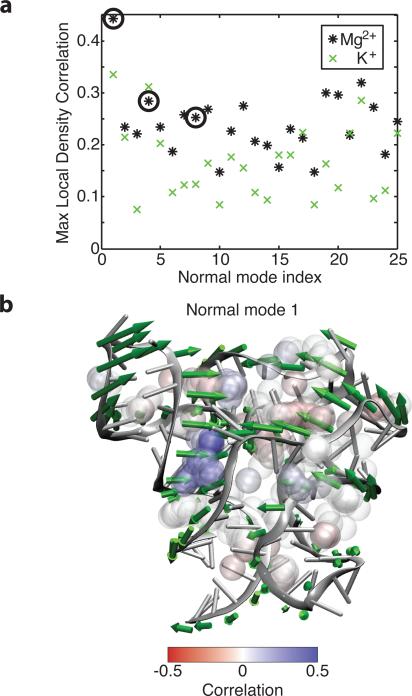
The effect of Mg²⁺ association events on local RNA conformation in turn affects the global conformation. Correlations were computed between the local density around association sites and the first 25 normal modes. The presence or absence of Mg²⁺ can account for 30% to 40% of RNA fluctuations along many normal modes (Figure 4a). Several of the lowest and most correlated normal modes are shown with the directions of motion along the normal mode. Normal mode 1 responds to bridging interactions in the P4 major groove (Figure 4b). When Mg²⁺ enters the blue region (positive correlation), progress along that coordinate increases, and the major groove of P4 surrounding those phosphates closes. (Correlations are opposite from Figure 3c because positive motion along the structural reaction coordinate is in opposite directions.) Normal mode 4 responds to competition between bridging interactions in the P3 and P4 major grooves (Figure S5c). Positive motion along normal mode 4 opens the P4 major groove and closes the P3 major groove, and the resulting correlations are as expected. Normal mode 8 responds to competing bridging interactions on opposite ends of the P4 major groove (Figure S5d). In normal mode 8, the P4 major groove opens on the loop end while closing on the P1 end. Correlations with the association sites in this groove reflect that difference: the loop end displays negative correlations; the P1 end shows positive correlations. Our results show that individual Mg²⁺ association events affect the global conformation by changing local conformation through bridging interactions between phosphates.

Figure 4.

Mg²⁺ association and resulting local bridging interactions also affect the global RNA conformation. (a) Correlations between normal mode projections and the most strongly correlated local Mg²⁺ density for each normal mode. Several of the first few normal modes are strongly correlated. Circled modes are shown in (b) and in Figure S5. The positive direction of motion along the normal mode is plotted as green arrows. Densities in regions which close upon positive motion along the normal mode are generally positively correlated (blue), while densities in regions which open are generally negatively correlated (red). We note that in the case of the P4 major groove described earlier, positive motion along the normal mode corresponds to a decrease in P-P distance. Thus, a negative correlation between the Mg²⁺ density and the P-P distance corresponds to a positive correlation between the Mg²⁺ density and positive motion along the normal mode. Balls represent association sites, and are plotted one quarter scale as in Figure 3.

3.2 Characterization of Outer-Sphere Mg²⁺

3.2.1 Ionic Concentrations and Preferential Interaction Coefficients

Since RNA is strongly charged, it attracts excess ions to balance its charge. The excess number of each species of ion i that an RNA molecule attracts into its local environment is called the preferential interaction coefficient Γ_i.¹⁶ Preferential interaction coefficients are of interest because they are experimentally measurable,⁴⁹ and allow connection between the simulations and experiment. Electroneutrality requires the preferential interaction coefficients to balance the net RNA charge according to Z = Σq_iΓ_i, where Z is the magnitude of the RNA charge and q_i is the charge of each ionic species i.^50,51 Within this constraint, Γ_i for each species can vary with bulk ionic concentrations due to the availability of various ions.

Simulations were run at several varying concentrations. Table 1 shows the number of ions included in simulations as well as the concentrations and preferential interaction coefficients (Γ_i) for each species i. The number of ions in the box is the sum of ions contributing to the concentration and the excess ions Γ. Since Γ_i varies with concentration, the number of ions in the box had to be chosen through repeated trials to obtain the desired bulk concentrations. Concentrations as a function of time are computed by counting the number of “bulk” ions B_Mg²⁺ and water molecules B_H2O more than 20 Å from any RNA atom and taking their ratio. While this technically gives the molality rather than the molarity, we note that the molarity and molality are very close for low ionic concentrations in water. The concentration of an ionic species is given by the time average of the ratio of these molecule counts multiplied by the molarity of pure water.

$${\left[{\mathrm{Mg}}^{2+}\right]}^{\ast }=55.51\mathrm{M}\frac{B_{{\mathrm{Mg}}^{2+}}}{B_{{\mathrm{H}}_2\mathrm{O}}}$$ (1)

Since only 95% of the charge is balanced out by 20 Å in 100 mM KCl, the computed concentrations will not sum to zero because some charge density must remain in the rest of the box to balance the residual RNA charge. However, unlike the case near the RNA where ions interact differently with the RNA due to large electrostatic potentials, at 20 Å, the electrostatic potential is a smooth, small perturbation. Ion densities in a small potential well will respond linearly with their concentration, charge, and the well depth. The corrected bulk concentrations (which must be electroneutral) are given by

$$\left[i\right]={\left[i\right]}^{\ast }-q_i{\left[i\right]}^{\ast }\frac{{\sum }_j{q}_j{\left[j\right]}^{\ast }}{{\sum }_j{q_j}^2{\left[j\right]}^{\ast }}$$ (2)

$$\left[{\mathrm{Mg}}^{2+}\right]={\left[{\mathrm{Mg}}^{2+}\right]}^{\ast }-2{\left[{\mathrm{Mg}}^{2+}\right]}^{\ast }\frac{2{\left[{\mathrm{Mg}}^{2+}\right]}^{\ast }+{\left[{\mathrm{K}}^{+}\right]}^{\ast }-{\left[{\mathrm{Cl}}^{-}\right]}^{\ast }}{4{\left[{\mathrm{Mg}}^{2+}\right]}^{\ast }+{\left[{\mathrm{K}}^{+}\right]}^{\ast }+{\left[{\mathrm{Cl}}^{-}\right]}^{\ast }}$$ (3)

where q_i is the charge, [i]* denotes the raw concentration, and [i] denotes the corrected concentration. If the arbitrary definition of bulk ions as more than 20 Å from the RNA is varied, the corrected concentrations converge much more quickly than the raw concentrations. Once corrected concentrations are obtained, preferential interaction coefficients may be computed. Preferential interaction coefficients (Γ) are the ions in excess of the ions expected from the corrected concentration

$${\Gamma }_{{\mathrm{Mg}}^{2+}}=N_{{\mathrm{Mg}}^{2+}}-N_{{\mathrm{H}}_2\mathrm{O}}\frac{\left[{\mathrm{Mg}}^{2+}\right]}{55.51\mathrm{M}}$$ (4)

where N_Mg²⁺ is the total number of Mg²⁺ ions and N_H2O is the total number of water molecules.

Preferential interaction coefficients (Γ) are experimentally measurable.⁴⁹ For a purine riboswitch with 72 residues at 1 mM Mg²⁺ and 50 mM K⁺, Γ_Mg²⁺ varies from 13 to 18, depending on mutations and the switch state.^50,52 We observe a Γ_Mg²⁺ of 10.5 at this Mg²⁺ concentration. A lower prediction is expected in the simulation since it has twice as much K⁺ competing to balance the RNA charge. There are additional factors that complicate the comparison between experiment and simulation. NMR experiments generally show nearly all K⁺ remains fully hydrated, while in most molecular dynamics simulations (including ours) approximately half of the excess K⁺ partially dehydrates and contacts RNA directly.⁵³ Our simulations show 40% to 50% of Γ_K⁺ is partially dehydrated (Figure S11).

We emphasize that our ion parameters produce very stable 2 microsecond trajectories. Removal of this population and proportional increase of the remaining populations of excess ions would raise Γ_Mg²⁺ for 1 mM Mg²⁺ from 10.5 to 14.7. We note that most of the Mg²⁺ contributing to Γ_Mg²⁺ are in the outer-sphere layer of ions, between the inner-sphere and diffuse regimes.

3.2.2 Distance Classes and Diffusion of Mg²⁺ Ions

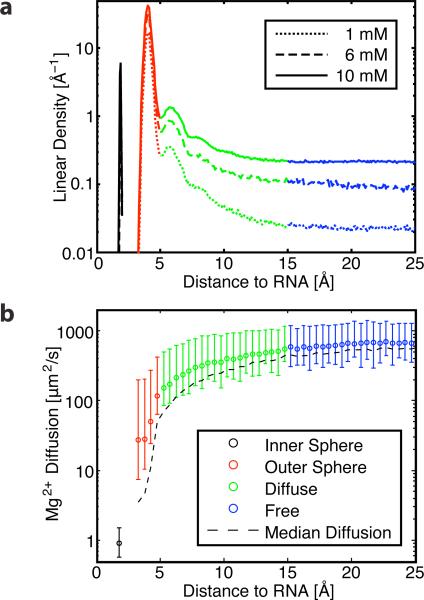
Mg²⁺ ions can be divided into classes based on distance from RNA^9,10 (Figure 5a). Inner-sphere ions are the closest and make direct contact with the RNA. Mg²⁺ typically has an octahedral geometry and coordinates with six waters. Each inner-sphere contact with RNA replaces one of these waters. Inner-sphere ions can be further divided into monodentate and chelated ions based on whether they make one or multiple inner-sphere contacts with RNA. The next layer is outer-sphere. These Mg²⁺ retain all their inner-sphere waters, and are only separated from the RNA by this single hydration layer. This layer accounts for most of the Mg²⁺ in our simulations, 80% to 85% of Γ_Mg²⁺ (Table 2). Ions in this layer fluctuate on time scales comparable with RNA fluctuations, and couple to the RNA. These Mg²⁺ ions cannot condense closer than this layer without paying substantial dehydration costs. There are several hints that this layer behaves as an ionic glass (Section 3.2.4). The next layer is diffuse. Diffuse ions are separated from RNA by two or more hydration shells, are poorly ordered, and are well described by continuum models. The furthest group of ions is free. The divide between diffuse and free ions is ambiguous. For the present analysis we simply subtract inner-sphere and outer-sphere ions from Γ_Mg²⁺. Population enrichment (Figure 5a) and reduced diffusion (Figure 5b) suggest between 10 and 20 Å as a reasonable boundary for these two classes.

Figure 5.

Four classes of Mg²⁺ based on RNA distance emerged during our analysis: inner-sphere (black) at 2 Å outer-sphere (red) at 3 to 5 Å, and diffuse (green) at 5 to 15 Å, blending into free (blue). (a) The population of Mg²⁺ as a function of distance from the RNA. The outer-sphere population, which has previously received little attention, composes 80% to 85% of Γ_Mg²⁺ (Table 2). (b) The diffusion of Mg²⁺ as a function of distance from the RNA. Closer Mg²⁺ ions show decreased values of mobility. Bars reflect the variance of instantaneous diffusion above and below the mean. The uncertainty from bootstrap analysis averages approximately 3%. The median instantaneous diffusion is plotted as a dashed line. While the median is comparable to the mean in most regimes, it is substantially below the mean for outer-sphere Mg²⁺ because rare dissociation events dominate the mean. Values are from the 10 mM simulation.

Table 2.

The number and percentage of ions in the distance classes in Figure 5. Predicted chelated ions are a subset of the inner-sphere class. Note that the outer-sphere population contains 80% to 85% of the excess Mg²⁺ ions Γ_Mg²⁺.

	1 mM	6 mM	10 mM
Γ Mg2+	10.5	18.7	27.2
Number of Mg2+
Inner-Sphere	1.0	1.0	1.0
Outer-Sphere	8.6	16.0	22.3
Diffuse	0.9	1.7	3.9
Percent of ΓMg2+
Inner-Sphere	9.5	5.4	3.7
Outer-Sphere	81.8	85.8	81.8
Diffuse	8.7	8.9	14.5

Diffuse ions are well represented by NLPB distributions due to their low density and rapid dynamics. Outer-sphere ions may be analogous to Manning counterions that condense as close to the RNA as possible and screen its charge. They are dense, have internal correlations, and couple strongly with the RNA. Reasonable thermodynamic agreement with experiment has been obtained by combining a few chelated sites with a NLPB representation of diffuse ions.^7,8,54 The Tightly Bound Ion method treats outer-sphere ions thermodynamically resulting in improved calculations of stability.⁶ Our results show that Mg²⁺ also exerts substantial kinetic control. In contexts where RNA kinetics are of interest, the kinetic effects of outer-sphere Mg²⁺ must be carefully considered.

The kinetic effects are highlighted by the different diffusive behavior between Mg²⁺ distance classes (Figure 5b). The diffusion of Mg²⁺ ions was computed as follows. The RNA was first fit to a reference structure, because otherwise the lower Mg²⁺ diffusion values were washed out by the bulk RNA diffusion, which was on the order of 10 μm²/s. The distance to the nearest RNA heavy atom was found for every frame. The squared displacement for 2 ns periods starting every 200 ps was computed, and then averaged within bins based on starting distance from the RNA. The mean squared displacement was then fit within each distance bin to 〈x²〉 = 6Dt to obtain diffusion. Instantaneous diffusion could be determined by fitting the mean squared displacement before averaging within distance bins.

The Mg²⁺ ion in the inner sphere class has the lowest diffusion. This ion does not move relative to the RNA during the simulation so its diffusion is nearly zero, and the plotted value of 1 μm²/s indicates our method's precision. The outer-sphere Mg²⁺ ions have a diffusion coefficient (20 to 30 μm²/s) roughly two orders of magnitude below bulk. As mentioned before, outer-sphere ions account for most of the Mg²⁺ associated with the RNA. Depending on the site, they can remain associated from a few ns to several thousand ns.

Due to heterogeneous sites, glassy dynamics, and escape to regions with higher diffusion, the diffusion of the inner-sphere regime is complex. Rare escape events dominate the average diffusion, while the median of the instantaneous diffusion is nearly an order of magnitude lower than the average.

A very steep increase in diffusion occurs between the outer-sphere and diffuse regimes. The diffuse Mg²⁺ helps with charge balancing, but its diffusion is higher because it is not associated very strongly with any particular site. Values for the free Mg²⁺ come close to the experimental value of 1100 μm²/s for MgCl₂ diffusion. The disconnect between diffusion rates emphasizes the uniqueness of the outer-sphere regime, which occupies a region of low mobility between the essentially immobile inner sphere Mg²⁺ ion and the more rapidly diffusing diffuse regime.

In the X-ray structure, there is density nearby A10 and U64 assigned to a Mg²⁺ ion. Due to the resolution of this structure, it is difficult to assign certainty to this density, much less ascertain its chelation state. Our starting initial configuration includes this ion, which we call inner sphere due to its close proximity to the RNA. We note that the use of the term inner sphere itself is approximate due to the resolution of the X-ray structure. In our simulations, the inner sphere Mg²⁺ ion connects the partially buried non-bridging phosphate oxygens of residues A10 and U64 for the duration of the simulation, suggesting that the ion may be chelated. The chelation site is consistent with the crystal structure, and has been suggested to be important for stability.^4,38 Our prediction that this ion is chelated is also based on the need for a positive ion to bridge the repulsion of two phosphate oxygens separated by 4.24 Å, the need to offset the cost of partial burial of the phosphate on U64, and the destabilization and disordering of the riboswitch, especially the P4 helix, in simulations lacking an ion in this position. Whether we are correct about magnesium chelation at this site remains to be seen experimentally.

In bulk solution, Mg²⁺ ions exchange their inner-shell contacts on a time scale of 1.5 μs,^55,56 so we did not expect this Mg²⁺ to unbind from the RNA. During the course of our simulations, none of the Mg²⁺ exchanged any of their waters, whereas we may have expected some exchange events to occur. Simulations of even longer durations will be able to more directly address this. We note that this is not necessarily a major limitation for our system, since dehydration of Mg²⁺ is energetically costly,¹⁰ and RNAs of this size have few electrostatic wells deep enough to pay the substantial dehydration cost for Mg²⁺. Such sites, which frequently occur at buried backbone phosphates, are more common in larger RNAs. For RNAs of this size at physiological concentrations, inner-sphere Mg²⁺ is likely only a small contributor to the preferential interaction coefficient Γ_Mg²⁺ or energetic stabilization (ΔG_Mg²⁺) compared to outer-sphere and diffuse Mg²⁺.³

3.2.3 Spatial Characterization of Outer-Sphere Mg²⁺

The distribution functions of Mg²⁺ about the RNA reveal three molecular principles of Mg²⁺-RNA association. First, Mg²⁺ shows a strong preference for the backbone and major groove. Second, Mg²⁺ is positioned by hydration layers. Finally, Mg²⁺ is positioned by an attraction for the most electronegative RNA atoms: non-bridging phosphate oxygens (NBPOs), and atoms Purine N7, Uridine O4, and Guanine O6 of the nucleotide bases.

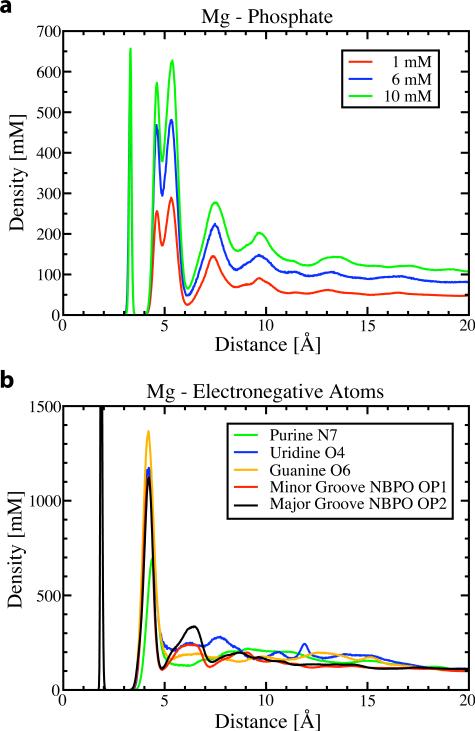
Radial distribution functions (RDF) reveal where Mg²⁺ resides during the simulations (Figure 6). The top panel shows the RDF for the central phosphorous of the phosphate group. The inner peak at 3.2 Å is the distance for the inner sphere Mg²⁺ ion which did not exchange. The double peak near 5 Å corresponds to hydrated, outer-sphere ions. The double peak suggests there is anisotropic substructure unexplained by this RDF. Most of the ions in the second and third hydration peaks are more closely associated with other phosphates. The substructure of the outer-sphere layer can be attributed to interactions with electronegative atoms of the RNA, in particular, base atoms Purine N7, Uridine O4, Guanine O6, and especially the non-bridging phosphate oxygens (NBPO) (Figure 6b). All of these RDFs have a single peak at 4.2 Å from the first hydration layer, revealing it is the electronegative atoms, not the phosphate centers, which control the Mg²⁺ distribution.

Figure 6.

Plotted are several radial distribution functions for Mg²⁺. (a) The RDF with the phosphorous atom at several concentrations. The dual peak at 5 Å indicates substructure. This substructure is clarified in (b) the RDF with several electronegative RNA atoms (10 mM simulation), including the phosphate oxygens. See Figure 7b for a 3D representation of electronegative atoms.

These radial distributions are consistent with previous results. A previously computed phosphate RDF averaged over four phosphates⁵⁷ shows qualitative agreement with the phosphate RDF and double peak. The RDF about specific electronegative atoms that explains this double peak has not been previously computed, but shows reasonable similarity to the RDF of water about Mg²⁺.^58,59 The main difference is that the inner-sphere peak in Figure 6b is much lower than the inner-sphere peak for water due to the high free energy cost of dehydrating Mg²⁺ ions.

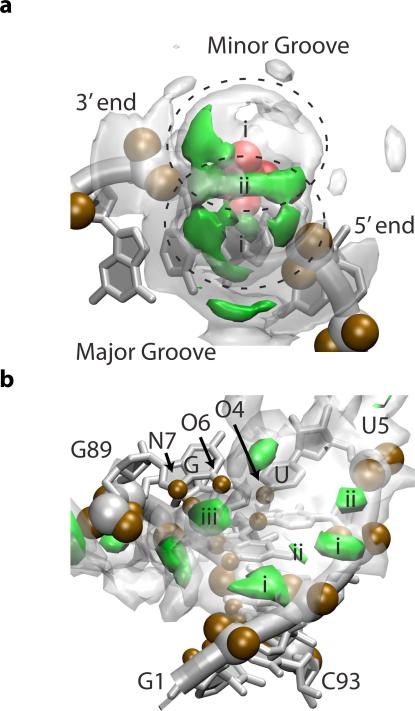
The spatial distribution functions (SDF) provide a more detailed picture of the Mg²⁺ distribution and corroborate the three principles controlling it (Figure 7). As noted in previous crystallographic studies,⁶⁰ the SDFs show that Mg²⁺ has a strong preference for the major groove.

Figure 7.

Spatial distribution functions (SDF) of Mg²⁺ about SAM-I. In our study, simulations were performed with 0 mM, 1 mM, 6 mM and 10 mM magnesium concentration. Here, we show magnesium density isosurfaces, displaying localized regions of high magnesium concentration. Specifically, Mg²⁺ density surfaces of 1.4 M and 7 M are shown in transparent white and solid green respectively (10 mM simulation with SAM). The density of the outer-sphere Mg²⁺ distribution is expressed in molarity to highlight the more than 700-fold enrichment of Mg²⁺ above the bulk concentration of 10 mM. See SI Section 8 for more details. (a) The average Mg²⁺ SDF about a phosphate (red). A representative backbone is shown for reference. Several hydration layers and a preference for the major groove are visible. Regions (i) and (ii) correspond to the two peaks in Figure 6a (b) The Mg²⁺ SDF about helix P1. Electronegative atoms controlling the distribution are labeled and shown in brown. Sites occur along the backbone (i&ii) or within the major groove near the brown electronegative atoms (iii).

Figure 7a shows the average SDF around phosphate groups. The SDF about the single phosphate shows two lobes (i) around the NBPOs as would be expected from Figure 6b. (The dual peak in Figure 6a arises because different parts of these lobes are different distances from the central phosphorus.) These lobes are modulated in density by preference for the major groove and by other electronegative atoms. As a result, the belt (ii) joining the lobes is particularly strong, as is the lobe around the major groove NBPO. The lobe around the minor groove NBPO is weaker, and polarized towards the 3’ terminus, due to the major groove NBPO of the neighboring residue. Secondary shells separated by two and three hydration layers are visible where Mg²⁺ can interact more closely with other electronegative atoms, especially the bases in the major groove.

Figure 7b (the P1 helix) shows typical ways that Mg²⁺ associates with helices. Again the preference for the major groove is strongly visible. There are sites along the backbone where Mg²⁺ sits in the belt (ii) between two NBPOs or in a notch (i) between neighboring phosphates, as suggested by Figure 7a. Several association sites within the major groove where Mg²⁺ interacts with the bases are visible. Electronegative atoms are again key in positioning these sites. One particularly strong site (iii) is at the G·U wobble pictured at the top of this helix. G·U wobbles have been previously noted to form Mg²⁺ association sites.^5,60 The molecular basis for this is immediately apparent: the G·U wobble forms a depression in the major groove surrounded by an N7 and an O6 on the guanine and an O4 on the uracil. The canonical base pairs only have two of these three electronegative atoms. A preliminary analysis of our data does show some clustering of K+ ions at similar N7 positions as observed in previous studies of monovalent ion interactions with RNA by Chen, et al.¹¹

3.2.4 Glassy Character of Outer-Sphere Mg²⁺

Outer-sphere Mg²⁺ ions are not quite bound and not quite un-bound. These ions are localized to the RNA, but hop from site to site in a glass-like manner. That is, the energy landscape for these ions exhibits a high degree of frustration, where one site of localization for a Mg²⁺ ion may be as favorable as another site, causing the ion to migrate from site to site, without being trapped in one specific site. Our measured diffusion and distribution of the outer-sphere Mg²⁺ suggest they behave in a glassy manner.

The presence of several ordered peaks in the RDF between Mg²⁺ and NBPOs in the major and the minor grooves of the RNA (Figure 6b) is consistent with glass-like behavior. Furthermore, the RDF between Mg²⁺ and the phosphorous atoms (Figure 6a) indicates a split peak at 4.2 Å and 5.1 Å, that is followed by peaks at 7.5 Å and 9.5 Å, and a lack of noticeable peaks for distances larger than 14 Å. This indicates that the system is locally amorphous, and likely an ionic glass.⁶¹

If the distance between these outer-sphere ions is less than or equal to the Debye screening length, these counterions strongly interact with each other and behave as a strongly correlated ionic liquid,²⁶ with corresponding diffusion and shear properties.⁶² In our simulations the average distance between outer-sphere ions is on the same order as the Debye length (both are approximately 6.5 Å), suggesting that the ions are strongly correlated. The diffusion coefficient of the outer-sphere ions is around one hundred fold smaller than the diffusion coefficient of the free ions (Figure 5b), also indicating that these ions have the properties of a strongly-coupled liquid consistent with glass-like behavior.

4 Conclusion

Mg²⁺ has a strong effect on RNA stability and dynamics. Through molecular dynamics simulation of a folded RNA riboswitch, we demonstrated that the dynamics of Mg²⁺ and RNA can couple because Mg²⁺ and RNA fluctuations occur on the same time scale. This coupling was substantiated by the correlation of the RNA's motion with Mg²⁺ association events. Increasing Mg²⁺ concentration was shown to slow fluctuations of the RNA. In fact, preliminary results suggest outer-sphere Mg²⁺ behaves in a glassy manner. Because Mg²⁺ couples to the RNA, phase changes in the glassy Mg²⁺ ions may result in changes in RNA kinetics. Further work is needed to fully characterize the glassy dynamics of outer-sphere Mg²⁺ ions.

To form a deeper physical understanding of the molecular basis for Mg²⁺-RNA interactions, we have focused on the spatial distribution and diffusion of Mg²⁺ itself. Over 80% of excess Mg²⁺ ions are in the outer-sphere regime, separated from the RNA by a single hydration layer, rather than in the diffuse regime. These outer-sphere ions are positioned by electronegative RNA atoms, hydration layers, and a preference for the major groove. The 100-fold slower kinetics within the outer-sphere regime demonstrates how different these ions are from the canonical diffuse Mg²⁺. The outer sphere Mg²⁺ occupy a region of intermediate mobility between inner sphere and diffuse, which allows them to couple to the RNA.

Previously, the interplay between Mg²⁺ and RNA has frequently been modeled by chelation sites and a diffuse ion cloud. Diffuse ions are well represented by NLPB distributions due to their low density and rapid dynamics. In contrast, outer-sphere ions may be more reminiscent of Manning counterions that condense as close to the RNA as possible. Our simulations include explicitly discrete ion effects, internal correlations, and kinetic coupling between outer-sphere Mg²⁺ and the RNA. Since outer-sphere Mg²⁺ are the dominant population and have a substantial effect on RNA dynamics, we propose a new view of Mg²⁺-RNA interactions where the outer-sphere Mg²⁺ class, with glass-like internal correlations, both thermodynamically stabilizes and exerts kinetic control on RNA. Future reduced treatments of Mg²⁺-RNA interactions need to consider the importance of the inherently discrete ion effects of the outer-sphere Mg²⁺.