Abstract
The circular chromosome of Escherichia coli has been suggested to fold into a collection of sequentially consecutive domains, genes in each of which tend to be co-expressed. It has also been suggested that such domains, forming a partition of the genome, are dynamic with respect to the physiological conditions. However, little is known about which DNA segments of the E. coli genome form these domains and what determines the boundaries of these domain segments. We present a computational model here to partition the circular genome into consecutive segments, theoretically suggestive of the physically folded supercoiled domains, along with a method for predicting such domains under specified conditions. Our model is based on a hypothesis that the genome of E. coli is partitioned into a set of folding domains so that the total number of unfoldings of these domains in the folded chromosome is minimized, where a domain is unfolded when a biological pathway, consisting of genes encoded in this DNA segment, is being activated transcriptionally. Based on this hypothesis, we have predicted seven distinct sets of such domains along the E. coli genome for seven physiological conditions, namely exponential growth, stationary growth, anaerobiosis, heat shock, oxidative stress, nitrogen limitation and SOS responses. These predicted folding domains are highly stable statistically and are generally consistent with the experimental data of DNA binding sites of the nucleoid-associated proteins that assist the folding of these domains, as well as genome-scale protein occupancy profiles, hence supporting our proposed model. Our study established for the first time a strong link between a folded E. coli chromosomal structure and the encoded biological pathways and their activation frequencies.
INTRODUCTION
It was discovered in 1970s that the Escherichia coli chromosome is organized into a collection of consecutive plectonemic DNA loops, each having its two ends connected with each other by binding with nucleoid-associated proteins (NAPs) (1,2). Each of such loops, also called a ‘supercoiled domain’ or simply ‘supercoil’, ranges between 10 and 100 kb in sequence length (3) and folds independent of the other loops into a negatively coiled conformation. It has been speculated that the folded chromosomal structure is dynamic (4), and the domain boundaries are distributed along the genome in a seemingly random manner (5). Imaging data have revealed that the folded conformation of the E. coli chromosome changes in response to the changing cellular and environmental conditions (6). For instance, the chromosome has substantially more supercoils during the exponential growth than during the stationary phase, suggesting that the physical organization of the chromosome may play a role in the regulation of gene expression (7,8). Interestingly, some of the NAPs, which can bend or bridge DNAs, are also transcription factors such as H-NS, FIS and IHF, providing further evidence about the possible links between chromosomal folding and transcription regulation.
The advent and maturation of various experimental techniques such as ‘CHIP-sequencing’ (9–12) techniques for identification of the DNA-binding sites of NAPs and the ‘chromatin conformation capture’ techniques (13–15) have clearly accelerated the study of the folded chromosomal structures, but mostly of eukaryotic organisms. As of now, only limited data on the folded E. coli chromosomal structures have been collected mostly focused on the binding of NAPs on the DNA. One recent study on bacterial chromosomes using high-resolution microscope revealed that H-NSs may play a more important role in bacterial chromosomal organization than the other NAPs (16).
A number of computational studies have also been carried out with the goal of understanding the folded structures of bacterial chromosomes. For instance, analyses of E. coli ‘omic’ data have revealed periodicities along the genome of co-expressed genes (4,17), as well as of co-evolved genes (18) and cis-regulatory elements (19,20), all seemingly related to the supercoils in the folded chromosomal structure. A model for the local arrangement of the E. coli chromosomal loci has been proposed based mostly on the geometric consideration (21). In addition, studies have been carried out aiming to capture the relationship among the loop domains based on a confinement and entropic repulsion model as well as the information about transcription regulation networks (22). While these studies have provided hints about possible links between sequence level signals and the folded chromosomal structures, none of them have established a clear definition of the individual folding domains with detailed boundary information, not to mention their dynamic nature with respect to different physiological conditions.
We have recently discovered that operons of more frequently activated pathways tend to group into fewer sequential clusters in a bacterial genome (23), and specifically they tend to minimize the overall genomic spread among the consecutive operons of the same metabolic and regulatory pathway (24,25) across all the pathways. One possible explanation of this discovery is that the E. coli chromosome is organized into consecutive domains that minimize the total number of the unfolding of these domains during the life cycle of the organism, where such a domain is unfolded when a biological pathway, consisting of genes encoded in this DNA segment, is being activated transcriptionally; here we use the total number of unfolding to approximate the total energy needed to unfold the relevant folded domains. This hypothesis has been strongly supported by our recent study of the global genomic arrangement of bacterial operons (23). Based on this hypothesis, we have predicted seven distinct sets of folding domains of the E. coli genome under seven different physiological conditions: exponential growth, stationary phase, anaerobiosis, heat shock, oxidative stress, nitrogen limitation and SOS responses. We found that (i) the predicted sets of folding domains are highly stable with respect to perturbations to the gene-expression data used to make the prediction; (ii) they are generally consistent with the limited experimental data on the folded supercoil structures collected under the exponential and stationary growth conditions; and (iii) their boundaries are consistent with the available NAP-binding sites and genome-scale protein occupancy data, hence supporting our prediction. We believe that this study provides an effective framework for elucidation of the chromosomal organization, its dynamic nature and its functional relationship to transcription regulation of E. coli and other bacteria.
MATERIALS AND METHODS
Data acquisition
We retrieved the genes encoding the 347 metabolic pathways of E. coli K12 from EcoCyc (26), and the expression data from the M3D database (27), which contain genome-scale expression data of E. coli collected under 466 conditions. In all, 527 cis-regulatory binding sites of six NAPs (Fis, H-NS, HU, IHF, Lrp and StpA) in the E. coli genome were downloaded from RegulonDB (28), and 537 binding regions of H-NS under stationary growth conditions are downloaded from (9). In addition, 253 highly expressed genes were obtained from HEG-DB (29), and 272 extensive protein occupancy domains (EPODs) of the E. coli genome are downloaded from (30).
Identification of the M3D growth condition groups associated with different folded structures of the chromosome
Based on the knowledge that the E. coli chromosome folds into different conformations during the exponential and stationary growths, we expect that under some other growth conditions, the chromosome may fold into alternate conformations to facilitate the efficient activation of the genes for pathways required for each such class of growth conditions. For each folded structure engendered under certain growth conditions, we anticipate that there should be a set of gene responses consistent across these conditions. We call each such class of conditions as a M3D growth condition (MGC) group, and this set of genes as its ‘marker genes’. The determination of each set of marker genes is made based on literature research (31–38) and our understanding of different growth conditions (see Supplementary Method S1). The detailed gene list for each of the seven conditions is given in Supplementary Table S1.
We have used the following procedure to identify the MGC group for each growth condition, collectively denoted as  , along with the associated gene-expression data in M3D. Let
, along with the associated gene-expression data in M3D. Let  denote the entire gene set of E. coli and
denote the entire gene set of E. coli and 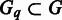 be a list of specified marker genes whose activations we suspect should require a distinct folded structure of the chromosome, with
be a list of specified marker genes whose activations we suspect should require a distinct folded structure of the chromosome, with 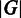 and
and 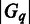 representing the number of genes in
representing the number of genes in  and
and 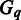 , respectively. Also let
, respectively. Also let 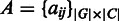 denote the whole M3D dataset, with
denote the whole M3D dataset, with 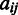 representing the expression value of gene i under condition j and
representing the expression value of gene i under condition j and 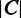 representing the number of conditions in the M3D dataset, and
representing the number of conditions in the M3D dataset, and 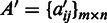 be a 0/1 matrix, with
be a 0/1 matrix, with 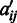 being 1 if
being 1 if 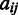 is among the highest (or the lowest depending on specific applications) 25% of the values in
is among the highest (or the lowest depending on specific applications) 25% of the values in 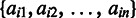 , otherwise 0, where
, otherwise 0, where 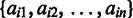 is the ith row of matrix
is the ith row of matrix 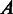 , i.e. the expression levels of gene i under all the conditions. Our goal is to identify MGCs as maximal subsets of
, i.e. the expression levels of gene i under all the conditions. Our goal is to identify MGCs as maximal subsets of  under which the majority of the marker genes in each
under which the majority of the marker genes in each 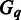 are highly expressed, i.e. their corresponding values in
are highly expressed, i.e. their corresponding values in 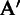 being 1. Specifically, we define
being 1. Specifically, we define
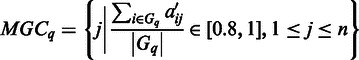 |
for each given 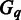 . In case an
. In case an 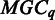 is empty, we will go back to adjust the threshold in
is empty, we will go back to adjust the threshold in 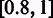 so each
so each 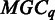 is a non-empty set.
is a non-empty set.
Prediction of the folding domains for each MGC group
Our main hypothesis (see ‘Introduction’ section) implies that (i) the genome of E. coli is partitioned into a set of contiguous domains, each independently folded into a compact structure in the folded chromosome; and (ii) under different growth conditions, the chromosome forms different sets of such folding domains, where the domain regions are so determined that minimizes the total number of unfolding of the folded domains to make their genes transcriptionally accessible when needed. Based on these, we have made a computational prediction of the domain boundaries along the genome by formulating the problem as a constrained optimization problem below.
Based on the published literature, we assume that the folding domains range L = 10 kb and U = 100 kb in length (3), and the domain boundaries can be only in inter-operonic regions. So our problem formulation is to find a partition of the E. coli K12 circular genome so that the following objective function is minimized:
| (1) |
with
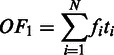 |
(2) |
and
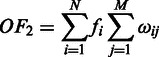 |
(3) |
where 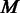 is the number of to-be-identified folding domains;
is the number of to-be-identified folding domains; 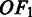 is the number of unfolding of the predicted domains to make the relevant pathways transcriptionally accessible (we assume that each domain will refold after the transcription of its relevant genes is all done so the unfolding is needed again when its genes need to be transcribed later); N is the number of known metabolic pathways encoded in the organism;
is the number of unfolding of the predicted domains to make the relevant pathways transcriptionally accessible (we assume that each domain will refold after the transcription of its relevant genes is all done so the unfolding is needed again when its genes need to be transcribed later); N is the number of known metabolic pathways encoded in the organism; 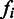 represents the activation frequency of the
represents the activation frequency of the 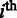 pathway, estimated from the gene expression data in M3D using the method given in (24);
pathway, estimated from the gene expression data in M3D using the method given in (24); 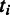 is the number of predicted folding domains that have genes encoding the ith pathway and
is the number of predicted folding domains that have genes encoding the ith pathway and 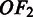 approximates the unfolding energy ‘wasted’ on unfolding the folded domains under the current condition (here we assume that (i) the effort (or energy) in unfolding a folding domain is proportional to the number of operons it contains; and (ii) the energy wasted is proportional to the number of operons contained in the domain but not involved in the pathway being activated under the current condition). For the jth domain (
approximates the unfolding energy ‘wasted’ on unfolding the folded domains under the current condition (here we assume that (i) the effort (or energy) in unfolding a folding domain is proportional to the number of operons it contains; and (ii) the energy wasted is proportional to the number of operons contained in the domain but not involved in the pathway being activated under the current condition). For the jth domain (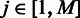 ) containing
) containing 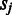 operons,
operons, 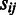 is the number of operons in the jth domain and in the ith pathway;
is the number of operons in the jth domain and in the ith pathway; 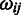 = 0 if
= 0 if 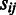 = 0, otherwise
= 0, otherwise 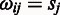 −
− 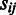 ;
; 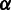 is a scaling factor whose value can be adjusted with its default value set at 1.
is a scaling factor whose value can be adjusted with its default value set at 1.
We noted that the pathway information alone does not constrain the domain prediction problem to a satisfactory level, making the problem a highly under-constrained optimization problem with a large number of solutions; hence, we included co-expression data as an additional constraint to further constrain the prediction problem. Intuitively we expect that genes in the same folding domain should be co-expressed more frequently than genes not in the same domain. We therefore developed the following objective term 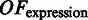 over domain boundaries (
over domain boundaries (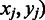 , with
, with 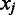 and
and 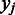 being two adjacent genes separated by an inter-operonic region, representing the last and the first gene of the to-be-identified jth and (j + 1)th folding domains under the current growth condition, respectively:
being two adjacent genes separated by an inter-operonic region, representing the last and the first gene of the to-be-identified jth and (j + 1)th folding domains under the current growth condition, respectively:
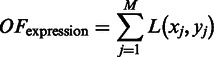 |
(4) |
where L() is designed to measure the overall co-expression level among gene pairs across each domain boundary 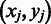 , which can be determined as to find a set of M gene pairs
, which can be determined as to find a set of M gene pairs 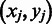 as potential domain boundaries so
as potential domain boundaries so 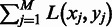 is minimized,
is minimized,
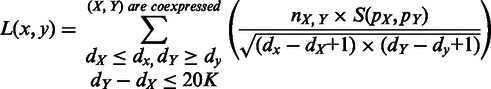 |
(5) |
where M > 0 is to be determined through solving this minimization problem; 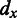 represents the genomic location of gene
represents the genomic location of gene 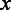 ;
; 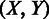 denotes all the gene pairs across the inter-genic region between genes x and y with distance
denotes all the gene pairs across the inter-genic region between genes x and y with distance  20 kb;
20 kb; 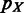 and
and 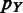 are vectors of expression levels of
are vectors of expression levels of 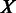 and
and 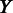 under the current growth condition;
under the current growth condition; 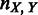 is the number of MGCs under which
is the number of MGCs under which 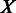 and
and 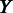 are co-expressed; and
are co-expressed; and 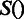 is the Spearman rank correlation coefficient (39).
is the Spearman rank correlation coefficient (39).
Now our enhanced formulation of the domain identification problem is defined as ‘to find a partition of the given circular genome to minimize the following’
| (6) |
where S and E represent the first and the last inter-operonic regions of the genome, respectively.
This optimization problem can be solved using a dynamic programming approach. Specifically, we have the following recursive relationship, which can be proved without a substantial effort:
| (7) |
which gives rise to a straightforward dynamic programming algorithm for solving this optimization problem, and further gives rise to the predicted domain boundaries under the specified growth conditions.
Measuring distance between two sets of predicted folding domains
To assess the prediction performance of the above algorithm, we need a capability to estimate the distance between two different sets of predicted folding domains (i.e. the distance between two different genomic partitions). Consider two sets of predicted domain boundaries (each represented as a set of inter-operonic regions), 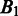 and
and 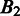 , of the same (circular) genome. Let
, of the same (circular) genome. Let 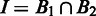 and
and 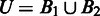 represent the intersection and union of
represent the intersection and union of 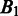 and
and 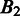 , respectively. Note that the distance between
, respectively. Note that the distance between 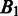 and
and 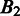 should be 0 if
should be 0 if 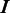 and
and 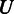 are identical. The larger the difference between
are identical. The larger the difference between 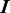 and
and 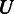 is, the larger the distance between
is, the larger the distance between 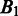 and
and 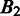 should be. In defining the distance, we consider that the distance between
should be. In defining the distance, we consider that the distance between 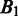 and
and 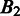 is larger when boundaries in
is larger when boundaries in  are more spread out across the genome when
are more spread out across the genome when 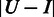 is fixed. Let
is fixed. Let 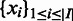 and
and 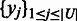 denote the sets of predicted boundaries of
denote the sets of predicted boundaries of 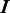 and U, respectively, ordered clockwise along the circular genome starting at the origin of replication, and
and U, respectively, ordered clockwise along the circular genome starting at the origin of replication, and 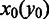 and
and 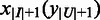 be the origin of replication. For any two consecutive boundaries in
be the origin of replication. For any two consecutive boundaries in 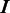 ,
, 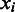 and
and 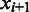 , the number of boundaries in
, the number of boundaries in  between
between 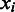 and
and 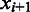 is denoted as
is denoted as 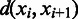 so the average value is
so the average value is 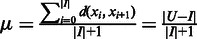 . Clearly the larger the
. Clearly the larger the 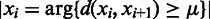 value is, the more spread out across the genome the boundaries in
value is, the more spread out across the genome the boundaries in  are. We define the distance between
are. We define the distance between 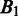 and
and 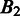 as
as
| (8) |
We can see that the more similar two genomic partitions are, the smaller the distance will be.
RESULTS
Generation of MGC groups
Knowing that the E. coli chromosome folds into different structures during exponential growth and stationary growth (1), we identified the subset of the 466 growth conditions in M3D associated with each of these two growth phases. Specifically, we used the expression levels of 54 ribosomal protein genes to define the two corresponding MGC groups: conditions under which most of these ribosomal proteins are highly expressed and conditions under which ribosomal proteins are overall lowly expressed, respectively (see ‘Materials and Methods’ section). These two MGC sets are referred to as two groups of growth conditions. We further hypothesize that other classes of growth conditions may also give rise to distinctly folded chromosomal structures. Specifically, we have considered the following five widely studied classes of growth conditions associated with anaerobiosis, oxidative stress, heat shock, nitrogen limitation and SOS response, and derived corresponding MGCs for each of them using marker genes known to be upregulated under each such condition (31–38). Table 1 lists the marker genes for each of these seven classes of growth conditions along with the associated information (for more details, see Supplementary Tables S1 and S2). Overall, seven MGC groups are identified covering 325 out of the 466 growth conditions in M3D, for each of which we made the prediction of the folding domain boundaries of the E. coli genome.
Table 1.
Information of the seven classes of growth conditions with the marker genes used for identifying the growth condition classes in M3D listed in the second column (with the gene number following in the brackets) and the number of MGC sets for each growth condition class shown in the third column
| Growth conditions | Marker genes (number of genes) | Number of MGC datasets |
|---|---|---|
| Exponential growth | Ribosomal proteins (54) | 45 |
| Stationary growth | Ribosomal proteins (54) | 131 |
| Heat shock | Heat shock proteins (14) | 54 |
| Oxidative stress | OxyR and SoxRS regulons (61) | 30 |
| Anaerobiosis | Partial Fnr regulons (53) | 55 |
| SOS response | LexA regulon (56) | 57 |
| Nitrogen limitation | NtrC and Nac regulon (65) | 34 |
| Random | N/A | 100 |
The ‘Random’ growth conditions (the last line in Table 1) correspond to 100 randomly selected MGCs from all the available MGC in the M3D database.
Prediction of folding domains of E. coli under a specified class of growth conditions
We predicted the folding-domain boundaries of the E. coli genome under each of the seven classes of growth conditions shown in Table 2. One hundrerd forty-six folding domains are predicted for the exponential growth, 84 for the stationary growth, 116 for heat shock, 95 for nitrogen limitation, 94 for oxidative stress, 102 for anaerobiosis and 114 for SOS response. Figure 1a shows the predicted domains under stationary growth along the E. coli K12 genome. Figure 1b is an expanded view of the genomic region (0–1.2 M) in Figure 1a. From Figure 1b, we can see that the predicted folding domains indeed show higher levels of co-expression than gene pairs across the domain boundaries as desired, with the detailed data shown in Figure 1c. An example of the predicted domains and associated co-expression data can be found in Supplementary Example S1 and Supplementary Table S3.
Table 2.
Properties of the folding-domain boundaries predicted for each MGC group
| MGC groups | Number of folding- domain boundaries | ALD (kb) | ALB (bp) | ALNB (bp) | #HEG | #NAP | #Transcription factories | #Fis |
|---|---|---|---|---|---|---|---|---|
| Exponential growth | 146 | 31.4 | 402 | 271 | 13 | 43 | 6 | 33 |
| Stationary growth | 84 | 54.9 | 351 | 276 | 10 | 24 | 3 | 16 |
| Heat shock | 116 | 39.6 | 424 | 193 | 13 | 31 | 6 | 19 |
| Oxidative stress | 94 | 48.9 | 344 | 276 | 3 | 31 | 2 | 15 |
| Anaerobiosis | 102 | 45 | 424 | 272 | 13 | 33 | 8 | 21 |
| SOS response | 114 | 40.2 | 471 | 269 | 6 | 34 | 1 | 20 |
| Nitrogen limitation | 95 | 48.5 | 344 | 276 | 4 | 26 | 1 | 18 |
ALD, average length of the predicted folding domains; ALB, average length of the inter-operonic regions containing folding-domain boundaries; ALNB, average length of the remaining inter-operonic regions. #HEG is the number of highly expressed genes encoded in the predicted folding-domain boundary regions. #NAP is the number of NAP binding sites in the inter-operonic regions containing a predicted folding-domain boundary. #Transcription factories is the number of superstructures near predicted folding-domain boundaries formed by NAPs associated with the ribosomal RNA operons. #Fis is for the number of Fis binding sites in the inter-operonic regions containing a predicted folding-domain boundary.
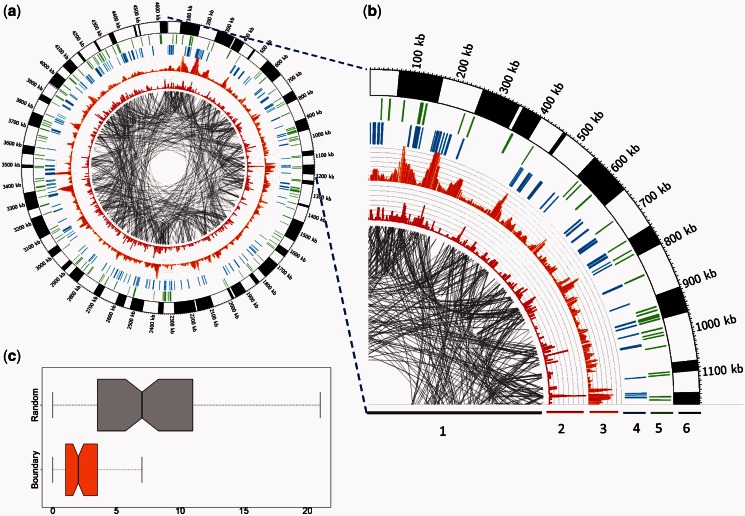
Figure 1.
(a) Circos plots of predicted folding domains along the genome of E. coli K12 during the stationary growth phase. The alternating black and white bands in the outermost ring represent the partition of the E. coli genome into folding domains. (b) An expanded view of the genomic region (0–1.2 M). From the inside out, the six rings are labeled with numbers: (1) Each pair of genes involved in the same EcoCyc pathway are connected using gray lines; (2) the red histogram shows the number of pathways in which the target gene is involved; (3) the orange histogram shows the number of the coexpressed gene pairs; (4) each blue bar represents the presence of a highly expressed gene; (5) each green bar represents the presence of a known NAP-binding site, which should fall in domain boundary regions; and (6) predicted folding domains represented as alternating black-and-white bands in the seventh ring. Two thick bars are used to distinguish the adjacent folding domains as the boundaries are not visible at genome scale. (c) A comparison between the numbers of coexpressed gene pairs in the flanks of the predicted domains (orange box) and a set of randomly picked intergenic regions (gray box).
Overall, 409 out of 2367 inter-operonic regions in the E. coli genome (40) serve as a boundary of at least one predicted domain (B), while the remaining 1958 do not (NB). We also noted that 45.3% of the predicted boundaries are shared by at least two MGC groups and 23.5% by at least three MGC groups. The detailed boundary information of the predicted domains, along with other related information is given in Supplementary Table S4.
Stability of the predicted folding-domain boundaries
As there are no large-scale experimental data collected on the folded E. coli chromosomal structures to valid our prediction, we have to assess the reliability of the predicted folding domains mostly computationally. Specifically, we have assessed the stability of each predicted set of domains by perturbing the gene expression dataset used to make the prediction. The approach was to replace a fraction of the used MGC set by the same number of unrelated conditions randomly selected from the remaining growth conditions out of the 466 in M3D. We would expect that a correctly predicted set of folding domains should be highly consistent and reproducible, whereas randomly or incorrectly predicted domains should not.
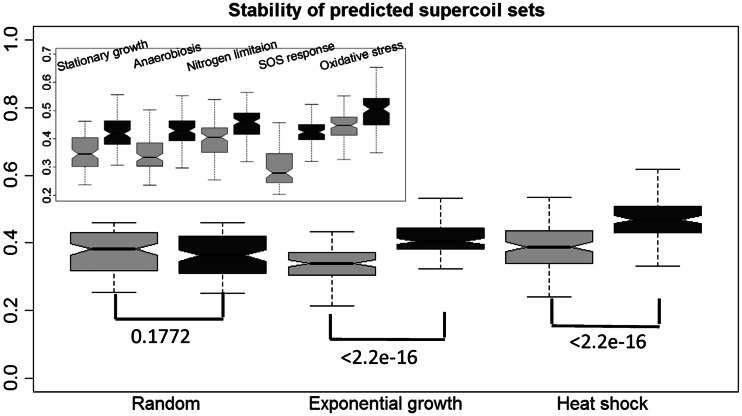
We used the following procedure, along with the distance measure defined in ‘Materials and Methods’ section, to assess the prediction stability. Let C be the condition set used to predict a set of folding domains. We randomly selected 50% of the conditions from C, denoted it as S1 and let S2 contain 25% of conditions randomly selected from C and the same number of conditions randomly selected from the remaining portion of the 466 conditions after removing C. We then predicted the set of folding domains under conditions C, S1 and S2, denoting the three sets of predicted domains as P, P1 and P2, respectively. We performed such predictions 1000 times for each C corresponding each condition class given in Table 2 and calculated the distance distributions between P and P1 and between P and P2. Figure 2 shows the box plots of the two distributions for each of the seven classes of conditions, plus a randomly selected condition set C out of 466, with the same number of conditions to that of the above. We can clearly see that the distance between P and P1 is significantly smaller than that between P and P2 (all achieving Wilcoxon test P < 2.2e-9, shown in Figure 2) for all the seven condition sets, and there is virtually no difference for the random set. Hence, we can conclude that each predicted folding-domain set based on any of the seven classes of conditions is highly statistically significant compared with domains predicted based on randomly selected conditions, hence suggesting the strong biological significance of the predicted domains.
Figure 2.
Boxplots showing stabilities of the predicted folding domains (exponential growth and heat shock) based on the selected MGC set versus a randomly selected MGC set as defined in the main text. The comparison among the other five pairs of predicted domain sets is shown in the left upper corner. Each box with lighter gray level represents the distance distribution between the domains predicted using the selected MGCs and domains predicted using half of the selected MGCs, and each box with darker gray level is defined similarly but against domains predicted based on randomly selected MGCs, where the y-axis is the distance axis. The Wilcoxon test P-values for each pair of distributions are shown in the top of boxes of each corresponding set of predicted folding domains.
Functional inference of genes located close to the predicted folding-domain boundaries
We have examined the predicted domains to check if genes located close to the domain boundaries may have distinct characteristics compared with other genes. We noted that such genes tend to have higher GC content and higher expression levels than the other genes. Specifically, we have calculated the P-value of the Wilcoxon test with the null hypothesis that such genes having no higher GC content and expression values than the other genes, which gives rise to P < 0.05 for the test. See Supplementary Figure S1 for the detailed information. Interestingly, previous studies have shown that there is a positive correlation between the expression value and GC content (41), providing an indirect evidence supporting our observation.
We have also performed a gene ontology ‘biological process’ (42) enrichment analysis on genes flanking the predicted folding-domain boundaries using DAVID (43). Our result indicates that some genes involved in nitrogen and sulfur metabolisms are enriched for five of the seven classes of conditions (except for anaerobiosis and oxidative stress). For instance, 76 out of the 494 genes flanking the domain boundaries during the exponential growth are involved in nitrogen, purine and amino acid metabolisms. In particular, this set of genes contains those encoding biosynthesis pathways of spermidine from glutamate, arginine degradation, nitrogen and sulfur assimilation, as well as proline and purine biosynthesis. The enrichment of these genes suggests that these genes are actively transcribed, which is consistent with our observation made in Supplementary Figure S1b that genes flanking the domain boundaries tend to express at higher levels than the other genes.
Comparisons among the seven sets of predicted domains
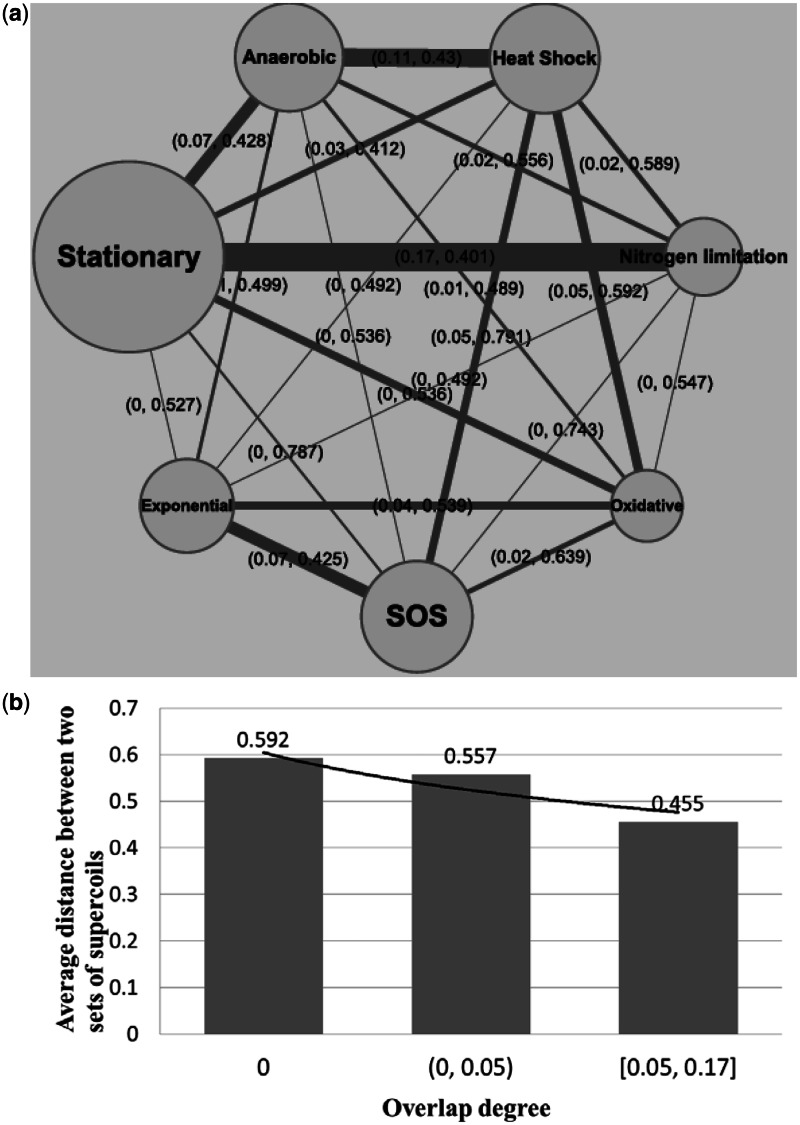
We have compared the seven sets of predicted folding domains based on seven sets of distinct MGCs defined earlier, using the following two measures: (i) the degree of overlap in growth conditions between two different MGC groups, and (ii) the distance between each pair of predicted domain sets. The ‘degree of overlap’ is defined as 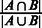 , where
, where 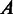 and
and 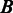 represent two MGC groups. First, we noted that >90% (19 out of
represent two MGC groups. First, we noted that >90% (19 out of 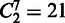 ) of the MGC group pairs have the degree of overlap scores <0.1, indicating that the seven classes of MGCs are largely independent of each other. As expected, a higher level of overlaps between two classes of MGCs tends to give rise to smaller distances between their predicted folding-domain sets, as shown in Figure 3b. For instance, the two classes of MGCs, stationary growth and nitrogen limitation, have the highest degree of overlap at 0.17 as shown in Figure 3a and also have the smallest distance, 0.401, between their predicted folding-domain sets among all the pairwise comparisons. This is not unexpected because in stationary phase, cells stop multiplying exponentially in part owing to limitation of some essential nutrients. Another two sets of domains with a small distance, 0.43, are under anaerobiosis and heat shock. Their corresponding MGC groups have the second largest degree of overlap 0.11. There are no overlapping MGCs between the classes of stationary growth and SOS response at all, and they have a relatively large distance at 0.787.
) of the MGC group pairs have the degree of overlap scores <0.1, indicating that the seven classes of MGCs are largely independent of each other. As expected, a higher level of overlaps between two classes of MGCs tends to give rise to smaller distances between their predicted folding-domain sets, as shown in Figure 3b. For instance, the two classes of MGCs, stationary growth and nitrogen limitation, have the highest degree of overlap at 0.17 as shown in Figure 3a and also have the smallest distance, 0.401, between their predicted folding-domain sets among all the pairwise comparisons. This is not unexpected because in stationary phase, cells stop multiplying exponentially in part owing to limitation of some essential nutrients. Another two sets of domains with a small distance, 0.43, are under anaerobiosis and heat shock. Their corresponding MGC groups have the second largest degree of overlap 0.11. There are no overlapping MGCs between the classes of stationary growth and SOS response at all, and they have a relatively large distance at 0.787.
Figure 3.
(a) Degrees of overlap between each pair of MGC groups. The node size represents the size of a MGC group, and the edge width represents the number of overlapping MGCs between the two corresponding nodes. The label of each edge has two values: the first being the degree of overlap between the two corresponding MGC groups and the second being the distance between two predicted folding-domain sets, and (b) relationship between the degree of overlap among MGC groups and the distance between the corresponding folding-domain sets.
Comparison between domain boundaries and experimental data
Using an in vivo protein occupancy experiment, 272 EPODs of the E. coli chromosome have been identified in (30). The EPODs are enriched with NAP-binding sites (see details in Supplementary Table S5) and play an important role in the folding of the E. coli chromosome. These domains can be grouped into two classes: the transcriptionally silent class (tsEPODs) and the highly expressed class (heEPODs). The 151 tsEPODs are located across the genome apparently randomly and has proved to have bigger influence on the organizational architecture of the folded E. coli chromosome than the heEPODs (30), totaling 121. In addition, we have also retrieved 537 H-NS binding regions under the stationary growth condition from (9), knowing that H-NSs play a key role in the formation of supercoil structures in the folded E. coli chromosome (16). These H-NS binding regions can be classified to long H-NS (loH-NSs) and short H-NS binding regions (shH-NSs), with the longer H-NSs wrapping around larger segments of the E. coli chromosome. We have compared the predicted folding-domain boundaries under the stationary growth condition [stationary folding domains (sFDs)] with these EPODs and H-NS binding regions as follows.
Let A denote all the inter-operonic regions in E. coli genome, and B be the subset of A that has been computationally predicted by our algorithm; C denotes the subset of A, which is experimentally identified. We use the following P-value calculation to assess the statistical significance of the level of coincidence between B and C. Specifically, if our prediction B is random, then the probability of B and C sharing exactly m inter-operonic regions is
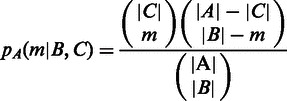 |
where |X| denotes the number of elements in X and m = 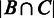 . Hence, the P-value in respect to the assumption is
. Hence, the P-value in respect to the assumption is 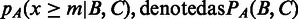 .
.
We note that the P-values PA(sFDs, EPODs) and PA(sFDs,tsEPODs) are both <0.05, but PA(sFDs,heEPODs) is not. Between sFDs and the H-NS binding regions, PA(sFDs,H-NSs) and PA(sFDs,loH-NSs) are <0.05 but PA(sFDs,shH-NSs) is not (see Table 3). These results indicate that our predicted folding domains have substantial overlaps with EPODs and H-NS–binding regions, and they tend to have higher level of overlap with the tsEPODs and loH-NSs, which are known to cast bigger influence on the folded chromosomal structures than heEPODs and shH-NSs. As a comparison, we have randomly picked a set of inter-operonic regions as potential domain boundaries and done the same calculation on sFDs, the P-values are consistently higher than those calculated using predicted domain boundaries as shown in Table 3.
Table 3.
Statistical significance of correlation coefficient between predicted domain boundaries and EPODs and H-NS binding regions
| EPODs | tsEPODs | heEPODs | H-NSs | loH-NSs | shH-NSs | |
|---|---|---|---|---|---|---|
| sFDs | 3.8e-03* | 2.6e-02* | 6.4e-02 | 1.1e-02* | 4.1e-02* | 8.3e-02 |
| Random set | 4.2e-01 | 2.3e-01 | 6.1e-01 | 9.7e-02 | 9.2e-02 | 5.4e-01 |
*P < 0.05.
DISCUSSION
Predicted folding domains under exponential and stationary growth conditions are generally consistent with the available experimental data
We have noted from Table 2 that the numbers of folding domains predicted under the exponential growth and the stationary growth conditions are generally consistent with the experimentally observed number of supercoils using electron microscopy (1). Specifically, the data indicate that the folded chromosomal structure has substantially more supercoils during the exponential growth than those during the stationary growth phase, which is consistent with our predicted numbers of folding domains under the two conditions, 146 versus 84. And some Fis-binding sites are exposed more frequently during the exponential growth than during the stationary growth, consistent with our predicted numbers 33 versus 16. In addition, there are more transcription factories operating during the exponential growth than during the stationary growth, consistent with the numbers 6 versus 3 based on our prediction, where a ‘transcription factory’ is defined as a spatially confined aggregation of RNA polymerase, transcription factors and NAPs in nucleoid (44). The detailed calculation of these numbers based on our predictions is given in Table 2.
Sequence features indicate a strong link between the predicted folding domains and supercoils in the folded chromosome
We have noted that the average length of the inter-operonic regions in B is 414 bp, which is significantly longer than the average length of NB, 250 bp (see ‘Materials and Methods’ section). This clearly makes sense as NAPs are expected to bind near the supercoil boundaries and hence require extra space in the binding-site containing inter-operonic regions (detailed comparisons can be found in Supplementary Figure S2). The higher expression levels of genes flanking the folding-domain boundaries (Supplementary Figure S1b) suggest that these genes are more actively transcribed compared with those in the internal portions of the folding domains. Hence, we speculate that the active transcription of genes flanking the boundaries might be accompanied by pushing the coiling toward the center of the supercoiled domains, hence making the middle portions of the supercoils more tightly coiled than the boundary regions, and reducing their accessibility by the RNA polymerases and the transcription levels.
Potential limitations of our predicted MGCs
For each of the seven physiological conditions, its set of marker genes is manually collected from the published studies on the seven conditions. While the seven identified subsets of conditions are biologically meaningful and statistically significant, the marker genes are not selected in a systematic manner and hence could have limited the effectiveness of our method. To examine this issue, we have carried out a de novo biclustering (45,46) of the expression data of E. coli in M3D and obtained 17 condition clusters with high statistical significance (shown in Supplementary Table S6). Out of these 17 clusters, six have low a degree of overlap with the seven MGC groups (<0.15), indicating that these subsets of conditions, not covered by current seven MGC groups, may correspond to certain physiological conditions that have not been systematically studied, and hence warrants further studies. We plan to carry a detailed and systematic analysis of the 17 biclusters to identify their corresponding physiological conditions as well as their potentially corresponding folded chromosomal structures of E. coli K12.
CONCLUDING REMARK
We have predicted a distinct set of folding domains of the E. coli K12 chromosome for each of seven sets of growth conditions based on the gene-expression data in M3D, the most comprehensive gene-expression dataset on E. coli, along with pathway information from EcoCyc. These predicted domains are highly stable with respect to perturbations to the expression data based on which the prediction is made. They also show good agreement with the available E. coli folded chromosomal structure data, including experimental observation and high-throughput NAP-binding regions. The results of the computation and analysis provided strong evidence supporting our main hypothesis that operons encoding E. coli metabolic pathways are arranged along the genome that tends to minimize the total effort, measured using the number of total unfolding of the folded domains, to make the genes of the needed pathways transcriptionally accessible. We believe that this study provides a framework for studying the functional constraints cast on the genomic organization of operons in E. coli and bacteria in general. We fully expect that the same study can be applied to other bacterial genomes, for which substantial amounts of gene-expression data collected under multiple conditions are available. Such predicted folding-domain boundaries, when fully validated by and applied in conjunction with the information derived from the emerging chromosome conformation capture techniques, could prove to be essential to understanding the detailed regulation mechanisms of transcription relating to dynamic supercoiling, as well as the general principles that govern the genomic locations of operons (24,25).
The program used to generate the data used in this article was written in ANSI C and tested using GCC (version 4.1.2) on Linux. The source code is available at: http://code.google.com/p/supercoil/.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online: Supplementary Tables 1–6, Supplementary Figures 1 and 2, Supplementary Method 1, Supplementary Example 1 and Supplementary References [1,3,6–8,13–16,47].
ACKNOWLEDGEMENTS
Y.X. conceived the basic idea and planned the project. Q.M. developed the software and carried out the experiments. Y.Y. and Q.M. analyzed the data and wrote the manuscript. M.S. proposed several good suggestions for the ‘Results’ section in the view of biology. G.L. designed and polished the algorithm. H.Z. contributed to the gene expression analysis. All authors edited the manuscript and approved the final manuscript.
FUNDING
National Science Foundation (#NSF DEB-0830024 and NSF MCB-0958172) (in part); the US Department of Energy’s BioEnergy Science Center (BESC) grant through the Office of Biological and Environmental Research. The BioEnergy Science Center is a U.S. Department of Energy Bioenergy Research Center supported by the Office of Biological and Environmental Research in the DOE Office of Science. Funding for open access charge: US Department of Energy's BioEnergy Science Center (BESC).
Conflict of interest statement. None declared.
REFERENCES
- 1.Dillon SC, Dorman CJ. Bacterial nucleoid-associated proteins, nucleoid structure and gene expression. Nat. Rev. Microbiol. 2010;8:185–195. doi: 10.1038/nrmicro2261. [DOI] [PubMed] [Google Scholar]
- 2.Benza VG, Bassetti B, Dorfman KD, Scolari VF, Bromek K, Cicuta P, Lagomarsino MC. Physical descriptions of the bacterial nucleoid at large scales, and their biological implications. Rep. Prog. Phys. 2012;75:076602. doi: 10.1088/0034-4885/75/7/076602. [DOI] [PubMed] [Google Scholar]
- 3.Noom MC, Navarre WW, Oshima T, Wuite GJ, Dame RT. H-NS promotes looped domain formation in the bacterial chromosome. Curr. Biol. 2007;17:R913–R914. doi: 10.1016/j.cub.2007.09.005. [DOI] [PubMed] [Google Scholar]
- 4.Postow L, Hardy CD, Arsuaga J, Cozzarelli NR. Topological domain structure of the Escherichia coli chromosome. Genes Dev. 2004;18:1766–1779. doi: 10.1101/gad.1207504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Luijsterburg MS, Noom MC, Wuite GJ, Dame RT. The architectural role of nucleoid-associated proteins in the organization of bacterial chromatin: a molecular perspective. J. Struct. Biol. 2006;156:262–272. doi: 10.1016/j.jsb.2006.05.006. [DOI] [PubMed] [Google Scholar]
- 6.Stein RA, Deng S, Higgins NP. Measuring chromosome dynamics on different time scales using resolvases with varying half-lives. Mol. Microbiol. 2005;56:1049–1061. doi: 10.1111/j.1365-2958.2005.04588.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rocha EP. The organization of the bacterial genome. Annu. Rev. Genet. 2008;42:211–233. doi: 10.1146/annurev.genet.42.110807.091653. [DOI] [PubMed] [Google Scholar]
- 8.Browning DF, Grainger DC, Busby SJ. Effects of nucleoid-associated proteins on bacterial chromosome structure and gene expression. Curr. Opin. Microbiol. 2010;13:773–780. doi: 10.1016/j.mib.2010.09.013. [DOI] [PubMed] [Google Scholar]
- 9.Kahramanoglou C, Seshasayee AS, Prieto AI, Ibberson D, Schmidt S, Zimmermann J, Benes V, Fraser GM, Luscombe NM. Direct and indirect effects of H-NS and Fis on global gene expression control in Escherichia coli. Nucleic Acids Res. 2011;39:2073–2091. doi: 10.1093/nar/gkq934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Grainger DC, Aiba H, Hurd D, Browning DF, Busby SJ. Transcription factor distribution in Escherichia coli: studies with FNR protein. Nucleic Acids Res. 2007;35:269–278. doi: 10.1093/nar/gkl1023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Grainger DC, Hurd D, Goldberg MD, Busby SJ. Association of nucleoid proteins with coding and non-coding segments of the Escherichia coli genome. Nucleic Acids Res. 2006;34:4642–4652. doi: 10.1093/nar/gkl542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Prieto AI, Kahramanoglou C, Ali RM, Fraser GM, Seshasayee AS, Luscombe NM. Genomic analysis of DNA binding and gene regulation by homologous nucleoid-associated proteins IHF and HU in Escherichia coli K12. Nucleic Acids Res. 2012;40:3524–3537. doi: 10.1093/nar/gkr1236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Simonis M, Klous P, Splinter E, Moshkin Y, Willemsen R, de Wit E, van Steensel B, de Laat W. Nuclear organization of active and inactive chromatin domains uncovered by chromosome conformation capture-on-chip (4C) Nat. Genet. 2006;38:1348–1354. doi: 10.1038/ng1896. [DOI] [PubMed] [Google Scholar]
- 14.Dekker J, Rippe K, Dekker M, Kleckner N. Capturing chromosome conformation. Science. 2002;295:1306–1311. doi: 10.1126/science.1067799. [DOI] [PubMed] [Google Scholar]
- 15.Zhao Z, Tavoosidana G, Sjolinder M, Gondor A, Mariano P, Wang S, Kanduri C, Lezcano M, Sandhu KS, Singh U, et al. Circular chromosome conformation capture (4C) uncovers extensive networks of epigenetically regulated intra- and interchromosomal interactions. Nat. Genet. 2006;38:1341–1347. doi: 10.1038/ng1891. [DOI] [PubMed] [Google Scholar]
- 16.Wang W, Li GW, Chen C, Xie XS, Zhuang X. Chromosome organization by a nucleoid-associated protein in live bacteria. Science. 2011;333:1445–1449. doi: 10.1126/science.1204697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Deng S, Stein RA, Higgins NP. Organization of supercoil domains and their reorganization by transcription. Mol. Microbiol. 2005;57:1511–1521. doi: 10.1111/j.1365-2958.2005.04796.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wright MA, Kharchenko P, Church GM, Segre D. Chromosomal periodicity of evolutionarily conserved gene pairs. Proc. Natl Acad. Sci. USA. 2007;104:10559–10564. doi: 10.1073/pnas.0610776104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kepes F. Periodic transcriptional organization of the E. coli genome. J. Mol. Biol. 2004;340:957–964. doi: 10.1016/j.jmb.2004.05.039. [DOI] [PubMed] [Google Scholar]
- 20.Jeong KS, Ahn J, Khodursky AB. Spatial patterns of transcriptional activity in the chromosome of Escherichia coli. Genome Biol. 2004;5:R86. doi: 10.1186/gb-2004-5-11-r86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Buenemann M, Lenz P. Geometrical ordering of DNA in bacteria. Commun. Integr. Biol. 2011;4:291–293. doi: 10.4161/cib.4.3.14891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fritsche M, Li S, Heermann DW, Wiggins PA. A model for Escherichia coli chromosome packaging supports transcription factor-induced DNA domain formation. Nucleic Acids Res. 2012;40:972–980. doi: 10.1093/nar/gkr779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ma Q, Ying X. Global genomic arrangement of bacterial genes is closely tied with the total transcriptional efficiency. Genomics Proteomics Bioinformatics. 2013;11:66–71. doi: 10.1016/j.gpb.2013.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yin Y, Zhang H, Olman V, Xu Y. Genomic arrangement of bacterial operons is constrained by biological pathways encoded in the genome. Proc. Natl Acad. Sci. USA. 2010;107:6310–6315. doi: 10.1073/pnas.0911237107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang H, Yin Y, Olman V, Xu Y. Genomic arrangement of regulons in bacterial genomes. PLoS One. 2012;7:e29496. doi: 10.1371/journal.pone.0029496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Karp PD, Riley M, Saier M, Paulsen IT, Collado-Vides J, Paley SM, Pellegrini-Toole A, Bonavides C, Gama-Castro S. The EcoCyc Database. Nucleic Acids Res. 2002;30:56–58. doi: 10.1093/nar/30.1.56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Faith JJ, Driscoll ME, Fusaro VA, Cosgrove EJ, Hayete B, Juhn FS, Schneider SJ, Gardner TS. Many Microbe Microarrays Database: uniformly normalized Affymetrix compendia with structured experimental metadata. Nucleic Acids Res. 2008;36:D866–D870. doi: 10.1093/nar/gkm815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gama-Castro S, Salgado H, Peralta-Gil M, Santos-Zavaleta A, Muniz-Rascado L, Solano-Lira H, Jimenez-Jacinto V, Weiss V, Garcia-Sotelo JS, Lopez-Fuentes A, et al. RegulonDB version 7.0: transcriptional regulation of Escherichia coli K-12 integrated within genetic sensory response units (Gensor Units) Nucleic Acids Res. 39:D98–D105. doi: 10.1093/nar/gkq1110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Puigbo P, Romeu A, Garcia-Vallve S. HEG-DB: a database of predicted highly expressed genes in prokaryotic complete genomes under translational selection. Nucleic Acids Res. 2008;36:D524–D527. doi: 10.1093/nar/gkm831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Vora T, Hottes AK, Tavazoie S. Protein occupancy landscape of a bacterial genome. Mol. Cell. 2009;35:247–253. doi: 10.1016/j.molcel.2009.06.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lindquist S, Craig EA. The heat-shock proteins. Annu. Rev. Genet. 1988;22:631–677. doi: 10.1146/annurev.ge.22.120188.003215. [DOI] [PubMed] [Google Scholar]
- 32.De Maio A. Heat shock proteins: facts, thoughts, and dreams. Shock. 1999;11:1–12. doi: 10.1097/00024382-199901000-00001. [DOI] [PubMed] [Google Scholar]
- 33.Tolla DA, Savageau MA. Regulation of aerobic-to-anaerobic transitions by the FNR cycle in Escherichia coli. J. Mol. Biol. 2010;397:893–905. doi: 10.1016/j.jmb.2010.02.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kang Y, Weber KD, Qiu Y, Kiley PJ, Blattner FR. Genome-wide expression analysis indicates that FNR of Escherichia coli K-12 regulates a large number of genes of unknown function. J. Bacteriol. 2005;187:1135–1160. doi: 10.1128/JB.187.3.1135-1160.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cabiscol E, Tamarit J, Ros J. Oxidative stress in bacteria and protein damage by reactive oxygen species. Int. Microbiol. 2000;3:3–8. [PubMed] [Google Scholar]
- 36.Michel B. After 30 years of study, the bacterial SOS response still surprises us. PLoS Biol. 2005;3:e255. doi: 10.1371/journal.pbio.0030255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ninfa AJ, Jiang P, Atkinson MR, Peliska JA. Integration of antagonistic signals in the regulation of nitrogen assimilation in Escherichia coli. Curr. Top. Cell. Regul. 2000;36:31–75. doi: 10.1016/s0070-2137(01)80002-9. [DOI] [PubMed] [Google Scholar]
- 38.Muse WB, Bender RA. The nac (nitrogen assimilation control) gene from Escherichia coli. J. Bacteriol. 1998;180:1166–1173. doi: 10.1128/jb.180.5.1166-1173.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kharchenko P, Church GM, Vitkup D. Expression dynamics of a cellular metabolic network. Mol. Syst. Biol. 2005;1:2005.0016. doi: 10.1038/msb4100023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mao F, Dam P, Chou J, Olman V, Xu Y. DOOR: a database for prokaryotic operons. Nucleic Acids Res. 2009;37:D459–D463. doi: 10.1093/nar/gkn757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kudla G, Lipinski L, Caffin F, Helwak A, Zylicz M. High guanine and cytosine content increases mRNA levels in mammalian cells. PLoS Biol. 2006;4:e180. doi: 10.1371/journal.pbio.0040180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gene Ontology Consortium. The Gene Ontology in 2010: extensions and refinements. Nucleic Acids Res. 2010;38:D331–D335. doi: 10.1093/nar/gkp1018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Huang da W, Sherman BT, Lempicki RA. Bioinformatics enrichment tools: paths toward the comprehensive functional analysis of large gene lists. Nucleic Acids Res. 2009;37:1–13. doi: 10.1093/nar/gkn923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Cook PR. A model for all genomes: the role of transcription factories. J. Mol. Biol. 2009;395:1–10. doi: 10.1016/j.jmb.2009.10.031. [DOI] [PubMed] [Google Scholar]
- 45.Li G, Ma Q, Tang H, Paterson AH, Xu Y. QUBIC: a qualitative biclustering algorithm for analyses of gene expression data. Nucleic Acids Res. 2009;37:e101. doi: 10.1093/nar/gkp491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zhou F, Ma Q, Li G, Xu Y. QServer: a biclustering server for prediction and assessment of co-expressed gene clusters. PLoS One. 2012;7:e32660. doi: 10.1371/journal.pone.0032660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Li G, Liu B, Ma Q, Xu Y. A new framework for identifying cis-regulatory motifs in prokaryotes. Nucleic Acids Res. 2011;39:e42. doi: 10.1093/nar/gkq948. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.