Translational Pharmacokinetic-Pharmacodynamic Modeling from Nonclinical to Clinical Development: A Case Study of Anticancer Drug, Crizotinib

Abstract

Attrition risk related to efficacy is still a major reason why new chemical entities fail in clinical trials despite recently increased understanding of translational pharmacology. Pharmacokinetic-pharmacodynamic (PKPD) analysis is key to translating in vivo drug potency from nonclinical models to patients by providing a quantitative assessment of in vivo drug potency with mechanistic insight of drug action. The pharmaceutical industry is clearly moving toward more mechanistic and quantitative PKPD modeling to have a deeper understanding of translational pharmacology. This paper summarizes an anticancer drug case study describing the translational PKPD modeling of crizotinib, an orally available, potent small molecule inhibitor of multiple tyrosine kinases including anaplastic lymphoma kinase (ALK) and mesenchymal-epithelial transition factor (MET), from nonclinical to clinical development. Overall, the PKPD relationships among crizotinib systemic exposure, ALK or MET inhibition, and tumor growth inhibition (TGI) in human tumor xenograft models were well characterized in a quantitative manner using mathematical modeling: the results suggest that 50% ALK inhibition is required for >50% TGI whereas >90% MET inhibition is required for >50% TGI. Furthermore, >75% ALK inhibition and >95% MET inhibition in patient tumors were projected by PKPD modeling during the clinically recommended dosing regimen, twice daily doses of crizotinib 250 mg (500 mg/day). These simulation results of crizotinib-mediated ALK and MET inhibition appeared consistent with the currently reported clinical responses. In summary, the present paper presents an anticancer drug example to demonstrate that quantitative PKPD modeling can be used for predictive translational pharmacology from nonclinical to clinical development.

Electronic supplementary material

The online version of this article (doi:10.1208/s12248-012-9436-4) contains supplementary material, which is available to authorized users.

INTRODUCTION

Pharmacokinetic-pharmacodynamic (PKPD) modeling is a useful mathematical approach linking drug exposure to pharmacologic response as a function of time, providing a quantitative assessment of in vivo drug potency with mechanistic insight of drug action (1–4). PKPD modeling is being applied to virtually all phases of drug discovery and development such as 1) drug candidate selection with most favorable PKPD properties and 2) prediction of exposure-response in patients with the aim to optimize clinical trial design. For setting the first-in-human (FIH) dose and subsequent dosing regimen recommendation, several factors, which may vary among therapeutic areas, are carefully taken into consideration. For example, a FIH dose of an anticancer drug would basically be recommended by nonclinical safety study results, such as no observed adverse effect level (NOAEL) and highest non-severely toxic dose (HNSTD), together with an overall risk assessment based on nonclinical data (Fig. 1) (5). In phase I dose-escalation studies, one of the most important questions is whether systemic exposures in patients are enough to achieve the expected antitumor efficacy. Therefore, PKPD understanding is particularly key to support a decision to move clinical drug candidates forward, ultimately to evaluate their clinical efficacy in phase II trials (6). The use of PKPD modeling in this context relies on the prediction of the time-course of drug action in patients based on quantitative PKPD data and understanding in nonclinical models. A full evaluation of the PD system, which converts in vivo responses related to its target (e.g., target modulation and subsequent biomarker response) to pharmacological response (e.g., antitumor efficacy), is among the key translational considerations from nonclinical models to patients. Accordingly, a quantitative PKPD model-based approach to translational pharmacology can provide valuable opportunities to accelerate the evaluation of drug candidates in the clinic (7–9).

Fig. 1.

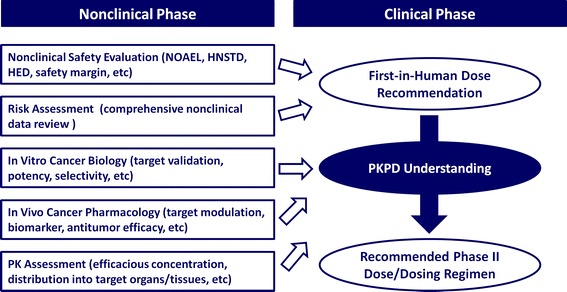
Main work streams for setting the first-in-human starting dose and subsequent phase II dose/dosing regimen recommendation in cancer therapeutics. NOAEL, no observed adverse effect level; HNSTD, highest non-severely toxic dose; HED, human equivalent dose

Despite recently increased understanding of translational pharmacology, attrition risk related to efficacy is still a major reason why new chemical entities fail in clinical trials (10,11). In the case of anticancer drugs, numerous agents have shown effective, and sometimes even spectacular in vivo antitumor efficacy in nonclinical models. Unfortunately, such nonclinical results are often followed by efficacy failure in clinical trials, or only modest efficacy even if the drug is successful (12,13). Thus, there appears to be a continuing lack of clear understanding about translational pharmacology of anticancer agents. The value of any nonclinical models ultimately depends upon their ability to predict clinically relevant responses accurately. Human tumor xenograft mouse models are extensively used as the most common nonclinical antitumor efficacy model and have played an important role for drug discovery and development. The advantages and disadvantages of the use of xenograft models have been discussed extensively (12–16). Historically, human tumor xenograft models have been developed and validated using cytotoxic cancer agents. In contrast, most anticancer agents under current development (e.g., tyrosine kinase inhibitors) are designed to inhibit or interfere with specific molecular targets or pathways. Accordingly, a growing emphasis is being placed upon the incorporation of biomarker responses into translational pharmacology, because a certain degree of biomarker response, as driven by unbound drug concentration at target site, should be quantitatively related to antitumor efficacy. This more sophisticated approach may naturally lead to some questions: what is the value of in vivo xenograft models; whether antitumor efficacy evaluation in tumor cell cultures is enough for clinical drug candidates, etc. On the contrary, human tumor xenograft models are currently valuable to determine in vivo PKPD relationships of drug concentration (exposure) to target modulation, subsequent biomarker response and/or antitumor efficacy. Therefore, tumor xenograft mouse models are used extensively to evaluate in vivo PKPD relationships of molecularly targeted agents (14–16), often in conjunction with a mathematical modeling approach (17–22). For translational pharmacology of molecularly targeted agents, it would be crucial to select appropriate human tumor cell lines and in vivo xenograft models by considering several factors such as target gene, its related pathway, clinical indication and intended patient population. It would also be vital to understand molecular pathway and genetic events occurring in individual patients by identifying mutations, amplification, overexpression or translocation in oncogenic proteins such as epidermal growth factor receptor (EGFR), mesenchymal-epithelial transition factor (MET, also named cMet or HGFR) and anaplastic lymphoma kinase (ALK). These oncogenic proteins are potentially involved in tumor initiation and progression; therefore, personalized targeted cancer therapy can be considered a clinically effective alternative strategy to conventional therapy.

To achieve a reliable extrapolation of PKPD relationships from in vivo nonclinical xenograft models to patients, there are obviously several important assumptions that need to be made and evaluated. One of the main assumptions is that the tumor microenvironment is functionally comparable between subcutaneous tumor xenograft models and human tumors growing in particular sites of organs or tissues. This assumption also presumes a similar overall drug distribution between xenograft models and human tumors. A marked difference in tumor growth rate between xenograft models and patients may have a significant impact on the evaluation of drug-related antitumor efficacy. A different effect of tumor burden on therapeutic efficacy between nonclinical models and cancer patients may also be considered carefully. Ultimately, the most important question in translational pharmacology is whether PKPD relationships of drug exposure, target occupancy or modulation and pharmacological effects are quantitatively translatable from nonclinical models to patients. When this assumption is reasonably valid, two of the subsequent important questions are whether 1) a sufficient drug exposure is achieved in patients to elicit its desired pharmacological effects at the target site of action over a desired time period, and 2) a required target occupancy or modulation (or its surrogate biomarker, if reasonably available and applicable) is achieved in patients to elicit its desired pharmacological effects. When a drug candidate in clinical trials meets these criteria, its clinical development can be carried out in a rational way through translational pharmacology, thus minimizing attrition risk. Therefore, the pharmaceutical industry is clearly moving toward proactive utilization of more mechanistic and quantitative PKPD modeling to gain a deeper understanding of translational pharmacology (6).

Crizotinib (previously known as PF02341066, marketed as Xalkori®) was identified as an orally available, potent ATP-competitive small molecule inhibitor of multiple tyrosine kinases including ALK and MET (23). Crizotinib phase I dose-escalation study started in 2006 in patients with solid tumors primarily as a MET inhibitor (24,25). After the discovery of ALK gene rearrangement such as echinoderm microtubule-associated protein-like 4 (EML4)-ALK in non-small cell lung cancer (NSCLC) in 2007 (26,27), the first ALK-positive NSCLC patient enrolled in the dose-escalation trial in 2007 followed by the second patient in 2008. Promising clinical responses in both the patients treated with crizotinib prompted to add an additional ALK-positive NSCLC expanded cohort to the ongoing clinical studies in 2008 in parallel with screening for MET-positive patients, e.g., MET-mutation and amplification (24,25). Subsequently, an overall response rate of 61% (confirmed complete and partial responses) was observed in an expanded cohort of 143 NSCLC patients carrying ALK rearrangements (24,28). Crizotinib has recently been approved by the Food and Drug Administration (FDA) for the treatment of patients with locally advanced or metastatic NSCLC that is ALK-positive as detected by an FDA-approved test. The companion diagnostic test kit to detect ALK rearrangements (i.e., a breakapart fluorescence in situ hybridization assay) has also been developed in parallel with clinical trials of crizotinib (25,29). Investigations into the clinical responses derived from crizotinib-mediated MET inhibition are still ongoing with case reports describing clinical activity in some patients with MET-amplified NSCLC, gastroesophageal carcinoma and glioblastoma (25).

We previously reported the PKPD modeling of crizotinib for the inhibition of ALK phosphorylation and antitumor efficacy in athymic nu/nu mice implanted with H3122 NSCLC or severe combined immunodeficient (SCID) mice implanted with Karpas299 anaplastic large cell lymphomas (22) and for the inhibition of MET phosphorylation and antitumor efficacy in athymic nu/nu mice implanted with GTL16 gastric carcinomas (GC) or U87MG glioblastomas (21). The objective of this case study is to review the translational pharmacology of crizotinib from nonclinical models to patients based on quantitative PKPD modeling in each ALK- and MET-driven tumor xenograft model, i.e., H3122 NSCLC and GTL16 GC xenograft model, respectively (21,22). Furthermore, several factors contributing to the projection of clinically efficacious concentrations and dosing regimens of anticancer drugs are discussed from the perspective of PKPD modeling and simulation.

METHODS

In Vivo PKPD Study

The detailed experimental designs and methods of crizotinib in vivo PKPD studies were previously reported (21,22). In this paper, we focused on four separate multiple oral-dose PKPD studies, that were conducted with crizotinib in athymic nu/nu mice implanted with H3122 NSCLC (studies ALK-1 and ALK-2) or GTL16 GC (studies MET-1 and MET-2). Mice were orally treated with crizotinib at the doses of 25 to 200 mg/kg once daily in studies ALK-1 and ALK-2 and at the doses of 6.25 to 50 mg/kg once daily in studies MET-1 and MET-2. In the original report (21), three separate studies of crizotinib were conducted in mice implanted with GTL16 GC, i.e., two studies for MET inhibition and one study for tumor growth inhibition (TGI). To avoid confusion in this paper, two studies for MET inhibition were combined and indicated as study MET-1, whereas one TGI study was indicated as study MET-2. In order to accurately estimate the PKPD relationship, it would be important to select an appropriate dose range showing negligible/weak to maximal effects. A subset of mice was humanely euthanized at 1, 4, 7 and 24 h after the last dose to collect blood and tumor samples (n = 3/time point). To perform robust PKPD modeling, it would be important to have a reasonable number of animals and time points, considering a balance between minimizing cost and labor resources versus maximizing accuracy and precision of the exposure-response (PKPD) estimation. Although study design generally depends upon several factors, such as compound, target and xenograft model tested, the author’s recommendation based on prior experience is at least 3 animals per time point, 4 doses (plus control group) and 5 time points to perform relevant PKPD modeling. Once any PKPD data are available, the design of subsequent studies can be optimized by simulation based on previous data set. The protein levels of phosphorylated ALK (ALK phosphorylation) or MET (MET phosphorylation) in tumors were determined using a capture enzyme-linked immunosorbent assay (studies ALK-1 and MET-1), and then normalized by mean values of the vehicle control group; therefore, the levels of ALK and MET phosphorylation were expressed as the ratios to their baseline (i.e., unity). It is important for modelers to understand assay sensitivity, lower limit of quantitation, precision and accuracy of biomarker assay to properly perform PKPD modeling. Tumor volume of each animal was measured during the treatment period by electronic Vernier calipers and was calculated as the product of its length × width² × 0.4 (studies ALK-2 and MET-2). The author would recommend measurement of tumor volumes at least every other day during the treatment period to accurately characterize the tumor growth rate, which could be one of the most important parameters for PKPD modeling, as will be mentioned later.

Crizotinib PK Analysis

The detailed quantitative crizotinib assay method and its PK analysis in mouse xenograft models were previously reported (21,22). In general, assay method for drug candidates might not be validated yet in the early stage of drug discovery, where most nonclinical PKPD studies were conducted. However, it would be important to have a robust assay method with reasonable accuracy and precision. In our assay method, the calibration curve range was 1 to 1,000 or 2,500 ng/mL with precision and accuracy of the quality control samples of less than ±15%. The back calculated calibration standard concentrations were within ±15% of their theoretical concentrations with coefficients of variation of less than ±15%. The assay method in the clinic is typically developed based on nonclinical assay method, and then fully validated to determine clinical PK parameters. Crizotinib assay method used in the clinical studies was also validated prior to FIH studies (30). The quantitative range, precision and accuracy in the crizotinib assay method used in nonclinical studies were comparable to that used in the clinic.

A naïve-pooled PK analysis was performed in the present nonclinical studies, since a subset of mice (n = 3/time point) was humanely euthanized at each time point to collect blood samples. Therefore, all individual plasma concentrations of crizotinib (one sample per animal) at each dose were pooled together to perform PK analysis as if they came from a single individual (31). This approach has been widely used when a full plasma concentration-time profile from each animal was not available. In the present studies, this approach provided a better fitting compared to non-linear PK model with Michaelis-Menten elimination (data not shown). A standard one-compartment PK model was used to determine estimates for the absorption rate constant (k_a, h⁻¹), oral clearance (CL/F, L/h/kg) and oral volume of distribution (V/F, L/kg). The pharmacokinetic parameters obtained were used to simulate plasma concentrations as a function of time following oral administration to drive the time-dependent PD models. It should be noted that the estimated variability for crizotinib PK in nonclinical models was not used for the subsequent PKPD simulation in patients (described later) because it was not generally considered as meaningful for translational modeling.

PKPD Modeling for Target Modulation

In general, two types of PKPD models, the link model and the indirect response model, have been proposed and extensively used to characterize PKPD relationship for drug concentrations and biomarker response, especially when a time-delay of biomarker response relative to drug concentration was observed (32–34). In the link model, the rates of onset and offset of the biomarker response are assumed to be governed by the rate of drug distribution to and from a hypothetical effect site. However, the time-delay of biomarker response is often caused by other reasons, particularly because of indirect mechanisms of action such as stimulation or inhibition of formation (k_in) or loss (k_out) of substance controlling the physiological response. The indirect response model, which is based on the turnover concept, accounts for delays caused by the time needed for changes in k_in or k_out to be fully reflected in the physiological response. These two types of PKPD models were applied to characterize ALK or MET phosphorylation in tumor to plasma concentration of crizotinib (21,22).

In the link model (henceforth referred to as model I), the effect site concentration of crizotinib (C_e, ng/mL) was first calculated by the following differential equation:

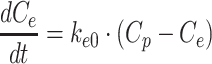1

where k_e0 is the rate constant for equilibration with the effect site (h^-1) and C_p is the plasma concentration of crizotinib (ng/mL).

Then, the biomarker response in tumor to plasma concentration of crizotinib was characterized to determine EC₅₀ by the following equation:

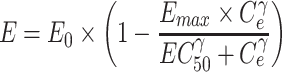2

where E is the ratio of ALK or MET phosphorylation to its baseline (E₀), E_max is maximum effect, EC₅₀ is the concentration causing one-half E_max (ng/mL) and γ is the Hill coefficient.

In the indirect response model (henceforth referred to as model II), ALK or MET phosphorylation at baseline is assumed to be maintained by the balance of formation and degradation rates as mentioned above. The addition of crizotinib was considered to inhibit the biomarker’s formation rate, because crizotinib was a competitive ATP-binding inhibitor. Therefore, the following differential equation was used to determine EC₅₀ required for crizotinib-mediated ALK or MET inhibition:

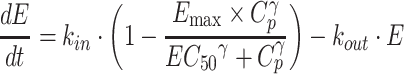3

where k_in is the zero-order formation rate constant (h^-1) and k_out is the first-order degradation rate constant (h^-1).

Drug-Disease Modeling for Antitumor Efficacy

In general, the time-dependent behavior of in vivo tumor growth curves in xenograft models can be described as an exponential growth in the early phase followed by a linear growth and then a plateau phase (35,36). This growth inhibition is considered as being mainly caused by insufficient oxygen and nutrient supplies due to a large tumor mass. The full temporal profile of in vivo tumor growth curves can thus be described by either a logistic (37) or Gompertz model (36). Recent modeling approaches based on transduction processes for antitumor efficacy evaluation include cell distribution and signal transduction models (38–40). Whether these models are applicable to each data set largely depends upon available experimental results measured over a certain period of time with a certain interval. In the present study, antitumor efficacy to crizotinib plasma concentration was characterized by a modified indirect response model based on either exponential or logistic models, where crizotinib was assumed to ultimately inhibit tumor growth rate (21,22). When individual tumor volumes of control animals were exponentially increased over the time of experimental period, the response of tumor volume (T) to crizotinib plasma concentration (C_p) was modeled by the following differential equation based on the exponential growth model (henceforth referred to as model III):

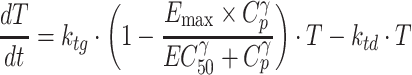4

where T is tumor volume, k_tg is the first-order tumor growth rate constant (h^-1), k_td is the first-order tumor death rate constant (h^-1).

On the other hand, when the individual tumor volumes were increased linearly or reached a plateau phase over the time of experimental period, the following differential equation based on the logistic growth model was used for drug-disease modeling (henceforth referred to as model IV):

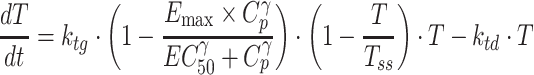5

where T_ss represents the maximum sustainable tumor volume (carrying capacity), which is assumed to be constant whereas the carrying capacity may change over time.

In the logistic growth model, the tumor growth rate is roughly first-order (i.e., exponential growth) when T is relatively small. The tumor growth rate thereafter decreases with the increase in T, and then finally approaches zero when T reaches T_ss (i.e., carrying capacity). Mathematically, a logistic model with large T_ss relative to the observed maximal tumor volume nearly equals to an exponential growth model. In our approach, both models were typically applied to compare the goodness-of-fit of individual tumor growth curves, and then a better model was selected as a final model. The logistic and exponential growth models were used in studies ALK-2 and MET-2, respectively, because of the goodness-of-fit. The difference in tumor growth curves between these studies may simply reflect baseline tumor growth dynamics that differ among a variety of xenograft models. Hill coefficients (γ) were fixed to be unity in both studies.

Integrated Drug-Disease Modeling for Antitumor Efficacy

To further investigate the PKPD relationships of crizotinib in the xenograft models, a recently proposed integrated drug-disease model, i.e., the integration of mathematical modeling from biomarker to pharmacological response (20), was applied to comprehensively characterize the relationships between crizotinib C_p, target modulation (ALK or MET) and TGI. This integrated model differs from the stepwise approach described above, where target modulation and TGI are modeled separately based on crizotinib plasma concentration. In the integrated model, the PD parameters obtained by the link model were used to simulate the ALK or MET phosphorylation (ratio to baseline) as a function of time. Antitumor efficacies in studies MET-2 and ALK-2 were then modeled using an “inhibition index” (1/E-1) as the variable driving the effect based on the exponential growth model (Eq. 6) and the logistic model (Eq. 7), respectively:

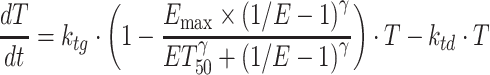6

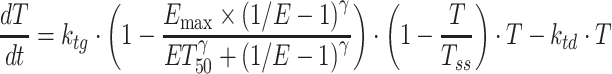7

where, as before, E is the ALK or MET phosphorylation ratio to its baseline and ET₅₀ corresponds to the ALK or MET inhibition index producing 50% of E_max. These integrated drug-disease models are henceforth referred to as model V and VI, respectively.

PKPD Simulation in Patients

For anticancer agents, phase I studies are generally conducted in a manner of dose escalation to determine safety profiles including maximal tolerated dose (MTD), dose-limiting toxicities, PK profiles and the recommended phase II dose (RP2D). Clinical PKPD relationships of systemic drug exposure to target modulation and/or its surrogate biomarker response (e.g., proof of mechanism) should be established in phase I studies such as an expanded cohort setting of selected patients at MTD. However, tumor biopsy samples, especially serial samples, are currently difficult to obtain from patients. In addition, most human tumors are highly heterogeneous, being a complex mixture of multiple cell types, and target modulation/biomarker responses typically show large variability in the clinic (41,42). Despite these limitations, it has been reported that phase I dose-escalation study of the poly(ADP-ribose) polymerase inhibitor (PARP), AG014699, was conducted to establish the PARP inhibitory dose using a target modulation as the primary endpoint (43). This approach can maximize potential benefits and minimize possible risks of anticancer drugs in patients, but unfortunately is a rare practice in the field. If an inhibitory dose was established for a first-in-class candidate drug based on its target modulation and/or biomarker response, it can be valuable for subsequent drug candidates to conduct dose-escalation studies safely and effectively. The quantitative understanding of translational pharmacology is key to make this approach successful. In this context, clinical crizotinib PKPD relationship in phase I dose-escalation study (e.g., a starting dose of 50 mg once daily to the highest dose of 300 mg twice daily) had been simulated based on nonclinical PKPD data with the predicted/observed crizotinib plasma concentrations. Particularly, the projection of crizotinib PKPD relationship at the RP2D, 250 mg twice daily (500 mg/day), was crucial to make the decision to move forward. It is worth noting that no clinical data regarding crizotinib-mediated ALK- or MET-related biomarker responses are available. For crizotinib PKPD simulation, crizotinib plasma concentrations were first simulated as a function of time in patients following the twice-daily doses of 250 mg for 14 days using a one-compartment PK model with CL/F of 70 L/h, V/F of 1,500 L and k_a of 0.75 h⁻¹ (22). Since crizotinib steady-state plasma concentrations were higher than simulated from single-dose PK parameters (i.e., nonlinear kinetics from single to multiple doses), these one-compartment PK parameters were adjusted from the clinically observed single-dose PK parameters to simulate comparable steady-state plasma concentrations to the clinically observed results previously reported (30): the differences in the maximum plasma concentration (C_max) and the area under the plasma concentration-time curve during the dosing interval of 12 h (AUC_0-τ) at steady-state between the simulated (342 ng/mL and 3,570 ng · h/mL, respectively) and observed values (368 ng/mL and 3,641 ng · h/mL, respectively) were within 10%. Based on the simulated crizotinib plasma concentrations, crizotinib-mediated ALK or MET inhibition in patient tumors were projected using the pharmacodynamic characteristics determined in nonclinical ALK- or MET-driven xenograft models. Given that human tumor cells were subcutaneously inoculated into animals to establish nonclinical xenograft models, the dynamic PD parameters (e.g., k_e0) for the PKPD simulation were used without any correction. In contrast, the assumption was made that unbound EC₅₀ values were comparable between nonclinical xenograft models and patients, in keeping with “free drug hypothesis”. Thus, EC₅₀ values estimated in nonclinical models were appropriately adjusted accounting for plasma protein binding differences between species: crizotinib unbound fractions in plasma; (f_u,plasma) were 0.093 and 0.036 in humans and mice, respectively.

Data Analysis

PK and PKPD modeling analyses were performed with NONMEM version VI (University of California at San Francisco, San Francisco, CA). The subroutine ADVAN2 with TRANS2 implemented in NONMEM was used for a one-compartment PK analysis whereas the subroutines ADVAN6 and ADVAN8 were used for the PKPD analyses with the link and indirect response models, respectively. The subroutine ADVAN8 was also used for the drug-disease model and PKPD simulation. The initial conditions at time zero were the dose amount (mg/kg or mg) in the dosing compartment, the baseline ratio (i.e., unity) for E and the measured initial individual tumor volume (mm³) for T. Residual variability was characterized by a proportional error model. The source of inter-animal variability (described with an exponential variance model) was assumed as either k_tg or k_td in the drug-disease model. As is customary, model selection was based on a number of criteria such as the NONMEM objective function values (OFV), parameter estimates, standard errors, and scientific plausibility, as well as exploratory analysis of standard goodness-of-fit plots. One of the advantages to perform nonclinical PKPD modeling with NONMEM is the extensive use of this software by most clinical pharmacologists. This improves the sharing of model structures, technical discussions and translation between organizations.

RESULTS

In Vivo Crizotinib PK

A one-compartment PK model sufficiently described plasma concentration-time courses of crizotinib in both H3122 NSCLC and GTL16 GC xenograft models following multiple oral doses (21,22). PK parameter estimates for crizotinib are summarized in Supplemental Table S1. The coefficient variability of the majority of PK parameters were relatively small (<40%). The CL/F values in all studies tended to be higher at the lower doses than at the higher doses, suggesting nonlinear PK in xenograft models at the dose range tested. The observed dose-dependent PK was likely associated with an inhibition of crizotinib hepatic/intestinal clearance because crizotinib was reported to be a substrate and inhibitor of CYP3A isozymes with a negligible renal excretion (44).

In the clinic, the steady-state crizotinib C_max and AUC_0-τ were 368 ng/mL and 3,641 ng · h/mL, respectively, in cancer patients (n =6) at the RP2D of 250 mg twice daily (500 mg/day) (30). The average steady-state unbound plasma concentration (C_ave,u), that was calculated from AUC_0-τ divided by a dosing interval followed by the correction for f_u,plasma, ranged from 50 to 60 nM free. Nonclinical dose level corresponding to the C_ave,u in patients at the RP2D was approximately 50 mg/kg once daily in the present studies.

PKPD Relationships for Target Modulation and Antitumor Efficacy

Crizotinib plasma concentrations reached C_max at 1 to 4 h post-dose and slowly declined thereafter in both H3122 NSCLC (study ALK-1) and GTL16 GC (study MET-1) xenograft models, while crizotinib-mediated ALK or MET inhibition was sustained throughout most of the dosing interval of 24 h. The ALK or MET inhibition was particularly pronounced at higher doses. Thus, temporal disconnects between crizotinib plasma concentrations and target modulations were observed in both xenograft models. Such a time-delay between systemic exposure and biomarker response is often described as hysteresis, and can be analyzed with appropriately defined PKPD models that explicitly incorporate a provision for time-delay. A link model (model I) reasonably fit the time-courses of target modulation with EC₅₀ of 233 ng/mL in study ALK-1 and EC₅₀ of 18.5 ng/mL in study MET-1 (Table I). Pharmacodynamic half-lives in studies ALK-1 and MET-1 were 23 and 5.1 h, respectively, as quantified by k_e0 values of 0.030 and 0.135 h⁻¹, respectively. In contrast to the link model, an indirect response model (model II) did not fit the time-courses of ALK or MET inhibition well in both studies ALK-1 and MET-1, resulting in higher OFVs of −132 and −265, respectively, compared to those in the link models (−153 and −322, respectively). Accordingly, the link model was selected as the final PKPD model for crizotinib-mediated ALK or MET inhibition.

Table I.

Pharmacodynamic Parameter Estimates of Crizotinib-Mediated ALK or MET Inhibition in Mouse Xenograft Models with H3122 NSCLC or GTL16 GC Cells Following Once Daily Oral Administration

Study	Model	EC 50	E 0	E max	k e0	γ
		ng/mL			h −1
ALK-1	I	233 (153)	1 (fixed)	1 (fixed)	0.030 (0.013)	0.56 (0.11)
MET-1	I	18.5 (2.65)	1 (fixed)	1 (fixed)	0.135 (0.020)	1 (fixed)

Precision of the estimates is expressed as S.E. in parentheses

Study ALK-1: athymic nu/nu mice bearing H3122 NSCLC xenografts; Study MET-1: athymic nu/nu mice bearing GTL16 GC xenografts

Results are cited from previous reports (21,22)

The drug-disease models (i.e., model III and IV) adequately fit the individual tumor growth curves during crizotinib multiple-dose treatment in both H3122 NSCLC (study ALK-2) and GTL16 GC (study MET-2) xenograft models with the EC₅₀ of 255 and 213 ng/mL, respectively (Table II). The EC₅₀ value for TGI in H3122 NSCLC xenograft model was comparable with that for ALK inhibition (233 ng/mL). In contrast, the EC₅₀ value for TGI in GTL16 GC xenograft model was approximately 10-fold higher than that for MET inhibition (18.5 ng/mL). As a result, the EC₅₀ value for TGI was roughly comparable to the EC₉₀ for MET inhibition (167 ng/mL). A recently proposed integrated PKPD modeling was applied to further characterize the PKPD relationships of crizotinib for ALK or MET inhibition to antitumor efficacy in the xenograft models (Table II). The integrated PKPD models (i.e., model V and VI) also reasonably fit the individual tumor growth curves in all groups of studies ALK-2 and MET-2. The relationships between the observed and predicted tumor volumes were almost super-imposable to those estimated from the drug-disease model alone: the correlation coefficients of linear regression analyses for the integrated and drug-disease models were 0.973 and 0.972, respectively, for H3122 NSCLC xenograft model, and 0.991 and 0.990, respectively, for GTL16 GC xenograft model. These findings indicated that the integrated PKPD model did not introduce any bias to the drug-disease modeling. The OFVs of the integrated PKPD models in H3122 NSCLC and GTL16 GC xenograft models (4010 and 2404, respectively) were also comparable to those from the drug-disease model alone (4011 and 2404, respectively). The ET₅₀ value in a H3122 NSCLC model was estimated to be 1.03, indicating E of approximately 0.50 (i.e., 50% inhibition) corresponded to 50% TGI. In contrast, the ET₅₀ value in a GTL16 GC model was estimated to be 15.8, indicating E of approximately 0.06 (i.e., 94% inhibition) corresponded to 50% TGI. Collectively, the integrated PKPD modeling results suggest that target modulation required for significant antitumor efficacy (>50% TGI) is >50% ALK inhibition in H3122 NSCLC xenograft model and >94% MET inhibition in GTL16 GC xenograft model. This finding confirmed to an extent the results previously obtained with the sequential PKPD modeling.

Table II.

Pharmacodynamic Parameter Estimates of Crizotinib for Biomarker Response to Tumor Growth Inhibition in Mouse Xenograft Models with H3122 NSCLC or GTL16 GC Cells Following Once Daily Oral Administration

Study	Model	EC 50	ET 50	E max	E 0	k e0	k tg	k td	T ss
		ng/mL				h −1	h −1	h −1	h −1
ALK-2	IV	255 (22)	–	1 (fixed)	–	–	0.0126 (0.0008)	0.00115 (0.000003)	1410 (155)
	VI	–	1.03 (0.023)	1 (fixed)	1 (fixed)	0.030a (fixed)	0.0126a (0.0008)	0.00115a (0.000003)	1410a (155)
MET-2	III	213 (123)	–	1 (fixed)	–	–	0.0130 (0.0021)	0.00672 (0.00243)	–
	V	–	15.8 (1.2)	1 (fixed)	1 (fixed)	0.135a (fixed)	0.0130a (0.0021)	0.00672a (0.00243)	–

Precision of the estimates is expressed as S.E. in parentheses. –, not applicable

Study ALK-2: athymic nu/nu mice bearing H3122 NSCLC xenografts; Study MET-2: athymic nu/nu mice bearing GTL16 GC xenografts

Results are cited from previous reports (21,22)

^aThe values were estimated by the corresponding link and drug-disease models

Overall, the PKPD relationships among crizotinib systemic exposure, ALK or MET inhibition, and TGI in H3122 NSCLC and GTL16 GC xenograft models were characterized well in a quantitative manner using mathematical models to understand nonclinical PKPD (exposure-response) relationships (Fig. 2). The present modeling effort suggests that crizotinib-mediated target modulation of >50% ALK inhibition or >90% MET inhibition would be required to achieve significant anti-tumor efficacy (>50%).

Fig. 2.

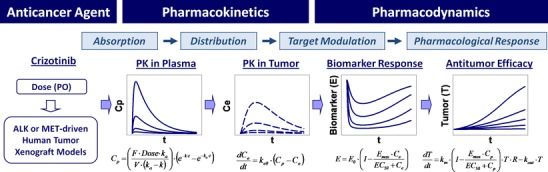
PKPD modeling summary of crizotinib-mediated target modulation and antitumor efficacy in human tumor xenograft models. C _p, plasma concentration; F, oral bioavailability; k _a, absorption rate constant; V, volume of distribution; k, elimination rate constant; t, time after dosing; C _e, effect-site concentration; k _e0, rate constant for equilibration with the effect site; E, biomarker response ratio to baseline (E ₀); EC ₅₀, concentration causing 50% of maximum effect (E _max); T, tumor volume; R, logistic function (1-T/T _ss), where T _ss is a maximum sustainable tumor volume (R = 1 for exponential growth model)

PKPD Simulation in Patients

A simulation for crizotinib plasma concentration and subsequent ALK or MET inhibition in tumors was performed in a population of patients at the RP2D of 250 mg twice daily (500 mg/day) for 14 days. Crizotinib PKPD parameters used for the simulation are summarized in Table III. Crizotinib EC₅₀ values for ALK and MET inhibition were assumed to be 90 and 7.2 ng/mL total, respectively, that were calculated from the EC₅₀ estimates of 233 and 18.5 ng/mL total from the nonclinical models by accounting for the species-difference in f_u,plasma as indicated in Methods. The simulation result projected that the crizotinib-mediated ALK and MET inhibition in patients was sustained during drug treatment. The simulated ALK inhibition reached approximately 75% whereas the simulated MET inhibition rapidly reached near-complete inhibition (∼98%). Thus, the simulated target modulation for ALK and MET in tumor of cancer patients at the RP2D was higher than the projected minimal required target modulation (i.e., >50% ALK and >90% MET) to achieve the expected antitumor efficacy. In addition, the simulation of crizotinib-mediated ALK inhibition was performed in a population of patients at the doses of 200 mg twice daily (400 mg/day) and 250 mg once daily (250 mg/day), since the reduction to these dosing regimens has been recommended in the prescription of Xalkori® based upon individual safety and tolerability if necessary. The simulated ALK inhibition reached approximately 65% at the dose of 200 mg twice daily and 60% at the dose of 250 mg once daily. Thus, the simulated ALK inhibition at these reduced dosing regimens was still enough to achieve the expected antitumor efficacy in patients.

Table III.

Summary of Crizotinib Pharmacokinetic and Pharmacodynamic Parameters for the Projection of Crizotinib-Mediated ALK and MET-Inhibition in Patients

Species	Target	Dosea	CL/F b	V/F b	k a b	k e0 b	EC 50,total b	EC 50,free	f u,plasma
		mg/kg/day	L/h/kg	L/kg	h −1	h −1	ng/mL	ng/mL
Xenograft	ALK	25 to 200	1.9 to 4.4	1.0 to 17	0.1 to 1.8	0.030	233	8.4	0.036
	MET	6.3 to 50	1.5 to 14	3.2 to 56	0.24 to 0.34	0.135	18.5	0.67
Patients	ALK	7.1	1.0	21	0.75	0.030	90	8.4	0.093
	MET					0.135	7.2	0.67

^aDaily dose in patients was calculated from clinically recommended dose (500 mg/day) with a body weight of 70 kg

^bPharmacodynamic parameters in xenograft models were estimated in athymic nu/nu mice bearing H3122 NSCLC (ALK) or GTL16 GC (MET). Results are cited from previous reports (21,22). Pharmacokinetic parameters in patients were adjusted from the clinically observed single-dose PK parameters to simulate comparable steady-state plasma concentrations to the clinically observed results previously reported (30). The EC _50,total values in patients were calculated from those estimated in the xenograft models following the correction for the difference in unbound fraction in plasma (f _u,plasma) between mice and humans. Other pharmacodynamic parameters such as E _max, E ₀ and γ were fixed as unity for the simulation in patients

DISCUSSION

Building PKPD Understanding in Nonclinical Models

Crizotinib in vivo EC₅₀ and EC₉₀ estimates for ALK, MET and TGI in xenograft models, along with in vitro ALK and MET EC₅₀ estimates are summarized in Table IV. It is important to examine in vitro-in vivo correlations for key PKPD parameters such as EC₅₀. The estimated in vivo EC₅₀ values in the nonclinical xenograft models tend to be lower than their in vitro EC₅₀ values. Crizotinib-mediated ALK inhibition in H3122 NSCLC xenograft model was achieved with an in vivo EC₅₀ of 19 nM free, that was approximately 3-fold lower than in vitro EC₅₀ of 60 nM (45). In GTL16 GC xenograft models, crizotinib-mediated MET inhibition was achieved with an in vivo EC₅₀ of 1.5 nM free, that was approximately 7-fold lower than in vitro value (10 nM) (46). While there are several potential reasons for such a disconnect between in vitro and in vivo EC₅₀ estimates, a correction for non-specific binding of crizotinib in the in vitro cell-based assay might be the one to be considered since crizotinib showed relatively high non-specific binding (∼90%) in hepatic microsomes and hepatocytes, along with high plasma protein binding of 91 to 96% across species (47). Another potential contributing factor could be the impact of subcutaneous inoculation of tumor cells on the expression levels of drug-metabolizing enzymes and transporters in mouse xenograft models (48), since crizotinib has been characterized as a substrate of CYP3A isozymes and multidrug-resistance transport protein, P-glycoprotein (44). As a general lesson in drug discovery and development programs, it is important to investigate whether there is an in vitro-in vivo correlation of EC₅₀ estimates for target modulation and/or biomarker response. If there was a poor correlation, we might need to further investigate several factors involved in biochemical or functional in vitro assay systems and in vivo xenograft models in addition to compound’s physicochemical and ADME (absorption, distribution, metabolism and excretion) properties.

Table IV.

Summary of Crizotinib Effective Concentration Estimates for Target Modulation and Antitumor Efficacy in Mouse Xenograft Models with H3122 NSCLC or GTL16 GC Cells

Xenograft Model	PD Parameter	EC 50,vitro	EC 50,vivo	EC 90,vivo
		nM free	nM free	nM free
H3122 NSCLC	ALK	60	19	–
	TGI	–	20	–
GTL16 GC	MET	10	1.5	13
	TGI	–	17	–

–, not calculated

Characterizing an anticancer agent’s ADME properties is definitely crucial to understand its antitumor efficacy in vivo. As shown in Fig. 2, pharmacodynamic evaluation is strongly linked to traditional ADME evaluation; therefore, this requires an intimate collaboration between biologists, modelers and ADME scientists. For example, when pharmacologically active metabolites were present, the metabolites should also be incorporated into the extrapolation of translational pharmacology from nonclinical models to patients, by taking account species-difference in the metabolite formation and excretion. Moreover, the rate and degree of anticancer agent’s distribution into tumors could be strongly associated with the rate (e.g., onset and offset) and extent of target modulation and/or biomarker response. When anticancer agent was a substrate of any transporter proteins (e.g., P-glycoprotein and breast cancer resistance protein, BCRP) and its pharmacological targets were expressed within the cells, we might need to further investigate the concentration of anticancer agent within the cells relative to systemic exposure. If we could accurately predict molecularly targeted anticancer agent’s ADME properties including drug distribution into tumors (e.g., target site), testing in vivo xenograft model might not even be required for further development.

It would be of great value to relate the ADME properties of a molecule to its pharmacodynamic characteristics. Crizotinib consistently showed a relatively large V_ss (13 to 25 L/kg) across species including humans after an intravenous administration, and crizotinib C_max was occurred at relatively later time point (e.g., 4 to 6 h) after an oral administration across species (44,47). Crizotinib has an extensive tumor distribution profiles with an approximate tumor/plasma AUC ratio of 4 at steady-state (in-house data). In the in vitro cell-based assay systems, the inhibition of both ALK- and MET phosphorylation by crizotinib was relatively rapid (<1 h) (46,49). However, in vivo pharmacodynamic half-lives estimated by the link model were 23 and 5.1 h for crizotinib-mediated ALK and MET inhibition, respectively, demonstrating the observed substantial hysteresis. Based on these findings, the main reason for the observed hysteresis between crizotinib plasma concentration and target modulation is likely a rate-limiting distribution from plasma to the effect site (i.e., tumors). This appears to be in line with a theoretical hypothesis of the link model. That is, the rates of onset and offset of biological response are governed by the rate of drug distribution to and from a hypothetical effect site (34). There are also some circumstances where the indirect response model may mimic a direct pharmacological response because of a relatively short lag time to develop its response (50). Therefore, the factors controlling target modulation, i.e., crizotinib-mediated ALK- and MET-inhibition, may be of little importance to the observed hysteresis in the present nonclinical models. The intermediary components between drug concentration and PD response in an effect site (e.g., drug distribution to the effect site, indirect pharmacological mechanisms, cascading transduction steps and others) are generally not known in advance. To be able to distinguish between the different processes contributing to the drug distribution rate and the indirect pharmacodynamic response, it requires intensive sampling at multiple doses in relation to the half-lives of k_e0 and the rate of biosignal turnover, in addition to understanding of compound’s ADME property and biological mechanism. The complexities of signaling networks within cancer cells during tumorigenesis and tumor progression have been intensely studied (26,51), whereas the recent PKPD models rarely contain the degree of such mechanistic detail. It is also possible for these networks to undergo adaptive changes in response to anticancer agents. It would be difficult, if not impossible, to completely understand the effects of these factors on PKPD relationships; therefore, it is important to properly design and run nonclinical studies by selecting appropriate xenograft models (based, e.g., upon clinical disease understanding, or relevance to patient population) (16,52). It is also required to evaluate study results quantitatively based on appropriate experimental endpoints. Mechanistic PKPD modeling (and also dynamic systems modeling approach) is often required to correctly analyze these endpoints in a quantitative manner, and can greatly facilitate a deeper understanding of translational pharmacology. In contrast, tumor biopsies from cancer patients during drug treatment are quite challenging to acquire under most practical circumstances, and the primary endpoint in clinical trials is generally overall survival with progression free survival as secondly (or surrogate) endpoint in most cases (53). Therefore, any surrogate markers from accessible tissues, such as plasma, peripheral blood, mononuclear cells and skin, which would be modulated in vivo by the drug, would be of great value to quantitatively evaluate in vivo drug potency. Ultimately, if a quantitative PKPD relationship was deeply understood and well established in appropriate nonclinical models, drug concentration in plasma from patients could even be used as a reliable surrogate marker for pharmacological response.

Projection of Crizotinib Antitumor Efficacy in Patients

In drug discovery and development, a target efficacious concentration (C_eff) of clinical drug candidate is routinely projected by characterizing a quantitative PKPD relationship in nonclinical pharmacological models. We generally target >50% TGI as the minimum required antitumor efficacy in nonclinical xenograft models. This was defined based on in house historical data and appeared to be consistent with a recently reported analysis of antitumor efficacy of anticancer agents between nonclinical xenograft models and cancer patient (54). This analysis suggests that anticancer agents that lead to >60% TGI in nonclinical xenograft models at clinically relevant exposures are more likely to lead to antitumor efficacy in the clinic. It should be noted that target TGI% would depend upon several factors, such as the nonclinical xenograft models used, a possible attainable maximum TGI%, a relationship of biomarker response to TGI, and clinical indication/unmet need. These factors should be carefully considered to set a target TGI% for the minimal C_eff projection, and tumor stasis or even regression might be an appropriate target in some cases.

It could be instructive to draw a comparison of EC₅₀ values required to achieve target modulation and antitumor efficacy. As mentioned above, the EC₅₀ for ALK inhibition (19 nM free) was comparable to the EC₅₀ required for TGI (20 nM free) in H3122 NSCLC xenograft model, whereas the EC₅₀ for MET inhibition (1.5 nM free) was approximately 10-fold lower than the EC₅₀ required for TGI (17 nM free) in GTL16 GC xenograft model. Therefore, the EC₉₀ value (13 nM free) for MET inhibition was roughly comparable to the EC₅₀ for TGI. These relationships appeared to be consistent among different xenograft models such as Karpas299 anaplastic large cell lymphoma model for ALK inhibition (22) and U87MG glioblastoma model for MET inhibition (21). To further characterize these PKPD relationships, the integrated PKPD modeling was performed for linking target modulation to antitumor efficacy with crizotinib exposure, by simultaneously accounting for an effect of ALK or MET inhibition on TGI. The integrated PKPD modeling results suggested that 50% ALK inhibition and 94% MET inhibition would be required for 50% TGI in H3122 NSCLC and GTL16 GC xenograft models, respectively. Thus, these results from the integrated PKPD modeling were consistent with a direct comparison of EC₅₀ values between the link and drug-disease model. The integrated PKPD model is more mechanistic approach, and can in principle cover the full dynamic PD range to properly estimate the PKPD relationship (e.g., exposure-to-response or response-to-response). This model can also link some different biomarker responses to a pharmacological response, and simultaneously estimate/simulate biomarker and pharmacological responses. Assuming comparable PKPD relationships between the xenograft models and patients, crizotinib PKPD relationships between target modulation and antitumor efficacy suggest that targeting ALK would be more effective than MET to achieve similar levels of antitumor efficacy in cancer patients. In fact, crizotinib has been approved by FDA for the treatment of ALK-positive patients with locally advanced or metastatic NSCLC as a “single agent”.

The overview of crizotinib minimal target C_eff projection for ALK and MET inhibition in cancer patients are graphically illustrated in Figs. 3 and 4, respectively. Crizotinib minimal target C_eff for ALK-positive patients was projected as the steady-state crizotinib plasma concentrations required for >50% TGI (i.e., TGI EC₅₀ = 255 ng/mL total or 20 nM free) which corresponded to >50% ALK inhibition (i.e., ALK EC₅₀ = 255 ng/mL total or 19 nM free) in H3122 xenograft models (Fig. 3). Similarly, crizotinib minimal target C_eff for MET-positive patients was projected as the plasma concentrations required for >50% TGI (i.e., TGI EC₅₀ = 213 ng/mL total or 17 nM free) which corresponded to >90% MET inhibition (i.e., MET EC₉₀ = 167 ng/mL total or 13 nM free) in GTL16 GC xenograft models (Fig. 4). In phase I dose-escalation study, this projected crizotinib minimal target C_eff based on the nonclinical PKPD relationships was set to be targeted for steady-state oral exposure to achieve the expected significant antitumor efficacy in cancer patients. Based on the observed results in phase I dose-escalation studies from a starting dose of 50 mg once daily to the highest dose of 300 mg twice daily, crizotinib C_ave,u reached the projected minimal target C_eff for ALK and MET inhibition at the dose of 200 mg once daily. The observed crizotinib steady-state plasma concentrations (50 to 60 nM free as C_ave,u) at the RP2D of 250 mg twice daily were 2 to 3-fold higher than the minimal target C_eff for the ALK and MET inhibition. Consistently, the predicted crizotinib-mediated ALK (>75%) and MET inhibition (>95%) by the PKPD modeling based on the clinically observed steady-state plasma concentrations at the RP2D was higher than their projected minimal required target modulation, i.e., >50% for ALK and >90% for MET inhibition (Figs. 3 and 4, respectively). Assuming linear pharmacokinetics, the simulated ALK inhibition at steady-state would reach near 90% at twice daily doses of 600 mg (1,200 mg/day). In principle, it would be interesting to compare target modulation and/or subsequent biomarker responses between nonclinical models and patients. However, no clinical data regarding clinical ALK- or MET-related biomarker responses are available. Up to this point, the promising clinical responses by crizotinib as a single agent have been reported in ALK-positive NSCLC patients, the majority of whom had received multiple previous therapies (24,28). Interestingly, a preliminary analysis of clinical study results indicated a positive correlation between the proportion of patients with clinically observed objective response rate (ORR) and crizotinib steady-state trough concentration (44): the proportion of patients with ORR was increased with the increase in the crizotinib concentration. In addition, this analysis suggests that a maximal effect of the proportion of patients with ORR has not been achieved yet at the RP2D. That is, higher clinical response rate may be attainable at higher doses, where greater than 75% ALK inhibition (e.g., near maximal inhibition) by crizotinib can be projected by the present PKPD modeling. Thus, despite the lack of ALK- or MET-related biomarker data in cancer patients, the approach to apply the PKPD simulation to phase I dose-escalation study supported the RP2D selection and associated systemic exposure that later demonstrated promising clinical responses (24,55). Promising clinical response in MET-positive patients could also be expected on the basis of projected crizotinib-mediated MET inhibition of >95% at steady-state along with the recent case reports describing clinical activity in some patients with MET-amplified NSCLC, gastroesophageal carcinoma and glioblastoma (25); however, extensive clinical results have not been reported yet. Overall, it is believed that the projection of crizotinib minimal target C_eff based on nonclinical quantitative PKPD modeling has been and will be helpful in guiding dose escalation and/or de-escalation to maintain efficacious exposure to crizotinib in cancer patients.

Fig. 3.

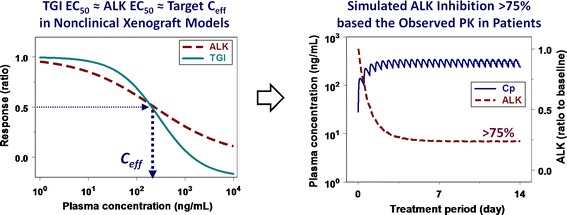
Overview of the projection of crizotinib minimum efficacious concentration (C _eff) in patients based on the exposure-response relationships for ALK inhibition versus antitumor efficacy in nonclinical xenograft models. Concentration-response curves for crizotinib-mediated ALK inhibition and tumor growth inhibition (TGI) were simulated at the concentration range of 1 to 10,000 ng/mL with sigmoidal E _max model using the pharmacodynamic parameters (EC ₅₀, E _max and γ) obtained from a mouse xenograft model with H3122 NSCLC cells

Fig. 4.

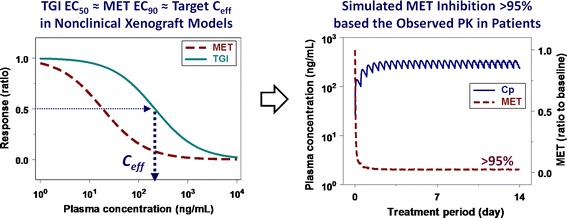
Overview of the projection of crizotinib minimum efficacious concentration (C _eff) in patients based on the exposure-response relationships for MET inhibition versus antitumor efficacy in nonclinical xenograft models. Concentration-response curves for crizotinib-mediated MET inhibition and tumor growth inhibition (TGI) were simulated at the concentration range of 1 to 10,000 ng/mL with sigmoidal E _max model using the pharmacodynamic parameters (EC ₅₀, E _max and γ) obtained from a mouse xenograft model with GTL16 GC cells

CONCLUSION

Based on the lessons learned from this case study, the general main work streams required for projection of clinically efficacious concentration and dose as translational pharmacology are summarized in Fig. 5. PKPD modeling and simulation is key to translate in vivo drug potency from nonclinical models to patients by providing a quantitative assessment of in vivo drug potency with mechanistic insight of drug action. The present paper presents crizotinib as an anticancer drug example to demonstrate that quantitative PKPD modeling can be used for predictive translational pharmacology from nonclinical to clinical development.

Fig. 5.

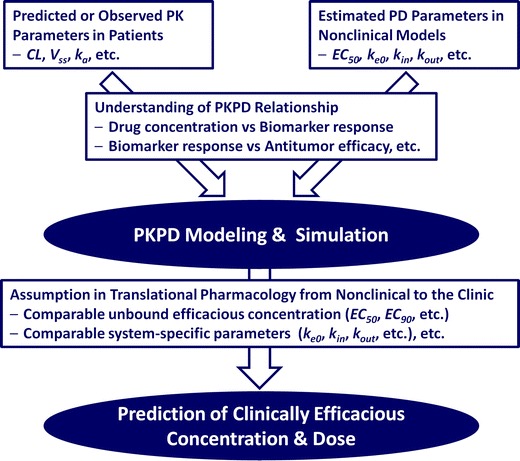
Main work streams to predict clinically efficacious concentration and dose by PKPD modeling and simulation

Electronic supplementary material

Below is the link to the electronic supplementary material.