Discussion on the validity of NIR spectral data in non-invasive blood glucose sensing

Abstract

In this paper, the effects of two-dimensional correlation spectroscopy (2DCOS) on chance correlations in the spectral data, generated from the correlations between glucose concentration and some undesirable experimental factors, such as instrument drift, sample temperature variations, and interferent compositions in the sample matrix, are investigated. The aim is to evaluate the validity of the spectral data set, instead of assessing the calibration models, and then to provide a complementary procedure for better verifying or rejecting the data set. It includes tracing back to the source of the chance correlation on the chemical basis, selecting appropriate preprocessing methods before building multivariate calibration models, and therefore may avoid invalid models. The utility of the proposed analysis is demonstrated with a series of aqueous solutions using near-infrared spectra over the overtone band of glucose. Results show that, spectral variations from chance correlations induced by those experimental factors can be determined by the 2DCOS method, which develops avenues for prospectively accurate prediction in clinical application of this technology.

1. Introduction

Diabetes mellitus is one of the most widespread global diseases threatening human health. In order to keep the blood glucose in a normal level thus reduce the complications of diabetes, self-monitoring of glucose (SMG) is necessary for diabetic patients. However, the frequent acupunctures for glucose testing bring discomfort and suffering, and may cause infections to them [1–4]. Therefore, a non-invasive continuous blood glucose measurement methodology would be highly desirable. Near-infrared (NIR) spectroscopy, with its fast and non-destructive superiorities, has been widely regarded as an effective and promising tool for non-invasive blood glucose measurements [5].

However, for the complex measuring system, especially for the case of non-invasive blood glucose sensing in the human body tissue, the changes of physiological background and experimental condition are extremely indeterminate, ambiguous, and uncontrolled. It has been reported that a chance temporal correlation, such as a correlation caused by temporal phenomena that have correlation with blood glucose changes by chance, tends to happen easily [6]. The variations from such undesirable experimental factors may be analogous to that of glucose and in some cases even cover the information of the analyte. Based on that, a certain multivariate calibration algorithm such as partial least-squares (PLS) regression is usually applied to correlate NIR spectral variation with the corresponding glucose information at multiple wavelengths. However, the correlation based statistical methods have the propensity to incorporate the latent variables maximized to correlate between spectral variances and analyte’s concentration within the spectral data set. They have little regard for the chemical basis of measurement selectivity and specificity, and cannot confirm the variations in the spectral data are really based on the variations of analyte but not on the spurious correlations. So it may lead to a situation in which apparently functional models are actually futile on the basis of spurious chance temporal correlations associated with variations in nonanalyte spectral features within the spectral data.

Particularly, several groups including Arnold, Xu, Barman, Dingari and associates, among many others [7–10], have already called the reliability of the transcutaneous glucose measurement calibration models based on NIR absorption spectroscopy or Raman spectroscopy into question. In some studies, pure component selectivity analysis (PCSA) [11–14], which comparing the regression coefficient vector of the PLS calibration model and the net analyte signal (NAS) vector of analyte, was used as a tool in order to characterize the chemical basis of selectivity for the PLS calibration models. As, the NAS vector is derived directly from the analyte absorption spectrum, it can be used to confirm that the PLS calibration vector originates from the analyte molecule. However, those methods are proposed as a general technique for assessing the selectivity for multivariate calibration models but not the validity of the spectral data. During the regression procedure, certain preprocessing methods, such as smoothing, multiplicative scatter correction, et al., are usually adopted to optimize the calibration models. Remarkably, these steps only make sense if the spectral data are based on the true causation. Therefore, not every data set can be used as calibration data set for a calibration regression model, especially for the low signal-to-noise ratio analytical system. But relatively few studies specify the reasons for the observed confusion and errors induced by chance temporal correlations, clarify the effects of various factors influencing the spectra, and ‘open the black box’ and discover it from variances at each wavelength. Attempts on the verification of the spectral data containing chance correlations can aid in better selecting of appropriate band selection preprocessing methods prior to multivariate regression, leading to the decision either accept or reject the data set to build a model. Thus it can be seen that the assessment of the validity of the spectral data before submitting it to a regression step is extremely a more effective way.

Two-dimensional correlation spectroscopy (2DCOS) [15–22], which was initially proposed and extended to the generalized form by Noda, spreads peaks along the second dimension which results in greatly improved apparent spectral resolution and selectivity. By combining the generalized correlation spectra, the hetero 2D correlation spectra, and taking advantage of Noda’s rules, the specificity of the characteristic information of glucose would be enhanced in the highly overlapped spectra. The primary purpose of this paper is to propose a method to verify that the spectral variations in the spectral data originate from the analyte of interest or chance correlations and to assess the validity of the spectral data, so that further analysis through various chemometrics techniques may be possible. By taking advantage of 2DCOS, it can be applied as an effective means for chance correlation analysis with much more superior features than the traditional one-dimensional ways. In this work, the chance correlations in the NIR spectroscopy data caused by instrumental drift, temperature variations and interferent compositions are elucidated. NIR spectra of sets of aqueous solutions with series concentrations of glucose and with constant glucose concentrations while varying instrumental status or sample temperature are studied and investigated by 2DCOS.

2. Materials and methods

2.1 Instrumentation

The NIR transmission spectra are recorded on two spectrometers individually.

A custom-built NIR spectrometer with a tungsten-halogen lamp of 100 W (PG64623, OSRAM, Germany) is used as the light source. The system is equipped with a non-collinear acoustic-optic tunable filter (AOTF) (TEAF10-1.0-1.8-S, VFI-80-50-DDS-B1-C2-E, Brimrose Company, USA) as the light splitting element to provide a spectral response range from 8707 to 5781 cm⁻¹ (1148.5-1729.8 nm) with a resolution of 10 cm⁻¹, a InGaAs PIN photodiode (G5851-21, Hamamatsu Photonics K.K., Japan), and a 16-bit data acquisition board (PCI-MIO-16XE-50, National Instrument Inc., USA).

A Fourier transforms infrared (FT-IR) spectrometer (GX, Perkin-Elmer, USA), equipped with a 50 W tungsten-halogen lamp, quartz beam splitters, and a liquid nitrogen-cooled InSb detector, is also used. NIR spectra are collected by averaging 8 scans from 10000 to 4000 cm⁻¹ (1000-2500 nm) with a resolution of 1 cm⁻¹.

Quartz cells with the path length of 1mm and a programmable temperature circulating water bath apparatus with a resolution of 0.1 °C are used in the experiments.

2.2 Instrumental drift experiments

Two experiments are conducted to investigate spectral variations induced by instrumental drift and glucose concentration change, respectively. All samples are prepared with deionized water purified with a Milli-Q Reagent Water system. The first experiment is a repetitive measurement, where the aqueous solution with the glucose concentration of 100 mg/dL and pure water solution are used as the samples. The single-beam spectra of the glucose solution and pure water are measured alternatively for 30 times by the custom-built spectrometer and the FT-IR spectrometer, separately, which last approximately 4 hours. In all, 60 spectra of glucose solution at 100 mg/dL (30 for the custom-built spectrometer and 30 for the FT-IR spectrometer) and 60 spectra of pure water (30 for the custom-built spectrometer and 30 for the FT-IR spectrometer) are obtained. In the second experiment, 30 aqueous solutions with series of glucose concentrations varying randomly over a range of 40-330 mg/dL with a mean concentration of 158.4 mg/dL and a standard deviation of 88.9 mg/dL are prepared as the samples. The transmission spectra are collected by the custom-built spectrometer. Random sampling is adopted to minimize the correlation between the time-dependent variations and the concentration of analyte. Background spectra originated from pure water are collected immediately after each sample to calculate absorbance units as described below. A total of 60 single-beam spectra (30 for the samples and 30 for the background solution) are obtained for further processing. Sample temperature is maintained at 22.0 ± 0.1 °C by the circulating water bath. A digital thermometer is used to monitor the sample temperature while collecting spectra.

2.3 Temperature variation experiments

Two experiments are conducted by the FT-IR spectrometer. In the first experiment, the NIR transmission spectra of pure water and aqueous solution with glucose of 100 mg/dL are measured with a temperature circulating water bath apparatus under the temperatures from 10 to 50 °C with 5 °C intervals. Another empty cell serving as an air reference spectrum is measured immediately following each sample measurement to eliminate the influences of instrumental drift and the possible temperature effects of the cell on the spectra. The spectra are then converted to absorbance. In the second experiment, another series of aqueous solutions with glucose concentrations ranging from 100 to 900 mg/dL with intervals of 100 mg/dL are collected at a constant temperature of 22 °C, which is maintained by using the circulating water bath. The digital thermometer is also used to monitor the sample temperature during the experiments.

2.4 Interferent compositions experiments

The aqueous solutions are composed of randomized concentrations of glucose (10-500 mg/dL) and hemoglobin (0-1000 mg/dL). Two kinds of condition are investigated: (1) a correlation between glucose and hemoglobin concentrations; and (2) an uncorrelation between glucose and hemoglobin concentrations. For each experiment, 30 mixture samples are included. R-squared values for the concentration correlations between glucose and hemoglobin are 0.991 and 0.0135 for conditions (1) and (2), respectively. All statistical testing of significance uses the standard t-test at the 95% confidence level. Pure water is used as the background. It should be noted that the spectra acquired are not time-dependent with respect to the concentration of any solutes. The transmission spectra of samples (glucose aqueous solution) and backgrounds (water) are measured by the FT-IR spectrometer alternatively. In total, 30 single-beam spectra of samples and 30 repeated spectra of pure water are collected.

2.5 Theoretical calculations and data analysis

Two-dimensional correlation spectroscopy (2DCOS) is directly related to the spectral features and perturbations, and analyzes the variations in the spectral intensities induced by the applied perturbation. It simplifies overlapping spectral information and enhances spectral resolution by spreading peaks over the second dimension.

In general, a spectral matrix X (s_×v) is composed of s samples spectra in rows and v variables per spectrum. The average spectrum of the spectra is subtracted from each of the collected spectra, and synchronous and asynchronous correlation spectra are then calculated from these dynamic spectra using the Hilbert transform H suggested by Noda. The synchronous Φ(v₁,v₂) and asychronous Ψ(v₁,v₂) variable-variable correlation spectra are calculated as:

$$\Phi (v_1,v_2)=1/(s-1)X^{T}X$$ (1)

$$\Psi (v_1,v_2)=1/(s-1)X^{T}HX$$ (2)

where the superscripted T denotes transposition. The synchronous correlation spectrum is used to investigate in-phase correlations between the spectral intensity changes, which can be regarded as a table of the correlation coefficients between the dynamic vectors of a given spectral matrix. The autopeaks in the synchronous map indicate that the corresponding variables exhibit great variability. The appearance of cross-peaks in the synchronous map reveals that the associated two variables vary in the same direction (positive cross-peaks) or in reverse directions (negative cross-peaks). While the asynchronous correlation spectrum represents the scalar products between the data and their orthogonalized forms, being regarded as a measurement of out-of-phase of the spectral intensity variations. Hybrid 2D correlation is a further development of the so-called hetero 2D correlation [23]. In hybrid correlation, a type of spectroscopic measurement is usually carried out under two different perturbation variables. By analogy to the generalized 2D correlation spectroscopy, X₁ and X₂ are two separate spectral matrices measured under separate perturbation conditions, respectively. The principles of autopeaks and cross-peaks appeared in the hybrid 2D correlation maps are consistent with those of the generalized 2D correlation spectra.

Shaded areas on the contour map represent negative intensity regions. The calculations of preprocessing and the generalized 2D correlation spectra analysis are performed in MATLAB R2010a (The Math Works Inc.).

In some cases, the raw single-beam spectra collected from the samples are used directly for the 2DCOS analysis. However, in another cases, the resulting transmittance values are converted to absorbance units (AU), where spectra matrices are generated from the ratio between each sample spectrum and the adjacent background spectrum of water or air and then taking the negative logarithm. Unless noted otherwise, the absorbance spectra refers to the data generated from the background correction mentioned above, hereinafter.

3. Results and discussion

3.1 Chance correlation induced by instrumental drift study

Normally, it takes 3-4 hours or more to obtain the large quantity of spectra required for regression modeling and prediction, especially for human experimentations. As a result, instrumental drift, which may result in similar changes to the calibration spectra as the analyte of interest and even mask information regarding the analyte, should be taken into consideration.

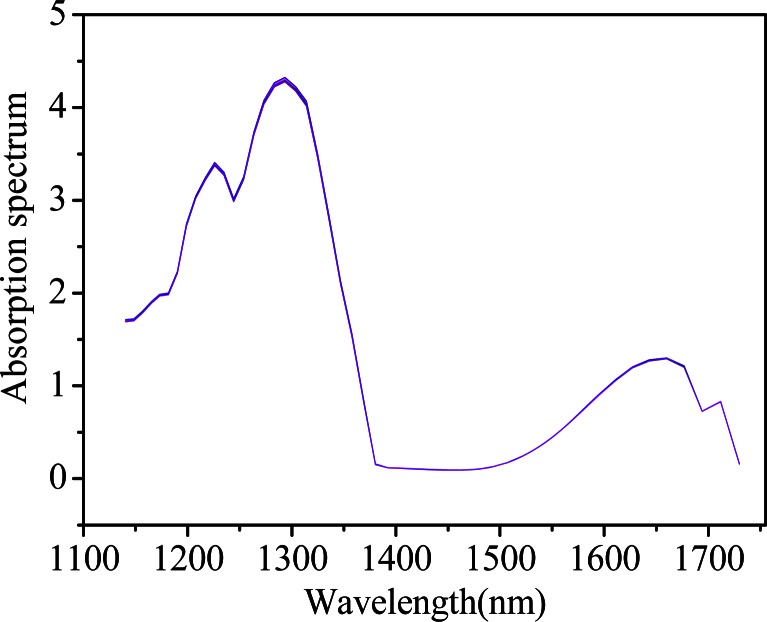
For the first experiment described in 2.2, Fig. 1 shows the raw spectra of repetitive measurements of aqueous solution with a glucose concentration of 100 mg/dL by the custom-built spectrometer, where all 30 curves are overlapped with broad and relatively small changes. In view of this, it looks difficult to interpret the spectral variations induced by some uncontrolled and time-dependent experimental parameters from the conventional one-dimensional (1D) stacking of the spectra straightforwardly. In addition, similar results can be obtained for the pure water (data not shown).

Fig. 1.

Spectra of aqueous solution with a glucose concentration of 100 mg/dL (the custom-built spectrometer).

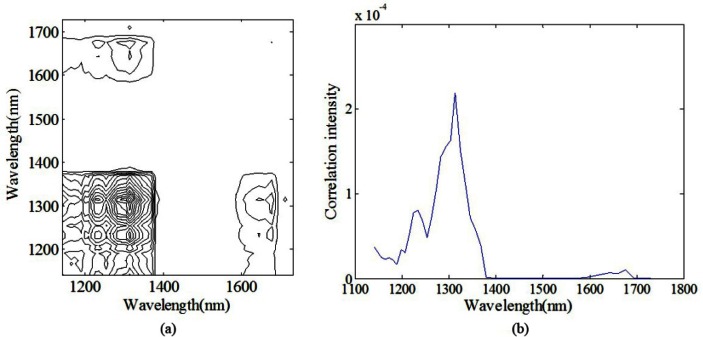
Figure 2(a) shows synchronous 2D correlation spectra constructed from the spectra of aqueous solutions with a glucose concentration of 100 mg/dL mentioned above under the perturbation of time. And the corresponding slice spectrum for the improvement of the clarity of synchronous correlations is presented in Fig. 2(b), which can be viewed as an intensity spectrum of variations. Asynchronous 2D correlation contour map is not shown here. The instrumental drift plays a dominant role since the chemical composition concentration is fixed during the measurement. Therefore, the autopeaks in the 2D correlation spectra represent those wavelengths that are sensitive to instrumental drift. As evident in Fig. 2, autopeaks can be obviously observed in the synchronous spectrum of the 2D correlation analysis at 1199, 1235, and 1314 nm, and less clearly at 1659 nm, indicating that spectra at those wavelengths varied as a function of the order of acquisition time. Moreover, the positive cross-peaks at (1235, 1314), (1235, 1659), and (1314, 1659) reveal that the variances at these points, which all attributed to the instrumental drift, are correlated and in same trend. Notice that those autopeaks reflect the wavelength drift features of instrument rather than the absorption characteristics of glucose (~1595 nm) or water (~1450 nm).

Fig. 2.

Schematic contour map of (a) synchronous (b) slice 2D correlation spectra of aqueous solutions with a glucose concentration of 100 mg/dL (the custom-built spectrometer).

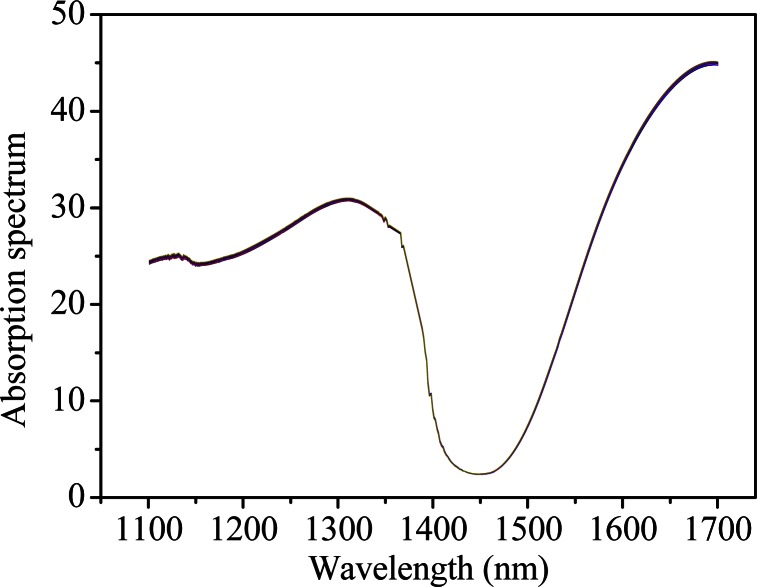
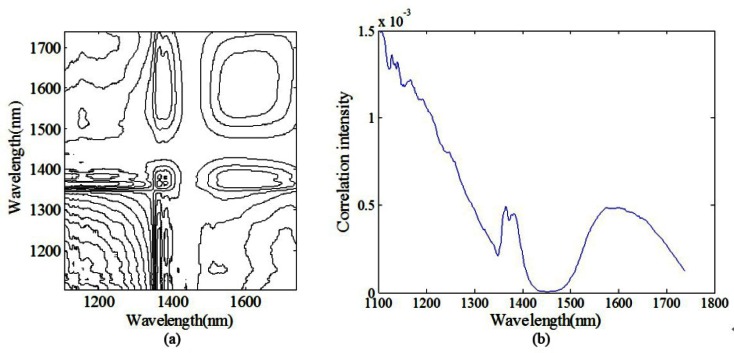
To investigate the autopeak differences originated from instrument to instrument, similar repetitive experiment is conducted on the FT-IR spectrometer. Figure 3 shows the raw spectra of pure water of repetitive measurements from 1100 to 1700 nm. Similar results can be obtained for the glucose solution at the constant concentration (data not shown here). The 2D contour map and slice 2D correlation map of pure water under the perturbation of time are shown in Figs. 4(a) and 4(b), respectively. The synchronous map shows autopeaks near 1107, 1366, 1383, and 1595 nm, which suggests that instrumental drift has influence on spectral variation. This is consistent with the result of the custom-built spectrometer. However, it is evident that the location, and intensity of autopeaks in Fig. 4 are different from those in Fig. 2, which verifies the specificity of the autopeaks subject to respective instruments.

Fig. 3.

Spectra of pure water (the FT-IR spectrometer).

Fig. 4.

Schematic contour map of (a) synchronous (b) slice 2D correlation spectra of pure water (the FT-IR spectrometer).

In addition, there is little difference between the 1D spectra of pure water and the glucose solution with fixed concentration. As we know, measurements of aqueous samples are often complicated by the strong NIR absorption properties of water, which exist in large amounts, even in matrices as complex as whole blood. Moreover, the unique absorption of glucose is at least 1-2 magnitude lower than that of water. So the background correction is usually applied in near-infrared spectroscopy.

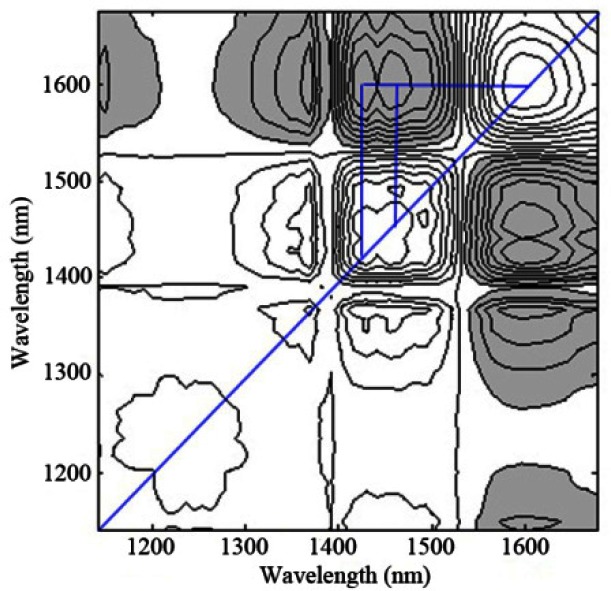
For the second experiment described in 2.2, pure water and glucose aqueous solutions with different concentrations are measured by the custom-built spectrometer. Then the mean-centered absorbance spectra of glucose are applied to compute the 2D correction spectroscopy under the perturbation of glucose concentration. The synchronous map is shown in Fig. 5, where the synchronous map shows strong autopeaks near 1595 nm, indicating that the spectral features at that position vary greatly according to concentration-dependent intensity changes, followed by the feature around 1429 and 1454 nm. It is totally different from either Fig. 2(a) or Fig. 4(a). The dominant water absorption bands centered at approximately 1450 nm at room temperature cover the broad bands centered at 1429 and 1454 nm, and the band at 1595 nm is assigned as the overtone absorption band of glucose [22]. In the synchronous spectra, the appearance of negative cross-peaks at (1429, 1595) and (1454, 1595) between the autopeaks reveals that they originated from different molecules and changes are in opposite directions. It corresponds to displacement of water by dissolution of glucose, i.e., displacement from the relative decreasing of water concentration with the increasing of glucose concentration. The autopeaks coexisted at the absorption bands of both glucose and water, which is indicative of the in-phase variation with each other.

Fig. 5.

Synchronous 2D correlation spectra of aqueous solutions with series of glucose concentrations after background correction (the custom-built spectrometer).

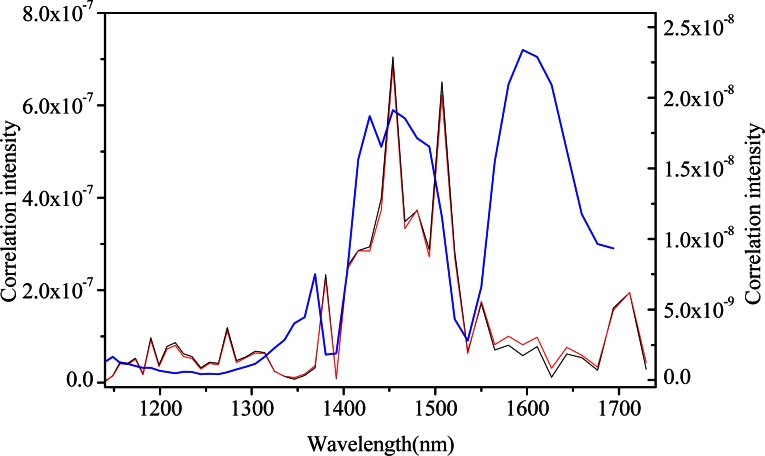
The plots presented in Fig. 6 provide a comparison of these synchronous slice spectra for aqueous glucose solutions with background correction (blue), without background correction (red), and pure water (black). The spectra of pure water can be regarded as the spectra only induced by the instrumental drift. The overall shapes of the pure water and glucose solutions without background correction slice vectors are nearly identical except for subtle discrepancies in the magnitude of the absorption band at approximately 1600 nm associated with glucose. It indicates that it is difficult to distinguish the information variations generated from the two spectral data. And autopeaks at 1500 and 1700 nm which are not corresponding to glucose can be inferred as the instrumental drift. Although the slice spectrum is decreased in one order of magnitude with background correction, the obvious presence of the blue line suggests the presentation of high resolution characteristics of glucose and of weaker autopeaks of instrumental drift and water after background correction, whatsoever. The reason may be that the absorptivity coefficient of water is 1-2 magnitude greater than that of glucose in the NIR region. Such preprocessing can reduce the error caused by instrumental drift-induced chance correlations as well as highlight the absorption characteristics of glucose, which will definitely benefit the specific extraction of glucose information.

Fig. 6.

Comparison of 2D correlation slice spectra of aqueous glucose solutions with background correction (blue, assigned to the right ordinate), without background correction (red, assigned to the left ordinate), and pure water (black, assigned to the left ordinate) (the custom-built spectrometer).

Overall, it can be seen that instrument drift can be interpreted fairly well from a synchronous 2D correlation spectra and the corresponding slice spectrum. If autopeaks appear at the waveband that not associated with the analyte of interest or any known interferent compositions, a conclusion that the instrumental drift have not been corrected in the sample spectral data can be drawn. Even if the autopeaks also show at the waveband that belonging to glucose, it’s absolutely essential to correct the background from the sample spectral data because of faint spectral variations caused by glucose concentration changes and the severe impact of the background drift. Background correction is required, provided autopeaks associated with instrumental drift appears apparently in the 2D contour map. In addition, in regards to data acquisition, random sampling is also recommended to minimize the potential chance correlation relationship between the time-dependent variations and the concentration of analyte of interest in controlled experiments [7,9,24].

3.2 Chance correlation induced by temperature variation study

The effects of temperature variation are widely investigated in NIR spectroscopy due to its serious influence and great importance [12,25–32]. Chance correlation between temperature variance and spectrum variances induced by glucose concentrations is often ignored in the implicit calibration methods. However, as noted in the bibliography [25], only 1 °C change in temperature could induce about 500 mg/dL errors in the prediction of the glucose concentration. According to previous research, temperature can influence intermolecular relationships, for example, the rotation and vibration of hydrogen bonding (H-bonding) in water changes as a function of temperature variations which may result in band broadening or shift. Generally, band broadening and shift vary non-linearly with temperature.

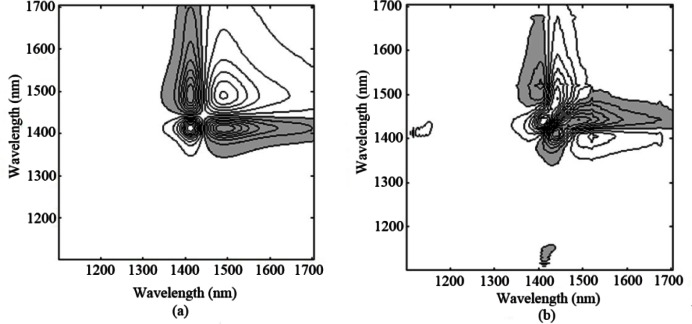
In this work, the 2DCOS of the absorbance spectra under the perturbation of temperature is calculated. The synchronous correlation spectrum (Fig. 7(a)) of pure water shows the apparent dominating autopeaks at around 1410 and 1495 nm that correspond to the O-H band shift from long wavelength to short wavelength coupled with some intensity increases, which is attributed to the fact that the intermolecular H-bonds are generally weakened with temperature elevation. Such cluster pattern is commonly known as the four-leaf-clover pattern cluster. Especially for such four-way non-symmetric pattern, it can be referred to as the angel pattern with cross-peak wings [20]. On the other hand, we can observe the development of cross-peaks in the asynchronous correlation spectra (Fig. 7(b)). The elongated asynchronous cross-peaks near the diagonal are now distributed closer to the stronger autopeak side, which encompass the 2D spectral regions of both positive and negative synchronous correlation intensities. This provides a clear indication that these peaks are generated from a band shift and from a gradual increase in the intensity with temperature elevation rather than simple intensity changes of two overlapped bands, which is consistent with previous result [22,30].

Fig. 7.

(a) Synchronous (b) asynchronous 2D correlation spectra of pure water under temperature perturbation (the FT-IR spectrometer).

As we know, while the glucose concentration in aqueous increases, the concentration of water will decrease due to the displacement between glucose and water, which will lead to the change of spectral peak intensity but no band shift occurs in the area around the water absorption band. However, under the perturbation of temperature, the band shift is coupled with a simultaneous peak intensity variation, which is complex but characteristic features comprising of clusters of multiple correlation peaks from a single band of varying position and intensity in the 2D correlation spectra. Obviously, they are significantly distinct from the spectral variation from the perturbation of time and composition. So the 2DCOS method, which has been proven to be an approach for exploring the evolution of spectral changes induced by some perturbations, enables the ability to discern whether or not the chance correlations are induced by temperature variations. Similar results can be obtained from the 2D contour maps of glucose solution with fixed concentration, indicating that the glucose molecular is less sensitive to temperature variation than water.

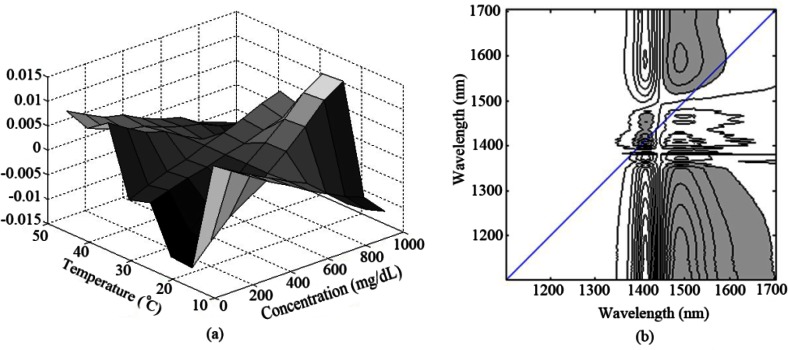
For further analysis, a hybrid 2D correlation [20,33] for a single type of spectroscopic measurement under two perturbations (concentration and temperature) is then studied. Figure 8 shows the synchronous hybrid 2D correlation contour maps between the two spectral data of pure water in the temperature range of 10-50 °C and aqueous glucose solution in the concentration range of 100-900 mg/dL at a constant temperature of 22 °C. Synchronous sample-sample hybrid correlation in Fig. 8(a) reveals that the temperature- and concentration-dependent spectral variations show dissimilar trends regarding these two different external variables. Moreover, synchronous variable-variable hybrid correlation in Fig. 8(b) provides complementary information by indicating which wavelength pairs are responding to the two different perturbations in similar manners. As expected, no obvious autopeak or symmetric cross-peaks are observed along the diagonal line, which is indicative of distinct spectral variations under the two permutations at each wavelength. It means that the 2DCOS analysis present here can be considered as an efficient discrimination method for chance correlations induced by temperature variations.

Fig. 8.

Synchronous (a) sample-sample (b) variable-variable hybrid 2D correlation spectra under perturbations of concentration and temperature. (the FT-IR spectrometer).

From the generalized phenomenon, in the synchronous and asynchronous correlation spectra of spectral data, when the autopeaks and cross-peaks with angel pattern appear around the absorption band of water, we can argue that temperature variations occur in the spectral data. To build a predictive calibration model, some temperature correction methods, such as background or reference spectrum subtraction [34], or a reference-wavelength-based method [35], should be adopted. Moreover, both of the ambient and sample temperature must be strictly controlled during the spectra acquisition.

3.3 Chance correlation induced by interferent compositions study

Except the chance correlations induced by time- and temperature-dependent perturbations, another challenge in non-invasive glucose detection is the complexity of the blood components in the samples. Due to the implicity of the PLS regression, information of both the analyte of interest and other interferential components are usually included into the model. Specifically, there are two different conditions regarding the concentration correlations between the analyte of interest and inference which cannot be removed by background correction. One is an acceptable beneficial signal enhancement generated from the correlation. For example, the concentration correlations between glucose and water due to the displacement. This is a correlation relationship that is maintained throughout the other samples. Another is a detrimental and temporary correlativity, such as the chance correlation between the analyte and other interferent compositions, which cannot be simply discerned by 1D spectrum or multivariate calibration regression technologies. Despite these temporal correlations, accurate analyte measurements are possible so long as the correlations in the prediction data set keep consistent with that in the calibration data set. However, once conditions change or such relationships absent of true causation are no longer maintained, accurate calibration models cannot be generated and undesirable errors may result.

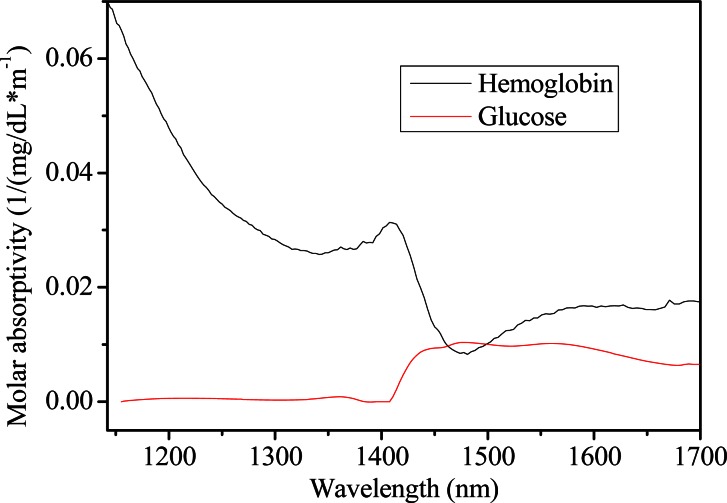
In this section, chance concentration correlation between glucose and hemoglobin is discussed. For clarity, individual molar absorptivities are presented in Fig. 9 for each solute, which are calculated from a standard solution of 100 mg/dL for the solute with an optical path length of 1 mm. Critical features for each component are highlighted by the spectra, including several significant broad bands centered at approximately 1100-1200 nm for hemoglobin, and ~1595 nm for glucose.

Fig. 9.

Molar absorptitives for the solute of hemoglobin (black) and glucose (red).

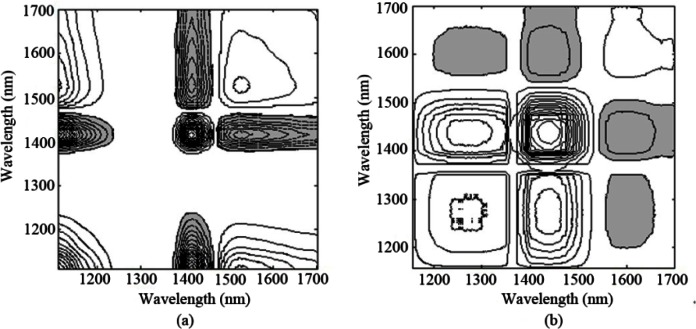
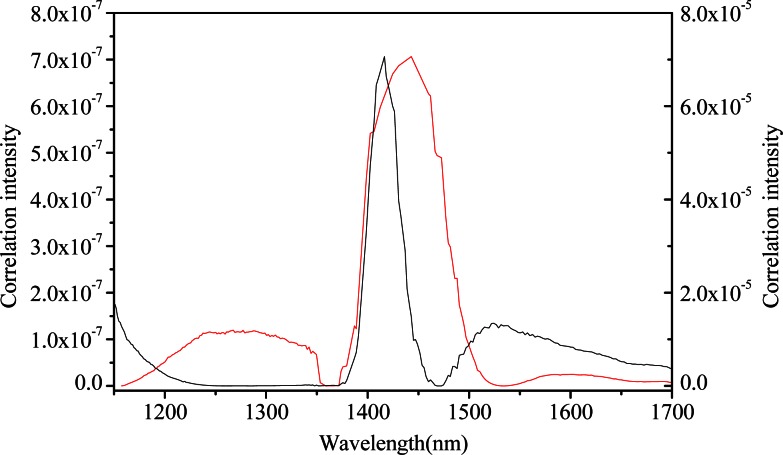
As described in 2.4, two different correlation conditions between glucose and hemoglobin concentrations are considered, one of which has a noticeable R-squared value of 0.991 and the other with an R-squared value of 0.0135. Net analyte signal (NAS) analysis of glucose is determined for each absorbance spectra to produce the NAS matrix according to glucose concentrations. NAS, defined by Lorber, corresponds to the component of the analyte spectrum that is orthogonal to the spectral features of the interfering compounds [36,37]. NAS can be utilized to understand figure of merit such as sensitivity, chemical selectivity from overlapping spectra [11–14]. Obviously, NAS of glucose is free from interference. Ideally, in the case when the interferent’s concentration is uncorrelated with the glucose, the selectivity for glucose is very high and the influences of all nonanalyte spectral variations within the data set can be removed via NAS analysis. However, if the interferent’s concentrations are highly correlated with glucose, the selectivity for glucose would be influenced by the intereferent and be very low. Then, 2D correlation spectra based on the NAS matrices of glucose are calculated under the perturbation of glucose concentration to further characterize the two groups of spectra. The synchronous correlation spectra under two kinds of correlation condition are presented in Figs. 10(a) and 10(b), respectively. Furthermore, Fig. 11 plots their corresponding synchronous slice spectra.

Fig. 10.

Synchronous 2D correlation spectra of (a) correlation (b) uncorrelation between glucose and hemoglobin (the FT-IR spectrometer).

Fig. 11.

Slice spectra of correlation (black, assigned to the left ordinate) and uncorrelation (red, assigned to the right ordinate) between glucose and hemoglobin (the FT-IR spectrometer).

As is known, the molar absorptivities of glucose, water and hemoglobin are highly overlapping in the wavelength of 1100-1700 nm. Comparing the contour maps and plots in Figs. 10 and 11, major differences occur in the absorption region below 1200 nm, which is associated with hemoglobin. As expected from the overlapping of the absorption coefficients, absorption spectral features for hemoglobin cover that of glucose with principal absorption bands nominally located in the vicinity of 1250 nm, with less strong autopeaks emerging in the region of 1100-1200 nm. Its appearance put forward the presence of hemoglobin. Figure 10(a) and the black line in Fig. 11 provide evidence for this. In addition, autopeaks located around 1525 nm also show that the information of hemoglobin still exists in NAS of glucose, indicating that concentrations between glucose and hemoglobin are highly correlated.

Nevertheless, when the concentrations of hemoglobin are irrelevant with that of glucose, spectral variance induced by hemoglobin can be removed from NAS analysis of glucose. This is evident by the decrease in autopeak intensity within the region below 1200 nm and around 1595 nm, as noted in Fig. 10(b) and the red line in Fig. 11. Obviously, higher autopeak centered at 1595 nm appears to be associated with glucose, which at least give prominence to the glucose-specific information relative to water and other interferents, although the slice spectrum has lower amplitude as the signals of hemoglobin are not a part of the useful signals any more.

These findings verify the validity of the spectral data set that there are not any interferents correlated to glucose concentrations in condition (2) and, as a result, can be treated as the calibration set to build a regression model. Whereas a rejection is received for the data set in condition (1), where a destructive correlation is found and some steps such as waveband selection can be adopted in order to reduce the influences of hemoglobin. In all, NAS combined with the 2DCOS analysis is an effective way to discover the chance correlation between the analyte of interest and other compositions. From a practical standpoint, especially, reasonable experiment design is necessary for in vitro experiments, as described in references [9,38].

4. Conclusions

In this paper, the validity of NIR spectral data over the overtone band of glucose in non-invasive glucose sensing is investigated. We mainly focus on the variations generated from chance temporal correlations between glucose concentrations and some undesirable experimental factors, such as instrumental drift, sample temperature variations, and interferent compositions, and generalized 2DCOS and hybrid 2DCOS are applied to determine the validity of data. Through a systematic investigation of the spectral data by using 2DCOS analysis, the impact of the overlapped peaks, which cannot be detected by the traditional one-dimensional spectral analysis, can be excluded with the 2D correlation analysis. It gives us substantial information on the dynamic behavior of the spectra, and will definitely enhance the specificity of glucose from the complicated spectral data set. The utility of the proposed analysis is demonstrated with a series of aqueous glucose solutions. It can lead to the contribution to find out the causal attributions of the chance correlations. It is advised to adopt different preprocessing methods for different situations ahead of regression. Background correction should be taken first if the autopeaks associated with instrumental drift appear apparently in the 2D contour map; Temperature correction should be taken if the autopeaks and cross-peaks with angel pattern appear around the absorption band of water; The data set should be rejected for calibration set, or waveband selection should be taken if the autopeaks appear at any other wavebands corresponding to the interferential compositions.

Therefore, it can be seen that the assessment of the validity of the spectral data is extremely a more effective way than evaluating the calibration regression models. It is not only to avoid building spurious calibration models, but also to further the improvements of multivariate regression steps through appropriate preprocessing by calibration data evaluation, and thereby improve model performances and optimize the data acquisition and experimental design. Those results maybe intended to encourage the widespread use of the proposed analysis in the biomedical optics field. Though the results are promising, in order to assess the validity of the spectral data comprehensively, future work must include experiments involving the spectral variances induced by other resources such as changes of humidity, pressure, and etc., and the application of the 2DCOS should be performed in more complex matrices with highly overlapping spectral features.