Abstract
We report a cross-referencing method to quickly and accurately characterize the optical properties of nanoparticles including the extinction, scattering, absorption and backscattering cross sections by using an OCT system alone. Among other applications, such a method is particularly useful for developing nanoparticle-based OCT imaging contrast agents. The method involves comparing two depth-dependent OCT intensity signals collected from two samples (with one having and the other not having the nanoparticles), to extract the extinction and backscattering coefficient, from which the absorption coefficient can be further deduced (with the help of the established scattering theories for predicting the ratio of the backscattering to total scattering cross section). The method has been experimentally validated using test nanoparticles and was then applied to characterizing gold nanocages. With the aid of this method, we were able to successfully synthesize scattering dominant gold nanocages for the first time and demonstrated the highest contrast enhancement ever achieved by the gold nanocages (and by any nanoparticles of a similar size and concentration) in an in vivo mouse tumor model. This method also enables quantitative analysis of contrast enhancement and provides a general guideline on choosing the optimal concentration and optical properties for the nanoparticle-based OCT contrast agents.
OCIS codes: (110.4500) Optical coherence tomography, (170.3880) Medical and biological imaging, (290.0290) Scattering, (290.5820) Scattering measurements
1. Introduction
The imaging contrast of optical coherence tomography (OCT) is determined by the optical properties of biological tissue (i.e. scattering and absorption) and is often dominated by scattering. Unfortunately, the intrinsic OCT imaging contrast can be very weak in many cases for discerning pathological change. As in all clinical imaging modalities, the use of exogenous contrast agents have been investigated for improving OCT imaging contrast and potentially gaining molecular specificity. An ideal contrast agent is expected to have a small size (i.e. less than 100 nm) for effective systemic delivery, and should be strong in backscattering in order to reflect more photons towards the detector. In addition, the contrast agents should be biocompatible and easy to conjugate for active targeting. Several types of contrast agents, such as core-shell microsphere, air-filled micro-bubbles, dyes and structured gold nanoparticles, have been developed for improving OCT contrast [1–8]. However, most of these contrast agents are either too large or are dominated by absorption (i.e., absorbing the imaging photons as opposed to enhancing backscattering). Gold nanocages are a relatively new class of structured nanoparticles [3]. Compared to most other nanoparticle contrast agents, gold nanocages have a much larger total optical extinction cross section (i.e., the sum of scattering and absorption) in the near infrared (NIR) region while maintaining a relatively small size (i.e. 80 nm or less). Furthermore, the optical properties of gold nanocages can be tailored by modulating the nanostructure geometric parameters including size, wall thickness and wall porosity.
A critical step in the development of any OCT contrast agents is the assessment of the optical properties of the agents. Ideally the characterization process should be simple and quick yet accurate so that synthesis conditions could be retuned in order to optimize the optical properties of the contrast agents (e.g., with stronger scattering than absorption and a larger backscattering cross section, etc.). Typically the method of choice is the integrating sphere method, which has been used for quantitatively characterizing optical properties of scattering samples [9]; however, the results are sensitive to many experimental parameters and can often have large fluctuations. Thus a new and easy-to-use method is needed for rapid characterization of the contrast agents. Characterization of optical properties using an OCT system has been investigated [10–12]. However, the effect of a focused incident beam in a scattering sample has not been carefully considered or eliminated in those models, which would reduce the accuracy of measurement results.
In this paper, we report a new generic method for quickly and accurately characterizing the optical properties of OCT contrast agents, including the total extinction, scattering, absorption and backscattering cross sections, by using an OCT system itself. The feasibility of the new method was validated by comparing the characterization results with both the theoretical calculations (i.e., Mie theory for spherical particles [13] and discrete dipole approximation (DDA) for non-spherical ones [14]) and the traditional integrating sphere measurements. With the aid of this new method, we have successfully developed a new class of gold nanocages, which, for the first time, offer stronger scattering than absorption at wavelengths around 800 nm among gold nanoparticles [15]. As a result, significant contrast enhancement was observed in OCT imaging of a mouse tumor model in vivo by the newly developed gold nanocages.
2. Theoretical analysis
It is well known that the depth-dependent OCT backscattering intensity can be modeled as:
| (1) |
where z is the imaging depth, φand θ are respectively the azimuthal and polar angle in a spherical coordinate system, Θis the half collection cone angle of the objective lens in the sample arm (and , NA is the numerical aperture of the imaging objective lens), is the angular dependent differential scattering coefficient, is the total extinction coefficient, is a system constant which depends on the detection system (such as the incident power and photo detector gain etc.), and is the geometric factor function describing both the focusing and scattering effects on the imaging beam in a turbid medium as described in [2,16]. Considering the scattering is azimuthally symmetric in highly scattering samples and the NA of the imaging lens in most OCT systems is small (i.e. around 0.1 or even smaller), the equation can be reduced to [2,16,17]:
| (2) |
where is backscattering coefficient and is a new system constant. We notice that there are three unknowns (i.e. K, , ) and one function (i.e. ) in Eq. (2). Extracting the unknowns, particularly those in a multiplicative form, from this equation by multi-parameter fitting generally yields very large errors and is not always feasible.
In order to overcome the challenges involved with direct curve fitting, the basic principle is to introduce one type of scattering nanoparticles, of which the optical properties (i.e. scattering, absorption, and backscattering cross-sections or coefficients) can be conveniently calculated (e.g. using Mie theory or DDA). Two identical samples (phantoms) made of the given nanoparticles (e.g. silica nanospheres) with a known concentration are first prepared. The test nanoparticles (i.e. gold nanocages in our case) are then added to one of the phantoms (named test phantom), while the other phantom serves as the reference phantom. OCT imaging is then performed over the test and reference phantoms under the same experimental conditions (i.e., with the same incident power, focused spot size, focusing depth, etc.). The corresponding OCT signals are:
| (3) |
Here and are the backscattering (and extinction) coefficients of reference and test phantoms, respectively; and are the geometric factor functions in the reference and test phantom, respectively. If the scattering properties between reference and test phantoms do not differ dramatically (e.g., within an order of magnitude), it can be reasonably assumed (as confirmed experimentally in this paper) that the difference in the geometric factor function between the test and reference phantoms is negligible, i.e., . Therefore, by subtracting the logarithm of the two OCT signals in Eq. (3), we cancel out both the system constant and the geometric factor function and obtain the following depth-dependent cross-referencing function:
| (4) |
Linear fitting can then be applied to Eq. (4) with respect to the imaging depth z, the slope of which gives the total extinction coefficient of the test phantom. In addition, we will also obtain the y-intercept of the Eq. (4) (at z = 0) from the linear fitting, denoted as. Since the backscattering coefficient of the reference phantom can be precisely calculated by the scattering theory (or experimentally measured), the backscattering coefficient of the test sample can then be easily found, i.e.
| (5) |
The next parameter to consider is the total scattering coefficient of test nanoparticles, which can be deduced from the backscattering coefficient of the test nanoparticles using , where k can be derived by the scattering theory for nanoparticles of a given size and shape (and by averaging over the nanoparticle orientations if the nanoparticle does not have a spherical shape). The absorption coefficient of the test nanoparticles is then given by. This algorithm is fast and only involves OCT measurements. The above linear fitting procedure is very robust compared to the multivariable curve fitting procedure. More importantly, the new algorithm can provide a whole set of optical properties of the phantom made by the test nanoparticles, including,, and .
3. Algorithm verification
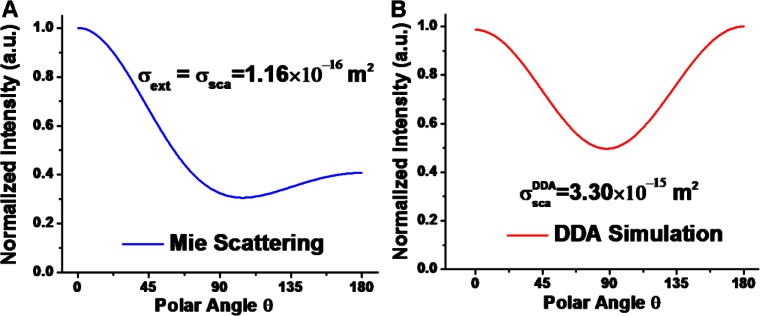
Before applying the above characterization algorithm to gold nanocages, we performed an experiment to verify it on mock nanoparticles. In this experiment, we used home synthesized silica nanospheres of a nm diameter as the reference nanoparticles. The reference and test phantoms were made of 5% gelatin embedded with 50 and 100 mg/mL silica nanospheres, respectively. Therefore, the test and the reference nanoparticles are both at a concentration of 50 mg/mL in the 5% gelatin phantom. The optical properties, including the scattering (no absorption) and backscattering cross sections, of the fused silica nanosphere at the given concentration in the medium can be analytically predicted by the Mie scattering theory, and the angular dependent scattering pattern as shown in Fig. 1(A). OCT imaging was conducted using a 7-fs Ti:Sapphire laser as the light source with a center wavelength at 825 nm and a 3dB spectral bandwidth of ~150 nm. The NA of the imaging lens in the sample arm was about 0.1 and the averaged power on the sample arm was ~4 mW. OCT images of the two phantoms were acquired by scanning an imaging beam across the two side-by-side phantoms under the same experimental conditions.
Fig. 1.
(A) Angular dependent scattering pattern of 180 nm silica nanospheres in a 5% gelatin phantom at the wavelength of 825 nm calculated by the Mie scattering theory. (B) Angular dependent scattering pattern of 75 nm gold nanocages in a 5% gelatin phantom at the wavelength of 825 nm calculated by a numerical method based on discrete dipole approximation (DDA). The scattering pattern is averaged over various nanoparticle orientations.
After OCT imaging of both phantoms, A-scan OCT intensity signals were obtained as a function of imaging depth by averaging along the B-scan direction in order to remove heterogeneity of the phantom samples and reduce the speckle noise. The first step is to extract the total extinction and back scattering coefficients from the averaged A-line signals (e.g., averaged over 500 A-lines). By applying the aforementioned algorithm to the test and reference A-scan OCT intensity signals, the extinction coefficient of test silica nanospheres was extracted in the test phantom (at a mass concentration of 50 mg/mL) as . To deduce the extinction cross section of a single fused silica nanosphere, we first need find out the molar concentration of the silica nanospsheres in the test phantom by converting the mass concentration to the molar concentration. And the molar concentration was found to be . The extinction cross section of a fused silica nanosphere is then given by (where is Avogadro constant). This extinction cross section is very close to the theoretical value predicted by the Mie theory. The ratio of the backscattering coefficients of the test to the reference nanoparticles denoted by can be found from Eq. (5), and the resulted value is 0.96 which is very close to the theoretical limit of 1 in this case (considering test and reference silica nanospheres had the same concentration in this experiment). We notice that the accuracy of the algorithm in determining the extinction coefficient and the backscattering ratio of the test and the reference nanoparticles is excellent; warranting that neglecting the geometric factor function in Eq. (4) is safe.
The next step is to separate the total scattering and absorption coefficient of the test silica nanospheres from the total extinction coefficient. Since the backscattering coefficient of reference silica nanospheres was calculated by the Mie theory as , we were able to deduce the backscattering coefficient of test silica nanospheres to be (from Eq. (5)). From the scattering pattern predicted by the Mie theory (as shown in Fig. 1(A)), the ratio of the total scattering to the backscattering coefficient is. Therefore, the total scattering coefficient of test silica nanospheres is, and the absorption coefficient of the test silica phantom is (which, in theory, should be zero). It is noted that the relative errors in the extinction coefficient between the experimental measurements and theoretical predictions are within 7%, demonstrating the feasibility of the proposed cross-referencing method for optical properties characterization.
Similar experiments of different concentrations of fused silica nanospheres were repeated three times and all results showed that the relative measurement errors (i.e. the variation in the characterization results) in the extinction and backscattering cross sections were no more than 3% among experiments, confirming the robustness of this method for optical properties characterization.
4. Experimental results
4.1 Characterization of optical properties of gold nanocages
After verifying the accuracy of the algorithm, we used it to fully characterize the optical properties of the newly developed gold nanocages, aiming to provide quick feedback to optimize nanocage synthesis conditions for achieving scattering dominating optical properties and thus OCT imaging contrast enhancement with the nanocages. Similar to the above feasibility experiments, two identical phantoms were made by embedding 50 mg/mL silica nanospheres into 5% gelatin, whose optical properties again can be calculated using the Mie theory. Gold nanocages were added to one of the phantoms at a nominal concentration of 1.0 nM. OCT imaging of the test (with nanocages) and reference (without nanocages) phantoms was performed under the same conditions as mentioned in the previous section.
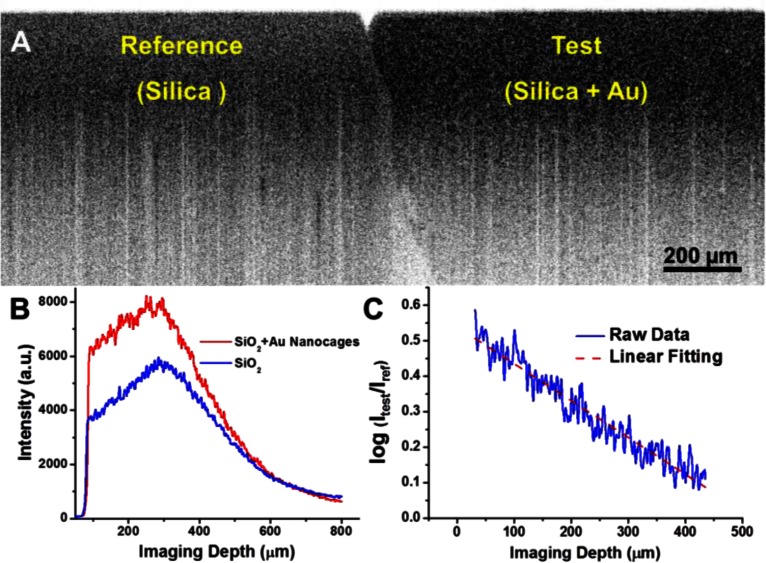
Figure 2(A) shows the OCT images of the reference phantom (on the left) and the test phantom (on the right), respectively, and the decay curves of the OCT intensity along imaging depth in both cases are given in Fig. 2(B). Using the cross-referencing method, the extinction coefficient and the backscattering coefficient of gold nanocages in the test phantom were calculated from the slope and y-intercept of Eq. (4), and the resulted values are and , where the backscattering coefficient of the reference nanoparticles (silica nanospheres) predicted by Mie theory was used for Eq. (5). Figure 2(C) shows the ratio of the two depth-dependent signals shown in Fig. 2(B), and the nearly perfect linear relationship of this ration versus imaging depth also implies that the potential difference in of the test and reference phantoms can be safely neglected. To calculate the scattering coefficient of the nanocages from the backscattering coefficient, we need first to find the relationship constant k in. A numerical simulation method based on DDA was used to calculate the orientation averaged, angular dependent scattering pattern and the result is shown in Fig. 1(B), from which the parameter is found to be 1.385. The scattering coefficient of nanocages is then given by. The absorption coefficient is thus . We notice that the ratio of the scattering to the absorption coefficient is about 1.31, showing the scattering dominance in the optical extinction coefficient. To independently validate the optical properties obtained from OCT phantom imaging, integrating sphere experiments were performed to directly measure the optical properties of the nanocages, where the ratio of scattering to absorption coefficient was found to be ~1.27 at the central wavelength (825 nm) of the OCT source, and this ratio was very close to the one obtained by cross-referencing OCT method. Taking into account the nanocage concentration (1 nM), the corresponding cross sections of a gold nanocage can be found as, , and . It is noted that the measured cross sections differ from the ones predicted by DDA simulations (i.e. and). One major reason accounting for this discrepancy is the potential loss of gold nanocages during sample preparation which was inevitable; thus the actual concentration could be lower than the nominal one, underestimating the overall cross section values.
Fig. 2.
(A) OCT images of the phantoms without nanocages (left) and with nanocages (right). (B) Intensity plots of the OCT signals on a linear scale as a function of imaging depth. (C) Ratio of the two signals in (B) on a logarithmic scale as a function of imaging depth.
4.2 Contrast enhancement of gold nanocages for OCT imaging of tumor in vivo
We examined the feasibility of using the very first scattering-dominant gold nanocages as a contrast agent for in vivo OCT imaging of tumor on a xenograft mouse model. Three male Balb/c nude mice, 6–8 weeks of age and about 25 g of average weight, were obtained from the Taconic Farmer (One Hudson City Centre, Hudson). Approximately human epidermoid carcinoma cells (A-431) suspended in 50 µL PBS were injected subcutaneously into the ear of the mice and the ear tumors developed on two of the three mice. 10 days after tumor cell inoculation, OCT imaging of the mouse tumor on the ear was performed before and after 4 fractionated tail vein injections (24 hours apart) of PEGylated gold nanocages (150μL of 1nM solution per injection). The animal experimental procedures in this study were approved by the Institutional Animal Care and Use Committee at the Johns Hopkins University.
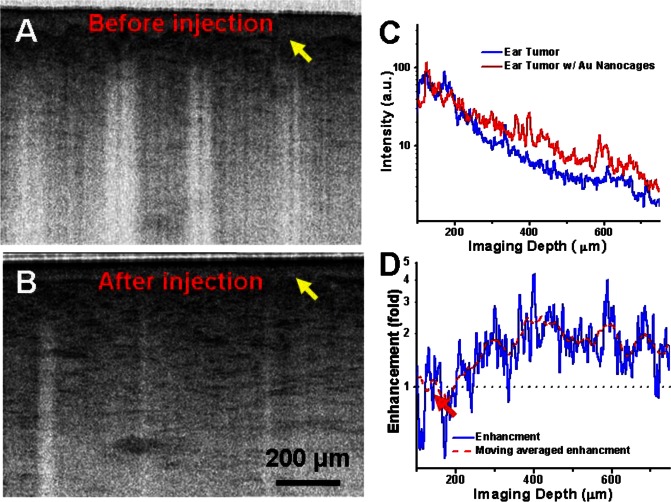
Figures 3(A) and 3(B) show a representative OCT image of the tumor before and after the administration of gold nanocages, respectively, and the corresponding decay curves on a logarithm scale are shown in Fig. 3(C). It is evident that the presence of gold nanocages increases the backscattering in the tumor, thus enhancing OCT imaging contrast. More interestingly, fine structures were able to be observed after the injection of gold nanocages (as shown in Fig. 3(B)). It is noted that the contrast enhancement is approximately ~2.4 dB on average, and to the best of our knowledge, this is the highest OCT contrast enhancement by nanoparticles of a similar size and at a similar concentration. The contrast enhancement (in dB) and its moving average versus imaging depth are shown in Fig. 3(D), which suggest that the accumulation of the gold nanocages started ~70 µm below the epidermis (where the tumor boundary is supposed to be as indicated by the arrows in Figs. 3(A), 3(B) and 3(D)) and reached its peak around 300 µm beneath the surface.
Fig. 3.
(A) In vivo OCT images of a mouse ear tumor (induced with A431 cell line) before (A) and after (B) intravenous injection of gold nanocages, respectively. (C) Depth-dependent OCT intensity plots from the tumor on a logarithm scale before (blue curve) and after (red curve) the administration of gold nanocages. (D) The ratio of the two curves in (C) and its moving-average results on a logarithm scale.
5. Discussion
Several issues need to be considered in order to use the cross-referencing method properly. Firstly, in order to linearly fit the difference curve represented by Eq. (4), the A-scan OCT intensity signals from the reference and the test phantom need to be significantly above the noise floor of the OCT system. An alternative is to choose a segment from the entire depth profile of the OCT intensity.
Secondly, although the method was initially developed for an imaging system with a small NA as discussed in the Algorithm session, it should be applicable, in principle, to a large NA imaging system as well. Instead of using a single backscattering coefficient at 180°, a definite integral of the differential scattering coefficient over the entire collection angle (NA) should be used to get a new parameter k that relates the total scattering coefficient to the backscattering coefficient.
Thirdly, the cross-referencing method assumes an approximation that the difference in the geometric factor function in the test and reference phantom is negligible. In addition to the depth-dependent transparent-medium-equivalent point-spread function [18], also takes into account the scattering effect on the point-spread function in a turbid medium [16]. In theory, would change as the scattering property changes and thus the two ’s would not perfectly cancel out each other in the two A-scan signals (from Eq. (3) to Eq. (4)). However, from what we experimentally observed (see Section 3), the change in was negligible even the scattering coefficient changed by about 2 mm−1 from the reference to test phantom. When using gold nanocages for enhancing OCT imaging contrast, the concentration of the gold nanocages in tissue would be on the order of nM or less considering the small systemic injection volume (100-200 uL) and low concentration (1 nM). The resulted change in scattering coefficient would thus be small (e.g. ) compared to the scattering coefficient of highly scattering biological tissues (i.e. [19]). Hence it is safe to neglect the change in before and after the administration of gold nanocages and consequently the cross-referencing characterization method (Eq. (4)) is applicable.
Moreover, the cross-referencing method (Eq. (4)) also enables semi-quantitative analysis of the OCT contrast enhancement when using contrast agents and thus can provide a general guideline on choosing the optimal concentration and optical properties for nanoparticle-based contrast agents. We notice that there are two competing effects generated by the contrast agents in biological tissue: contrast enhancement (by the backscattering coefficient) and intensity attenuation (by the total extinction coefficient). Here we propose a simple model for semi-quantitatively analyzing the balance between these two effects in order to gain a maximal contrast enhancement. By comparing the OCT intensity signal before and after the administration of contrast agents, we have:
| (6) |
where and are respectively the extinction and backscattering coefficient of the contrast agent, and is the backscattering coefficient of tissue. Substituting and into Eq. (7) where Cand are the molar concentration and extinction cross section of a given contrast agent, respectively, and is the Avogadro constant, we have the following equation:
| (7) |
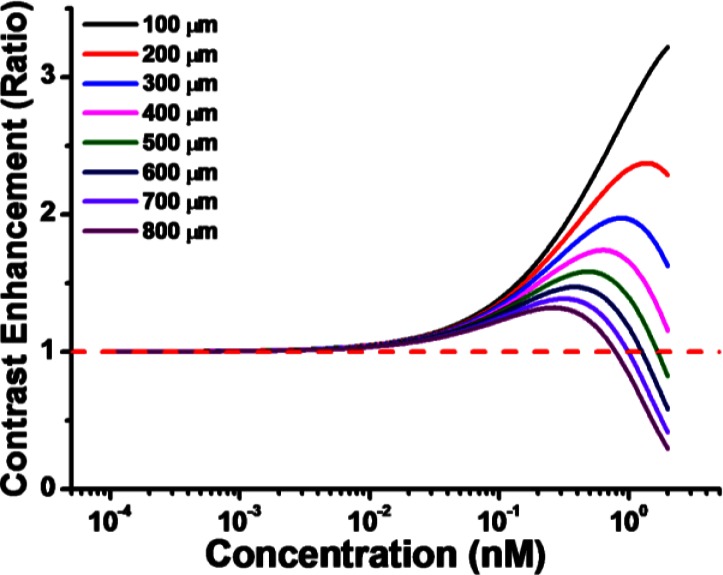
where is the ratio of the scattering to absorption coefficient for the contrast agent and k is the ratio of backscattering to total scattering coefficient of the contrast agent. In order to observe contrast enhancement in tissue, Eq. (7) has to be greater than unity. To perform numerical calculations, we first need to estimate the backscattering coefficient. For most tissues in the NIR region, the backscattering coefficient varies from 0.1 to [20]. And we choose the backscattering coefficient to be here. For the gold nanocages, we have and . With these parameters, the contrast enhancement curves versus contrast agent concentration at different imaging depths were calculated using Eq. (7) and the results are shown in Fig. 4. We find that all the curves start from unity when the concentration is very low (i.e., 1 pM), and the contrast enhancement increases slowly as the concentration of agents increases. When the concentration continues increasing, the contrast enhancement curves at different depths begin to deviate from each other and the contrast starts decreasing versus concentration owing to the increase in the extinction coefficient (and thus signal attenuation) by the contrast agent. As seen in Fig. 4, most of the curves reach their peaks when the concentration is around 0.3-0.4 nM. The peak of contrast enhancement curves decreases as the imaging depth increases, from >3 fold at 100 µm to <1.5 fold at 800 µm. When contrast agent concentration keeps increasing, the contrast enhancement is compromised and eventually it will drop below unity (i.e. negative contrast).
Fig. 4.
The estimation of contrast enhancement with respect to the concentration of OCT contrast agent at different imaging depths.
Equation (7) also shows that better contrast enhancement can be achieved by increasing the parameter and, suggesting the benefit of having a scattering dominating contrast agent (i.e. a large parameter r) and an agent with a large backscattering cross section. For gold nanocages, the overall cross sections of gold nanocages are at least one order of magnitude higher than other OCT contrast agents at the same size due to the unique structure of nanocages [21]. In other words, only a smaller size is needed with gold nanocages compared to other contrast agents for the same cross sections. The small size of gold nanocages in fact leads to a larger ratio k of the backscattering to the total scattering cross section, which is beneficial for OCT contrast enhancement. Furthermore, our newly synthesized gold nanocages are scattering dominant (r>1), which further helps improve the backscattered OCT signal.
6. Conclusion
In summary, we developed a generic cross-referencing method to offer accurate, quick and full characterization of the optical properties of nanoparticles as an OCT contrast agent by using a standard OCT system alone. The accuracy of the method was confirmed by phantom experiments using fused silica nanospheres and predictions by the Mie theory. With the aid of this method, synthesis conditions of gold nanocages were fine-tuned, resulting in scattering dominance in the optical properties for the first time with the ratio of scattering over absorption of about , which was consistent with the results from the integrating sphere measurements. In vivo animal tumor model imaging with systemic administration of the gold nanocages was also performed, demonstrating significant contrast enhancement (i.e. by ~2.4 dB). This generic optical properties characterization method can be, in principle, applied to any other nanoparticle based OCT contrast agents. The same principle can also be used in in vivo tissue imaging to provide a semi-quantitative guideline for choosing a proper concentration of a given contrast agent in order to achieve optimal contrast enhancement.
Acknowledgments
The authors would like to thank Du Le and Dr. Jessica Ramella-Roman at the Department of Biomedical Engineering, Catholic University of America for helping perform the integrating sphere measurements of the gold nanocages. The authors would also like to acknowledge the funding support from the National Institutes of Health (NIH) (R01EB007636). Publication of this article was funded in part by the Open Access Promotion Fund of the Johns Hopkins University Libraries.
References and links
- 1.Barton J. K., Hoying J. B., Sullivan C. J., “Use of microbubbles as an optical coherence tomography contrast agent,” Acad. Radiol. 9(Suppl 1), S52–S55 (2002). 10.1016/S1076-6332(03)80395-1 [DOI] [PubMed] [Google Scholar]
- 2.Cang H., Sun T., Li Z.-Y., Chen J., Wiley B. J., Xia Y., Li X. D., “Gold nanocages as contrast agents for spectroscopic optical coherence tomography,” Opt. Lett. 30(22), 3048–3050 (2005). 10.1364/OL.30.003048 [DOI] [PubMed] [Google Scholar]
- 3.Chen J., Saeki F., Wiley B. J., Cang H., Cobb M. J., Li Z.-Y., Au L., Zhang H., Kimmey M. B., Li X. D., Xia Y., “Gold nanocages: bioconjugation and their potential use as optical imaging contrast agents,” Nano Lett. 5(3), 473–477 (2005). 10.1021/nl047950t [DOI] [PubMed] [Google Scholar]
- 4.Gobin A. M., Lee M. H., Halas N. J., James W. D., Drezek R. A., West J. L., “Near-infrared resonant nanoshells for combined optical imaging and photothermal cancer therapy,” Nano Lett. 7(7), 1929–1934 (2007). 10.1021/nl070610y [DOI] [PubMed] [Google Scholar]
- 5.Lee T. M., Oldenburg A. L., Sitafalwalla S., Marks D. L., Luo W., Toublan F. J.-J., Suslick K. S., Boppart S. A., “Engineered microsphere contrast agents for optical coherence tomography,” Opt. Lett. 28(17), 1546–1548 (2003). 10.1364/OL.28.001546 [DOI] [PubMed] [Google Scholar]
- 6.Troutman T. S., Barton J. K., Romanowski M., “Optical coherence tomography with plasmon resonant nanorods of gold,” Opt. Lett. 32(11), 1438–1440 (2007). 10.1364/OL.32.001438 [DOI] [PubMed] [Google Scholar]
- 7.Xu C., Ye J., Marks D. L., Boppart S. A., “Near-infrared dyes as contrast-enhancing agents for spectroscopic optical coherence tomography,” Opt. Lett. 29(14), 1647–1649 (2004). 10.1364/OL.29.001647 [DOI] [PubMed] [Google Scholar]
- 8.Hao F., Nehl C. L., Hafner J. H., Nordlander P., “Plasmon resonances of a gold nanostar,” Nano Lett. 7(3), 729–732 (2007). 10.1021/nl062969c [DOI] [PubMed] [Google Scholar]
- 9.L. M. Hanssen and K. A. Snail, “Integrating spheres for mid- and near infrared reflection spectroscopy,” in Handbook of Vibrational Spectroscopy, J. M. Chalmers and P. R. Griffiths, eds. (John Wiley & Sons, Ltd, 2002), pp. 1175–1192. [Google Scholar]
- 10.Bosschaart N., Faber D. J., van Leeuwen T. G., Aalders M. C. G., “Measurements of wavelength dependent scattering and backscattering coefficients by low-coherence spectroscopy,” J. Biomed. Opt. 16(3), 030503 (2011). 10.1117/1.3553005 [DOI] [PubMed] [Google Scholar]
- 11.Robles F. E., Wax A., “Separating the scattering and absorption coefficients using the real and imaginary parts of the refractive index with low-coherence interferometry,” Opt. Lett. 35(17), 2843–2845 (2010). 10.1364/OL.35.002843 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Xu C., Marks D., Do M., Boppart S., “Separation of absorption and scattering profiles in spectroscopic optical coherence tomography using a least-squares algorithm,” Opt. Express 12(20), 4790–4803 (2004). 10.1364/OPEX.12.004790 [DOI] [PubMed] [Google Scholar]
- 13.W. Hergert and T. Wriedt, The Mie Theory: Basics and Applications (Springer, 2012). [Google Scholar]
- 14.Draine B. T., Flatau P. J., “Discrete-dipole approximation for scattering calculations,” J. Opt. Soc. Am. A 11(4), 1491–1499 (1994). 10.1364/JOSAA.11.001491 [DOI] [Google Scholar]
- 15.Y. P. Chen, J. F. Xi, J. C. Ramella-Roman, and X. D. Li, “The first scattering-dominant structured gold nanoparticles for enhancing OCT backscattering and imaging contrast,” in Biomedical Optics and 3-D Imaging, OSA Technical Digest (Optical Society of America, 2012), BTu3A.94. [Google Scholar]
- 16.van Leeuwen T. G., Faber D. J., Aalders M. C., “Measurement of the axial point spread function in scattering media using single-mode fiber-based optical coherence tomography,” IEEE J. Sel. Top. Quantum Electron. 9(2), 227–233 (2003). 10.1109/JSTQE.2003.813299 [DOI] [Google Scholar]
- 17.Schmitt J. M., Knuettel A. R., Gandjbakhche A. H., Bonner R. F., “Optical characterization of dense tissues using low-coherence interferometry,” Proc. SPIE 1889, 197–211 (1993). 10.1117/12.155715 [DOI] [Google Scholar]
- 18.Ralston T. S., Marks D. L., Scott Carney P., Boppart S. A., “Interferometric synthetic aperture microscopy,” Nat. Phys. 3(2), 129–134 (2007). 10.1038/nphys514 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.L. V. Wang and H.-I. Wu, Biomedical Optics: Principles and Imaging (Wiley-Interscience, 2007). [Google Scholar]
- 20.Schmitt J. M., Kumar G., “Optical scattering properties of soft tissue: a discrete particle model,” Appl. Opt. 37(13), 2788–2797 (1998). 10.1364/AO.37.002788 [DOI] [PubMed] [Google Scholar]
- 21.Jain P. K., Lee K. S., El-Sayed I. H., El-Sayed M. A., “Calculated absorption and scattering properties of gold nanoparticles of different size, shape, and composition: applications in biological imaging and biomedicine,” J. Phys. Chem. B 110(14), 7238–7248 (2006). 10.1021/jp057170o [DOI] [PubMed] [Google Scholar]