Chiral imaging of collagen by second-harmonic generation circular dichroism

Abstract

We provide evidence that the chirality of collagen can give rise to strong second-harmonic generation circular dichroism (SHG-CD) responses in nonlinear microscopy. Although chirality is an intrinsic structural property of collagen, most of the previous studies ignore that property. We demonstrate chiral imaging of individual collagen fibers by using a laser scanning microscope and type-I collagen from pig ligaments. 100% contrast level of SHG-CD is achieved with sub-micrometer spatial resolution. As a new contrast mechanism for imaging chiral structures in bio-tissues, this technique provides information about collagen morphology and three-dimensional orientation of collagen molecules.

1. Introduction

Chirality, lack of mirror symmetry, is an important and fundamental structural property of matter, and can be extensively found in various biological molecules, such as proteins, nucleic acids, and saccharides. Collagens, which are the most abundant proteins in vertebrates, are composed of three polypeptide strands, and are intrinsically chiral due to their right-handed triple-helical structures [1]. The structural changes of collagen due to misfoldings of the triple helices can be associated with severe diseases [2], so it is important to study those variations of collagens in tissues. In addition, the 3D orientation and arrangement of collagen is strongly associated with biological functions of the tissues. For example, the mechanical properties of cartilage and cornea are highly dependent on the orientation of the embedded collagen molecules [3,4]. The pathological characterization of collagenous fibrosis required precise 3D analysis of local collagen orientations [5]. Furthermore, the 3D structures of collagen molecules in malignant tissues have been found to be significantly different from that in normal tissues [6].

Conventionally, the structural changes of collagens and the subsequent subtle changes in their chiroptical responses can be studied by optical circular dichroism (CD) spectroscopy [7,8]. The contrast in CD arises from different optical absorption for left- and right-hand circularly polarized (LCP/RCP) light. However, the contrast in CD experiments is typically less than 1%, since CD arises from the weak interaction of light with the electric-quadrupole or magnetic-dipole moments of the molecules [8].

Second-harmonic generation (SHG) is a nonlinear optical phenomenon, in which two photons at frequency ω are annihilated in a medium, and a new photon with doubled frequency/energy 2ω is generated. A brief review of SHG in biological tissues can be found in [9]. The fact that collagen fibers exhibit exceptionally strong SHG response was discovered more than 30 years ago [10], and has been extensively studied ever since [6,11–18]. It has also been shown that chirality can give rise to different efficiency of SHG for LCP and RCP light, resulting in SHG-CD responses [19,20]. Because nonlinear optical activity effects are allowed through electric-dipole interactions [21], the contrast of SHG-CD can approach unity, which is beneficial for imaging applications [22–25]. Nevertheless, although the intrinsic chirality of collagens is well known, only a few studies have reported chiroptical SHG responses from collagens [26,27]. The earlier works have either involved only theoretical studies, or have not been applicable to imaging. Only very recently, SHG-CD and two-photon luminescence CD imaging have been demonstrated, but suffered still from poor contrast [25,28].

In this report, we perform SHG-CD microscopy of individual collagen fibers. We show that collagens can give rise to strong SHG-CD responses, with 100% contrast level, under a polarized nonlinear optical microscope. A theoretical model is established for explaining the tensorial SHG responses from collagens, which links the varying SHG-CD responses to the 3D orientation of the fibers. The results show that SHG-CD microscopy can provide 3D molecular information of individual collagen fibers in tissues.

2. Theory

Quantitative calculations of molecular hyperpolarizability tensors of proteins are beyond the reach of current theoretical capabilities and computational power [29]. But recent theoretical and experimental works suggest that the nonlinear responses of proteins can be qualitatively approximated as sums of the nonlinear responses of their elementary building blocks, harmonophores [14,30]. Following these recent advances, we formulate a microscopic model to predict and explain the measured SHG responses from our protein sample. In essence, the macroscopic susceptibility χ⁽²⁾ of the protein is assumed to be the sum of the microscopic hyperpolarizabilities (β) of the harmonophores. This simple additive rule can be assumed to apply when there is no excitonic coupling between the active molecules. We also assume the distances between the harmonophores to be much smaller than wavelength, so that retardation effects can be neglected.

This approach is basically a generalization of the usual connection between the microscopic and macroscopic responses, where instead of averaging over the orientations of several molecules, we consider harmonophores and their relative orientations. We can then write an equation to connect the susceptibility χ⁽²⁾ of an arbitrary macroscopic object to the microscopic responses β as

$${\chi }_{IJK}^{(2)}={\displaystyle \sum _{m=1}^N{\displaystyle \sum _{ijk}{[c_{Ii}{c}_{Jj}{c}_{Kk}{\beta }_{ijk}]}_m,}}$$ (1)

where (I,J,K) and (i,j,k) correspond to the macroscopic and molecular spatial coordinates and factors c_Ii represent the direction cosines that project the responses of the harmonophores to the macroscopic frame. The summation over (i,j,k) is performed over the tensor components of the hyperpolarizability of the m^th harmonophore. The other summation is performed over N harmonophores. With the knowledge of the arrangement of the harmonophores in the material of interest, it is then possible to use Eq. (1) to estimate the susceptibility.

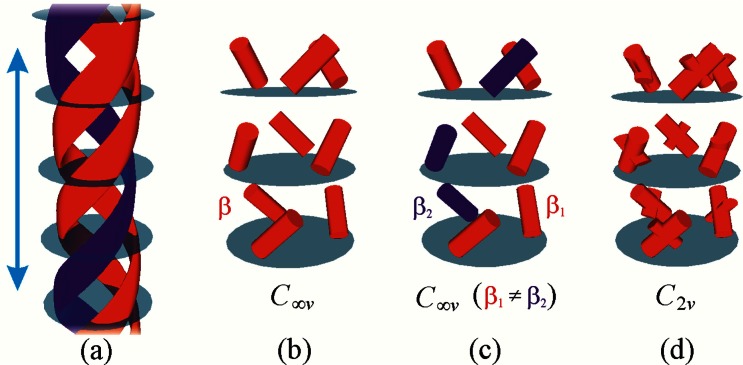
For the case of type-I collagen, the molecular structure is fairly well-known to consist of a left-handed helical polypeptide [α1(I)₂] α2(I) heterotrimer, which forms a right-handed triple helix, as shown in Fig. 1(a). For the current study, we follow the approach of Loison et al. and consider the peptide bonds as our harmonophores [29], which are organized in right-handed triple helical structures, as shown in Fig. 1(b). In the susceptibility calculations, the peptide pitch angle is chosen to be 45° to match recent optical measurements [15,31]. Note that the effects of larger structures, such as super-coils, are not taken into account here.

Fig. 1.

(a) Schematic representation of the collagen triple helix, consisting of a heterotrimer of alpha peptides. The red and blue colors correspond to α1 and α2 chains, respectively. Scale bar corresponds to 10 nm. Model susceptibilities of the collagen were formed by summing up (b) homotrimers or (c) heterotrimers of harmonophores with C_∞ symmetry. Also (d) homotrimers with C_2v symmetry were considered.

In order to get qualitative information on the effects of the symmetry group of the harmonophore to the resulting symmetry of the susceptibility, we considered harmonophores with two simplest symmetries, and the results are shown in Table 1. Here, β₁ and β₂ are the hyperpolarizabilities of the α1 and α2 chains, respectively. β_ijk in Eq. (1) signifies that certain tensor component defined by the indices (i,j,k) while β₁ and β₂ signifies the whole nonlinear tensor. The C_∞v symmetry corresponds to rod-like achiral harmonophores, as illustrated in Figs. 1(b) and 1(c), whereas the C_2v symmetry corresponds to anisotropic but achiral harmonophores, shown in Fig. 1(d).

Table 1. The Symmetry Groups and Corresponding Non-Zero Molecular Hyperpolarizabilities of the Harmonophores Together with the Symmetry Groups of the Calculated Susceptibilities^a.

Symmetry of the harmonophore	Non-zero β components	Symmetry of susceptibility	SHG-CD response
C∞v, (β2 = β1)	zzz, zxx = zyy, xxz = xzx = yyz = yzy	C∞v	no
C∞v, (β2 ≠ β1)	zzz, zxx = zyy, xxz = xzx = yyz = yzy	C∞	yes
C2v, (β2 = β1)	zzz, zxx, zyy, xxz = xzx, yyz = yzy	C∞	yes

^aThe possibility for SHG-CD responses is shown in the last column.

For the case of harmonophores with C_∞v symmetry with equally strong optical responses for the α1 and α2 chains (i.e. β₂ = β₁), the symmetry of the calculated susceptibility is also C_∞v, which is the most commonly assumed symmetry used for analyzing the SHG responses from collagenous samples [32]. For this case, however, no SHG-CD response can occur. On the other hand, if β₂ ≠ β₁, the symmetry of the susceptibility of collagen becomes C_∞, and a non-zero SHG-CD response should be observed.

Please note that in the first column, the symmetry is for a single harmonophore. Therefore, independent of whether β₁ is equal to β₂ or not, the symmetry of a single harmonophore is C_∞v. Nevertheless, the symmetry of the nonlinear susceptibility is related to the ensemble effect of multiple harmonophores in the collagen molecular chain. So the symmetry of the nonlinear susceptibility is different from the symmetry of a single harmonophore.

For the case of anisotropic harmonophores with 180^○ rotational symmetry about the long axis (C_2v symmetry), a SHG-CD response also exists. These calculations reflect how the fine structure of collagen triple-helices might affect the SHG responses. It is interesting to note that in our model, the chirality of collagen is predicted to arise from the helical structures of tropocollagen, and does not thus require chirality of the individual harmonophores. This agrees well with the recent studies on the origin of chiral SHG responses from anisotropic molecular structures [9]. Another noteworthy point is that only the case of isotropic and identical harmonophores, corresponding to a homotrimer structure, will lead to achiral susceptibility of collagen, and thus to a vanishing SHG-CD response.

3. SHG-CD experiment setup

The setup for the home-built laser scanning SHG microscope has been reported elsewhere [33]. An Yb:fiber mode-locked laser (Uranus 005, PolarOnyx, CA) with central wavelength fixed at 1040-nm is used. To generate circularly polarized excitation beam from our linearly polarized laser, a quarter-wave plate (10RP04-λ-32, Newport, US) was inserted before the scanning system. The scanning system was composed of silver-coated mirrors, operated at small angles of incidence in order to keep the incident polarization circular. The purity of circular polarization was measured after focusing the beam with an objective (UPLSAPO 60XW) and consequent collimation with a condenser. For both RCP and LCP, the power ratio between the major and the minor axes of polarizations were better than 1: 1.05.

Anterior cruciate ligaments were harvested from the knees of freshly slaughtered young pigs. Sections of the ligaments were prepared by embedding the ligament explants in an optimal cutting temperature (OCT) compound and sliced on a cryosectioning system. The slice thickness was 10 µm with about 1 mm² area. The specimens were kept frozen. Before experiment, the OCT was rinsed off with saline and the samples were sealed on microscope slides with abundant water.

4. Results and discussions

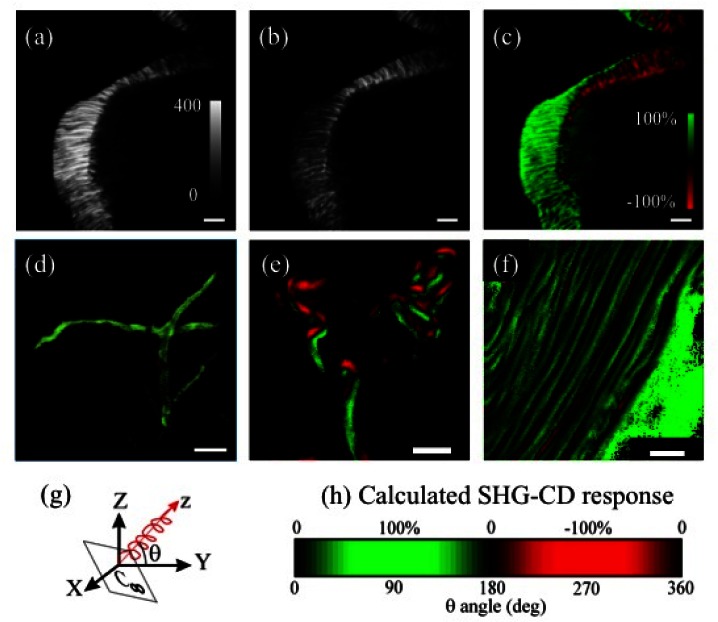
Figures 2(a) and 2(b) show the SHG images of a ligament with LCP and RCP excitations, respectively. The SHG signal mainly originates from type-I collagens in the ligament, and thus no labeling is required [34]. It is clear that the shapes of these two images are the same, but SHG signal using LCP excitation [I_LCP(2ω)] is significantly different from SHG signal using RCP excitation [I_RCP(2ω)]. Similar to conventional CD, the contrast of SHG-CD response is defined as the difference between I_LCP(2ω) and I_RCP(2ω), divided by their average, given as [35]:

$$I_{SHG-CD}=\frac{[I_{LCP}(2\omega )-I_{RCP}(2\omega )]}{[I_{LCP}(2\omega )+I_{RCP}(2\omega )]/2}.$$ (2)

The equation is commonly used for quantifying OA effects when circular input polarizations are used [36]. By calculating I_SHG-CD values pixel-wise from Figs. 2(a) and 2(b), a SHG-CD image of the sample is formed, presented in Fig. 2(c). With the aid of a high numerical aperture (NA = 1.20) water-immersion objective, the lateral and axial resolutions are 340 nm and 860 nm, respectively. The value of SHG-CD contrast reaches 100%, which is at least two orders of magnitude larger value than commonly achieved in conventional CD measurements.

Fig. 2.

(a) and (b) are the lateral (x-y) SHG images of the ligament illuminated by excitations in LCP and RCP, respectively. The gray bars describe the SHG intensity counted by PMT. (c) is the SHG-CD image calculated pixel-wise from (a) and (b) with ImageJ software. The green and red colors indicate the SHG-CD value with positive sign and negative sign, respectively. (d) to (f) show results from different ligaments, demonstrating the reproducibility of SHG-CD responses. All scale bars are 5 μm. (g) θ is defined as the angle between the collagen molecular orientation z and the transverse XY-plane. Z denotes the direction of excitation. (h) Calculated SHG-CD responses as a function of the θ angle.

Compared with a recent work of SHG-CD on collagen [25], our contrast is 10-fold higher. Since SHG-CD response requires that phase differences exist between different tensor components and the imaginary part of the susceptibility should thus be non-zero [37], the responses could be enhanced closer to resonant conditions. It is known that collagen fiber bundles exhibit an autofluorescence peak around 500 nm [38], which is about half of our excitation wavelength. Thus our 10-fold increase for the contrast compared with the previous study might be attributed to the different excitation wavelength. It is also very interesting that there are both positive and negative SHG-CD values in Fig. 2(c), while the signal contrast is quite high.

To confirm the reproducibility and study the origins of the SHG-CD responses, more than 10 independent sample sources were studied. Examples of the results are shown in Figs. 2(d)–2(f). Two crossed fibers are observed in Fig. 2(d) with similar contrast value, showing that the effect of residual linear polarization is diminishing. Figures 2(e) and 2(f) further demonstrate the coexistence of positive and negative SHG-CD values.

One possible explanation for the positive and negative SHG-CD is that the orientation of the fiber affects the value of the SHG-CD. Because the contrast of SHG-CD originates from chirality of collagen fibers, SHG-CD contrast should be maximized (minimized) when input polarization is perpendicular (parallel) to the longitudinal axis of collagen triple helix. That is, we can interpret the axial orientation of local collagen molecules based on SHG-CD contrast. To validate this assumption, SHG-CD responses were calculated using Green’s function approach as a function of the fiber orientation [39]. For simplicity, only free-space Green’s functions were considered. The fiber angle θ is defined as the angle between the long axis of the fiber (z) and the macroscopic XY-plane (the transverse scanning plane), as illustrated in Fig. 2(g). In the calculations, we used relative values of zzz = 1, zxx = zyy = 0.63 and xxz = 0.48 for the non-zero susceptibility components of the fiber, where z was the fiber direction. The values corresponded to previously measured values [15]. For a non-zero SHG-CD responses to occur, a complex chiral component xyz = −0.14-0.19i was iteratively found, resulting in a relatively good agreement with the measurements as seen in Fig. 2(h). To our knowledge, a technique has been recently proposed to provide real part of second order tensor elements [40], but generalization of the technique into the complex domain is still lacking. Our result features an attempt to extract the complex content of optical nonlinearity in collagen.

It is interesting to notice that the calculations with C_∞ symmetry and the given tensor predict the sign changes of SHG-CD responses when the fiber orientation flips from downward to upward. This can be qualitatively understood by e.g. rotating the C_∞ fiber 180 degrees in xz-plane. Then Cartesian coordinates x and z change their sign, but y-component remains unchanged. The tensor components zzz, xxz = yyz, zxx = zyy thus change sign, but the chiral components xyz = -yxz do not. Since the SHG-CD responses are due to interference effects between the achiral and chiral parts of the overall responses, these sign changes of the tensor components explain the sign flip of the SHG-CD responses.

As shown in Fig. 2(c), the experimental image shows the sign flip when the collagen fiber flips in space. Note that by simply looking at the SHG intensity images in Figs. 2(a) and 2(b), no such orientation information can be obtained, unless by resorting to more complicated polarization analysis [41]. Additional experimental SHG-CD data is shown in Figs. 2(e) and 2(f), demonstrating that SHG-CD sign flips seem to be correlated with the fiber flips also in other samples. Based on these results, SHG-CD microscopy provides a sensitive contrast for three-dimensional (3D) collagen molecular orientation, and might even provide more quantitative morphological information if the full complex susceptibility tensor of the collagen would be known.

Since the ellipticity of our circular polarization is less than 5%, the maximum SHG-CD inaccuracy should be less than 10%. We also performed a control experiment by using a 500-μm thick film of lithium niobate (LiNbO₃), which is anisotropic but achiral. In the upper surface, the SHG-CD approaches zero as expected. In the lower surface, the SHG-CD response is still less than 20%, which might be induced by the birefringence of the anisotropic crystal [42]. The anisotropy Δn of LiNbO₃ and collagen is about 0.1 and 3 × 10⁻³, respectively [43,44]. The thickness of our collagen samples is about 10 μm, so the corresponding birefringence phase retardation is less than 0.05 λ for our experimental setup, resulting in negligible polarization rotation effect.

Another potential effect that may reduce the quality of circular polarization is the oblique incidence introduced by laser scanning. Please note that the deflection angle in our scanning system is less than 1°, so the depolarization effect should be negligible. This can be seen in Figs. 2(d) and 2(f), which show nearly uniform SHG-CD values at the extreme angles of the scanning image. In addition, in the result of LiNbO₃ film, SHG-CD is less than 15% both in the center and the corner of the image, manifesting the uniform quality of circular polarization across the image.

Since the SHG-CD values in collagen are much larger than 10%, the SHG-CD signals should arise from chiral structures present in the samples, instead of arising from polarization impurities and sample anisotropy. Given the large values of SHG-CD responses, the effects of linear CD or optical rotatory dispersion from the remaining part of the sample can be ignored. In addition, based on rigorous vector diffraction calculations, the depolarization effect due to tight focusing does not compromise the SHG-CD results. In fact tight focusing increases the coupling of light to the nonlinear tensor of the sample [45].

One major advantage of SHG microscopy is its intrinsic optical sectioning capability. With our setup, both the lateral and the axial resolutions are less than 1-μm, as shown in Fig. 3 (Media 1 ^{(461.6KB, MOV)} ). Our technique reveals the complicated 3D molecular orientation inside a collagen fiber. It is interesting to note that the measured signals in each pixel practically arises from a sub-femtoliter volume, and that the required laser dwell time per pixel can be less than 4 μs. Both the sample volume and integration time in SHG-CD experiment are much less than what is typically required for conventional chiroptical techniques. In traditional techniques, e.g. Raman OA or Rayleigh OA effects have been utilized to study morphological/structural changes in biological systems [7,8], but unfortunately due to poor contrast, these techniques are not well suited for microscopy. Thus high-resolution and fast imaging of chiral molecules becomes possible only with nonlinear chiroptical techniques.

Fig. 3.

Optical sections of SHG-CD in a collagen fiber (Media 1 ^{(461.6KB, MOV)} ).

Note that at a specific wavelength, the positive and negative values of SHG-CD responses do not directly relate to the enantiomerism of the chiral sample. The handedness, as well as the secondary structure of molecules, could be deduced only after acquiring the full SHG-CD spectrum and comparing that with simulations based on quantum mechanical calculations.

The measured non-zero SHG-CD responses show that the intrinsic chirality of collagen, and the non-zero imaginary part of the susceptibility should be considered when SHG responses are analyzed. At this point, though, we cannot distinguish which microscopic model would better correspond to the physical reality, since both models predicting the SHG-CD responses also predict the same overall C_∞ symmetry for the macroscopic susceptibility. Therefore, further theoretical and experimental work is necessary.

4. Summary

We have observed SHG-CD responses from collagens, with a contrast level approaching 100%, a value much larger than conventional CD contrast or previous demonstration [25]. We explain our results qualitatively by proposing SHG models, which take the chirality of collagens into account. In addition, we have demonstrated the potential of utilizing SHG-CD responses as a chirality-sensitive morphological contrast mechanism for tissue imaging. SHG-CD imaging not only provides intrinsic 3D sub-micrometer spatial resolution, but also opens the possibility of determining the local 3D orientation of collagen molecules information. Our work is an important step towards fully understanding the origins of the achieved contrast and towards developing SHG-CD microscopy for biologically relevant applications.