Entangled Valence Electron-Hole Dynamics Revealed by Stimulated Attosecond X-ray Raman Scattering

Abstract

We show that broadband x-ray pulses can create wavepackets of valence electrons and holes localized in the vicinity of a selected atom (nitrogen, oxygen or sulfur in cysteine) by stimulated resonant Raman scattering. The subsequent dynamics reveals highly correlated motions of entangled electrons and hole quasiparticles. This information goes beyond the time-dependent total charge density derived from x-ray diffraction.

X-ray diffraction in crystals provides electron density maps that are widely used to determine high resolution molecular structures. In this technique hard x-ray photons scatter elastically off a static or time-dependent molecular charge density. New attosecond x-ray sources^1–3 have the short duration and high intensity to create resonant, time-resolved excitations of core electrons.⁴ Even though core-excited states are of fundamental interest, their high transition energies and short lifetimes (~ 7.1 fs for nitrogen, ~ 4.9 fs for oxygen,⁵ and ~ 1.1 fs for sulfur⁶) due to Auger decay make them less attractive targets for time-resolved experiments than the valence electronic states which directly participate in ordinary chemical processes. Attosecond resonant x-ray pulses, however, can be used to prepare valence excitations by a second-order inelastic stimulated Raman scattering. The evolution of these states reflects the dynamics of electron-hole excitations in the molecule. The idea draws on the analogy with the optical regime; some of the earliest applications of femtosecond pulses when they became available in the eighties involved the preparation and monitoring of vibrational wavepackets.⁷ Thanks to their broader bandwidth (FWHM 14.2 eV for a 128 as pulse), attosecond pulses can be similarly used to impulsively create and control wavepackets of valence electrons, providing a novel window into the chemical and optical properties of molecules. In the x-ray Raman technique the core excitations merely serve as a fast trigger for the valence excitations in the same why that excited valence excitations act as a trigger for the slower vibrational motions in the optical regime.

Here we demonstrate the possible excitation selectivity offered by recently developed x-ray sources and how by preparing localized particle-hole excitations and monitoring their subsequent quantum evolution they can provide an unprecedented window into the many-body dynamics of valence excitations.

In a stimulated x-ray Raman process, a core electron is excited into an unoccupied virtual orbital for a very short time. A second valence electron is then stimulated to fill the core hole, resulting in a valence electron-hole pair.^8,9 The impulsive x-ray pulse creates a coherent superposition of such pairs, as allowed by its bandwidth. Shaping of the pulse envelopes can be used to further manipulate the wavepacket. The short core-hole lifetime is not a problem, provided the pulse is sufficiently intense and short.

A valence excitation initially localized to a selected atom can be created by tuning the x-ray pulse to be resonant with its core transition

The ground (|g_o〉), core-excited (|e〉) and valence excited (|g′〉) states of cysteine are calculated using Restricted Excitation Window Time-dependent Density Functional Theory (REW-TDDFT)^10–13 calculated using a modified version of NWChem ¹⁴ (unpublished results). We focus on the purely electronic dynamics and neglect nuclear motions. This is justified for short time-scales (< 20 fs). The pulse prepares the molecule in a wavepacket of valence excited states |g′〉

$$\mid \psi (\tau )\rangle =\sum _{g^{\prime }}{\alpha }_{g^{\prime }{g}_o}{e}^{-i{\epsilon }_{g^{\prime }}\tau }\mid g^{\prime }\rangle .$$ (1)

Here α is the effective x-ray polarizability for the stimulated Raman process

$${\alpha }_{j;g^{\prime }{g}^{″}}={\int }_{\infty }^{\infty }\frac{(V_{g^{\prime }e}·V_{e{g}^{″}}){\mathcal{E}}_j^{\ast }({\omega }_2){\mathcal{E}}_j({\omega }_2+{\omega }_{g^{\prime }{g}^{″}})}{{\omega }_2+{\omega }_j-{\omega }_{{eg}^{\prime }}+i{\mathrm{\Gamma }}_e}\text{d}{\omega }_2$$ (2)

where ℰ_j(ω) is the Fourier transform of the temporal envelope of the j’th pulse, V_g′e,V_eg″ are the dipole matrix elements, ω_j is the pulse central frequency, Γ_e is the lifetime decay of the core-excited state and ω_eg′ = ε_e − ε_g′ is the energy difference between |e〉 and |g′〉.

A compact representation of the time-evolving state can be derived using superpositions of pairs of particle-hole natural orbitals^15,16

$$\mid \psi (\tau )\rangle =\sum _{\xi =1}^N{w}_{\xi }(\tau )c_{\xi }^{†}(\tau )d_{\xi }(\tau )\mid g_o\rangle .$$ (3)

We define a creation operator $c_a^{†}$ for an electron at the initially vacant valence orbital φ_a(r), and an annihilation operator c_i for an electron from the occupied valence orbital φ_i(r). $c_{\xi }^{†}(\tau )={\sum }_a{V}_{a,\xi }(\tau )c_a^{†}$ and $d_{\xi }={\sum }_i{U}_{i,\xi }^{\ast }(\tau )c_i$ represent corresponding operators for the natural orbitals ξ. The transformation matrices V_a,_ξ (τ) and U_i,ξ (τ) as well as the coefficients w_ξ(τ) may be obtained by Singular Value Decomposition¹⁷ (SVD). These orbitals provide the most compact representation of the evolving state and therefore depend on time. Each $c_{\xi }^{†}(\tau )d_{\xi }(\tau )$ operator creates a pair of particle (electron) ( $c_{\xi }^{†}$) and hole (d_ξ) natural orbitals. The reduced electron and hole density matrix weights w_ξ(τ) are positive and we use the normalization ${\sum }_{\xi }{w}_{\xi }^2(\tau )=1$.

The net charge-density change measured by x-ray diffraction is the difference of the electron and hole densities. By revealing the electron and hole densities separately, stimulated Raman excitation contains signatures of their correlation and spatial coherence across the molecule; which are not otherwise available. Correlation driven migration of an electron hole in the valence band of a molecule were simulated in earlier studies^18–21 in which ultrafast hole motion was predicted. Those simulations assumed an initial, nonstationary state in which a core hole was prepared manually by simply removing an electron from a core orbital. Here we show how the entangled electron-hole state depends on the attosecond pulse envelope and further examine the dynamics of these coupled quasiparticles.

The spatial distribution of the particle (electron)

$${\sigma }_p(\mathbf{r})=\sum _{\xi }{\left|\sum _a{w}_{\xi }(\tau )V_{\xi ,a}(\tau ){\phi }_a(\mathbf{r})\right|}^2$$ (4)

, and the hole

$${\sigma }_h(\mathbf{r})=\sum _{\xi }{\left|\sum _i{w}_{\xi }(\tau )U_{\xi ,i}(\tau ){\phi }_i(\mathbf{r})\right|}^2,$$ (5)

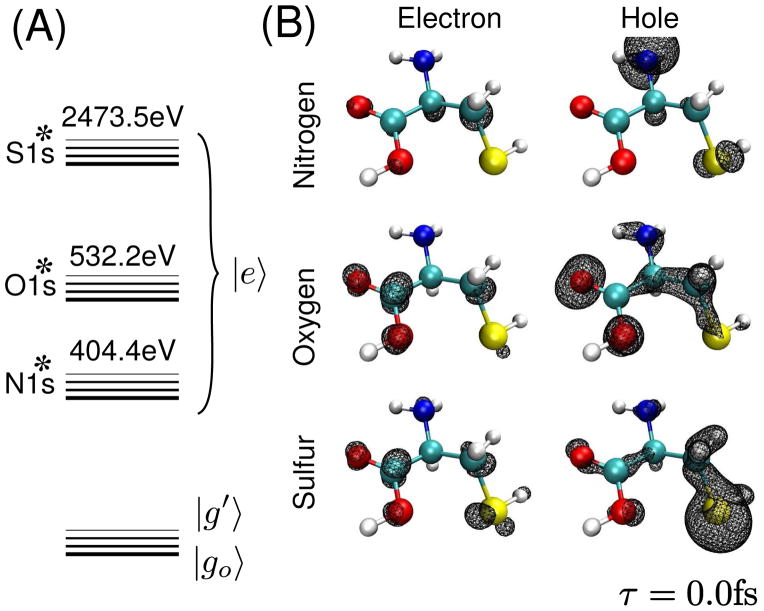
created in the excited cysteine molecule after an x-ray excitation with a Gaussian pulse (FWHM 128 as; 14.2 eV) resonant with either the N, O or S K-edge are shown in Fig. 1. At the nitrogen K-edge, the hole is localized on the nitrogen with little spread onto the neighboring carbon backbone, the particle is spread between the neighboring carboxyl and thiol groups. Excitation at the oxygen creates an electron with a strong π character local to the carboxyl group, and a hole density distributed over σ-type excitations of the carboxyl and backbone. Sulfur excitation produces a particle and a hole with densities spread between the sulfur and the carboxyl group, with the hole showing a projection onto the σ-bond of the amide backbone. Several effects compete in creating these distributions. Selection rules in the K-edge x-ray Raman process favor final states with strong electron-hole projections onto the p orbitals of the resonant core atom. If the exciting pulse bandwidth is very broad, then the particle and hole should have mostly p-orbital excitation character. However, if transition densities with opposite phases on neighboring orbitals occur only at higher energies beyond the exciting pulse bandwidth, or no orbitals with significant projection onto the p-orbitals of the resonant core lie within the bandwidth of the pulse, then these particle or hole densities may be spread over neighboring atoms. Lower energy states should have a high probability for finding the electron on the electronegative carboxyl group, and the hole on either the amine or thiol groups. By adjusting the exciting pulse to cover low energy states, we can select states with this preference.

Figure 1.

(A) The level scheme for the nitrogen (N1s^*), oxygen (O1s^*) and sulfur (N1s^*) core-excited states at the K-edge (B) reduced electron and hole density contours σ_p,h(r) = 0.005 a.u. for a wavepacket directly after excitation with a pulse tuned to the nitrogen (top), oxygen (middle) and sulfur (bottom) K-edges.

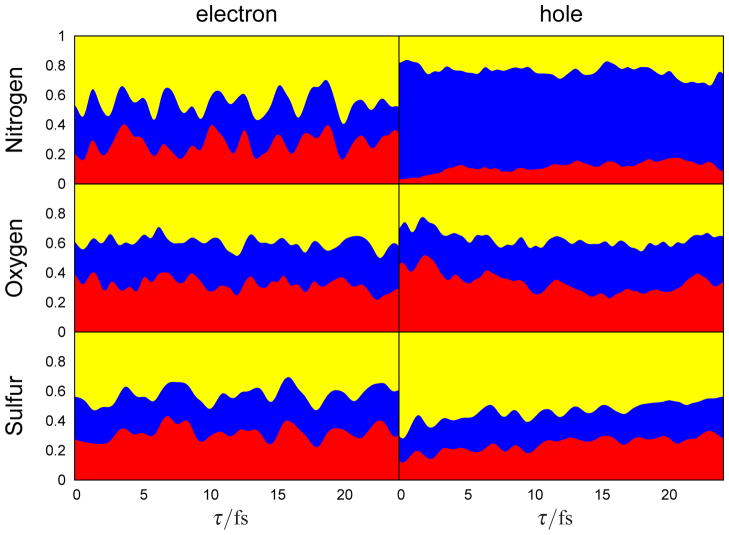
A ~25 fs movie of the time-evolution of the electron and hole densities following the Raman excitation is given in the supplementary information. In all three cases the electron resides preferentially on the carboxyl functional group. A few snapshots of the nitrogen K-edge excited density are shown in Fig. 2. The electron probability distribution moves between the more electronegative carboxyl and thiol groups, while the hole created on the amine group remains there. To visualize the time-evolution of the density for each of the techniques we have divided the nearly tetrahedral cysteine molecule into three regions containing the -CO₂H, -NH₂ and -CH₂SH functional groups, and integrated the reduced densities inside these regions. This projection is depicted in Fig. 3, details are given in the supplementary information. The integrated intensity reveals the charge redistribution in the excited molecule. The particle densities are spread over the molecule, with the odds of finding the electron near the oxygen (39.5%) or sulfur (42.4%) after excitation at these groups slightly greater than in the other regions of the molecule. The nitrogen particle has a smaller density (33.5%) on the amine group than on the carbon in the sulfur group (44.2%). The hole densities show a much stronger projection local to the resonant core: 78.8% for nitrogen, 45.4% for oxygen and 69.6% for sulfur. From the subsequent evolution we find that the hole created after excitation on the nitrogen remains on that functional group, while the holes and particles excited on oxygen and sulfur are more evenly delocalized between the three regions. By comparing the isosurface evolution for the electron probability after excitation at the nitrogen in Fig. 2 with the integrated density in Fig. 3, we see that at times the electron has an equal probability of being localized on either the amine or carboxyl, the isosurface encloses less area near the amine.

Figure 2.

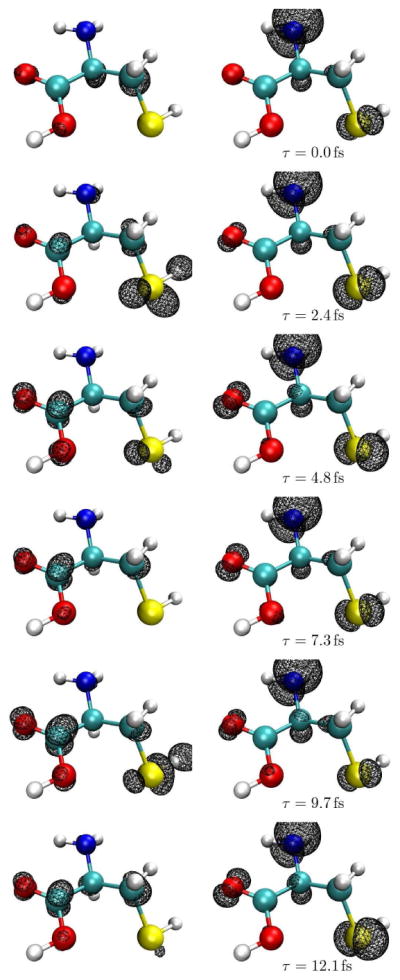
Six snapshots of the movie shown in the supplementary information of the nitrogen pumped wavepacket from τ = 0.0 fs to τ ≃ 12 fs.

Figure 3.

The distribution of the reduced electron (left column) and hole (right) densities over the carboxyl (red), amine (blue) and thiol (yellow) functional groups in cysteine after excitation with x-ray pulses tuned to the nitrogen (top row), oxygen (middle) and sulfur (bottom) K-edges. Computational details of this projection are given in supplementary information.

The Raman excited wavepackets contain a wealth of information regarding the correlated electron-hole motion that goes beyond their charge density alone

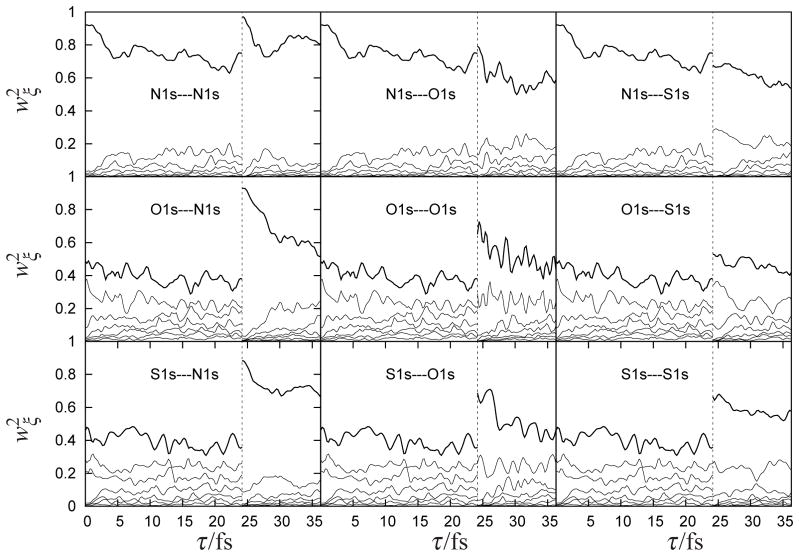
The natural orbital basis provides the most compact representation of electron-hole excitations. Both the number N of pairs included in the wavepacket and the natural orbital shapes themselves evolve with time. N = 1 signifies that the electrons and holes move independently and are uncorrelated; larger N indicates a higher degree of correlation.^22,23 Additional pulses tuned to be resonant with different atoms can further manipulate the electron-hole wavepacket. In the following simulations we applied two pulses separated by a delay τ=24 fs. There are nine possible combinations of two pulses each tuned to either the N, O or S K-edges: N1s—O1s implies that the first pulse is tuned to the nitrogen edge, and the second tuned to oxygen, and so forth. The squares of the time-dependent SVD weights $w_{\xi }^2(\tau )$ shown in Fig. 4 reveal the multi-particle character of the entangled system. Initially the electron and hole are local to the resonant atom, and the time evolution of the natural orbitals reveals how they become delocalized with time. The many-body wavepacket involves several electron-hole pairs and represents a highly entangled state of these quasiparticles. For nitrogen excitation the leading pair has 91% of the total weight, whereas for O and S it is only 49% and 46%, respectively. We have used two measures for the degree of entanglement between the bipartite electron and hole systems. The participation ratio,

Figure 4.

(top)Time variation of the normalized natural orbital SVD weights $w_{\xi }^2(\tau )$ for each particle-hole pair ξ with wavepackets created by pulses at τ = 0 followed by a second pulse at τ = 24.2 fs (dashed line). Each of these pulses can be tuned to be resonant with either the N,O or S K-edges, giving rise to the nine scenarios, as indicated.

$$R^{-1}(\tau )=\frac{1}{{\sum }_{\xi }{w}_{\xi }^4(\tau )}$$ (6)

varies between 1 (uncorrelated electron-hole motion described by a single electron-hole product), and d where d is the number of possible excitations in the basis. The concurrence

$$C(\tau )=\sqrt{2(1-R(\tau ))}$$ (7)

is another measure of entanglement commonly used in the field of quantum information²⁴ and varies between 0 (no entanglement) and $\sqrt{\frac{2(d-1)}{d}}$.

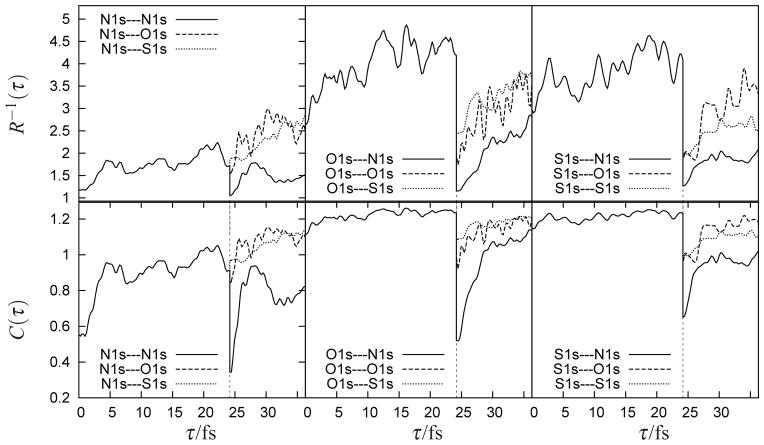
The time evolution of both measures of entanglement are displayed in Fig. 5. All panels show the relaxation from single- to many-excitation character of the wavepacket with time. Of the three resonant cores, nitrogen excitation has the least electron-hole entanglement during the first time-evolution period, and the largest jump in the single-particle character when the second pulse is tuned to this transition, leading to the lowest participation ratio and concurrences. The N1s—O1s panel shows a marked increase in the participation ratios and concurrence after the second pulse relative to the N1s—S1s signal. The same trend is observed if the first pulse is tuned to sulfur (S1s—O1s and S1s—S1s), but not for the O1s—O1s and O1s—S1s configurations, which both have similar participation ratios for the second time-interval.

Figure 5.

Measures of electron-hole entanglement: the time-dependent participation ratio R⁻¹(τ) (top) and the concurrence C(τ) (bottom). Notation and pulse sequence is as in Fig. 4, the first pulse is tuned to the nitrogen (left), oxygen (middle) and sulfur (right) K-edge.

In summary, we have demonstrated the capacity of attosecond x-ray pulses to prepare electronic wavepackets with electron and hole densities local to the resonant core atom. These densities were calculated immediately after the excitation at the nitrogen, oxygen and sulfur K-edges of cysteine, and movies of the time-evolving natural orbitals, the reduced electron and hole densities, and their degree of entanglement (natural orbital participation ratio and concurrence) illustrate the single particle character of the x-ray pulse, and the subsequent dynamic many-body entanglement of quasiparticles. The time-dependent participation ratios show a rapid decay of the single particle-hole character of the excitation and the buildup of electron correlations in the valence excited states. Time-dependent particle hole occupations carry additional information on these correlations through both the reduced densities of the electrons and holes themselves, and the cross-correlation between them. Identifying more detailed measures of these correlations, and designing the optimal stimulated Raman, photoelectron or other experimental techniques to measure this entanglement constitutes an interesting future challenge.