Systems Factorial Technology provides new insights on global–local information processing in autism spectrum disorders

Abstract

Previous studies of global–local processing in autism spectrum disorders (ASDs) have indicated mixed findings, with some evidence of a local processing bias, or preference for detail-level information, and other results suggesting typical global advantage, or preference for the whole or gestalt. Findings resulting from this paradigm have been used to argue for or against a detail focused processing bias in ASDs, and thus have important theoretical implications. We applied Systems Factorial Technology, and the associated Double Factorial Paradigm (both defined in the text), to examine information processing characteristics during a divided attention global–local task in high-functioning individuals with an ASD and typically developing controls. Group data revealed global advantage for both groups, contrary to some current theories of ASDs. Information processing models applied to each participant revealed that task performance, although showing no differences at the group level, was supported by different cognitive mechanisms in ASD participants compared to controls. All control participants demonstrated inhibitory parallel processing and the majority demonstrated a minimum-time stopping rule. In contrast, ASD participants showed exhaustive parallel processing with mild facilitatory interactions between global and local information. Thus our results indicate fundamental differences in the stopping rules and channel dependencies in individuals with an ASD.

1. Introduction

Autism Spectrum Disorders (ASDs) are characterized by a triad of symptoms: impaired social interactions, deficits in communication, and the presence of repetitive behaviours and interests. This spectrum encompasses a wide range of clinical presentations, symptom severity, and associated strengths and disabilities. Autistic Disorder, Asperger’s Disorder, and Pervasive Developmental Disorder, Not Otherwise Specified (DSM-IV-TR American Psychiatric Association, 2000) typically comprise the autism spectrum. Although much research has focused on characterizing atypical behaviour in ASDs, there has been less progress in revealing the cognitive or perceptual mechanisms that underlie the core differences. Given the heterogeneity of the spectrum, observed symptoms and features may well have various explanations. There is growing discussion of multiple “autisms” and thus, an increased focus on identifying and characterizing meaningful subgroups, or “informative phenotypes” (see Szatmari et al., 2007). An important step toward this goal is the elucidation of mechanisms that underlie core features of behaviour. This knowledge may lead to the identification of an informative phenotype of ASD, as well as provide critical information for the development of interventions that can be individually tailored according to this information.

The current study characterizes information processing approaches in ASDs in one standard perceptual task using sophisticated, theoretically driven mathematical modeling techniques. Our central experimental paradigm, the global–local task, has proven extremely useful in basic cognitive and perceptual research, as well as in a wide array of applied studies, including the perceptual–cognitive functioning of ASD patients. Nonetheless, even in the ‘basic’ domain, the information processing mechanisms underpinning performance on this paradigm have never been uncovered. In this investigation, we utilized theory-driven methodologies that can identify these mechanisms, as well as how they differ across individuals and clinical groups. The methodologies are quite powerful and robust since the classes of mathematical models are parameter-free. The latter statement is analogous to being able to perform multivariate ANOVAs without having to assume normality, homogeneity of variances, and so on. Our data and theoretical analyses identify striking differences between ASD and control participants that fail to support previous claims about how individuals with an ASD approach global–local processing.

Atypical perceptual and cognitive processes are a central feature of ASDs and have been the focus of much research in recent years. Although social deficits are the hallmark of ASDs, many previous findings indicate that differences in autism extend beyond social dysfunction and that understanding non-social features may provide important insights into the nature of the disorder. Furthermore, recent research (Happé & Ronald, 2008) indicates that the social and non-social features of ASDs are “fractionable” (i.e., do not necessarily co-occur or have a common genetic basis), suggesting that examining specific non-social differences in ASDs is warranted. It is also possible that there are relationships between some aspects of non-social processing and social deficits that may be elucidated through characterization of basic perceptual and cognitive processes.

Clinically, individuals with an ASD are often highly attuned to details and demonstrate narrow interests and repetitive behaviours. In the laboratory, many studies have examined perceptual processing in ASDs, and results strongly suggest a “detail focused processing style” (for a review, see Happé & Frith, 2006). One explanation for these findings argues that attention is biased toward details, rather than the whole or gestalt, and is referred to as the Weak Central Coherence theory of ASD (WCC; Frith, 1989; Frith & Happé, 1994; Happé & Frith, 2006)). Central coherence refers to the ability to integrate various pieces of information into a meaningful whole. This ability, according to research findings, is “weaker” in those with an ASD relative to their typically developing peers. The bias toward attending to details may occur at the expense of the overall meaning or the whole. Alternatively, some researchers (Mottron, Burack, Iarocci, Belleville, & Enns, 2003; Plaisted, Dobler, Bell, & Davis, 2006) have stated that processing of configurations/gestalt is intact, but individuals with an ASD also demonstrate enhanced processing of features. Although these explanations are quite similar and both can account for many of the reported differences in the processing of details in ASDs, there is a subtle and important difference between them. The WCC theory assumes an atypical bias toward details rather than configurations or gestalt, whereas the “Enhanced Perceptual Functioning” view emphasizes superior processing of details in the context of typical gestalt/configural processing. It is important to note, however, that both theories predict atypical global–local processing in ASDs and that local processing, in particular, would be expected to differ relative to performance by controls. These claims were examined in the current study.

For some tasks, such as visual search, attention to detail lends itself to superior performance in those with an ASD (O’Riordan & Plaisted, 2001; Plaisted, O’Riordan, & Baron-Cohen, 1998). One example that contributed to the development of the WCC theory of ASDs was the finding of superior performance on the Children’s Embedded Figures Test (Shah & Frith, 1983). Participants with an ASD showed more accurate identification of a smaller figure embedded within a meaningful larger figure than control participants, presumably because the larger figure interfered less for the ASD group relative to the controls. It is important to note, however, that not all studies have demonstrated support for WCC (e.g. Rinehart, Bradshaw, Simon, Brereton, & Tonge, 2000; Rutherford, Richards, Moldes, & Sekuler, 2007). These studies suggest typical attention to details, rather than a bias for processing and attending to details, and suggest that there is still much to be learned about the contexts in which a local processing bias may be present or absent in ASDs. Furthermore, it is not yet clear if a detail focused bias or enhanced processing of details is a common feature of individuals with an ASD or present in only a subset.

Perceptual processing of parts versus wholes has been studied extensively in non-clinical populations using hierarchical figures. A robust set of findings supports the global-precedence hypothesis (Navon, 1977) which proposes that people process the global stimulus information prior to or without interference from the local stimulus details (for a review, see Kimchi, 1992). To examine this effect, hierarchical stimuli are employed in a cognitive paradigm often referred to as a global–local task (Navon, 1977). Hierarchical stimuli are visual objects consisting of a global shape formed by an appropriate configuration of local elements. For example, a set of local elements might be the typed character 2 (the size of this text) arranged into a single, larger number 2.

In a typical global–local selective attention task, participants are instructed to identify the local or global level stimuli from a set of two target choices (e.g., are the local elements 1’s or 2’s?). Global–local divided attention tasks require participants to attend to both the global and local levels simultaneously (e.g., is there a 1 present anywhere?). There are two typical findings on these tasks in control participants supporting the global-precedence hypothesis: global advantage and global interference. Global advantage, or global superiority, is the empirical finding that people make faster responses and fewer errors when identifying the global configuration, relative to local elements. Global interference arises from employing a Stroop-like or Garner (1974) interference task, in which the global and local levels may be congruent (e.g. global number 1 composed of local number 1 elements) or incongruent (e.g. global number 1 composed of local number 2 elements). Global interference is the empirical finding that conflicting information within incongruent stimuli results in more errors and slower responses to the local elements, but no such inhibitory interference is evident in the global responses. Together, global interference and global advantage are interpreted as evidence that image processing proceeds in a global-to-local fashion.

Returning to cognitive theories of ASDs, it was proposed that global–local processing in ASDs is characterized by an absence of global precedence, as well as a lack of interaction between global and local information (Mottron & Belleville, 1993). However, global–local experimental findings to date are inconsistent, which may reflect the variability and limitations of the methods employed. Studies that have examined global–local processing of hierarchical stimuli with selective attention tasks have generally found conflicting results. For example, Plaisted, Swettenham, and Rees (1999) found no differences between ASDs and typically developing participants, indicating global advantage and global interference for both groups. Rinehart and colleagues (Rinehart et al., 2000) also demonstrated global advantage and global interference in ASDs. However, they also found that two ASD subgroups (high-functioning autism and Asperger’s Disorder) exhibited slower global response times (RTs) when local information was incongruent than when local information was congruent, indicating a local interference effect. Rinehart and colleagues concluded that their findings provided evidence for a lack of global precedence, as described by Mottron and Belleville (1993). Studies using a divided attention global–local task have shown a lack of global advantage in ASDs (Plaisted et al., 1999) and a deficit in shifting attention from local to global, but not in the opposite direction (Rinehart, Bradshaw, Moss, Brereton, & Tonge, 2001).

Although the few studies that have been completed in ASDs suggest atypical global–local processing, perhaps consistent with a detail focused processing style, there are limitations with the foregoing studies. Importantly, certain essential ingredients of the paradigms used in cognitive psychological investigations (the discussion of which is beyond the scope of the current paper) appear to have been lost in the translation to studies of clinical samples. We are currently pursuing a deeper investigation of these paradigms and their impact on conclusions about global–local perception in ASDs. Furthermore, there is currently no information about the mechanisms that may contribute to atypical global–local processing.

The bias to attend to details appears to be relatively robust in ASDs, but, as we have described, is not always supported by research findings. The theory of WCC, as well as the concept of Enhanced Perceptual Functioning, appeals to ASD researchers and clinicians because these ideas capture important features of ASDs and help explain some of the core symptoms. Given the emphasis on WCC in the current literature, it is critical that we begin to examine this aspect of cognitive processing in ASDs by using rigorous empirical and theoretical approaches. Happé and Frith (2006) suggested that the bias for attending to details versus the gestalt or gist can be viewed as existing on a continuum. Although individuals with an ASD appear to be more likely to have a bias at the details end of this continuum, not all individuals demonstrate this bias (Jarrold & Russell, 1997). This is not surprising given the heterogeneity of the autism spectrum and suggests that studies with a focus on individual performance are warranted. It is important to understand which individuals prefer details and in what contexts, as this information may allow us to predict the situations in which details will be most salient.

The current study is our initial investigation of information processing mechanisms in high-functioning children and adolescents with an ASD. As stated, we utilized a global–local paradigm for this purpose. We investigated four specific features of information processing (see below for a description) using the models and measures of Townsend and colleagues’ Systems Factorial Technology (SFT) and the associated, well-developed Double Factorial Paradigm (DFP; Townsend & Ashby, 1983; Townsend & Nozawa, 1995). It is worth noting that despite the broad usefulness of the global–local paradigm and the multitude of studies that have employed it, up until now, the underlying processing mechanisms and how they operate have not been open to identification even in the general experimental milieu. The present investigation is the first to identify critical features of information processing associated with this valuable paradigm in a clinical sample.

1.1. Human information processing systems

Models of human information processing systems often address questions about four fundamental characteristics of cognitive (perceptual, memory, decision making, etc.) processing: architecture, stopping rule, (in)dependence, and capacity. In the following definitions, we assume that a given cognitive task engages a set of subprocesses, which we refer to as processing channels.² Architecture defines the spatiotemporal arrangement of the channels. The two canonical model architecture classes we consider here are parallel (simultaneously operating channels) and serial (sequentially operating channels). The stopping rule specifies how many channels must complete processing before the system can make a response. Of particular interest to our current work are minimum-time, sometimes called first-terminating, and exhaustive stopping rules. Dependence within the system describes if and how the channels interact with each other. Finally, capacity describes how efficiently the channels/system responds to changes in workload demands. These characteristics will be defined more rigorously later.

The Systems Factorial Technology, and associated Double Factorial Paradigm, provide a rigorous, mathematically well-defined framework for characterizing the above aspects of information processing within a single experiment (Townsend & Ashby, 1983; Townsend & Nozawa, 1995; Townsend & Wenger, 2004). Within the SFT framework, we assume that each facet of a given task (e.g., identification of each object in a visual search display) is subserved by a corresponding processing channel. Given the nature of global–local processing tasks, we will restrict our consideration here to models consisting of two channels, one associated with global object identification and the other dedicated to local feature processing.³ We further assume that physical manipulations of global features and local features influence only the processing speed of the global channel and local channel, respectively. This latter assumption is known as the assumption of selective influence (Dzhafarov, 1997; Schweickert, 1978; Schweickert & Giorgini, 1999; Schweickert, Giorgini, & Dzhafarov, 2000; Townsend, 1984; Townsend & Nozawa, 1995) and we specify it in more detail below.

As noted above, one of the strengths of the SFT approach is its non-parametric nature. The measures that assess architecture, stopping rule, and capacity make no assumptions about the distributions underlying the response time processes. They are based on transformations of the empirical response time distributions. However, the SFT does operate under the aforementioned assumption of selective influence. Stemming from Donders’ (1869/1969) method of subtraction and Sternberg’s (1969) additive factors method, selective influence theoretically specifies that physical (stimulus) variables affect one and only one cognitive process. Let A be the cognitive channel processing physical factor α, and let B be the cognitive channel processing physical factor β. In our modern terminology selective influence means both that (1) physical manipulation of α affects the processing rate of Channel A and physical manipulation of β affects the processing rate of Channel B, and (2) the physical manipulation of α does not affect processing in Channel B, and the physical manipulation of β does not affect processing in Channel A (Ashby & Townsend, 1980; Townsend & Nozawa, 1995; Townsend & Thomas, 1994).

For example, in a simple visual detection task, we can present a single lighted dot to each visual field and further manipulate the luminance of each dot. If the assumption of selective influence is met, changing the brightness of the left dot would not influence the speed of detecting the right dot and vice versa (for empirical results on this task, see Townsend & Nozawa, 1995). Selective influence in a global–local task holds when changes to the global configuration influence only global processing and changes to the local elements affect only local processing. We might anticipate, given previous findings of global interference on local processing (Navon, 1977, 1981), that the assumption of selective influence may not be met under some global–local testing conditions.

More technically, we can empirically assess selective influence by examining response time data, because the actions of experimental factors that change the rates of processing manifest as shifts in the response time cumulative distribution functions (CDFs).⁴ We define influence per se as the measurable changes in response time distributions resulting from manipulation of experimental factors. Influence implies an ordering of the RT distributions, such that factors manipulated to slow processing result in slower response times across the entire distribution. When more than one channel is being assessed by multiple experimental factors, selective influence implies an ordering in the marginal CDF of a given channel while the distributions of the other channels remain unchanged. Let A₁ and A₂ denote the Channel A processing rates when α is at level 1 and level 2, respectively, and denote the marginal CDF of response times for Channel A at a given level by F_Ai(t), for i = 1, 2. If A₁ is faster than A₂, selective influence is supported by F_A1(t) ≤ F_A2(t) or equivalently S_A1(t) ≤ S_A2(t) where S_k(t) = 1 – F_k(t) is the survivor function of process k. We note that while the CDFs may be equal at some time, under selective influence, there exists at least one measurable time interval (t₁, t₂) with t₁ < t₂ where the ordering is strict, so that F_A1(t) > F_A2(t) on that interval.⁵

A necessary, but not sufficient, condition for the assumption of selective influence is the ordering of response time distributions. A system that shows crossings of its CDFs violates the assumption of selective influence and may have strong dependencies between its processing channels. Hence, we tested for violations of selective influence by examining orderings of our empirical CDFs.

There are two types of selective influence violations that can occur, direct and indirect, and both imply some form of dependency in the processing system. First, a direct violation of selective influence on, say, Channel A, occurs when manipulation of factor β affects Channel A without mediation through Channel B. In the global–local testing framework, direct non-selective influence would be present if changes to the global configuration directly affect the processing of local elements or vice versa (for example, at the early input or perceptual encoding stages of processing). Direct non-selective influence results in an input-based correlation between the channel processing times (Townsend & Thomas, 1994), and its presence also negates the assumptions of the Systems Factorial Technology theorems. Careful construction of the stimuli should prevent direct selective influence violations.

Non-selective influence can occur indirectly when physical manipulation of β directly affects only Channel B, but Channel B in turn affects Channel A via interchannel statistical dependence.⁶ Note that channel dependencies can be facilitatory in nature, with one channel accelerating the processing in another, or inhibitory, with one channel slowing another. Either form qualifies as indirect non-selective influence. Note also that stochastic dependencies can occur in both serial and parallel channels. If indirect non-selective influence occurred in a global–local experiment, it would mean that although the global channel processes only global inputs and the local channel processes only local inputs, the speed of processing in one channel affects the speed of the other channel.

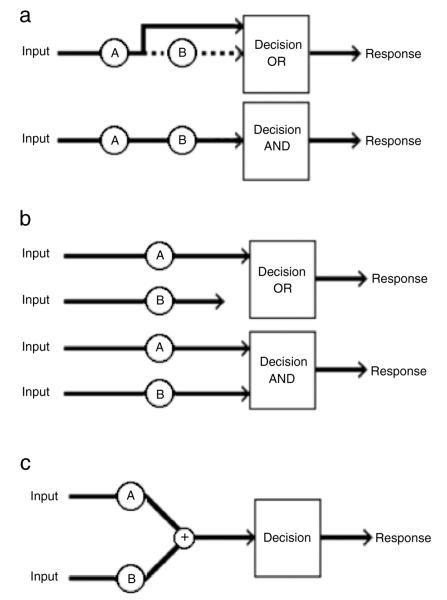
As mentioned above, the architecture of a processing system defines the spatiotemporal arrangement of channels or subprocesses. The canonical architectures considered here are depicted in Fig. 1. If the channels proceed in a sequential manner, with one channel completing its processing before the next begins, then the system possesses a serial architecture (Fig. 1(a)). If, however, the channels operate simultaneously, with decisions made on each channel separately, then the system possesses a parallel architecture (Fig. 1(b)). We also consider a special case of parallel processing known as the coactive architecture, wherein channels operating in parallel feed into a single decision channel (Fig. 1(c)). Responses in the coactive system are based on the pooled information from all the channels rather than individual decisions being made on each channel as observed in standard parallel processing.

Fig. 1.

Schematic illustrations of the three canonical processing architectures: (a) serial, (b) parallel, and (c) coactive. For the serial and parallel models, both the minimum-time (OR) and exhaustive (AND) stopping rules are illustrated. For the serial OR model, the dashed line indicates that completion of the associated item (channel, etc.) was not needed, because the system responded to the first item processed. In the coactive model, decisions are made when the summed information from the two items exceeds some threshold.

Logically distinct from architecture and often governed by task demands, the stopping rule specifies how many channels must reach completion for the system to make a correct response. If only a single channel needs to be completed, such as in the case of visual searching for one target item in a display of only target items, then the system is operating with a minimum-time stopping rule, also known as an OR-gate. When all subprocesses must be completed, such as visual search for a target item in a display of only distractor items, then the system is operating under an exhaustive stopping rule or AND-gate. Note that coactive architectures do not employ one of these traditional stopping rules. In this case, a single decisional threshold exists on the decision channel, and the system responds when the pooled information reaches that threshold.

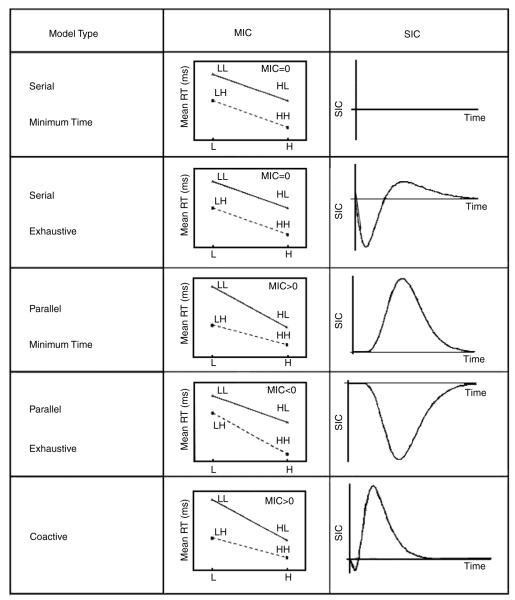
Two measures have been developed to identify the processing architecture and stopping rule: the Mean Interaction Contrast (MIC) and the Survivor Interaction Contrast (SIC) functions (Townsend & Nozawa, 1995). These measures are based on the RT patterns from the processing of double targets whose processing speeds have been factorially manipulated. Factorially combining two targets at two levels of salience creates four critical conditions for assessing architecture. We denote these conditions by HH, HL, LH, and LL, where, in the present global–local task, the first letter refers to the manipulation of global target salience and the second letter indicates the salience manipulation of the local targets. An H “high” salience manipulation facilitates faster target processing, while an L “low” salience manipulation slows processing relative to the H manipulation. Under the assumption of selective influence, double-target processing speeds exhibit the following predictable orders: HH > {HL, LH} > LL. The MIC, then, is defined by the double difference of the double-target mean RTs:

$$\mathit{MIC}=[{\stackrel{‒}{\mathit{RT}}}_{\mathit{LL}}-{\stackrel{‒}{\mathit{RT}}}_{\mathit{LH}}]-[{\stackrel{‒}{\mathit{RT}}}_{\mathit{HL}}-{\stackrel{‒}{\mathit{RT}}}_{\mathit{HH}}].$$ (1)

Analogous to the MIC, the SIC is defined by the double difference of survivor functions for the four factorially manipulated redundant target conditions:

$$\mathit{SIC}\left(t\right)=\left[S_{\mathit{LL}}\right(t)-S_{\mathit{LH}}(t\left)\right]-\left[S_{\mathit{HL}}\right(t)-S_{\mathit{HH}}(t\left)\right].$$ (2)

Note that while the MIC provides a single number, the SIC is a function of time and produces a curve for each model.⁷

Each architecture and stopping rule pair makes a unique prediction for the combination of MIC value and SIC shape. Aside from the coactive architecture, which uses a single decisional threshold, there are four distinct logical combinations of the architectures and stopping rules defined above. These are: (1) serial minimum-time, (2) serial exhaustive, (3) parallel minimum-time, and (4) parallel exhaustive. Fig. 2 illustrates the MIC and SIC signatures for each of these five models with independent channels (Townsend & Nozawa, 1995). Because of their non-parametric nature, these are descriptive model predictions, providing guidelines for the qualitative patterns that may be observed empirically in each participant’s RT data. Again, the five MIC/SIC combinations in Fig. 2 assume selective influence, and in previous applications of these techniques, empirical support for selective influence has been observed consistently (e.g., Fifić, unpublished; Ingvalson & Wenger, 2005; Townsend, Fifić, & Neufeld, 2007; Townsend & Nozawa, 1995; Wenger & Townsend, 2001). Anticipating our results for global–local processing, which appears to lend itself to channel dependencies as evidenced by global interference, we will encounter evidence of indirect non-selective influence through the crossover of a single empirical survivor function. Such violations, termed single-factor reversals, were developed theoretically by Townsend and Thomas (1994); we will return to the implications of the single-factor reversal in the results.

Fig. 2.

MIC and SIC function predictions for the four combinations of parallel and serial processing architectures with minimum-time and exhaustive stopping rules, as well as the predictions for the coactive architecture. MIC alone cannot distinguish between minimum-time and exhaustive serial models (both MIC = 0), nor can it distinguish parallel minimum-time and coactive processing (both MIC > 0). The SIC provides a unique signature over time for each model. Note that the abscissas for the MIC plots give the manipulations on experimental Factor 1, and the solid and dashed lines in each plot indicate the manipulations on experimental Factor 2. The full factorial combination of these factors produces the four critical stimuli conditions (HH, HL, LH, LL) for the MIC and SIC measures. These basic predictions assume independent processing of two channels under the assumption of selective influence (see Townsend & Nozawa, 1995, for more details).

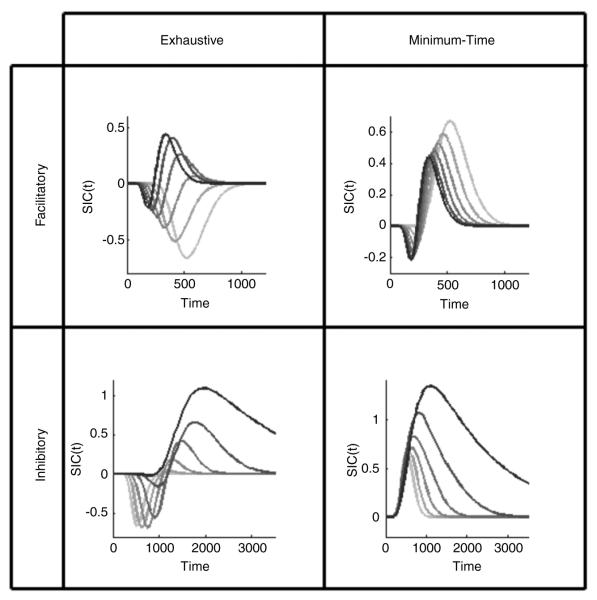
As discussed above, indirect non-selective influence occurs through channel dependencies. In order to then model the processing systems under non-selective influence, we applied the theory of parallel interactive processing (Townsend & Wenger, 2004). A lack of evidence from both our current results and a group of adult controls (Blaha, Johnson, & Townsend, 2007) for serial processing suggests we may reasonably restrict ourselves to parallel interactive models. Interactive parallel processing is defined by the presence of stochastic dependencies between parallel processing channels (Townsend & Wenger, 2004). These systems differ from the aforementioned coactive processing models in that the interactive parallel models are still defined with separate decision mechanisms for each channel. Allowing interactions between parallel channels results in a wide range of SIC predictions. For example, as can be seen in Fig. 3, both inhibitory and facilitatory exhaustive models with minimal to moderate interactions can produce entirely negative SIC functions or S-shaped SIC functions that have a large negativity followed by a small positivity. Under high interactions, exhaustive models produce an S-shaped SIC similar to the coactive shape in Fig. 2 (for more detailed model predictions, see Eidels, Houpt, Pei, Altieri, & Townsend, in preparation). More detail on the behaviours of interactive parallel processing models will be presented in the Results.

Fig. 3.

Range of SIC predictions for two-channel interactive parallel models. Data were simulated by the Poisson parallel interactive model (PPIM), which defines each channel to be a Poisson accumulator. Channels interact by probabilistically sharing information. Curve darkness corresponds to the degree of interaction in each model. The lightest gray curve in each plot represents the prediction for independent processing (probability of interaction equals zero), matching the parallel minimum-time and parallel exhaustive predictions shown in Fig. 2. The black curve represents the highest possible degree of interaction (probability of interaction equals one). For details of the PPIM see the Appendix and Eidels et al. (in preparation).

In addition to architecture, stopping rule and processing dependence, we can use SFT to evaluate the system’s workload capacity, which describes the efficiency of processing as the amount of work to be done (i.e., the number of channels operating) increases. If, as the number of active target-present channels increases, processing rates within each channel are unchanged, the system is described as exhibiting unlimited capacity at the channel level. If channel processing slows under increasing workload, the system is described as limited in capacity, and if processing speeds up, the system is said to exhibit super-capacity (Townsend, 1972, 1974; Townsend & Ashby, 1978, 1983; Wenger & Townsend, 2000).

We measure processing workload capacity by the capacity coefficient ratio (Townsend & Nozawa, 1995; Townsend & Wenger, 2004; Wenger & Townsend, 2000), defined for global–local processing by

$$C\left(t\right)=\frac{H_{\text{Double}}\left(t\right)}{H_{\text{Global}}\left(t\right)+H_{\text{Local}}\left(t\right)}$$ (3)

where $H_i\left(t\right)={\int }_0^t{h}_i\left(\tau \right)\mathrm{d}\tau$ is the cumulative hazard function for target condition i.⁸ The hazard function $h\left(t\right)=\frac{f\left(t\right)}{S\left(t\right)}$ defines the conditional probability that processing completes at time t given that the system has not yet finished processing before time t. While the hazard function provides a measure of instantaneous energy (termed “power” in physics) in the system at each point of time, the cumulative hazard function provides a measure of the dispersed energy or total amount of work completed by the system at each point in time. The capacity coefficient, then, provides a comparison of the amount of work that is completed by the system while processing double targets (here, targets at both the global and local level) with the summed amount of work that is completed in the same amount of time by each single target processed individually. The denominator is the prediction made by an unlimited capacity, independent parallel (UCIP) model, providing an unlimited capacity efficiency benchmark: C(t) = 1. This type of processing seems closest to what is generally meant by the term “parallel processing”. Thus, we accept this variety as exemplifying a standard parallel model.

C(t) provides a fine-grained indicator of capacity over the entire range of RTs. As mentioned above, if C(t) = 1, the work completed in t time on double targets was equal to the summed amount of work completed on each of the single targets in the same amount of time.⁹ This is the case of unlimited capacity, and again it implies that the system is acting like a standard parallel model in terms of its workload efficiency. If C(t) < 1, processing is limited in capacity. Finally, if C(t) > 1, then processing is super-capacity. Note that capacity hovering around C(t) = ½ can be caused by a serial system, working on global, then local levels or vice versa; or, C(t) = ½ could be associated with a parallel system which divides up a fixed resource across the two operating channels, one local, and the other global (e.g. Townsend & Nozawa, 1995; Townsend & Wenger, 2004). Examining C(t) together with the MIC/SIC tests of architecture allows us to disambiguate these possibilities.

2. Method

To model the information processing system supporting hierarchical form processing, we adapted the Double Factorial Paradigm (DFP) for divided attention identification of global and local stimulus features. New compound arrows were designed according to the DFP criteria. The first target factor manipulated was the presence of a target right-pointing arrow at either the global or local stimulus level or both. The absence of a target at either level was the presence of a neutral (dash-shaped) distractor. This first factor, the number of targets present/absent, provides the workload manipulation to determine the capacity of the global–local processing system. The second factorial manipulation was the salience of the target arrows relative to the shape of the distractor dash. This second factor enables the assessment of processing architecture by modeling the responses to the redundant target trials. We employed a basic divided attention OR-decision task (see Townsend & Ashby, 1983; Townsend & Nozawa, 1995). We did not employ Stroop-like incongruent distractors (left-pointing arrows), as our goal was to minimize perceptual and cognitive interference (i.e., to minimize possible dependence) in modeling the basic structures of the global–local processing system.

2.1. Participants

Participants were 10 high-functioning adolescents and young adults with a diagnosis of an autism spectrum disorder (ASD; 6 males, 4 females) and 11 typically developing controls (5 males, 6 females) matched for age and cognitive ability (see Table 1). Diagnoses were established according to the Autism Diagnostic Interview-Revised (ADI-R; Lord, Rutter, & Le Couteur, 1994) and the Diagnostic and Statistical Manual for Psychiatric Disorders, Fourth Edition, Text Revision (DSM-IV-TR; American Psychiatric Association, 2000). The groups were similar in age, gender composition, and estimated intellectual abilities (Wechsler Abbreviated Scale of Intelligence; Wechsler, 1999). In addition, we utilized a parent-report (Baron-Cohen, Wheelwright, Skinner, Martin, & Clubley, 2001) and self-report (Baron-Cohen, Hoekstra, Knickmeyer, & Wheelwright, 2006) version of the Autism Spectrum Quotient (AQ) to gather information about autism symptom severity. As expected, the ASD group means were significantly higher than controls, indicating more symptoms of autism, on both versions of this measure. Exclusion criteria for both groups included parent- or self-report of histories of significant head trauma, major neurological disorders, lack of normal or corrected-to-normal vision, and systemic diseases that might affect the central nervous system.

Table 1.

Mean and standard deviation of age, WASI scores, and AQ parent- and self-report.

Measure	ASD group		Control group		t-value	P-value
	Mean	SD	Mean	SD
Age (years)	16.3	2.3	14.3	2.6	1.86	.08
WASI two-subtest IQ	112.4	9.6	114.6	10.3	.45	.66
Vocabulary (t-score)	59.9	8.4	61.2	7.5	.41	.73
Matrix reasoning (t-score)	54.2	6.3	55.4	6.4	.36	.69
AQ parent-report	34.3	3.6	12.7	6.0	9.22	<.001
AQ self-report	21.8	7.5	15.1	3.8	2.54	<.05

WASI = Wechsler Abbreviated Scale of Intelligence (Wechsler, 1999); AQ = Autism Spectrum Quotient (Baron-Cohen et al., 2006, 2001).

2.2. Stimuli and apparatus

Visual stimuli were presented on a 17 inch Dell Trinitron monitor (refresh rate ≈ 100 Hz), and responses were made using a standard two-button mouse. A Dell Intel Pentium II computer controlled stimulus presentation and recorded responses using DMDX software.¹⁰

The hierarchical images were large (global) arrows composed of smaller (local) arrows. The arrow shapes were either a right-pointing arrow or a dash. At the viewing distance of 50 cm, global elements subtended a horizontal visual angle ranging from 3.88 degrees (global dash) to 4.98 degrees (global high salience arrow). All global objects subtended a vertical visual angle of 1.48 degrees. Each local element subtended 0.55 by 0.37 horizontal by vertical degrees of visual angle.

The first factorial manipulation was the presence or absence of an arrow. Consequently, we used all combinations of global and local right-pointing arrows mixed with global and local dashes, as seen in Fig. 4. The absence of a right-pointing arrow was defined by the presence of a dash. Thus, stimuli either contained no targets (dash composed of dashes), a single target (global arrow with local dashes or global dash with local arrows), or double targets (global arrow consisting of local arrows).

Fig. 4.

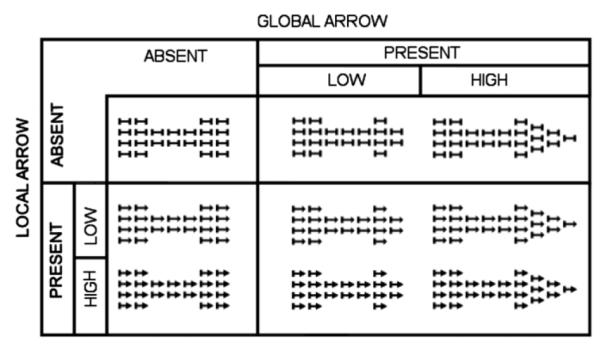
DFP stimuli. Targets were right-pointing arrows. Factor 1 was the presence/absence of a right-pointing arrow at the local and global levels. The single-target stimuli were those containing either Local Arrow Present only or Global Arrow Present only (the upper right and lower left quadrants). The lower right quadrant shows the double-target stimuli. Factor 2 was a salience manipulation of the arrows, where high salience arrows were easily distinguished from dashes (arrow absent) and low salience arrows were more difficult to distinguish due to their similarity to the dashes. Factorial combinations of both arrow presence and arrow salience form the critical conditions for SFT measures.

The second factorial manipulation was the salience of the arrows relative to the dashes. Low salience arrows were right-pointing arrows visually similar to the shape of the dash; high salience arrows had a more distinct arrow shape, including a longer point. Salience manipulations influenced processing speed, which allowed us to directly assess both the processing architecture and stopping rule. High salience arrows encourage faster processing than low salience arrows, because they are easier to identify.

Fig. 4 depicts the full set of double-factorial stimuli, including all factorial combinations of arrows present/absent and arrow salience. As shown here, the stimuli were black figures presented on a white background.

2.3. Procedure

Participants were asked to complete a standard divided attention, or OR-gate, task in which all stimuli containing a target (a right-pointing arrow of any salience at either the global or local stimulus level) mapped to a target-present response, and the stimulus containing only distractors (dashes) mapped to a target-absent response. Participants were instructed to respond ‘yes’ with a right mouse button press if a right-pointing arrow was present at any level (global or local or both) in the stimulus, and ‘no’ with a left mouse button press if no arrows were present (the global dash composed of local dashes).

A single trial began with an approximately 80 ms tone and central fixation. Immediately following this, a single stimulus was randomly presented either at fixation or in one of four off-centered locations within 7.94 by 3.7 horizontal by vertical degrees of fixation. Stimuli were presented for 65 ms, and then replaced by a blank screen until a mouse button response was made. When an incorrect response was made, the word “wrong” was displayed for 2400 ms; no feedback was given when a correct response was made. The blank screen inter-stimulus interval (ISI) was 1000 ms.

All participants completed 2560 trials in total. These trials were presented in four separate runs, with each run containing 4 blocks of 160 trials. Typically, a participant completed the study in two separate testing sessions that comprised two runs (8 blocks) of the task. Within each block, the prior probabilities of target-absent, global target only, local target only, and double-target trials were equated, as were the four types of double-target stimuli and the high and low salience stimuli for the single-target trials.

At the beginning of each testing session, participants completed two blocks of practice trials. In the first block of 27 trials, stimuli were presented centrally and remained on screen until a response was made. In the second block of 27 practice trials, stimuli were presented in the testing manner described above. If participants had a practice error rate over 5%, they repeated the two practice blocks.

2.4. Data analysis

Global advantage at the group level was assessed by repeated measures analysis of variance (ANOVA) with the within-subjects factor of Target Location (Local Only, Global Only, Double Targets) and the between-subjects factor of Group (ASD, Controls). Repeated measures ANOVAs were applied to both the group-averaged RT data and the group-averaged error rates. Individual participant global RT advantage was assessed by three two-sample, two-tailed Kolmogorov–Smirnov tests for differences in CDFs (Double Targets v. Local Only, Double Targets v. Global Only, Local Only v. Global Only).¹¹ Individual participant error rates were not analyzed because individual error rates were too low to permit meaningful comparisons.

Evidence for selective influence was assessed by a series of non-parametric two-sample, one-tailed Kolmogorov–Smirnov tests between pairs of double-target conditions (denoted HH, HL, LH, LL). Under the assumption of selective influence, double-target RT survivor functions exhibit the ordering S_HH (t) ≤ {S_HL(t), S_LH (t)} ≤ S_LL(t), which translates into five distinct orderings that must be tested. In the two-sample Kolmogorov–Smirnov test, the null hypothesis is that two empirical distributions are equal, and the alternative is that the two distributions are ordered in some way. To assess selective influence, we performed the following set of tests for each participant individually:

1. H₀: S_HH(t) = S_HL(t)v:H_a: S_HH(t) < S_HL(t),

2. H₀: S_HH(t) = S_LH (t)v:H_a: S_HH(t) < S_LH (t),

3. H₀: S_HH(t) = S_LL(t)v:H_a: S_HH(t) < S_LL(t),

4. H₀: S_HL(t) = S_LL(t)v:H_a: S_HL(t) < S_LL(t),

5. H₀: S_LH(t) = S_LL(t)v:H_a: S_LH(t) < S_LL(t).

A significant Kolmogorov–Smirnov test statistic, rejecting the null hypothesis, provides evidence supporting the assumption of selective influence. Kolmogorov–Smirnov test statistics and exact p-values were calculated using MATLAB.

All Systems Factorial Technology measures, including C(t), mean interaction contrast and survivor interaction contrast defined above, were applied to individual participants’ response time data.

3. Results

3.1. Group-averaged results

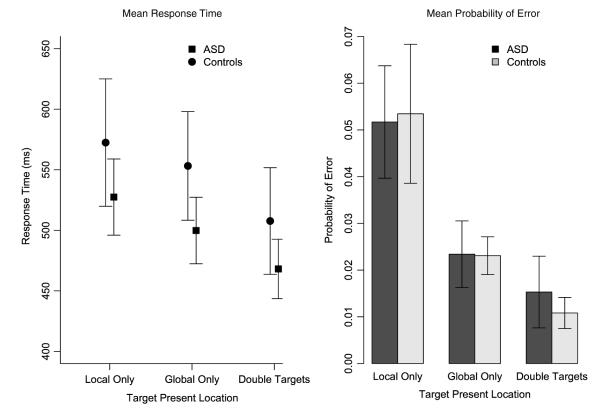
Mean response time (RT) results are plotted in Fig. 5. There was a significant effect of Target Location (F (2, 38) = 57.14, p < .001). Post hoc paired t-tests indicated that responses to Global Only stimuli (${\stackrel{‒}{\mathit{RT}}}_{\text{Global}}=527.8\mathrm{ms}$) were significantly faster than responses to Local Only stimuli (${\stackrel{‒}{\mathit{RT}}}_{\text{Local}}=551.0\mathrm{ms}$; t(20) = 3.54, p = 0.001). Responses to Double Targets (${\stackrel{‒}{\mathit{RT}}}_{\text{Double}}=488.8\mathrm{ms}$) were significantly faster than both Local Only targets (t(20) = 9.12, p < 0.001) and Global Only targets (t(20) = 11.09, p = 0.001). There was no difference between the mean RTs of the groups (F (1, 19) = 0.67, p = 0.42), and there was not a significant interaction of Target Location and Group (F (2, 38) = 0.69, p = 0.51). Thus, at the group level, both the ASD and control groups demonstrated global advantage. Both groups also showed a decrease in RT, or redundancy gain, when targets were present at both the global and local levels compared to targets presented at either level alone.

Fig. 5.

Group-averaged mean RT results and group-averaged mean probability of error for all target-present conditions (Local Arrows Only, Global Arrow Only, Double Target (Redundant) Arrows). Error bars show ± one standard error of the mean.

Mean probabilities of error are plotted in Fig. 5. There was a significant effect of Target Location (F (2, 38) = 16.64, p < 0.001). Post hoc paired t-tests show that significantly more errors were made on Local Only trials (${\stackrel{‒}{E}}_{\text{Local}}=0.053$) than on both Global Only trials (${\stackrel{‒}{E}}_{\text{Global}}=0.023$; t(20) = 3.78, p < 0.001) and Double-Target trials (${\stackrel{‒}{E}}_{\text{Double}}=0.013$; t(20) 4.48 p < 0.001) Significantly more errors were made on Global Only trials than on Double-Target trials (t(20) = 3.89, p < 0.001). There was no difference in the probabilities of error between Group (F (1, 19) = 0.01, p = 0.9), and there was not a significant interaction of Target Location and Group (F (2, 38) = 0.10, p = 0.91).

3.2. Individual analyses and models

Results of the individual participant analyses are summarized in Tables 2 and 3.

Table 2.

Single-target versus double-target individual analyses.

	RT distribution ordering			Capacity
	Double v. Global Only	Double v. Local Only	Global Only v. Local Only
ASD1	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) > FLocal(t)***	Limited
ASD2	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) > FLocal(t)***	Super→Limited
ASD3	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) > FLocal(t)**	Super→Limited
ASD4	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) > FLocal(t)*	Limited
ASD5	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) > FLocal(t)***	Super→Limited
ASD6	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) ≈ FLocal(t)	Super→Limited
ASD7	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) ≈ FLocal(t)	Limited
ASD8	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) > FLocal(t)***	Super→Limited
ASD9	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) > FLocal(t)***	Super→Limited
ASD10	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) > FLocal(t)***	Super→Limited
CON1	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) > FLocal(t)***	Limited
CON2	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) > FLocal(t)***	Limited
CON3	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) ≈ FLocal(t)	Limited
CON4	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) > FLocal(t)*	Limited
CON5	FDouble(t) > FGlobal(t)**	FDouble(t) > FLocal(t)***	FGlobal(t) < FLocal(t)***	Limited→Unlimited
CON6	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) > FLocal(t)***	Super→Limited
CON7	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) > FLocal(t)*	Limited
CON8	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) > FLocal(t)***	Super→Limited
CON9	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) < FLocal(t)*	Limited
CON10	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) < FLocal(t)*	Limited
CON11	FDouble(t) > FGlobal(t)***	FDouble(t) > FLocal(t)***	FGlobal(t) < FLocal(t)*	Limited

Note that the arrow→indicates the progression of time, t → ∞, over the range of RTs.

^*p < 0.15

^**p < 0.05

^***p < 0.01

Table 3.

Double-target trial individual analyses.

	S(t) ordering	MIC	SIC	Candidate systems
ASD1	Predicted ordering	Overadditive	S-shaped Overadditive	Coactive Facilitatory parallel exhaustive
ASD2	Predicted ordering	Overadditive	S-shaped Overadditive	Coactive Facilitatory parallel exhaustive
ASD3	Predicted ordering	Overadditive	S-shaped Overadditive	Coactive Facilitatory parallel exhaustive
ASD4	Predicted ordering	Overadditive	S-shaped Overadditive	Coactive Facilitatory parallel exhaustive
ASD5	Predicted ordering	Underadditive	S-shaped Underadditive	Facilitatory parallel exhaustive
ASD6	Multiple S(t) crossings	Crossover	Positive	Cannot conclude
ASD7	Multiple S(t) crossings	Crossover	Positive	Cannot conclude
ASD8	Predicted ordering	Overadditive	Positive	Coactive Facilitatory parallel exhaustive
ASD9	Predicted ordering	Underadditive	S-shaped Underadditive	Facilitatory parallel exhaustive
ASD10	Multiple S(t) crossings	Crossover	Positive	Cannot conclude
CON1	Crossing type II	Underadditive ${\stackrel{‒}{\mathit{RT}}}_{\mathit{LL}}={\stackrel{‒}{\mathit{RT}}}_{\mathit{LH}}$	Pos→Neg Underadditive	Inhibitory parallel exhaustive
CON2	Crossing type I	Crossover	Positive	Inhibitory parallel minimum-time
CON3	Crossing type I	Crossover	Positive	Inhibitory parallel minimum-time
CON4	Crossing type I	Crossover	Neg→Pos→Neg	Inhibitory parallel minimum-time
CON5	Crossing type I	Overadditive ${\stackrel{‒}{\mathit{RT}}}_{\mathit{HL}}={\stackrel{‒}{\mathit{RT}}}_{\mathit{HH}}$	Positive	Inhibitory parallel minimum-time
CON6	Crossing type I	Crossover	Neg→Pos→Neg	inhibitory parallel minimum-time
CON7	Crossing type I	Crossover	Neg→Pos→Neg	Inhibitory parallel minimum-time
CON8	Crossing type I	Crossover	Positive	Inhibitory parallel minimum-time
CON9	Crossing type I	Overadditive ${\stackrel{‒}{\mathit{RT}}}_{\mathit{HL}}={\stackrel{‒}{\mathit{RT}}}_{\mathit{HH}}$ ${\stackrel{‒}{\mathit{RT}}}_{\mathit{LH}}={\stackrel{‒}{\mathit{RT}}}_{\mathit{LL}}$	S-shaped Overadditive	Inhibitory parallel minimum-time
CON10	Crossing type I	Crossover	S-shaped Overadditive	Inhibitory parallel minimum-time Inhibitory parallel exhaustive
CON11	Crossing type II	Crossover	Negative	Inhibitory parallel exhaustive

Note that the arrow→indicates the progression of time, t → ∞, over the range of RTs.

Predicted ordering: S_HH(t) ≤ S_HL(t) ≤ S_LH(t) ≤ S_LL(t).

Crossing type I: S_HH(t) crosses S_HL(t) ≤ S_LH(t) ≤ S_LL(t).

Crossing type II: S_HH(t) ≤ S_HL(t) ≤ S_LH(t) crosses S_LL(t).

Global advantage and redundancy gain

All participants exhibited a response time (RT) redundancy gain at the cumulative distribution level, where F_Double(t) > F_Global(t) and F_Double(t) > F_Local(t). Eight of ten ASD participants exhibited a global RT advantage at the distribution level, with F_Global(t) > F_Local(t). The remaining two participants showed at least a marginal global RT advantage at the mean level (ASD6: ${\stackrel{‒}{\mathit{RT}}}_{\text{Global}}=393.1$, ${\stackrel{‒}{\mathit{RT}}}_{\text{Local}}=401.5$, t(1154) = 1.13, p < 0.13; ASD7: ${\stackrel{‒}{\mathit{RT}}}_{\text{Global}}=435.4$, ${\stackrel{‒}{\mathit{RT}}}_{\text{Local}}=449.9$ t(1222) = 0.83, p = 0.21). Only six of 11 controls exhibited a global RT advantage with at least marginal significance. One control exhibited F_Global(t) = F_Local(t) at the distribution level, and a non-significant difference at the mean level (CON3: ${\stackrel{‒}{\mathit{RT}}}_{\text{Global}}=656.9$, ${\stackrel{‒}{\mathit{RT}}}_{\text{Local}}=669.9$, t(1222) = 0.83, p = 0.21). Four controls showed a reversal such that F_Global(t) < F_Local(t) with at least marginal significance at the distribution level. Thus, global advantage did not hold for several individuals in the control group.

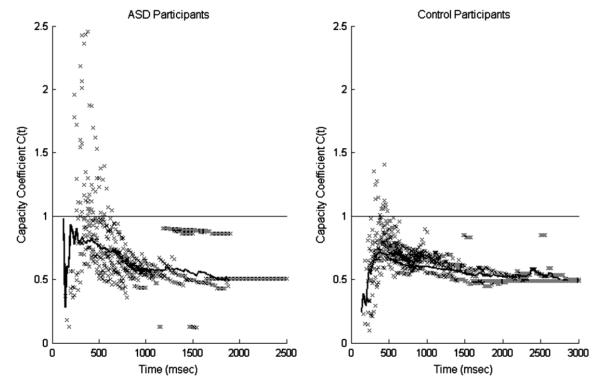
Capacity

Capacity coefficient values for ASD and control participants are plotted in Fig. 6 and summarized in Table 2. For both groups of participants, C(t) < 1 over most of the RT range, with three ASD participants exhibiting C(t) < 1 for all times t. Seven ASD participants showed super-capacity C(t) > 1 for early processing times (responses faster than approximately 450 ms) before dropping to limited capacity processing.

Fig. 6.

Capacity coefficient values at all times for all participants (scatter points) plotted together with the C(t) values for pooled data (solid line) for the ASD and control groups. The straight line at C(t) = 1 is the reference level of unlimited capacity processing, as predicted by the UCIP model. C(t) < 1 indicates limited capacity processing, while C(t) > 1 indicates super-capacity. Note that the pooled data line represents the distribution of all participants’ amalgamated data, not the average of the distributions from each participant.

The majority (9 of 11) of the control participants exhibited C(t) < 1 for all times t, shown in Fig. 6. Two control participants showed C(t) ≥ 1 for very early RTs followed by limited capacity C(t) < 1 after 450 ms. For both groups, the lower bound of observed capacity coefficient values was C(t) = ½, approximately fixed capacity.

Selective influence

Seven of ten ASD participants exhibited evidence supporting selective influence with survivor function orderings S_HH(t) ≤ S_HL(t) ≤ S_LH (t) ≤ S_LL(t), with a strict ordering of all survivor functions holding for at least some range of time. In particular, these seven participants exhibited strict orderings of their fast RTs, in the range of 200–450 ms after the onset of stimulus. Following this early strict ordering, each participant had some period of time in which S_HH (t) < S_LL(t), but S_HH(t) ≈ S_HL(t) or S_LH (t) ≈ S_LL(t) or both, indicating that global dimension processing dominated local dimension processing. It is important to note that while the survivor functions were not strictly ordered at all times, they did not show violations (survivor function crossings) of the above ordering.¹²

Three of the ten ASD participants exhibited violations of the selective influence assumption, with response time distributions that were either equal or crossed. These survivor function crossings occurred between multiple conditions and at multiple points in time in no obviously predictable pattern. Consequently we were unable to examine the processing architecture employed by these individuals.

All control participants showed evidence of non-selective influence through distribution misorderings. Nine of 11 controls exhibited the ordering S_HL(t) ≤ S_LH(t) ≤ S_LL(t) with S_HH(t) crossing at least S_HL(t) if not all the other distributions at some point in time. That is, S_HH (t) was the smallest survivor function at early times but then slowed over processing to be larger than at least one of the other three double-target conditions.

Two controls showed a survivor function ordering such that S_HH(t) ≤ S_HL(t) ≤ S_LH (t) all cross S_LL(t) at some point in time. This type of misordering could indicate that channel processing rates within the LL condition increased over the course of a trial, but this is unlikely given the nature of the low salience stimulus manipulations. A more parsimonious explanation is that the above misorderings resulted from processing in the HH, HL and LH conditions that was slower than predicted by selective influence. That is, the channel processing rates decreased over the course of a trial through interchannel inhibition.

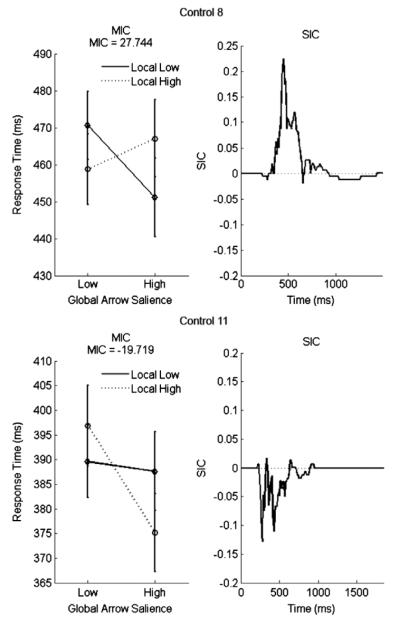
The systematic violations of selective influence exhibited by all controls are indicative of particular types of interactions between the processing channels. Specifically, orderings of early response times followed by the crossover of a single distribution suggests that the control participants were processing under single-factor reversal indirect non-selective influence (Townsend & Thomas, 1994). Mathematically, a single-factor reversal is defined at the mean level by E(T_HL) < E(T_HH), E(T_LH) > E(T_LL), or both. That is, for either the local or global arrows, the low salience arrows were processed faster than the high salience arrows, resulting in the reversal of a factor ordering. Single-factor reversals are generally evident as crossovers in the mean interaction contrast (MIC). The MIC results, summarized in Table 3 and depicted for two control participants in Fig. 7, reflected such reversals for 8 of 11 control participants and mean RT equalities for the three other control participants. For all participants, the reversal was observed on the salience of the local arrows, where responses to low salience local arrows were faster than high salience local arrows. According to Townsend and Thomas’ Theorem 1, a sufficient condition for the occurrence of a single-factor reversal within a parallel model is the presence of negative stochastic dependence between subprocesses.

Fig. 7.

MIC and SIC results for two typical control participants. Both participants have a crossover MIC, indicating a single-factor reversal violation of selective influence. Control 8 has a strictly positive SIC which, together with the MIC result, is indicative of inhibitory parallel minimum-time processing. Control 11 has a strictly negative SIC which, together with the MIC result, is evidence for inhibitory parallel exhaustive processing.

Architecture and stopping rule

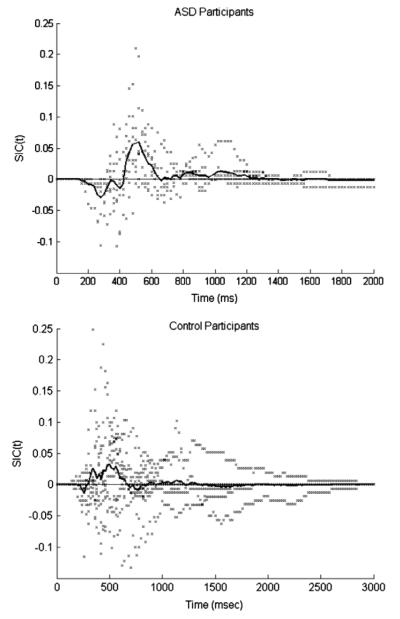
The survivor interaction contrast (SIC) functions for the seven ASD participants supporting selective influence, together with the pooled SIC curve, are plotted in Fig. 8 and summarized in Table 3. As depicted in the scatter points for the individual participants, mirrored in the group curve, the SIC functions exhibited an S-shaped characteristic of coactive or parallel interactive processing. The SIC functions for all participants were negative for early processing times and positive for later processing times. Exhaustive serial processing requires that the early negative region be equal to the subsequent positive area (see Fig. 2), and we did not observe this pattern for any participant.

Fig. 8.

Survivor interaction contrast (SIC) functions for the seven ASD participants whose data could be modeled and all control participants. Individual participants are plotted with the points. The solid lines represent the overall SIC for the pooled group data. Most ASD individual SICs and the ASD group SIC show an S-shaped signature, dipping negatively before going positive, with a larger positive area than negative. This signature is characteristic of a coactive processing architecture or facilitatory parallel exhaustive processing. The control group’s SIC is predominantly positive, consistent with parallel minimum-time processing. The individual SICs of the control participants show more variable behaviours, ranging from strictly positive, to S-shaped to all strictly negative, consistent with inhibitory parallel processing. Note that the pooled data line represents the distribution of all participants’ amalgamated data, not the average of the distributions from each participant.

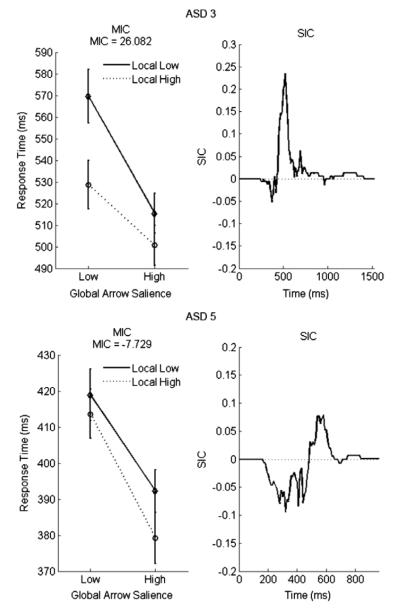
Considering each individual participant, there was evidence for two different processing architectures within the ASD group. Examples of these trends from two typical participants are plotted in Fig. 9. Five ASD participants had overadditive (positive) MIC values with S-shaped SIC functions that were negative for short, early periods of time and then predominantly positive for later times (Fig. 9, ASD3). This pattern is evidence for a coactive processing architecture (see Fig. 2) or facilitatory parallel exhaustive processing.

Fig. 9.

MIC and SIC results for two typical ASD participants. ASD3 exhibits an S-shaped SIC consistent with either a coactive architecture or facilitatory parallel exhaustive processing. ASD5 shows an S-shaped SIC with a much larger negative portion than positive portion. This pattern is indicative of facilitatory parallel exhaustive processing.

The remaining two ASD participants showed the combination of underadditive (negative) MIC values with S-shaped SIC functions that were negative for a much longer period of time than they were positive (Fig. 9, ASD5). This pattern, together with ordered survivor functions, is predicted by parallel exhaustive processing with mild facilitatory interactions. The facilitation was not strong enough to cause any survivor function misorderings but resulted in late positivity in the SIC curves which would not be found in strictly independent parallel exhaustive processing (Townsend & Nozawa, 1995). Thus we can conclude that all ASD participants were using either coactive or facilitatory exhaustive parallel processing in our global–local task.

Non-selective influence was consistently observed for control participants, meaning that we were unable to determine architecture from our non-parametric MIC and SIC measures. While we have identified these violations as single-factor reversals, Townsend and Thomas (1994) did not have a state space model to consider processing models that might account for these patterns. We utilized a Poisson counter model instantiation of parallel interactive processing (Eidels et al., in preparation) to simulate and fit these data. These more intricate models, which do not assume selective influence and allow for stochastic dependencies, provided a means of explicating the differences in processing systems between the control and ASD participants. Details of the structure and implementation of the Poisson parallel interactive models can be found in the Appendix.

Poisson parallel interactive models (PPIMs)

Intuitively, PPIMs act as a system of parallel accumulators, building evidence for or against the presence of targets in each channel (Eidels et al. (in preparation); see also the Appendix and Fig. 10). Channels are able to stochastically interact with each other, either accelerating accumulation by sending evidence-supporting information between channels, or slowing accumulation by sending competing information between channels. We considered four classes of PPIMs: facilitatory minimum-time systems, facilitatory exhaustive systems, inhibitory minimum-time systems, and inhibitory exhaustive systems. Double-target conditions were modeled by two accumulators, one representing global information and one representing local information. The two accumulators could either mutually facilitate or mutually inhibit each other. Single-target conditions were modeled as an accumulator in the presence of a competing (inhibitory) accumulator representing distractor information. The presence of inhibitory distractor information bounded the speed of single-target processing. Consequently, both facilitatory and inhibitory PPIMs produced redundancy gains similar to the redundancy gains observed in the data. These models predict a variety of SIC patterns, depicted in Fig. 3, depending on the nature and degree of channel interactions. Despite the relative generality of the interactive models, the predicted SIC patterns are still highly constrained. At least one type of PPIM was predicted by each participant’s data.

Fig. 10.

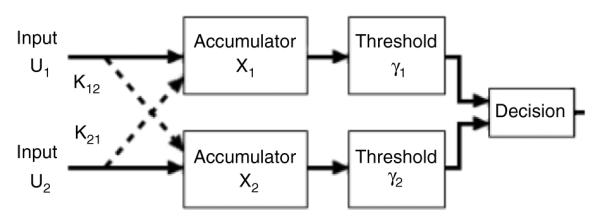
Poisson parallel interactive model (PPIM) with two channels. The current activation state of each channel, X_i, is the accumulation of total channel counts, U_i and information shared between channels, K_ij. In facilitatory PPIMs, K_ij is added; in inhibitory PPIMs, K_ij is subtracted. Information accumulates until a channel reaches its threshold, γ_i. The model makes a decision when one channel (Minimum-Time Processing) or both channels (Exhaustive Processing) have reached their respective thresholds. X_i, U_i, K_ij are random variables, and γ_i is a fixed parameter.

Table 3 provides a summary of candidate PPIMs together with the empirical findings for all participants (control participants in the lower panel). Facilitatory minimum-time PPIMs exhibit capacity coefficient values C(t) ≥ 1, with C(t) = 1 occurring when facilitations have been minimized or are 0. Thus we eliminated them as candidate models. Facilitatory exhaustive models, on the other hand, can exhibit C(t) < 1.¹³ However, no facilitatory PPIMs, exhaustive or minimum-time, show survivor function crossovers (a correlate, proven by Townsend & Thomas, 1994, showed this at the mean level). Specifically, because the double targets are positively interacting with each other, these models do not exhibit a slowing of the HH condition, as was observed. Consequently, we ruled out facilitatory exhaustive PPIMs and inferred that all control participants were processing with inhibitory interactions.

Stopping rules were determined by the shapes of the survivor interaction contrast (SIC) function under inhibitory crosstalk. The SIC results for all control participants are plotted in Fig. 8, and the SICs of two typical control participants are plotted in Fig. 7. By comparing their results with the predictions of the interactive models in Fig. 3, we conclude that the seven controls who exhibited a strictly positive or W-shaped SIC function (Fig. 7, Control 8) likely employed a minimum-time stopping rule. Two control participants exhibited negative SIC functions indicative of inhibitory exhaustive processing (Fig. 7, Control 11). Two control participants exhibited S-shaped SIC functions that were predicted by both minimum-time and exhaustive inhibitory PPIMs; so we cannot conclusively determine these individuals’ stopping rules under inhibitory parallel processing.

PPIMs also offer a second candidate model for the ASD data. Those participants who exhibited ordered survivor functions, S-shaped SIC functions, and limited capacity processing may have been utilizing a facilitatory exhaustive parallel processing system.

4. Discussion

In a divided attention global–local perception task, both the ASD and control groups showed response time and accuracy data supporting global advantage. Consistent with previous studies of global–local processing (see Kimchi, 1992, for a review), both groups were faster at responding to global level stimulus information than local information. These data do not support previous claims that individuals with an ASD have a local bias or show a lack of global advantage (Plaisted et al., 1999).

Despite these group similarities, we found fundamental differences between the ASD and control groups when we employed information processing models of response time data to examine four characteristics of global–local processing in individual participants. Differences were not evident in architecture; all participants across both groups used a parallel processing architecture. This finding is consistent with our previous study (Blaha et al., 2007), which demonstrated that a parallel minimum-time processing system was typically employed by adults performing the same divided attention global–local task.

Differences between groups were evident in the type of interaction between the parallel channels and the stopping rule employed. Participants in the control group all exhibited strong inhibitory (negative) interactions between global and local information and the majority (7/11) employed a minimum-time stopping rule. Two control individuals employed an exhaustive stopping rule, and the data were ambiguous as to the stopping rule for two others. Inhibitory parallel processing means that the control participants were processing global and local information simultaneously, but that information in these two channels was slowing the processing of each other. Generally, control participants responded as soon as enough information had been processed to make a correct decision (i.e., minimum-time stopping rule). The limited capacity coefficient values exhibited by each control participant offer additional evidence that global and local information were processed inefficiently, which is not surprising given the inhibition between channels.

Two candidate models were found within the ASD participant group: coactive processing under the assumption of selective influence and facilitatory exhaustive parallel processing when the assumption of selective influence is relaxed. Both candidate models predict the double-target survivor function orderings observed in the ASD data (Table 3). However, only the facilitatory exhaustive parallel processing system would predict the limited capacity C(t) values observed for each ASD participant. Typically, coactive architectures, operating on independent channels, result in highly efficient processing, evidenced by C(t) ≥ 1 (Townsend & Nozawa, 1995) or violations of the race-model bound on standard parallel processing response time distributions (Miller, 1982). Thus, a facilitatory exhaustive parallel processing system is most consistent with the response time patterns of the ASD participants. This means that the individuals with an ASD processed global and local information simultaneously and, unlike most of the control participants, waited until they had processed all available information before responding. In contrast to the controls, the presence of both global and local information actually benefitted processing rates through facilitatory interactions. That is, global target information sped up the processing of local target information and vice versa.

Additional analyses are possible to confirm our conclusions about dependencies and stopping rule in the parallel processing systems. In particular, comparisons may be made between each of the nine stimulus types employed in this task. Investigation of the response time distributions for all conditions show that processing of each double-target condition (HH, HL, LH, LL) is consistently faster than processing of each single-target condition, with response times to H targets being faster than those to L targets. The non-target object (dash composed of dashes) is the slowest response time distribution overall. For many participants, these results hold at the level of the integrated hazard function (Townsend, 1990), implying significant differences at the mean. Thus, comparisons between the individual stimulus conditions are consistent with the resulting Poisson parallel interactive model conclusions. These comparisons also offer additional support for the single-factor reversals observed in the control participants; as we see high salience manipulations are consistently faster than low salience manipulations in the presence of a distractor, but that the processing speed for high salience manipulations slows in the presence of targets. Although a full accounting of the results of these analyses is beyond the scope of this paper, data can be made available to the reader upon request.

As described earlier, previous studies of global–local processing in ASD have yielded mixed results. Our findings of global advantage for the majority of ASD participants are inconsistent with some previous findings (Plaisted et al., 1999), but consistent with others (Ozonoff, Strayer, McMahon, & Filloux, 1994; Rinehart et al., 2000). Given our adherence to methodological features that have been identified in cognitive psychological studies as critical to the global–local paradigm, we feel confident that our findings of global advantage are valid. The modeling results offer further insights into ASD performance. Importantly, the observed parallel architectures appear to be inconsistent with the Weak Central Coherence (WCC) theory of ASDs because they refute the use of any sequential global-to-local or local-to-global processing strategies. A recent conceptualization of WCC (Happé & Booth, 2008) suggested that some individuals with an ASD have difficulty constructing the global or whole percept out of the local elements (i.e., poor integration), implying a local-to-global processing order. Our current findings support neither a preference for first processing local information nor faster identification of local targets for any of the ASD participants. Further, parallel processing of global and local information in ASD participants was characterized by facilitatory rather than inhibitory interactions, indicating that global information and local information were not only processed simultaneously but interacted to accelerate responses. This positive interaction would not be predicted by WCC. Although we did not directly examine interference effects in this study (via incongruent distractors), our results do not suggest a local bias or local interference.

The information processing mechanisms revealed here are consistent with some previous studies in ASDs that have examined attention in contexts other than global–local perception. The use of exhaustive processing when not required is consistent with studies that have reported an inability to ignore irrelevant stimulus features in individuals with an ASD (e.g. Brian, Tipper, Weaver, & Bryson, 2003). Similarly, clinical observations of some individuals with an ASD indicate difficulty filtering information in the environment, such as sensory information. Additionally, Rutherford et al. (2007) demonstrated an advantage (less cost) in individuals with autism when dividing attention between central and peripheral task demands. This divided attention advantage might be attributable to facilitation or a lack of inhibition between the channels processing the central task and those processing the peripheral task. More research is needed to determine if individual participants with ASD demonstrate different processing characteristics under distinct task demands or if these characteristics are stable across cognitive and perceptual paradigms. Given the heterogeneity in ASDs, it will be important for future studies to begin to map modeling results onto clinical symptoms and associated features. A finding such as exhaustive processing on a particular task may provide important clues about more general underlying information processing approaches in certain individuals and a clear target for intervention.

Although our findings provide some important insights regarding basic information processing in ASDs they do not address the hallmark symptoms of this spectrum, social impairments. As stated earlier, we do not claim that the processing of non-social information is necessarily relevant for understanding social deficits, nor do we feel it is essential to link our findings to social dysfunction. However, we acknowledge that it is possible that understanding basic perceptual and cognitive processes may further our understanding of social deficits. For example, it is not difficult to imagine how challenging it would be to navigate social situations if information were always processed exhaustively. Timing of exchanges and the ability to identify and respond to the salient features of social interactions would likely suffer. In future studies, we plan to use SFT to examine processing of social stimuli in ASDs. Townsend, Wenger, Fifić and colleagues have already developed and employed tasks that use the Double Factorial Paradigm (DFP) for examining face processing in controls (e.g. Fifić, unpublished; Ingvalson & Wenger, 2005; Innes-Kerr, unpublished; Wenger & Townsend, 2001). It will be important to determine if individuals, both with and without ASDs, demonstrate similar processing approaches for non-social and social stimuli. The current findings are the initial step in a larger set of studies that will examine information processing in ASD and other clinical groups.

Not only do our findings further our understanding of ASDs, but several results have bolstered our knowledge of information processing models and advanced the sophistication of the tools with which we measure and model response time data. Findings from this study highlight the integral role of the assumption of selective influence to human information processing modeling, particularly the strong relationship between failures of selective influence and interchannel interactions. It is noteworthy that the majority of non-selective influences observed across control participants were single-factor reversals, which to date have only been discussed and developed theoretically (Townsend & Thomas, 1994). To our knowledge, ours is the first study to empirically demonstrate single-factor reversals, thus confirming the psychological validity of this modeling construct. Additional investigation is now called for at the distribution function level to enhance our understanding of how single-factor reversals may affect our DFP analyses, particularly the survivor interaction contrast function. This is a clear example of how the nature of clinical research engenders an environment in which to test the limits of mathematical models and to consider alternative approaches to explaining behaviour.

As noted in the introduction, most previous applications of the DFP have observed selective influence, and thus there has not been a need to adjudicate between processing systems under non-selective influence. These previous studies, though, have often employed either simplified psychophysical detection tasks, such as dots presented in separate visual fields (Townsend & Nozawa, 1995), or visual or memory targets with separate physical locations and/or structures, including face features (e.g., eyes, distance between eyes, Fifić, unpublished; Ingvalson & Wenger, 2005; Wenger & Townsend, 2001), halves of split faces (Innes-Kerr, unpublished), and different characters in strings of letters (Fifić, 2001; Townsend & Fifić, 2004). In a recent study using configural line figures, Eidels, Townsend, and Pomerantz (2008) demonstrated that selective influence was consistently violated unless the features of the configural figures were spatially separated. Together, these studies imply that some spatial separation of stimulus features facilitates selective influence.

The global configurations utilized in global–local tasks would not exist without the local elements of which they are composed, and, consequently, the two types of objects are always presented in a spatially contiguous manner. In this sense, global–local processing invites interactions during the course of processing. Prior evidence of global interference on local processing confirms that some degree of interaction typically occurs between global and local information (for a review, see Kimchi, 1992). Thus, it is not surprising that even under conditions in which we eliminated competing/incongruent non-target information, participants were susceptible to processing interactions. The presence of processing interactions suggests that these stimuli may be more integral than separable in nature, a factor shown to affect the architecture used for image classification (Fifić, Nosofsky, & Townsend, 2008).

With the exception of three ASD participants, we confirmed that the observed violations of selective influences were not the result of direct interactions at the stimulus input level because the survivor functions for all participants were ordered for fast response times (less than approximately 450 ms). The global–local processing channels received independent global and local input information, and during this early period of time, the accumulating effects of interchannel interactions had only a minimal effect on processing rates. The use of the Poisson parallel interactive models (PPIMs) enabled us to capture these patterns with interchannel dependencies. Further theoretical work is under way to explicate response time patterns for parallel interactive models in which the inputs are correlated.

The fact that our data exhibited various types and degrees of interaction allowed us to advance the theory development of parallel interactive processing models, specifically the Poisson counter instantiation. Although we (L.M.B. and J.W.H.) have been exploring PPIMs through simulations, this project provided the first opportunity to apply these models to empirical data. Constraining model behaviour to match the empirical patterns necessitated additional theoretical development of the PPIMs. In particular, basic interactive parallel processing treated single-target conditions as channels operating in isolation, with no other channels operating simultaneously and no interactions affecting the single-target processing (Townsend & Wenger, 2004). In practical application, these models, particularly the inhibitory models, could not produce response time distributions showing a redundancy gain because the single channels in isolation were generally faster than the double-target channels inhibiting each other. Yet all ASD and most control participants consistently exhibited redundancy gains for the double-target conditions. This can be attributed, at least partially, to the fact that the single targets (Global Only Arrows and Local Only Arrows) in this experiment were never presented in isolation but always in the presence of non-target distractors (neutral dashes at the non-target level), representing some information competing for processing resources.

To capture this aspect of the data, we introduced an inhibitory distractor channel to the single-target condition, modifying the Markov chains to slow the single-target conditions. Note that like the target channels, the distractor channels processed until reaching their thresholds, but the system could not respond to the distractor information.¹⁴ This new feature of the parallel interactive models makes them more flexible and will aid in the future applications of these models to other tasks with complex or integral stimuli.

5. Conclusion

The results of this study highlight the value of employing well-established mathematical modeling techniques to examine perceptual and cognitive processes in clinical populations. In this study, we assessed global–local processing in individuals with an ASD using Systems Factorial Technology and the associated Double Factorial Paradigm (Townsend & Ashby, 1983; Townsend & Nozawa, 1995). Utilizing these tools for the first time in the field of autism research, we were able to begin characterizing the differences in the information processing mechanisms employed by individuals with an ASD and their typically developing counterparts at the individual participant level. The results did not support a bias toward local information, as predicted by the Weak Central Coherence theory and some previous global–local studies in ASDs (Plaisted et al., 1999), but instead indicated a difference in interactions between global and local information processing channels and the stopping rules preferred by each group. This study illustrates the feasibility of applying these methods and models to children and adolescents, as well as developmental clinical samples, expanding the initial clinical applications of SFT by Neufeld, Townsend, and Jetté (2007); Townsend et al. (2007). Furthermore, expanding the application of these methods to samples other than “normal” adults yielded unexpected advances in our modeling techniques. This underscores the synergy that can be obtained by merging mathematical psychology and clinical science, a common theme of this special issue.

Appendix

A.1. Double-target processing

We model interactive parallel processing of double targets with two channels acting as simultaneous Poisson accumulators with some additional probability of information passing between the two channels. Fig. 10 provides a diagram of the two-channel system. Let U_i, i = 1, 2, be the random variable for the number of counts accumulated within a single channel i operating alone, and let U_i be distributed as a Poisson random variable with accumulation rate parameter λ_i, i = 1, 2, given by

$$P\left(U_i\right(t)=u_i)=f(u_i,{\lambda }_{i}t)=\{\begin{array}{cc}\hfill \frac{{\left({\lambda }_{i}t\right)}^{u_i}{\mathrm{e}}^{-{\lambda }_{i}t}}{u_i!}\hfill & \hfill {\lambda }_i,t\ge 0;u_i=0,1,2,\dots \hfill \\ \hfill 0\hfill & \hfill \text{otherwise}.\hfill \end{array}\phantom{\}}$$

Let γ_i, i = 1, 2, be the criterion for channel i, the number of counts that must accumulate for the channel to finish processing. Thus the model is defined over the γ₁ γ₂ state space. Channels are initialized at zero activation, denoted (0, 0); as processing proceeds, the density over the state space shifts toward the completion states.

Let K_j,i, i, j = 1, 2, i ≠ j be the random variable total amount of information shared from channel j to channel i. The probability that a single count is shared from channel j to channel i is distributed as a Bernoulli random variable:

$$P(k_{j,i},p_{j,i})=\{\begin{array}{cc}{p}_{j,i}\hfill & k_{j,i}=1\hfill \\ 1-p_{j,i}\hfill & k_{j,i}=0\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

The total amount of shared information, K_j,i, is distributed as a binomial distribution with

$$P(K_{j,i}=k_{j,i}\mid U_j=u_j)=\left(\begin{array}{c}\hfill u_j\hfill \\ \hfill k_{j,i}\hfill \end{array}\right)p_{j,i}^{k_{j,i}}{(1-p_{j,i})}^{u_j-k_{j,i}}$$

where k_j,i and p_j,i are defined as above. Note that when p_j,i = p_i,j = 0, the system is a standard, independent parallel processing model.

Let X_i, i = 1, 2, be the random variable representing the total activation (total number of counts) in a single channel. If the interchannel interactions are facilitatory, then k_j,i(t) is added to the channel activation: X_i = U_i + K_j,i; if the interactions are inhibitory, then k_j,i(t) is subtracted: X_i = U_i – K_j,i. Criterion γ_i acts as an absorbing state; so the channel will cease accumulating when x_i(t) = γ_i. Thus, for a given channel i, its position in the state space at a given time t will be defined by 0 ≤ u_i(t) ± k_j,i(t) ≤ γ_i.

Responses of the whole system are made according to a predetermined stopping rule; here we implement the two canonical stopping rules possible within the global–local task: minimum-time (respond after processing global or local) and exhaustive (stop after processing both global and local). In the minimum-time (OR-gate) models, a response is made (the channels stop accumulating information and the state space is reset to (0, 0)) when any single channel reaches its criterion. In the exhaustive (AND-gate) models, both channels must reach their respective criteria before the system responds and the state space is reset to (0, 0).

Facilitatory exhaustive processing

Facilitatory exhaustive processing is modeled with two channels that mutually facilitate each other (i.e., x_i = u_i+k_j,i), each of which must reach their criterion for the model to respond. Let T_i, i = 1, 2, be the channel completion time of channel i. We readily arrive at an analytic solution for the facilitatory exhaustive model, given by the joint cumulative distribution function shown in Box I. The four terms in the cumulative probability function give the probabilities for the four mutually exclusive ways the system might reach its exhaustive criteria. The first term is the probability of the system responding when both channels required counts from the other channel to reach their respective thresholds. The second term is the probability that Channel 1 required shared counts to reach its threshold and Channel 2 completed through the Poisson accumulator alone. Similarly, the third term reflects Channel 1 completing by the Poisson accumulator alone and Channel 2 requiring shared counts to reach threshold. Finally, the fourth term is the joint probability that both channels reach their respective thresholds by the Poisson processes without requiring shared counts.

Box I.

$$\begin{array}{cc}\hfill P(T_1<t\text{AND}{T}_2<t)=& \sum _{u_1=0}^{{\gamma }_1-1}\sum _{u_2=0}^{{\gamma }_2-1}\frac{{\left({\lambda }_{1}t\right)}^{u_1}{\mathrm{e}}^{-{\lambda }_{1}t}}{u_1!}\frac{{\left({\lambda }_{2}t\right)}^{u_2}{\mathrm{e}}^{-{\lambda }_{2}t}}{u_2!}\left[1-\sum _{k_{2,1}=0}^{\min (u_2,{\gamma }_1-u_1-1)}\left(\begin{array}{c}\hfill u_2\hfill \\ \hfill k_{2,1}\hfill \end{array}\right)p_{2,1}^{k_{2,1}}{(1-p_{2,1})}^{u_2-k_{2,1}}\right]\hfill \\ \hfill & \times \left[1-\sum _{k_{1,2}=0}^{\min (u_1,{\gamma }_2-u_2-1)}\left(\begin{array}{c}\hfill u_1\hfill \\ \hfill k_{1,2}\hfill \end{array}\right)p_{1,2}^{k_{1,2}}{(1-p_{1,2})}^{u_1-k_{1,2}}\right]\hfill \\ \hfill & +\sum _{u_1=0}^{{\gamma }_1-1}\frac{{\left({\lambda }_{1}t\right)}^{u_1}{\mathrm{e}}^{-{\lambda }_{1}t}}{u_1!}\left[1-\sum _{k_{2,1}=0}^{\min ({\gamma }_2,{\gamma }_1-u_1-1)}\left(\begin{array}{c}\hfill {\gamma }_2\hfill \\ \hfill k_{2,1}\hfill \end{array}\right)p_{2,1}^{k_{2,1}}{(1-p_{2,1})}^{{\gamma }_2-k_{2,1}}\right]\left[1-\sum _{u_2=0}^{{\gamma }_2-1}\frac{{\left({\lambda }_{2}t\right)}^{u_2}{\mathrm{e}}^{-{\lambda }_{2}t}}{u_2!}\right]\hfill \\ \hfill & +\sum _{u_2=0}^{{\gamma }_2-1}\frac{{\left({\lambda }_{2}t\right)}^{u_2}{\mathrm{e}}^{-{\lambda }_{2}t}}{u_2!}\left[1-\sum _{k_{1,2}=0}^{\min ({\gamma }_1,{\gamma }_2-u_2-1)}\left(\begin{array}{c}\hfill {\gamma }_1\hfill \\ \hfill k_{1,2}\hfill \end{array}\right)p_{1,2}^{k_{1,2}}{(1-p_{1,2})}^{{\gamma }_1-k_{1,2}}\right]\left[1-\sum _{u_1=0}^{{\gamma }_1-1}\frac{{\left({\lambda }_{1}t\right)}^{u_1}{\mathrm{e}}^{-{\lambda }_{1}t}}{u_1!}\right]\hfill \\ \hfill & +\left[1-\sum _{u_1=0}^{{\gamma }_1-1}\frac{{\left({\lambda }_{1}t\right)}^{u_1}{\mathrm{e}}^{-{\lambda }_{1}t}}{u_1!}\right]\left[1-\sum _{u_2=0}^{{\gamma }_2-1}\frac{{\left({\lambda }_{2}t\right)}^{u_2}{\mathrm{e}}^{-{\lambda }_{2}t}}{u_2!}\right]\hfill \end{array}$$

where u₁, u₂, λ₁, λ₂, γ₁, γ₂, p_2,1, and p_1,2 have been defined previously.

Facilitatory minimum-time processing

Facilitatory OR processing is modeled by the complement of the cumulative probability that neither channel has reached criterion at time t. We, again, readily arrive at an analytic formulation for facilitatory minimum-time processing as shown in Box II. The terms in this equation give first the probability that within-channel count u_i(t) < γ_i, i = 1, 2, and second, the probability that the shared counts are not enough for the total to reach criterion, i.e., x_i(t) = u_i(t) + k_j,i(t) < γ_i, i = 1, 2, i ≠ j.

Box II.

$$\begin{array}{cc}\hfill P(T_1<t\text{OR}{T}_2<t)=& 1-P(T_1>t\text{AND}{T}_2>t)\hfill \\ \hfill =& 1-\{\sum _{u_1=0}^{{\gamma }_1-1}\sum _{u_2=0}^{{\gamma }_2-1}\frac{{\left({\lambda }_{1}t\right)}^{u_1}{\mathrm{e}}^{-{\lambda }_{1}t}}{u_1!}\frac{{\left({\lambda }_{2}t\right)}^{u_2}{\mathrm{e}}^{-{\lambda }_{2}t}}{u_2!}\phantom{\}}\hfill \\ \hfill & \times \sum _{k_{2,1}=0}^{\min (u_2,{\gamma }_1-u_1-1)}\left(\begin{array}{c}\hfill u_2\hfill \\ \hfill k_{2,1}\hfill \end{array}\right)p_{2,1}^{k_{2,1}}{(1-p_{2,1})}^{u_2-k_{2,1}}\hfill \\ \hfill & \phantom{\{}\times \sum _{k_{1,2}=0}^{\min (u_1,{\gamma }_2-u_2-1)}\left(\begin{array}{c}\hfill u_1\hfill \\ \hfill k_{1,2}\hfill \end{array}\right)p_{1,2}^{k_{1,2}}{(1-p_{1,2})}^{u_1-k_{1,2}}\}\hfill \end{array}$$

where u₁, u₂, λ₁, λ₂, γ₁, γ₂, p_2,1 and p_1,2 are defined as above.

Inhibitory processing

In defining the facilitatory models, we took advantage of the fact that the total activation in a channel is a monotonically increasing function of time. However, with inhibition it is possible for the total activation in a channel to decrease. To accommodate this behaviour, we utilize a different formalism: the Markov chain. See Diederich and Busemeyer (2003) for a tutorial on the use of Markov models of information accumulation.

Let U_i, K_j,i, X_i, and λ_i, i, j = 1, 2, i ≠ j, be defined as above, and let Δt be a sufficiently small increment of time. Note that we constrain λ_i and Δt such that P[u_i(t + Δt) > 1] < 0.01 to bound the error on the Poisson approximation. Transitions in the two-dimensional state space are made as x₁ and/or x₂ increase or decrease; failure of both channels to increase or decrease their total activation in a single time step Δt results in a “stationary” transition. Let P[m, n] denote the transition probability such that, at time t + Δt, x_i has changed by m and x_j has changed by n. The transition probabilities for all possible transitions of the inhibitory AND Markov chain are defined, for i, j = 1, 2, i ≠ j, by

$$\begin{array}{cc}\hfill P[0,0]=& P\left[x_i\right(t+\Delta t)=x_i(t)\text{AND}\hfill \\ \hfill & x_j(t+\Delta t)=x_j\left(t\right)]\hfill \\ \hfill =& (1-{\lambda }_i\Delta t)(1-{\lambda }_j\Delta t)+{\lambda }_i{\lambda }_j{\left(\Delta t\right)}^2{p}_{i,j}{p}_{j,i}\hfill \\ \hfill P[1,-1]=& P\left[x_i\right(t+\Delta t)=x_i(t)+1\text{AND}\hfill \\ \hfill & x_j(t+\Delta t)=x_j\left(t\right)-1]\hfill \\ \hfill =& {\lambda }_i\Delta t(1-{\lambda }_j\Delta t)p_{ij}\hfill \\ \hfill P[1,0]=& P\left[x_i\right(t+\Delta t)=x_i(t)+1\text{AND}\hfill \\ \hfill & x_j(t+\Delta t)=x_j\left(t\right)]\hfill \\ \hfill =& \left({\lambda }_i{\lambda }_j\right){\left(\Delta t\right)}^2{p}_{i,j}(1-p_{j,i})+{\lambda }_i\Delta t(1-{\lambda }_j\Delta t)(1-p_{i,j})\hfill \\ \hfill P[1,1]=& P\left[x_i\right(t+\Delta t)=x_i(t)+1\text{AND}\hfill \\ \hfill & x_j(t+\Delta t)=x_j\left(t\right)+1]\hfill \\ \hfill =& \left({\lambda }_i{\lambda }_j\right){\left(\Delta t\right)}^2{p}_{i,j}(1-p_{i,j})(1-p_{j,i})\hfill \\ \hfill P[0,-1]=& P\left[x_i\right(t+\Delta t)=x_i(t)\text{AND}\hfill \\ \hfill & x_j(t+\Delta t)=x_j\left(t\right)-1]\hfill \\ \hfill =& 0\hfill \\ \hfill P[-1,-1]=& P\left[x_i\right(t+\Delta t)=x_i(t)-1\text{AND}\hfill \\ \hfill & x_j(t+\Delta t)=x_j\left(t\right)-1]\hfill \\ \hfill =& 0.\hfill \end{array}$$

Note that P[0, 1], P[−1, 1] and P[−1, 0] are obtained by proper rearrangement of the subscripts i, j in the equations for P[1, 0], P[−1, 1] and P[0, −1], respectively.

To intuit the basis of these distributions, consider the possible ways the model would make a stationary transition (P[0, 0]). Either both channels gain a within-channel count (i.e., u₁(t + Δt) = u₁(t) + 1 and u₂(t + Δt) = u₂(t) + 1) and share that count, subtracting it from the other (i.e., k_1,2(t + Δt) = k_2,1(t + Δt) = −1) with probability (λ_iλ_j(Δt)²(1 – p_i,j)(1 – p_i,j)), or neither channel gains a within-channel count with probability (1 – λ_iΔt)(1 – λ_jΔt). As these are disjoint events, the probability of either occurring is just their sum as given in P[0, 0] above.

We assume x_i(t) ≥ 0, i = 1, 2, for all t. Thus, if channel i shares an inhibitory count with channel j ≠ i, i.e., k_i,j(t + Δt) = 1, when x_j(t) = 0 and u_j(t + Δt) = 0, then x_j remains at 0. In order to ensure valid probability density functions over the rows of the transition matrix, we set the probability that x₁ increases while x₂ stays at zero to be P[1, 0]+P[1, −1]. Likewise, we set the probability that x₂ increases while x₁ stays at zero to be P[0, 1] + P[−1, 1].

Inhibitory exhaustive processing

Exhaustive processing requires that processing continues until both x₁(t) = γ₁ and x₂(t) = γ₂, which results in a single absorbing state (γ₁, γ₂) in the transition matrix. Assume that if at time t_γ, x_i(t_γ) = γ_i, i = 1, 2, then for all t > t_γ, x_i(t) = γ_i. It follows that, for all remaining time steps, k_i,j(t + Δt) = 0. Thus, if x₂(t) = γ₂ then the probability of x₁ decreasing is 0 (k_2,1(t + Δt) = 0), P[x₁(t + Δt) = x₁(t)] = P[0, 0] + P[0, 1] + P[−1, 1] = 1 – λ₁Δt, and P[x₁(t + Δt) = x₁(t) + 1] = P[1, 0] + P[1, 1] + P[1, −1] = λ₁Δt.

With the transition probabilities defined above and the absorbing state (γ₁, γ₂), we can state the model in terms of its transition matrix T. Table A.1 gives an example T for a system where γ₁ = γ₂ = 2. The transition matrix can be then partitioned into the transient [(γ₁+1)(γ₂+1)−1]×[(γ₁+1)(γ₂+1)−1] state matrix Q and the [(γ₁+1)(γ₂+1)−1]×1 absorbing vector R, such

Table A.1.

Transition matrix for inhibitory exhaustive processing, γ₁ = γ₂ = 2.

Activation state at time t	Activation state at time t + Δt
	(0, 0)	(0, 1)	(0, 2)	(1, 0)	(1, 1)	(1, 2)	(2, 0)	(2, 1)	(2, 2)
(0, 0)	P[0, 0]	P[0, 1] + P[−1, 1]	0	P[1,0] + P[1,−1]	P[1, 1]	0	0	0	0
(0, 1)	0	P[0, 0]	P[0, 1] + P[−1, 1]	P[1,−1]	P[1, 0]	P[1, 1]	0	0	0
(0, 2)	0	0	P[0, 0] + P[0, 1] + P[−1, 1]	0	0	P[1, 0] + P[1,−1] + P[1, 1]	0	0	0
(1, 0)	0	P[−1, 1]	0	P[0, 0]	P[0, 1]	0	P[1, 0] + P[1, −1]	P[1, 1]	0
(1, 1)	0	0	P[−1, 1]	0	P[0, 0]	P[0, 1]	P[1, −1]	P[1, 0]	P[1, 1]
(1, 2)	0	0	0	0	0	P[0, 0] + P[0, 1] + P[−1, 1]	0	0	P[1, 0] + P[1,−1] + P[1, 1]
(2, 0)	0	0	0	0	0	0	P[0, 0] + P[0, 1] + P[−1, 1]	P[0, 1] + P[−1, 1] + P[1, 1]	0
(2, 1)	0	0	0	0	0	0	0	P[0, 0] + P[0, 1] + P[−1, 1]	P[0, 1] + P[−1, 1] + P[1, 1]
(2, 2)	0	0	0	0	0	0	0	0	1

Table A.2.

Transition matrix for inhibitory minimum-time processing, γ₁ = γ₂ = 2.

Activation state at time t	Activation state at time t + Δt
	(0, 0)	(0, 1)	(0, 2)	(1, 0)	(1, 1)	(1, 2)	(2, 0)	(2, 1)	(2, 2)
(0, 0)	P[0, 0]	P[0, 1] + P[−1, 1]	0	P[1, 0] + P[1,−1]	P[1, 1]	0	0	0	0
(0, 1)	0	P[0, 0]	P[0, 1] + P[−1, 1]	P[1, −1]	P[1, 0]	P[1, 1]	0	0	0
(0, 2)	0	0	1	0	0	0	0	0	0
(1, 0)	0	P[−1, 1]	0	P[0, 0]	P[0, 1]	0	P[1, 0] + P[1,−1]	P[1, 1]	0
(1, 1)	0	0	P[−1, 1]	0	P[0, 0]	P[0, 1]	P[1,−1]	P[1, 0]	P[1, 1]
(1, 2)	0	0	0	0	0	1	0	0	0
(2, 0)	0	0	0	0	0	0	1	0	0
(2, 1)	0	0	0	0	0	0	0	1	0
(2, 2)	0	0	0	0	0	0	0	0	1

that 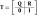. R represents the transition probabilities from any state in which the model has not completed to an absorbing state, and Q represents the transitions between non-completion states in the Markov chain. Under the assumption of sufficiently small, equal, discrete time steps Δt, the cumulative distribution of finishing times is given by (Kemeny & Snell, 1976)

$$\mathbf{C}\left(N\right)={(\mathbf{I}-\mathbf{Q})}^{-1}\ast (\mathbf{I}-{\mathbf{Q}}^{N+1})\mathbf{R}$$

where N is the total number of transitions made in the Markov chain. Note that the cumulative distribution, given the initial activation state (0, 0), is the first entry of vector C(N).

Inhibitory minimum-time processing

The inhibitory minimum-time model finishes when either x₁(t) = γ₁ or x₂(t) = γ₂, resulting in multiple absorbing states. It follows that R is a [(γ₁γ₂)]×[(γ₁ + γ₂ + 1)] matrix with each column representing the probability of transitioning into a different completion state. Transient matrix Q has dimension [(γ₁γ₂)]×[(γ₁γ₂)]. An example transition matrix T for the γ₁ = γ₂ = 2 case is given in Table A.2.

Let C(N) be defined as above. Under the minimum-time stopping rule, the cumulative distribution of finish times is the sum across the row in the resulting matrix C(N) corresponding to the initial activation state (0, 0).

A.2. Single-target processing

We assume that processing of an uninformative distractor will either process independently or with inhibitory interactions with the target. We again implement our two-channel Markov chain. Let x_i, i ∈ {1, 2}, be the total activation state of target channel i, with within-channel Poisson accumulation rate λ_i, probability p_ij of channel i sharing information with channel j, and target threshold γ_i. Note that λ_i, p_ij, and γ_i are properties of channel i, and are fixed regardless of the presence of a target or distractor in channel j. Again, let Δt be a sufficiently small increment of time.

Define d_j, j ∈ {1, 2}, j ≠ i, to be the activation state of channel j when processing a distractor, with within-channel Poisson accumulation rate λ_dj and threshold _dj. Let the probability of the distractor sharing information with target channel i be given by p_dj. Although channel j can finish processing the distractor when d_j(t) = γ_dj, the system can only respond when x_i(t) = γ_i.

Let the transition matrix 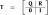be defined analogously to the inhibitory exhaustive model above, but using transition probabilities calculated with λ_dj and p_dj instead of λ_j and p_ji. The transient state matrix Q has dimension [(γ_i + 1)γ_dj × (γ_i + 1)γ_dj]. R is the [(γ_i + 1)γ_dj × (γ_dj + 1)] set of transition probability vectors from transient activation states to target completion activation states. C(N) is defined as above, and the cumulative distribution of total processing times for the initial activation state (0, 0) is the sum over the first row of C(N).

Note that, save for the error due to our approximation, this model reduces to a Poisson process on target channel i when either p_dj = 0 or λ_dj = 0.