Abstract
Purpose: Prostate cancer ranks as one of the most common malignancies and currently represents the second leading cancer-specific cause of death in men. The current use of single modality transrectal ultrasound (TRUS) for biopsy guidance has a limited sensitivity and specificity for accurately identifying cancerous lesions within the prostate. This study introduces a novel prostate cancer imaging method that combines TRUS with electrical impedance tomography (EIT) and reports on initial clinical findings based on in vivo measurements.
Methods: The ultrasound system provides anatomic information, which guides EIT image reconstruction. EIT reconstructions are correlated with semiquantitative pathological findings. Thin plate spline warping transformations are employed to overlay electrical impedance images and pathological maps describing the spatial distribution of prostate cancer, with the latter used as reference for data analysis. Clinical data were recorded from a total of 50 men prior to them undergoing radical prostatectomy for prostate cancer treatment. Student's t-tests were employed to statistically examine the electrical property difference between cancerous tissue and benign tissue as defined through histological assessment of the excised gland.
Results: Example EIT reconstructions are presented along with a statistical analysis comparing EIT and pathology. An average transformation error of 1.67% is found when 381 spatially coregistered pathological images are compared with their target EIT reconstructed counterparts. At EIT signal frequencies of 0.4, 3.2, and 25.6 kHz, paired-testing demonstrated that the conductivity of cancerous regions is significantly greater than that of benign regions ( p < 0.0304).
Conclusions: These preliminary clinical findings suggest the potential benefits electrical impedance measurements might have for prostate cancer detection.
Keywords: electrical impedance tomography, image coregistration, prostate cancer
INTRODUCTION
Prostate cancer ranks as one of the most common malignancies and in 2012 represented the second leading cancer-specific cause of death in men.1 Excessive levels of serum prostate specific antigen (PSA) and abnormal digital rectal examination (DRE) represent the current clinical screening methods for prostate cancer. Positive findings reported from either of these procedures are typically followed by transrectal ultrasound (TRUS) guided biopsy, which is the standard protocol for establishing diagnosis and staging disease. Because both PSA and DRE-based diagnoses have low sensitivity (<30%),2, 3 diagnostic confirmation of prostate cancer relies solely on these TRUS-guided biopsy findings with histology-based measurements including Gleason grade4 and tumor involvement largely influencing therapeutic staging. Unfortunately, numerous studies report a lack of concordance between Gleason grades pathologically assigned for biopsy and those assigned for prostatectomy specimens;5 this arises due to spatial sampling shortcomings of the biopsy procedure and suggests that current biopsy-based diagnosis is not sufficiently accurate to determine the stage of the cancer in all cases. Further, TRUS imaging has limited sensitivity and specificity (a miss rate of approximately 40% reported in one study6) for identifying the pathology of focal lesions during these biopsy procedures.7
Multiple ex vivo studies report that significant electrical property differences exist between cancerous and benign tissues in the prostate.8, 9 Specifically, cancerous tissue has a lower conductivity ( σ) than benign tissue ( p < 0.05) at frequencies ranging from 0.1 to 100 kHz, and a larger permittivity ( ɛ) at 100 kHz ( p < 0.0001) in ex vivo studies.10 Significant contrasts in electrical properties have also been reported between different grade prostate cancers.11 These electrical property differences result from morphological variations present between cancer and benign tissues. Cancerous tissues consist of a large number of small, deformed, epithelial cell-lined lumens with decreased levels of extracellular fluids as compared to benign tissue, where fewer cells, more uniform luminal structures, and higher levels of extracellular fluids are found. Conductivity is typically associated with ionic charge transfer through biological fluids, while permittivity is associated with charge storage at cellular membranes. The low levels of extracellular fluid and high density of cells in cancerous prostate are hypothesized to lead to the lower conductivity and higher permittivity observed, respectively, under ex vivo conditions. These contrasts suggest that methods capable of measuring these properties in vivo may prove useful for cancer detection.
Electrical impedance tomography (EIT) is an imaging modality capable of estimating the internal spatial distribution of conductivity and permittivity based on measured physical quantities (currents and voltages) recorded from electrodes positioned on an object's surface. In medical EIT applications, a number of electrodes are attached to a patient's surface. Low amplitude alternating currents (AC) are injected into the patient and voltages are measured on some or all of the electrodes simultaneously. The boundary currents and voltages, along with the geometry of the object, are used to mathematically estimate the internal conductivity and permittivity by solving a severely ill-posed, nonlinear “Calderón's Inverse Problem”12 using a finite element method (FEM) approach.13, 14
An ultrasound coupled transrectal electrical impedance tomography (TREIT) system15 with a dedicated reconstruction algorithm16 has been developed for prostate imaging. The imaging system consists of an EIT data acquisition module, a TRUS imaging module, a system control computer, a visual display monitor, and a medical-grade isolated power supply.17 Ultrasound provides a priori anatomical information to guide EIT image reconstruction. Thirty gold-plated electrodes are printed on a 1 mil thick flexible Kapton circuit board and configured along the periphery of a rectangular opening (20 × 60 mm). This flexible circuit is wrapped around the shaft of the TRUS probe such that the opening is aligned with the probe's acoustic window and held in place by a pressure sensitive adhesive layer. The window size exceeds that of the TRUS probe's field-of-view (FOV) and enables TREIT imaging of any sized prostate that fits within the TRUS FOV. The addition of this thin flexible circuit does not appreciably increase the diameter of the TRUS probe so no additional patient discomfort is experienced. A circular external ventral electrode is placed on the patient's lower abdomen to provide a return path for currents directed away from the prostate (Fig. 1).
Figure 1.
System electrodes. Thirty electrodes are plated on a flexible circuit, which was applied on the surface of a TRUS probe (left). Ventral electrode for placement on a patient's lower abdomen (right).
Previous imaging studies have demonstrated that this TREIT system is able to detect high contrast inclusions of 1.0 cm in diameter, positioned 2.3 cm away from the probe surface. The system is also capable of differentiating inclusions with 20% contrast to the background,15 which is less than the reported electrical impedance contrast observed between cancer and benign prostate.10 This report presents a method to evaluate the TREIT system's ability to detect cancer in the prostate based on correlating electrical properties found in EIT reconstruction with the pathological findings.
METHODS
In vivo patient imaging protocol
In vivo ultrasound and TREIT data have been acquired from a total of 50 men diagnosed with prostate cancer prior to their undergoing radical prostatectomy. A cancer diagnosis was made based on histological review of tissue cores extracted during prostate biopsy at least 6 weeks prior to surgery and the average PSA (± one standard deviation) of the men undergoing robot-assisted radical prostatectomy (RALP) in this study was 8.1 ± 7.6 ng/ml (range: 1.4–53 ng/ml). Ultrasound gel and an electrically translucent natural membrane sheath18 were applied to interface the TREIT probe to the patient's rectum. The shape and size of the prostate was captured by 3D TRUS, which consisted of 13 or 61 frames of 2D transverse images. Following TRUS imaging, impedance data were recorded. Two electrodes were selected as current source and sink to drive the excitation signals into the patient's prostate and passive voltage levels were sensed on the remaining 29 electrodes. Voltage and current signals were recorded for all current driving electrode combinations at excitation frequencies of 0.4, 3.2, 25.6, and 102.4 kHz. Following surgical resection, the prostate was sectioned and microscopically examined to assess the actual cancer distribution. Cancer diagnosis was confirmed through histological evaluation of the excised prostates. TNM staging criteria was used to define the extent of cancer invasion19 when available, lymph node invasion was also reported. In addition, primary and secondary Gleason grades were assigned to the prostate and the percentage of tumor volume within the prostate was noted. This investigational imaging study has been approved by the Committee for the Protection of Human Subjects, Dartmouth College's local Institutional Review Board.
EIT reconstruction with a priori information
Ultrasound image stacks consist of 13 or 61 frames of 2D cross-sectional transverse images (depending on a specified slice spacing of 5 or 1 mm) recorded from each patient. The image stack is ported to a commercial medical image processing software Mimics 13.1 (Materialise Group, Leuven, Belgium) and each 2D transverse frame is manually segmented. After all frames are segmented, a surface mesh with configurable density and smoothness is generated to accurately match the US-based anatomic geometry of the prostate (Fig. 2).
Figure 2.

Segmenting the prostate with Mimics. (a) Original 2D cross-sectional transverse ultrasound image of the prostate. (b) Manually segmented prostate boundary on the same slice. (c) Resulting 3D surface mesh of the prostate from multiple 2D cross-sectional segmentations.
The US derived prostate surface is embedded into a 3D cylindrical mesh containing the probe and electrode geometry (Fig. 3). A priori anatomic information provided by the embedded prostate is used to guide EIT image reconstruction.20 The ultrasound image stack is coregistered with the cylindrical mesh for reconstruction using a rigid transformation to maintain its correct position in relation to the TRUS probe.21 After the prostate surface mesh is properly oriented and positioned relative to the probe, the coupled geometric surfaces are processed to generate a volumetric FEM mesh containing the TRUS probe, electrodes, and correctly positioned prostate. Each tetrahedron in the mesh is assigned a value to reflect the complex conductivity (relative to the 0.1 S/m reference saline tank) and the vertices of each tetrahedron represent a voltage potential.
Figure 3.
Prostate embedded mesh for EIT reconstruction. The solid region within the mesh represents the prostate.
In this application, difference imaging is employed for EIT reconstruction in order to minimize systematic errors from the imaging system. A reference data set is recorded by imaging a saline bath with a conductivity of 0.1 S/m immediately following clinical data acquisition. 3D reconstructions are computed based on the impedance differences measured between the reference data set and patient data set using the algorithms described in detail by Borsic et al.16
Briefly, for sufficiently low frequencies of injected currents (<1 MHz), a quasistatic approximation is used to model the potential field due to an injected current pattern. In this case, the fundamental equation in EIT becomes
| (1) |
where , ω is the frequency of the injected current, and u is the scalar potential field in an enclosed body Ω. For simplicity, the complex admittivity γ = σ + jωε can be used to represent the conductivity and permittivity. Assuming that a voltage Vl is applied on electrode El ( l = 1, 2, 3, …, L) located on the domain's surface, ∂Ω, this leads to the following boundary conditions:
| (2) |
| (3) |
| (4) |
where zl is the contact impedance between the electrode and body surface, n is the outward normal vector extending from the surface, Sl is the surface area of electrode El, and Il is the current measured at electrode El.12, 22 Estimating internal conductivity and permittivity from finite observed measurements on the surface represents an ill-conditioned inverse problem that often leads to unstable solutions due to amplification of errors from both measurements and numerical rounding. In practice, Tikhonov regularization is used to penalize the oscillatory conductivities in solving the inverse problem.23
In this case, the conductivity distribution is reconstructed by fitting the calculated measurements Mcal to the real measurements Mreal and minimizing the error in L2 norm
| (5) |
The penalty term is added to regularize the inverse problem by assuming that the conductivity changes gradually inside the imaging volume. L is a matrix of partial differential operators (a Laplacian is used here) and γref is a reference admittivity (known from estimation or anatomic structure). In this study, the scalar regularization factor, α, was empirically chosen to be 200. Note that this method of regularization imposes a degree of spatial averaging due to the nodal-weighting provided through the Laplacian matrix, but is necessary for solving the ill-posed inverse problem.
A coarse FEM mesh (with fewer elements) is typically used in EIT to reduce the ill-conditioning of the inverse problem (due to the small number of measurements) and the computational complex parameter estimation.16 In this TREIT application, the high-density patient specific prostate volume mesh (which contains tens of thousands of tetrahedra) is discretized into an 8 × 8 × 8 pixelated coarse mesh for parameter estimation as a compromise between sensitivity (influencing image resolution) and noise (larger negative impact with denser meshes).20
This choice is driven by both the computational considerations and the available contrast provided by electrical impedance. For a larger sized 50 cm3 prostate, each voxel of the 8 × 8 × 8 coarse mesh represents an approximately 4.6 × 4.6 × 4.6 mm cube (97.4 mm3). For a smaller sized 25 cm3 prostate, the voxel represents a 3.6 × 3.6 × 3.6 mm cube (46.7 mm3). Previous ex vivo studies have reported that a 3.5 mm diameter by ∼5 mm tall cylindrical sample of tissue (48.1 mm3) consisting of >50% cancerous tissue can be identified with electrical impedance measurements to contain cancer with a high level of sensitivity and specificity (∼70%).10 The 8 × 8 × 8 coarse mesh elements represent similar volumes to these previous findings and were chosen to potentially enable pixel-based cancer identification of cancer in a computationally efficient way.
The cuboidal coarse mesh circumscribes the prostate region and is uniformly discretized to 8 pixels in each of the x, y, and z directions to provide a uniform resolution in all directions. The reconstruction algorithm constrains the complex conductivity to a single value within each of the coarse pixels. In addition, the complex conductivity of all the mesh elements outside the prostate region is estimated as single background value during reconstruction. The complex conductivity distribution γ is linearly solved by
| (6) |
where J is the Jacobian of Mcal(γ) evaluated at γ0 and δM = Mreal − Mcal(γ0).
Correlating pathological findings and EIT images
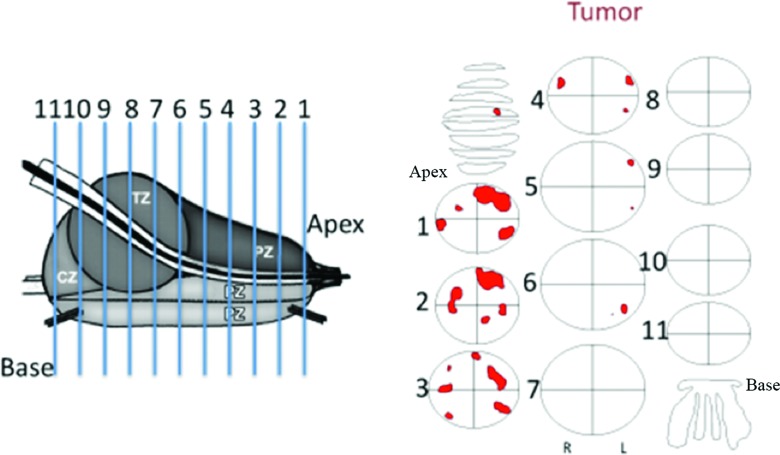
Resected prostates were examined by a pathologist to document cancer distribution within the gland. Each prostate specimen is sectioned along its axis into 7–15 slices depending on the prostate volume, with slices measuring approximately 3–5 mm in thickness. Each sectioned slice is processed for microscopic evaluation following routine clinical procedures for radical prostatectomy specimens. Cancerous regions are identified on each micrograph, and maps indicating those regions are constructed (Fig. 4). In these pathological maps, the outlined regions designate cancerous tissue and white background in the ellipse represents benign prostate tissue. The exact shape of the prostate slice is not recorded in the pathological maps; instead, prostate slices are represented by ellipses of different sizes. Despite small fluctuations in slice thickness (±1 mm), the prostate is assumed to be uniformly sliced for this analysis. In order to correlate estimated conductivity and permittivity profiles of the prostate to the actual histological findings, the TREIT-based reconstructed prostate volume is sectioned along the axis at equal intervals to generate a number of 2D cross-sectional transverse plane views of the electrical properties. The number of the planes is selected to be the same as the number of slices sectioned clinically so that each electrical property image corresponds to a single pathology map.
Figure 4.
The prostate is sliced into 7–15 sections. In pathological reports, each prostate slice is represented by an ellipsoid and cancerous regions are outlined by hand based on microscopic evaluation.
Before corresponding images can be compared, the elliptical slices in the pathological maps are spatially transformed to match the actual shape of the prostate as defined by ultrasound; this shape is reflected in the stack of sampled 2D EIT reconstruction planes. A thin plate spline transformation technique is used to morphologically transform the pathological maps.24 Multiple landmark points are selected on the prostate boundary from each slice of both the EIT images and pathological maps. These points are equally spaced around the periphery of the prostate in both images. Based on the multiple pairs of landmark points, each point in the pathology map is transformed to a correspondingly new position. Finally, the morphed pathological maps are resized to match the corresponding EIT 2D plane so that the prostate in both images is equivalently scaled, which is essential for a pixel based data analysis (Fig. 5).
Figure 5.

The thin plate spline transformation of pathological maps to match EIT slices. Example represents the transformation obtained when 20 landmark points were selected.
Data analysis
For data analysis purposes, the pathological map can be overlaid onto the EIT 2D plane image to specify cancerous and benign regions within the EIT image. For each individual patient and frequency, all pixels within the EIT slices identified as cancer are averaged to produce a single mean cancer conductivity, σc (or permittivity, ɛc); likewise, pixels identified as benign are averaged to produce a single mean benign conductivity, σb (or permittivity, ɛb). This provides a single value of cancer conductivity (and permittivity) and of benign conductivity (and permittivity) for each patient and frequency.
Paired Student's t-tests are used to statistically examine the hypothesis that cancerous and benign tissues have an equal mean conductivity or permittivity. Specifically, for the kth patient (1 ⩽ k ⩽ N, N being the total number of cases), the mean conductivity in cancerous and benign tissue are denoted as and , respectively. A sample of conductivity differences, σδ_k was constructed for all the patients: . A one-sample, paired Student's t-test was used to examine the hypothesis that the mean of the conductivity difference () is equal to 0; the alternative hypothesis stated that mean was greater than 0 (one-tailed test). If the alternative hypothesis is true, this would suggest that cancer has a statistically larger conductivity (or permittivity) than benign prostate in the kth patient. The Student's t-test analysis was conducted using the MATLAB R2010b (Natick, Massachusetts) statistical toolbox and Stata 12 (College Station, Texas). The confidence level used in this analysis is 1 − α = 0.95.
In addition, mean conductivity, , and permittivity, , for all patients are computed from averaging the individual conductivity and permittivity means [i.e., ], where N is the total number of cases. Standard deviations are also calculated from the individual means to evaluate cross-patient variability.
RESULTS
Image transformation
The number of landmark points sufficient for accurately performing the pathological map transformation was determined by morphing one map to match its corresponding EIT slice using 4, 8, 20, and 50 landmark points (Fig. 6). Each row of Fig. 6 represents the transformation process for a specific number of landmark points. The individual columns represent the landmark point locations on the EIT prostate boundary (target, column 1), these same points on the original pathology-based prostate map boundary (column 2), the pathological map before (column 3) and after (column 4) transformation, and a comparison between the original and transformed boundaries (column 5). In the comparison images (column 5), red, green, and blue represent transformed, target, and original prostate boundaries, respectively. The transformation performance can be visually assessed by examining the overlap (yellow) of the transformed boundary and the target boundary. As indicated in the comparison images, the transformation accuracy improves with increased landmark points. In the transformation using only four landmark points, there is shape mismatch (lower right) due to insufficient sampling along the prostate boundary (Fig. 6). The effect that the number of landmark points has on the transformation is quantified by calculating the percentage of pixels falling outside the target boundary (i.e., transformation error). Specifically, binary images ( Itg and Itr) are defined for both the target and transformed image such that the pixels within the prostate boundary are assigned “1” while the pixels outside the prostate boundary are assigned “0.” The mismatch image is defined as Imismatch = Itg ⊕ Itr, where ⊕ designates pixel-based XOR operation. The transformation error is calculated as the ratio of the number of “1”s in the mismatch image to the number of “1”s in the target image. In addition, computation time to calculate the transformation is recorded. As expected, the transformation error decreases and computation time increases with the growing number of landmark points (Table 1). A total of 381 pathological map transformations were performed for clinical data analysis using 20 landmark points; the average transformation error for warping this cohort of images is 1.67%.
Figure 6.

Thin plate spline transforms based on different number of landmark points. The transformed, target, and original prostate boundary in the right column are designated by red, green, and blue.
Table 1.
Overlapping pixel ratio and computation time for pathological map transformation with different number of landmark points.
| Number of control points | Transformation berror (%) | Computation time (s) |
|---|---|---|
| 4 | 7.61 | 1.57 |
| 8 | 4.42 | 1.70 |
| 20 | 1.50 | 1.91 |
| 50 | 1.30 | 2.55 |
Clinical data
Of the 50 men enrolled in this protocol, the majority (31 cases) had tumor confined to the prostate (4 with pT2a and 27 pT2c). Of the remaining 19 cases, 15 had pT3a, 3 pT3b, and 1 pT4 stage disease based on the TNM criteria. Lymph node invasion was observed in one case (four of ten lymph nodes extracted had evidence of tumor involvement). Gleason grades of all the subjects were ≥ 6 (3+3). The majority of the subjects (80.0%) had a Gleason grade of 7 (34 of 3+4 and 6 of 4+3), while 9 (18%) and 1 (2%) patients had a Gleason grade of 6 (3+3) and 9 (4+5), respectively. Out of the 50 patients, 13 (26%), 17 (34%), 15 (30%), 4 (8%), and 1 (2%) patients had tumor involvement of less than 5%, between 5% and 10%, 10% and 20%, 20% and 50%, and 50% and 100% in their prostates, respectively.
Intraoperative imaging required approximately 10 min to complete prior to surgery for both ultrasound and EIT measurements. In a number of the initial cases, the EIT data sets had moderate levels of noise arising from a number of hardware and protocol issues; these included hardware communication errors, poor cable contact, poor electrode-tissue contact, and patient movement during data collection. When these issues occurred there was insufficient time to remedy the source of the noise and repeat the data collection because time was limited in the OR environment. These instances were identified and removed from data analysis. As a result, images acquired from 42, 45, 45, and 39 of the 50 men were available for statistical analysis at frequencies of 0.4, 3.2, 25.6, and 102.4 kHz, respectively (Table 2).
Table 2.
Student's t-test result for all patients (σ: conductivity, ε: permittivity).
| σcancer > σbenign |
εcancer > εbenign |
||||
|---|---|---|---|---|---|
| Frequency (kHz) | Number patients | Result | p value | Result | p value |
| 0.4 | 42 | Y | 0.0015 | N | 0.7011 |
| 3.2 | 45 | Y | 0.0021 | N | 0.5436 |
| 25.6 | 45 | Y | 0.0304 | N | 0.1372 |
| 102.41 | 39 | Y | 0.0342 | N | 0.5740 |
For 102.4 kHz, the condition tested was σcancer < σbenign.
In 12 cases, the TRUS probe was positioned suboptimally within the rectum such that only part of the prostate was within the imaging field of view (i.e., only the apical half of the prostate was imaged). For these cases, only the pathological slices actually imaged by TREIT are included for analysis.
Example EIT reconstructions are shown in Figs. 78. The 3D reconstruction (Fig. 7) shows the segmented prostate (blue) and detected cancerous region (identified as nodes with conductivity greater than 0.26 S/m, red) embedded within the high density FEM mesh (∼100 000 nodes and 600 000 elements). Transverse cross sections, sliced perpendicular to the TRUS probe axis and prostatic urethra in the 3D reconstruction image, are displayed with corresponding pathological maps (Fig. 8). The cancerous regions in the EIT slices are enclosed by red lines indicating their locations based on the warped pathological maps. Pixel colors spanning from blue to red represent reconstructed conductivities from low to high, respectively. In the reconstructed image, most regions of elevated conductivity correspond to cancer locations. The small cancerous regions in the anterior prostate (in the distant imaging field) were not observed in these conductivity images. In other cases (not shown here), cancer foci were distributed throughout the prostate with foci present in both right and left hemispheres and in anterior and posterior aspects of the prostate depending on a particular man's particular prostate cancer profile. The same assessment procedures were employed independent of where the cancers were identified in pathology.
Figure 7.
Example conductivity reconstruction from a single patient at 3.2 kHz. Cancerous regions detected in 3D conductivity reconstruction are highlighted in red. Blue region indicated the segmented prostate, and red region indicates the cancer (based on a patient-specific conductivity threshold of 0.26 S/m).
Figure 8.
Five consecutive transverse cross sections of reconstructed conductivity (3.2 kHz) of a single patient's prostate from Fig. 7 with corresponding pathological maps. Cross-sections span from apex (left) to the base (right) of the prostate.
Within each individual patient, 30 out of 42 (71.4%), 30 out of 45 (66.7%), and 31 out of 45 (68.9%), had a mean tumor pixel conductivity (σc) exceeding that of the mean benign pixel conductivity (σb) at frequencies of 0.4, 3.2, and 25.6 kHz, respectively. At 102.4 kHz, the mean σc was found to be less than the mean σb in 25 out of 39 (64.1%) patients. When the sample of differences (), are compared across patients, paired one-sample Student's t-tests revealed several significant differences when the valid data from all patients were analyzed (Table 2). At lower frequencies of 0.4, 3.2, and 25.6 kHz, the t-test suggests that the conductivity of cancerous regions is greater than that of benign tissue on a per patient basis, while at 102.4 kHz the conductivity of tumor is less ( p = 0.0315, Table 2) than that of benign tissues. No significant permittivity differences were observed between the two tissue types at any of the four frequencies.
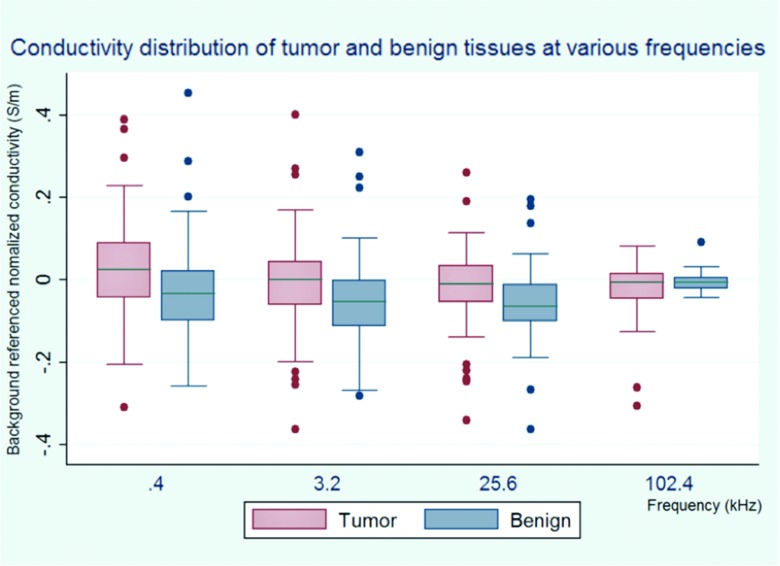
The mean (and standard deviation) of conductivity and permittivity for both tissue types across patients (, , , and ) are tabulated in Table 3 and graphed in Figs. 910. While not significantly different, mean tumor conductivity is greater than that of benign tissues at frequencies lower than 102.4 kHz (33.5 mS/m vs −19.7 mS/m at 0.4 kHz, −2.7 mS/m vs −48.9 mS/m at 3.2 kHz, and −28.2 mS/m vs −61.7 mS/m at 25.6 kHz). Mean permittivity differences between tumor and benign prostatic tissue are not observed to be significant in this cohort. This lack of significance in σ and ɛ when all patients are grouped arises from the considerable standard deviations as compared to the averaged means for both tissue types; this suggests that there is a moderately large patient-to-patient variability.
Table 3.
Means and standard deviations for reconstructed conductivities and relative permittivity for all patients. Note that these values represent the σ and ε different relative to the reference saline solution.
| Conductivity (mS/m) |
Relative permittivity |
|||
|---|---|---|---|---|
| Frequency (kHz) | Tumor | Benign | Tumor | Benign |
| 0.4 | 33.5 ± 141.2 | −19.7 ± 136.1 | 0.7 ± 171.6 | 8.0 ± 148.7 |
| 3.2 | −2.7 ± 140.5 | −48.9 ± 121.6 | 7.5 ± 159.6 | 6.5 ± 131.6 |
| 25.6 | −28.2 ± 123.9 | −61.7 ± 102.9 | −45.4 ± 143.8 | −58.6 ± 104.6 |
| 102.4 | −27.5 ± 76.4 | −3.5 ± 24.3 | −15.9 ± 56.7 | −13.8 ± 17.3 |
Figure 9.
The conductivity distribution of different tissue types at various frequencies. The central mark is the median, the edges of the box are the 25th and 75th percentiles, the whiskers extend to the most extreme data points not considered outliers, and outliers are plotted individually in the form of dots.
Figure 10.
The permittivity distribution of different tissue types at various frequencies. The central mark is the median, the edges of the box are the 25th and 75th percentiles, the whiskers extend to the most extreme data points not considered outliers, and outliers are plotted individually in the form of dots.
DISCUSSION
Pathological maps based on a tissue's morphological appearance are considered the reference for defining cancer distribution in this study. Although small errors may exist in drawing the cancerous regions by hand, the pathological maps still depict cancer location within a prostate slice with a sufficiently high degree of precision. By providing a histology-based reference, the correlation algorithm presented here is robust in the sense that it can also be applied to verify and evaluate other medical imaging methods.
Twenty landmark points were used in transforming the pathological map for clinical data analysis. This choice represented a compromise between accuracy and speed; the prostate shape was largely maintained (transformation error = 1.67%) while computational effort was ∼25% more efficient than using 50 landmark points.
The in vivo electrical property differences observed between malignant and benign tissues detected by the TREIT imaging system suggest potential clinical value in identifying cancerous regions. Paired-testing revealed that at frequencies ranging from 0.4 to 25.6 kHz, the conductivity in cancerous tissue is typically larger than that of normal tissue (Table 2). This finding is contradictory to that reported previously in multiple ex vivo studies.8, 9 These reports have suggested that cancerous tissue has a lower conductivity than benign tissue ( p < 0.05) at frequencies ranging from 0.1 to 100 kHz, and that the permittivity of cancerous tissue is greater than that of normal tissues at 100 kHz ( p < 0.0001).10 These contradictory findings may stem from differences between in vivo and ex vivo tissue properties. While not confirmed in this particular study, it is hypothesized that this relationship may arise from the larger blood volume present in the highly vascularized cancerous regions; blood has a higher conductivity than normal prostatic tissues [0.6 S/m (Ref. 25) vs 0.2 S/m (Ref. 10)]. The effect of blood-concentrated vascularization may be the dominating factor influencing the electrical properties within the cancer region in in vivo tissues, while under ex vivo conditions the blood leaves the prostate and tissue architecture and cell density become the primary factors affecting electrical properties. Besides higher levels of vascularization, lower hematocrit values within the cancer region and increased levels of plasma and electrolyte (ionic) concentration within the cancer cells may also explain the higher conductivity found in the cancer tissue.26
It is worth noting that conductivity relationships at 102.4 kHz in this in vivo study were opposite from that observed at the lower frequencies. Specifically, tumor conductivity is smaller than in benign tissue ( p = 0.0315), which possibly results from a more prominent effect from cell morphology at the higher frequency following the trend reported in previous ex vivo studies.8, 9, 10 Further studies recording electrical properties from both in vivo and ex vivo prostate tissue are needed to better understand the opposing findings at lower frequencies.
When pixel values from all men are combined, conductivity differences between cancer and benign regions were not observed to be significant (i.e., is not significantly different from ). This is due to considerably large variation (standard deviation from Table 3) as compared to the mean conductivities (i.e., 33.5 mS/m vs 141.2 mS/m at 0.4 kHz, Table 3). This large interpatient variability stems from a number of patient dependent conditions that occur during data acquisition including: different electrode and tissue contact impedances associated with fluid content within the rectum, slight variations in pressure applied between the imaging probe and rectal wall, minor differences in quantity and distribution of acoustic gel applied to the electrodes and TRUS probe, and the inherent patient-to-patient prostate tissue variation, which was also observed in previous ex vivo studies.10 The conductivity variability reported here may make it difficult to identify a single threshold for discriminating tissue types for a general population; but, because there is a significant difference found within individual patients, it may be possible to find a patient-specific threshold for each EIT scan. For example, binary classifying algorithms (i.e., k-means, receiver-operator characteristics) could be developed to separate pixels into two categories (tumor and benign) if there is sufficient contrast within an individual image. This contrast appears to be present (Table 2) which would enable these algorithms to extract a patient-specific threshold. These are high-speed algorithms that could be applied to the data in real-time to assess cancer presence and uniquely identify image pixels containing cancerous tissue.
The use of a patient-specific threshold is quite common in medical practice in which physicians leverage baseline or background measurements for a given patient. For instance, in gray-scale TRUS, lesions suspicious of being cancer are not typically defined by the acoustic impedance or velocity during imaging by an urologist; rather, these lesions are noted to be suspicious based on their echogenicity with respect to the background. In ∼60% of cases, cancerous lesions present as hypoechoic lesions while in up to 40% of case they are either iso- or hyperechoic.27 Interestingly, this study demonstrated a similar relationship for TREIT; in 60%–70% of the cases, cancer was found to have hyperimpedance with respect to the background (at frequencies <102.4 kHz) and to have either iso- or hypoimpedance in 30%–40% of the cases.
A challenge currently facing urologists is discriminating between aggressive and indolent tumors in the prostate.28 It has been established that cancer volume within the prostate is significantly correlated to the disease stage.29 In this context, TREIT is being envisioned as an adjunct to TRUS for prostate biopsy guidance. Compared to traditional gray-scale TRUS-guided biopsy [sensitivity 41%, specificity 85.0%, and accuracy 67% (Ref. 30)], TREIT may help to enhance prostate cancer detection rates by leveraging the larger conductivity observed in cancer tissues (i.e., σδ > 0) at frequencies lower than 102.4 kHz; σc was larger than σb in more than 66.67% of all cases. Specifically, TREIT may be an effective tool for accurately identifying moderate and large sized tumors with the use of the coarse mesh. Tumor volumes exceeding a certain size and revealed by TREIT may be potentially used to target suspicious regions in the prostate during biopsy procedure. Two potential approaches could be used clinically based on the findings from these TREIT images: (1) additional biopsies could be extracted from regions of suspicion which would potentially reduce the number of repeat biopsy's and decrease the lack of concordance between biopsy and prostatectomy specimen assessment,31 and (2) a currently standard 12 core protocol could be reduced to a fewer core biopsy template (i.e., 6 core protocol) followed by extracting additional samples from TREIT based regions of suspicion; this would potentially decrease morbidities (i.e., hemorrhage and infection) associated with core extraction and provide a more representative assessment of the disease within the gland.
There are several limitations to this study that should be considered. The patient population was moderately homogeneous since it included only men undergoing prostatectomy. The majority of men had organ-confined disease (31 of 50 cases), with cancer making up less than 20% of the prostate (45 of 50 cases), and only one case had a Gleason score >7. This homogeneity is expected in a population of men being treated with RALP for curative therapy; men with high Gleason scores and high probability of extraprostatic extension, lymph node involvement, or metastasis are not generally considered good candidates for radical prostatectomy. For this study, this population of patients was chosen in order to be able to directly correlate image findings with organ pathology. Additional studies, employing TREIT in a more standard prostate biopsy population are needed to further evaluate the technology.
The pathological slices are assumed to be of equal thickness; however, in practice the whole prostate is sliced manually with slice thicknesses ranging from 3 to 5 mm. This imprecision may lead to small errors in correlating EIT images with pathology maps since there may be small offsets between the actual axial location of an EIT slice in relation to the pathological slice. Recording the exact thickness of each slice might mitigate this error, which should be considered in future research.
Variations in the quantity of ultrasound gel and thickness of the porous membrane sheath interfacing the TREIT probe to the patient may influence the recorded impedance data. Previous phantom imaging experiments have demonstrated that the interfacing material had a minor impact on EIT reconstructions; only the region close to the probe (∼1 mm) demonstrated increased conductivity.18
EIT is a relatively low resolution imaging modality compared to CT or MRI due to the underlying physics defined by a diffusely propagating current through an electrically heterogeneous volume. Most current EIT research focuses on solving closed domain problems, where the imaging field is enclosed by a number of electrodes. However, for a TRUS-based imaging system, most electrodes are located on the probe surface and only one ventral electrode is located far from this surface. This open imaging domain poses additional challenges to image reconstruction in EIT due to the lack of cross-prostate currents sensed far from the probe's surface. As a result, the sensitivity deteriorates with distance from this surface.32 Due to these open domain challenges and the systematic measurement errors, we were not able to reconstruct accurate absolute EIT images. Instead, difference imaging with a reference saline bath was employed to reduce the systematic errors of the imaging system.33, 34 Although the conductivity of the saline bath (0.1 S/m) may be different from the prostate tissue, it provides a uniform background for the reconstruction and the contrast between cancerous and benign tissue still exists in the reconstructed images. One way of potentially mitigating low sensitivity of open domain EIT is to include additional intraprostatic sensors, by coupling EIT electrodes to a standard biopsy needle;35 this approach is currently being explored to provide more transprostatic current, increase the distal sensitivity, and ultimately enhance transrectal electrical impedance tomography.32
The prostate case illustrated in Figs. 78 was characterized primarily by a large, discrete tumor mass. Although the TREIT imaging system was characterized to be able to detect a high contrast object of at least 1 cm in diameter,15 subtle, smaller tumors may be challenging to define and isolate from background benign tissue (e.g., the smaller anterior tumor was not observed in TREIT image in Fig. 8). Another reason these anterior foci were not observed may be due to the limited sensitivity to deep structures >3 cm from the probes surface. We demonstrate in Ref. 15 that the system is able to detect contrast up to ∼3 cm from the probe surface. By incorporating needle electrodes to the imaging system, the sensitivity in these anterior regions will likely be enhanced and an overall increased resolution may help to detect smaller tumors.35
CONCLUSION
This study presents a novel method for imaging the electrical properties of prostate and for correlating reconstructed EIT images and pathological findings. Cancerous tissue is found to be more conductive than normal tissue at frequencies ranging from 0.4 to 25.6 kHz, while the permittivity of both tissue types is not found to be significantly different. The findings pertaining to conductivity imaging suggest that TREIT-based prostate imaging is worth exploring for use in identifying tissue regions suspicious of being prostate cancer during TRUS/TREIT guided prostate biopsy procedures.
ACKNOWLEDGMENT
This research was supported by the US National Institutes of Health through award #'s 5RC1EB0011000 and 5R01CA124925.
References
- Siegel R., Naishadham D., and Jemal A., “Cancer statistics, 2012,” Ca-Cancer J. Clin. 62(1), 10–29 (2012). 10.3322/caac.20138 [DOI] [PubMed] [Google Scholar]
- Brawer M. K., Chetner M. P., Beatie J., Buchner D. M., Vessella R. L., and Lange P. H., “Screening for prostatic carcinoma with prostate specific antigen,” J. Urol. 147(3 Pt 2), 841–845 (1992). [DOI] [PubMed] [Google Scholar]
- Hoogendam A., Buntinx F., and de Vet H. C., “The diagnostic value of digital rectal examination in primary care screening for prostate cancer: A meta-analysis,” Fam. Pract. 16(6), 621–626 (1999). 10.1093/fampra/16.6.621 [DOI] [PubMed] [Google Scholar]
- Borley N. and Feneley M., “Prostate cancer: Diagnosis and staging,” Asian J. Androl. 11(1), 74–80 (2009). 10.1038/aja.2008.19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epstein J. I. and Herawi M., “Prostate needle biopsies containing prostatic intraepithelial neoplasia or atypical foci suspicious for carcinoma: Implications for patient care,” J. Urol. 175(3), 820–834 (2006). 10.1016/S0022-5347(05)00337-X [DOI] [PubMed] [Google Scholar]
- Catalona W. J., Richie J. P., Ahmann F. R., Hudson M. A., Scardino P. T., Flanigan R. C., deKernion J. B., Ratliff T. L., Kavoussi L. R., and Dalkin B. L., “Comparison of digital rectal examination and serum prostate specific antigen in the early detection of prostate cancer: Results of a multicenter clinical trial of 6,630 men,” J. Urol. 151(5), 1283–1290 (1994). [DOI] [PubMed] [Google Scholar]
- Kantoff P. W. and Taplin M., “Clinical presentation, diagnosis, and staging of prostate cancer,” Waltham, MA, 2010. (available URL: http://www.uptodate.com/contents/clinical-presentation-and-diagnosis-of-prostate-cancer).
- Lee B. R., Roberts W. W., Smith D. G., Ko H. W., Epstein J. I., Lecksell K., Partin A. W., and Walsh P. C., “Bioimpedance: Novel use of a minimally invasive technique for cancer localization in the intact prostate,” Prostate 39, 213–218 (1999). [DOI] [PubMed] [Google Scholar]
- Halter R. J., Hartov A., Heaney J. A., Paulsen K. D., and Schned A. R., “Electrical impedance spectroscopy of the human prostate,” IEEE Trans. Biomed. Eng. 54(7), 1321–1327 (2007). 10.1109/TBME.2007.897331 [DOI] [PubMed] [Google Scholar]
- Halter R. J., Schned A., Heaney J., Hartov A., and Paulsen K. D., “Electrical properties of prostatic tissues: I. Single frequency admittivity properties,” J. Urol. 182(4), 1600–1607 (2009). 10.1016/j.juro.2009.06.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halter R. J., Schned A. R., Heaney J. A., and Hartov A., “Passive bioelectrical properties for assessing high- and low-grade prostate adenocarcinoma,” Prostate 71(16), 1759–1767 (2011). 10.1002/pros.21393 [DOI] [PubMed] [Google Scholar]
- Uhlmann G., “Electrical impedance tomography and Calderón's problem,” Inverse Probl. 25(12), 123011 (2009). 10.1088/0266-5611/25/12/123011 [DOI] [Google Scholar]
- Murai T. and Kagawa Y., “Electrical impedance computed tomography based on a finite element model,” IEEE Trans. Biomed. Eng. BME-32, 177–184 (1985). 10.1109/TBME.1985.325526 [DOI] [PubMed] [Google Scholar]
- Bagshaw A. P., Liston A. D., Bayford R. H., Tizzard A., Gibson A. P., Tidswell T. A., Sparkes M. K., Dehghani H., Binnie C. D., and Holder D. S., “Electrical impedance tomography of human brain function using reconstruction algorithms based on the finite element method,” Neuroimage 20(2), 752–764 (2003). 10.1016/S1053-8119(03)00301-X [DOI] [PubMed] [Google Scholar]
- Wan Y., Halter R., Borsic A., Manwaring P., Hartov A., and Paulsen K., “Sensitivity study of an ultrasound coupled transrectal electrical impedance tomography system for prostate imaging,” Physiol. Meas. 31(8), S17–S29 (2010). 10.1088/0967-3334/31/8/S02 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borsic A., Halter R., Wan Y., Hartov A., and Paulsen K., “Electrical impedance tomography reconstruction for three dimensional imaging of the prostate,” Physiol. Meas. 31(8), S1–S16 (2010). 10.1088/0967-3334/31/8/S01 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan Y., “Development of a combined ultrasound and electrical impedance imaging system for prostate cancer detection,” Ph.D. theses (Dartmouth College, 2012).
- Manwaring P. K., Wan Y., Halter R. J., and Hartov A., “A natural membrane material enabling multi-layer saline tank phantoms for use in EIT,” in Proceedings of the International Conference on Electrical Bioimpedance, Gainesville, FL, April 2010.
- American Joint Committee on Cancer, AJCC Cancer Staging Manual, 6th ed. (Springer, New York, NY, 2003). [Google Scholar]
- Syed H., “Subvolume reconstruction algorithm for electrical impedance tomography,” M.S. thesis, Dartmouth College, New Hampshire, 2011. [Google Scholar]
- Ghali S., Introduction to Geometric Computing, 1st ed. (Springer, London, 2008), pp. 35–50. [Google Scholar]
- Scherzer O., Handbook of Mathematical Methods in Imaging, 1st ed. (Springer, New York, NY, 2010). [Google Scholar]
- Holder D., “Electrical Impedance Tomography: Methods, History and Applications,” IOP Publishing, Bristol, UK, 2005.
- Bookstein F. L., “Principle warping: Thin-plate splines and the decomposition of deformations,” IEEE Trans. Pattern Anal. Mach. Intell. 11(6), 567–585 (1989). 10.1109/34.24792 [DOI] [Google Scholar]
- Faes T., van der Meij H., de Munck J., and Heethaar R., “The electric resistivity of human tissues (100 Hz-10 MHz): A meta-analysis of review studies,” Physiol. Meas. 20(4), R1–R10 (1999). 10.1088/0967-3334/20/4/201 [DOI] [PubMed] [Google Scholar]
- Foster C. S. and Bostwick D. G., Pathology of the Prostate (W.B. Souders Company, Philadelphia, PA, 1998). [Google Scholar]
- Vo T., Rifkin M. D., and Peters T. L., “Should ultrasound criteria of the prostate be redefined to better evaluate when and where to biopsy,” Ultrasound Q. 17, 171–176 (2001). 10.1097/00013644-200109000-00005 [DOI] [PubMed] [Google Scholar]
- Moyer V. A., “Screening for prostate cancer: U.S. Preventive service task force recommendation statement,” Ann. Intern. Med. 157, 120–134 (2012). 10.7326/0003-4819-157-2-201207170-00459 [DOI] [PubMed] [Google Scholar]
- Epstein J. I., Walsh P. C., Carmichael M., and Brendler C. B., “Pathological and clinical findings to predict tumor extent of non palpable stage (T1 c) prostate cancer,” JAMA, J. Am. Med. Assoc. 271, 368–374 (1994). 10.1001/jama.1994.03510290050036 [DOI] [PubMed] [Google Scholar]
- Kuligowska E. et al. , “Predictors of prostate carcinoma: Accuracy of gray-scale and color Doppler US and serum markers,” Radiology 220, 757–764 (2001). 10.1148/radiol.2203001179 [DOI] [PubMed] [Google Scholar]
- Scattoni V. et al. , “Extended and saturation prostatic biopsy in the diagnosis and characterization of prostate cancer: A critical analysis of the literature,” Eur. Urol. 52, 1309–1322 (2007). 10.1016/j.eururo.2007.08.006 [DOI] [PubMed] [Google Scholar]
- Borsic A., Halter R., Wan Y., Hartov A., and Paulsen K., “Sensitivity study and optimization of a 3D electric impedance tomography prostate probe,” Physiol. Meas. 30(6), S1–S18 (2009). 10.1088/0967-3334/30/6/S01 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheney M., Isaacson D., and Newell J. C., “Electrical impedance tomography,” SIAM Rev. 41(1), 85–101 (1999). 10.1137/S0036144598333613 [DOI] [Google Scholar]
- Bayford R. H., “Bioimpedance tomography (electrical impedance tomography),” Annu. Rev. Biomed. Eng. 8, 63–91 (2006). 10.1146/annurev.bioeng.8.061505.095716 [DOI] [PubMed] [Google Scholar]
- Halter R. J., Mishra V., Bouayad H., Manwaring P., Heaney J., and Schned A., “Electrical property-based biopsy for prostate cancer detection and assessment,” Proc. SPIE 7901, Energy-based Treatment of Tissue and Assessment VI, 79010U (Feb. 23, 2011); San Francisco, CA, 2011. 10.1117/12.876489 [DOI]